Dynamic Self-Adaptive Modeling for Real-Time Flood Control Operation of Multi-Reservoir Systems
Abstract
:1. Introduction
2. Methodology
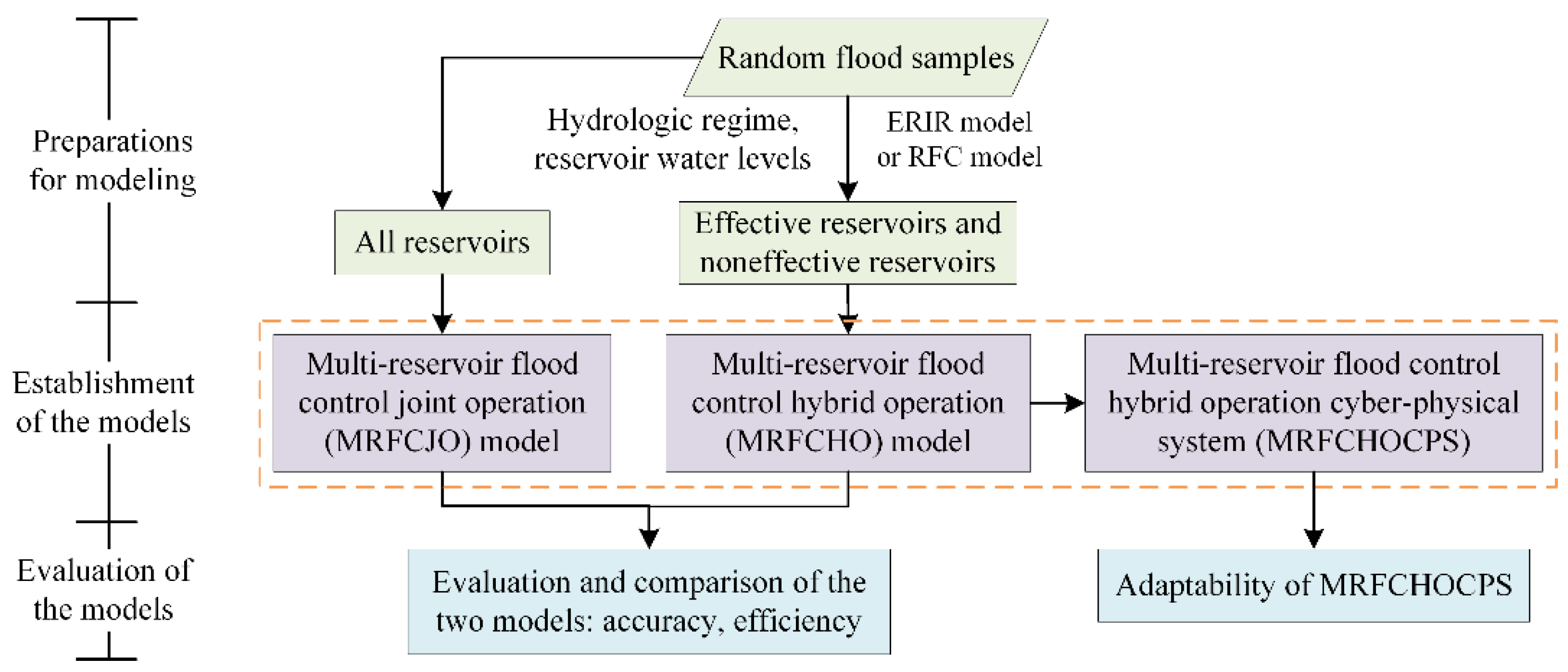
2.1. Generation of Flood Samples and Establishment of Operation Models
2.1.1. Generation of Random Flood Samples
2.1.2. Establishment of the Operation Models
- (a)
- Water balance equation:
- (b)
- Reservoir release capacity limits:
- (c)
- Reservoir water level limits:
- (d)
- End water level limits:
- (e)
- Reservoir release fluctuation limits:
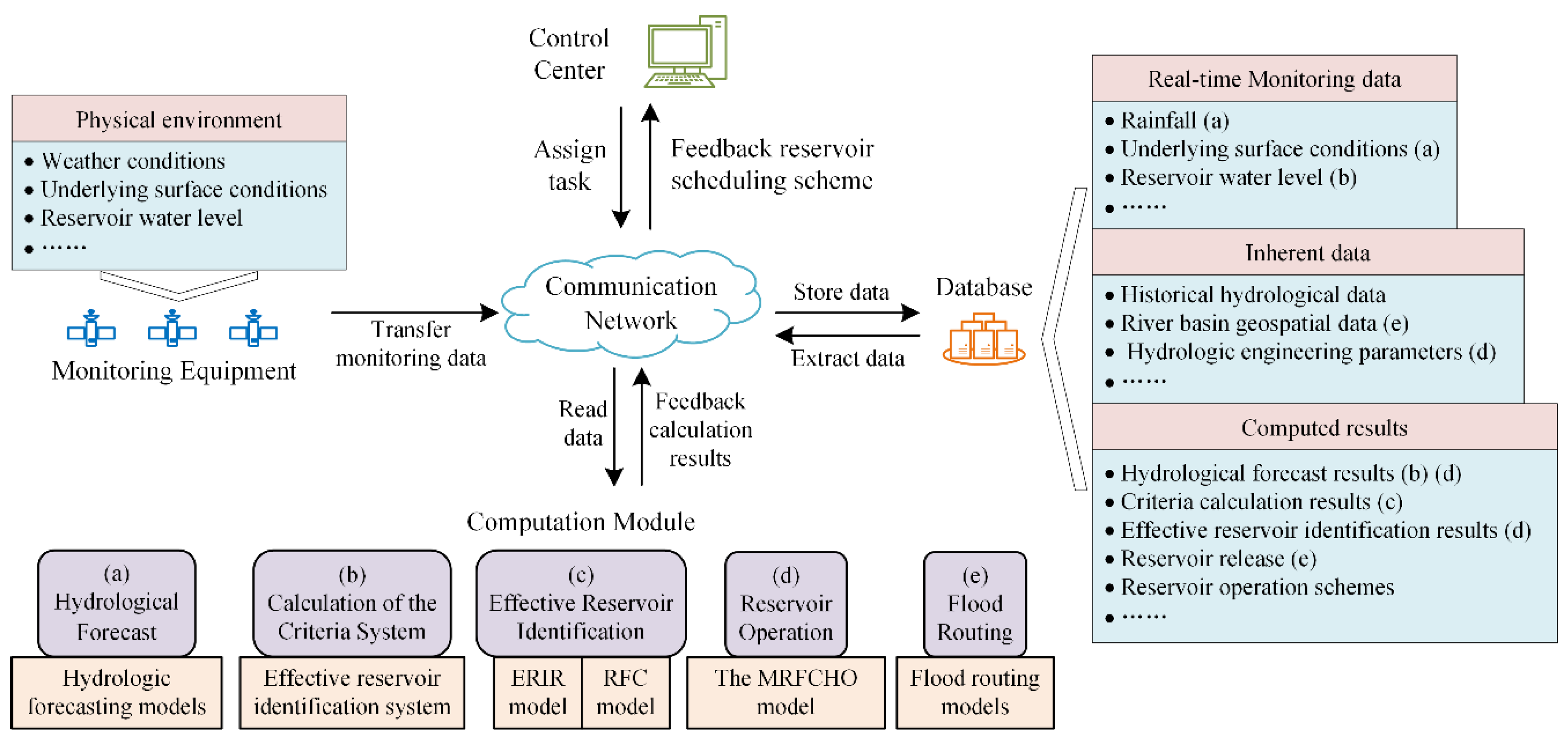
2.2. Establishment of the Multi-Reservoir Flood Control Hybrid Operation Cyber–Physical System
2.2.1. Framework Design of the MRFCHOCPS
2.2.2. Functions of Each Component of MRFCHOCPS
- (1)
- Monitoring equipment
- (2)
- Database
- (3)
- Communication network
- (4)
- Computation module
- (5)
- Control center
2.3. Evaluation of the MRFCHO Model
2.3.1. Evaluation of the Model Accuracy
2.3.2. Evaluation of the Model Solving Efficiency
3. Case Study
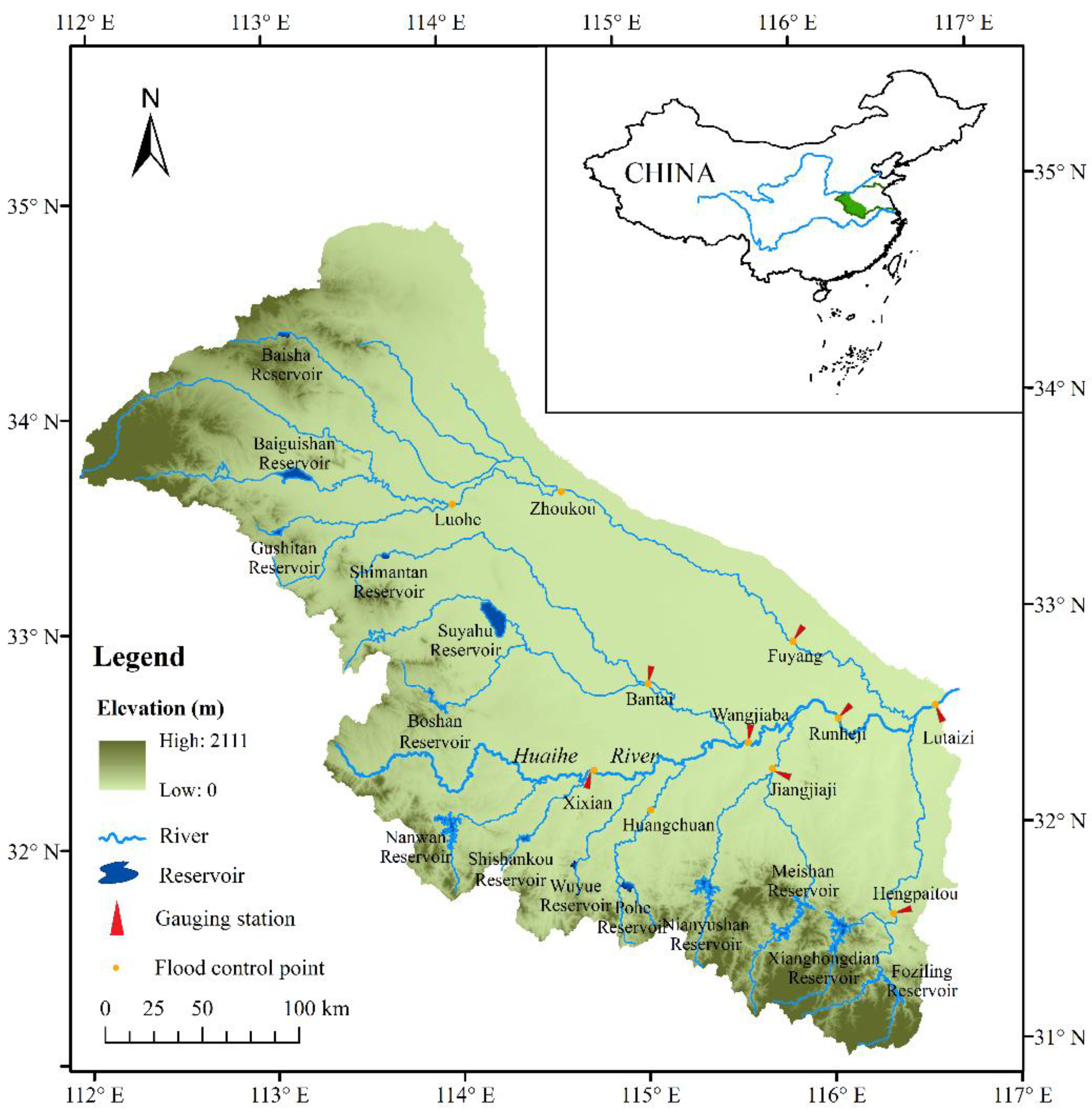
3.1. Study Area
3.2. Data
4. Results and Discussion
4.1. Accuracy of the MRFCHO Model
4.2. Solving Efficiency of the MRFCHO Model
4.3. Adaptability of MRFCHOCPS
5. Conclusions
- (1)
- Among 1000 random flood samples, the equivalent qualified rate of the MRFCHO model is 84.9%. It shows that in the future real-time flood control operation, it is highly reliable to establish the MRFCHO model for flood control operation on the basis of identifying effective reservoirs.
- (2)
- The operation results of floods with different magnitudes show that the equivalent qualified rate decreases with the decrease of flood magnitude. When the peak discharge of the Lutaizi point is more than 7000 m3/s, the equivalent qualified rate is more than 90%. The MRFCHO model is more suitable for basin-wide floods.
- (3)
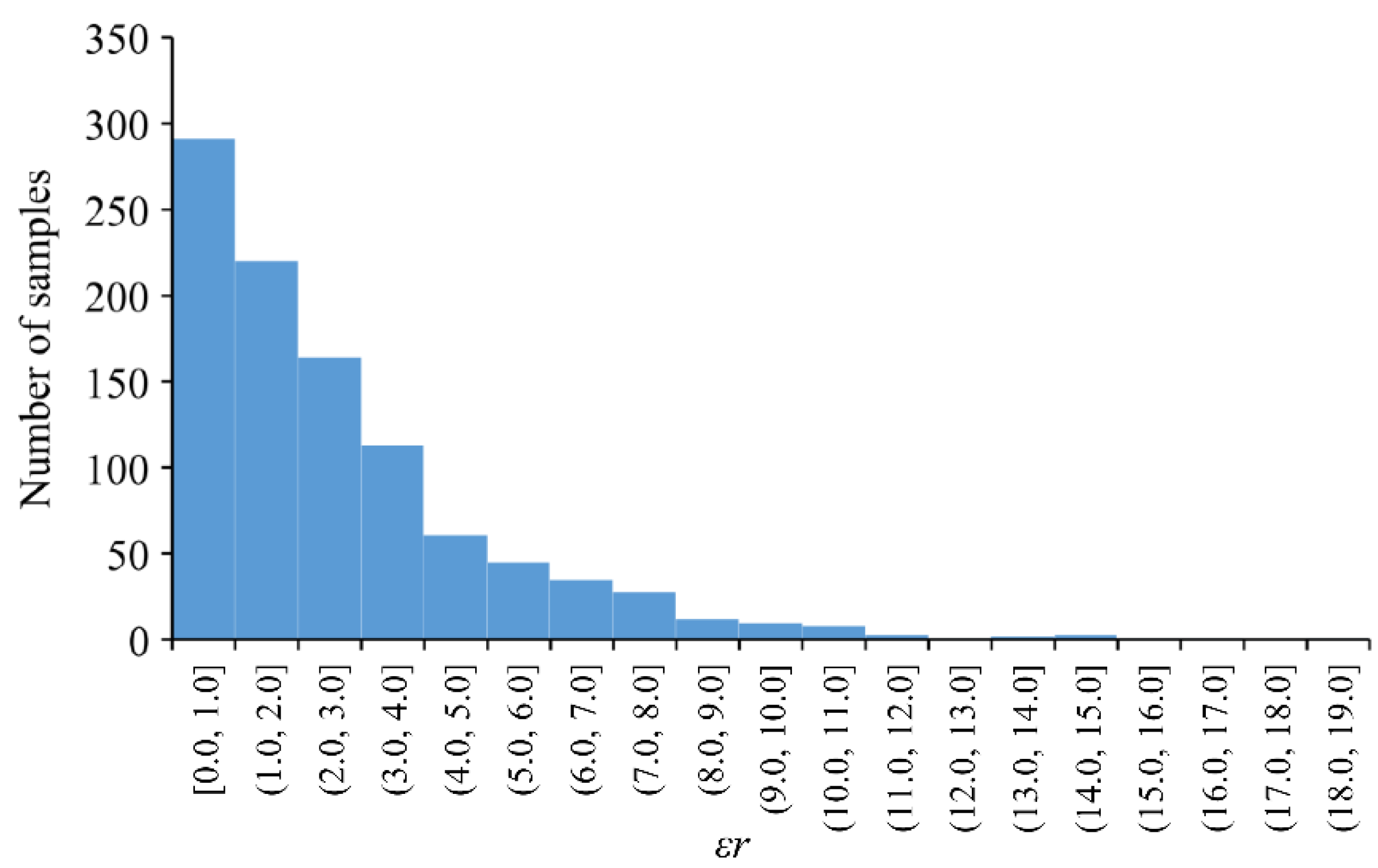
- In random flood samples, the number of effective reservoirs is generally 4–7, and the maximum number is not more than 11. Compared with the MRFCJO model, the space and time complexity of the MRFCHO model is reduced drastically.
- (4)
- The solving efficiency of the MRFCHO model is significantly improved compared with that of the MRFCJO model under the premise of ensuring the flood control effect. The MRFCHO model provides a reliable method for the real-time operation of basin-wide floods.
- (5)
- MRFCHOCPS has better adaptability in the real-time operation of large-scale multi-reservoir systems because it can realize the intelligent identification of effective reservoirs and dynamical modeling according to the rain and flood information.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, F.; Valeriano, O.C.S.; Sun, X. Near Real-Time Optimization of Multi-Reservoir during Flood Season in the Fengman Basin of China. Water Resour. Manag. 2013, 27, 4315–4335. [Google Scholar] [CrossRef]
- Donyaii, A.; Sarraf, A.; Ahmadi, H. Application of a New Approach in Optimizing the Operation of the Multi-Objective Reservoir. J. Hydraul. Struct. 2020, 6, 1–20. [Google Scholar]
- Yu, Y.; Zhao, R.; Zhang, J.; Yang, D.; Zhou, T. Multi-objective game theory optimization for balancing economic, social and ecological benefits in the Three Gorges Reservoir operation. Environ. Res. Lett. 2021, 16, 85007. [Google Scholar] [CrossRef]
- Avesani, D.; Zanfei, A.; Di Marco, N.; Galletti, A.; Ravazzolo, F.; Righetti, M.; Majone, B. Short-term hydropower optimization driven by innovative time-adapting econometric model. Appl. Energy 2022, 310, 118510. [Google Scholar] [CrossRef]
- De Ladurantaye, D.; Gendreau, M.; Potvin, J. Optimizing profits from hydroelectricity production. Comput. Oper. Res. 2009, 36, 499–529. [Google Scholar] [CrossRef] [Green Version]
- Ficchì, A.; Raso, L.; Dorchies, D.; Pianosi, F.; Malaterre, P.O.; Van Overloop, P.J.; Jay-Allemand, M. Optimal Operation of the Multireservoir System in the Seine River Basin Using Deterministic and Ensemble Forecasts. J. Water Res. Plan. Manag. 2016, 142, 5015005. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.; Zhong, P.; Xu, B.; Chen, J.; Sun, Y.; Liu, W.; Li, T. Stochastic multi-criteria decision making based on stepwise weight information for real-time reservoir operation. J. Clean. Prod. 2020, 257, 120554. [Google Scholar] [CrossRef]
- Opan, M. Irrigation-energy management using a DPSA-based optimization model in the Ceyhan Basin of Turkey. J. Hydrol. 2010, 385, 353–360. [Google Scholar] [CrossRef]
- Cheng, C.; Wu, H.; Wu, X.; Shen, J.; Wang, J. Power Generation Scheduling for Integrated Large and Small Hydropower Plant Systems in Southwest China. J. Water Res. Plan. Manag. 2017, 143, 4017021–4017027. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, X.; Qin, H. Optimal operation of multi-reservoir hydropower systems using enhanced comprehensive learning particle swarm optimization. J. Hydro-Environ. Res. 2016, 10, 50–63. [Google Scholar] [CrossRef]
- Ladanu, A.A.; Akanmu, S.; Adeyemo, J. Enhancing Artificial Neural Network with Multi-Objective Evolutionary Algorithm for Optimizing Real Time Reservoir Operations: A Review. Am. J. Water Resour. 2020, 8, 118–127. [Google Scholar]
- Chen, H.; Wang, W.; Chen, X.; Qiu, L. Multi-objective reservoir operation using particle swarm optimization with adaptive random inertia weights. Water Sci. Eng. 2020, 13, 136–144. [Google Scholar] [CrossRef]
- Wang, W.; Jia, B.; Simonovic, S.P.; Wu, S.; Fan, Z.; Ren, L. Comparison of Representative Heuristic Algorithms for Multi-Objective Reservoir Optimal Operation. Water Resour. Manag. 2021, 35, 2741–2762. [Google Scholar] [CrossRef]
- Avesani, D.; Galletti, A.; Piccolroaz, S.; Bellin, A.; Majone, B. A dual-layer MPI continuous large-scale hydrological model including Human Systems. Environ. Modell. Softw. 2021, 139, 105003. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Zhao, B. Real-time reservoir operation using recurrent neural networks and inflow forecast from a distributed hydrological model. J. Hydrol. 2019, 579, 124229. [Google Scholar] [CrossRef]
- Wei, C.; Hsu, N. Derived operating rules for a reservoir operation system: Comparison of decision trees, neural decision trees and fuzzy decision trees. Water Resour. Res. 2008, 44, W02428. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, H.; Zhang, Z.; Yao, L.; Wang, Y.; Li, J.; Liu, G.; Zhou, J. Deriving reservoir operation rule based on Bayesian deep learning method considering multiple uncertainties. J. Hydrol. 2019, 579, 124207. [Google Scholar] [CrossRef]
- Ahmadi, M.; Bozorg Haddad, O.; Mariño, M.A. Extraction of Flexible Multi-Objective Real-Time Reservoir Operation Rules. Water Resour. Manag. 2014, 28, 131–147. [Google Scholar] [CrossRef]
- Levy, J.K. Multiple criteria decision making and decision support systems for flood risk management. Stoch. Environ. Res. Risk Assess. 2005, 19, 438–447. [Google Scholar] [CrossRef]
- Qi, H.; Altinakar, M.S. A GIS-based decision support system for integrated flood management under uncertainty with two dimensional numerical simulations. Environ. Modell. Softw. 2011, 26, 817–821. [Google Scholar] [CrossRef]
- Che, D.; Mays, L.W. Application of an Optimization/Simulation Model for Real-Time Flood-Control Operation of River-Reservoirs Systems. Water Resour. Manag. 2017, 31, 2285–2297. [Google Scholar] [CrossRef]
- Li, J.; Zhong, P.A.; Yang, M.; Zhu, F.; Chen, J.; Xu, B.; Liu, W. Dynamic and intelligent modeling methods for joint operation of a flood control system. J. Water Res. Plan. Manag. 2019, 145, 0401904410. [Google Scholar] [CrossRef]
- Li, J.; Zhong, P.; Yang, M.; Zhu, F.; Chen, J.; Liu, W.; Xu, S. Intelligent identification of effective reservoirs based on the random forest classification model. J. Hydrol. 2020, 591, 125324. [Google Scholar] [CrossRef]
- Derler, P.; Lee, E.A.; Vincentelli, A.S. Modeling cyber-physical systems. Proc. IEEE 2012, 100, 13–28. [Google Scholar] [CrossRef]
- Kuang, Z.J.; Hu, L.; Zhang, C. Characteristic analyzation of cyber physical systems. Appl. Mech. Mater. 2014, 484–485, 427–430. [Google Scholar] [CrossRef]
- Peng, Y.; Jolfaei, A.; Yu, K. A Novel Real-Time Deterministic Scheduling Mechanism in Industrial Cyber-Physical Systems for Energy Internet. IEEE T. Ind. Inform. 2022, 18, 5670–5680. [Google Scholar] [CrossRef]
- Mohanty, S.P. Advances in transportation cyber-physical system (T-CPS). IEEE Consum. Electron. Mag. 2020, 9, 4–6. [Google Scholar] [CrossRef]
- Wang, Z.; Song, H.; Watkins, D.W.; Ong, K.G.; Xue, P.; Yang, Q.; Shi, X. Cyber-physical systems for water sustainability: Challenges and opportunities. IEEE Commun. Mag. 2015, 53, 216–222. [Google Scholar] [CrossRef] [Green Version]
- Taormina, R.; Galelli, S.; Tippenhauer, N.O.; Salomons, E.; Ostfeld, A. Characterizing cyber-physical attacks on water distribution systems. J. Water Res. Plan. Manag. 2017, 143, 040170095. [Google Scholar] [CrossRef]
- Li, J.; Zhong, P.; Wang, Y.; Yang, M.; Fu, J.; Liu, W.; Xu, B. Risk analysis for the multi-reservoir flood control operation considering model structure and hydrological uncertainties. J. Hydrol. 2022, 612, 128263. [Google Scholar] [CrossRef]
- Feng, Z.K.; Niu, W.J.; Cheng, C.T.; Shen, J.J.; Wu, X.Y. Study on dimension reduction for optimal operation of large-scale hydropower system I: Theoretical analysis. J. Hydraul. Eng. 2017, 48, 146–156. (In Chinese) [Google Scholar]
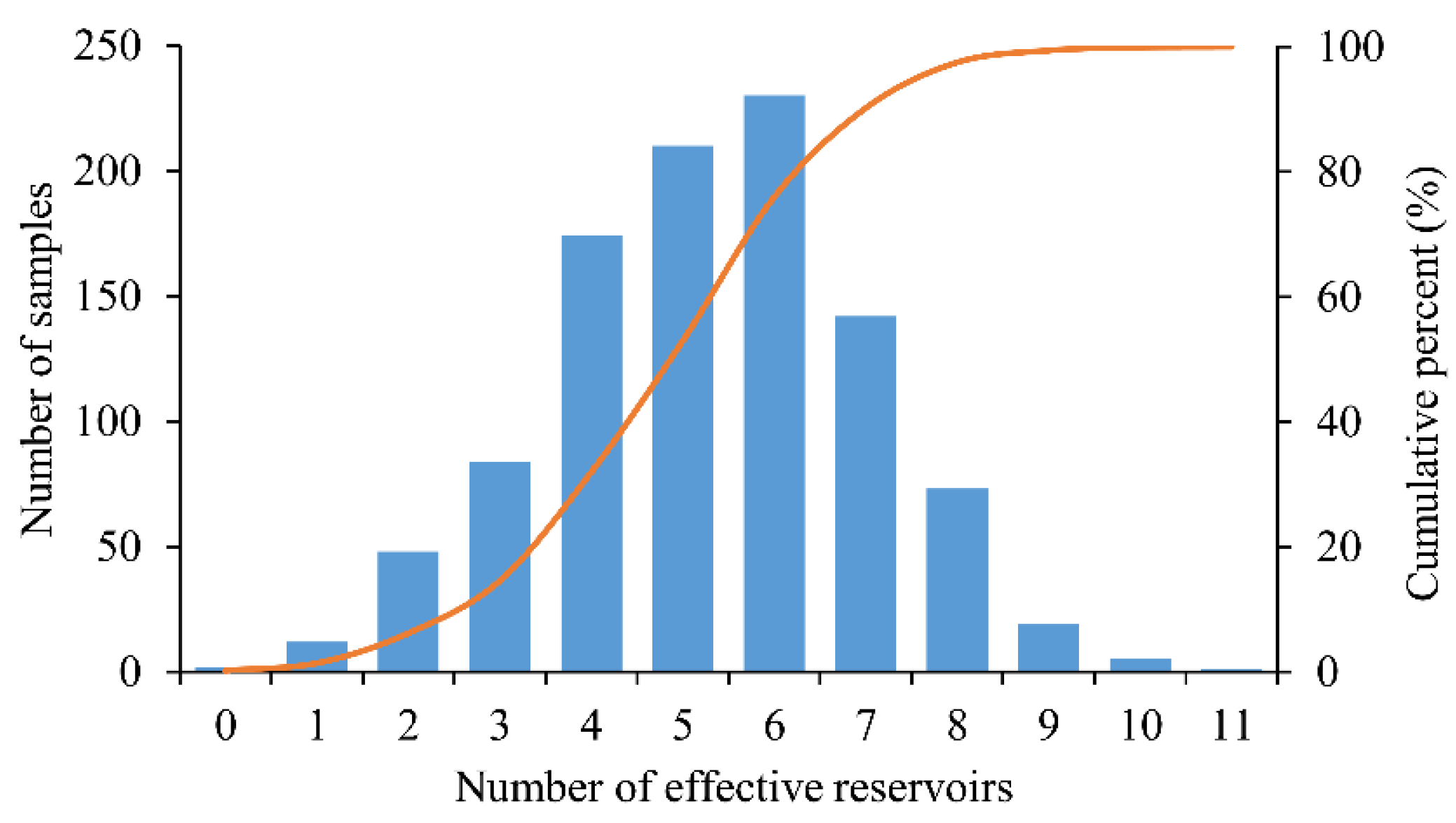
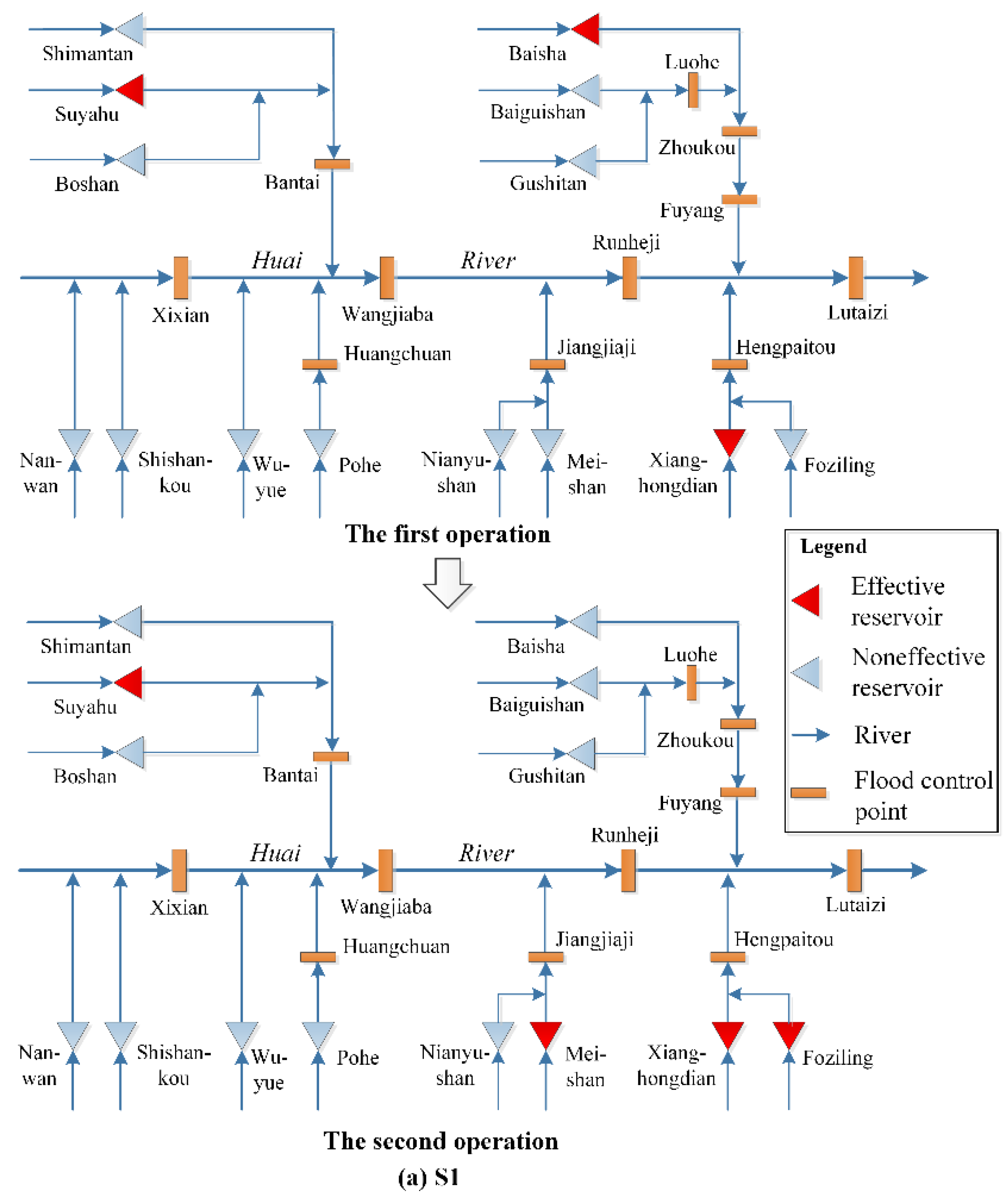


| Serial Number | Location of Rainstorm Center | Flood Magnitude |
|---|---|---|
| 1 | centralizing in the whole basin | medium |
| 2 | centralizing in the whole basin | medium |
| 3 | centralizing in the southeast | large |
| 4 | centralizing in the whole basin | large |
| 5 | centralizing in the southeast | large |
| 6 | centralizing in the southeast | medium |
| 7 | centralizing in the southeast | small |
| 8 | centralizing in the southeast | small |
| 9 | centralizing in the upstream of the main stream | medium |
| 10 | centralizing in the southeast | small |
| 11 | centralizing in the whole basin | medium |
| 12 | centralizing in the upstream of the main stream | small |
| 13 | centralizing in the whole basin→centralizing in the southeast | large |
| Peak Discharge at the Lutaizi Point (m3/s) | Number of Samples | Number of Qualified Samples | Equivalent Qualified Rate (%) | Non-Qualified Rate (%) |
|---|---|---|---|---|
| QCm ≥ 10,000 | 50 | 50 | 100 | 0 |
| 9000 ≤ QCm < 10,000 | 47 | 45 | 95.74 | 4.26 |
| 8000 ≤ QCm < 9000 | 65 | 63 | 96.92 | 3.08 |
| 7000 ≤ QCm < 8000 | 120 | 109 | 90.83 | 9.17 |
| 6000 ≤ QCm < 7000 | 172 | 149 | 86.63 | 13.37 |
| 5000 ≤ QCm < 6000 | 216 | 183 | 84.72 | 15.28 |
| 4000 ≤ QCm < 5000 | 185 | 153 | 82.70 | 17.30 |
| 3000 ≤ QCm < 4000 | 112 | 73 | 65.18 | 34.82 |
| QCm < 3000 | 33 | 24 | 72.73 | 27.27 |
| MRFCHO Model | MRFCJO Model | ||
|---|---|---|---|
| POA | space complexity | O(6k6) | O(14k14) |
| time complexity | O(6ITk6) | O(14ITk14) | |
| GA | space complexity | O(6NT) | O(14NT) |
| time complexity | O(6INT) | O(14INT) |
| MRFCJO | MRFCHO | Relative Error (%) | ||
|---|---|---|---|---|
| S1 | (1) | 7320 | 7590 | 3.69 |
| (2) | 4540 | 4610 | 1.54 | |
| S2 | (1) | 12,600 | 13,000 | 3.17 |
| (2) | 9260 | 9470 | 2.27 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Zhong, P.-a.; Wang, Y.; Liu, Y.; Zheng, J.; Yang, M.; Liu, W. Dynamic Self-Adaptive Modeling for Real-Time Flood Control Operation of Multi-Reservoir Systems. Water 2022, 14, 3740. https://doi.org/10.3390/w14223740
Li J, Zhong P-a, Wang Y, Liu Y, Zheng J, Yang M, Liu W. Dynamic Self-Adaptive Modeling for Real-Time Flood Control Operation of Multi-Reservoir Systems. Water. 2022; 14(22):3740. https://doi.org/10.3390/w14223740
Chicago/Turabian StyleLi, Jieyu, Ping-an Zhong, Yuanjian Wang, Yanhui Liu, Jiayun Zheng, Minzhi Yang, and Weifeng Liu. 2022. "Dynamic Self-Adaptive Modeling for Real-Time Flood Control Operation of Multi-Reservoir Systems" Water 14, no. 22: 3740. https://doi.org/10.3390/w14223740





