Improving Lake Level Prediction by Embedding Support Vector Regression in a Data Assimilation Framework
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Collection
2.2. Problem Formulation
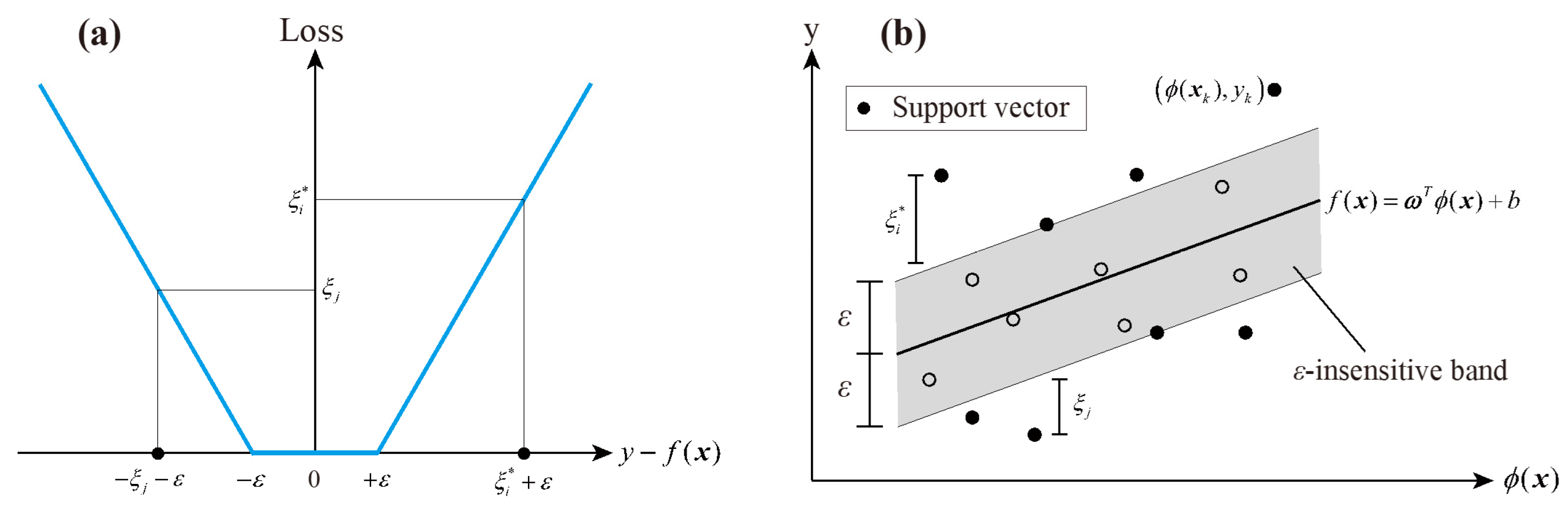
2.3. Support Vector Regression
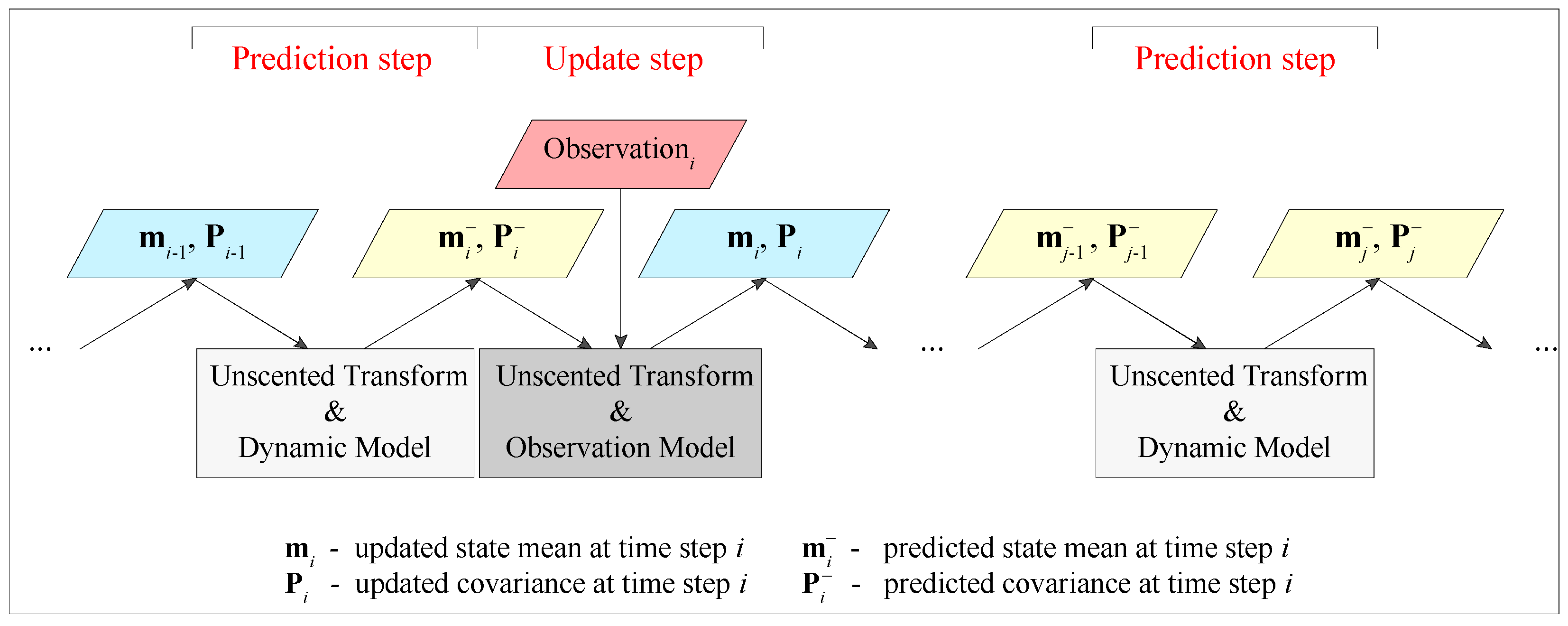
2.4. Unscented Kalman Filter
3. Results and Discussion
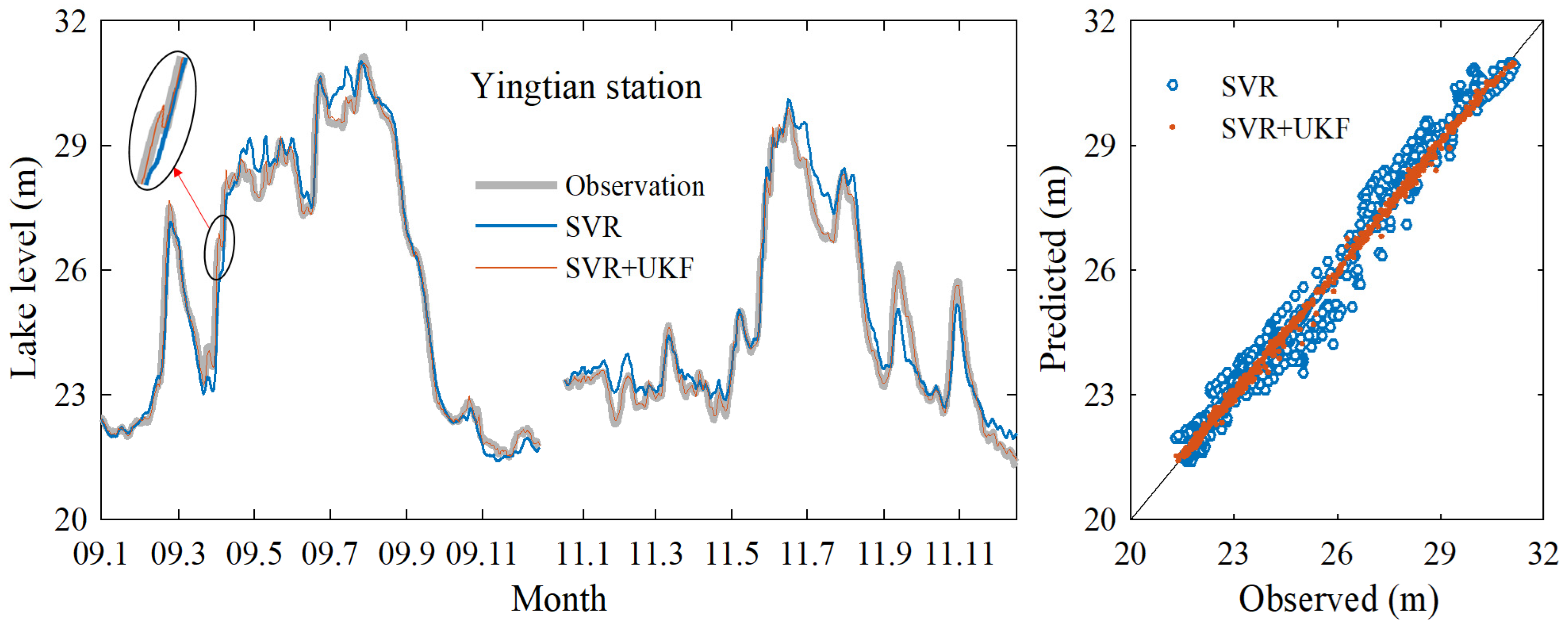
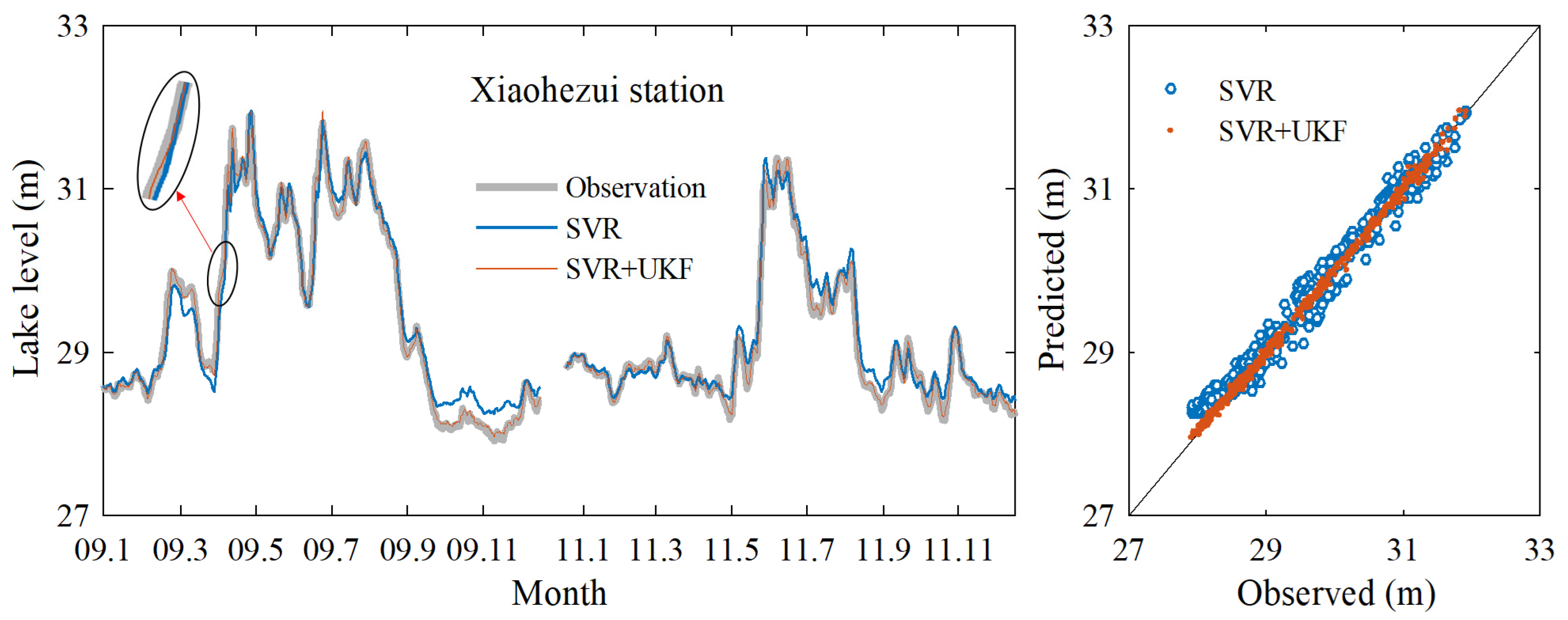
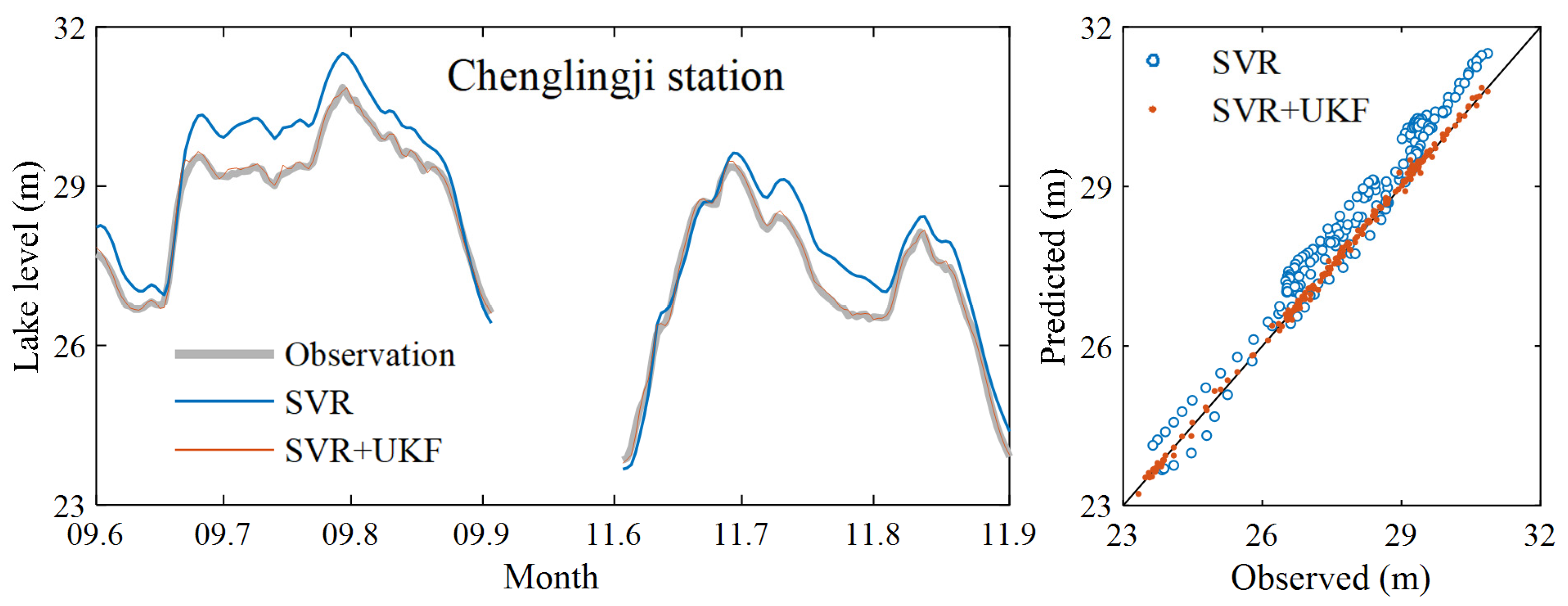
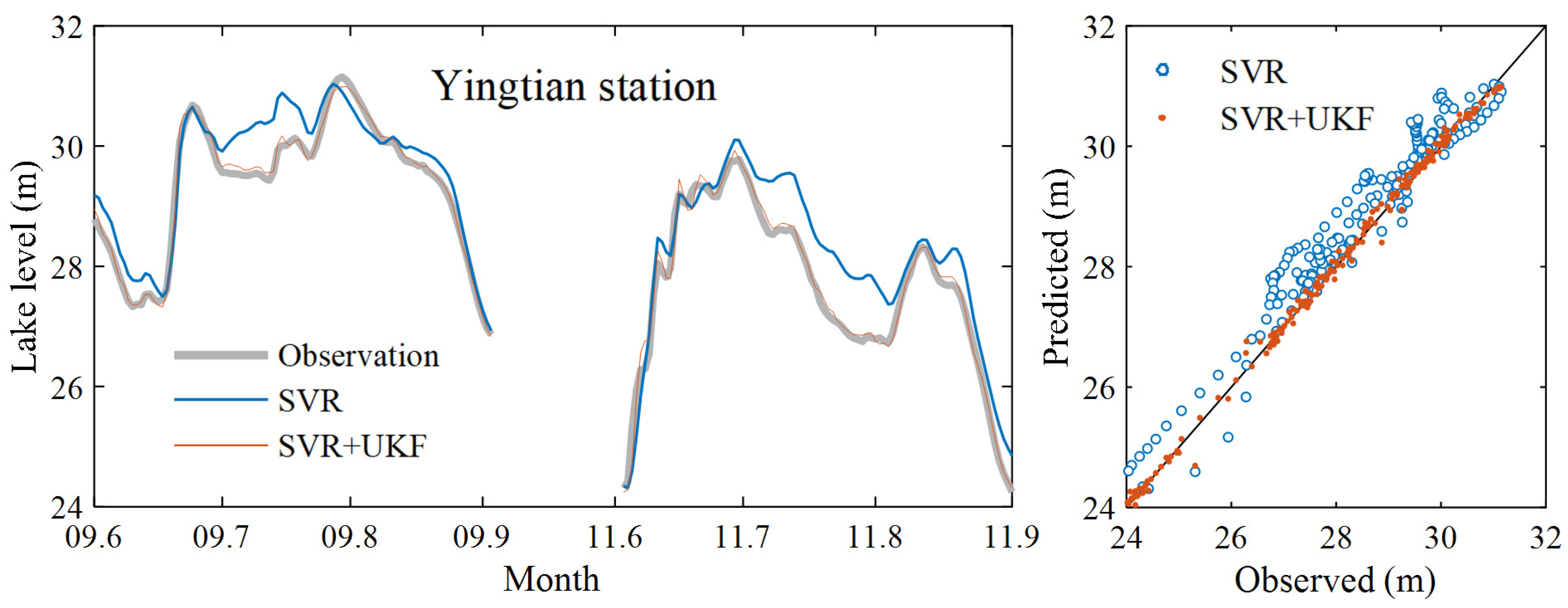
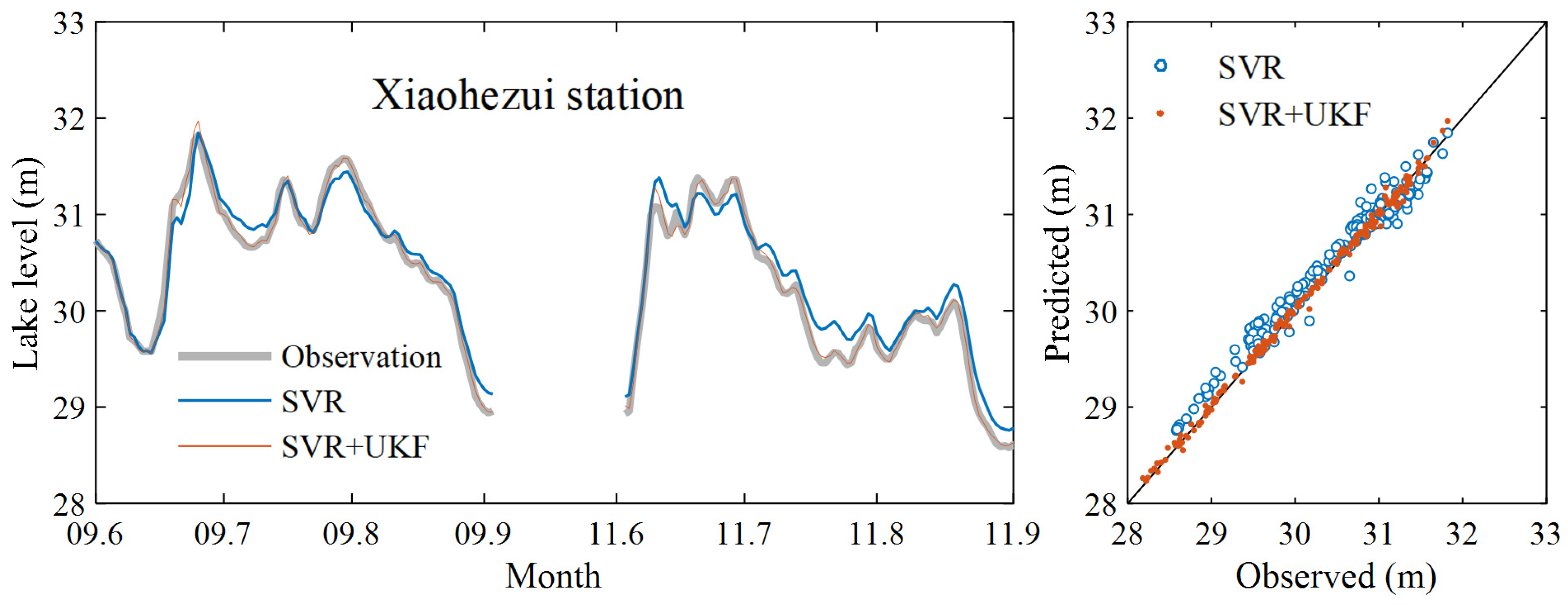
3.1. Data Assimilation Model Prediction Results
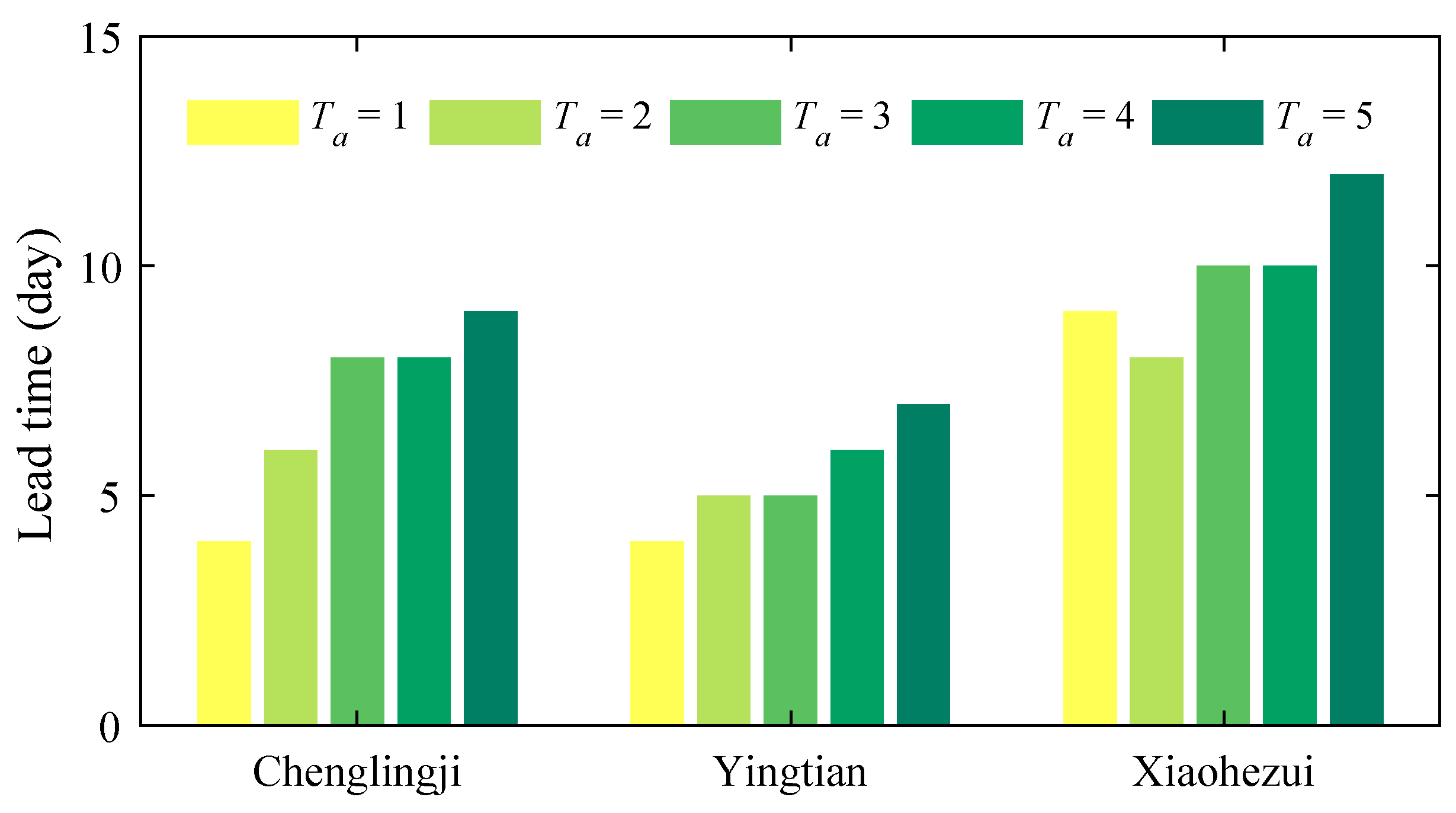
3.2. Further Model Testing
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Govindaraju, R.S. Artificial Neural Networks in Hydrology. I: Preliminary Concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar]
- Govindaraju, R.S. Artificial Neural Networks in Hydrology. II: Hydrologic Applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar]
- Abebe, A.J.; Price, R.K. Information Theory and Neural Networks for Managing Uncertainty in Flood Routing. J. Comput. Civil. Eng. 2004, 18, 373–380. [Google Scholar] [CrossRef]
- van den Boogaard, H.; Mynett, A. Dynamic Neural Networks with Data Assimilation. Hydrol. Process. 2004, 18, 1959–1966. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods Used for the Development of Neural Networks for the Prediction of Water Resource Variables in River Systems: Current Status and Future Directions. Environ. Modell. Softw. 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Moayedi, H.; Armaghani, D.J. Optimizing an ANN Model with ICA for Estimating Bearing Capacity of Driven Pile in Cohesionless Soil. Eng. Comput. 2018, 34, 347–356. [Google Scholar] [CrossRef]
- Cimen, M.; Kisi, O. Comparison of Two Different Data-Driven Techniques in Modeling Lake Level Fluctuations in Turkey. J. Hydrol. 2009, 378, 253–262. [Google Scholar] [CrossRef]
- Khan, M.S.; Coulibaly, P. Application of Support Vector Machine in Lake Water Level Prediction. J. Hydrol. Eng. 2006, 11, 199–205. [Google Scholar] [CrossRef]
- Gu, R.C.; McCutcheon, S.; Chen, C.J. Development of Weather-Dependent Flow Require-ments for River Temperature Control. Environ. Manag. 1999, 24, 529–540. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural Networks for the Prediction and Forecasting of Water Resources Variables: A Review of Modelling Issues and Applications. Environ. Modell. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Zhang, X.; Liang, F.; Srinivasan, R.; Van Liew, M. Estimating Uncertainty of Streamflow Simulation Using Bayesian Neural Networks. Water Resour. Res. 2009, 45, W02403. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, H.; Peng, A.; Wang, W.; Li, B.; Huang, X. Quantifying the Uncertainties in Data-Driven Models for Reservoir Inflow Prediction. Water Resour. Manag. 2020, 34, 1479–1493. [Google Scholar] [CrossRef]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An Evaluation Framework for Input Variable Selection Algorithms for Environmental Data-Driven Models. Environ. Modell. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef]
- Kingston, G.B.; Lambert, M.F.; Maier, H.R. Bayesian Training of Artificial Neural Networks Used for Water Resources Modeling. Water Resour. Res. 2005, 41, W12409. [Google Scholar] [CrossRef]
- Quilty, J.; Adamowski, J.; Boucher, M.-A. A Stochastic Data-Driven Ensemble Forecasting Framework for Water Resources: A Case Study Using Ensemble Members Derived from a Database of Deterministic Wavelet-Based Models. Water Resour. Res. 2019, 55, 175–202. [Google Scholar] [CrossRef]
- Newhart, K.B.; Holloway, R.W.; Hering, A.S.; Cath, T.Y. Data-Driven Performance Analyses of Wastewater Treatment Plants: A Review. Water Res. 2019, 157, 498–513. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Diks, C.G.H.; Gupta, H.V.; Bouten, W.; Verstraten, J.M. Improved Treatment of Uncertainty in Hydrologic Modeling: Combining the Strengths of Global Optimization and Data Assimilation. Water Resour. Res. 2005, 41, W01017. [Google Scholar] [CrossRef]
- Liu, Y.; Gupta, H.V. Uncertainty in Hydrologic Modeling: Toward an Integrated Data Assimilation Framework. Water Resour. Res. 2007, 43, W07401. [Google Scholar] [CrossRef]
- Liu, Y.; Weerts, A.H.; Clark, M.; Franssen, H.-J.H.; Kumar, S.; Moradkhani, H.; Seo, D.-J.; Schwanenberg, D.; Smith, P.; van Dijk, A.I.J.M.; et al. Advancing Data Assimilation in Operational Hy-drologic Forecasting: Progresses, Challenges, and Emerging Opportunities. Hydrol. Earth Syst. Sci. 2012, 16, 3863–3887. [Google Scholar] [CrossRef]
- Mao, J.Q.; Lee, J.H.W.; Choi, K.W. The Extended Kalman Filter for Forecast of Algal Bloom Dynamics. Water Res. 2009, 43, 4214–4224. [Google Scholar] [CrossRef]
- Zamani, A.; Azimian, A.; Heemink, A.; Solomatine, D. Non-Linear Wave Data Assimilation with an ANN-Type Wind-Wave Model and Ensemble Kalman Filter (EnKF). Appl. Math. Model. 2010, 34, 1984–1999. [Google Scholar] [CrossRef]
- Gill, M.K.; Kemblowski, M.W.; McKee, M. Soil Moisture Data Assimilation Using Support Vector Machines and Ensemble Kalman Filter. J. Am. Water Resour. Assoc. 2007, 43, 1004–1015. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, D.; Lu, H.; Fu, X.; Xiang, L.; Zhu, Y. A Multi-Layer Soil Moisture Data Assimilation Using Support Vector Machines and Ensemble Particle Filter. J. Hydrol. 2012, 475, 53–64. [Google Scholar] [CrossRef]
- Kalman, R. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 35–45. [Google Scholar] [CrossRef]
- Lee, J.H.W.; Mao, J.Q.; Choi, K.W. The Extended Kalman Filter for Short Term Prediction of Algal Bloom Dynamics. In Advances in Water Resources and Hydraulic Engineering; Zhang, C.K., Tang, H.W., Eds.; Tsinghua Univ Press: Beijing, China, 2009; Volume 1–6, pp. 513–517. [Google Scholar]
- Evensen, G. Sequential Data Assimilation with a Nonlinear Quasi-geostrophic Model Using Monte Carlo Methods to Forecast Error Statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. A New Extension of the Kalman Filter to Nonlinear Systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–24 April 1997; Kadar, I., Ed.; SPIE—International Society Optical Engineering: Bellingham, WA, USA, 1997; Volume 3068, pp. 182–193. [Google Scholar]
- Qi, J.; Sun, K.; Wang, J.; Liu, H. Dynamic State Estimation for Multi-Machine Power System by Unscented Kalman Filter with Enhanced Numerical Stability. IEEE Trans. Smart Grid 2018, 9, 1184–1196. [Google Scholar] [CrossRef]
- Ahani, A.; Shourian, M.; Rad, P.R. Performance Assessment of the Linear, Nonlinear and Nonparametric Data Driven Models in River Flow Forecasting. Water Resour. Manag. 2018, 32, 383–399. [Google Scholar] [CrossRef]
- Shu, C.; Ouarda, T.B.M.J. Flood Frequency Analysis at Ungauged Sites Using Artificial Neural Networks in Canonical Correlation Analysis Physiographic Space. Water Resour. Res. 2007, 43, W07438. [Google Scholar] [CrossRef]
- Haque, A.; Rahman, S. Short-Term Electrical Load Forecasting through Heuristic Configuration of Regularized Deep Neural Network. Appl. Soft. Comput. 2022, 122, 108877. [Google Scholar] [CrossRef]








| Station | Dataset a | Minimum Value (m) | Maximum Value (m) | Mean Value (m) | Standard Deviation (m) |
|---|---|---|---|---|---|
| Chenglingji | Training | 20.21 | 33.40 | 25.66 | 3.95 |
| Testing | 20.43 | 30.86 | 24.13 | 2.94 | |
| Yingtian | Training | 21.21 | 33.67 | 26.69 | 3.66 |
| Testing | 21.32 | 31.15 | 25.05 | 2.75 | |
| Xiaohezui | Training | 27.89 | 34.93 | 29.99 | 1.68 |
| Testing | 27.91 | 31.91 | 29.27 | 1.02 |
| Type | Source |
|---|---|
| Structural uncertainty | Insufficient degree of freedom of the approximator used |
| Unreasonable input variable selection | |
| Parameter uncertainty | Dependency of parameter values on data division |
| Absence of representativeness of training samples | |
| Difficulty in finding globally optimal parameters | |
| Equifinality problem | |
| Overfitting problem | |
| Data uncertainty | Input and output measurement noise |
| Lack of representativeness |
| Station | SVR | SVR+UKF | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE (m) | MRE | R2 | RMSE (m) | MRE | |
| Chenglingji | 0.982 | 0.395 | 0.012 | 0.999 | 0.068 | 0.002 |
| Yingtian | 0.975 | 0.436 | 0.013 | 0.999 | 0.105 | 0.003 |
| Xiaohezui | 0.976 | 0.159 | 0.004 | 0.998 | 0.042 | 0.001 |
| Station | SVR | SVR+UKF | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE (m) | MRE | R2 | RMSE (m) | MRE | |
| Chenglingji | 0.949 | 0.487 | 0.017 | 0.999 | 0.073 | 0.002 |
| Yingtian | 0.961 | 0.412 | 0.016 | 0.998 | 0.116 | 0.004 |
| Xiaohezui | 0.984 | 0.103 | 0.003 | 0.999 | 0.037 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Hu, T.; Zhang, P.; Huang, W.; Mao, J.; Xu, Y.; Shi, Y. Improving Lake Level Prediction by Embedding Support Vector Regression in a Data Assimilation Framework. Water 2022, 14, 3718. https://doi.org/10.3390/w14223718
Wang K, Hu T, Zhang P, Huang W, Mao J, Xu Y, Shi Y. Improving Lake Level Prediction by Embedding Support Vector Regression in a Data Assimilation Framework. Water. 2022; 14(22):3718. https://doi.org/10.3390/w14223718
Chicago/Turabian StyleWang, Kang, Tengfei Hu, Peipei Zhang, Wenqin Huang, Jingqiao Mao, Yifan Xu, and Yong Shi. 2022. "Improving Lake Level Prediction by Embedding Support Vector Regression in a Data Assimilation Framework" Water 14, no. 22: 3718. https://doi.org/10.3390/w14223718
APA StyleWang, K., Hu, T., Zhang, P., Huang, W., Mao, J., Xu, Y., & Shi, Y. (2022). Improving Lake Level Prediction by Embedding Support Vector Regression in a Data Assimilation Framework. Water, 14(22), 3718. https://doi.org/10.3390/w14223718








