A Modified Two-Parameter Monthly Water Balance Model for Runoff Simulation to Assess Hydrological Drought
Abstract
:1. Introduction
2. Methodology
2.1. Modified TPMWB Model
2.2. Calculation of Standardized Drought Index
2.3. Identification of Drought Events and Characteristics
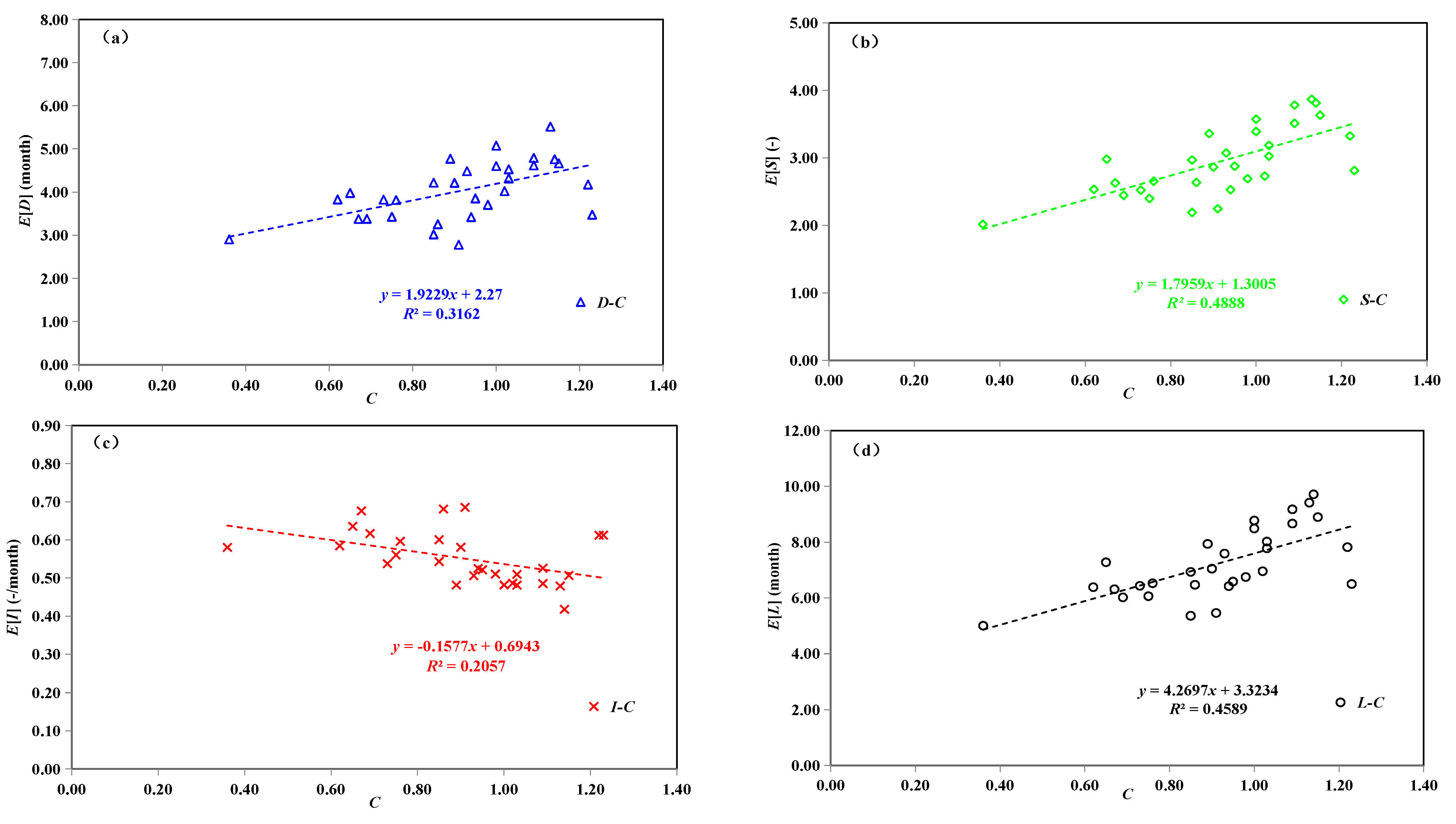
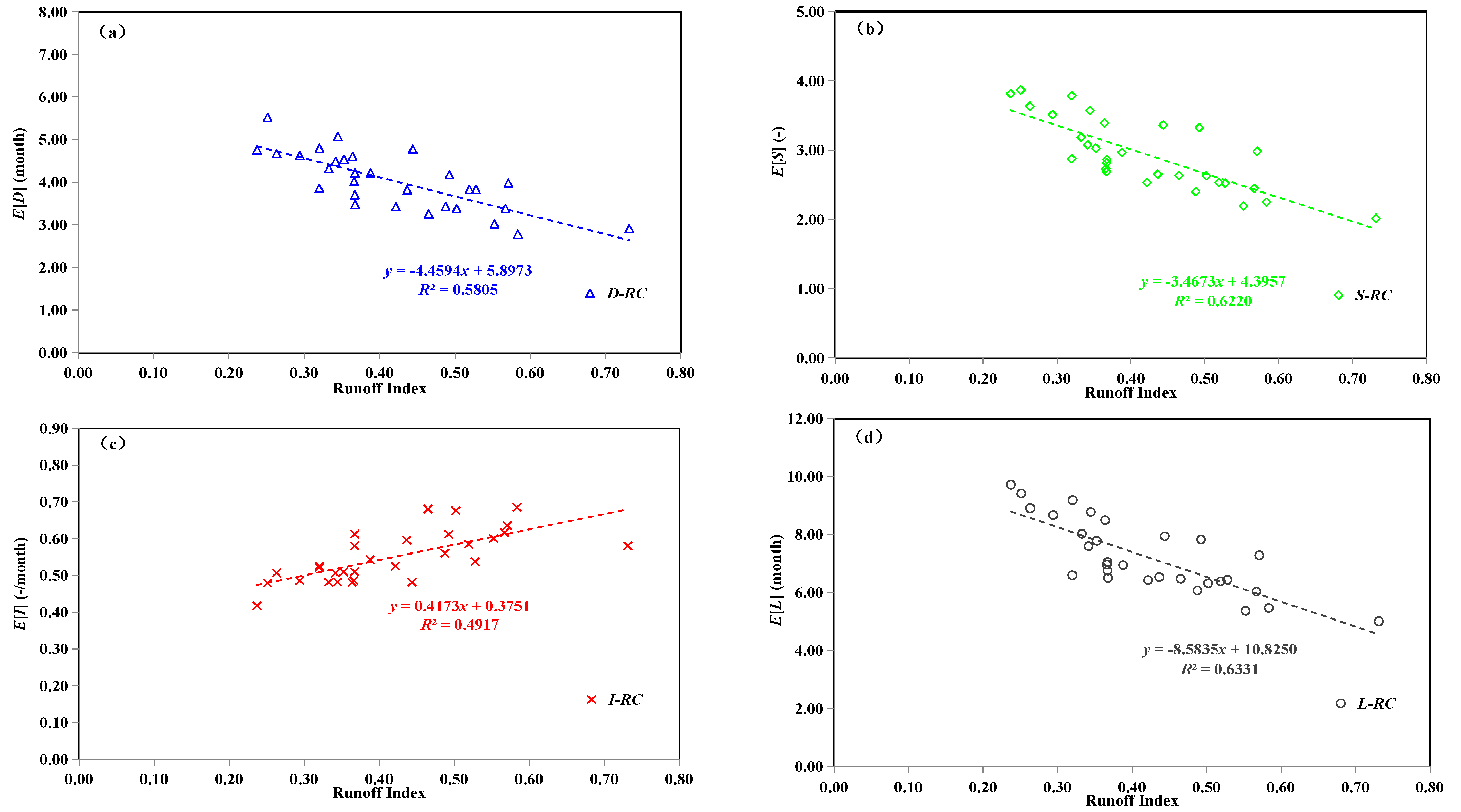
2.4. Correlation Analysis between Drought Characteristics and Watershed Features
3. Study Area and Data
3.1. Study Area
3.2. Data
4. Results and Discussion
4.1. Performance of the Modified TPMWB Model
4.2. Hydrological Drought Assessment Based on Standardized Drought Indices
4.2.1. Calculation of Standardized Drought Indices
4.2.2. Drought Characteristics (DC) Analysis
4.3. Impacts of Watershed Features on Drought Characteristics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fleig, A.K.; Tallaksen, L.M.; Hisdal, H.; Demuth, S. A global evaluation of streamflow drought characteristics. Hydrol. Earth Syst. Sci. 2006, 10, 535–552. [Google Scholar] [CrossRef] [Green Version]
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef] [Green Version]
- Hong, X.; Guo, S.; Xiong, L.; Liu, Z. Spatial and temporal analysis of drought using entropy-based standardized precipitation index: A case study in Poyang Lake basin, China. Theor. Appl. Climat. 2015, 122, 543–556. [Google Scholar] [CrossRef]
- Rahmat, S.N.; Jayasuriya, N.; Bhuiyan, M. Assessing droughts using meteorological drought indices in Victoria, Australia. Hydrol. Res. 2015, 46, 463–476. [Google Scholar] [CrossRef]
- Portela, M.M.; Dos Santos, J.F.; Silva, A.T.; Benitez, J.B.; Frank, C.; Reichert, J.M. Drought analysis in southern Paraguay, Brazil and northern Argentina: Regionalization, occurrence rate and rainfall thresholds. Hydrol. Res. 2015, 46, 792–810. [Google Scholar] [CrossRef]
- de Freitas, G.N. São Paulo drought: Trends in streamflow and their relationship to climate and human-induced change in Cantareira watershed, Southeast Brazil. Hydrol. Res. 2015, 51, 750–767. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, X.; Zhang, Z.; Shi, P. Evolution of hydrological drought under the regulation of two reservoirs in the headwater basin of the Huaihe River, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 487–499. [Google Scholar] [CrossRef]
- Hong, X.; Guo, S.; Wang, L.; Yang, G.; Liu, D.; Guo, H.; Wang, J. Evaluating water supply risk in the middle and lower reaches of Hanjiang river basin based on an integrated optimal water resources allocation model. Water 2016, 8, 364. [Google Scholar] [CrossRef] [Green Version]
- Firoz, A.B.M.; Nauditt, A.; Fink, M.; Ribbe, L. Quantifying human impacts on hydrological drought using a combined modelling approach in a tropical river basin in central Vietnam. Hydrol. Earth Syst. Sci. 2018, 22, 547–565. [Google Scholar] [CrossRef] [Green Version]
- Tijdeman, E.; Hannaford, J.; Stahl, K. Human influences on streamflow drought characteristics in England and Wales. Hydrol. Earth Syst. Sci. 2018, 22, 1051–1064. [Google Scholar] [CrossRef]
- Fan, K.; Zhang, Q.; Gu, X.; Singh, V.P.; Xu, C.Y.; Shen, Z.; Wang, G. Global soil moisture drought identification and responses to natural and anthropogenic forcings. J. Hydrol. 2022, 610, 127993. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. Drought modeling—A review. J. Hydrol. 2011, 403, 157–175. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993. [Google Scholar]
- Tsakiris, G.; Vangelis, H. Establishing a drought index incorporating evapotranspiration. Euro. Water 2005, 9, 3–11. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Fischer, T.; Gemmer, M.; Su, B.; Scholten, T. Hydrological long-term dry and wet periods in the Xijiang River basin, South China. Hydrol. Earth Syst. Sci. 2013, 17, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Hong, X.; Guo, S.; Zhou, Y.; Xiong, L. Uncertainties in assessing hydrological drought using streamflow drought index for the upper Yangtze River basin. Stoch. Environ. Res. Risk Assess. 2015, 29, 1235–1247. [Google Scholar] [CrossRef]
- Sun, X.; Li, Z.; Tian, Q. Assessment of hydrological drought based on nonstationary runoff data. Hydrol. Res. 2020, 51, 894–910. [Google Scholar] [CrossRef]
- Yue, S.; Sheng, X.; Yang, F. Spatiotemporal evolution and meteorological triggering conditions of hydrological drought in the Hun River basin, NE China. Nat. Hazards Earth Syst. Sci. 2022, 22, 995–1014. [Google Scholar] [CrossRef]
- Nalbantis, I.; Tsakiris, G. Assessment of hydrological drought revisited. Water Resour. Manag. 2009, 23, 881–897. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate computation of a streamflow drought index. J. Hydrol. Eng. 2012, 17, 318–332. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardized precipitation index approach. Hydrol. Earth Syst. Sci. 2013, 17, 4769–4787. [Google Scholar] [CrossRef] [Green Version]
- Waseem, M.; Ajmal, M.; Kim, T.W. Development of a new composite drought index for multivariate drought assessment. J. Hydrol. 2015, 527, 30–37. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, S.; Huang, Q.; Leng, G.; Wang, H.; Wang, L. Assessment of drought evolution characteristics based on a nonparametric and trivariate integrated drought index. J. Hydrol. 2019, 579, 124230. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965. [Google Scholar]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35, L02405. [Google Scholar] [CrossRef] [Green Version]
- Staudinger, M.; Stahl, K.; Seibert, J. A drought index accounting for snow. Water Resour. Res. 2014, 50, 7861–7872. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, S. A two-parameter monthly water balance model and its application. J. Hydrol. 1999, 216, 111–123. [Google Scholar] [CrossRef]
- Guo, S.; Wang, J.; Xiong, L.; Ying, A.; Li, D. A macro-scale and semi-distributed monthly water balance model to predict climate change impacts in China. J. Hydrol. 2002, 268, 1–15. [Google Scholar] [CrossRef]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Stepwise development of a two-parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q.X. Water balance modeling over variable time scales based on the Budyko framework-Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Wang, Q.; Pagano, T.C.; Zhou, S.; Hapuarachchi, H.A.P.; Zhang, L.; Robertson, D.E. Monthly versus daily water balance models in simulating monthly runoff. J. Hydrol. 2011, 404, 166–175. [Google Scholar] [CrossRef]
- Vandewiele, G.L.; Xu, C.Y.; Win, N.L. Methodology and comparative study of monthly water balance models in Belgium, China and Burma. J. Hydrol. 1992, 134, 315–347. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V.P. A review on monthly water balance models for water resources investigations. Water Resour. Manag. 1998, 12, 20–50. [Google Scholar] [CrossRef]
- Vasiliades, L.; Loukas, A.; Liberis, N. A water balance derived drought index for Pinios River basin, Greece. Water Resour. Manag. 2011, 25, 1087–1101. [Google Scholar] [CrossRef]
- Li, S.; Xiong, L.; Dong, L.; Zhang, J. Effects of the Three Gorges Reservoir on the hydrological droughts at the downstream Yichang station during 2003–2011. Hydrol. Process. 2013, 27, 3981–3993. [Google Scholar] [CrossRef]
- Wang, W.; Wei, J.; Shao, Q.X.; Xing, W.; Yong, B.; Yu, Z.; Jiao, X. Spatial and temporal variations in hydro-climatic variables and runoff in response to climate change in the Luanhe River basin, China. Stoch. Environ. Res. Risk Assess. 2015, 29, 1117–1133. [Google Scholar] [CrossRef]
- Hu, Q.; Wang, Y.; Liu, K.; Wang, Z. Monthly runoff simulation based on improved two-parameter monthly water volume balance model. J. Hohai Univ. Nat. Sci. 2007, 35, 638–642. (In Chinese) [Google Scholar]
- Harman, C.; Troch, P.A. What makes Darwinian hydrology “Darwinian”? Asking a different kind of question about landscapes. Hydrol. Earth Syst. Sci. 2014, 18, 417–433. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.B.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in Darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef] [Green Version]
- Mo, K.C. Model-based drought indices over the United States. J. Hydrometeorol. 2008, 9, 1212–1230. [Google Scholar] [CrossRef]
- Wang, D.B.; Hejazi, M.; Cai, X.M.; Valocchi, A.J. Climate change impact on meteorological, agricultural, and hydrological drought in central Illinois. Water Resour. Res. 2011, 47, W09527. [Google Scholar] [CrossRef] [Green Version]
- Leng, G.; Tang, Q.; Rayburg, S. Climate change impacts on meteorological, agricultural, and hydrological droughts in China. Global Planet. Chang. 2015, 126, 23–34. [Google Scholar] [CrossRef]
- Guo, Y.; Huang, S.; Huang, Q.; Leng, G.; Fang, W.; Wang, L.; Wang, H. Propagation thresholds of meteorological drought for triggering hydrological drought at various levels. Sci. Total Environ. 2020, 712, 136502. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Tu, X.; Singh, V.P.; Chen, X.; Lin, K. Global data assessment and analysis of drought characteristics based on CMIP6. J. Hydrol. 2021, 596, 126091. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. Information theory and statistical mechanics, II. Phys. Rev. 1957, 108, 171–190. [Google Scholar] [CrossRef]
- Shannon, C.E. The mathematical theory of communications. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.E. Moment methods for decision analysis. Manag. Sci. 1993, 39, 340–358. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Entropy-based method for extreme rainfall analysis in Texas. J. Geophys. Res. Atmos. 2013, 118, 263–273. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Entropy-based method for bivariate drought analysis. J. Hydrol. Eng. 2013, 18, 780–786. [Google Scholar] [CrossRef]
- Mead, L.R.; Papanicolaou, N. Maximum entropy in the problem of moments. J. Math. Phys. 1984, 25, 2404–2417. [Google Scholar] [CrossRef] [Green Version]
- Zuo, D.D.; Hou, W.; Yan, P.C.; Feng, T.C. Research on drought in southwest China based on the theory of run and two-dimensional joint distribution theory. Acta Phys. Sin. 2014, 63, 230204. [Google Scholar]
- Wu, R.; Zhang, J.; Bao, Y.; Guo, E. Run theory and copula-based drought risk analysis for Songnen Grassland in Northeastern China. Sustainability 2019, 11, 6032. [Google Scholar] [CrossRef]
- Malagò, A.; Bouraoui, F.; De Roo, A. Diagnosis and treatment of the SWAT hydrological response using the budyko framework. Sustainability 2018, 10, 1373. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Guo, S.; Xu, C.Y.; Singh, V.P. Historical temporal trends of hydro-climatic variables and runoff response to climate variability and their relevance in water resource management in the Hanjiang basin. J. Hydrol. 2007, 344, 171–184. [Google Scholar] [CrossRef]
- Chen, H.; Guo, J.; Xiong, W.; Guo, S.; Xu, C.Y. Downscaling GCMs using the Smooth Support Vector Machine method to predict daily precipitation in the Hanjiang Basin. Adv. Atmos. Sci. 2010, 27, 274–284. [Google Scholar] [CrossRef]
- Xiong, L.; Yu, K.; Gottschalk, L. Estimation of the distribution of annual runoff from climatic variables using copulas. Water Resour. Res. 2014, 50, 7134–7152. [Google Scholar] [CrossRef]
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]


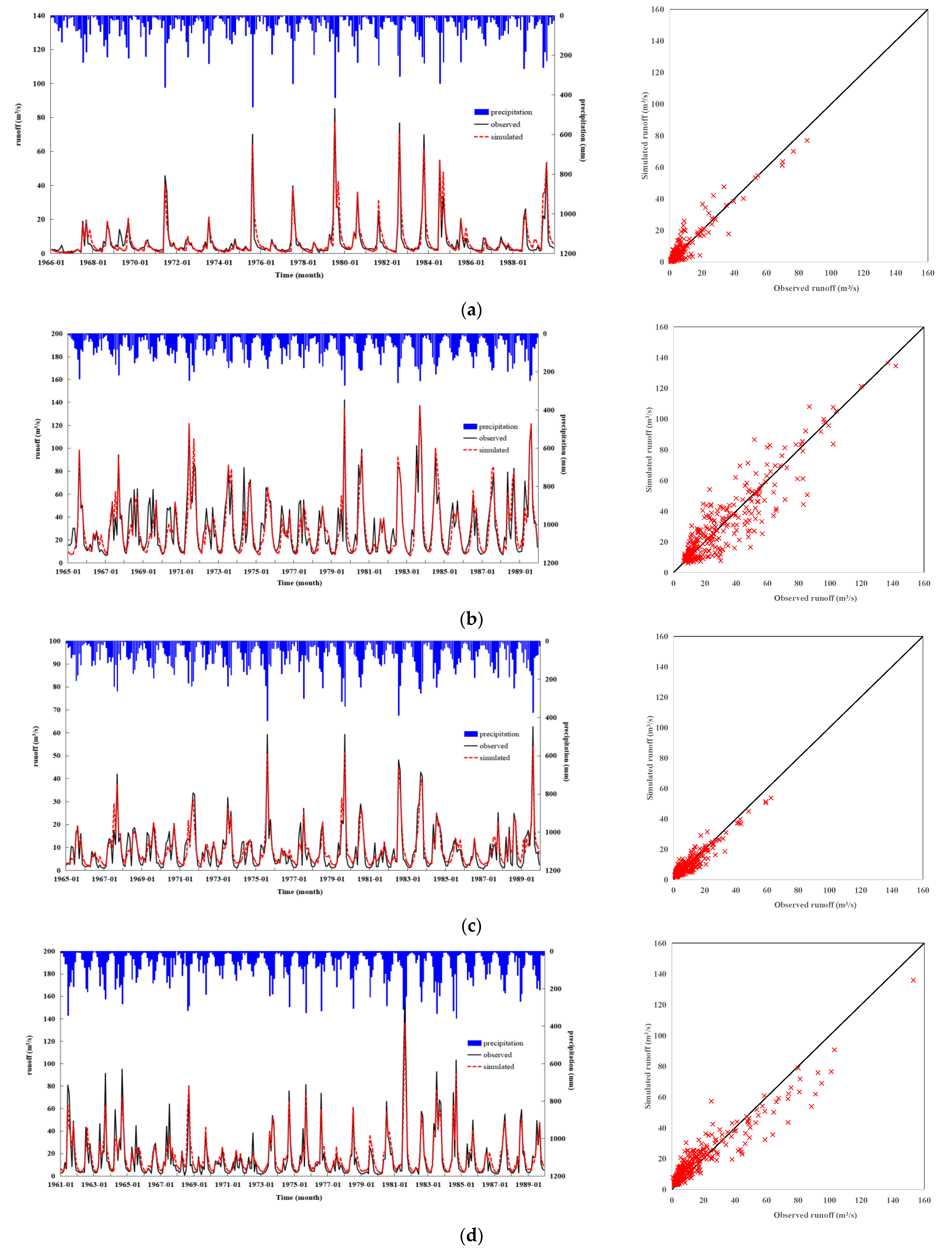
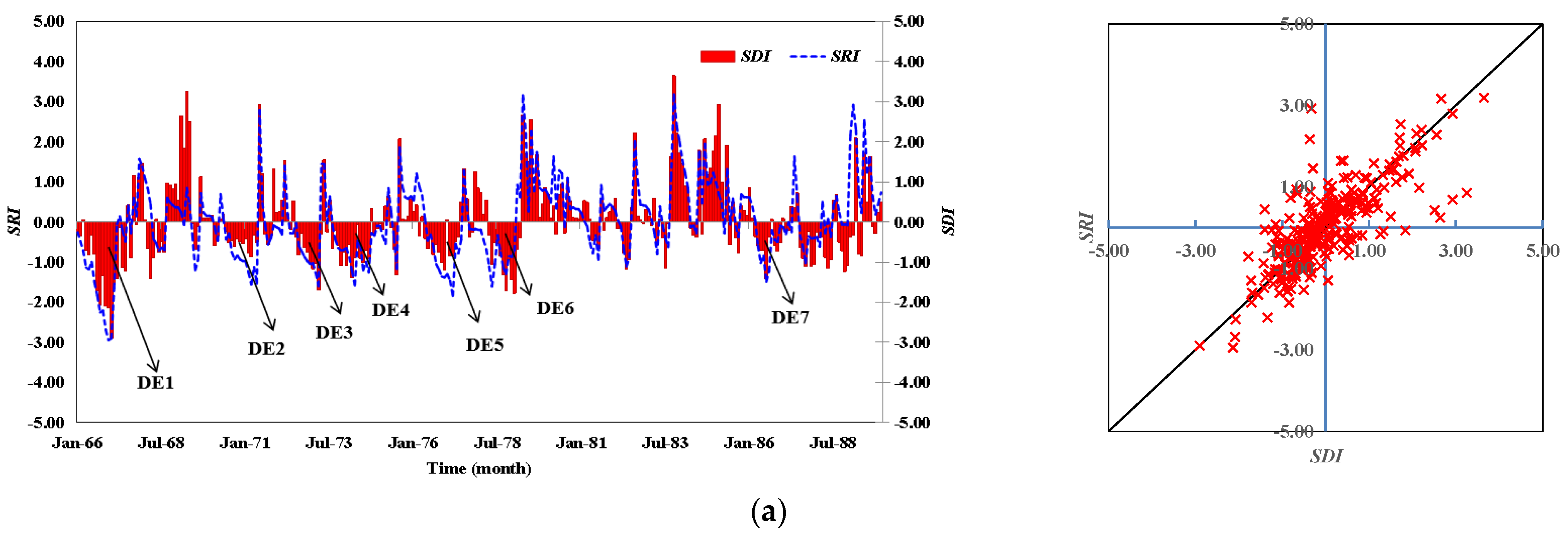

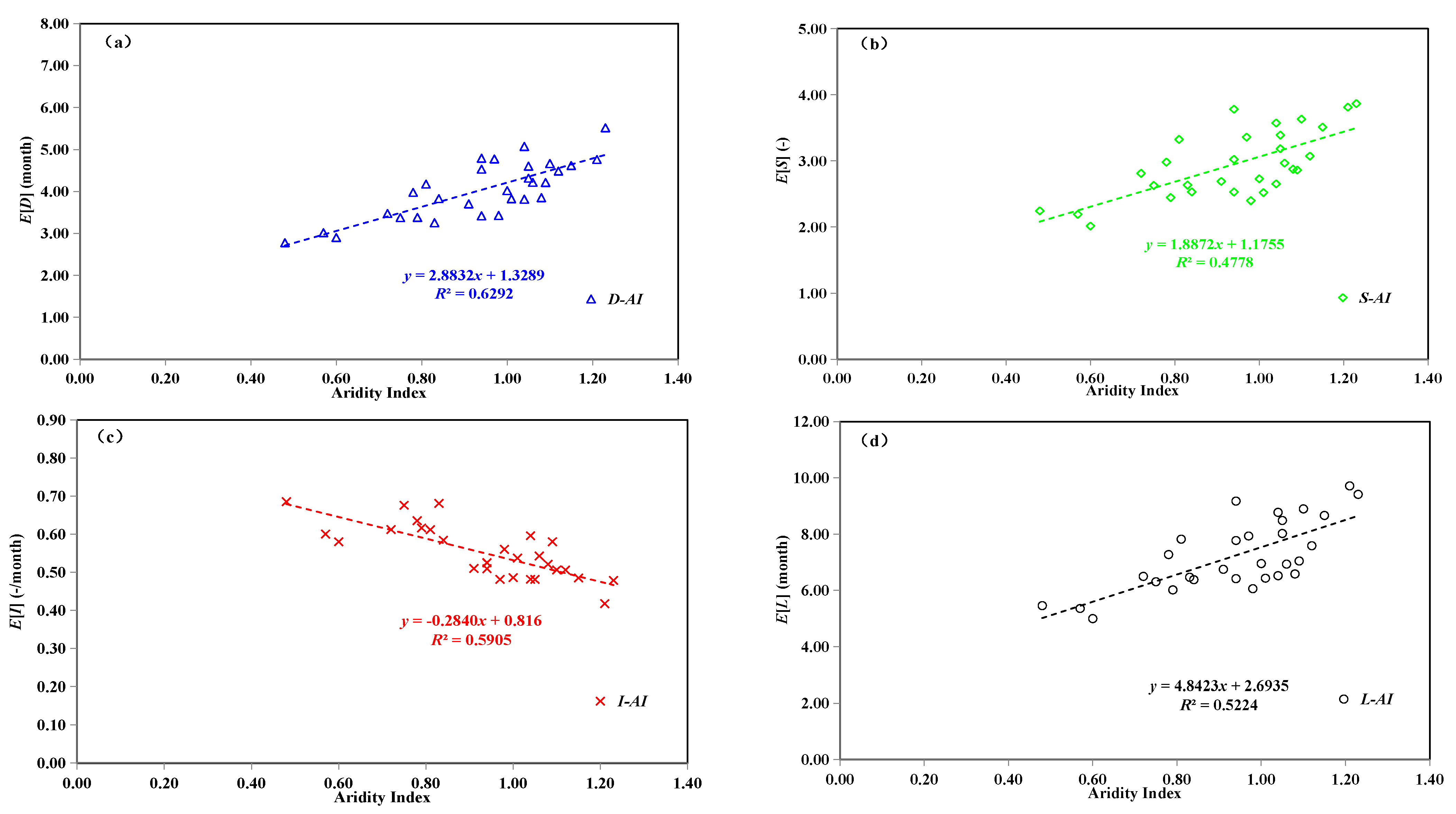
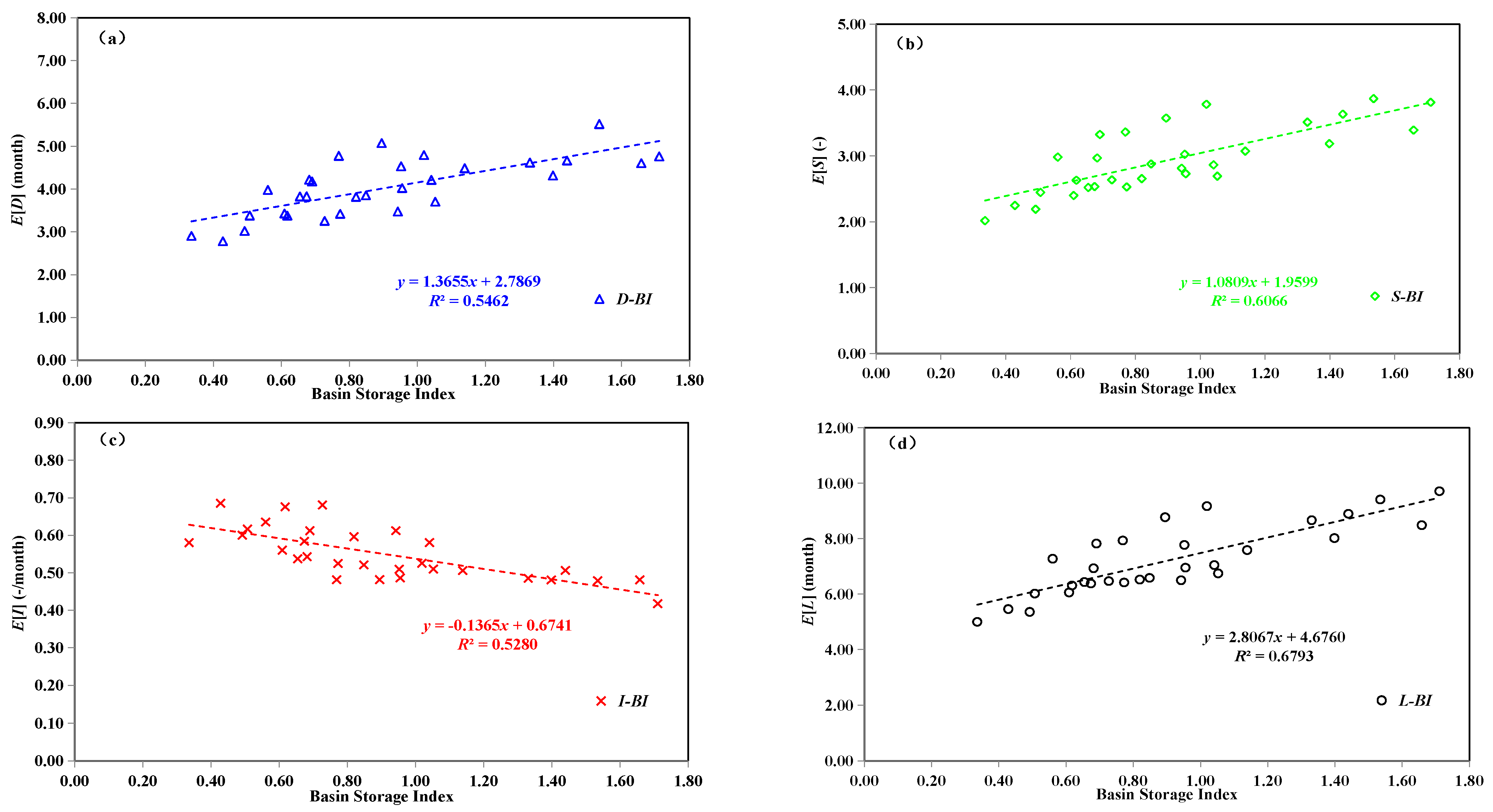
| No. | Watershed | Area (km2) | Data Period | P (mm∙yr−1) | PE (mm∙yr−1) | Q (mm∙yr−1) | AI (-) | RC (-) |
|---|---|---|---|---|---|---|---|---|
| 1 | Baitugang | 1134 | 1963–1989 | 923 | 864 | 389 | 0.94 | 0.42 |
| 2 | Baiyan | 690 | 1965–1989 | 779 | 708 | 286 | 0.91 | 0.37 |
| 3 | Bandian | 425 | 1955–1989 | 742 | 896 | 176 | 1.21 | 0.24 |
| 4 | Caodian | 683 | 1960–1987 | 1142 | 1205 | 443 | 1.06 | 0.39 |
| 5 | Chadianzi | 1683 | 1967–1989 | 868 | 624 | 319 | 0.72 | 0.37 |
| 6 | Chaiping | 2364 | 1969–1989 | 845 | 880 | 369 | 1.04 | 0.44 |
| 7 | Dazhuhe | 2651 | 1968–1989 | 1229 | 735 | 899 | 0.60 | 0.73 |
| 8 | Guihuayuan | 1275 | 1964–1989 | 859 | 721 | 446 | 0.84 | 0.52 |
| 9 | Houhui | 816 | 1958–1989 | 902 | 849 | 318 | 0.94 | 0.35 |
| 10 | Huayuan | 2601 | 1964–1987 | 1113 | 1207 | 356 | 1.08 | 0.32 |
| 11 | Jiajiafang | 1281 | 1960–1989 | 839 | 885 | 279 | 1.05 | 0.33 |
| 12 | Jiangwan | 781 | 1959–1989 | 849 | 890 | 309 | 1.05 | 0.36 |
| 13 | Kouzihe | 421 | 1963–1989 | 863 | 865 | 316 | 1.00 | 0.37 |
| 14 | Lianghekou | 2816 | 1967–1989 | 889 | 716 | 438 | 0.81 | 0.49 |
| 15 | Miping | 1404 | 1967–1989 | 794 | 875 | 209 | 1.10 | 0.26 |
| 16 | Nankuanping | 3936 | 1965–1989 | 773 | 869 | 264 | 1.12 | 0.34 |
| 17 | Nanshahe | 243 | 1967–1989 | 1208 | 585 | 705 | 0.48 | 0.58 |
| 18 | Pingshi | 748 | 1960–1989 | 975 | 1010 | 336 | 1.04 | 0.34 |
| 19 | Qingfeng | 2082 | 1963–1989 | 931 | 875 | 298 | 0.94 | 0.32 |
| 20 | Qingniwan | 1377 | 1965–1989 | 798 | 869 | 293 | 1.09 | 0.37 |
| 21 | Shengxiancun | 2143 | 1961–1988 | 890 | 738 | 414 | 0.83 | 0.47 |
| 22 | Sheqi | 1044 | 1966–1989 | 796 | 981 | 200 | 1.23 | 0.25 |
| 23 | Shuhe | 581 | 1969–1989 | 881 | 851 | 391 | 0.97 | 0.44 |
| 24 | Taikou | 2073 | 1965–1989 | 883 | 888 | 466 | 1.01 | 0.53 |
| 25 | Tiesuoguan | 433 | 1966–1989 | 1106 | 632 | 611 | 0.57 | 0.55 |
| 26 | Wanyugou | 560 | 1965–1989 | 1013 | 996 | 494 | 0.98 | 0.49 |
| 27 | Wuguan | 724 | 1959–1989 | 772 | 888 | 227 | 1.15 | 0.29 |
| 28 | Xianhekou | 772 | 1966–1989 | 974 | 733 | 489 | 0.75 | 0.50 |
| 29 | Xinzhou | 4660 | 1964–1989 | 1055 | 830 | 598 | 0.79 | 0.57 |
| 30 | Youshuijie | 911 | 1961–1989 | 939 | 734 | 536 | 0.78 | 0.57 |
| No. | Watershed | C (-) | SC (-) | NSE (%) | RE (%) |
|---|---|---|---|---|---|
| 1 | Baitugang | 0.94 | 300.63 | 0.83. | 10.4 |
| 2 | Baiyan | 0.98 | 301.01 | 0.75 | 12.8 |
| 3 | Bandian | 1.14 | 301.11 | 0.80 | 4.1 |
| 4 | Caodian | 0.85 | 302.08 | 0.84 | 15.5 |
| 5 | Chadianzi | 1.23 | 300.61 | 0.85 | 21.9 |
| 6 | Chaiping | 0.76 | 302.35 | 0.86 | 10.2 |
| 7 | Dazhuhe | 0.36 | 301.84 | 0.84 | 7.7 |
| 8 | Guihuayuan | 0.62 | 300.63 | 0.74 | 11.0 |
| 9 | Houhui | 1.03 | 302.78 | 0.82 | 7.8 |
| 10 | Huayuan | 0.95 | 302.08 | 0.81 | 15.2 |
| 11 | Jiajiafang | 1.03 | 390.16 | 0.80 | 1.8 |
| 12 | Jiangwan | 1.00 | 512.38 | 0.78 | 2.7 |
| 13 | Kouzihe | 1.02 | 301.83 | 0.86 | 14.4 |
| 14 | Lianghekou | 1.22 | 302.35 | 0.83 | 18.7 |
| 15 | Miping | 1.15 | 300.93 | 0.81 | 5.7 |
| 16 | Nankuanping | 0.93 | 300.63 | 0.84 | 12.2 |
| 17 | Nanshahe | 0.91 | 301.81 | 0.86 | 17.8 |
| 18 | Pingshi | 1.00 | 300.63 | 0.75 | 13.1 |
| 19 | Qingfeng | 1.09 | 303.66 | 0.80 | 2.1 |
| 20 | Qingniwan | 0.90 | 305.02 | 0.85 | 12.3 |
| 21 | Shengxiancun | 0.86 | 301.01 | 0.76 | 30.4 |
| 22 | Sheqi | 1.13 | 306.95 | 0.88 | 5.9 |
| 23 | Shuhe | 0.89 | 300.63 | 0.86 | 4.6 |
| 24 | Taikou | 0.73 | 305.02 | 0.81 | 1.2 |
| 25 | Tiesuoguan | 0.85 | 300.63 | 0.86 | 22.1 |
| 26 | Wanyugou | 0.75 | 300.93 | 0.86 | 5.8 |
| 27 | Wuguan | 1.09 | 302.08 | 0.82 | 6.7 |
| 28 | Xianhekou | 0.67 | 302.08 | 0.81 | 13.2 |
| 29 | Xinzhou | 0.69 | 303.13 | 0.82 | 3.8 |
| 30 | Youshuijie | 0.65 | 300.31 | 0.86 | 10.6 |
| Ave. | 0.91 | 311.91 | 0.82 | 10.7 | |
| Min. | 0.36 | 300.31 | 0.74 | 1.2 | |
| Max. | 1.23 | 512.38 | 0.88 | 30.4 | |
| No. | Watershed | Number (Times) | E[D] (Month) | E[S] (-) | E[I] (-/Month) | E[L] (Month) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SRI | SDI | RB(%) | SRI | SDI | RB(%) | SRI | SDI | RB(%) | SRI | SDI | RB(%) | SRI | SDI | RB(%) | ||
| 1 | Baitugang | 50 | 53 | −5.6 | 3.42 | 3.29 | 4.0 | 2.53 | 2.34 | 8.0 | 0.53 | 0.67 | −21.3 | 6.42 | 6.04 | 6.3 |
| 2 | Baiyan | 44 | 48 | −8.8 | 3.70 | 3.23 | 14.6 | 2.69 | 2.40 | 11.9 | 0.51 | 0.64 | −20.6 | 6.75 | 6.13 | 10.0 |
| 3 | Bandian | 42 | 48 | −12.9 | 4.76 | 4.94 | −3.6 | 3.81 | 4.28 | −10.9 | 0.42 | 0.50 | −15.9 | 9.71 | 8.56 | 13.5 |
| 4 | Caodian | 46 | 58 | −20.2 | 4.22 | 3.15 | 33.7 | 2.97 | 2.86 | 3.8 | 0.54 | 0.55 | −0.5 | 6.93 | 5.53 | 25.5 |
| 5 | Chadianzi | 40 | 40 | 0.0 | 3.48 | 3.68 | −5.6 | 2.81 | 2.75 | 2.2 | 0.61 | 0.59 | 3.8 | 6.50 | 6.83 | −4.8 |
| 6 | Chaiping | 38 | 34 | 11.8 | 3.82 | 4.09 | −6.7 | 2.65 | 3.03 | −12.3 | 0.60 | 0.62 | −4.1 | 6.53 | 7.18 | −9.1 |
| 7 | Dazhuhe | 52 | 52 | 0.0 | 2.90 | 2.70 | 7.5 | 2.02 | 1.94 | 4.2 | 0.58 | 0.66 | −12.1 | 5.00 | 4.98 | 0.4 |
| 8 | Guihuayuan | 47 | 51 | −7.9 | 3.83 | 2.83 | 35.5 | 2.53 | 2.35 | 7.7 | 0.58 | 0.71 | −17.7 | 6.38 | 6.03 | 5.9 |
| 9 | Houhui | 49 | 59 | −16.4 | 4.53 | 3.61 | 25.4 | 3.02 | 3.27 | −7.5 | 0.51 | 0.61 | −16.3 | 7.78 | 6.48 | 20.0 |
| 10 | Huayuan | 41 | 44 | −7.7 | 3.85 | 3.38 | 14.1 | 2.88 | 3.05 | −5.7 | 0.52 | 0.50 | 4.3 | 6.59 | 6.30 | 4.6 |
| 11 | Jiajiafang | 44 | 61 | −27.3 | 4.32 | 3.21 | 34.4 | 3.19 | 3.01 | 5.8 | 0.48 | 0.53 | −8.9 | 8.02 | 5.90 | 36.1 |
| 12 | Jiangwan | 43 | 44 | −3.2 | 4.60 | 4.07 | 13.1 | 3.39 | 2.95 | 15.1 | 0.48 | 0.51 | −5.6 | 8.49 | 8.21 | 3.4 |
| 13 | Kouzihe | 46 | 53 | −13.1 | 4.02 | 3.67 | 9.5 | 2.73 | 2.97 | −8.1 | 0.49 | 0.53 | −8.3 | 6.96 | 6.02 | 15.5 |
| 14 | Lianghekou | 34 | 49 | −30.8 | 4.18 | 2.70 | 54.6 | 3.32 | 2.89 | 15.0 | 0.61 | 0.77 | −20.3 | 7.82 | 5.53 | 41.5 |
| 15 | Miping | 30 | 35 | −14.2 | 4.67 | 4.10 | 13.9 | 3.63 | 4.02 | −9.6 | 0.51 | 0.57 | −11.3 | 8.90 | 7.77 | 14.5 |
| 16 | Nankuanping | 39 | 37 | 5.4 | 4.49 | 4.48 | 0.1 | 3.07 | 3.32 | −7.5 | 0.51 | 0.56 | −9.9 | 7.59 | 7.89 | −3.8 |
| 17 | Nanshahe | 50 | 48 | 4.2 | 2.78 | 2.81 | −1.1 | 2.25 | 2.30 | −2.4 | 0.69 | 0.72 | −5.0 | 5.46 | 5.69 | −4.0 |
| 18 | Pingshi | 40 | 51 | −21.7 | 5.08 | 3.79 | 34.0 | 3.57 | 3.59 | −0.5 | 0.48 | 0.57 | −14.9 | 8.78 | 6.99 | 25.6 |
| 19 | Qingfeng | 34 | 49 | −30.8 | 4.79 | 3.21 | 49.3 | 3.78 | 3.42 | 10.6 | 0.53 | 0.63 | −16.9 | 9.18 | 6.50 | 41.1 |
| 20 | Qingniwan | 42 | 41 | 3.3 | 4.21 | 3.93 | 7.3 | 2.86 | 2.85 | 0.4 | 0.58 | 0.62 | −5.6 | 7.05 | 7.15 | −1.5 |
| 21 | Shengxiancun | 51 | 62 | −18.3 | 3.25 | 2.70 | 20.6 | 2.63 | 2.68 | −1.7 | 0.68 | 0.67 | 1.8 | 6.47 | 5.32 | 21.7 |
| 22 | Sheqi | 29 | 39 | −25.2 | 5.52 | 4.02 | 37.2 | 3.87 | 3.57 | 8.3 | 0.48 | 0.50 | −4.7 | 9.41 | 7.32 | 28.6 |
| 23 | Shuhe | 31 | 32 | −3.6 | 4.77 | 3.83 | 24.6 | 3.36 | 3.09 | 8.9 | 0.48 | 0.69 | −29.9 | 7.94 | 7.59 | 4.6 |
| 24 | Taikou | 46 | 48 | −4.6 | 3.83 | 2.97 | 28.7 | 2.52 | 2.34 | 7.7 | 0.54 | 0.72 | −25.5 | 6.43 | 6.07 | 6.0 |
| 25 | Tiesuoguan | 53 | 51 | 3.9 | 3.02 | 3.09 | −2.4 | 2.19 | 2.28 | −3.9 | 0.60 | 0.67 | −10.3 | 5.36 | 5.59 | −4.1 |
| 26 | Wanyugou | 49 | 52 | −5.8 | 3.43 | 2.85 | 20.3 | 2.40 | 2.87 | −16.4 | 0.56 | 0.70 | −19.9 | 6.06 | 5.65 | 7.3 |
| 27 | Wuguan | 42 | 52 | −19.2 | 4.62 | 3.74 | 23.6 | 3.51 | 3.62 | −3.0 | 0.49 | 0.59 | −18.0 | 8.67 | 7.05 | 22.9 |
| 28 | Xianhekou | 45 | 49 | −8.5 | 3.38 | 2.82 | 19.8 | 2.63 | 2.97 | −11.5 | 0.68 | 0.68 | 0.0 | 6.31 | 5.75 | 9.7 |
| 29 | Xinzhou | 50 | 55 | −8.8 | 3.38 | 2.72 | 24.3 | 2.45 | 2.14 | 14.1 | 0.62 | 0.72 | −14.1 | 6.02 | 5.61 | 7.3 |
| 30 | Youshuijie | 47 | 50 | −6.2 | 3.98 | 3.57 | 11.4 | 2.98 | 2.63 | 13.5 | 0.64 | 0.63 | 1.5 | 7.28 | 6.88 | 5.8 |
| Ave. | 43.13 | 48.19 | −9.7 | 4.03 | 3.44 | 18.1 | 2.94 | 2.93 | 1.2 | 0.55 | 0.62 | −10.9 | 7.23 | 6.48 | 11.7 | |
| Min. | 29 | 32 | −30.8 | 2.78 | 2.70 | −6.7 | 2.02 | 1.94 | −16.4 | 0.42 | 0.50 | −29.9 | 5.00 | 4.98 | −9.1 | |
| Max. | 53 | 62 | 11.8 | 5.52 | 4.94 | 54.6 | 3.87 | 4.28 | 15.1 | 0.69 | 0.77 | 4.3 | 9.71 | 8.56 | 41.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, X.; Guo, S.; Chen, G.; Guo, N.; Jiang, C. A Modified Two-Parameter Monthly Water Balance Model for Runoff Simulation to Assess Hydrological Drought. Water 2022, 14, 3715. https://doi.org/10.3390/w14223715
Hong X, Guo S, Chen G, Guo N, Jiang C. A Modified Two-Parameter Monthly Water Balance Model for Runoff Simulation to Assess Hydrological Drought. Water. 2022; 14(22):3715. https://doi.org/10.3390/w14223715
Chicago/Turabian StyleHong, Xingjun, Shenglian Guo, Guiya Chen, Na Guo, and Cong Jiang. 2022. "A Modified Two-Parameter Monthly Water Balance Model for Runoff Simulation to Assess Hydrological Drought" Water 14, no. 22: 3715. https://doi.org/10.3390/w14223715







