Inverse Estimation of Soil Hydraulic Parameters in a Landslide Deposit Based on a DE-MC Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Unsaturated Soil Hydrology in Hydro-Mechanical Model
2.2. Differential Evolution Markov Chain (DE-MC)
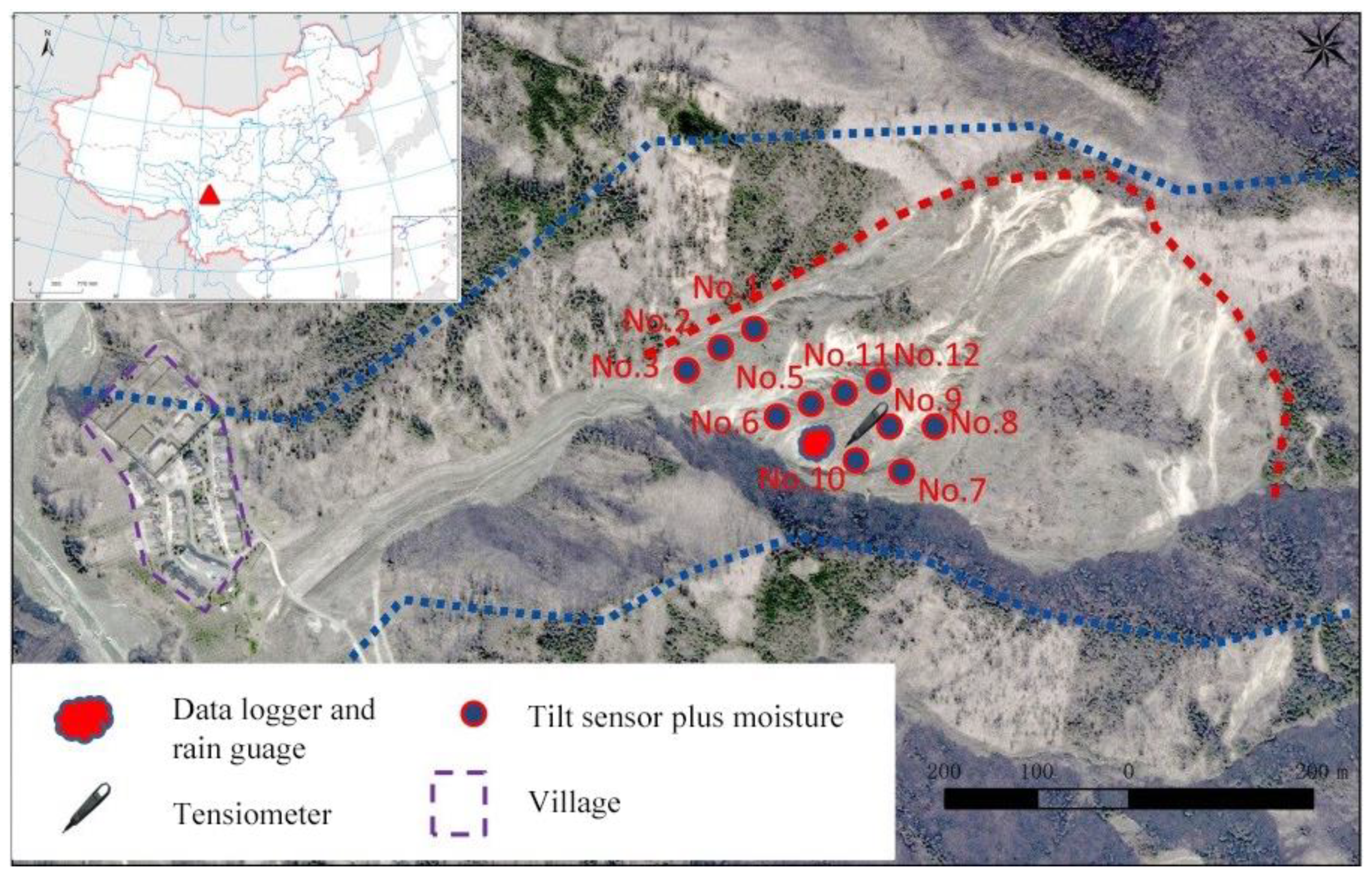
2.3. Study Area
2.4. Modeling Strategies
3. Results
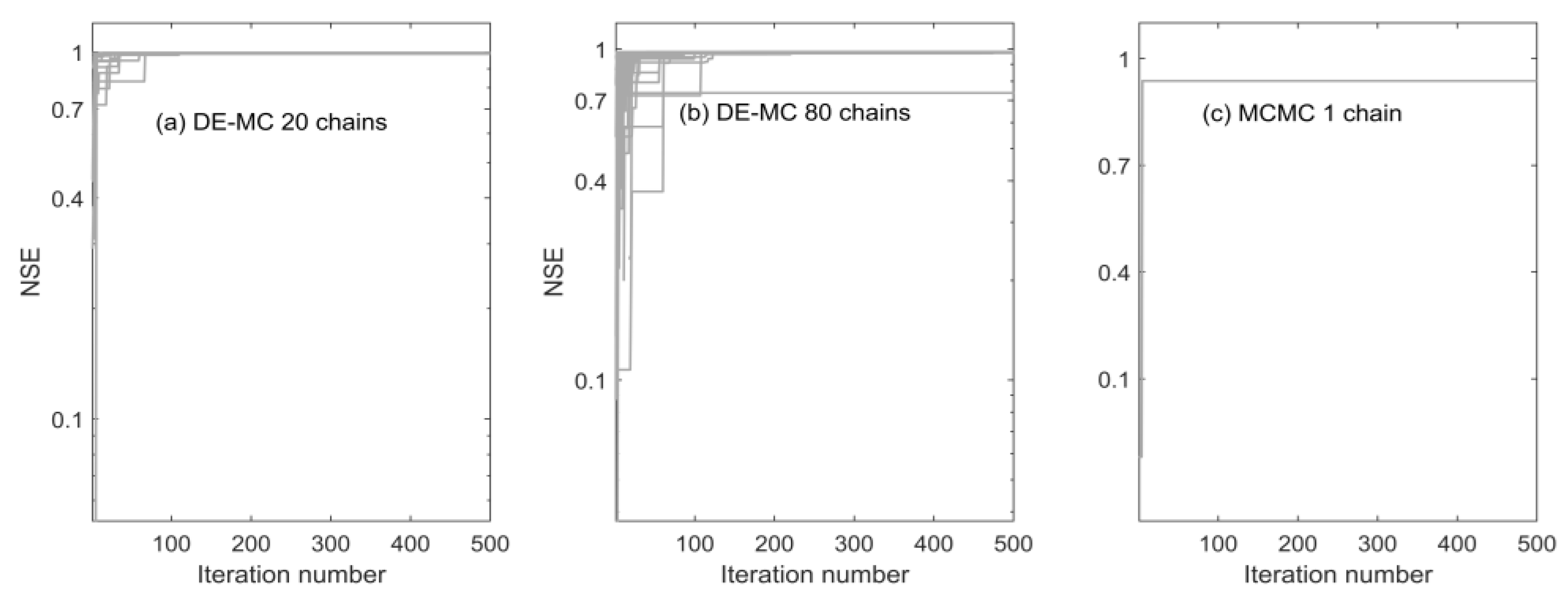
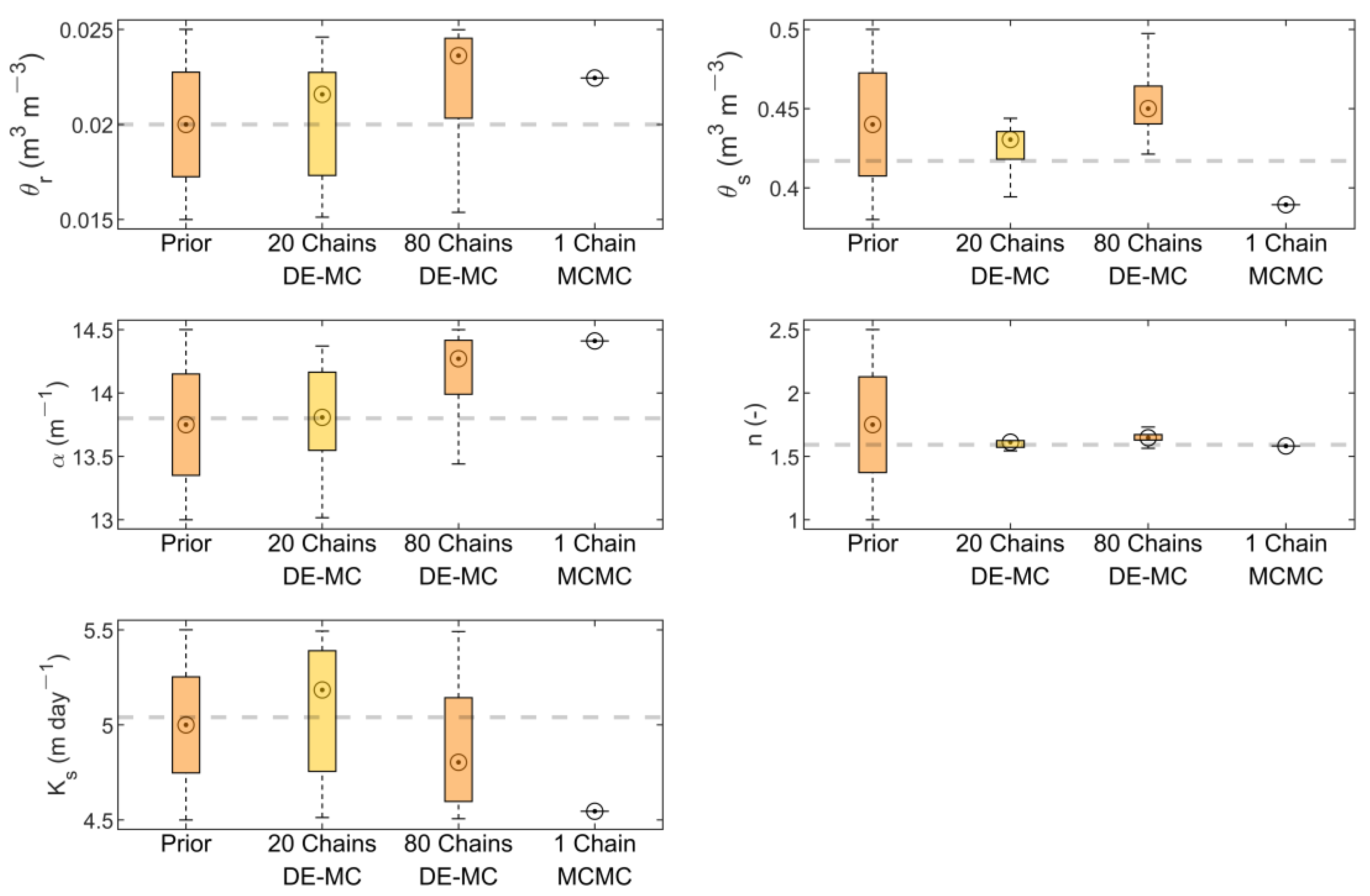
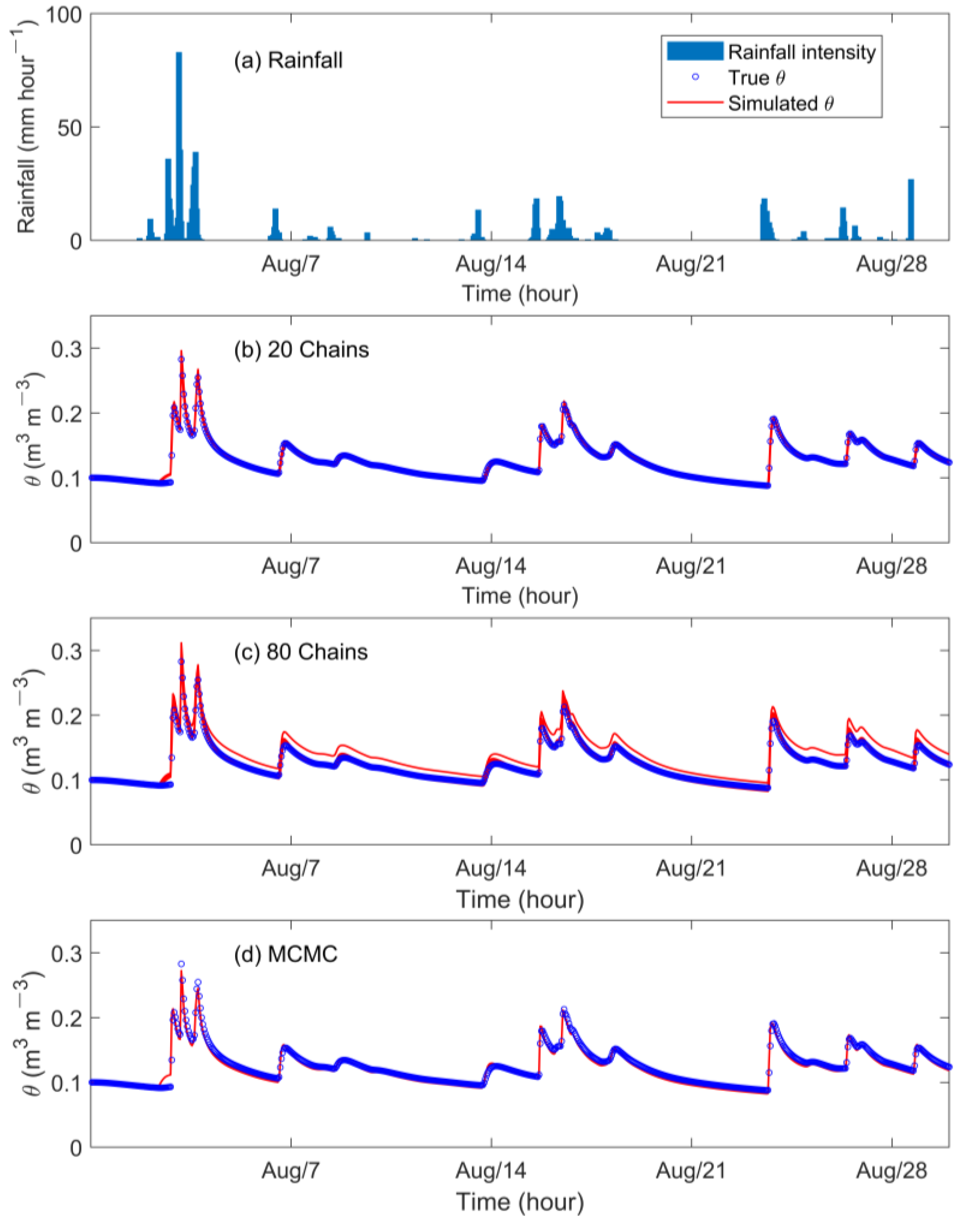
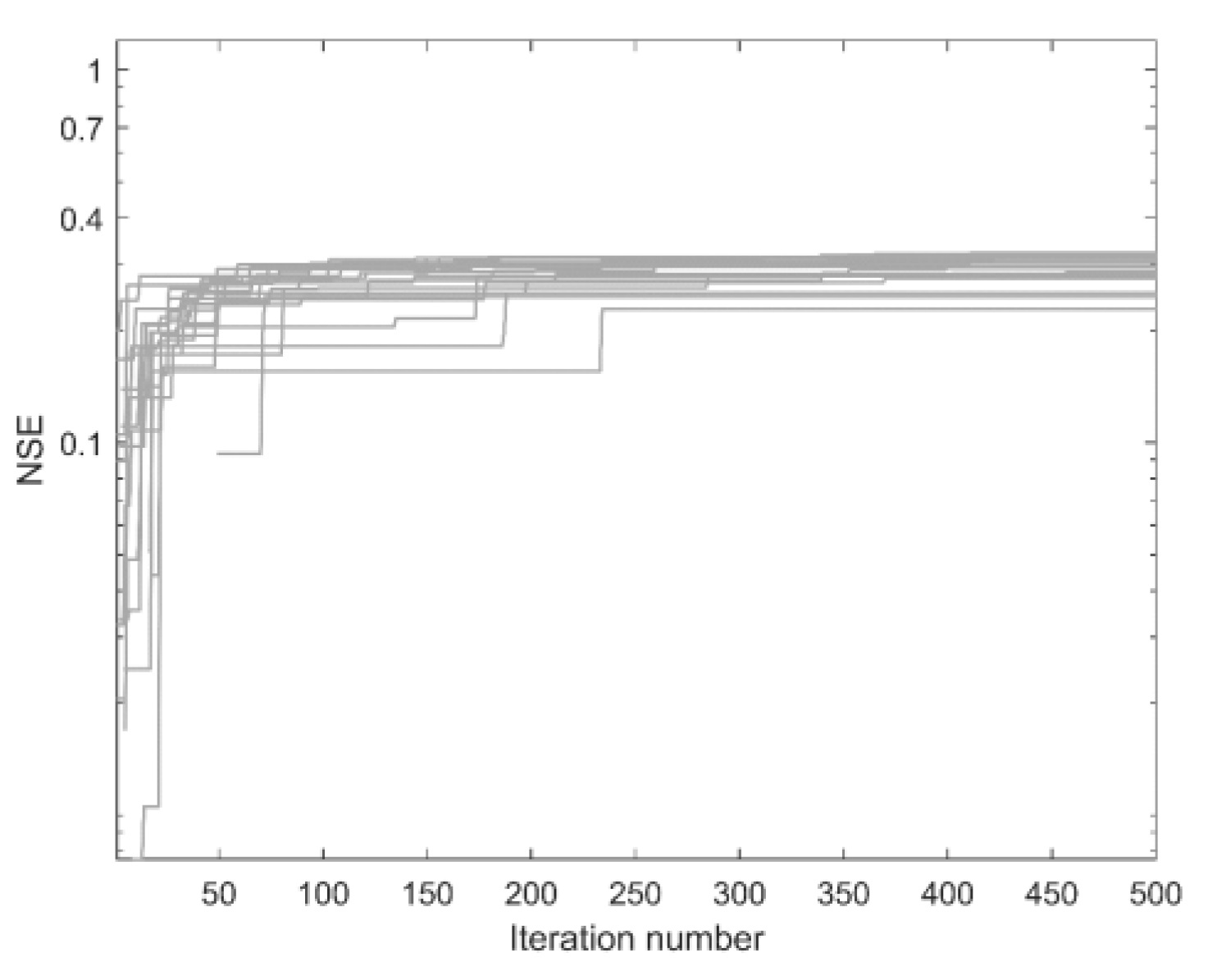
3.1. Synthetic Experiment
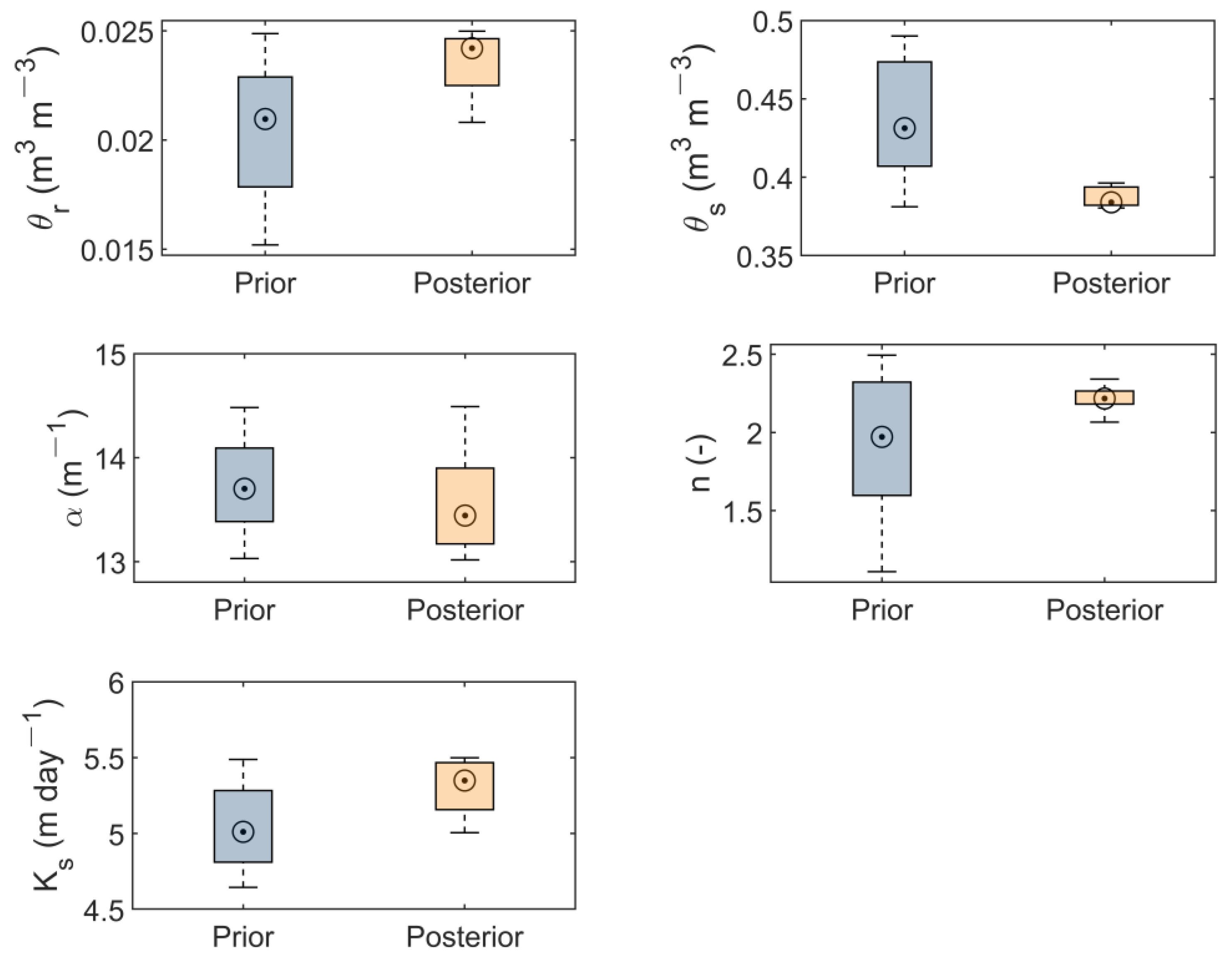
3.2. Real Case Simulation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Zhao, W.; Wang, L.; Liu, Y.; Liu, Y.; Feng, Q. Relationship between soil water content and soil particle size on typical slopes of the loess plateau during a drought year. Sci. Total Environ. 2019, 648, 943–954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. Earth Surf. 2010, 115, F03013. [Google Scholar] [CrossRef]
- Sidle, R.C.; Bogaard, T.A. Dynamic earth system and ecological controls of rainfall-initiated landslides. Earth-Sci. Rev. 2016, 159, 275–291. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y. Bayesian selection of slope hydraulic model and identification of model parameters using monitoring data and subset simulation. Comput. Geotech. 2021, 139, 104428. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, L.; Qiao, J.; Uchimura, T.; Wang, L. Application and verification of a multivariate real-time early warning method for rainfall-induced landslides: Implication for evolution of landslide-generated debris flows. Landslides 2020, 17, 2409–2419. [Google Scholar] [CrossRef] [Green Version]
- Larsen, M.C. Rainfall-triggered landslides, anthropogenic hazards, and mitigation strategies. Adv. Geosci. 2008, 14, 147–153. [Google Scholar] [CrossRef] [Green Version]
- Uyeturk, C.E.; Huvaj, N.; Bayraktaroglu, H.; Huseyinpasaoglu, M. Geotechnical characteristics of residual soils in rainfall-triggered landslides in Rize, Turkey. Eng. Geol. 2020, 264, 105318. [Google Scholar] [CrossRef]
- Görüm, T.; Fidan, S. Spatiotemporal variations of fatal landslides in Turkey. Landslides 2021, 18, 1691–1705. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Conte, E. A simplified analytical method to predict shallow landslides induced by rainfall in unsaturated soils. Water 2022, 14, 3180. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Conte, E. Rainfall threshold for shallow landslide triggering due to rising water table. Water 2022, 14, 2966. [Google Scholar] [CrossRef]
- Shao, W.; Yang, Z.; Ni, J.; Su, Y.; Nie, W.; Ma, X. Comparison of single- and dual-permeability models in simulating the unsaturated hydro-mechanical behavior in a rainfall-triggered landslide. Landslides 2018, 15, 2449–2464. [Google Scholar] [CrossRef]
- Hinds, E.S.; Lu, N.; Mirus, B.B.; Godt, J.W.; Wayllace, A. Evaluation of techniques for mitigating snowmelt infiltration-induced landsliding in a highway embankment. Eng. Geol. 2021, 291, 106240. [Google Scholar] [CrossRef]
- Lewis, R.W.; Ghafouri, H.R. A novel finite element double porosity model for multiphase flow through deformable fractured porous media. Int. J. Numer. Anal. Methods Geomech. 1997, 21, 789–816. [Google Scholar] [CrossRef]
- Chiu, C.F.; Yan, W.M.; Yuen, K.-V. Reliability analysis of soil–water characteristics curve and its application to slope stability analysis. Eng. Geol. 2012, 135–136, 83–91. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A. Effects of variability of unsaturated hydraulic properties on stability of residual soil slopes. In The Unsaturated Soil Mechanics-from Theory to Practice, Proceedings of the 6th Asia Pacific Conference on Unsaturated Soils, Guilin, China, 23–26 October 2015; CRC Press/Balkema: Boca Raton, FL, USA, 2015; pp. 401–406. [Google Scholar]
- Chirico, G.B.; Medina, H.; Romano, N. Uncertainty in predicting soil hydraulic properties at the hillslope scale with indirect methods. J. Hydrol. 2007, 334, 405–422. [Google Scholar] [CrossRef]
- Dong, J.; Steele-Dunne, S.C.; Ochsner, T.E.; van de Giesen, N. Determining soil moisture and soil properties in vegetated areas by assimilating soil temperatures. Water Resour. Res. 2016, 52, 4280–4300. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; Angulo-Jaramillo, R.; Schaap, M.G.; Vandervaere, J.-P.; van Genuchten, M.T. Using an inverse method to estimate the hydraulic properties of crusted soils from tension-disc infiltrometer data. Geoderma 1998, 86, 61–81. [Google Scholar] [CrossRef]
- Zhai, Q.; Rahardjo, H.; Satyanaga, A.; Zhu, Y.; Dai, G.; Zhao, X. Estimation of wetting hydraulic conductivity function for unsaturated sandy soil. Eng. Geol. 2021, 285, 106034. [Google Scholar] [CrossRef]
- Ma, C.; Tang, L.; Chang, W.; Jaffar, M.T.; Zhang, J.; Li, X.; Chang, Q.; Fan, J. Effect of shelterbelt construction on soil water characteristic curves in an extreme arid shifting desert. Water 2022, 14, 1803. [Google Scholar] [CrossRef]
- Minasny, B.; Field, D.J. Estimating soil hydraulic properties and their uncertainty: The use of stochastic simulation in the inverse modelling of the evaporation method. Geoderma 2005, 126, 277–290. [Google Scholar] [CrossRef]
- Scharnagl, B.; Iden, S.C.; Durner, W.; Vereecken, H.; Herbst, M. Inverse modelling of in situ soil water dynamics: Accounting for heteroscedastic, autocorrelated, and non-gaussian distributed residuals. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 2155–2199. [Google Scholar]
- Ines, A.V.M.; Droogers, P. Inverse modelling in estimating soil hydraulic functions: A genetic algorithm approach. Hydrol. Earth Syst. Sci. 2002, 6, 49–66. [Google Scholar] [CrossRef] [Green Version]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; IEEE: Piscataway, NJ, USA, 1995; pp. 39–43. [Google Scholar]
- Dai, Y.; Shangguan, W.; Duan, Q.; Liu, B.; Niu, G. Development of a China dataset of soil hydraulic parameters using pedotransfer functions for land surface modeling. J. Hydrometeorol. 2013, 14, 869–887. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Candela, A.; Noto, L.V.; Aronica, G. Influence of surface roughness in hydrological response of semiarid catchments. J. Hydrol. 2005, 313, 119–131. [Google Scholar] [CrossRef]
- Seifi, A.; Ehteram, M.; Nayebloei, F.; Soroush, F.; Gharabaghi, B.; Torabi Haghighi, A. GLUE uncertainty analysis of hybrid models for predicting hourly soil temperature and application wavelet coherence analysis for correlation with meteorological variables. Soft Comput. 2021, 25, 10723–10748. [Google Scholar] [CrossRef]
- Zhang, D.; Beven, K.; Mermoud, A. A comparison of non-linear least square and GLUE for model calibration and uncertainty estimation for pesticide transport in soils. Adv. Water Resour. 2006, 29, 1924–1933. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov Chain Monte Carlo simulation. Water Resour. Res. 2008, 44, W00B09. [Google Scholar] [CrossRef] [Green Version]
- Liang, F.; Wong, W.H. Real-parameter evolutionary Monte Carlo with applications to Bayesian mixture models. J. Am. Stat. Assoc. 2001, 96, 653–666. [Google Scholar] [CrossRef]
- Du, X.; Du, C.; Radolinski, J.; Wang, Q.; Jian, J. Metropolis-hastings Markov Chain Monte Carlo approach to simulate van genuchten model parameters for soil water retention curve. Water 2022, 14, 1968. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Liu, W.; Luo, X.; Huang, F.; Fu, M. Uncertainty of the soil–water characteristic curve and its effects on slope seepage and stability analysis under conditions of rainfall using the Markov Chain Monte Carlo method. Water 2017, 9, 758. [Google Scholar] [CrossRef] [Green Version]
- Braak, C.J.F.T. A Markov Chain Monte Carlo version of the genetic algorithm differential evolution: Easy Bayesian computing for real parameter spaces. Stat. Comput. 2006, 16, 239–249. [Google Scholar] [CrossRef]
- Ter Braak, C.J.F.; Vrugt, J.A. Differential Evolution Markov Chain with snooker updater and fewer chains. Stat. Comput. 2008, 18, 435–446. [Google Scholar] [CrossRef] [Green Version]
- Smith, T.J.; Marshall, L.A. Bayesian methods in hydrologic modeling: A study of recent advancements in Markov Chain Monte Carlo techniques. Water Resour. Res. 2008, 44, W00B05. [Google Scholar] [CrossRef] [Green Version]
- Carsel, R.F.; Parrish, R.S.; Jones, R.L.; Hanse, J.L.; Lamb, R.L. Characterizing the uncertainty of pesticide leaching in agricultural soils. J. Contam. Hydrol. 1988, 2, 111–124. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]



| Parameter | Synthetic Experiment | Real Case Simulation | |
|---|---|---|---|
| Prior Parameter Ranges | True | Prior Parameter Ranges | |
| 0.015~0.025 | 0.020 | 0.015~0.025 | |
| 0.380~0.500 | 0.417 | 0.350~0.50 | |
| 13.0~14.5 | 13.8 | 13.0~14.5 | |
| 1.000~2.00 | 1.592 | 1.000~2.500 | |
| 4.50~5.50 | 5.04 | 4.50~5.50 | |
| Parameter | Mean Value | Standard Deviation | ||||||
|---|---|---|---|---|---|---|---|---|
| Prior | Posterior | Prior | Posterior | |||||
| DE-MC 20 Chains | DE-MC 80 Chains | MCMC 1 Chain | DE-MC 20 Chains | DE-MC 80 Chains | MCMC 1 Chain | |||
| 0.020 | 0.020 | 0.022 | 0.022 | 0.003 | 0.003 | 0.003 | - | |
| 0.44 | 0.43 | 0.451 | 0.389 | 0.039 | 0.020 | 0.022 | - | |
| 13.75 | 13.814 | 14.189 | 14.41 | 0.476 | 0.413 | 0.264 | - | |
| 1.75 | 1.604 | 1.645 | 1.587 | 0.437 | 0.056 | 0.048 | - | |
| 5.00 | 5.082 | 4.874 | 4.546 | 0.293 | 0.349 | 0.304 | - | |
| Saturated Degree | True | DE-MC 20 Chains | DE-MC 80 Chains | MCMC | |
|---|---|---|---|---|---|
| = 0.2 | 2.039 | 1.854~2.382 | 1.803~2.461 | 2.039 | |
| = 0.5 | 1.324 | 1.251~1.482 | 1.210~1.524 | 1.324 | |
| = 0.8 | 0.808 | 0.783~0.871 | 0.756~0.895 | 0.808 | |
| = 0.2 | −4.268 | −5.110~−3.762 | −5.284~−3.723 | −4.365 | |
| = 0.5 | −1.884 | −2.345~−1.593 | −2.445~−1.576 | −1.957 | |
| = 0.8 | −0.531 | −0.792~−0.357 | −0.855~−0.349 | −0.592 | |
| Parameter | Mean Value | Standard Deviation | ||
|---|---|---|---|---|
| Prior | Posterior | Prior | Posterior | |
| 0.021 | 0.023 | 0.003 | 0.002 | |
| 0.437 | 0.391 | 0.035 | 0.016 | |
| 13.721 | 13.576 | 0.434 | 0.451 | |
| 1.913 | 2.209 | 0.461 | 0.101 | |
| 5.045 | 5.296 | 0.288 | 0.169 | |
| Saturated Degree | Prior | DE-MC 20 Chains | |
|---|---|---|---|
| = 0.2 | 1.296~7.211 | 1.350~1.607 | |
| = 0.5 | 0.975~3.593 | 1.011~1.118 | |
| = 0.8 | 0.701~1.696 | 0.711~0.751 | |
| = 0.2 | −8.435~−2.383 | −3.216~−2.509 | |
| = 0.5 | −4.061~−0.802 | −1.296~−0.888 | |
| = 0.8 | −1.707~−0.093 | −0.199~0.044 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Yan, H.; Shao, W.; Yu, W.; Wei, L.; Yang, Z.; Su, Y.; Kan, G.; Luo, S. Inverse Estimation of Soil Hydraulic Parameters in a Landslide Deposit Based on a DE-MC Approach. Water 2022, 14, 3693. https://doi.org/10.3390/w14223693
Chen S, Yan H, Shao W, Yu W, Wei L, Yang Z, Su Y, Kan G, Luo S. Inverse Estimation of Soil Hydraulic Parameters in a Landslide Deposit Based on a DE-MC Approach. Water. 2022; 14(22):3693. https://doi.org/10.3390/w14223693
Chicago/Turabian StyleChen, Sijie, Haiwen Yan, Wei Shao, Wenjun Yu, Lingna Wei, Zongji Yang, Ye Su, Guangyuan Kan, and Shaohui Luo. 2022. "Inverse Estimation of Soil Hydraulic Parameters in a Landslide Deposit Based on a DE-MC Approach" Water 14, no. 22: 3693. https://doi.org/10.3390/w14223693








