Study of Single Fracture Seepage Characteristics of Fault-Filled Materials Based on CT Technology
Abstract
:1. Introduction
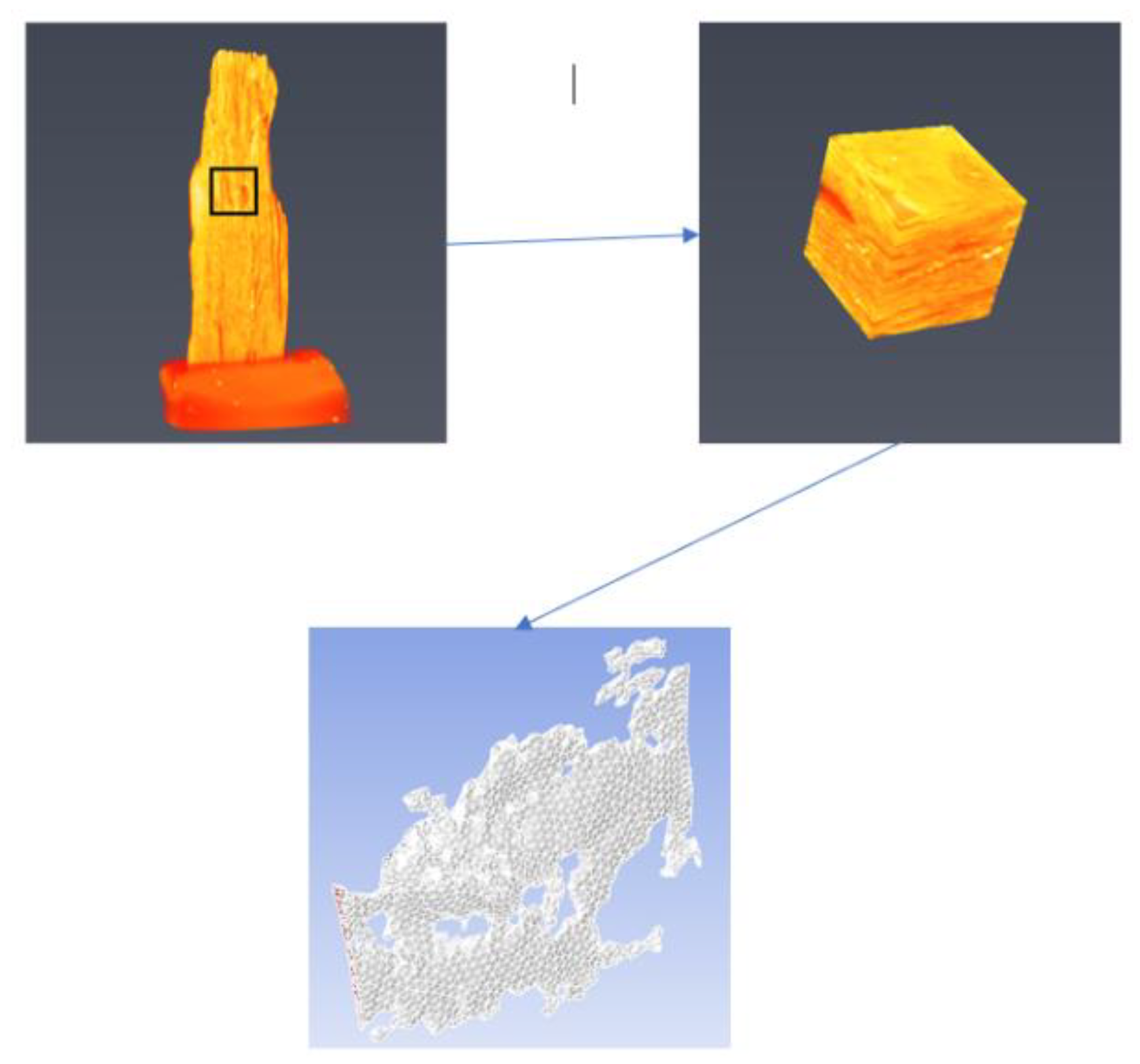
2. CT Scan and 3D Model Reconstruction
2.1. Pre-Processing of CT Scan Images
2.2. Fracture Extraction
3. Seepage Simulation
3.1. Condition Setting
3.2. Solver Model Selection
3.3. Experimental Design of Seepage Simulation
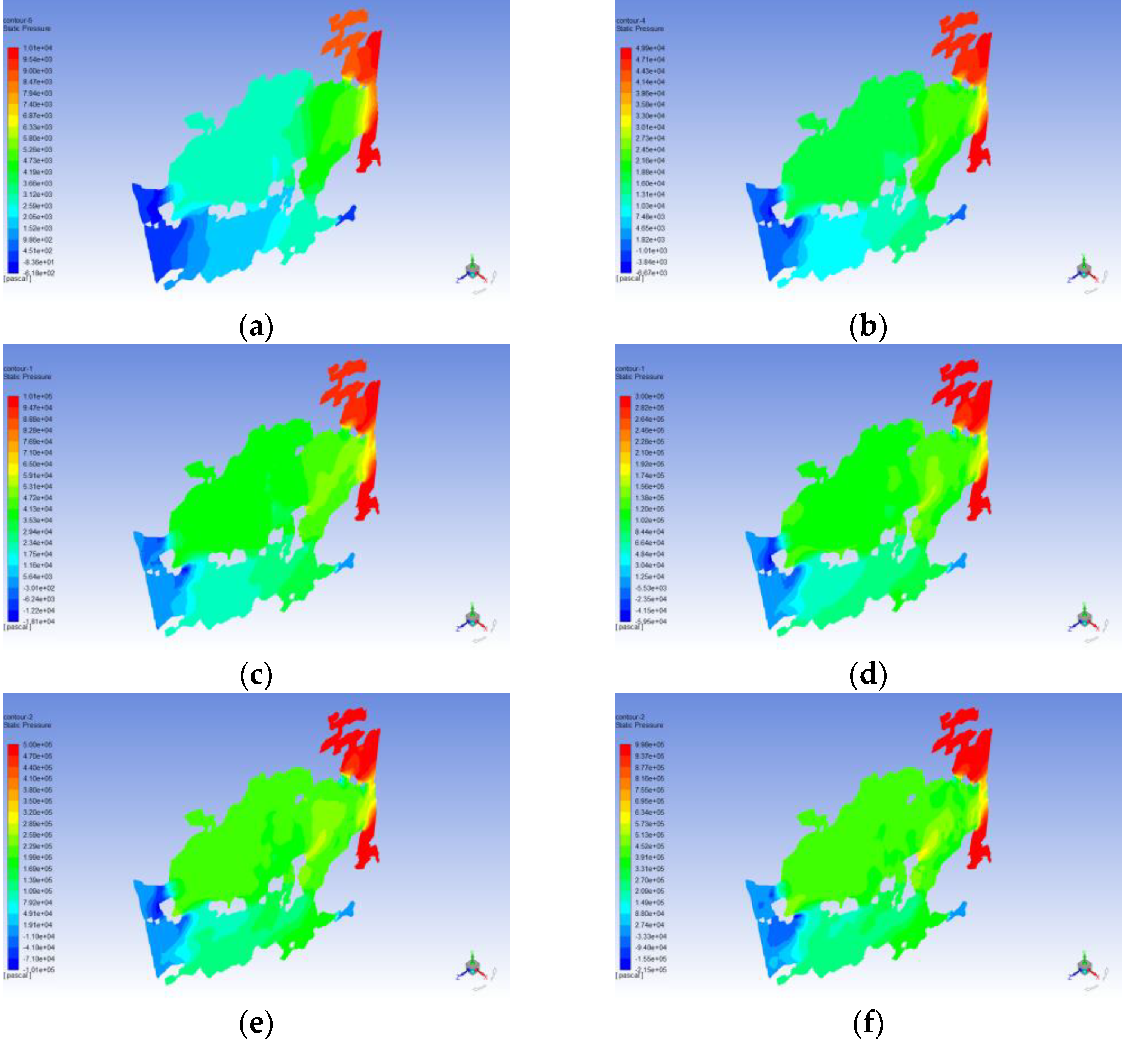
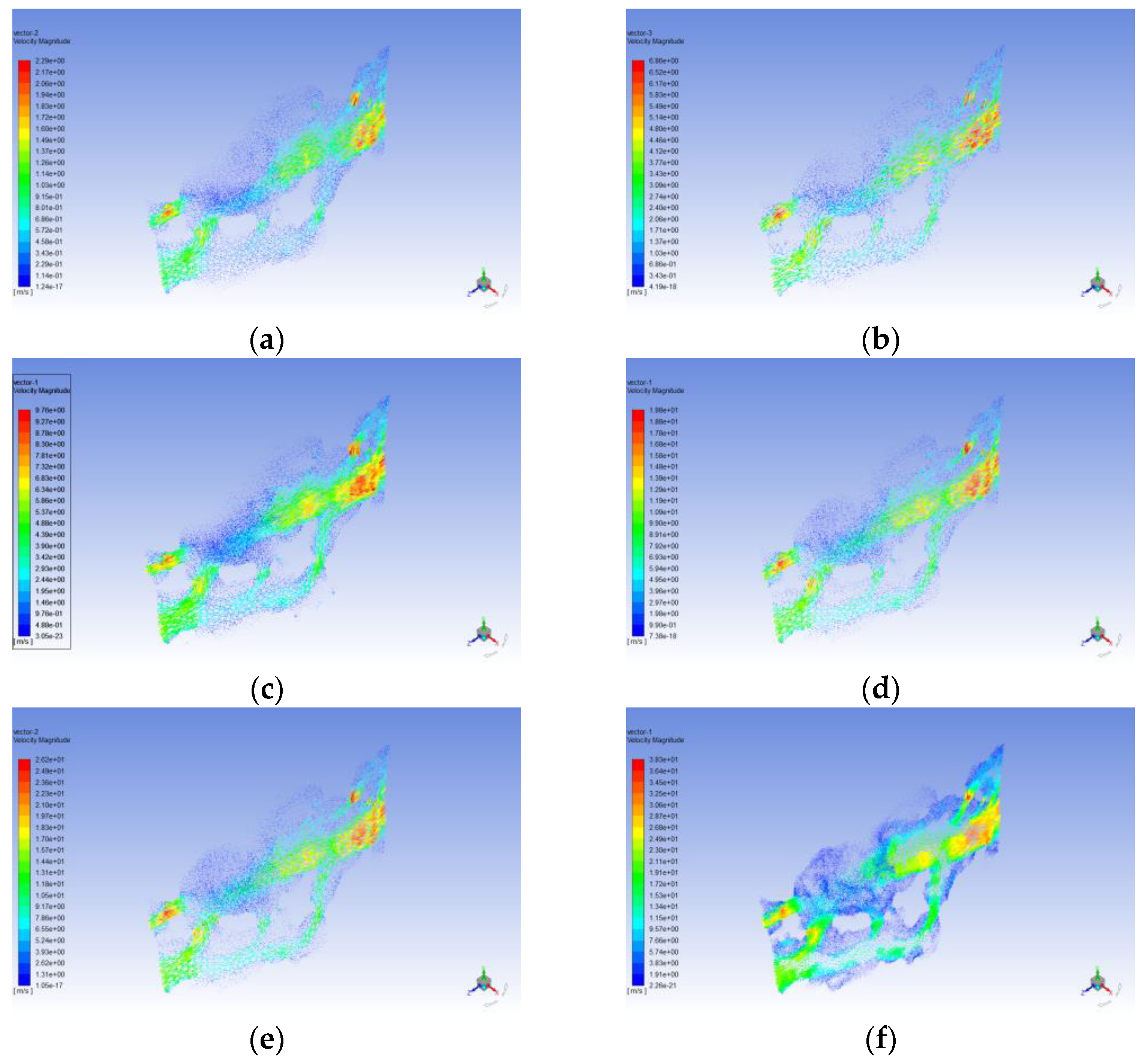
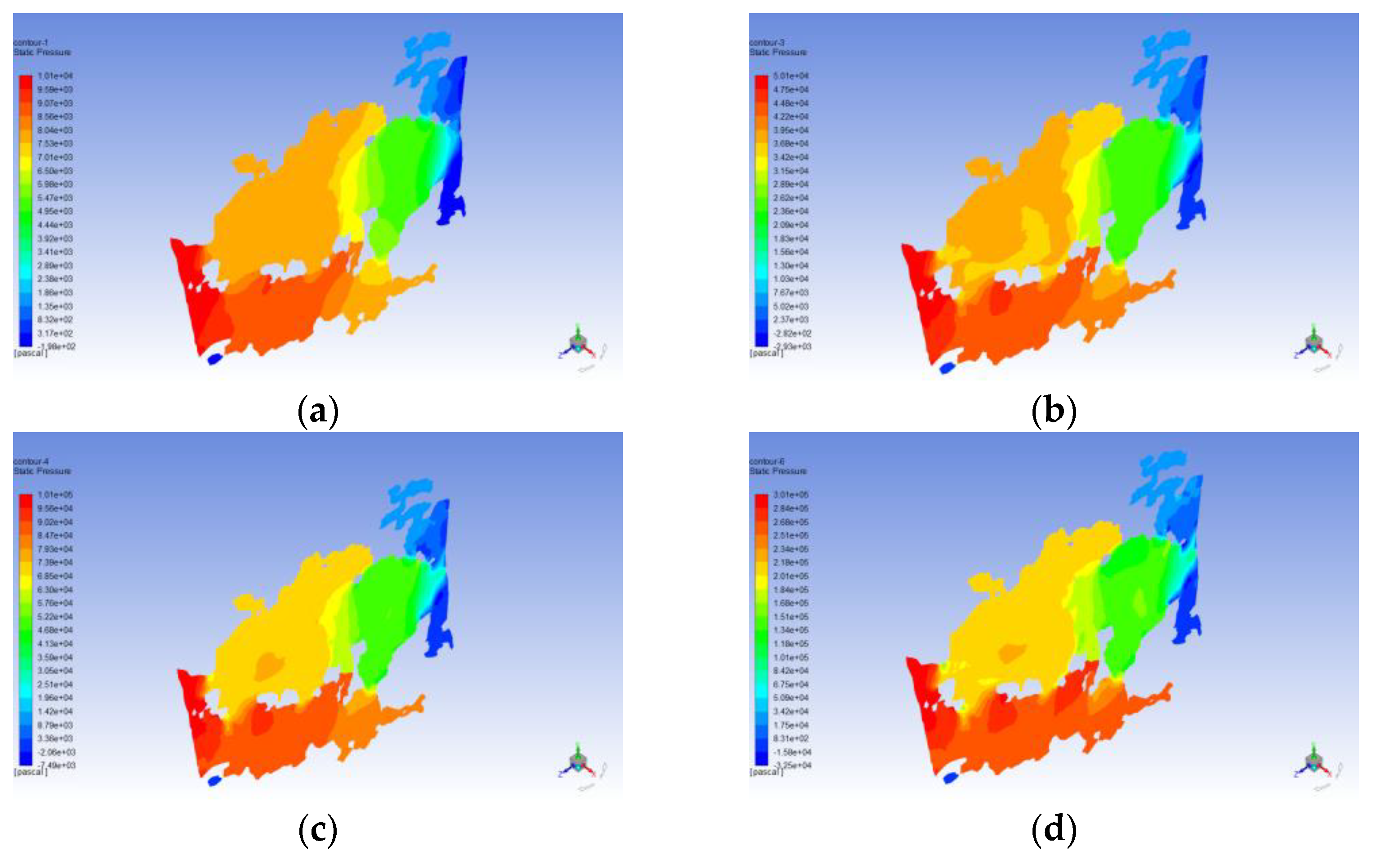
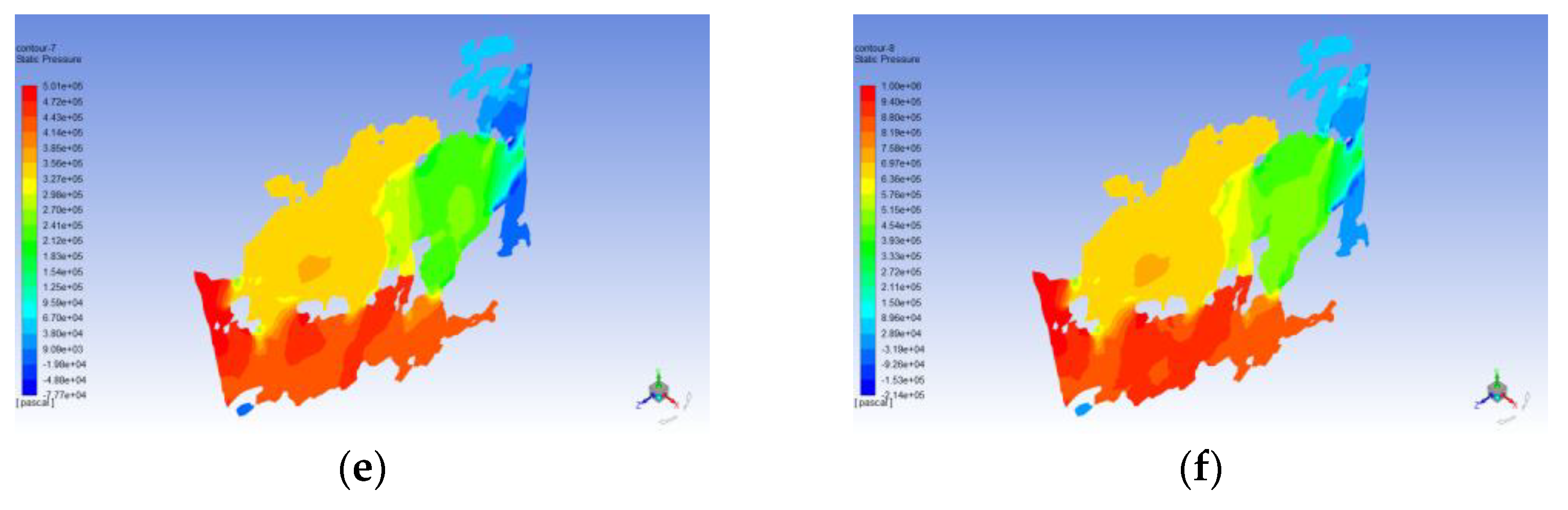
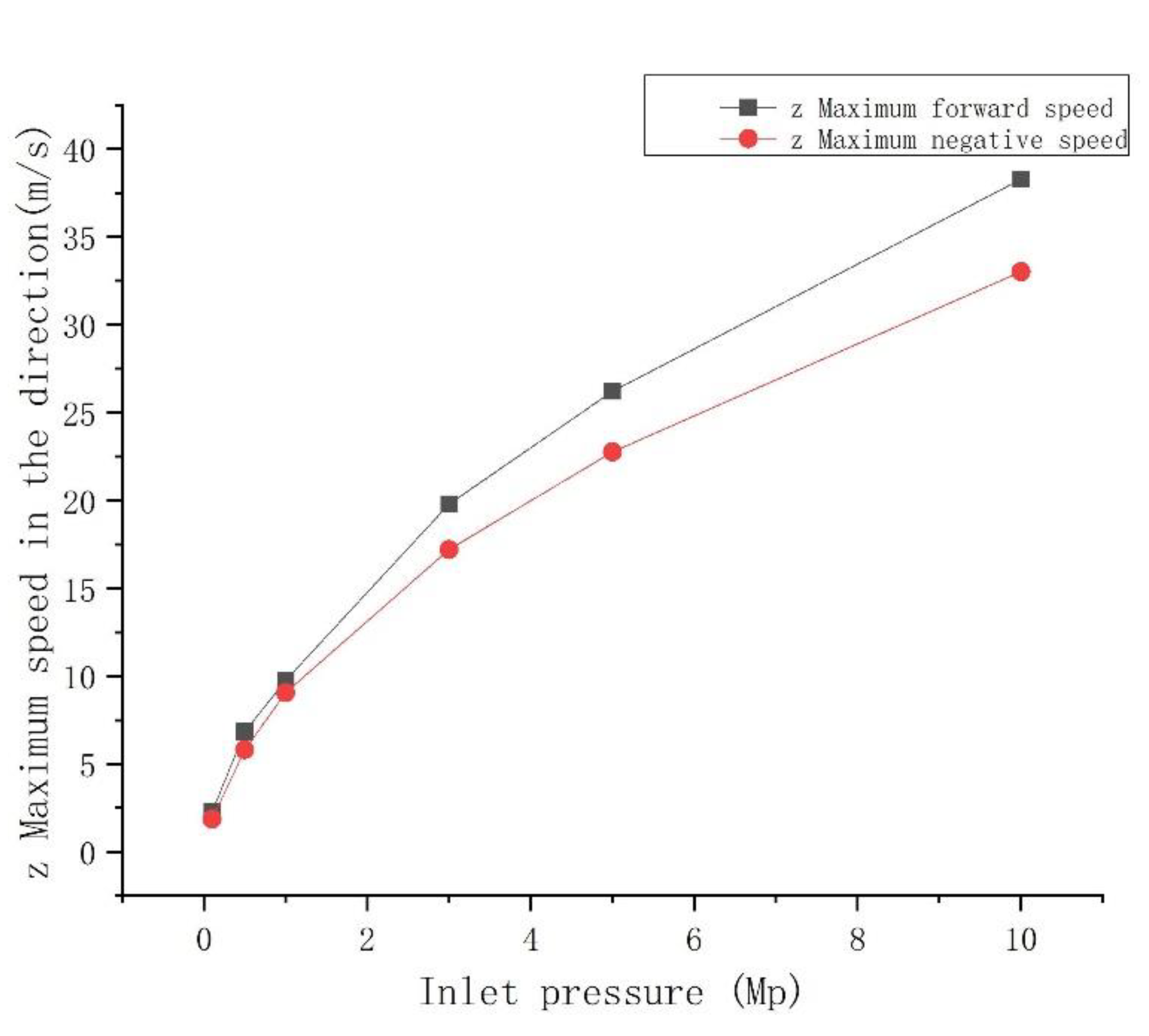
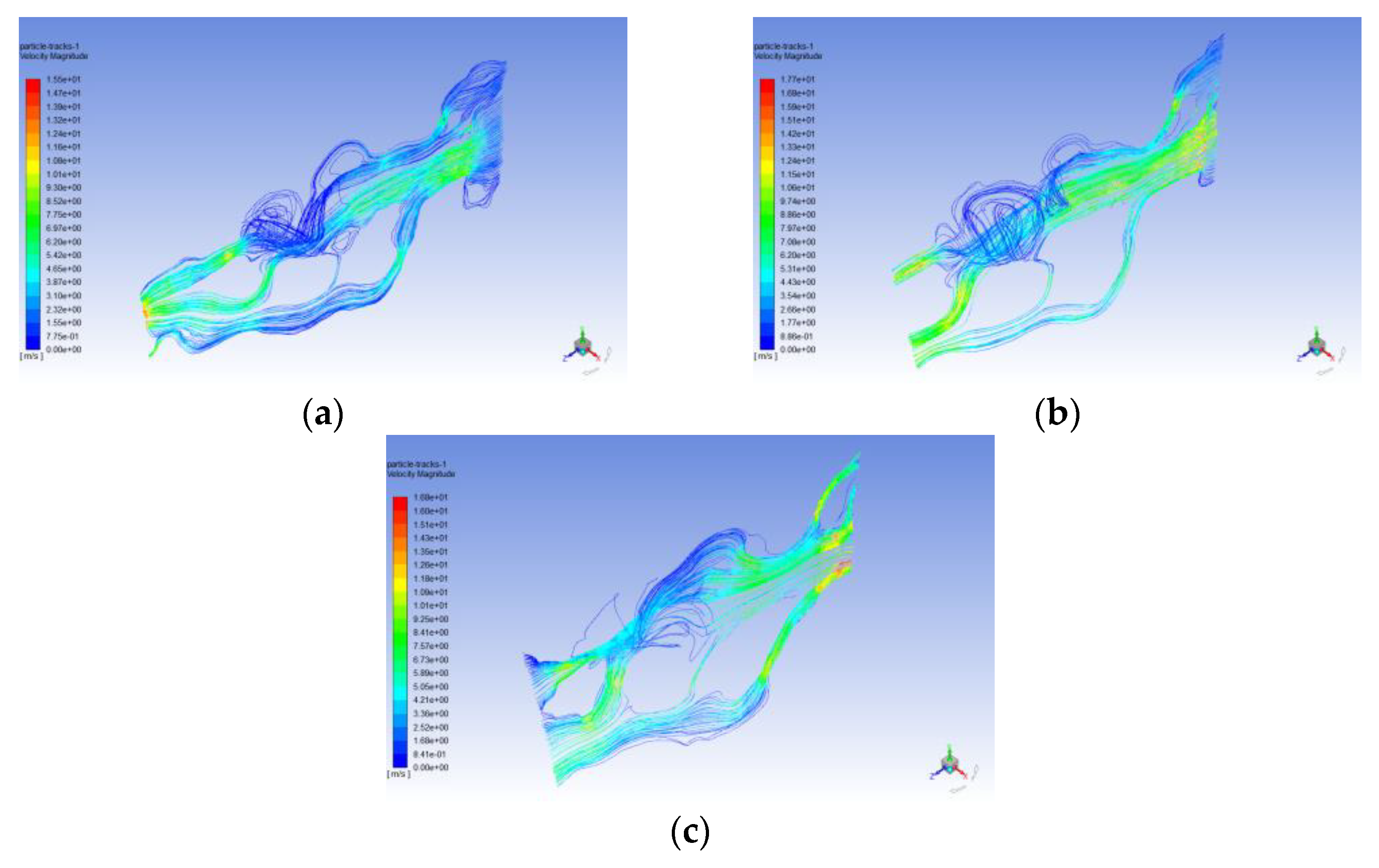
3.4. Seepage Simulation Results and Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, J.; Bo, L.; Chen, J.; Ning, J. Mechanism of Seepage-Stress Fault Water Inrush and Grouting Seal. Arab. J. Geosci. 2020, 13, 4259–4279. [Google Scholar] [CrossRef]
- Qian, Z.; Huang, Z.; Song, J. A case study of water inrush incident through fault zone in China and the corresponding treatment measures. Arab. J. Geosci. 2018, 11, 381. [Google Scholar] [CrossRef]
- Zheng, Z.; Yu, F.; Hao, W.; Jia, R.; Yu, L. The Non-Darcy Characteristics of Fault Water Inrush in Karst Tunnel Based on Flow State Conversion Theory. Therm. Sci. 2021, 25, 4415–4421. [Google Scholar]
- Wang, P.; Xu, J.; Li, C. Similar Simulation Test Study on Permeability Evolution Mechanism of Fault Sliding Fracture Zone. Arab. J. Geosci. 2022, 15, 548. [Google Scholar] [CrossRef]
- Shao, J.; Zhou, F.; Sun, W. Evolution Model of Seepage Characteristics in the Process of Water Inrush in Faults. Geofluids 2019, 2019, 4926768. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Z.; Niu, Z.; Que, X.; Liu, C.; He, Y.; Xie, X. Study on Permeability Characteristics of Rocks with Filling Fractures Under Coupled Stress and Seepage Fields. Water 2020, 12, 2782. [Google Scholar] [CrossRef]
- Shao, J.; Zhang, Q.; Wu, X.; Lei, Y.; Wu, X.; Wang, Z. Investigation on the Water Flow Evolution in a Filled Fracture under Seepage-Induced Erosion. Water 2020, 12, 3188. [Google Scholar] [CrossRef]
- Xue, S.; Yuan, L.; Wang, Y.; Xie, J. Numerical Analyses of the Major Parameters Affecting the Initiation of Outbursts of Coal and Gas. Rock Mech. Rock Eng. 2014, 47, 1505–1510. [Google Scholar] [CrossRef]
- Hao, Z.; Sun, G.; Zhang, G. Mechanism and Inducing Factors of Rockburst Events of Roadways Under Ultrathick Strata. Front. Earth. Sc-Switz. 2022, 10, 860929. [Google Scholar] [CrossRef]
- Zhang, Q.; Jiang, Q.; Zhang, X.; Wang, D. Model test on development characteristics and displacement variation of water and mud inrush on tunnel in fault fracture zone. Nat. Hazards. 2019, 99, 467–492. [Google Scholar] [CrossRef]
- Li, S.; Bu, L.; Shi, S.; Li, L.; Zhou, Z. Prediction for Water Inrush Disaster Source and CFD-Based Design of Evacuation Routes in Karst Tunnel. Int. J. Geomech. 2022, 22, 05022001. [Google Scholar] [CrossRef]
- Salzer, M.; Prill, T.; Spettl, A. Quantitative comparison of segmentation algorithms for FIB-SEM images of porous media. J. Microsc. Oxford 2014, 257, 23–30. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Li, Y.Z.; Qiao, W.G.; Fan, Z.W.; Zhang, S.; Chen, K.; Zhang, L. Water Seepage in Rocks at Micro-Scale. Water 2022, 14, 2827. [Google Scholar] [CrossRef]
- Ju, Y.; Xi, C.; Zheng, J.; Gong, W.; Wu, J.; Wang, S.; Mao, L. Study on three-dimensional immiscible water–Oil two-phase displacement and trapping in deformed pore structures subjected to varying geostress via in situ computed tomography scanning and additively printed models. Int. J. Eng. Sci. 2022, 171, 103615. [Google Scholar] [CrossRef]
- Wang, M.; Yang, S.; Li, J.; Zheng, Z.; Wen, J.; Ma, Q.; Wang, Q.; Chen, H. Cold water-flooding in a heterogeneous high-pour-point oil reservoir using computerized tomography scanning: Characteristics of flow channel and trapped oil distribution. J. Pet. Sci. Eng. 2021, 202, 108594. [Google Scholar] [CrossRef]
- Dong, C.; Nemkumar, B.; Wang, Q.; Sun, W. Investigation on porosity of partly carbonated paste specimens blended with fly ash through dual CT scans. Constr. Build. Mater. 2019, 196, 692–702. [Google Scholar]
- Yang, Y.; Yang, H.; Tao, L.; Yao, J.; Wang, W.; Zhang, K. Microscopic Determination of Remaining Oil Distribution in Sandstones with Different Permeability Scales Using Computed Tomography Scanning. J. Energy Resour. Technol. 2019, 141, 092903. [Google Scholar] [CrossRef]
- Zhou, G.; Zhang, Q.; Bai, R.; Ni, G. Characterization of Coal Micro-Pore Structure and Simulation on the Seepage Rules of Low-Pressure Water Based on CT Scanning Data. Minerals 2016, 6, 78. [Google Scholar] [CrossRef] [Green Version]
- Choi, C.; Lee, Y.; Song, J. Equivalent Pore Channel Model for Fluid Flow in Rock Based on Microscale X-ray CT Imaging. Materials 2020, 13, 2619. [Google Scholar] [CrossRef]
- Qiu, L.; Zhou, G.; Zhang, W.; Han, W. Simulations on the micro-seepage rules of gas and water based on micro-CT/CFD and the related contrastive analysis. Arab. J. Geosci. 2019, 12, 549. [Google Scholar] [CrossRef]
- Liu, W.; Wang, G.; Han, D.; Xu, H.; Chu, X. Accurate characterization of coal pore and fissure structure based on CT 3D reconstruction and NMR. J. Nat. Gas. Sci. Eng. 2021, 96, 104242. [Google Scholar] [CrossRef]
- Zhao, L.; Ni, G.; Wang, Y.; Jiang, H.; Wen, Y.; Dou, H.; Jing, M. Semi-homogeneous model of coal based on 3D reconstruction of CT images and its seepage-deformation characteristics. Energy 2022, 259, 125044. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Song, R. A Pore Scale Flow Simulation of Reconstructed Model Based on the Micro Seepage Experiment. Geofluids 2017, 2017, 7459346. [Google Scholar] [CrossRef]
- Wang, G.; Jiang, C.; Shen, J.; Han, D.; Qin, X. Deformation and water transport behaviors study of heterogenous coal using CT-based 3D simulation. Int. J. Coal. Geol. 2019, 211, 103204. [Google Scholar] [CrossRef]
- Wang, G.; Shen, J.; Liu, S.; Jiang, C.; Qin, X. Three-dimensional modeling and analysis of macro-pore structure of coal using combined X-ray CT imaging and fractal theory. Int. J. Rock. Mech. Min. 2019, 123, 104082. [Google Scholar] [CrossRef]
- Yao, B.; Chen, Z.; Wei, J.; Bai, T.; Liu, S. Predicting Erosion-Induced Water Inrush of Karst Collapse Pillars Using Inverse Velocity Theory. Geofluids 2018, 2018, 2090584. [Google Scholar] [CrossRef] [Green Version]
- Li, L.; Hu, J.; Li, S.; Qin, C.; Liu, H.; Chen, D.; Wang, J. Development of a Novel Triaxial Rock Testing Method Based on Biaxial Test Apparatus and Its Application. Rock. Mech. Rock. Eng. 2021, 54, 1597–1607. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Yu, B. On Full-Tensor Permeabilities of Porous Media from Numerical Solutions of the Navier-Stokes Equation. Adv. Mech. Eng. 2013, 5, 137086. [Google Scholar] [CrossRef] [Green Version]
- Shi, R.; Lin, J.; Yang, H. Distribution of Nanoparticles in a Turbulent Taylor–Couette Flow Considering Particle Coagulation and Breakage. Processes 2021, 9, 1789. [Google Scholar] [CrossRef]
- Zou, L.; Jing, L.; Cvetkovic, V. Modeling of flow and mixing in 3D rough-walled rock fracture intersections. Adv. Water Resour. 2017, 107, 1–9. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Wang, S.; Dong, F.; Xue, Y. Study of Single Fracture Seepage Characteristics of Fault-Filled Materials Based on CT Technology. Water 2022, 14, 3679. https://doi.org/10.3390/w14223679
Sun W, Wang S, Dong F, Xue Y. Study of Single Fracture Seepage Characteristics of Fault-Filled Materials Based on CT Technology. Water. 2022; 14(22):3679. https://doi.org/10.3390/w14223679
Chicago/Turabian StyleSun, Wenbin, Shaoyu Wang, Faxu Dong, and Yandong Xue. 2022. "Study of Single Fracture Seepage Characteristics of Fault-Filled Materials Based on CT Technology" Water 14, no. 22: 3679. https://doi.org/10.3390/w14223679




