SPI-Based Drought Classification in Italy: Influence of Different Probability Distribution Functions
Abstract
:1. Introduction
2. SPI Definition and Background
- compute the cumulative precipitation amounts for each month, with , using the time scale;
- fit the Gamma distribution to each calendar months, with the Maximum Likelihood Estimation (MLE) method;
- estimate the probability associated to each precipitation value;
- compute the SPI values by inverting the probability evaluated with the Gamma distribution with the standard normal function.
3. Case Study and Data
3.1. The Italian Climate Based on Köppen-Geiger
3.2. Daily Rainfall Data
3.3. Monthly Rainfall Main Statistics
4. Methodology
4.1. Tested Probability Distributions
4.2. Quantifying the Differences between the SPI Estimation Approaches
4.3. Test of Normality: The Shapiro-Wilk Test
- Shapiro-Wilk statistic () lower than 0.96;
- p-value associated to lower than 0.10;
- absolute value of the SPI median greater than 0.05;
4.4. Critical Drought Intensity-Duration-Frequency (IDF) Curves
- SPI estimation for each time scale to distinguish dry and wet periods and to identify drought events;
- determination of the critical drought severity for all the identified drought events;
- frequency analysis of critical drought severity with the identification of the best fit probability distribution function to describe each sample. Particularly, here we used the first two Extreme Value Distribution functions, that are, the Gumbel and the Fréchet, whose parameters are determined with the MSEN method, which also aim at defining the best fitting one;
- calculation of severity and/or intensity of critical drought of a given duration for a fixed return period from the best fit probability distribution (previously identified at point iii);
- drought intensity can be expressed, for each return period, by using a linear regression line: , where is the duration (which varies between 1 month and the maximum observed), while and are coefficients determinable with curve fitting.
5. Results
5.1. Fitting Performance
5.2. Comparison of the SPI Values Estimated with the Two Different Approaches
5.3. Drought Characteristics Comparison
5.4. Normality Test
5.5. Critical Drought IDF Curves
6. Discussion and Conclusions
- The Lognormal distribution resulted to be the best fit model to describe almost all the monthly precipitation samples, followed by the Weibull (for 1-month scale) and the Gamma. The Normal distribution, as expected, resulted as the best fitted for a very low percentage of stations, confirming its poor ability in modelling samples with a positive skewness;
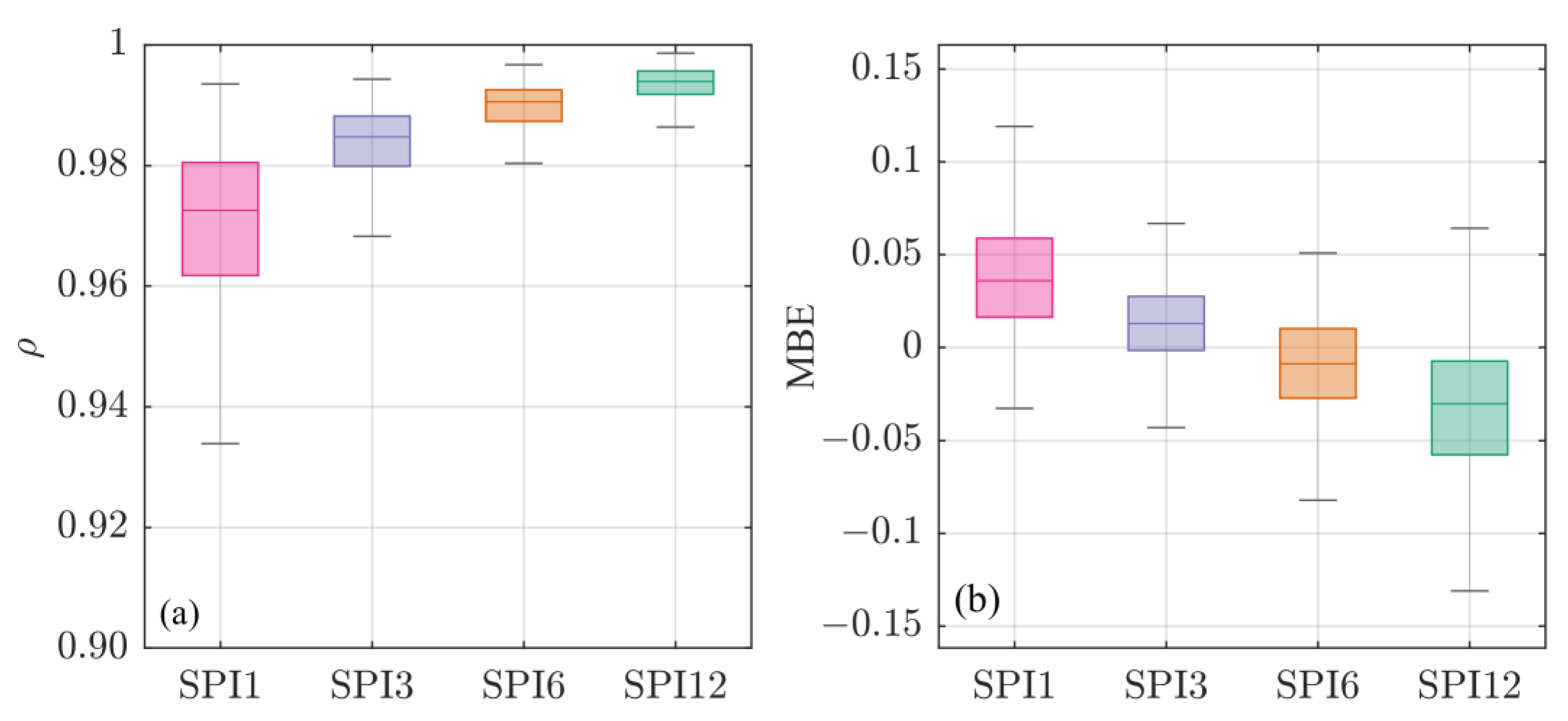
- the Pearson Correlation Coefficient ( evaluated on the entire SPI signal, showed an almost perfect agreement between the SPI signals estimated by the two tested approaches for 12-months time scale. Median values decrease by reducing the SPI’s time scale till 0.97 for SPI1 (Figure 2a);
- the Mean Bias Error (MBE) indicated an opposite behaviour for lower and higher SPI’s time scale. Indeed, for time scales up to 3-months, the BFA presented more severe SPI values than the SA, while the opposite was observed for 6- and 12-months scales;
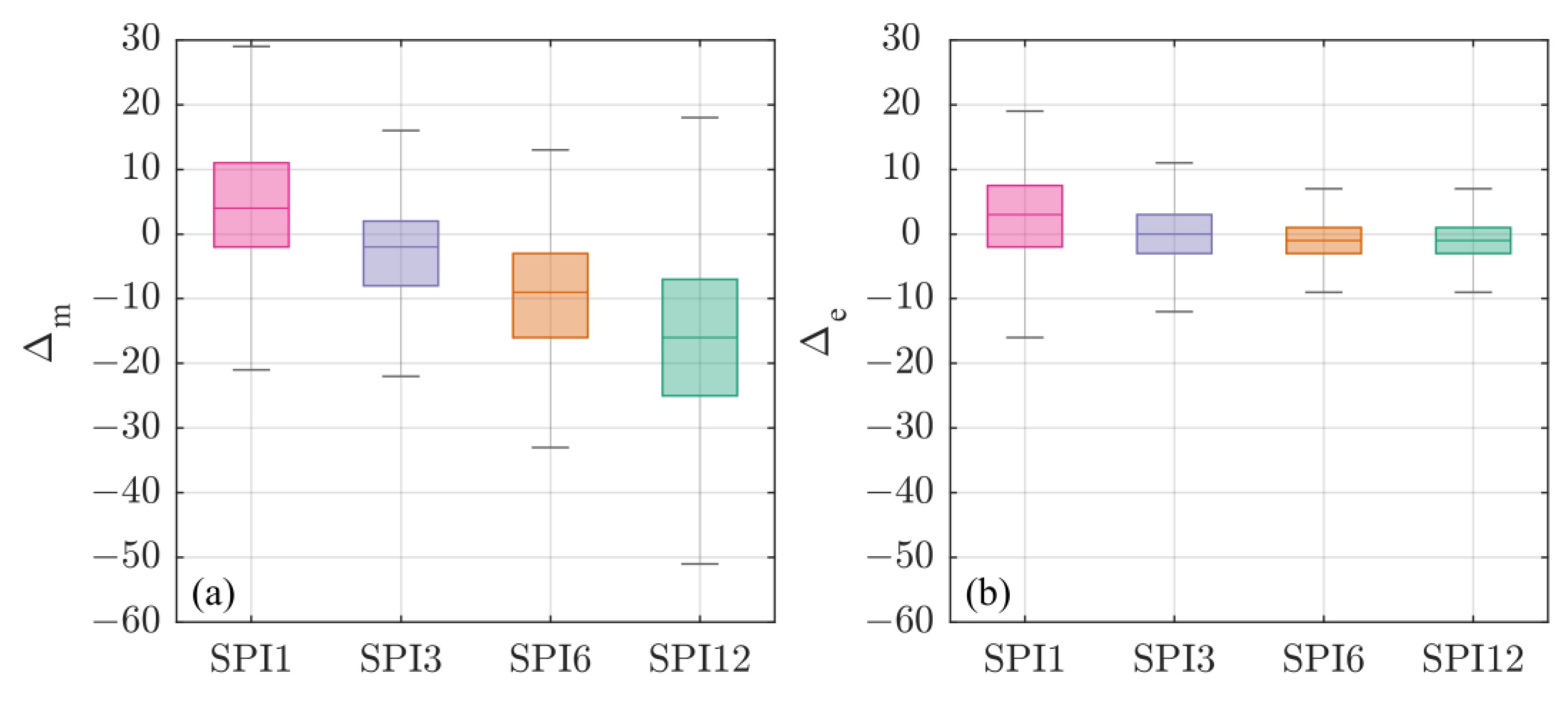
- by highlighting the differences between the two approaches in detecting both wet and dry periods, the Relative Error (RE) followed the behaviour of the MBE: the BFA tends to detect more extreme conditions than the SA for lower scales (i.e., SPI1 and SPI3), and vice versa for SPI6 and SPI12;
- the same patterns emerged from the analysis of the entire SPI signal are reflected on the analysis of drought events (i.e., SPI ≤ −1). Generally, the SA under-estimates all the drought characteristics (i.e., number of events and number of drought months (Figure 4), duration, severity and interarrival time (Table 5)) for small time scales (up to 3-months), while for longer time scale over-estimates the same characteristics. Clearly, we consider as a benchmark the BFA, since it is built to provide the best model to describe the empirical samples;
- the use of the BFA did not solve the SPI non-normality issue, indeed the percentage of non-normal SPIs is higher than the SA for all the months and all the time scales;
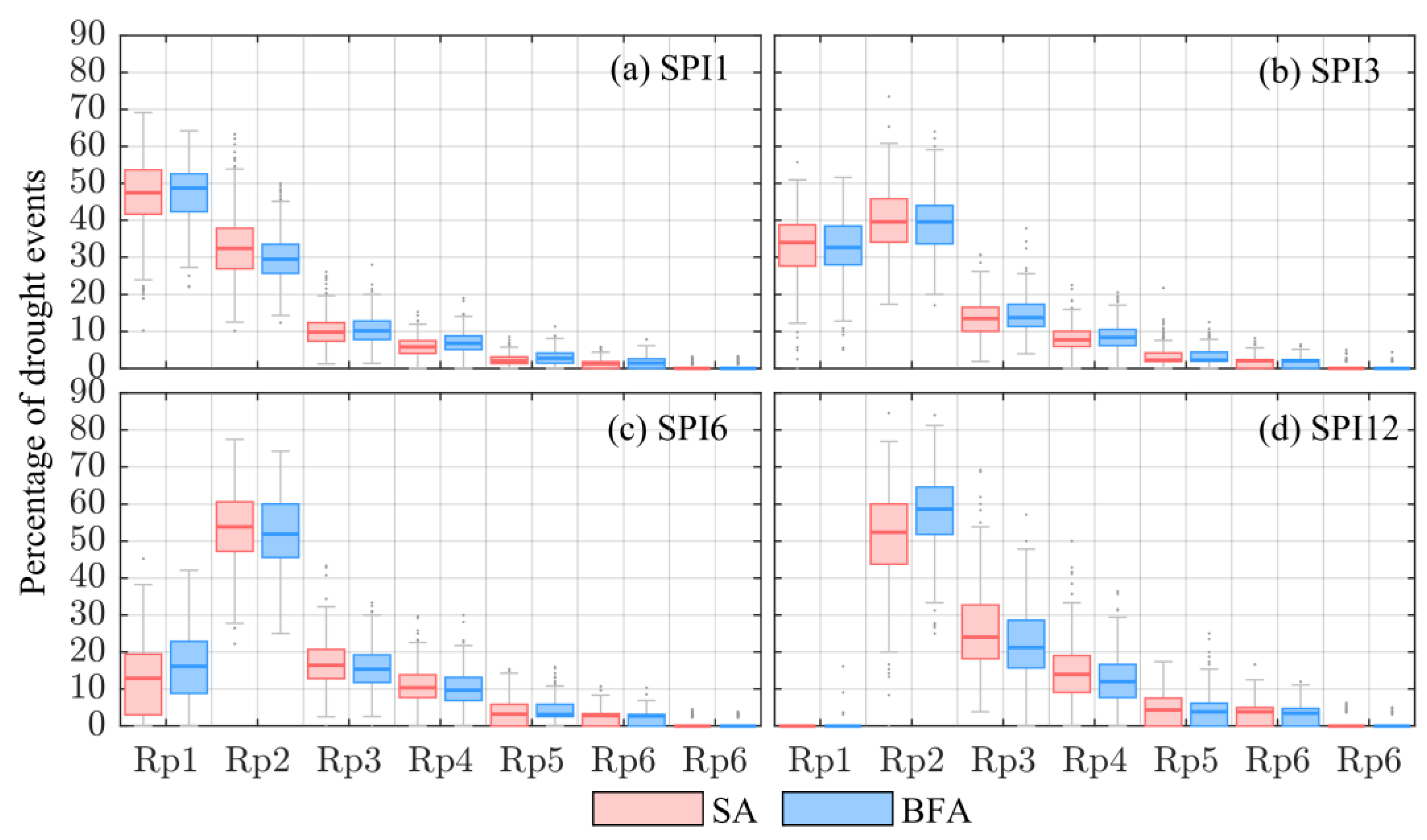
- despite the differences between the two approaches emerged in drought characteristics, the analyzed drought events lie in the same return period classes (Figure 6) for all the time scales.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Baronetti, A.; González-Hidalgo, J.C.; Vicente-Serrano, S.M.; Acquaotta, F.; Fratianni, S. A weekly spatio-temporal distribution of drought events over the Po Plain (North Italy) in the last five decades. Int. J. Climatol. 2020, 40, 4463–4476. [Google Scholar] [CrossRef]
- Cancelliere, A.; Salas, J.D. Drought length properties for periodic-stochastic hydrologic data. Water Resour. Res. 2004, 40, 1–13. [Google Scholar] [CrossRef]
- Kreibich, H.; Van Loon, A.F.; Schröter, K.; Ward, P.J.; Mazzoleni, M.; Sairam, N.; Abeshu, G.W.; Agafonova, S.; AghaKouchak, A.; Aksoy, H.; et al. The challenge of unprecedented floods and droughts in risk management. Nature 2022, 608, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Burgan, H.I.; Aksoy, H. Daily flow duration curve model for ungauged intermittent subbasins of gauged rivers. J. Hydrol. 2022, 604, 127249. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B.; Saunders, M.A. A drought climatology for Europe. Int. J. Climatol. 2002, 22, 1571–1592. [Google Scholar] [CrossRef]
- Garcia, M.; Ridolfi, E.; Di Baldassarre, G. The interplay between reservoir storage and operating rules under evolving conditions. J. Hydrol. 2020, 590, 125270. [Google Scholar] [CrossRef]
- American Meteorological Society (AMS). Statement on meteorological drought. Bull. Am. Meteorol. Soc. 2004, 85, 771–773. [Google Scholar]
- Kumar, M.N.; Murthy, C.S.; Sesha Sai, M.V.R.; Roy, P.S. On the use of Standardized Precipitation Index (SPI) for drought intensity assessment. Meteorol. Appl. 2009, 16, 381–389. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.F. Hydrological drought explained. WIREs Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Pan, Y.; Li, S.; Liu, Y.; Ma, Y. Agricultural drought monitoring: Progress, challenges, and prospects. J. Geogr. Sci. 2016, 26, 750–767. [Google Scholar] [CrossRef] [Green Version]
- Zhao, M.; Huang, S.; Huang, Q.; Wang, H.; Leng, G.; Xie, Y. Assessing socio-economic drought evolution characteristics and their possible meteorological driving force Assessing socio-economic drought evolution characteristics and their possible meteorological driving force. Geomat. Nat. Hazards Risk 2019, 10, 1084–1101. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate Distributions for Climatological Drought Indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Edwards, D.C.; McKee, T.B. Characteristics of 20th century drought in the United States at multiple time scales. In Atmospheric Science Paper 634; Department of Atmospheric Science, Colorado State University: Fort Collins, CO, USA, 1997. [Google Scholar]
- Papalexiou, S.M.; Rajulapati, C.R.; Andreadis, K.M.; Foufoula-Georgiou, E.; Clark, M.P.; Trenberth, K.E. Probabilistic Evaluation of Drought in CMIP6 Simulations. Earths Future 2021, 9, e2021EF002150. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The effect of the length of record on the standardized precipitation index calculation. Int. J. Climatol. 2005, 25, 505–520. [Google Scholar] [CrossRef] [Green Version]
- Guttman, N.B. Accepting the standardized precipitation index: A calculation algorithm. J. Am. Water Resour. Assoc. 1999, 35, 311–322. [Google Scholar] [CrossRef]
- Mineo, C.; Moccia, B.; Lombardo, F.; Russo, F.; Napolitano, F. Preliminary Analysis About the Effects on the SPI Values Computed from Different Best-Fit Probability Models in Two Italian Regions. In New Trends in Urban Drainage Modelling, Green Energy and Technology; Springer: Cham, Switzerland, 2018; pp. 958–962. [Google Scholar] [CrossRef]
- Sol’áková, T.; De Michele, C.; Vezzoli, R. Comparison between Parametric and Nonparametric Approaches for the Calculation of Two Drought Indices: SPI and SSI. J. Hydrol. Eng. 2014, 19, 04014010. [Google Scholar] [CrossRef]
- Angelidis, P.; Maris, F.; Kotsovinos, N.; Hrissanthou, V. Computation of Drought Index SPI with Alternative Distribution Functions. Water Resour. Manag. 2012, 26, 2453–2473. [Google Scholar] [CrossRef]
- Guenang, G.M.; Mkankam Kamga, F. Computation of the standardized precipitation index (SPI) and its use to assess drought occurrences in Cameroon over recent decades. J. Appl. Meteorol. Climatol. 2014, 53, 2310–2324. [Google Scholar] [CrossRef]
- Vergni, L.; Di Lena, B.; Todisco, F.; Mannocchi, F. Uncertainty in drought monitoring by the Standardized Precipitation Index: The case study of the Abruzzo region (central Italy). Theor. Appl. Climatol. 2017, 128, 13–26. [Google Scholar] [CrossRef]
- Mahmoudi, P.; Ghaemi, A.; Rigi, A.; Amir Jahanshahi, S.M. Recommendations for modifying the Standardized Precipitation Index (SPI) for Drought Monitoring in Arid and Semi-arid Regions. Water Resour. Manag. 2021, 35, 3253–3275. [Google Scholar] [CrossRef]
- Wu, H.; Svoboda, M.D.; Hayes, M.J.; Wilhite, D.A.; Wen, F. Appropriate application of the standardized precipitation index in arid locations and dry seasons. Int. J. Climatol. A J. R. Meteorol. Soc. 2007, 27, 65–79. [Google Scholar] [CrossRef]
- Rahmat, S.N.; Jayasuriya, N.; Bhuiyan, M. Development of drought severity-duration-frequency curves in Victoria, Australia. Aust. J. Water Resour. 2015, 19, 31–42. [Google Scholar] [CrossRef] [Green Version]
- Bonaccorso, B.; Cancelliere, A.; Rossi, G. An analytical formulation of return period of drought severity. Stoch. Environ. Res. Risk Assess. 2003, 17, 157–174. [Google Scholar] [CrossRef]
- Dalezios, N.R.; Loukas, A.; Vasiliades, L.; Liakopoulos, E. Severity-duration-frequency analysis of droughts and wet periods in Greece. Hydrol. Sci. J. 2000, 45, 751–769. [Google Scholar] [CrossRef]
- Bertini, C.; Buonora, L.; Ridolfi, E.; Russo, F.; Napolitano, F. On the Use of Satellite Rainfall Data to Design a Dam in an Ungauged Site. Water 2020, 12, 3028. [Google Scholar] [CrossRef]
- Aksoy, H.; Onoz, B.; Cetin, M.; Yuce, M.I. SPI-based Drought Severity-Duration-Frequency Analysis. In Proceedings of the 13th International Congress on Advances in Civil Engineering, Izmir, Turkey, 12–14 September 2018. [Google Scholar]
- Aksoy, H.; Cetin, M.; Eris, E.; Burgan, H.I.; Cavus, Y.; Yildirim, I.; Sivapalan, M. Critical drought intensity-duration-frequency curves based on total probability theorem-coupled frequency analysis. Hydrol. Sci. J. 2021, 66, 1337–1358. [Google Scholar] [CrossRef]
- Cavus, Y.; Aksoy, H. Critical drought severity/intensity-duration-frequency curves based on precipitation deficit. J. Hydrol. 2020, 584, 124312. [Google Scholar] [CrossRef]
- Song, S.; Singh, V.P.; Song, X.; Kang, Y. A probability distribution for hydrological drought duration. J. Hydrol. 2021, 599, 126479. [Google Scholar] [CrossRef]
- Desiato, F.; Lena, F.; Toreti, A. SCIA: A system for a better knowledge of the Italian climate. Boll. Geofis. Teor. Appl. 2007, 48, 351–358. [Google Scholar]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index: User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Fratianni, S.; Acquaotta, F. The Climate of Italy. In World Geomorphological Landscapes; Springer: Cham, Switzerland, 2017; pp. 29–38. ISBN 9783319261942. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlaysonm, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Moccia, B.; Papalexiou, S.M.; Russo, F.; Napolitano, F. Spatial variability of precipitation extremes over Italy using a fine-resolution gridded product. J. Hydrol. Reg. Stud. 2021, 37, 100906. [Google Scholar] [CrossRef]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Temperature and precipitation variability in Italy in the last two centuries from homogenised instrumental time series. Int. J. Climatol. 2006, 26, 345–381. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive automated quality assurance of daily surface observations. J. Appl. Meteorol. Climatol. 2010, 49, 1615–1633. [Google Scholar] [CrossRef] [Green Version]
- Arguez, A.; Durre, I.; Applequist, S.; Vose, R.S.; Squires, M.F.; Yin, X.; Heim, R.R.; Owen, T.W. Noaa’s 1981-2010 U.S. climate normals. Bull. Am. Meteorol. Soc. 2012, 93, 1687–1697. [Google Scholar] [CrossRef]
- Fioravanti, G.; Fraschetti, P.; Perconti, W.; Piervitali, E.; Desiato, F. Controlli di qualità delle serie di temperatura e precipitazione. In Rapporto ISPRA/Stato dell’Ambiente 66/2016; ISPRA: Roma, Italy, 2016. [Google Scholar]
- Nerantzaki, S.; Papalexiou, S.M. Assessing Extremes in Hydroclimatology: A Review on Probabilistic Methods. J. Hydrol. 2022, 605, 127302. [Google Scholar] [CrossRef]
- García-León, D.; Standardi, G.; Staccione, A. An integrated approach for the estimation of agricultural drought costs. Land Use Policy 2021, 100, 104923. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D.; Makropoulos, C. How extreme is extreme? An assessment of daily rainfall distribution tails. Hydrol. Earth Syst. Sci. 2013, 17, 851–862. [Google Scholar] [CrossRef] [Green Version]
- Moccia, B.; Mineo, C.; Ridolfi, E.; Russo, F.; Napolitano, F. Probability distributions of daily rainfall extremes in Lazio and Sicily, Italy, and design rainfall inferences. J. Hydrol. Reg. Stud. 2021, 33, 100771. [Google Scholar] [CrossRef]
- Gupta, N.; Chavan, S.R. Assessment of temporal change in the tails of probability distribution of daily precipitation over India due to climatic shift in the 1970s. J. Water Clim. Chang. 2021, 12, 2753–2773. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Series). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Thom, H.C.S. A Note on the Gamma Distribution. Mon. Weather. Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Barger, G.L.; Shaw, R.H.; Dale, R.F. Chances of Receiving Selected Amounts of Precipitation in the North Central Region of the United States; Agricultural and Home Economics Experimental Station: Ames, IA, USA; Iowa State University: Ames, IA, USA, 1959. [Google Scholar]
- Allan, R.P.; Hawkins, E.; Bellouin, N.; Collins, B. IPCC, 2021: Summary for Policymakers. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Zuo, D.D.; Hou, W.; Zhang, Q.; Yan, P.C. Sensitivity analysis of standardized precipitation index to climate state selection in China. Adv. Clim. Chang. Res. 2022, 13, 42–50. [Google Scholar] [CrossRef]



| SPI Values | SPI Classes | Probability (%) |
|---|---|---|
| Extremely wet | 2.3 | |
| 1.5 to 2.00 | Severely wet | 4.4 |
| 1.0 to 1.5 | Moderately wet | 9.2 |
| 0 to 1.0 | Mildly wet | 34.1 |
| −1.0 to 0 | Mildly drought | 34.1 |
| −1.5 to −1.0 | Moderate drought | 9.2 |
| −2.0 to −1.5 | Severe drought | 4.4 |
| Extreme drought | 2.3 |
| 1-month | 3-months | ||||||||||||
| P25 | P50 | P75 | SD | Skew | Pdry | P25 | P50 | P75 | SD | Skew | Pdry | ||
| month | 1 | 41.33 | 77.35 | 121.12 | 60.56 | 0.92 | 1.3% | 219.89 | 299.01 | 387.44 | 125.34 | 0.48 | 0% |
| 2 | 35.14 | 66.98 | 110.76 | 60.12 | 1.15 | 1.0% | 190.24 | 256.97 | 332.51 | 115.73 | 0.65 | 0% | |
| 3 | 38.51 | 71.00 | 113.26 | 54.54 | 0.86 | 1.3% | 161.94 | 229.09 | 309.63 | 116.03 | 0.77 | 0% | |
| 4 | 46.19 | 72.74 | 106.42 | 48.40 | 0.96 | 0.6% | 168.06 | 226.85 | 297.86 | 97.84 | 0.62 | 0% | |
| 5 | 35.48 | 58.67 | 89.13 | 43.12 | 1.15 | 1.4% | 164.54 | 217.10 | 277.25 | 85.09 | 0.54 | 0% | |
| 6 | 32.41 | 49.19 | 72.62 | 35.60 | 1.52 | 6.3% | 149.18 | 193.92 | 246.78 | 74.29 | 0.58 | 0% | |
| 7 | 22.04 | 35.92 | 56.22 | 30.22 | 1.52 | 19.1% | 116.45 | 152.24 | 198.02 | 63.72 | 0.89 | 0% | |
| 8 | 24.42 | 43.28 | 71.44 | 39.45 | 1.37 | 12.5% | 101.72 | 135.83 | 180.40 | 63.91 | 1.05 | 2% | |
| 9 | 32.93 | 62.99 | 106.11 | 58.97 | 1.25 | 2.5% | 106.64 | 153.13 | 209.85 | 82.32 | 0.96 | 1% | |
| 10 | 50.38 | 96.28 | 159.98 | 87.21 | 1.19 | 0.9% | 153.35 | 222.95 | 305.76 | 117.73 | 0.87 | 0% | |
| 11 | 64.44 | 108.52 | 164.74 | 80.37 | 1.04 | 0.5% | 212.44 | 295.89 | 389.32 | 134.99 | 0.68 | 0% | |
| 12 | 57.33 | 92.25 | 141.43 | 68.85 | 1.05 | 0.4% | 235.40 | 319.01 | 426.46 | 144.01 | 0.70 | 0% | |
| 6-months | 12-months | ||||||||||||
| P25 | P50 | P75 | SD | Skew | Pdry | P25 | P50 | P75 | SD | Skew | Pdry | ||
| month | 1 | 427.29 | 528.10 | 651.62 | 175.05 | 0.57 | 0% | 791.59 | 930.03 | 1090.20 | 217.87 | 0.48 | 0% |
| 2 | 455.31 | 560.20 | 676.80 | 173.94 | 0.57 | 0% | 796.53 | 929.64 | 1080.20 | 210.84 | 0.43 | 0% | |
| 3 | 457.76 | 564.55 | 679.86 | 174.98 | 0.46 | 0% | 801.08 | 927.79 | 1075.85 | 207.39 | 0.43 | 0% | |
| 4 | 431.31 | 533.26 | 643.87 | 160.70 | 0.51 | 0% | 801.33 | 926.70 | 1073.89 | 206.62 | 0.46 | 0% | |
| 5 | 387.32 | 478.80 | 581.76 | 150.44 | 0.52 | 0% | 799.72 | 928.24 | 1073.12 | 208.99 | 0.48 | 0% | |
| 6 | 345.38 | 431.96 | 531.22 | 142.70 | 0.50 | 0% | 799.64 | 930.59 | 1072.62 | 211.08 | 0.47 | 0% | |
| 7 | 313.15 | 387.86 | 475.85 | 122.77 | 0.51 | 0% | 800.96 | 930.18 | 1072.33 | 211.03 | 0.50 | 0% | |
| 8 | 294.92 | 362.40 | 435.90 | 106.68 | 0.52 | 0% | 804.86 | 931.36 | 1068.92 | 207.63 | 0.51 | 0% | |
| 9 | 290.58 | 357.29 | 433.19 | 108.07 | 0.54 | 0% | 799.60 | 924.47 | 1069.48 | 211.10 | 0.55 | 0% | |
| 10 | 302.38 | 384.35 | 481.85 | 136.38 | 0.70 | 0% | 793.61 | 923.40 | 1071.99 | 213.58 | 0.60 | 0% | |
| 11 | 347.39 | 438.48 | 546.24 | 152.75 | 0.65 | 0% | 794.80 | 925.10 | 1078.94 | 212.20 | 0.49 | 0% | |
| 12 | 383.97 | 487.93 | 605.93 | 170.45 | 0.58 | 0% | 794.46 | 930.71 | 1088.44 | 215.76 | 0.50 | 0% | |
| Probability Distribution | Cumulative Distribution Function | |
|---|---|---|
| (1) | ||
| (2) | ||
| (3) | ||
| (4) | ||
| Month | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| 1 | 17% | 30% | 17% | 21% | 27% | 18% | 21% | 26% | 18% | 18% | 20% | 23% | |
| 25% | 25% | 27% | 43% | 37% | 51% | 43% | 28% | 36% | 33% | 46% | 48% | ||
| 34% | 33% | 25% | 23% | 27% | 26% | 27% | 36% | 34% | 26% | 20% | 23% | ||
| 23% | 11% | 32% | 13% | 9% | 5% | 8% | 11% | 12% | 23% | 13% | 6% | ||
| 3 | 23% | 22% | 23% | 24% | 22% | 22% | 25% | 19% | 22% | 22% | 23% | 23% | |
| 39% | 53% | 51% | 42% | 37% | 41% | 49% | 45% | 41% | 45% | 44% | 40% | ||
| 24% | 15% | 15% | 24% | 29% | 26% | 21% | 28% | 25% | 19% | 22% | 27% | ||
| 14% | 10% | 11% | 10% | 12% | 11% | 5% | 8% | 12% | 14% | 11% | 11% | ||
| 6 | 24% | 16% | 19% | 15% | 15% | 22% | 20% | 19% | 22% | 22% | 17% | 21% | |
| 51% | 60% | 55% | 53% | 56% | 51% | 50% | 51% | 47% | 47% | 58% | 48% | ||
| 17% | 15% | 16% | 20% | 20% | 19% | 22% | 21% | 22% | 18% | 17% | 26% | ||
| 7% | 10% | 9% | 12% | 9% | 8% | 8% | 9% | 9% | 13% | 9% | 5% | ||
| 12 | 20% | 17% | 14% | 13% | 15% | 16% | 12% | 10% | 14% | 14% | 15% | 15% | |
| 52% | 56% | 57% | 57% | 61% | 62% | 61% | 64% | 61% | 60% | 55% | 55% | ||
| 18% | 19% | 18% | 21% | 17% | 14% | 15% | 15% | 15% | 17% | 19% | 20% | ||
| 10% | 8% | 11% | 9% | 6% | 8% | 11% | 11% | 10% | 8% | 10% | 9% | ||
| Standard Approach | Best Fit Approach | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SPI1 | SPI3 | SPI6 | SPI12 | SPI1 | SPI3 | SPI6 | SPI12 | ||
| D (month) | min | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| mean | 1.20 | 1.96 | 2.77 | 4.21 | 1.21 | 1.90 | 2.59 | 3.66 | |
| max | 7.00 | 14.00 | 26.00 | 51.00 | 8.00 | 14.00 | 23.00 | 46.00 | |
| sd | 0.49 | 1.31 | 2.34 | 4.69 | 0.51 | 1.27 | 2.14 | 4.14 | |
| S (mm) | min | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| mean | 1.89 | 3.06 | 4.27 | 6.29 | 2.08 | 3.13 | 4.07 | 5.43 | |
| max | 11.59 | 26.31 | 51.66 | 77.97 | 14.15 | 27.05 | 44.71 | 92.12 | |
| sd | 0.96 | 2.47 | 4.30 | 8.22 | 1.31 | 2.62 | 4.13 | 7.32 | |
| T (month) | min | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| mean | 8.26 | 11.36 | 15.52 | 22.31 | 7.94 | 11.42 | 16.26 | 24.17 | |
| max | 73.00 | 147.00 | 238.00 | 412.00 | 74.00 | 225.00 | 313.00 | 375.00 | |
| sd | 6.57 | 9.72 | 16.15 | 31.04 | 6.35 | 9.94 | 17.30 | 34.36 | |
| Month | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | ||
| SA | SPI1 | 2.4 | 1.2 | 3.6 | 4.8 | 4.8 | 11.4 | 22.0 | 18.7 | 3.6 | 4.2 | 4.5 | 3.9 |
| SPI3 | 2.7 | 2.1 | 1.8 | 4.5 | 1.8 | 4.5 | 1.2 | 2.1 | 0.6 | 4.5 | 3.0 | 2.7 | |
| SPI6 | 1.8 | 2.1 | 1.2 | 2.1 | 2.1 | 3.6 | 5.1 | 3.6 | 1.8 | 2.7 | 3.0 | 1.8 | |
| SPI12 | 1.2 | 2.4 | 1.5 | 2.1 | 3.9 | 4.2 | 3.3 | 4.2 | 2.4 | 2.1 | 1.8 | 2.7 | |
| BFA | SPI1 | 9.3 | 9.6 | 16.3 | 9.0 | 11.1 | 20.8 | 21.1 | 28.9 | 12.0 | 15.4 | 15.4 | 12.3 |
| SPI3 | 6.0 | 3.9 | 8.1 | 10.5 | 6.6 | 9.0 | 6.9 | 5.4 | 7.5 | 8.4 | 10.8 | 13.0 | |
| SPI6 | 5.4 | 4.8 | 5.4 | 5.4 | 4.5 | 5.7 | 4.8 | 5.7 | 4.2 | 4.2 | 5.7 | 3.3 | |
| SPI12 | 3.3 | 3.6 | 4.2 | 4.5 | 5.7 | 4.5 | 4.5 | 5.1 | 4.2 | 6.0 | 4.8 | 3.9 | |
| Δα | Δβ | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| SPI1 | SPI3 | SPI6 | SPI12 | SPI1 | SPI3 | SPI6 | SPI12 | ||
| Return periods | 2 | −0.95 | 1.12 | 0.43 | −0.97 | 0.47 | 0.42 | −0.94 | −3.03 |
| 5 | 3.72 | 3.57 | 1.77 | 0.48 | 3.73 | 2.09 | 0.16 | −1.96 | |
| 10 | 7.72 | 5.75 | 3.16 | 1.96 | 6.48 | 3.39 | 0.96 | −1.31 | |
| 25 | 13.53 | 8.76 | 5.06 | 3.76 | 10.56 | 5.23 | 2.00 | −0.52 | |
| 50 | 17.85 | 11.09 | 6.48 | 5.11 | 13.87 | 6.75 | 2.80 | 0.11 | |
| 100 | 21.84 | 13.35 | 7.83 | 6.39 | 17.27 | 8.44 | 3.66 | 0.83 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moccia, B.; Mineo, C.; Ridolfi, E.; Russo, F.; Napolitano, F. SPI-Based Drought Classification in Italy: Influence of Different Probability Distribution Functions. Water 2022, 14, 3668. https://doi.org/10.3390/w14223668
Moccia B, Mineo C, Ridolfi E, Russo F, Napolitano F. SPI-Based Drought Classification in Italy: Influence of Different Probability Distribution Functions. Water. 2022; 14(22):3668. https://doi.org/10.3390/w14223668
Chicago/Turabian StyleMoccia, Benedetta, Claudio Mineo, Elena Ridolfi, Fabio Russo, and Francesco Napolitano. 2022. "SPI-Based Drought Classification in Italy: Influence of Different Probability Distribution Functions" Water 14, no. 22: 3668. https://doi.org/10.3390/w14223668
APA StyleMoccia, B., Mineo, C., Ridolfi, E., Russo, F., & Napolitano, F. (2022). SPI-Based Drought Classification in Italy: Influence of Different Probability Distribution Functions. Water, 14(22), 3668. https://doi.org/10.3390/w14223668









