Experimental and Numerical Analysis of the Clearance Effects between Blades and Hub in a Water Wheel Used for Power Generation
Abstract
1. Introduction
2. Mathematical Model and Entropy Production Theory
2.1. Governing Equation
2.2. The VOF Method
2.3. Standard k-ε Turbulence Model
2.4. Entropy Production Theory
3. Simulation Setup and Experimental Validation
3.1. Computation Domain and Boundary Conditions
- (1)
- Inlet boundary: the water inlet boundary is set as the velocity inlet. The single variable method is adopted in that the inlet of water flow was set at 4 m/s to simulate the ultra-low head site condition. The direction of the inlet velocity is perpendicular to the inlet, and the turbulence intensity is set to a medium value of 5%. Considering that the water and air interface should be separated, the free surface level is set to the same height as the axis of rotation.
- (2)
- Outlet boundary: the outlet of water flow is set as the pressure outlet, which value is the same as atmospheric pressure.
- (3)
- Wall boundary: a no-slip wall is imposed on all other walls except the top of the area, which is set for symmetry [10].
- (4)
- During the calculation process, the influence of gravity is considered. The unsteady calculation method is used to simulate the gas–liquid two-phase, in which the sliding grid is used in the rotation field to ensure that the wheel rotates at 4 rpm.
3.2. Numerical Method
3.3. Grid Verification and Validation of Results
4. Performance and Flow Characteristics of Water Wheels
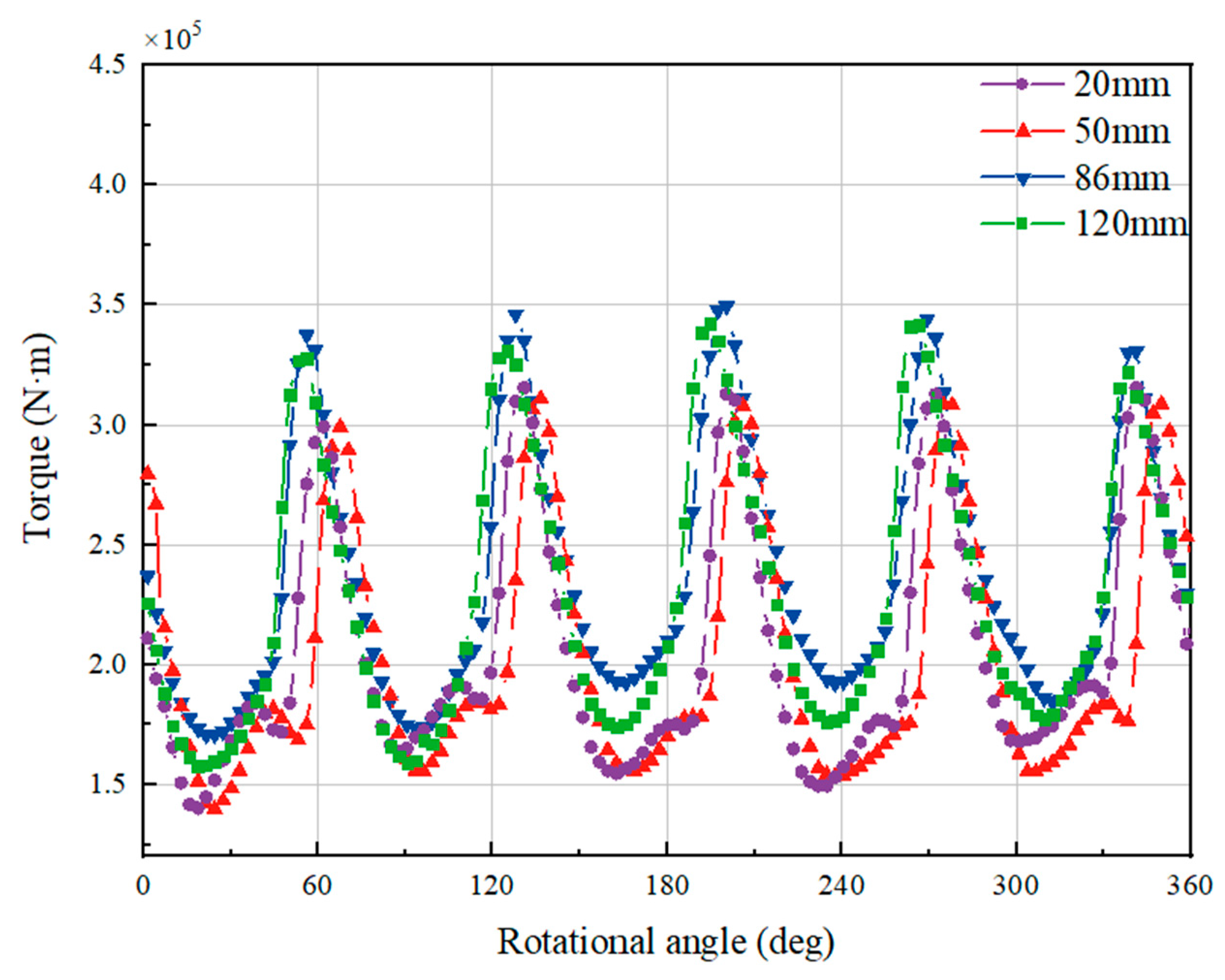
4.1. Water Wheels Performance and Power Fluctuation
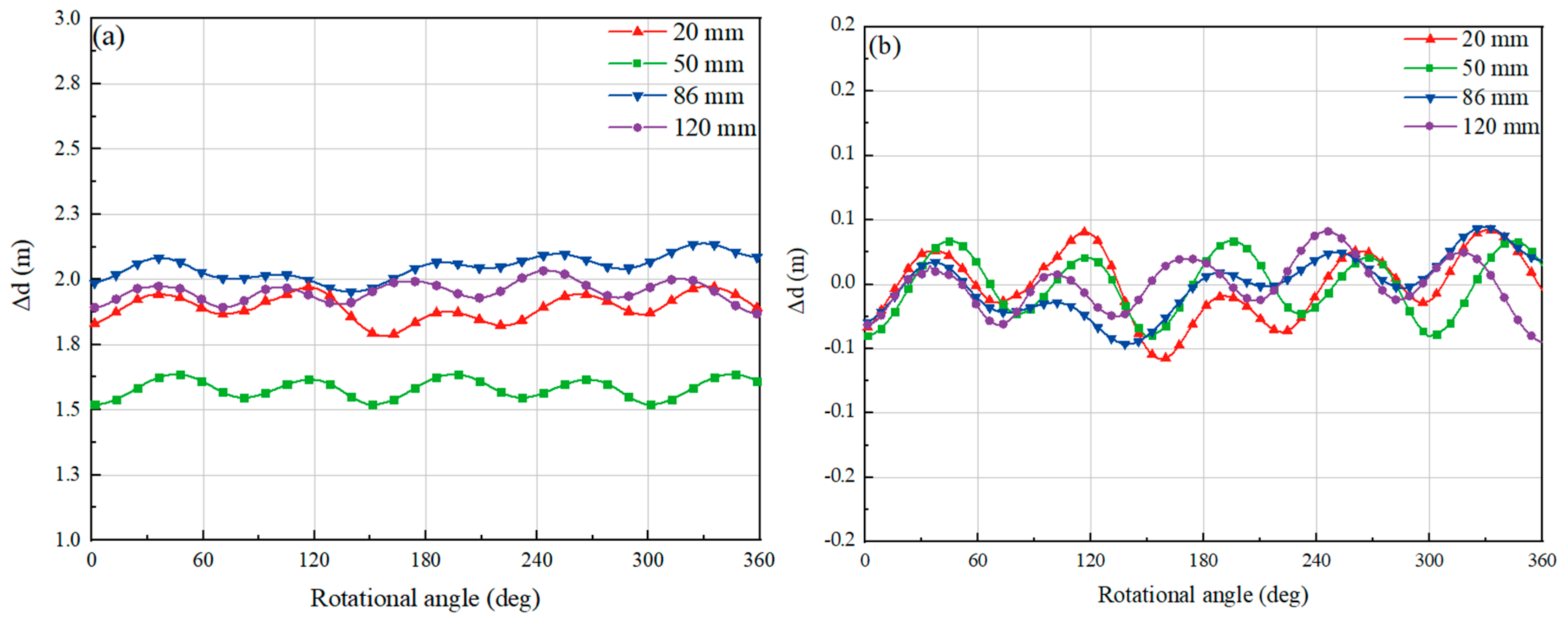
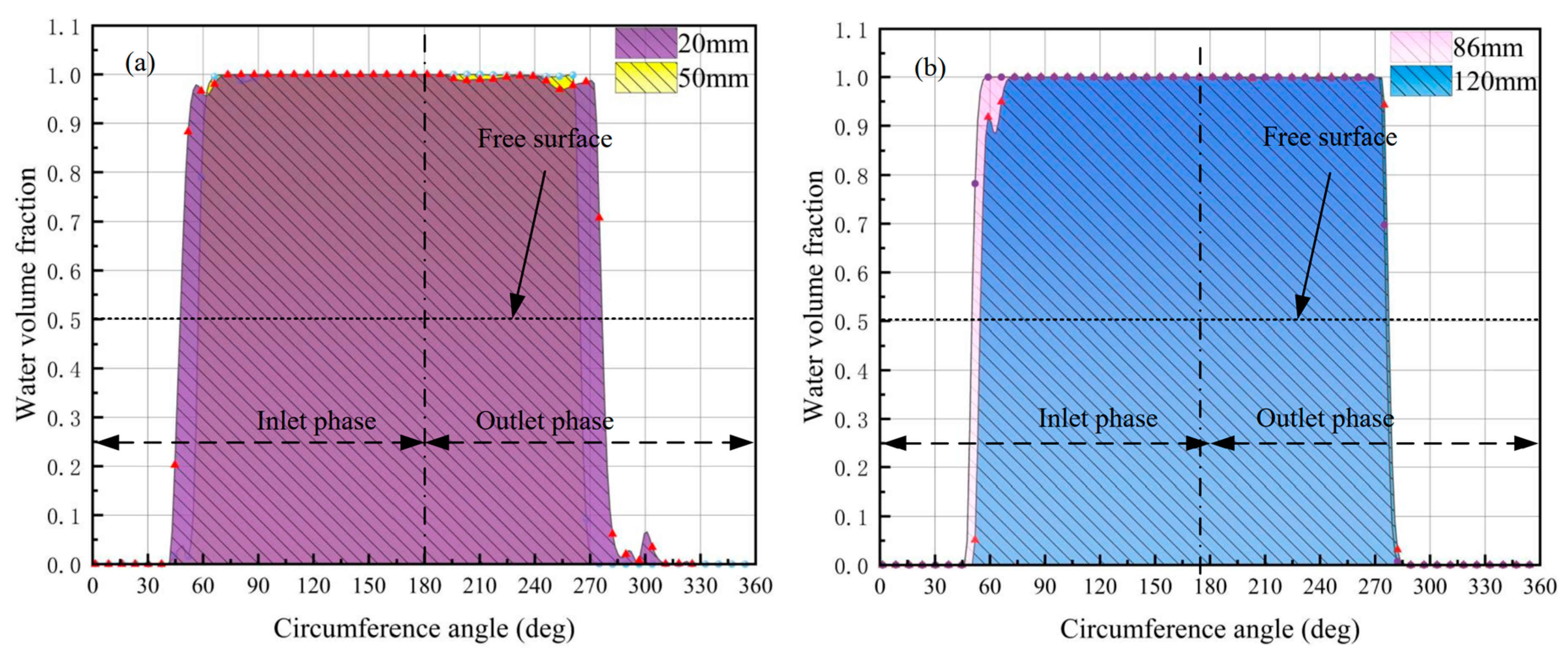
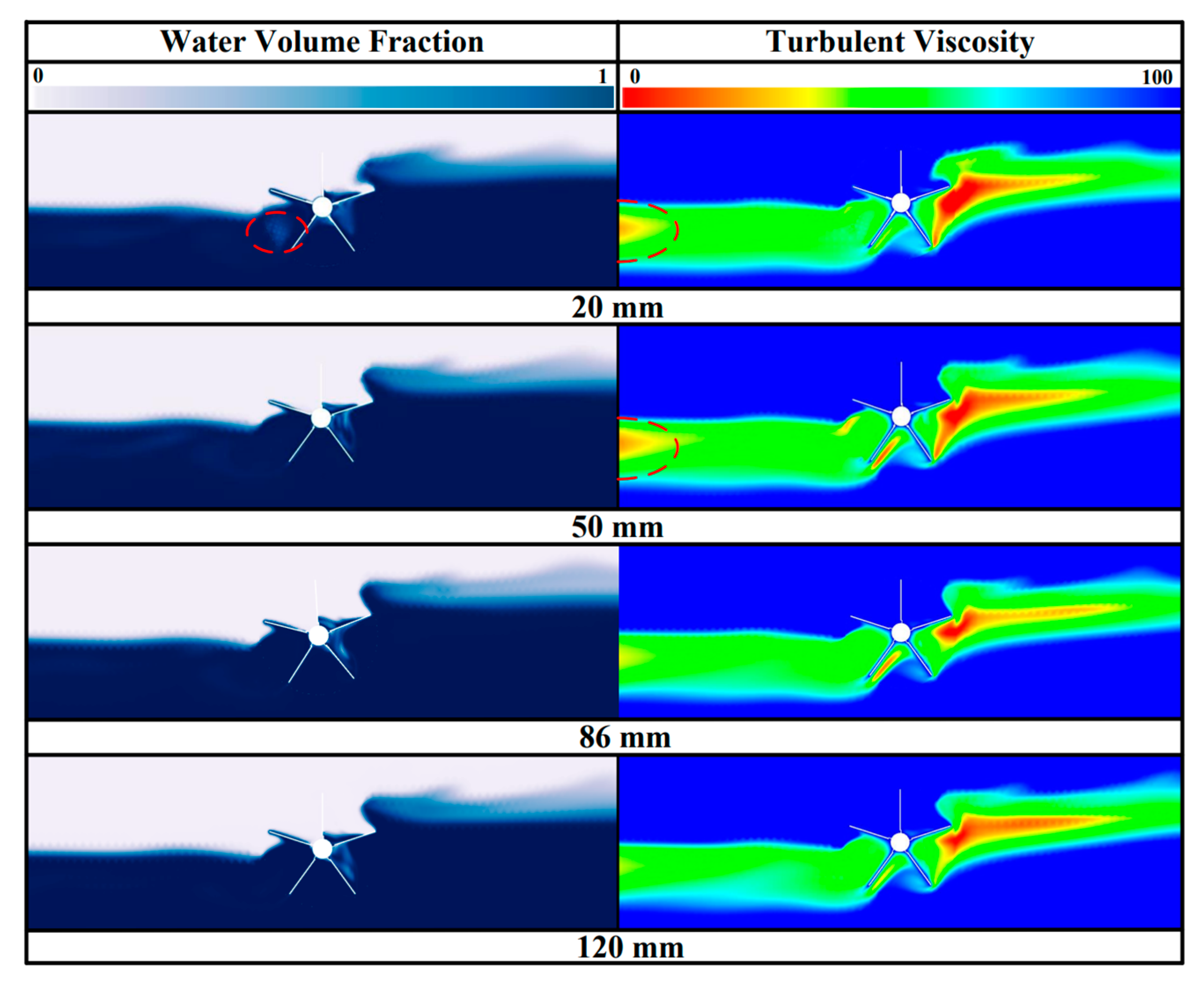
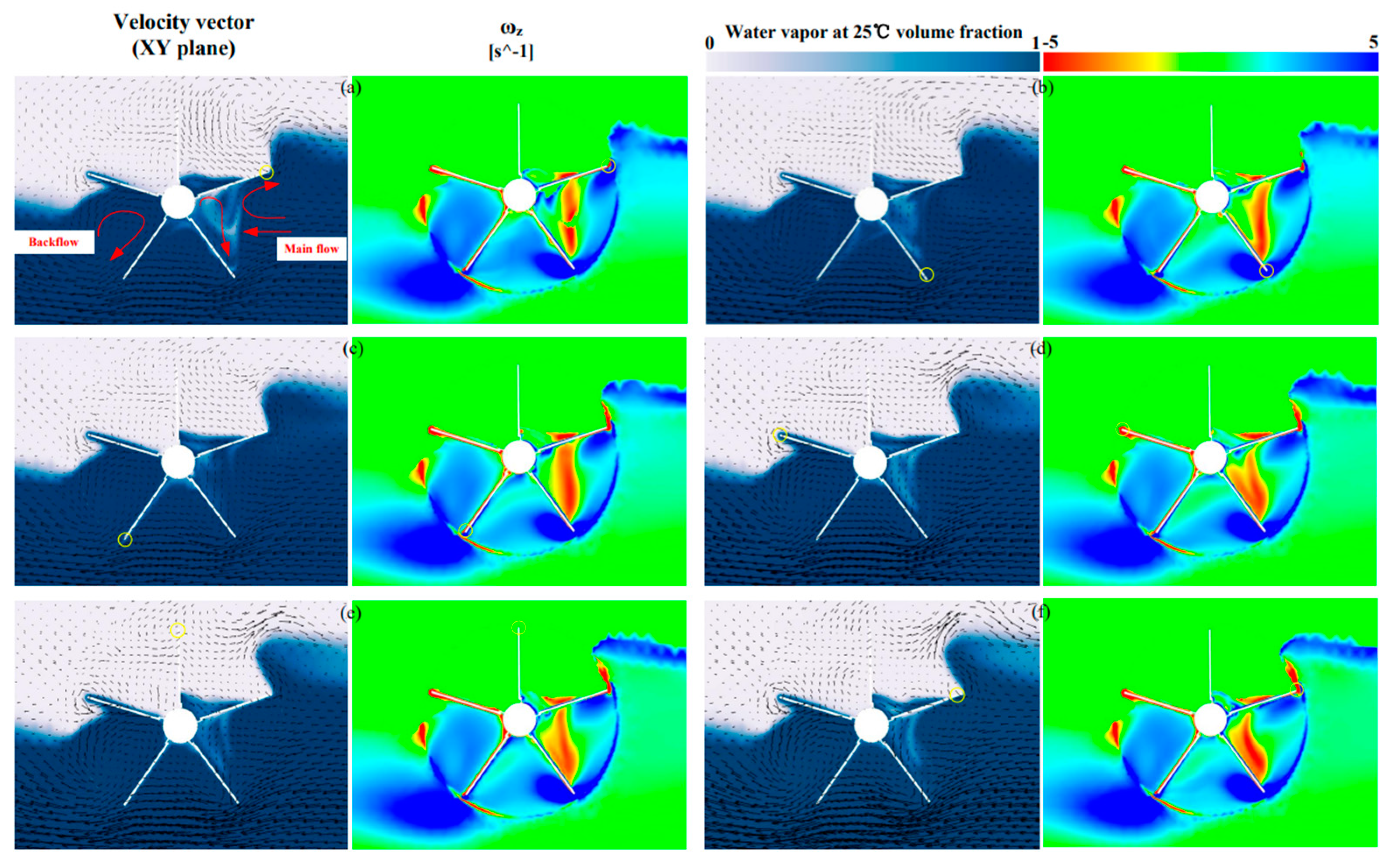
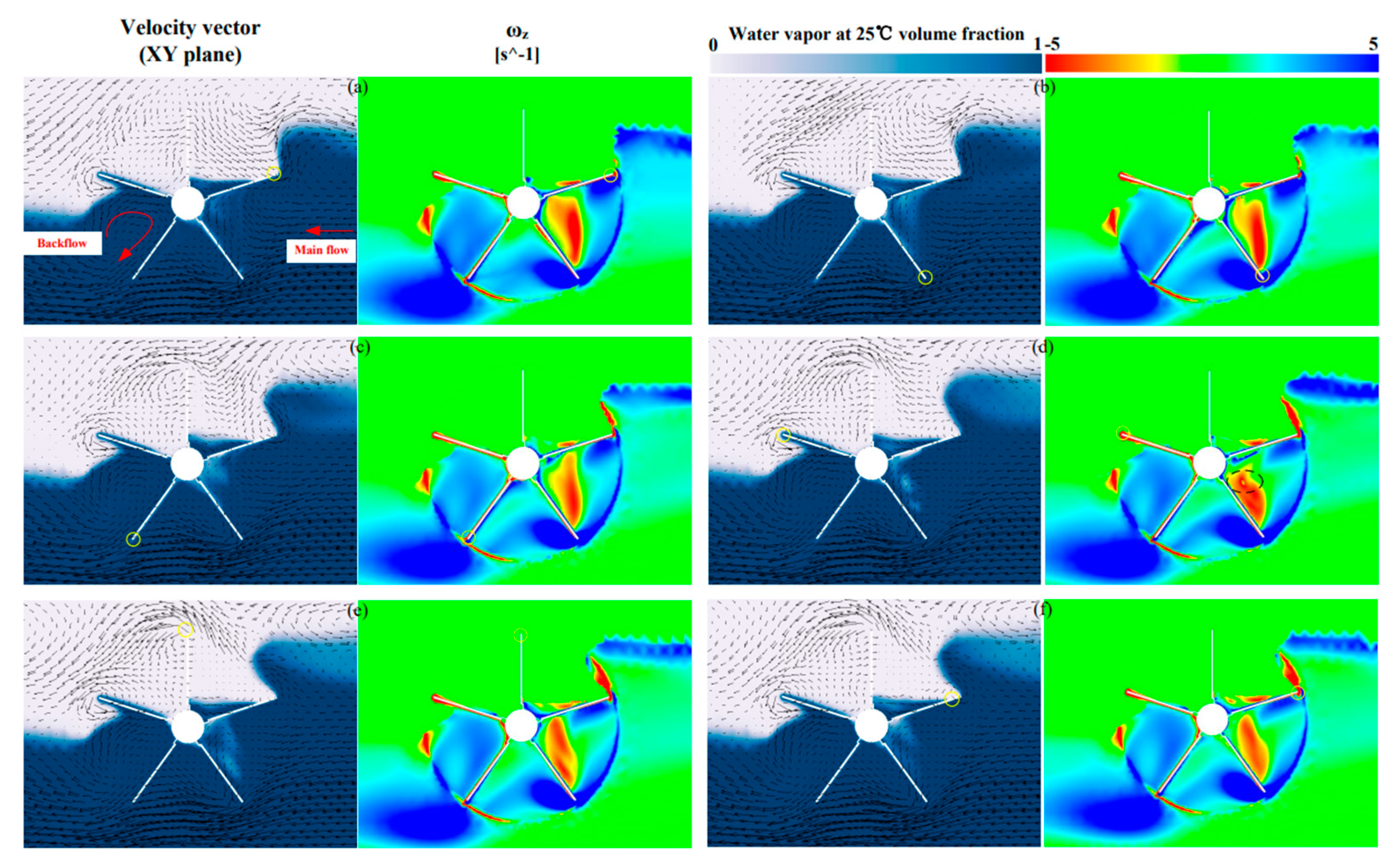
4.2. Analysis of Flow Fields
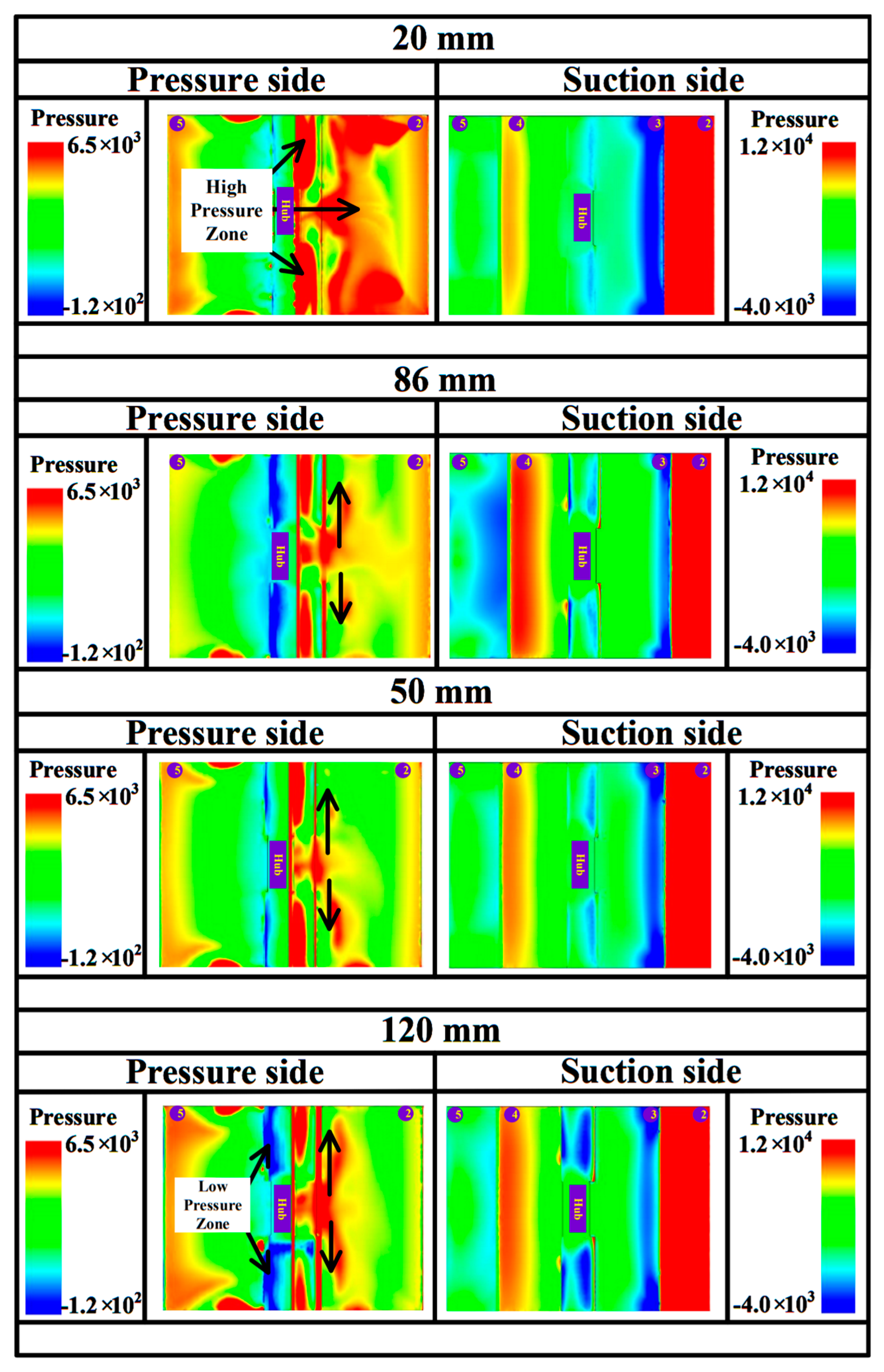
4.3. Energy Dissipation Analysis and Coupling Mechanism of Vorticity-Pressure
5. Characteristics and Distribution of Entropy Production
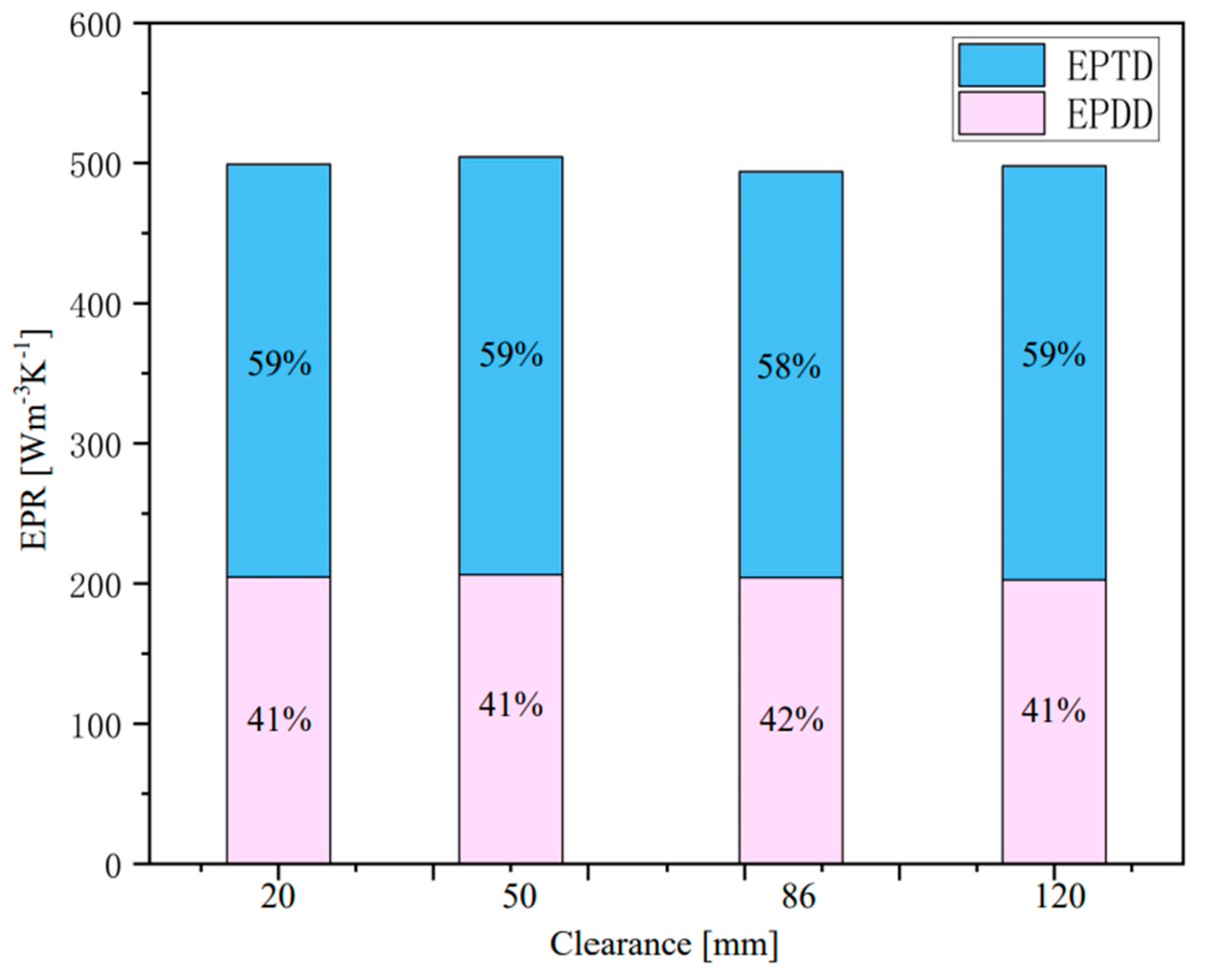
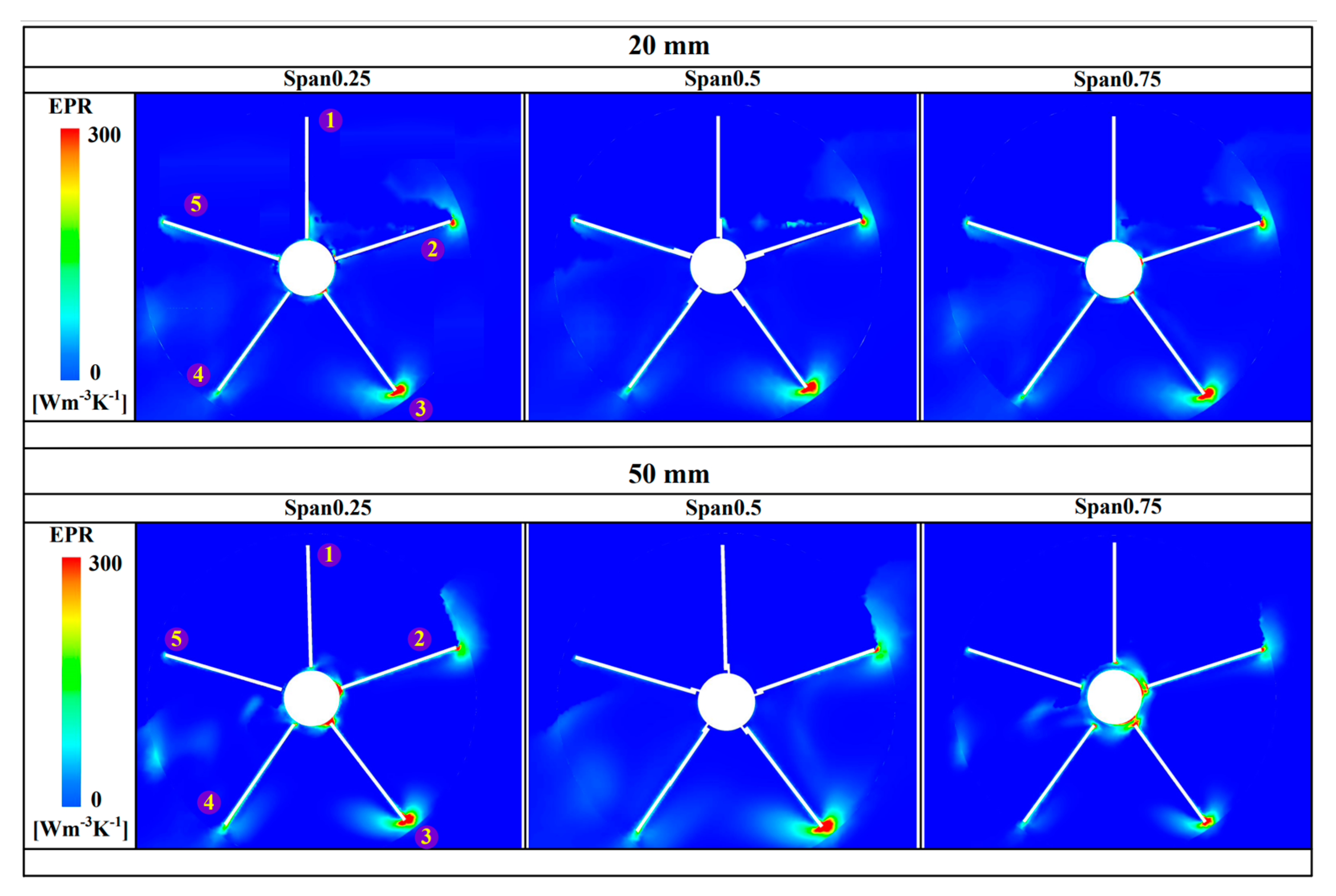
5.1. Distributions of EPR of Water Wheels
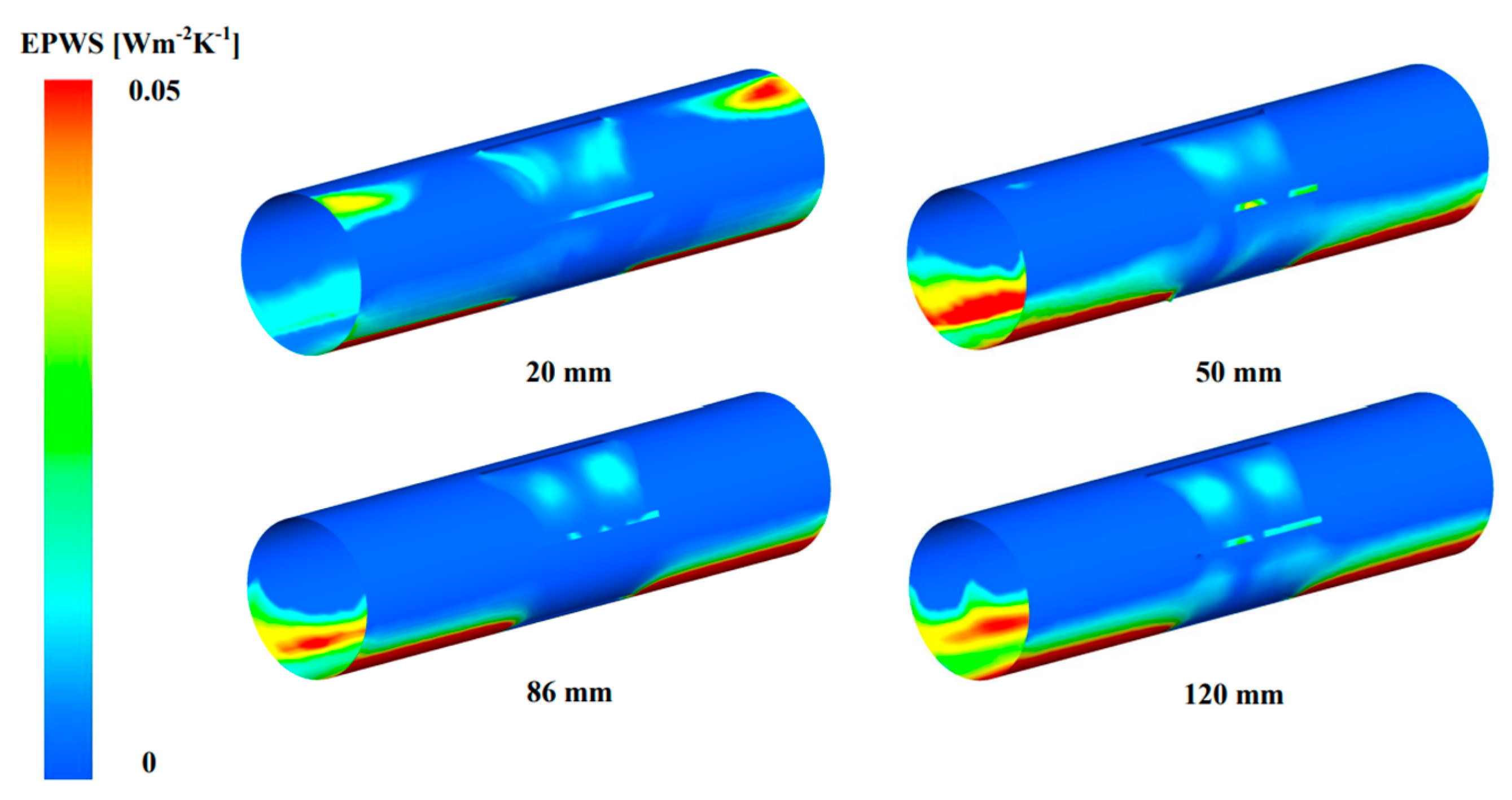
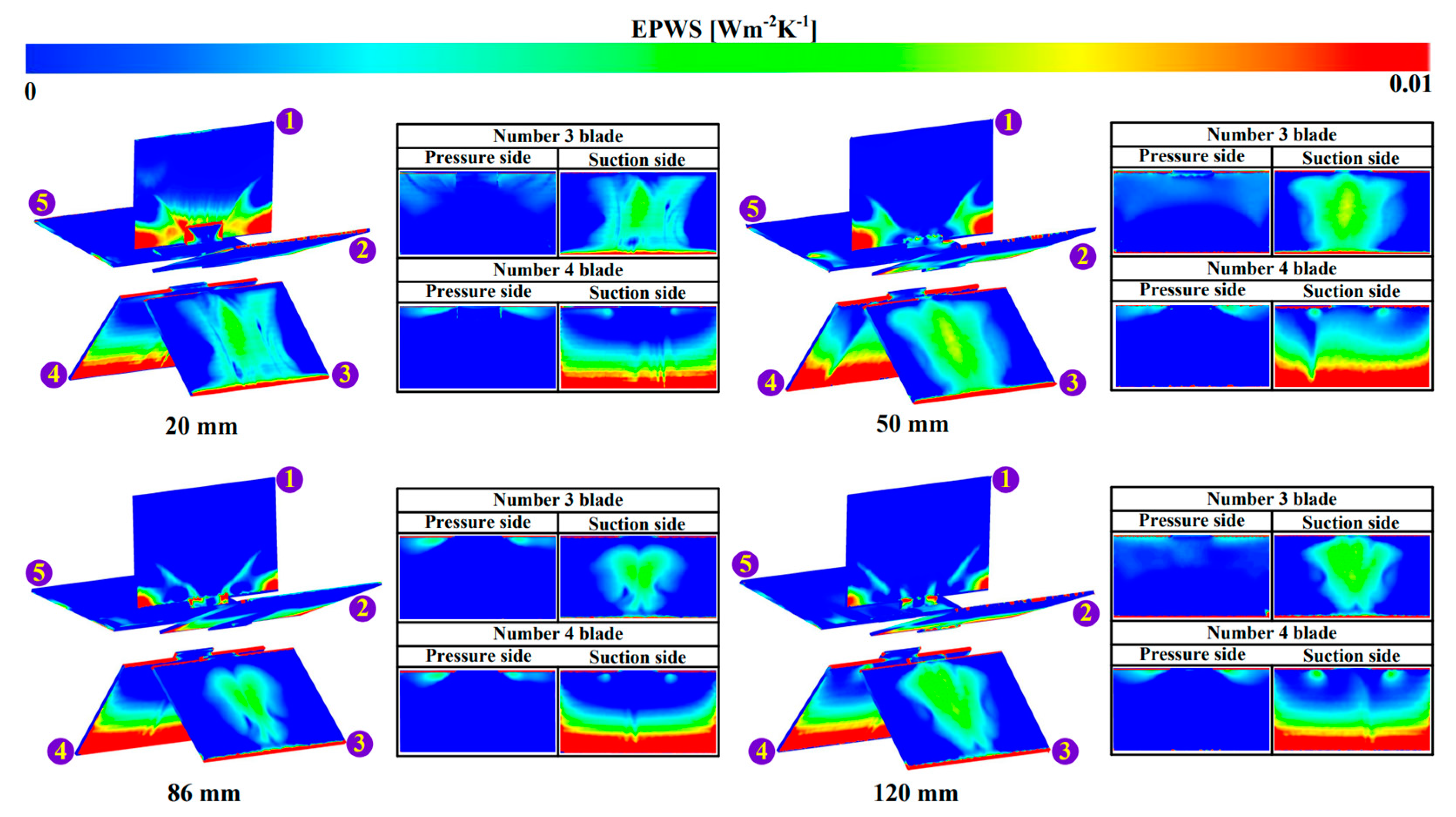
5.2. Distributions of EPWS of Water Wheels
6. Conclusions
- The numerical simulation and experimental results represent a relatively good agreement, with a maximum error of 3.5%.
- The torque of the water wheel has periodic transformation within a cycle of rotation, the maximum torque is reached at approximately 70.5° per period. Under the same working conditions, the performance of water wheels can be elevated by 8.7% by setting appropriate clearance.
- It was found that the average difference in water level is the highest in the water wheel with the 86 mm clearance configuration, and its fluctuation amplitude is the gentlest. The water wheels with 20 mm clearance and 120 mm clearance have a slight difference in the average difference in water level but the efficiency of maximum clearance (120 mm) is greater than that of minimum clearance (20 mm). The water wheel with optimal clearance can reduce air intruding into the water and attenuate the complexity of the water flow, potentially enhancing the performance of water wheels.
- It proved that the setting of water wheel clearance can attenuate outcomes of the blocking effect of the river channel and reduce the potential energy loss and kinetic energy dissipation while maintaining high efficiency. By comparing the most efficient two configurations of the vortex evolution and pressure distribution, it is illustrated that the optimal clearance can target eliminating vortical flow and improving flow adaptability, avoiding unnecessary energy losses, and decreasing the uneven pressure.
- As a new method, the irreversible energy loss characteristics can be intuitively diagnosed by using the entropy production method in water wheels under different clearance effects. The coupling mechanism of vorticity–pressure which will induce irreversible energy loss of the water wheel under different clearance effects is investigated. Hence, this research can provide a reference for the optimization of clearance between the hub and blade of water wheel performance.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Ui, V | velocity [m/s] |
| μ | dynamic viscosity [N·s/m2] |
| ρ | density [kg/m3] |
| F | Force [N] |
| T | torque [N·m] |
| g | Gravitational acceleration [m/s2] |
| α | volume fraction |
| r | radius [m] |
| q | heat flux [W/m2] |
| s | specific entropy [J/kg·K] |
| P | power [W] |
| ω | angular velocity [rev/s] |
| A | submerged water area [m2] |
| Δd | water depths [m] |
| θ | circumferential angle [deg] |
| CP | power coefficient |
| ɛ | turbulent dissipation rate [m2/s3] |
| entropy production by direct dissipation [W/K] | |
| entropy production by turbulent dissipation [W/K] | |
| entropy production by wall shear stress [W/K] | |
| Abbreviations | |
| HPZ | high-pressure zone |
| EPDD | entropy production rate by direct dissipation [W/(m3·K)] |
| EPTD | entropy production rate by turbulent dissipation [W/(m3·K)] |
| EPWS | entropy production rate by wall shear stress [W/(m2·K)] |
| Subscripts | |
| t | turbulent |
| - | Time-averaged value |
| i, j | direction of Cartesian coordinates |
| eff | Effective value |
References
- Cassan, L.; Dellinger, G.; Maussion, P.; Dellinger, N. Hydrostatic Pressure Wheel for Regulation of Open Channel Networks and for the Energy Supply of Isolated Sites. Sustainability 2021, 13, 9532. [Google Scholar] [CrossRef]
- Bachan, A.; Ghimire, N.; Eisner, J.; Chitrakar, S.; Neopane, H.P. Numerical analysis of low-tech overshot water wheel for off grid purpose. J. Phys. Conf. Ser. 2019, 1266, 012001. [Google Scholar] [CrossRef]
- Senior, J.; Saenger, N.; Müller, G. New hydropower converters for very low-head differences. J. Hydraul. Res. 2010, 48, 703–714. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. Gravity water wheels as a micro hydropower energy source: A review based on historic data, design methods, efficiencies and modern optimizations. Renew. Sustain. Energy Rev. 2018, 97, 414–427. [Google Scholar] [CrossRef]
- Paudel, S.; Saenger, N. Effect of channel geometry on the performance of the Dethridge water wheel. Renew. Energy 2018, 115, 175–182. [Google Scholar] [CrossRef]
- Quaranta, E.; Müller, G. Sagebien and Zuppinger water wheels for very low head hydropower applications. J. Hydraul. Res. 2017, 56, 526–536. [Google Scholar] [CrossRef]
- Ceran, B.; Jurasz, J.; Wróblewski, R.; Guderski, A.; Złotecka, D.; Kaźmierczak, Ł. Impact of the Minimum Head on Low-Head Hydropower Plants Energy Production and Profitability. Energies 2020, 13, 6728. [Google Scholar] [CrossRef]
- Quaranta, E.; Müller, G. Noise Generation and Acoustic Impact of Free Surface Hydropower Machines: Focus on Water Wheels and Emerging Challenges. Int. J. Environ. Res. Public Health 2021, 18, 13051. [Google Scholar] [CrossRef]
- Butera, I.; Fontan, S.; Poggi, D.; Quaranta, E.; Revelli, R. Experimental Analysis of Effect of Canal Geometry and Water Levels on Rotary Hydrostatic Pressure Machine. J. Hydraul. Eng. 2020, 146, 04019071. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Jeong, H.; Yang, C. A study on flow fields and performance of water wheel turbine using experimental and numerical analyses. Sci. China Technol. Sci. 2018, 61, 464–474. [Google Scholar] [CrossRef]
- Jasa, L.; Priyadi, A.; Purnomo, M.H. Experimental Investigation of Micro-Hydro Waterwheel Models to Determine Optimal Efficiency. Appl. Mech. Mater. 2015, 776, 413–418. [Google Scholar] [CrossRef]
- Tevata, A.; Inprasit, C. The Effect of Paddle Number and Immersed Radius Ratio on Water Wheel Performance. Energy Procedia 2011, 9, 359–365. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. Hydraulic Behavior and Performance of Breastshot Water Wheels for Different Numbers of Blades. J. Hydraul. Eng. 2016, 143, 0401607. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. CFD simulations to optimize the blade design of water wheels. Drink. Water Eng. Sci. 2017, 10, 27–32. [Google Scholar] [CrossRef]
- Quaranta, E.; Revelli, R. Performance Optimization of Overshot Water Wheels at High Rotational Speeds for Hydropower Applications. J. Hydraul. Eng. 2020, 146, 06020011. [Google Scholar] [CrossRef]
- Warjito, A.D.; Budiarso, P.A. The effect of bucket number on breastshot waterwheel performance. IOP Conf. Ser. Earth Environ. Sci. 2018, 105, 12031. [Google Scholar] [CrossRef]
- Licari, M.; Benoit, M.; Anselmet, F.; Kocher, V.; Clement, S.B.; Faucheux, P.L. Study of low-head hydrostatic pressure water wheels for harnessing hydropower on small streams. In Proceedings of the Congrès Français de Mécanique, Brest, France, 26–30 August 2019. [Google Scholar]
- Lin, T.; Li, X.; Zhu, Z.; Xie, J.; Li, Y.; Yang, H. Application of enstrophy dissipation to analyze energy loss in a centrifugal pump as turbine. Renew. Energy 2020, 163, 41–55. [Google Scholar] [CrossRef]
- Kock, F.; Herwig, H. Local entropy production in turbulent shear flows: A high-Reynolds number model with wall functions. Int. J. Heat Mass Transf. 2004, 47, 2205–2215. [Google Scholar] [CrossRef]
- Herwig, H.; Fabian, K. Direct and indirect methods of calculating entropy generation rates in turbulent convective heat transfer problems. Heat Mass. Tran. 2006, 43, 207–215. [Google Scholar] [CrossRef]
- Duan, L.; Wu, X.; Ji, Z.; Xiong, Z.; Zhuang, J. The flow pattern and entropy generation in an axial inlet cyclone with reflux cone and gaps in the vortex finder. Powder Technol. 2016, 303, 192–202. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Q.; Zhou, D. Entropy production analysis in thermodynamic cavitating flow with the consideration of local compressibility. Int. J. Heat Mass Transf. 2020, 153, 119604. [Google Scholar] [CrossRef]
- Yu, A.; Tang, Q.; Chen, H.; Zhou, D. Investigations of the thermodynamic entropy evaluation in a hydraulic turbine under various operating conditions. Renew. Energy 2021, 180, 1026–1043. [Google Scholar] [CrossRef]
- Zhao, M.; Zheng, Y.; Yang, C.; Zhang, Y.; Tang, Q. Performance Investigation of the Immersed Depth Effects on a Water Wheel Using Experimental and Numerical Analyses. Water 2020, 12, 982. [Google Scholar] [CrossRef]
- Acharyax, N.; Kim, C.G.; Thapa, B.; Lee, Y.H. Numerical analysis and performance enhancement of a cross-flow hydro turbine. Renew. Energy 2015, 80, 819–826. [Google Scholar] [CrossRef]
- Zhong, H.Z. Fluid’s Engineering Simulation Examples and Applications of Fluent; Beijing Institute of Technology Press: Beijing, China, 2004; ISBN 7564026049. (In Chinese) [Google Scholar]
- Setyawan, E.Y.; Djiwo, S.; Praswanto, D.H.; Suwandono, P.; Siagian, P.; Naibaho, W. Simulation model of vertical water wheel performance flow. IOP Conf. Ser. Mater. Sci. Eng. 2020, 725, 012020. [Google Scholar] [CrossRef]
- Adanta, D.; Muhammad, N.; Rizwanul, F.I.M. Comparison of standard k-ε and sst k-ωturbulence model for breastshot waterwheel simulation. J. Mech. Sci. Eng. 2020, 7, 39–44. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 2269–2289. [Google Scholar] [CrossRef]
- Li, D.; Wang, H.; Qin, Y.; Han, L.; Wei, X.; Qin, D. Entropy production analysis of hysteresis characteristic of a pump-turbine model. Energy Convers. Manag. 2017, 149, 175–191. [Google Scholar] [CrossRef]
- Yah, N.F.; Oumer, A.N.; Aziz, A.A.; Sahat, I.M. Numerical investigation on effect of blade shape for stream water wheel performance. IOP Conf. Ser. Mater. Sci. Eng. 2018, 342, 012066. [Google Scholar] [CrossRef]
- Tao, R.; Wang, Z. Comparative numerical studies for the flow energy dissipation features in a pump-turbine in pump mode and turbine mode. J. Energy Storage 2021, 41, 102835. [Google Scholar] [CrossRef]





| Elements (×106) | Averaged Torque (×105 N·m) | |
|---|---|---|
| Mesh 1 | 1.26 | 2.24 |
| Mesh 2 | 1.46 | 2.20 |
| Mesh 3 | 2.43 | 2.44 |
| Mesh 4 | 3.01 | 2.36 |
| Material | Number of Blades | Flow Velocity (m/s) | Rotational Speed (rpm) | Output in Experiments (KW) | Output in Numerical Result (KW) | Error (%) |
|---|---|---|---|---|---|---|
| Q235 steel | 5 | 1.3 | 5 | 0.34 | 0.35 | 2.9 |
| 6 | 0.55 | 0.57 | 3.5 | |||
| 7 | 0.67 | 0.69 | 4.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Zheng, Y.; Yu, A.; Tang, Q. Experimental and Numerical Analysis of the Clearance Effects between Blades and Hub in a Water Wheel Used for Power Generation. Water 2022, 14, 3640. https://doi.org/10.3390/w14223640
Feng W, Zheng Y, Yu A, Tang Q. Experimental and Numerical Analysis of the Clearance Effects between Blades and Hub in a Water Wheel Used for Power Generation. Water. 2022; 14(22):3640. https://doi.org/10.3390/w14223640
Chicago/Turabian StyleFeng, Wenjin, Yuan Zheng, An Yu, and Qinghong Tang. 2022. "Experimental and Numerical Analysis of the Clearance Effects between Blades and Hub in a Water Wheel Used for Power Generation" Water 14, no. 22: 3640. https://doi.org/10.3390/w14223640
APA StyleFeng, W., Zheng, Y., Yu, A., & Tang, Q. (2022). Experimental and Numerical Analysis of the Clearance Effects between Blades and Hub in a Water Wheel Used for Power Generation. Water, 14(22), 3640. https://doi.org/10.3390/w14223640







