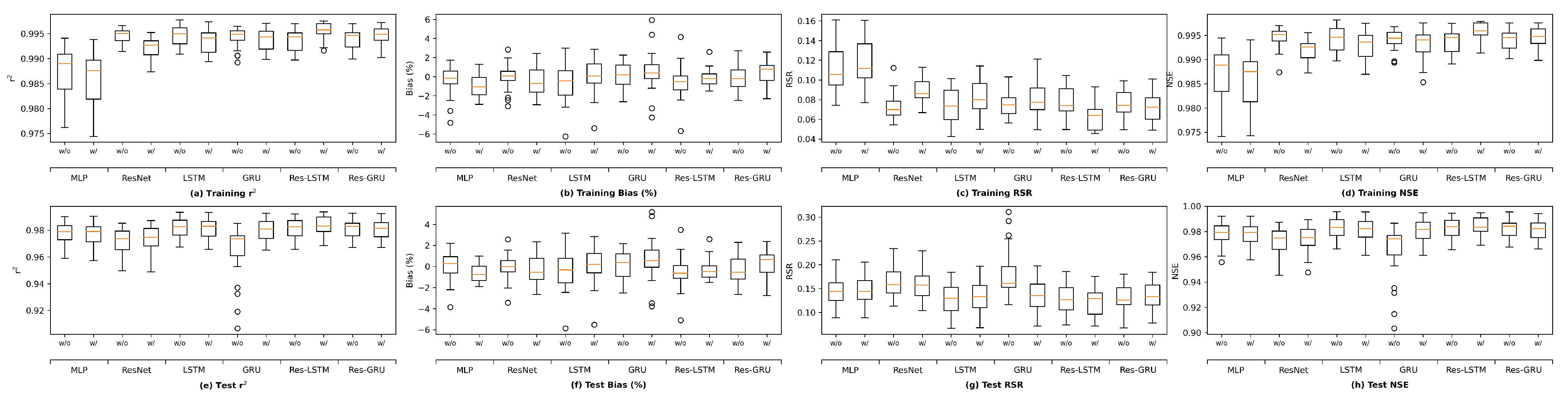
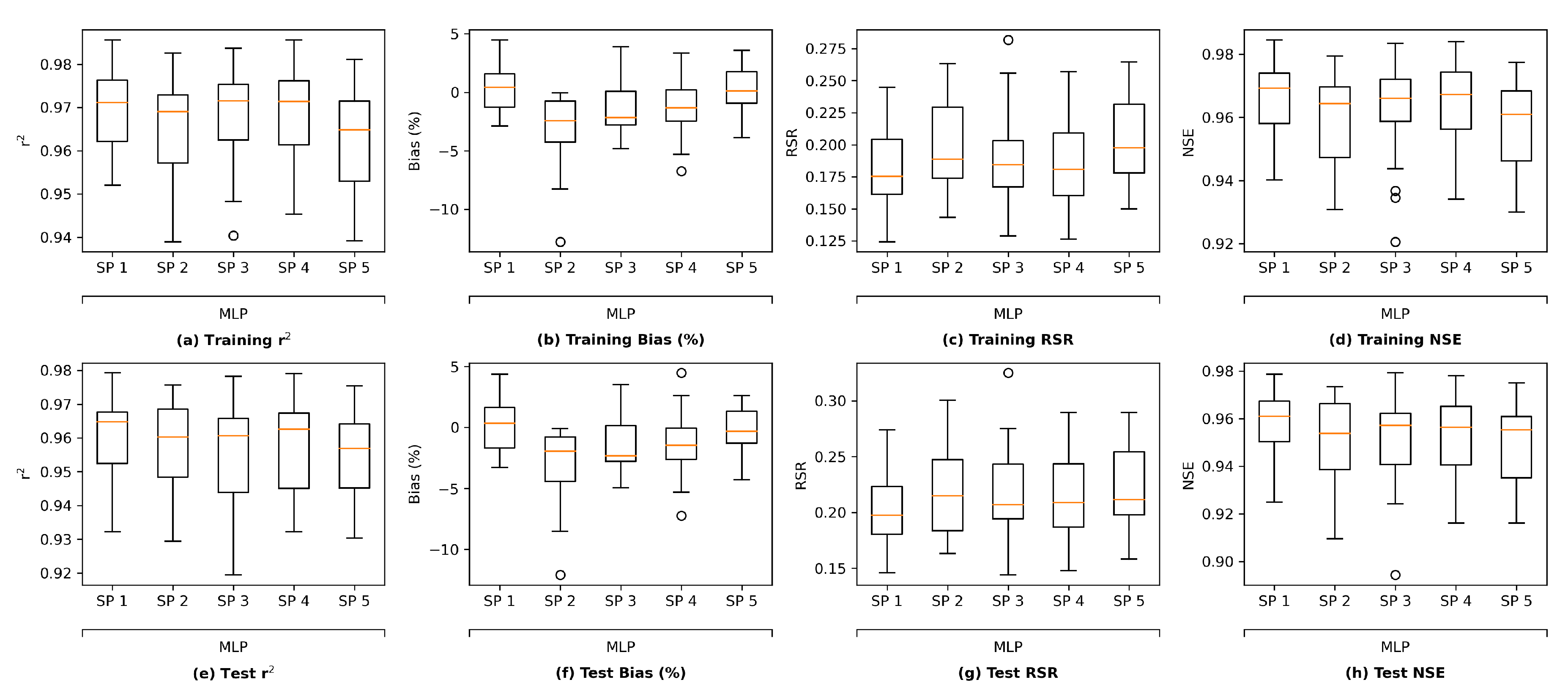
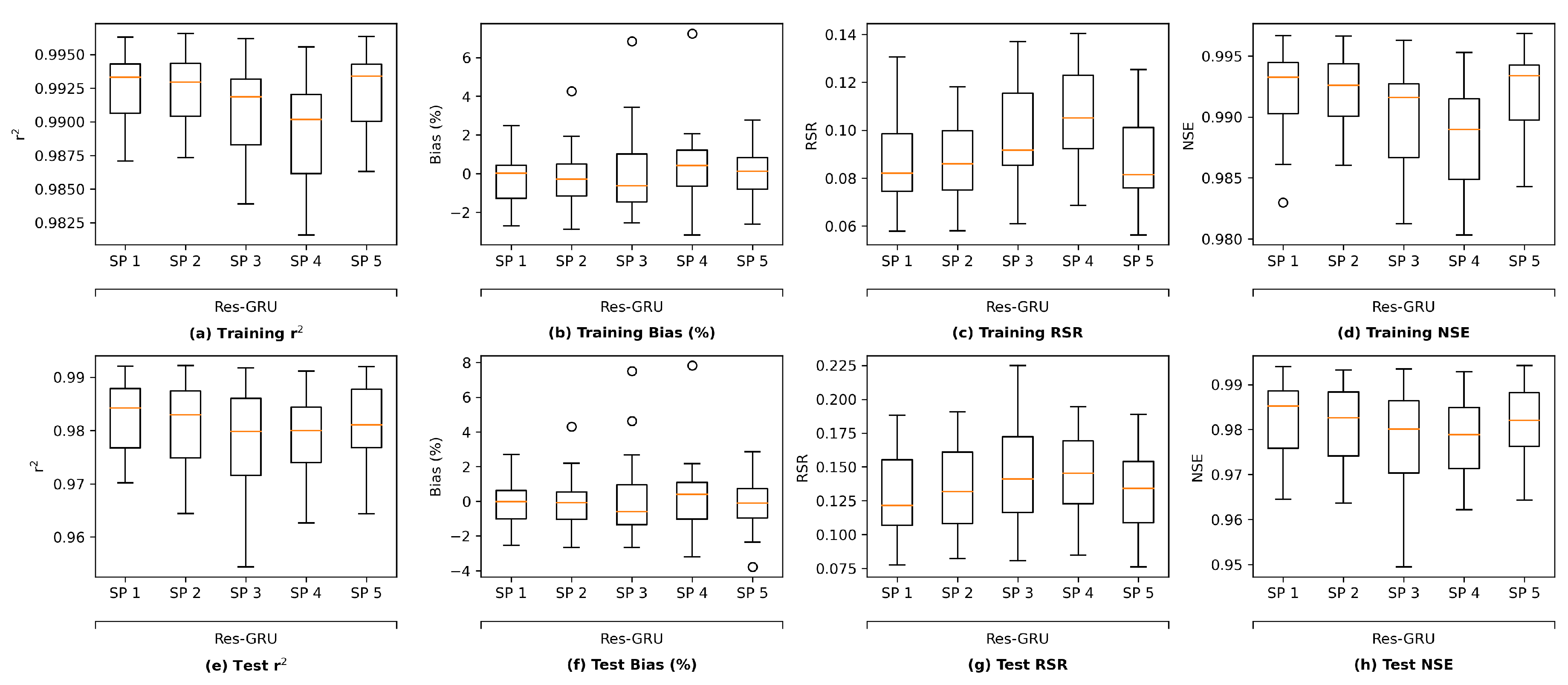
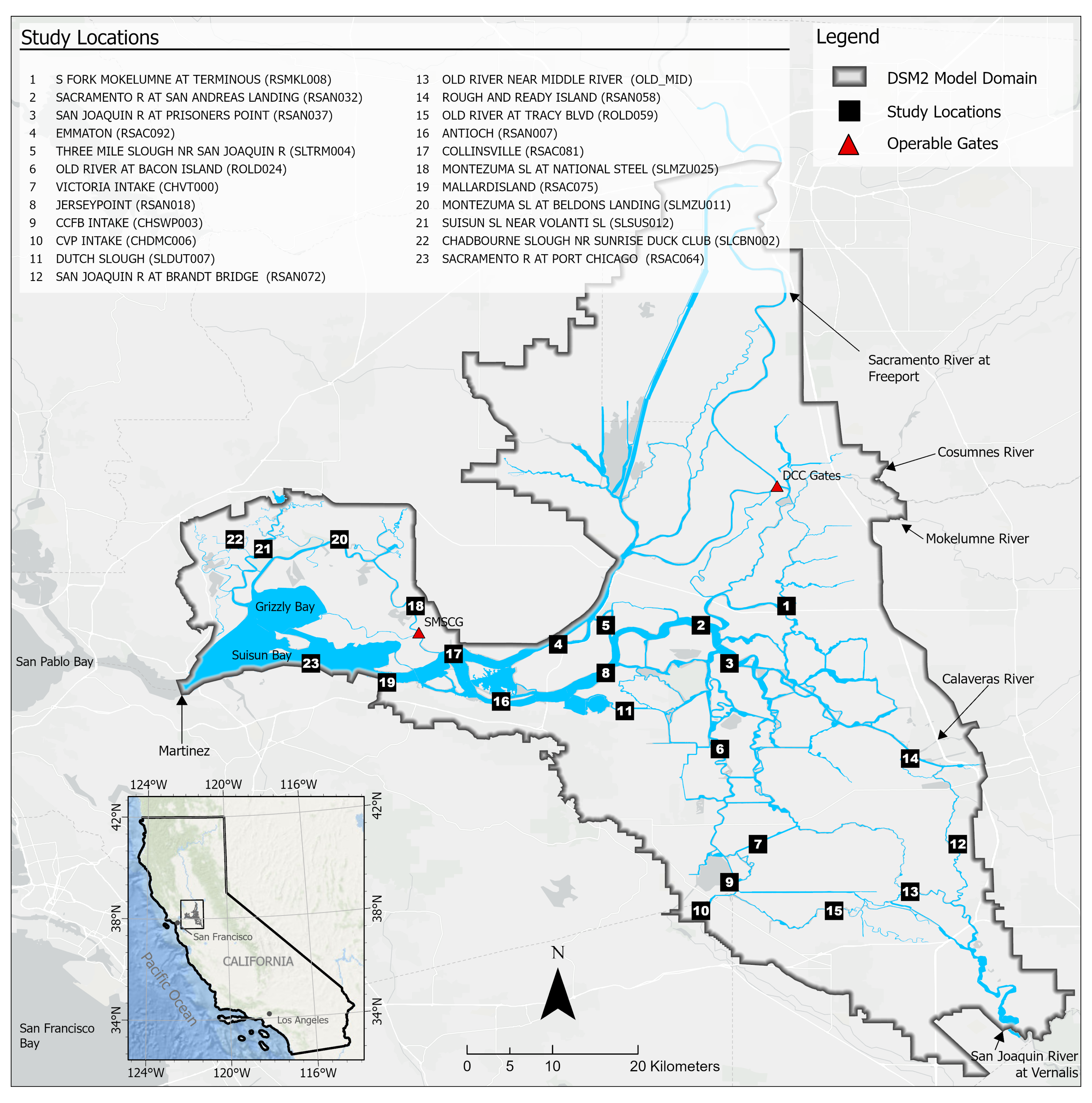
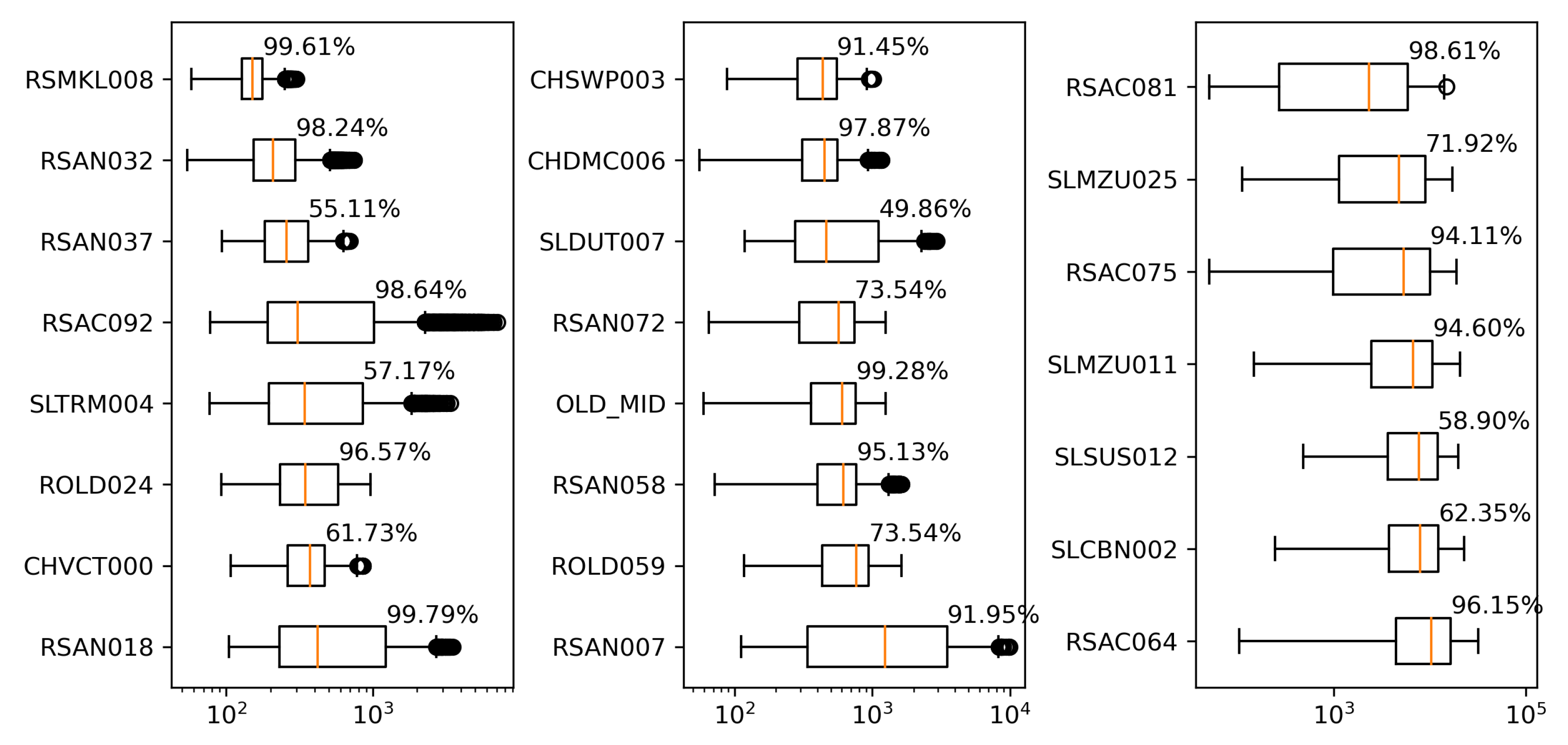
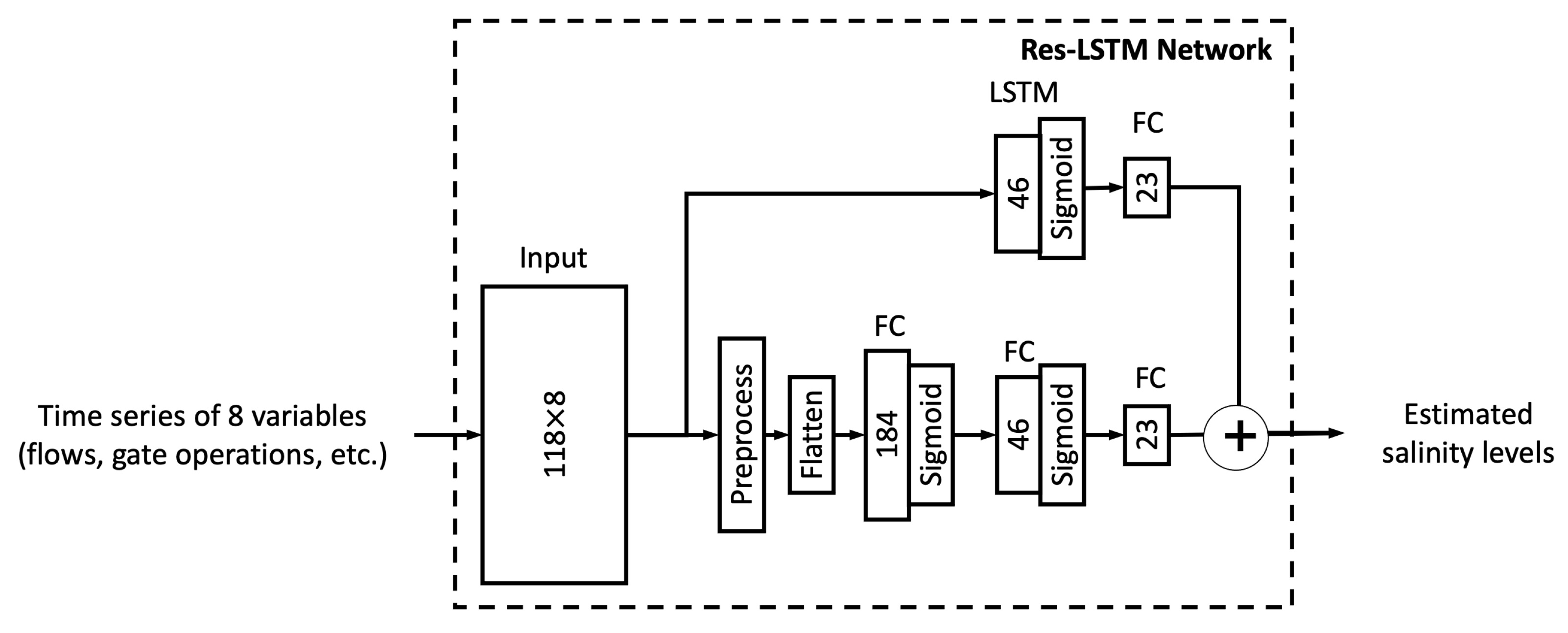
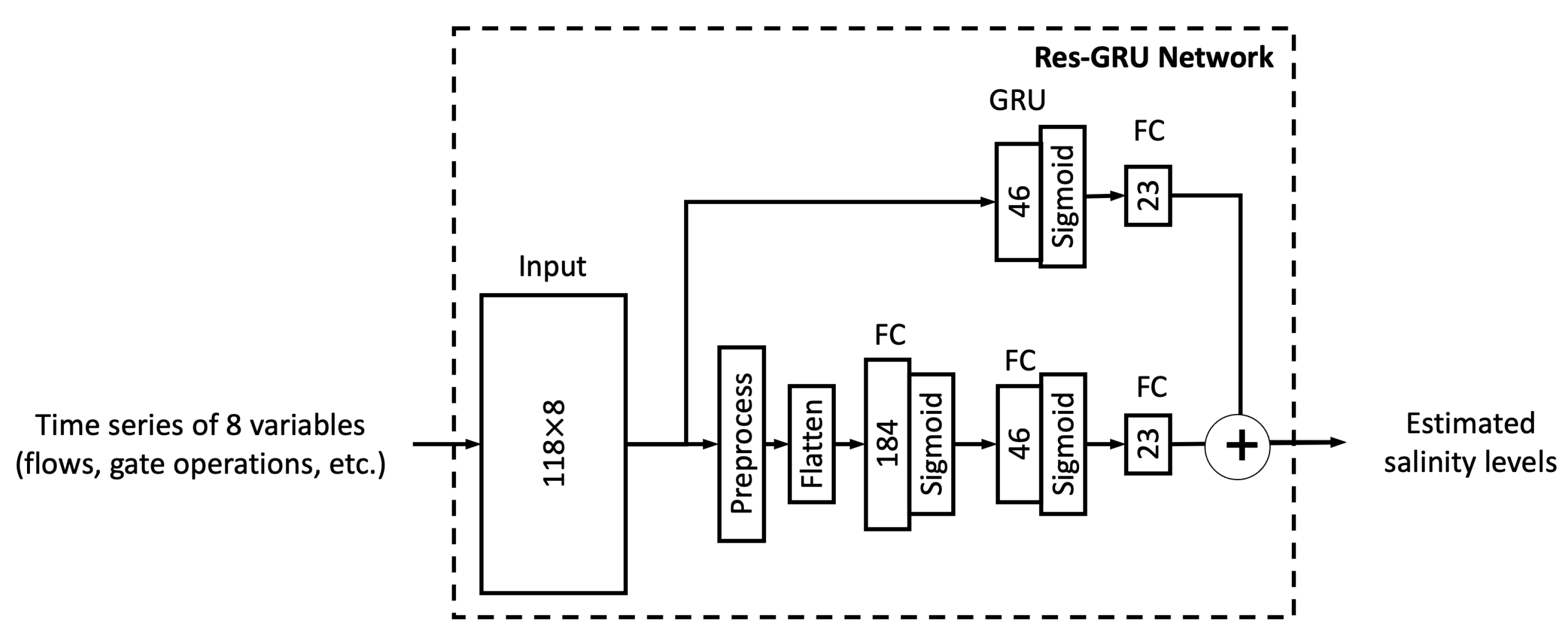
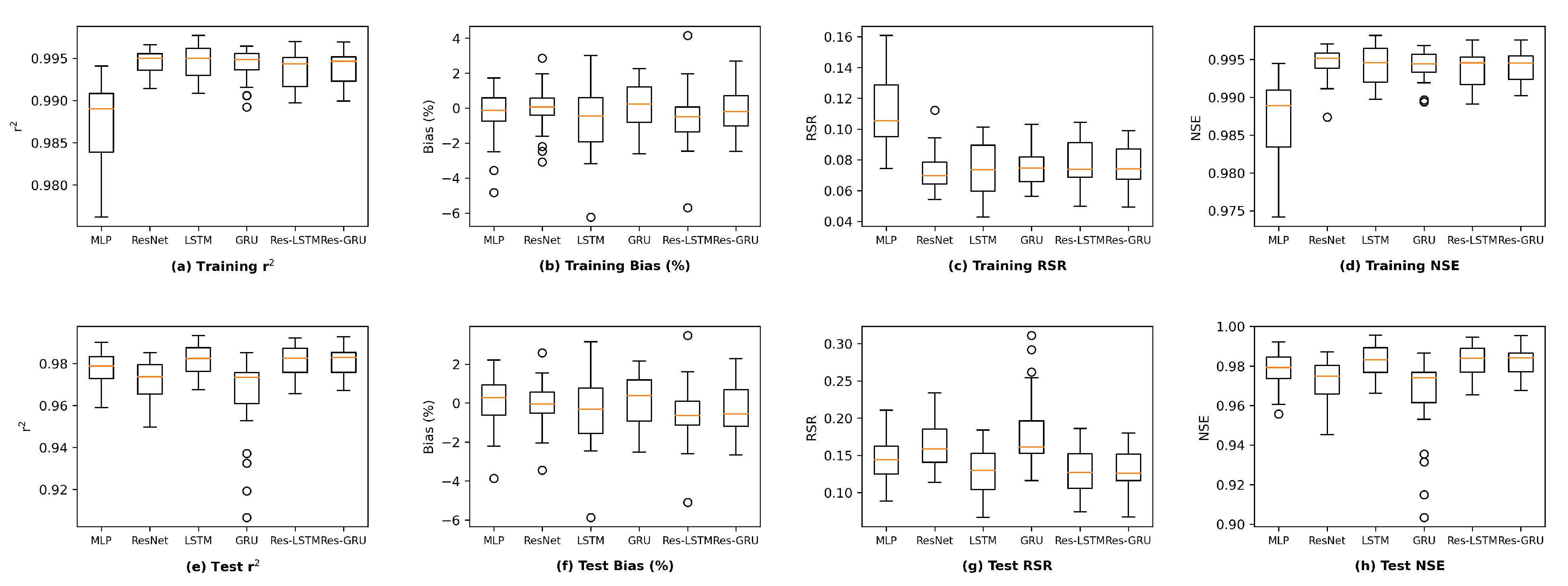
This section first discusses the overfitting potential of the ML models proposed in the study. Second, the performance of a selected ML model is compared with that of the process-based model DSM2, which is widely used to inform water operations in the Delta. Next, the section discusses the scientific and practical implications of the study, followed by discussions on study limitations and planned future work.
4.1. Overfitting Potential versus Model Complexity
Overfitting happens when a ML model picks up the details, including noise, and fits exactly on the training data but does not generalize well on unseen data [
58,
59]. Overfitting is a central problem in the field of data-driven ML, as it negatively impacts the model’s generalization performance on new data. Overfitting is more likely to occur when a model’s structure is too complex for the task. To avoid this problem, the number of neurons or units in the layers need to be determined carefully.
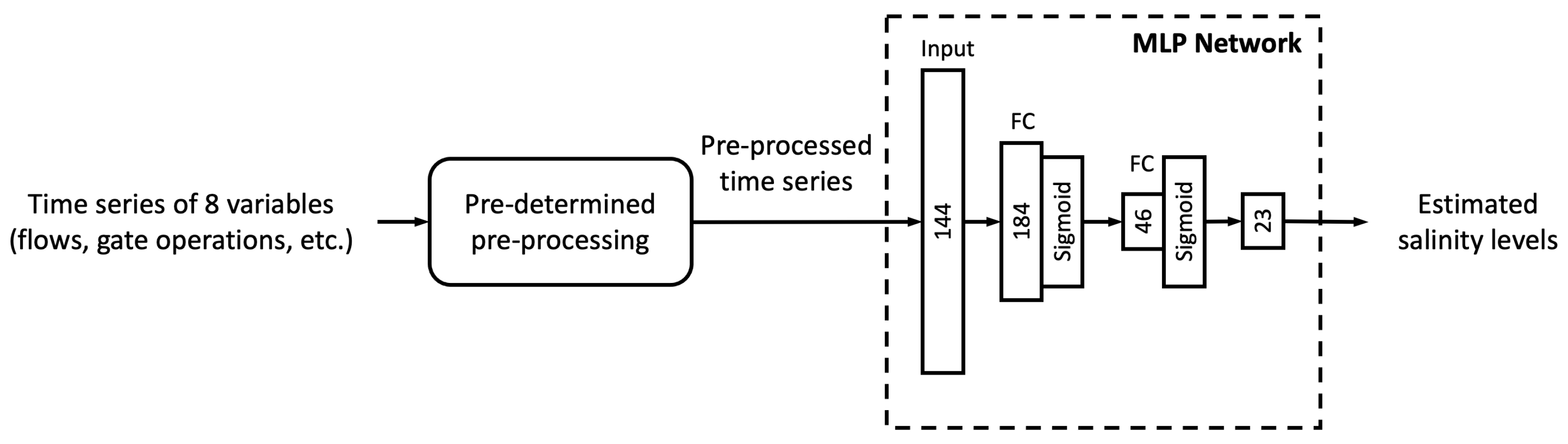
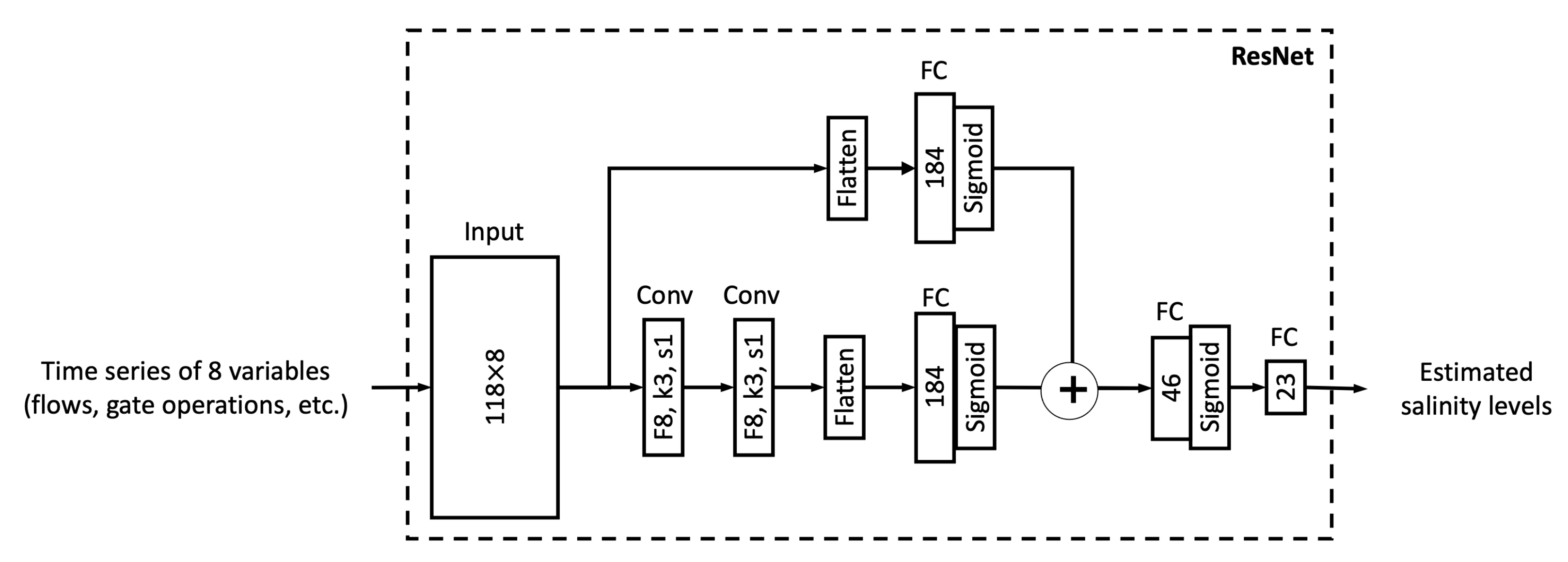
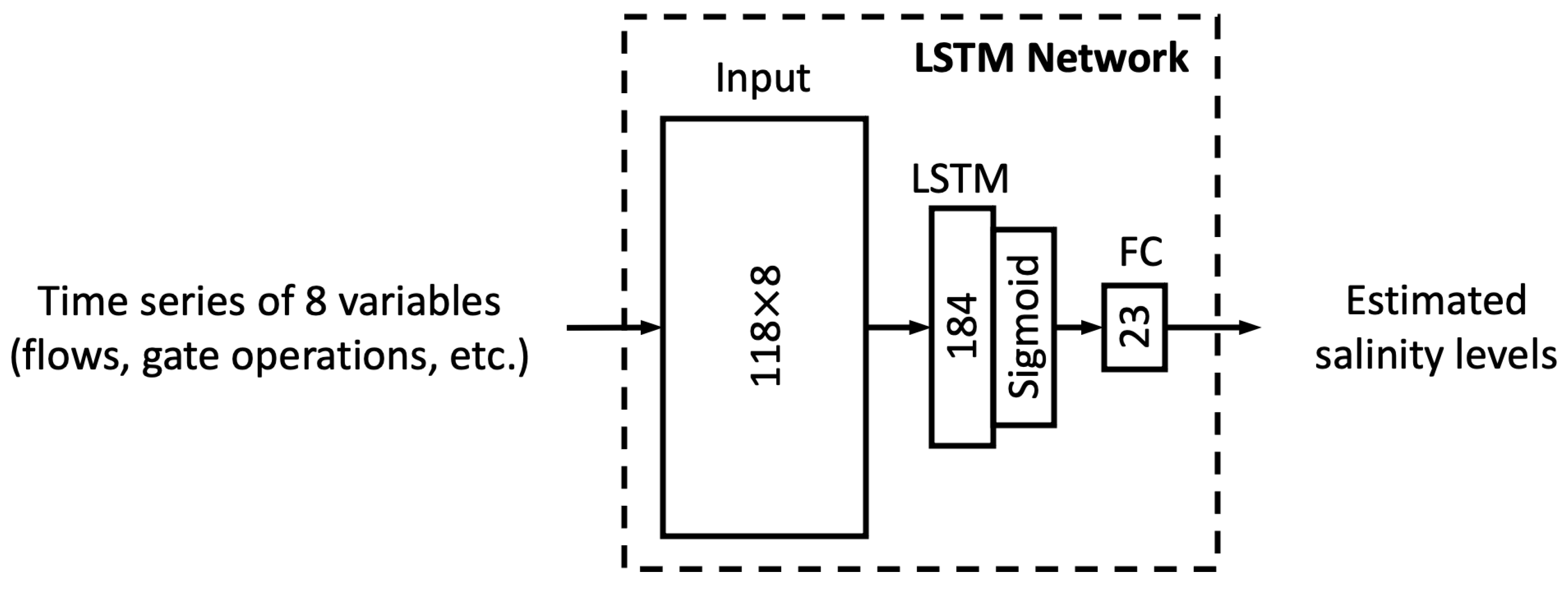
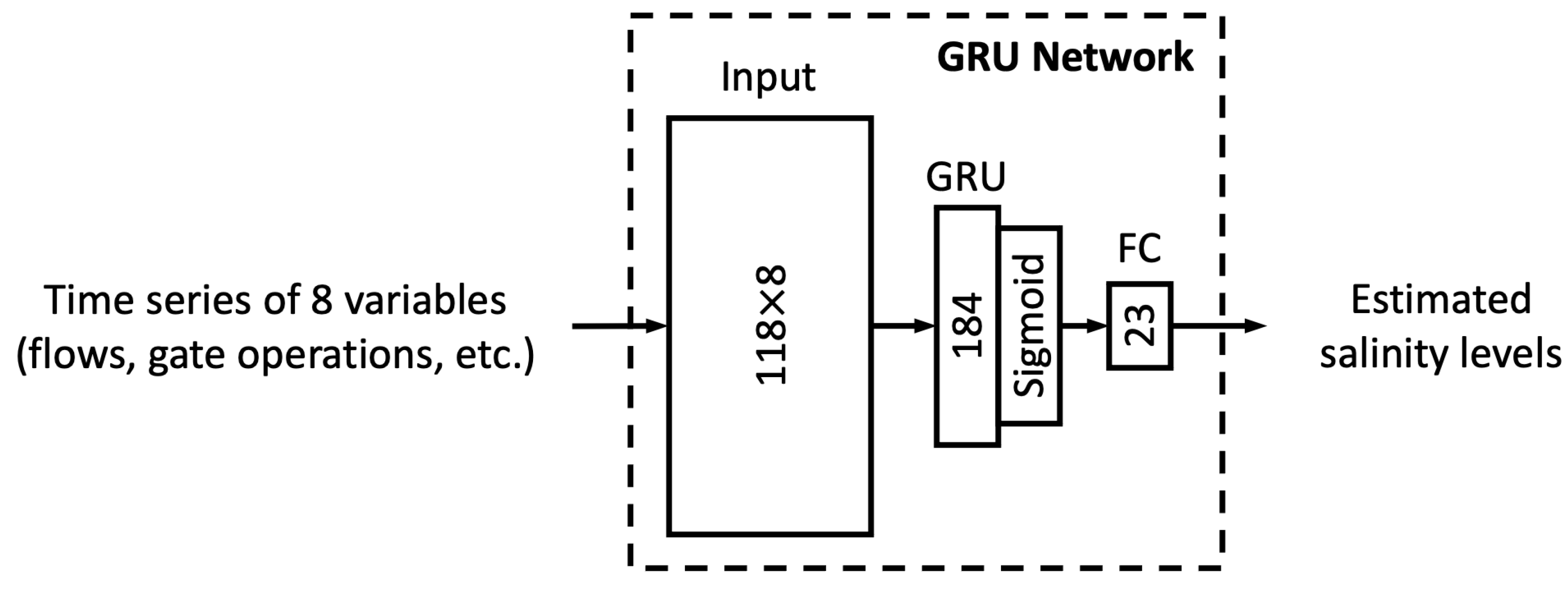
In this study, we proposed six different ML models. In this sub-section, we explore the relationship between model complexity and salinity estimation performance by reducing the number of neurons in the hidden layers of each model. For the MLP, ResNet, Res-LSTM and Res-GRU models, we adjust the number of neurons in two fully connected hidden layers in the main branch, depicted by
and
, respectively. In addition to the original settings, where
and
, we pick four combinations, including
,
,
and
to build four simplified versions as well as five additional combinations of
,
,
,
, and
that lead to complicated versions for each of the four models. For the vanilla LSTM and GRU models, we change the number of units in the recurrent layer from 184 units to 322, 276, 230, 138, 92, 46 or 23 units. A detailed list of the number of parameters in these models can be found in
Table A10 and
Table A11 of
Appendix E.
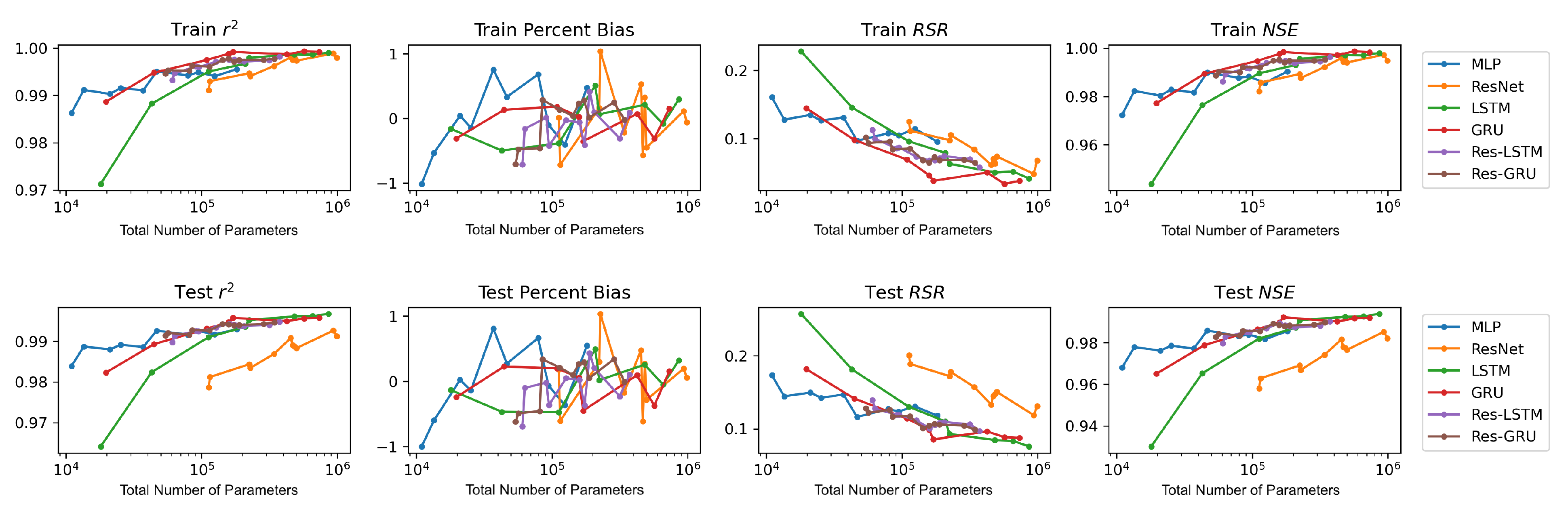
We plot the model performance (in terms of the average value of each evaluation metric across the 23 study locations) versus model complexity (in terms of number of parameters) in
Figure 13. In general, model performance improves as complexity grows. In both the training and test plots of
, RSR and NSE, MLP models show the best complexity–performance trade-off. Namely, the MLP model can achieve a comparable performance with other models with a relatively smaller number of parameters. However, during the grid search process when designing these models, we observed that the MLP model hits a performance plateau earlier than other models, namely, the test performance stops improving, even if we keep increasing the number of neurons in its hidden layers. In contrast, the ResNet model gives the worst complexity–performance trade-off because the extra FC hidden layer in its shortcut branch adds a large number of parameters to the model. Comparing the vanilla RNNs (i.e., LSTM and GRU) and their corresponding Res-RNN models, we see that the simple RNN module in the residual path ensures a satisfying model performance while bringing down the complexity.
In brief, model performance improves as the complexity grows but both training and test performance will hit a plateau at some point. No obvious overfitting was observed during our exploration, suggesting that the proposed models are not over-parameterized and well-trained.
It is worth noting that there are other methods that can be applied to assess the overfitting potential of machine learning models. The current study briefly explored two of those methods, namely data distortion and cross validation for demonstration purposes. The results (
Figure A5–
Figure A8 in
Appendix F) also indicated that no evident overfitting was observed.
4.2. Comparing with a Process-Based Model
It is shown in
Section 3 that the proposed ML models in this study, particularly the novel Res-LSTM and Res-GRU models, can simulate and predict real-world salinity in the Delta well. Traditionally, process-based models, including the operational hydrodynamics and water quality model DSM2, have been applied to simulate and predict the spatial and temporal variations of the salinity across the Delta. It is imperative to assess the performance of these ML models against that of the operational process-based models. For illustration purposes, this sub-section compares simulations from the Res-LSTM model and its counterparts from DSM2.
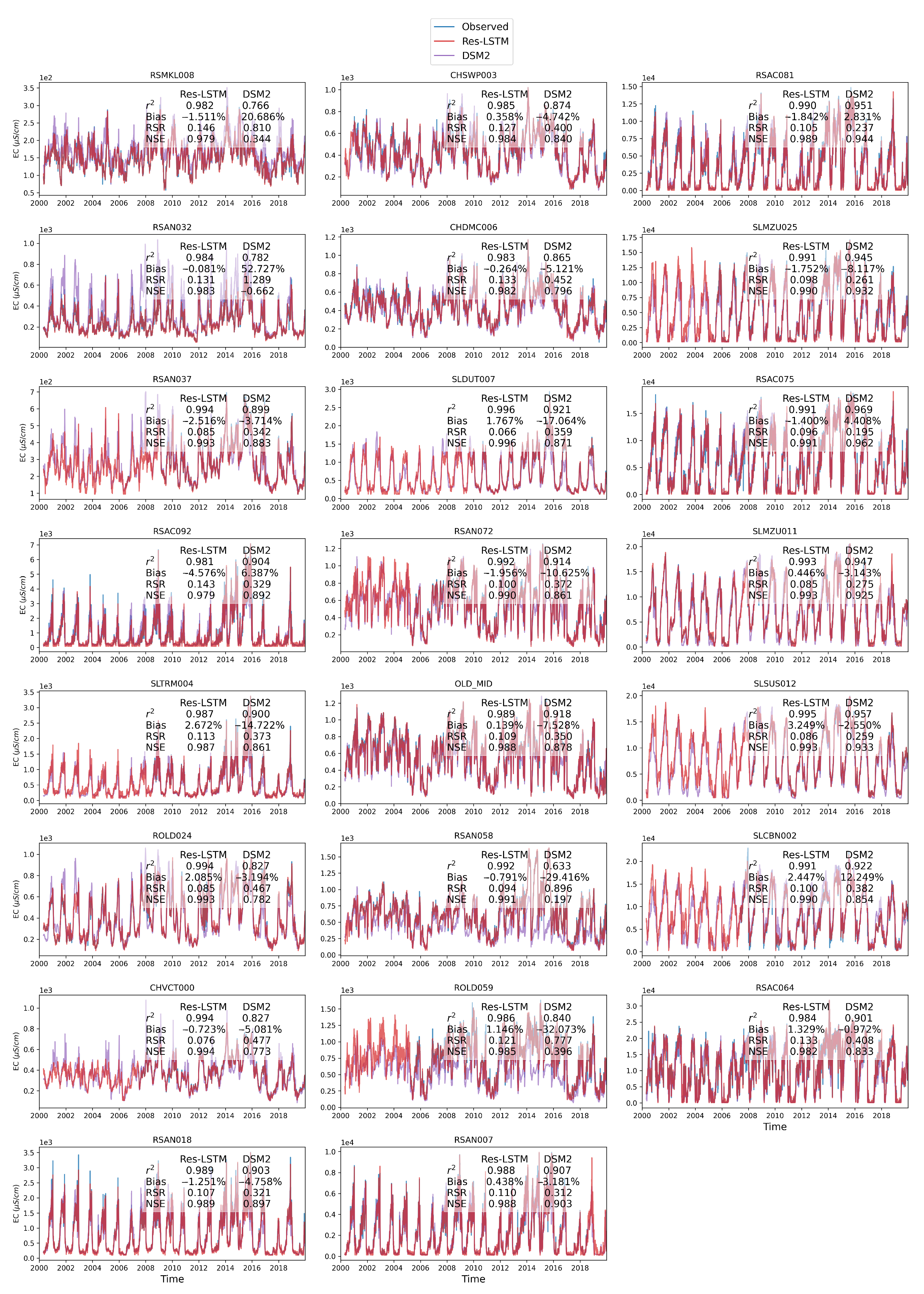
The comparison is conducted by means of both visual inspection and evaluating statistical metrics.
Figure 14 shows the comparison among time series plots of the measured DSM2-simulated and Res-LSTM-simulated EC data at six selected key stations. Four study metrics (
, Bias, RSR, NSE) of both sets of models are also displayed side-by-side to conduct quantitative comparison. The corresponding comparison for all 23 study locations is provided in
Appendix G. Both simulations mimic the target filed measurements of salinity very well via visually inspecting the time series plot. The overall biases of both models are generally small. For Res-LSTM, the absolute bias ranges from 0.3% to 4.6%. The
, RSR and NSE values of Res-LSTM are notably better than their counterparts of DSM2 for all six locations. Collectively, these observations indicate that Res-LSTM yields comparable or more desirable salinity simulations compared to the operational DSM2 model.
Nevertheless, it should be pointed out that DSM2 can generate salinity simulations not only at the 23 study locations, but at all channels across the Delta. The ML models proposed in the study can only be applied to study locations where they have been trained, and thus are not meant to be substitutes of process-based models, including DSM2.
4.3. Implications
This study has important scientific implications. Firstly, the study exemplifies the feasibility of applying ML, particularly deep learning models, as a new scientific exploratory tool to tackle a complex problem. Secondly, this study proposes two novel deep learning models (i.e., Res-LSTM and Res-GRU) that have never been explored before. These novel models can be applied to simulate other variables, including water temperature, suspended sediment, dissolved oxygen, and other water quality variables, that are important to guide water management practices in the Delta. Thirdly, this study illustrates the forecasting capability of newly developed deep-learning models. Effective and efficient forecasting models are valuable tools that can guide real-time operations in light of forecast near-term salinity conditions.
There are also important practical implications of this study. The study demonstrates that the proposed ML models are capable of generating desirable salinity simulations and predictions even on the hourly scale. The overall absolute biases are generally less than 5%. The correlation coefficients, RSR, and NSE values are generally satisfactory. They are either comparable or superior compared to the corresponding metrics of the DSM2 model. In addition to accuracy, the proposed ML models are also of high efficiency. DSM2 runs can take hours depending upon the simulation period length [
28], while the runtime for trained ML models for the same inputs is measured in seconds. This is particularly appealing, for instance, for real-time operations which require quick turn-around time and also studies that require running multiple scenarios during the historical period.
4.4. Limitations and Future Work
Despite those scientific and practical implications, this study has several limitations. First of all, the current study randomly splits the dataset into a training subset and a test subset. Though random split of training/testing in not uncommon in ML studies in the Delta [
2,
10,
26,
27,
28,
54], there are other data-split methods available. Ref. [
29] examined chronological split and manual split and found that the performance of the random split method yielded improved results over the other methods. Since the observed data are about one-third shorter than the simulated data used in [
29], this study did not employ the chronological/manual methods. In our future work focusing on larger datasets, we will explore chronological split and manual split methods. In addition, explainable artificial intelligence (XAI) is an active research area [
60]. There have been a number of XAI approaches developed. In our future work, we plan to explore various XAI approaches, including the gradient-based method [
61] and the backpropagation-based method [
62], and the input variable sensitivity analysis [
57], and conduct in-depth investigation of the importance of different inputs features in different regions and locations in the Delta.
This study used eight empirical variables as input features to the proposed models. They were shown to yield desirable salinity estimation at the study locations. However, other variables, including precipitation and wind speed, also influence the circulation and mixing of freshwater and sea water and thus affect the salinity level in the study area. In our future work, we will also explore the impacts of additional input features on the ability of the proposed models to estimate Delta salinity.
In this study, the ML models are trained and tested on historical time series. The selected range of data may not capture potential hydrologic extremes or increased water use. Climate change is expected to cause larger storm-driven streamflow and altered runoff timing [
63]. In addition, in the coming decades, municipal, industrial and agricultural water demand in California is projected to increase from increasing urbanization and changing agricultural practices [
64]. The models trained on historical data, therefore, will not be exposed to the range of inflows and operational constraints resulting from potential future conditions. Additionally, the ML models are trained using data from 23 study locations and can thus only be applied to those study locations. In the future, we will explore generic ML models capable of generating salinity estimates at locations they are not trained upon.
Exclusively using the historical record for training may also introduce shortcomings when conducting long-term planning studies, as the training dataset is not modified beyond the scope of historical operational considerations. In real-time operations and planning, measures such as emergency barriers and temporary operational regimes may be implemented to manage flow and salinity. Operational measures include emergency temporary barriers [
65] to manage salinity intrusion and maintain acceptable water quality at pumping locations. The historical time series reflects limited use of emergency operational measures and does not consider the operation of the Suisun Marsh Salinity Control Gates (SMSCG). The limitations associated with using a historical dataset during training will be addressed in future work, where the model will be trained using synthetically augmented datasets.
Data augmentation is a technique to generate synthetic data for model training, which incorporates an enlarged and diversified dataset to better represent extreme conditions and possible future conditions. In our ongoing preliminary tests, we use DSM2 historical simulation as the baseline, then apply several modifications, including (1) scaling the magnitude of major boundary flows; (2) temporally shifting major boundary flows; and (3) changing operations of key Delta structures, such as operable gates. All of the above aim to reduce overfitting and thus improve the generalization ability of the trained neural networks. Another benefit of data augmentation is that it can provide sufficient time series for chronological split training to bypass the limit of random split method.
In another follow-up work, we plan to explore the physics informed neural network (PINN), a cutting-edge neural network algorithm which can embed the knowledge of physical laws into data training. Most of the physical laws governing the dynamics of a system can be described by partial differential equations (PDEs). PINN adds the underlying PDE of the dynamics directly into the loss function of the neural network [
66,
67]. For our study, we plan on implementing PINN with the one-dimensional advection–dispersion equation for salinity transport [
14,
68].
PINN can be viewed as a regularization limiting the space of admissible solutions, through adding the prior knowledge of general physical laws in the training of neural networks. Its benefits include increasing the correctness of the function approximation, facilitating the learning algorithm to capture the right solution, generalizing well, even with a low amount of training examples, and providing a meshfree alternative to traditional approaches. PINN could also be viewed as a paradigm that bridges the gap between the process-based models, which are developed from the known PDEs of the dynamics, and the machine-learning models, which are driven purely by existing data. By integrating the best of both methods, namely, the physics information of the process-based models and the training data employed in the machine-learning models, PINN could learn the underlying solution of the dynamics more accurately and more efficiently.
Moreover, this study explored the forecasting capability of the two proposed novel ML models using historical data up to the forecast time only. The main reason is that we do not have forecasted input variables available. It is expected that the performance of the ML models would be even more satisfactory should forecasted model inputs be used to drive the models. In a follow-up study, we plan to collect archived forecasted inputs and salinity data from real-time operations, and develop ML models based on them, and test the trained model in a hindcasting mode.
Lastly, we are developing an interactive dashboard to integrate and visualize our modeling results. It is designed as a front-end to the trained neural network model engine, allowing users to customize data inputs, run the ANNs, and query results. The proposed dashboard could generate a visualization of the time-series output and their proposed metrics for all the specified locations across the Delta. This tool could facilitate management decisions in historical, real-time, and forecast applications.