1. Introduction
Flood frequency analysis (FFA) is considered as one of the most widely used approaches for estimation of design floods, which requires recorded streamflow data of adequate length at the site of interest. At many stream-gauging sites, the length of recorded flow data is quite short and furthermore there are numerous streams which are ungauged. For these ungauged catchments, regional flood frequency analysis (RFFA) is generally adopted to estimate design floods [
1,
2].
The linear RFFA models assume a linear relationship between the dependent variable (for example, flood quantile) and the predictor variables (physio-meteorological such as mean annual rainfall and catchment area). Hydrological processes are inherently complex in many ways, including nonlinearity [
2]. In many cases, the linearity assumption in hydrology may not be satisfied (for example, larger catchments behave differently than smaller ones and drier antecedent catchment state produces relatively smaller runoff than wetter one for a given rainfall). Non-linear methods have seen a limited application in RFFA. Several studies have tested several nonlinear methods to RFFA, e.g., [
3,
4,
5], and these studies have found that nonlinear methods outperform linear methods in general. Because of the development of new statistical tools and computer programmes, the use of more general non-linear methods, such as the generalised additive model (GAM) [
6,
7], has increased, e.g., [
8,
9]. GAMs have been successfully used in environmental studies [
10,
11], renewable energy assessment [
12], public health and epidemiological research [
13,
14].
GAM has been used in meteorology in a variety of ways. For example, Guan et al. [
15] used GAM to predict temperature in mountainous regions, while Haddad and Vizakos [
16] used GAMS to assess air quality pollutants and their relationship with meteorological variables in four suburbs of greater Sydney, Australia. Tisseuil et al. [
17] used statistical downscaling of general circulation model outputs to local-scale river flows using generalised linear model (GLM), GAM, aggregated boosted trees (ABT), and multi-layer perceptron artificial neural networks (ANN). When simulating fortnightly flow percentiles, they found that the non-linear models GAM, ABT, and ANN outperformed the linear GLM in general. GAM was used by Morton and Henderson [
18] to estimate nonlinear trends in water quality in the presence of serially correlated errors. They observed that GAM produced more reliable results and could more accurately estimate the variance structure. Asquith et al. [
19] used GAMs to develop prediction equations to estimate discharge and mean velocity from predictor variables at ungauged stream locations in Texas. According to Asquith et al. [
19], the incorporation of smooth functions is the strength of GAMs over simpler multilinear regression because appropriate smooth functions can accommodate components of a prediction model that are otherwise difficult to linear model. The developed GAM-based non-linear models were found to provide more accurate prediction in their study.
Wang et al. [
20] used non-stationary Gamma distributions and GAM to model summer rainfall from 21 rainfall stations in China’s Luanhe River basin. Galiano et al. [
21] used GAM to model droughts in southern Spain by fitting non-stationary frequency distributions. GAM was used by Shortridge et al. [
22] to simulate monthly streamflow in five highly seasonal rivers in Ethiopia. Dam reservoirs subjected to varying hydrological regimes frequently produce nonlinear runoff-sediment relationships that are difficult to describe using current reservoir indicators [
23]. The evolution of the runoff-sediment relationship in the Xiliu Valley, a tributary of the Upper Yellow River on China’s Northern Loess Plateau, was investigated in this study using tests for tendencies and abrupt changes. Runoff and sediment loads were simulated using GAMs as smooth functions of significant physical covariates such as reservoir indices. The results revealed significant downward trends in both annual runoff and sediment series, implying that GAMs should be adopted in changing environments dominated by nonlinearity. The use of GAM in RFFA has received little attention. Chebana et al. [
2] used a dataset of 151 hydrometrical stations from Quebec, Canada, to compare several RFFA methods (both linear and non-linear). They found that RFFA models based on GAM outperformed linear models, including the most used log-linear regression model. Smooth curves in GAM allowed for a more realistic understanding of the physical relationship between dependent and predictor variables in RFFA.
Rahman et al. [
24] used data from New South Wales (Australia) to test the applicability of the GAM model in RFFA and found promising results. Rahman et al. [
25] investigated the use of independent component analysis (ICA) in RFFA. This study analysed data from 88 catchments in New South Wales (NSW), Australia. The ICA was used in conjunction with both the quantile regression technique (QRT) and the parameter regression technique (PRT). As potential predictor variables, eight physio-climatic variables were used in this study. Independent components (IC) were used as predictor variables in ICA, and the best predictors were chosen using a ‘cumulative percent relevance’ criterion. A leave-one-out (LOO) validation by Haddad et al. [
26] used GAM to evaluate the performance of the competing models using a suite of statistical evaluation measures. The QRT model with four predictors and the PRT model with all the ICs as predictors were found to outperform the other candidate models. The results were comparable to the reported relative error values for the RFFA technique recommended in the Australian Rainfall and Runoff (ARR) handbook.
Isfahani and Modarres [
27] investigated non-stationary flood frequency analysis in non-stationary conditions using the GAM for parameter estimation for the location, scale, and shape of the GEV distribution for quantile estimation. Msilini et al. [
28] evaluated and compared several regional estimation models in this study. These models were then used for RFFA at ungauged catchments in the Montreal region of southern Quebec, Canada. To delineate homogeneous regions, two neighborhood approaches were used in this study: canonical correlation analysis (CCA) and the region of influence (ROI) method. For RFFA, three regression methods, namely log-linear regression model (LLRM), GAM, and multivariate adaptive regression splines (MARS), which were recently introduced in the RFFA context, were considered. The results showed that MARS and GAMS used in conjunction with the CCA approach outperformed all other regional approaches considered.
To summarise, GAM allows for the accounting of potential nonlinearities in RFFA, which cannot be achieved using linear models or simple variable transformations such as log or power methods. There has been little application of GAM in RFFA. To fill this knowledge gap, the aim of this study is to test the applicability of GAM to Victoria State of Australia and compare results with linear RFFA technique. This will assist to select more accurate RFFA technique for practical application in Victoria. The remainder of the paper is organised as follows:
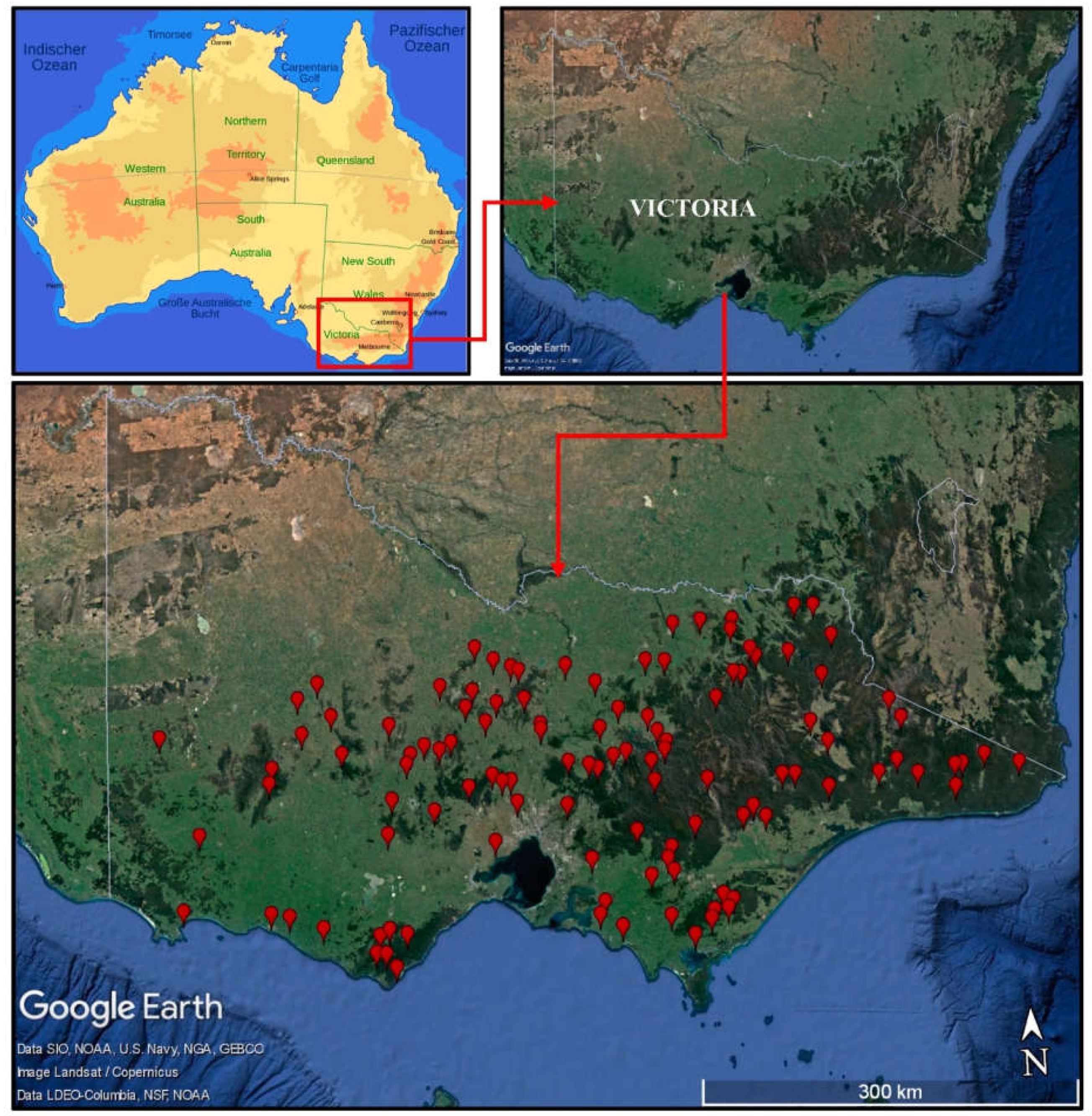
Section 2 presents the study area and dataset used;
Section 3 explains the methodology used in this study; and the results and discussion of the study are presented in
Section 4. Finally, discussion, and conclusions are provided in
Section 5 and
Section 6, respectively.
4. Results
The study is based on a variety of alternative groups, such as a combined group made up of all the 114 catchments and sub-groups formed by cluster analysis. Using hierarchical and k-means clustering techniques, four regions are formed: A1 (79 stations) and A2 (35 stations) from Wards-Manhattan clustering, and B1 (67 stations) and B2 (47 stations) from K-Means clustering. All these four groups and the combined sites in a single group are employed in the development of log-log linear models and GAM-based models.
Linear regression analysis is carried out using the dataset and backward stepwise procedure is followed to choose the catchment characteristics for model development.
Table 2 shows the overall model statistics for the 6 different ARIs. The major statistical measures used are coefficient of determination (
R2),
p-value and standard error of estimate (SEE).
R2 values range from 0.69 to 0.53, respectively for
Q2 to
Q100. The
R2 values are found to be particularly small for higher ARIs, indicating that the variance explained by catchment characteristics becomes smaller, resulting in higher model error variance of prediction for higher ARI flood estimation. All the
R2 values are modest to reasonable, indicating that the prediction equations are generally well-fitting. The SEE ranges from 0.22 to 0.32 for
Q2 to
Q100. SEE is found to be lowest in
Q2 and highest in
Q100. The predictor variables selected in the final model with the
p-statistics value of ≤0.05 are shown in
Table 2. From
Table 2, the area and I
6,2 appear to be the most important variables for estimating
Q for log-log linear model. These two variables are common with all the prediction equations. The next most important predictor variable is found as rain which appears in every prediction equation except for
Q2 and
Q5. Only for
Q2, sden is selected whereas rain is absent as predictor variable. For
Q5, both rain and sden are selected as predictor variable. Overall, the prediction equations show consistency in selection of independent variables except for
Q2 and
Q5.
Table 2 shows the variables of the developed prediction equations.
The log-log linear models are assessed using the
Qpred/
Qobs ratio and the median relative error (RE).
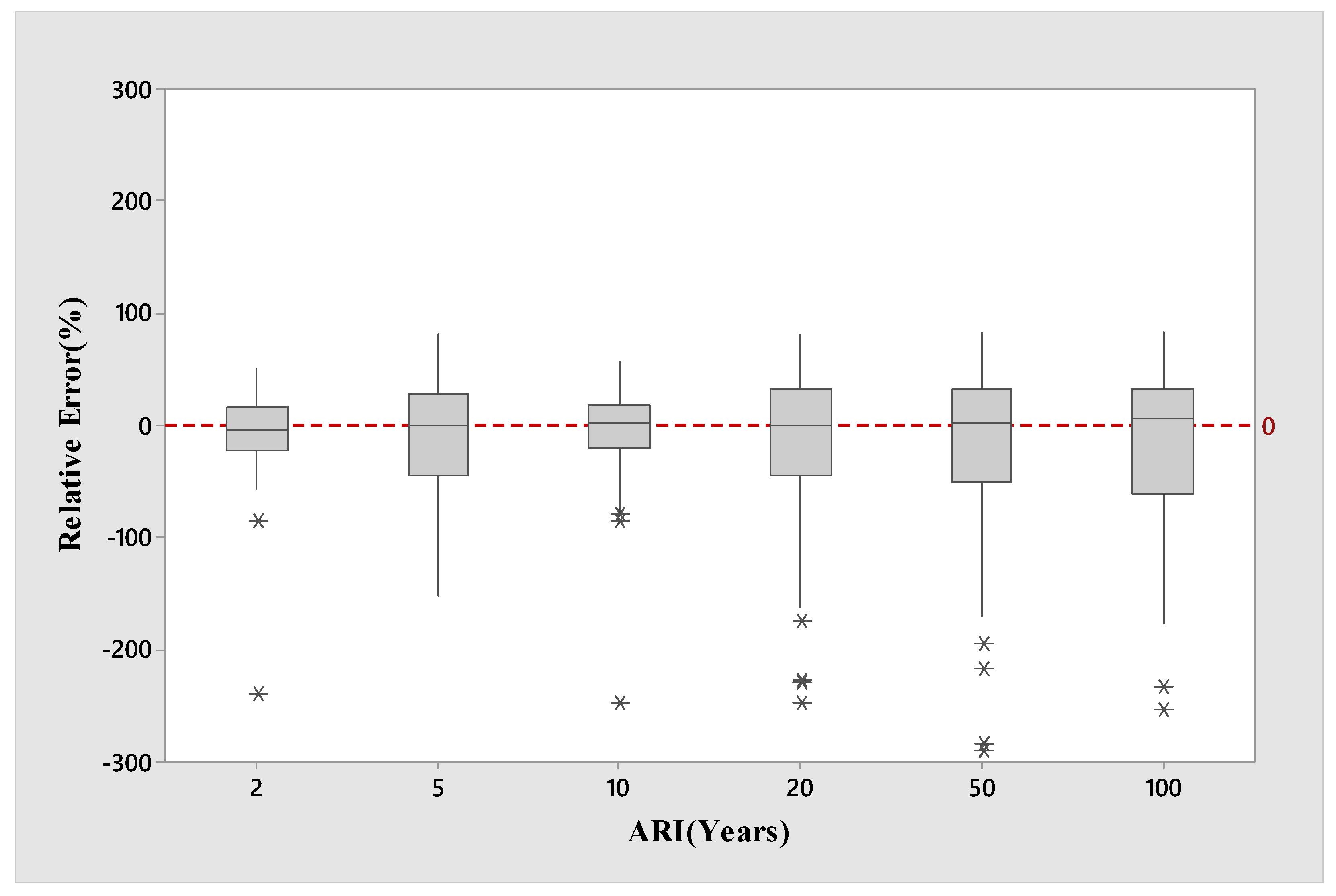
Figure 2 depicts boxplots of RE values for the log-log linear model for the combined group’s selected test catchments.
Figure 2 shows that the median RE values (represented by the black line within a box) match very well with the 0:0 line for ARIs of 5 and 20 years and are relatively good for ARIs of 10 and 50 years. Some underestimation is observed for ARI of 2 years. The underestimation is remarkable for an ARI of 100 years. The ARI of 2 years has the lowest spread in the RE band, which is represented by the total spread of the box. The RE band for ten years ARI is very similar to the RE band for two years ARI. The RE band for 100 years ARI is more than twice than the RE bands for 2 and 10 years. These results show that in terms of RE, 10 years ARI achieve the best results, followed by 2 years ARI. Higher ARI flood quantiles are associated with a higher degree of spread in the RE, which could indicate a higher standard deviation of the estimate. This matches the findings of Haddad and Rahman [
31] and Rahman et al. [
32]. This is generally the case in RFFA as essentially, we are making predictions beyond the limits of the original data space.
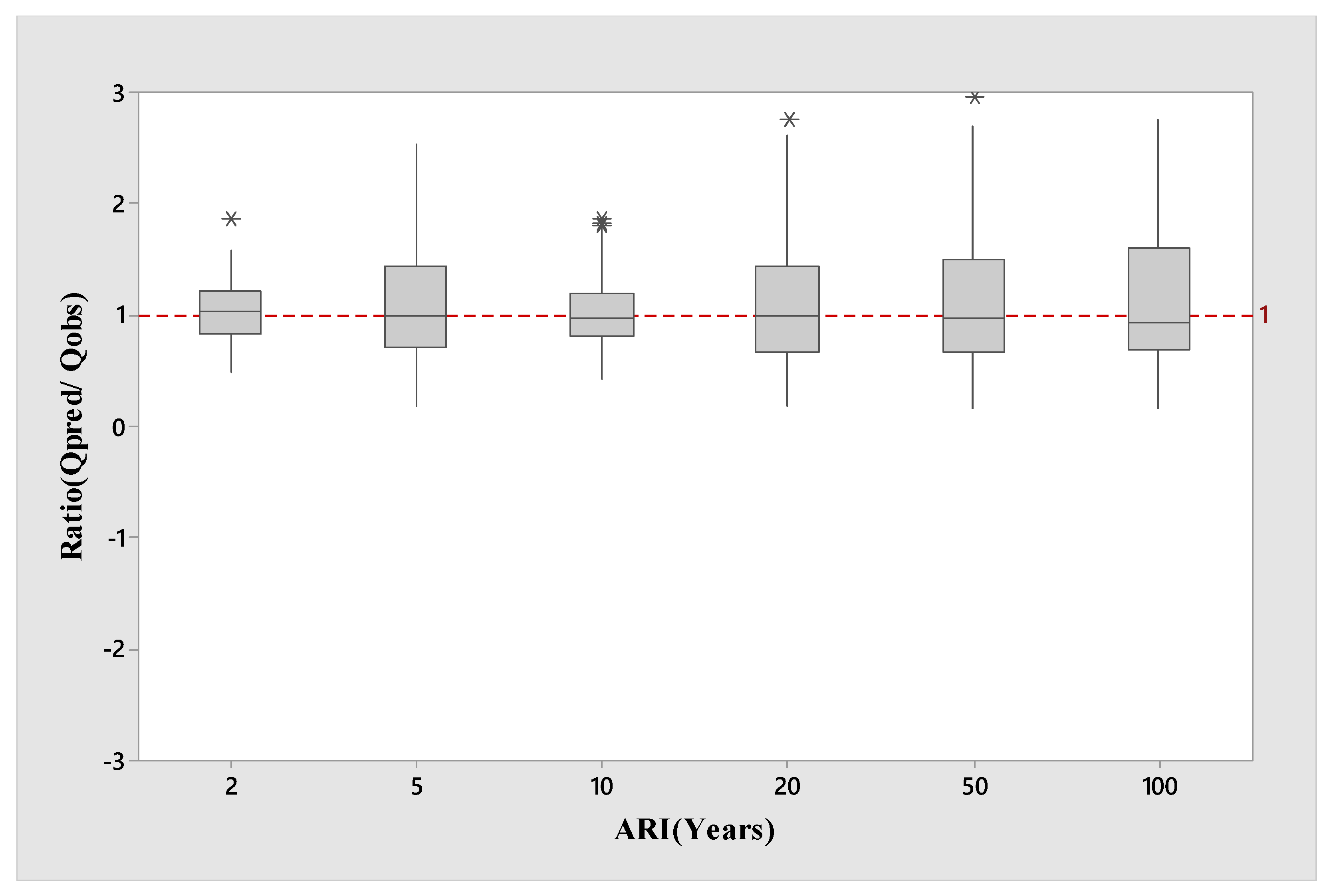
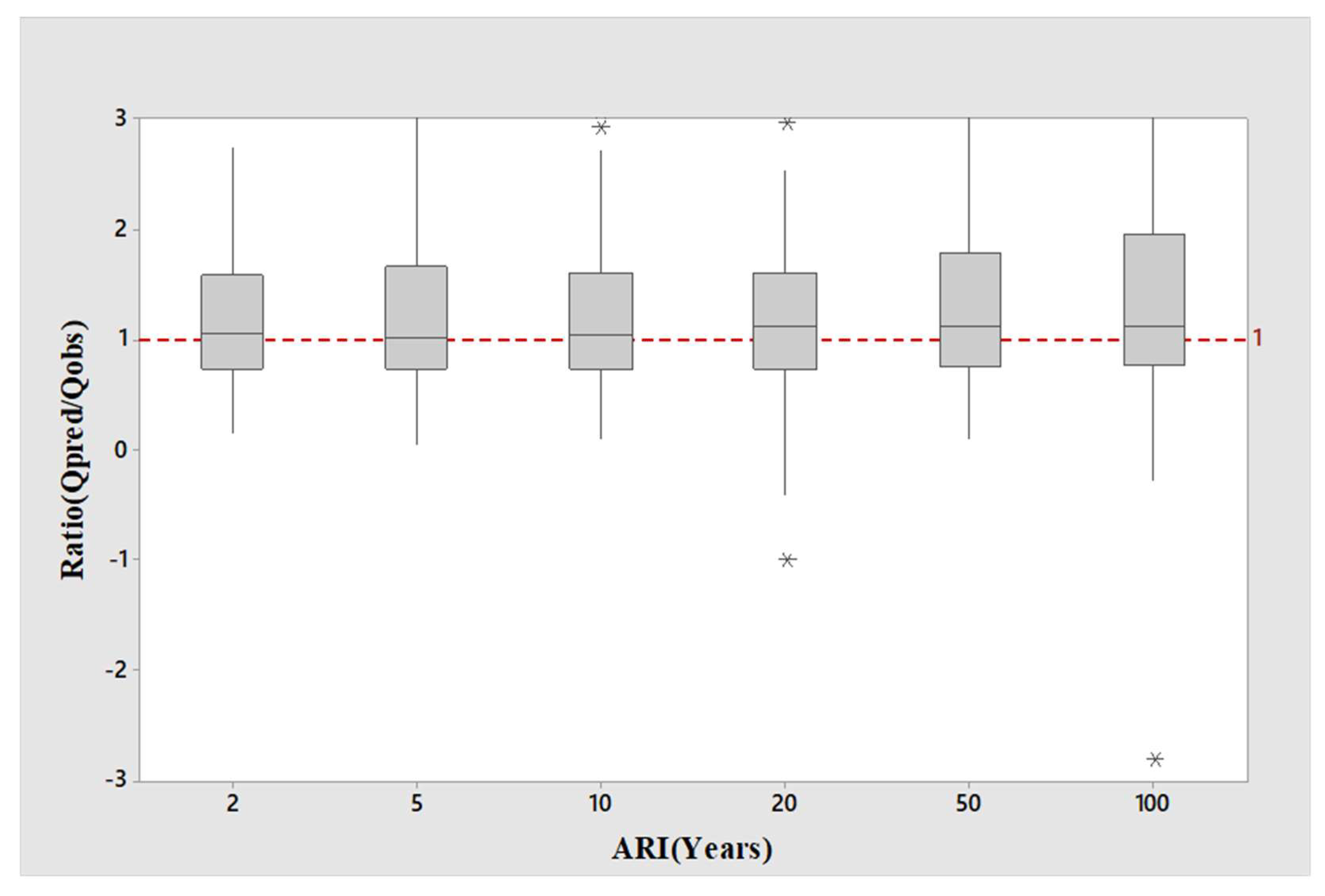
Figure 3 presents the boxplot of the
Qpred/
Qobs ratio values of the selected 114 catchments for the log-log linear model. It is found that the median
Qpred/
Qobs ratio values (represented by the thick black line within a box) are located closer to 1:1 line (the horizontal line in
Figure 3), for ARIs of 2, 5,10, 20 and 50 years (the best agreement is for ARI of 20 years). However, for ARI of 100 years, the median
Qpred/
Qobs ratio value is located a short distance below the 1:1 line, and for ARI of 2 years, the median
Qpred/
Qobs ratio value is located a short distance above the 1:1 line. In terms of the spread of the
Qpred/
Qobs ratio values, ARI of 2 years exhibits the lowest spread followed by ARI of 10 years. Furthermore, the spreads of the
Qpred/
Qobs ratio values for 50 and 100 years are very similar, which are remarkably larger than 2 and 10 years.
For developing GAM model, predictor variables are selected using backward stepwise procedure.
Table 3 shows overall GAM model (combined group) statistics for the 6 different ARIs. The major determinants are coefficient of determination (
R2), generalised cross-validation (GCV) statistic and
p-statistics. The
R2 values range from 0.69 to 0.44; particularly, smaller
R2 values are found for the higher ARIs indicating a weaker model. The
R2 values for lower ARIs seem to be quite reasonable (0.62–0.69). The GCV values vary from 501 to 82, 994 for
Q2 to
Q100. The lowest value of GCV is found for
Q2 and the highest one is found for
Q100. This indicates that the cross-validation error increases with increasing ARIs.
The predictor variables for the individual models are selected based on the
p-statistics of the predictor variables. The criterion of including a predictor variable in the final model is
p ≤ 0.05.
Table 3 contains all the selected predictor values for the models. The predictor variables area, I
6,2 and evap appear to be the most important variables for estimating flood quantiles using GAM, as these three variables are common in all the prediction equations. The next most important predictor variable is rain, which appears in all the prediction models except for
Q2. Another predictor variable, which is found statistically significant in
Q2,
Q5 and
Q10 is sden. Overall,
Q20,
Q50 and
Q100 models show a consistency in the selection of predictor variables (with area, I
6,2 and evap). The selected predictor variables are shown in
Table 3.
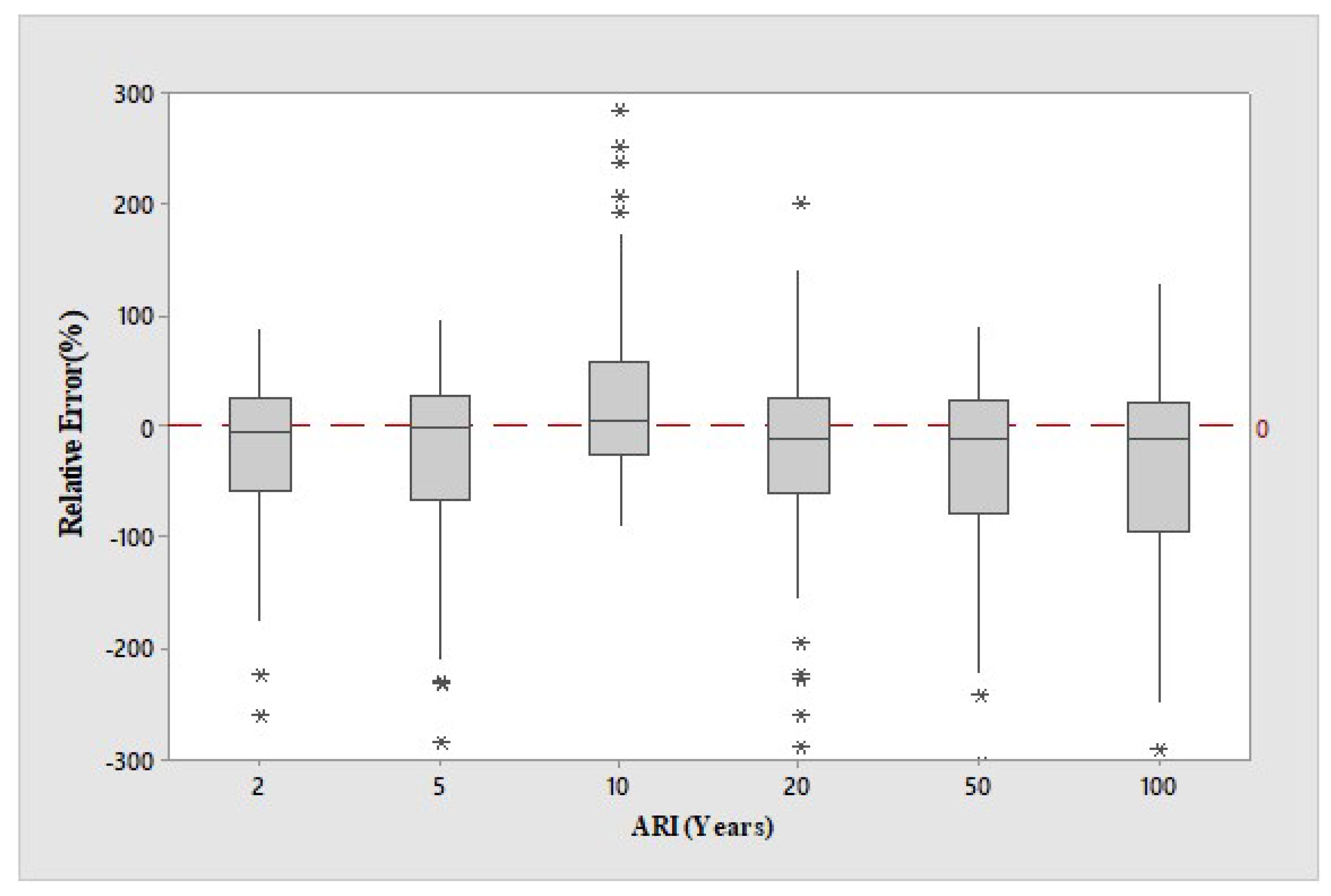
The boxplots of RE values for the GAM model of the combined group for the 6 ARIs are shown in
Figure 4. For ARIs of 5 years, the median RE values match the 0:0 line very well, and reasonably well for ARIs of 2 and 10 years, respectively. Except for 10 years ARI, the GAM models underestimate by a small to moderate amount. In terms of the RE band, the ARIs of 2 and 10 years have nearly identical spreads, which are also smaller than the remaining ARIs. The RE bands for 50 and 100 years of ARIs are very similar, which indicates a similar level of prediction error for these ARIs by the GAM. These results show that in terms of RE, the best overall result (for the combined group) for the GAM model is achieved for 2 years ARI. Overall, the performances of the GAM models (as indicated by the RE bands) for the combined group do not show a large variation across the six ARIs.
Figure 5 presents the boxplots of the
Qpred/
Qobs ratio values associated with the GAM models for the combined group for the six ARIs. It is found that the median
Qpred/
Qobs ratio values are located very close to 1:1 line, for ARIs of 5 and 10 years, showing the best agreement for ARI of 10 years. However, for all the ARIs, the median
Qpred/
Qobs ratio values are located within a short distance above the 1:1 line except for ARI of 100 years. For this ARI, there is a noticeable overestimation by the GAM model. These results indicate a slight to noticeable overestimation of the predicted flood quantiles for all the ARIs. In terms of the spread of the
Qpred/
Qobs ratio values, ARI of 2 years exhibits the lowest spread, whereas 10 and 20 years of ARIs show similar spread. Furthermore, the spreads of the
Qpred/
Qobs ratio values for 50 and 100 years of ARIs are very similar, which are remarkably larger than 2, 5 and 10 years of ARIs.
Table 4 compares the
R2 values of the ten different RFFA models. From
Table 4,
R2 values from GAM models are found to be higher than those from the respective log-log linear models for smaller ARIs. It has also been revealed that GAM models based on clustering groups produce better results, for example, models for smaller ARIs produce higher
R2 values. For example, the
R2 values of
Q2,
Q5, and
Q10 for GAM models in the combined group are 0.83, 0.73, and 0.70, respectively, which are 10%, 8%, and 4% higher than the respective log-log linear models. GAM models, on the other hand, have lower
R2 values than respective log-log linear models for higher ARIs (e.g., 0.67, 0.58 and 0.51, which are 1%, 10% and 17% lower than respective log-log linear model). Furthermore, the GAM models of clustering groups produce better results for
Q2 with a maximum value of 0.90. Overall, the log-log linear models give better performance for higher ARIs (i.e., 20, 50 and 100 years) and GAM models show better performance for smaller ARIs (i.e., 2, 5 and 10 years).
In
Table 5, the median RE values are summarised for the log-log linear and GAM models for the combined and four clustering groups. The median RE values are calculated considering the absolute relative error value (RE) of the test catchments. The highest RE is 59.94%, which is found for log-log linear model for the clustering group A2 for 100 years of ARI, and the lowest RE is 16.8%, which is found for the GAM model of group B1 data for 2 years ARI.
For the log-log linear models, median RE values range from 18.73% to 59.94%. The smallest and highest median RE values are found for the log-log linear models of the combined group for 2 years of ARI and clustering group A2 for 100 years ARI, respectively. From the overall median RE values for the log-log linear models, the smallest result is found from clustering group A1 with median RE of 31.11%. The overall highest median RE value for the log-log linear model is found from clustering group A2 with the value of 42.40%. The overall median RE values range from 31.11% to 42.40%, which indicate that the median RE does not differ much between different groups of the log-log linear models. Lowest values of RE are mostly found from 2 years of ARI for log-log linear model, which range from 18.73% to 30.33%, which are for the combined group and clustering group B1, respectively. The highest values of RE are found for 100 years ARI for the log-log linear models, which range from 37% to 59.94%, which are for clustering groups B1 and A2, respectively.
In the case of GAM, median RE values range from 16.8% to 53.38%. The smallest and highest median RE values are found for 2 years of ARI for clustering group B1, and for 100 years of ARI for clustering group A1, respectively. With respect to the overall median RE, the smallest value is found for the clustering group B1 with median RE of 35.10%. The overall highest median RE value is found for clustering group A2 (43.73%). The overall median RE values range from 35.10% to 43.73% for the GAM models. Lower values of median RE are mostly found for 2 years of ARI for the GAM, which range from 16.80% to 39.31% (for the clustering groups B1 and A2). The highest values of RE are found for 100 years of ARI for the GAM, which range from 39.04% (clustering group B2) to 53.38% (clustering group A1). It is observed that in most cases, the median RE values of GAM are greater than respective log-log linear models. For group A2, median RE values of the GAM models are lower than the log-log linear models for ARIs of 10, 20, 50 and 100 years. However, considering overall performance of median RE, log-log linear model is found to have better accuracy than GAM.
In
Table 6 median ratio (
Qpred/Qobs) values are summarised for 5 log-log linear models and 5 GAM models. The median ratio values are important as these are an effective indicator of overestimation or underestimation (i.e., a measure of bias) of the prediction model. The highest
Qpred/
Qobs ratio is 1.16, which is found for the log-log linear model for clustering group A1 for ARI of 50 years, and the lowest median
Qpred/
Qobs ratio is 0.83, which is found for GAM model for clustering group A2 data of 10 years of ARI.
For log-log linear models, median Qpred/Qobs ratio values range from 0.90 to 1.09. The smallest and highest median ratio values are found for 100 years of ARI for the log-log linear model of the clustering group B2 and log-log linear model of the clustering group B1, respectively. The overall smallest median Qpred/Qobs ratio values for the log-log linear models are found as 0.96, which is for the clustering group B2 and the highest median Qpred/Qobs ratio value for log-log linear model is found for the clustering group B1, which is 1.01. The overall median ratio values range from 0.96 to 1.01, which indicate a very small percentage of difference between different groups of the log-log linear models. Most of the median Qpred/Qobs ratio values obtained from the log-log linear model are in the range of 0.95 to 0.99, which indicate a slight underestimation in the prediction of flood quantiles. The best result is obtained for 20 and 5 years ARIs for the combined group, with the median ratio value of 1.00. In summary, log-log linear model-based RFFA techniques show a very reasonable and consistent median Qpred/Qobs ratio value.
In the case of GAM, median Qpred/Qobs ratio values range from 0.83 to 1.16. The smallest and highest median Qpred/Qobs ratio values are found for ARIs of 10 years for the clustering group A2 and 50 years ARI for the clustering group A1, respectively. The overall smallest median Qpred/Qobs ratio value for GAM is found for clustering group A2 with median Qpred/Qobs ratio of 0.97. The overall highest median Qpred/Qobs ratio value is found for combined group with median ratio of 1.08. The overall median Qpred/Qobs ratio value ranges from 0.98 to 1.08, which indicates that GAM tends to make an overestimation. Moreover, the overall median Qpred/Qobs ratio values for the GAM models are higher compared with respective log-log linear models. Most of the median Qpred/Qobs ratio values are found above 1.00 for the GAM models, which indicates again an overestimation. Lower values of median Qpred/Qobs ratio values for GAM are mostly found for the clustering group A2 that range from 0.83 to 1.14, which are comparatively lower than median Qpred/Qobs ratio values of the log-log linear models of the clustering group A2. For clustering group A2, median Qpred/Qobs ratio values are lower for the GAM than the log-log linear models for higher ARIs i.e., for 10, 20 and 50 years. However, in most cases, the median Qpred/Qobs ratio values of GAM are greater than the respective log-log linear models. Overall, median Qpred/Qobs ratio values indicate that the log-log linear models produce better predictions than GAM in the higher ARIs.