Separation Method of Main and Foreign Water for the Measuring Weirs of Danjiangkou Earth-Rock Dam
Abstract
:1. Introduction
2. Methodology
2.1. Statistical Model for Seepage Monitoring Considering Hysteresis Effect
2.2. Separation Method of Main and Foreign Water for the Measuring Weirs
2.3. Solution Method of Model Parameters
- (1)
- Encircle prey
- (2)
- Hunt
3. Results and Discussion
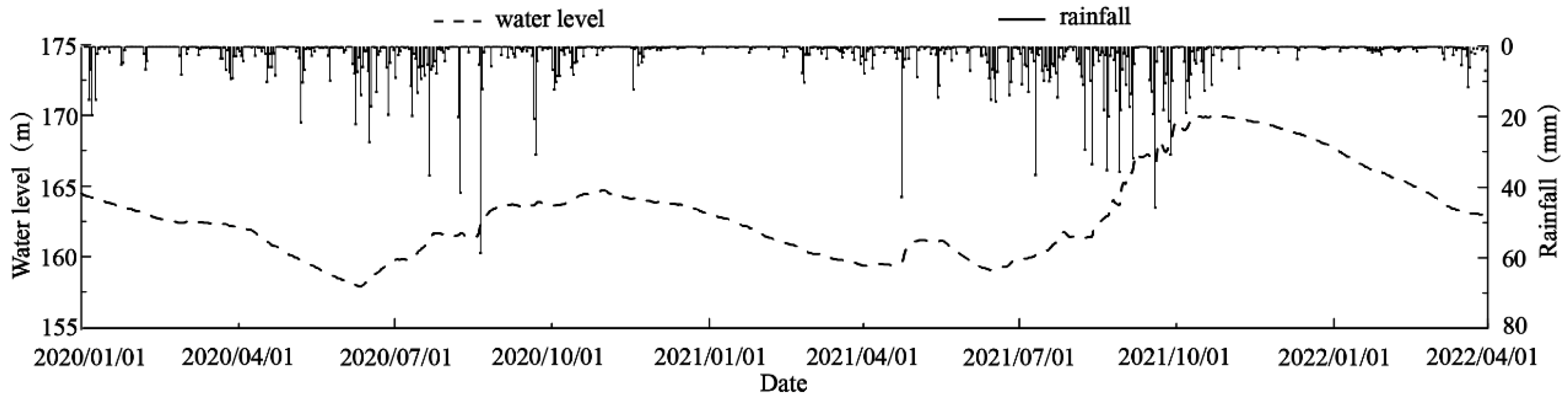
3.1. Project Overview
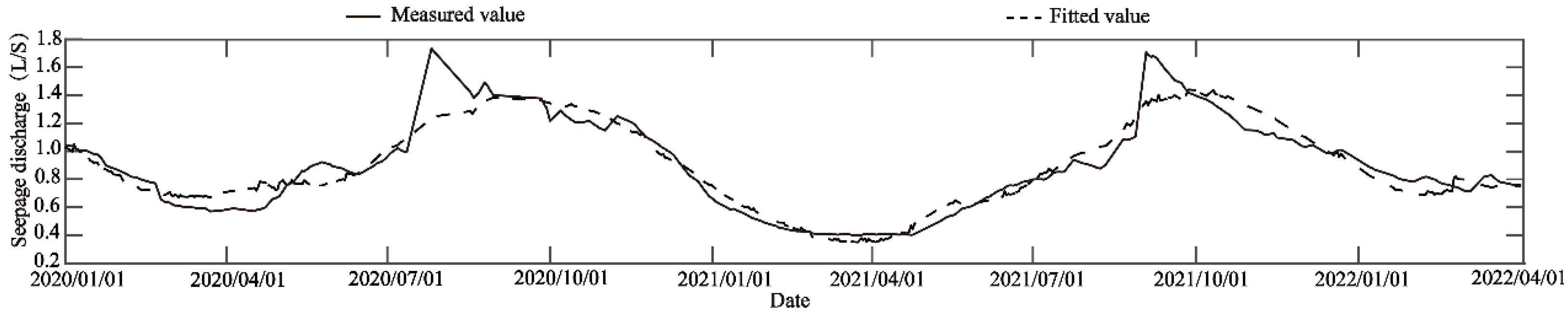
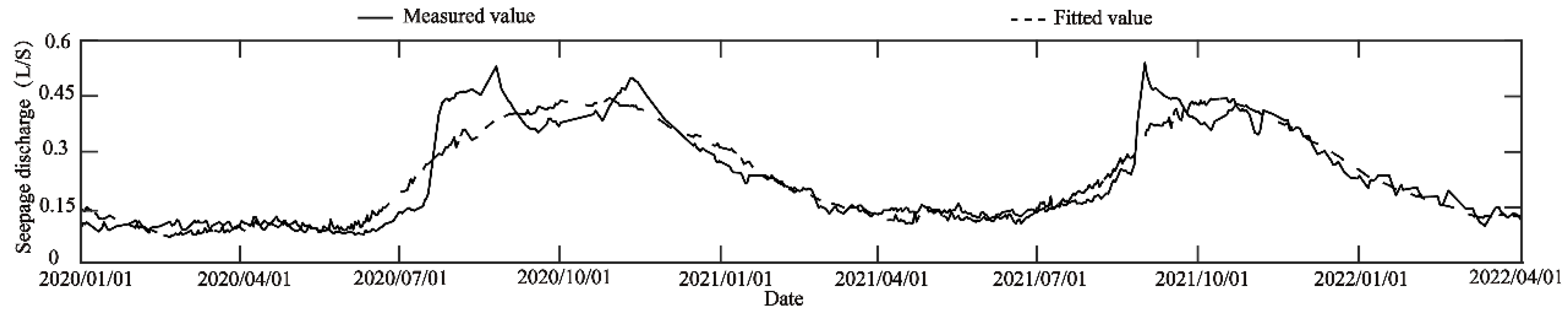
3.2. Statistical Model
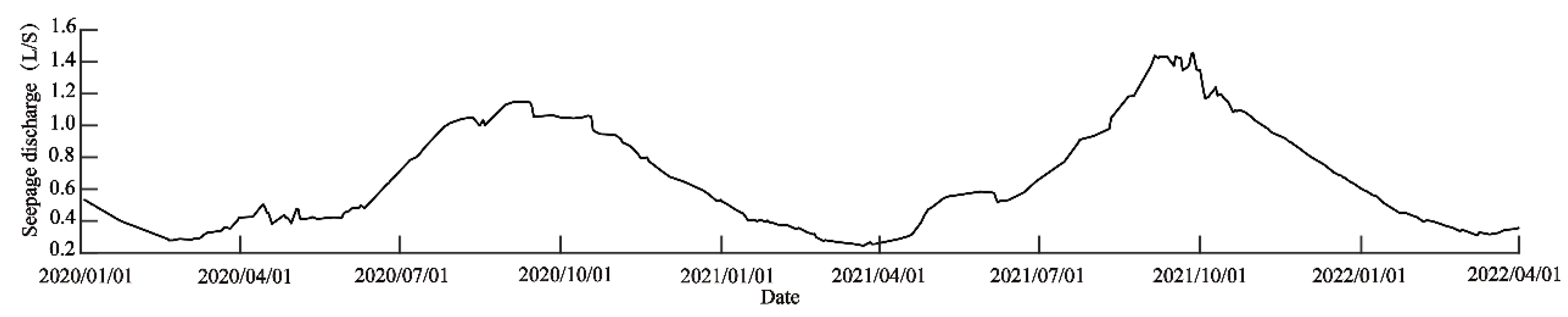
3.3. Separation of Main and Foreign Water for the Measuring Weirs
4. Conclusions
- (1)
- Normal distribution function and Rayleigh distribution function can effectively describe the lag effect of reservoir water level and rainfall on earth-rock dam seepage. The grey wolf algorithm can efficiently solve the optimal lag effect parameters of reservoir water level and rainfall.
- (2)
- The overall fitting accuracy of the statistical model is very high, the multi-correlation coefficients are about 0.95 and the residual standard deviations are smaller than 0.09. However, the fitting effect will be reduced and needs to be improved in the case of excessive rainfall leading to a seepage surge.
- (3)
- The correlation between the factors can be significantly reduced by extracting the influence factor components through the partial least square method, and then the main and foreign water of the seepage discharge of the measuring weir can be separated with higher accuracy.
- (4)
- The separated main and foreign water seepage discharge conform to the general law of earth-rock dam seepage, which verifies the effectiveness of this method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, H.Z.; Wen, Z.P.; Qian, C. Cellular automata-based analysis for seepage failure process of earth-rock dam. Struct. Control Health Monit. 2020, 27, e2553. [Google Scholar] [CrossRef]
- Jiang, S.H.; Fan, Z.W. Earth-rockfill dam safety classification and risk rate assessment on flood control. J. Hydraul. Eng. 2008, 39, 35–40. [Google Scholar]
- Beiranvand, B.; Rajaee, T. Application of artificial intelligence-based single and hybrid models in predicting seepage and pore water pressure of dams: A state-of-the-art review. Adv. Eng. Softw. 2022, 173, 103268. [Google Scholar] [CrossRef]
- Xiang, Y.; Fu, S.; Zhu, K.; Yuan, H.; Fang, Z. Seepage safety monitoring model for an earth rock dam under influence of high-impact typhoons based on particle swarm optimization algorithm. Water Sci. Eng. 2017, 10, 70–77. [Google Scholar] [CrossRef]
- Johari, A.; Talebi, A. Stochastic analysis of rainfall-induced slope instability and steady-state seepage flow using random finite-element method. Int. J. Geomech. 2019, 19, 04019085. [Google Scholar] [CrossRef]
- Cheng, X.S.; Zhang, W.L.; Fan, J.; Zhang, X.Y.; Liu, H.B.; Zhou, X.H. Seismic stability of Loess tunnel with rainfall seepage. Adv. Civ. Eng. 2020, 2020, 8147950. [Google Scholar] [CrossRef]
- Tian, D.F.; Zheng, H.; Liu, D.F. A 2D integrated FEM model for surface water-groundwater flow of slopes under rainfall condition. Landslides 2017, 14, 577–593. [Google Scholar] [CrossRef]
- Leshchinsky, B.; Vahedifard, F.; Koo, H.B.; Kim, S.H. Yumokjeong Landslide: An investigation of progressive failure of a hillslope using the finite element method. Landslides 2015, 12, 997–1005. [Google Scholar] [CrossRef]
- Liu, D.W.; Zheng, F.G.; Hu, S.W. Soil slope stability analysis under rainfall infiltration. J. Food Agric. Environ. 2013, 11, 713–717. [Google Scholar]
- Moayedi, H.; Huat, B.B.K.; Ali, T.A.M.; Asadi, A.; Moayedi, F.; Mokhberi, M. Preventing landslides in times of rainfall: Case study and FEM analyses. Disaster Prev. Manag. 2011, 20, 115–124. [Google Scholar] [CrossRef] [Green Version]
- Konishi, S.; Kitagawa, G. Information Criteria and Statistical Modeling; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Hu, J.; Ma, F. Statistical modelling for high arch dam deformation during the initial impoundment period. Struct. Control Health Monit. 2020, 27, e2638. [Google Scholar] [CrossRef]
- Yuan, D.; Wei, B.; Xie, B.; Zhong, Z. Modified dam deformation monitoring model considering periodic component contained in residual sequence. Struct. Control Health Monit. 2020, 27, e2633. [Google Scholar] [CrossRef]
- Yang, S.L.; Han, X.J.; Kuang, C.F.; Fang, W.H.; Zhang, J.F.; Yu, T.T. Comparative study on deformation prediction models of Wuqiangxi concrete gravity dam based on monitoring data. Comput. Model. Eng. Sci. 2022, 131, 49–72. [Google Scholar] [CrossRef]
- Wei, B.W.; Gu, M.H.; Li, H.K.; Xiong, W.; Xu, Z.K. Modeling method for predicting seepage of RCC dams considering time-varying and lag effect. Struct. Control Health Monit. 2018, 25, e2081. [Google Scholar] [CrossRef]
- Bao, T.F.; Wu, Z.R. Analysis of observed uplift pressure for xin an jiang dam. Hydropower Autom. Dam Monit. 2003, 27, 63–67. [Google Scholar]
- Nie, X.J.; Gu, C.S. Seepage behavior and its abnormality analysis for xiang hong dian dam. Hydropower Autom. Dam Monit. 2004, 28, 49–51, 55. [Google Scholar]
- Hu, J.; Ma, F.H. Comprehensive investigation method for sudden increases of uplift pressures beneath gravity dams: Case study. J. Perform. Constr. Facil. 2016, 30, 04016023. [Google Scholar] [CrossRef]
- Huo, J.X.; Song, H.Z.; Wu, Z.W.; Cheng, J. Seepage statistical model based on lag effect for pumped storage power stations. Hydropower Autom. Dam Monit. 2011, 35, 59–63. [Google Scholar]
- Zhang, Q.F.; Gu, C.S.; Wu, Z.R. Seepage flow monitoring model for rockfill-earth dams based on lag effect. J. Hydraul. Eng. 2001, 32, 85–90. [Google Scholar]
- Zhang, K.; Gu, C.; Zhu, Y.; Chen, S.; Dai, B.; Li, Y.; Shu, X. A novel seepage behavior prediction and lag process identification method for concrete dams using HGWO-XGBoost model. IEEE Access 2021, 9, 23311–23325. [Google Scholar] [CrossRef]
- Huang, H.; Chen, B. Dam seepage monitoring model based on dynamic effect weight of reservoir water level. Energy Procedia 2012, 16, 159–165. [Google Scholar] [CrossRef] [Green Version]
- Shi, Z.; Gu, C.; Zhao, E.; Xu, B. A novel seepage safety monitoring model of CFRD with slab cracks using monitoring data. Math. Probl. Eng. 2020, 2020, 1641747. [Google Scholar] [CrossRef]
- Zhao, M.; Jiang, H.; Chen, S.; Bie, Y. Prediction of seepage pressure based on memory cells and significance analysis of influencing factors. Complexity 2021, 2021, 5576148. [Google Scholar] [CrossRef]
- Wang, S.W.; Xu, Y.L.; Gu, C.S.; Bao, T.F. Monitoring models for base flow effect and daily variation of dam seepage elements considering time lag effect. Water Sci. Eng. 2018, 11, 344–354. [Google Scholar] [CrossRef]
- Wang, S.W.; Bao, T.F. Monitoring model for dam seepage based on lag effect. Appl. Mech. Mater. 2013, 353–356, 2456–2462. [Google Scholar] [CrossRef]
- Shi, Y.Q.; Zhao, C.; Peng, Z.Q.; Yang, H.Y.; He, J.P. Analysis of the lag effect of embankment dam seepage based on delayed mutual information. Eng. Geol. 2018, 234, 132–137. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Behfar, N. Earthfill dam seepage analysis using ensemble artificial intelligence based modeling. J. Hydroinformatics 2018, 20, 1071–1084. [Google Scholar] [CrossRef]
- Wang, A.; Yang, X.; Guo, D. The application of seepage flow prediction in Nuer dam based on the grey self-memory model. Geofluids 2022, 2022, 6211685. [Google Scholar] [CrossRef]
- Chen, S.; Gu, C.; Lin, C.; Wang, Y.; Hariri-Ardebili, M.A. Prediction, monitoring, and interpretation of dam leakage flow via adaptative kernel extreme learning machine. Measurement 2020, 166, 108161. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Suárez, B. Interpretation of dam deformation and leakage with boosted regression trees. Eng. Struct. 2016, 119, 230–251. [Google Scholar] [CrossRef] [Green Version]
- Song, J.; Yuan, S.; Duan, M.; Yang, J.; Zeng, Z.; Huag, Y. Earth-rock dams seepage pressure monitoring model based on the sparrow search algorithm and the hysteresis effect. Adv. Sci. Technol. Water Resour. 2022, 42, 52–57+120. [Google Scholar]
- Cheng, X.; Li, Q.; Zhou, W.; Zhou, Z. External deformation monitoring and improved partial least squares data analysis methods of high core rock-fill Dam (HCRFD). Sensors 2020, 20, 444. [Google Scholar] [CrossRef] [Green Version]
- Huang, H.; Chen, B.; Liu, C. Safety monitoring of a super-high dam using optimal kernel partial least squares. Math. Probl. Eng. 2015, 2015, 571594. [Google Scholar] [CrossRef] [Green Version]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- He, Z.H.; Jin, G.; Wang, Y.J. A novel grey wolf optimizer and its applications in 5G frequency selection surface design. Front. Inf. Technol. Electron. Eng. 2022, 23, 1338–1353. [Google Scholar] [CrossRef]









| WE01XFG | WE01ZXD | WE01YXD | |
|---|---|---|---|
| −6.12475 | −0.37834 | −1.62599 | |
| 0.02762 | 0.01090 | 0.03447 | |
| 0.00012 | 0.00005 | 0.00015 | |
| 196.15377 | −86.40445 | −284.75328 | |
| 0.02236 | 0.00752 | 0.03731 | |
| 0.00079 | 0.00074 | −0.00027 | |
| 28.02389 | 13.83270 | 26.42021 | |
| −0.26945 | 0.11529 | 0.27446 | |
| −0.22962 | 0.03136 | 0.10285 | |
| −0.00463 | −0.00170 | 0.00011 | |
| −0.15639 | −0.01281 | 0.03411 | |
| (Multi-correlation coefficient) | 0.95610 | 0.94490 | 0.94600 |
| (Residual standard deviation) | 0.06880 | 0.08870 | 0.07190 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, W.; Zhang, W.; Zhang, C.; Xie, Z.; Yu, T. Separation Method of Main and Foreign Water for the Measuring Weirs of Danjiangkou Earth-Rock Dam. Water 2022, 14, 3620. https://doi.org/10.3390/w14223620
Fang W, Zhang W, Zhang C, Xie Z, Yu T. Separation Method of Main and Foreign Water for the Measuring Weirs of Danjiangkou Earth-Rock Dam. Water. 2022; 14(22):3620. https://doi.org/10.3390/w14223620
Chicago/Turabian StyleFang, Weihua, Weiping Zhang, Chenghan Zhang, Zhiwen Xie, and Tiantang Yu. 2022. "Separation Method of Main and Foreign Water for the Measuring Weirs of Danjiangkou Earth-Rock Dam" Water 14, no. 22: 3620. https://doi.org/10.3390/w14223620





