Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction
Abstract
1. Introduction
2. Selection of Statistical Models for Dam Deformation Prediction
3. Wavelet Threshold-EMD-Based Data Noise Reduction Method
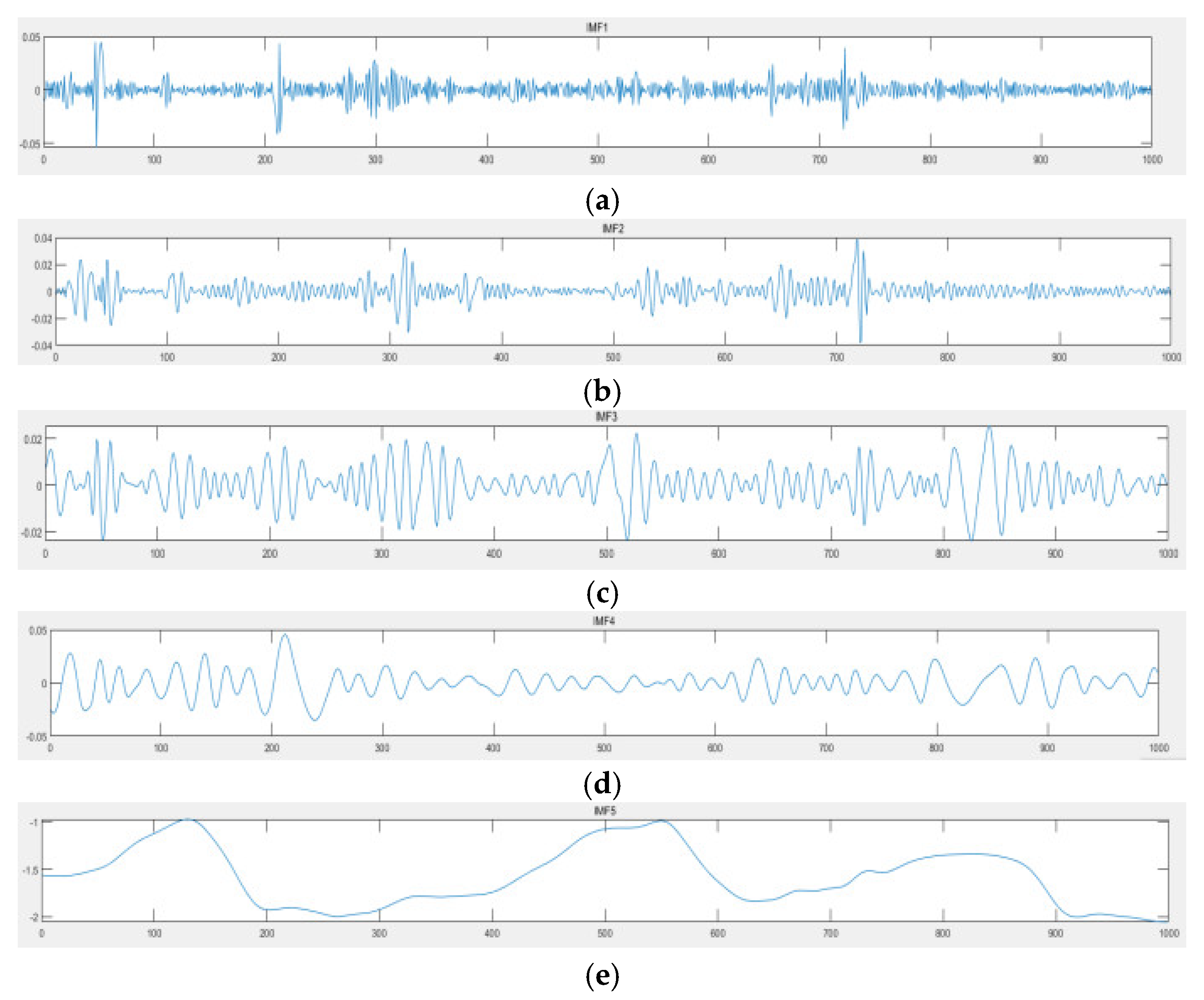
3.1. Empirical Mode Decomposition
3.2. Wavelet Threshold Noise Reduction
4. The Prediction Model Based on Optimized LSTM Model with Sparrow Search Algorithm
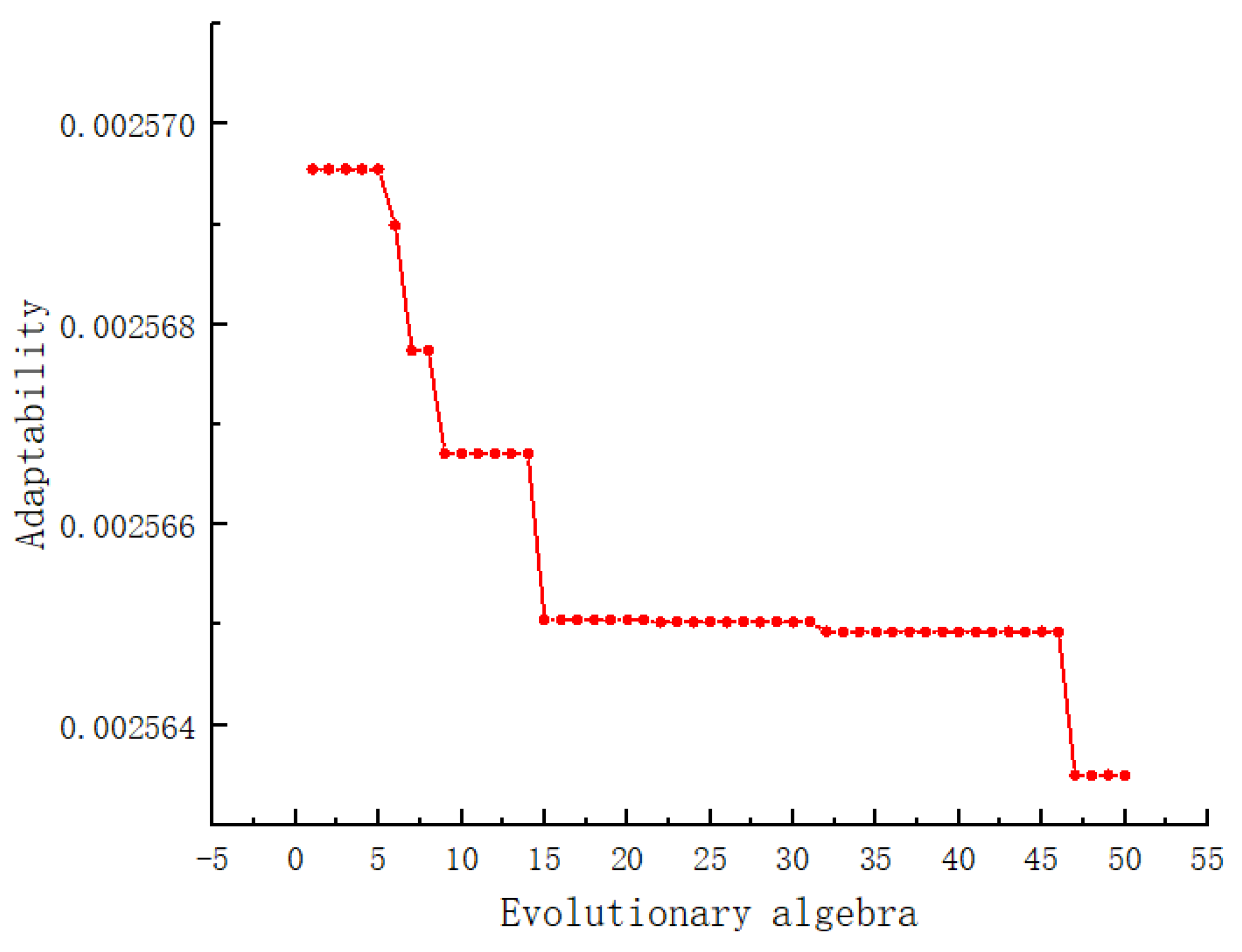
4.1. Sparrow Search Algorithm
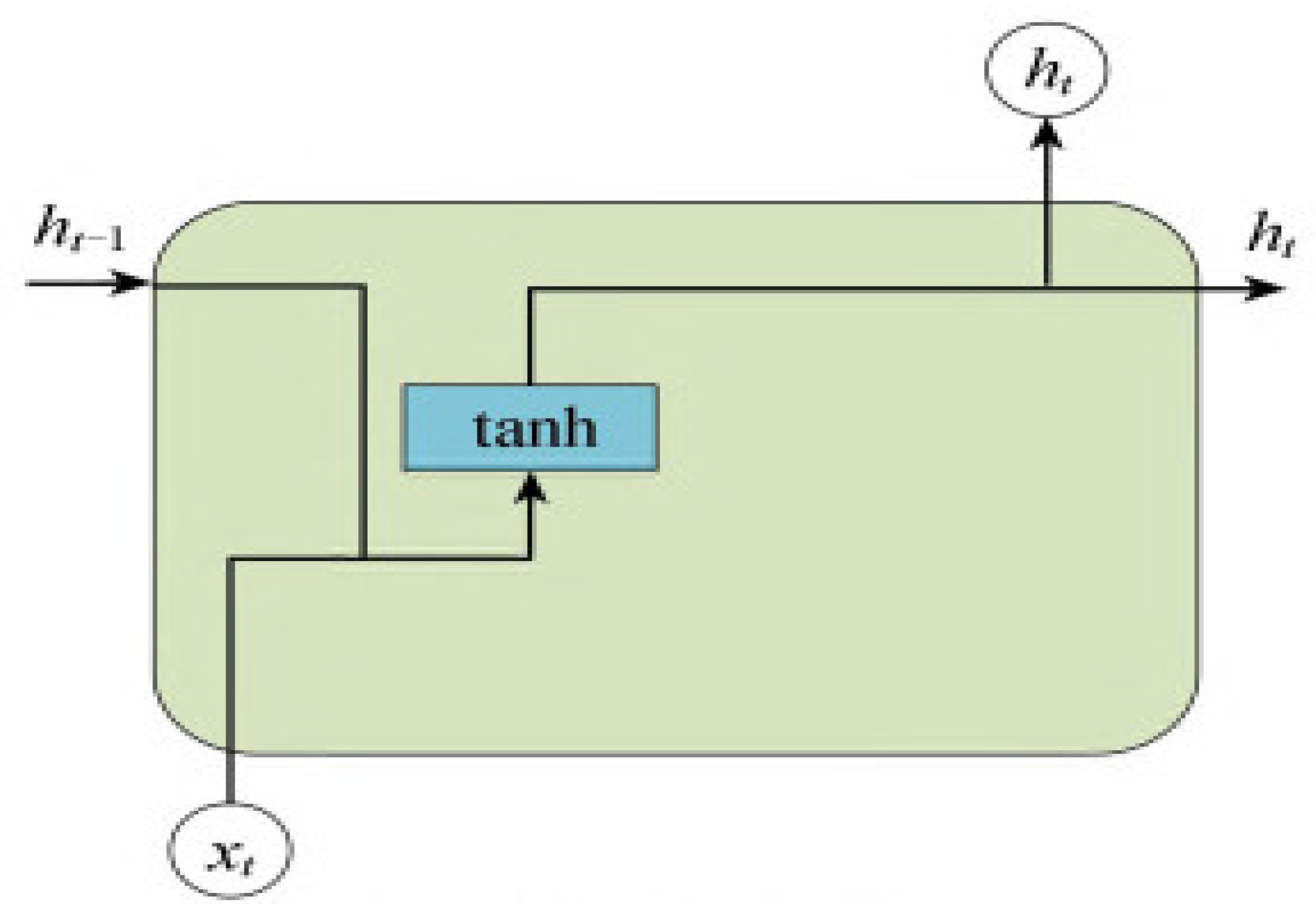
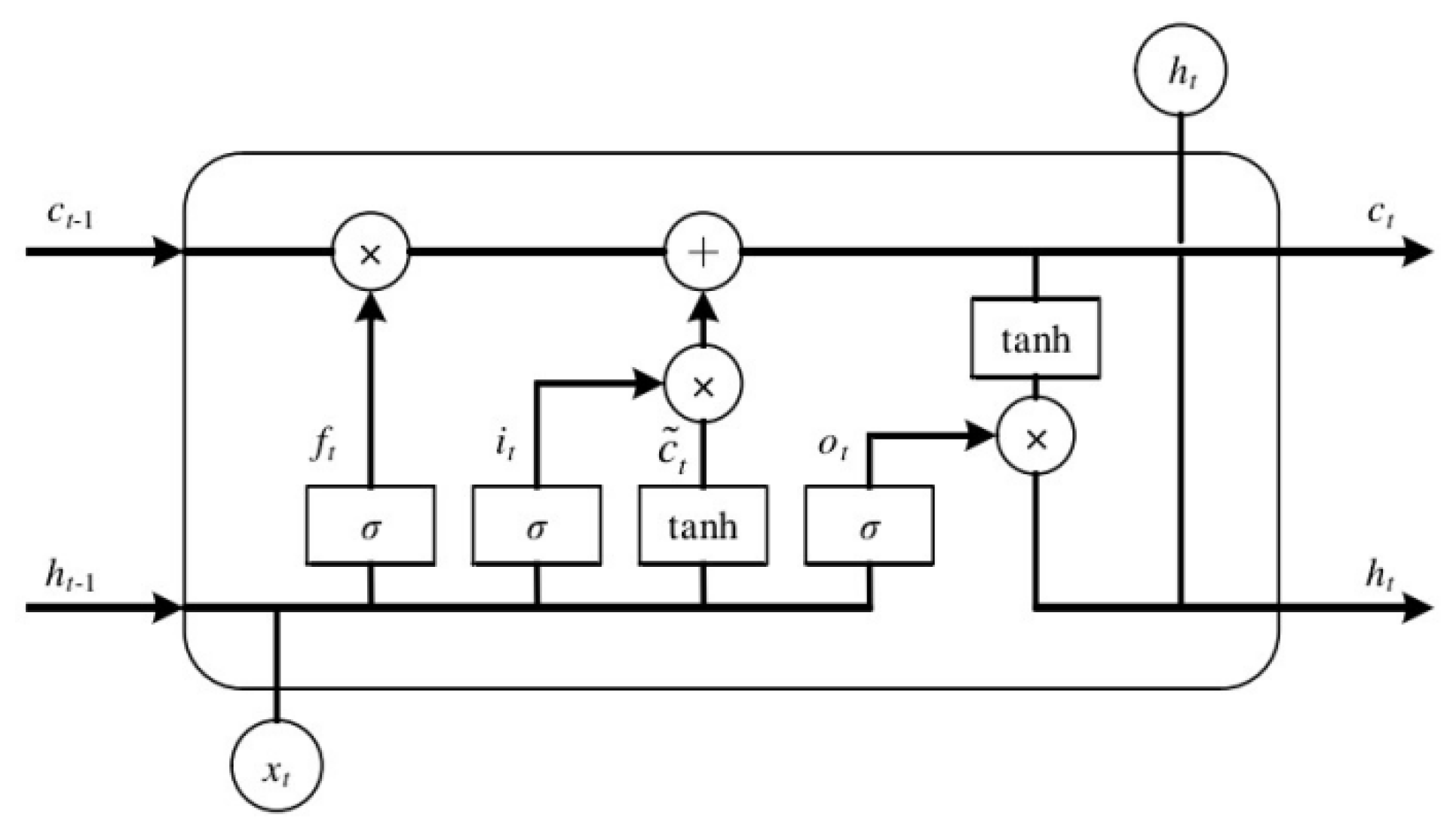
4.2. LSTM Neural Networks
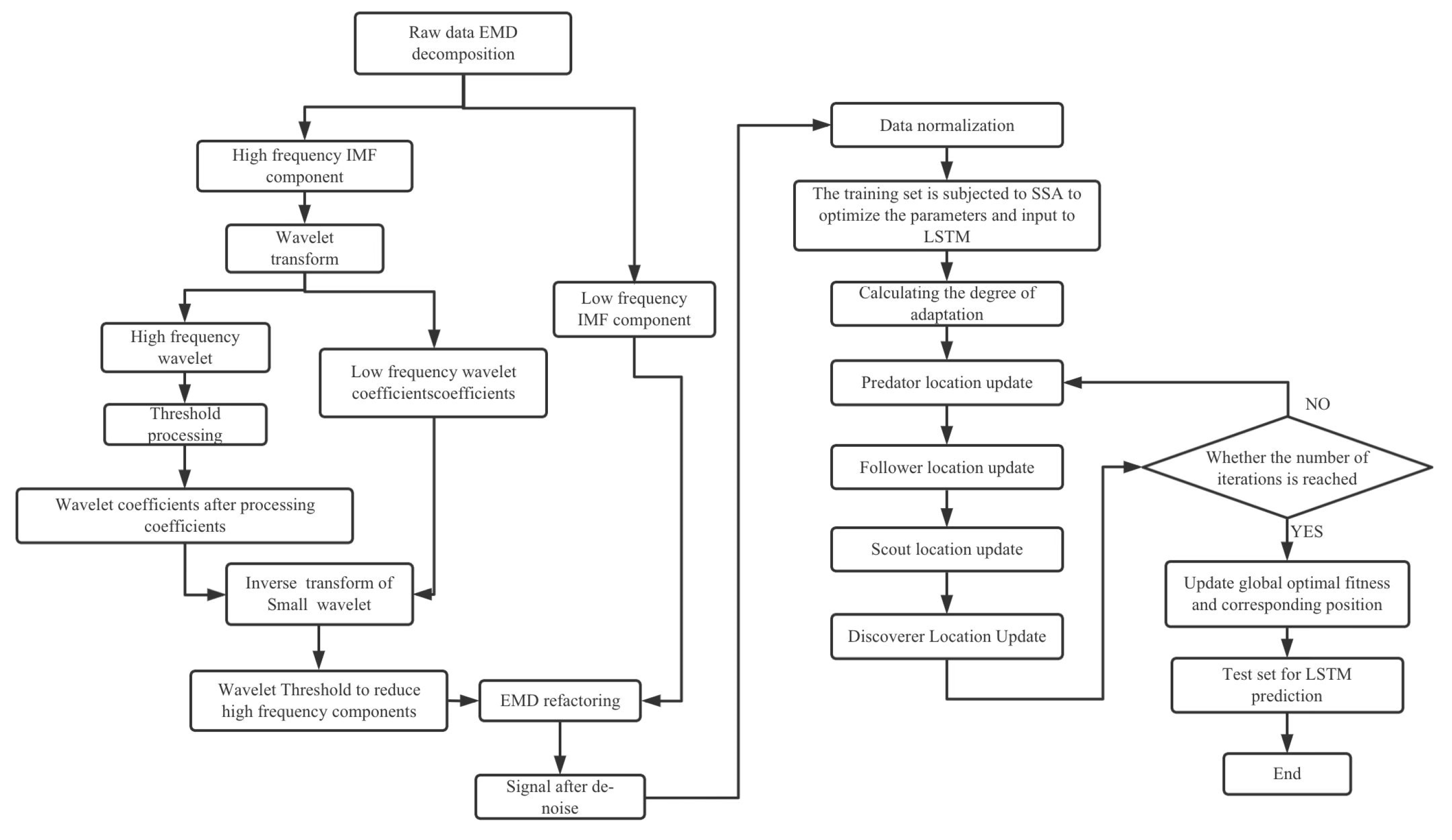
5. Construction of the Model
- Step 1: The monitored raw data are decomposed by EMD, and the IMF components obtained from the decomposition are distributed from high to low. Perform wavelet threshold noise reduction on high-frequency IMF components, reconstruct the high-frequency IMF components after noise reduction and low-frequency IMF components, and obtain the data after noise reduction;
- Step 2: Initialize and normalize the denoised data. Determine the following parameters: length of LSTM time window, number of hidden layer cells, sparrow population size and the number of iterations. Subsequently, initial safety threshold and sparrow position;
- Step 3: Use the predicted value of the LSTM algorithm and the root mean square of the sample data to determine the fitness value of each sparrow;
- Step 4: Update the sparrow position, get a new fitness value, and search for the optimal position of the population and the global optimal value;
- Step 5: Perform iterations, determine whether the maximum number of iterations is reached, and obtain the optimal individual solution. Stop the iteration if the maximum value is reached and determine the optimal parameters of the LSTM. If not, repeat the loop step;
- Step 6: Substitute the obtained LSTM parameters into the training grid to make predictions.
6. Case Study
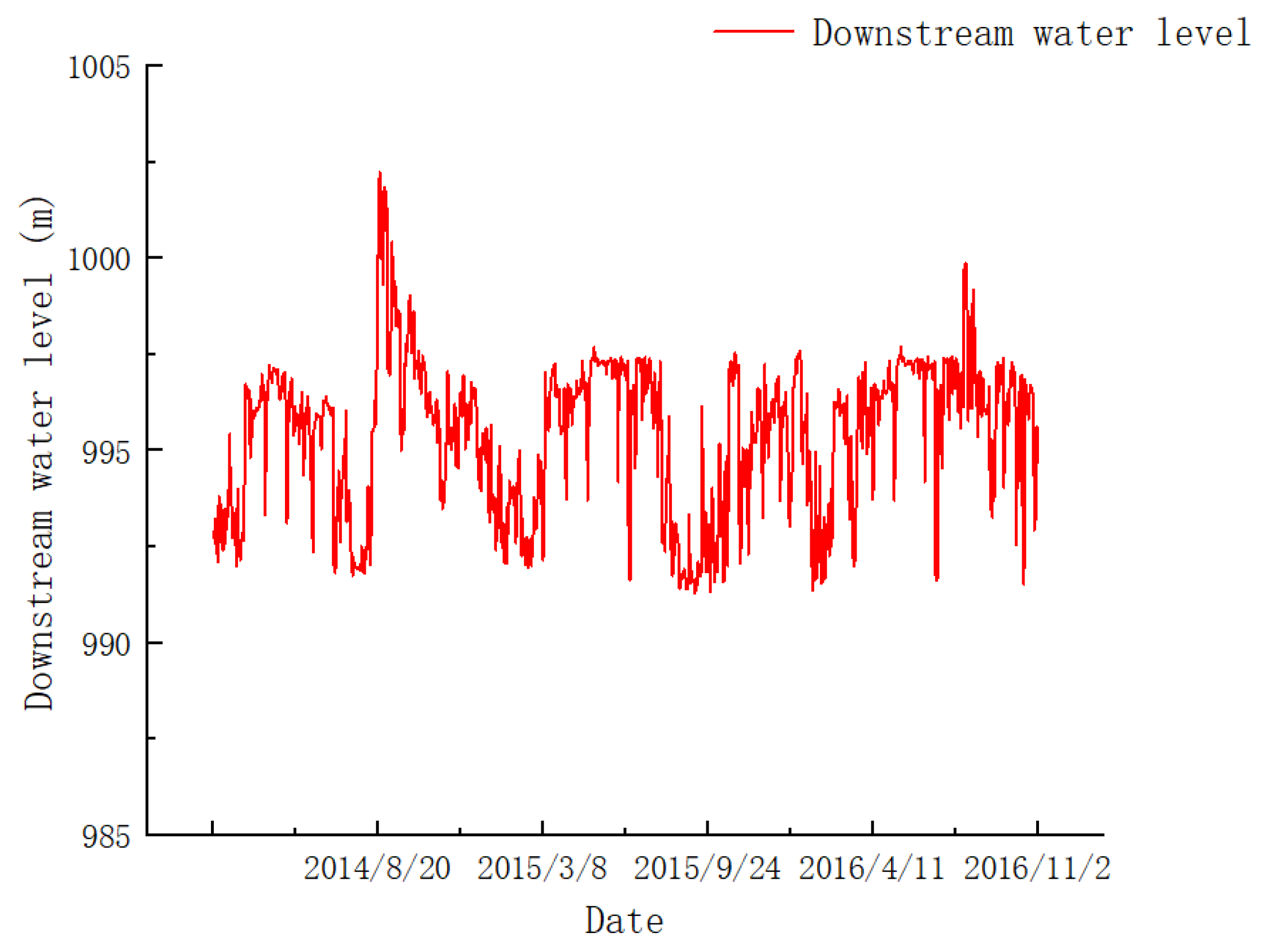
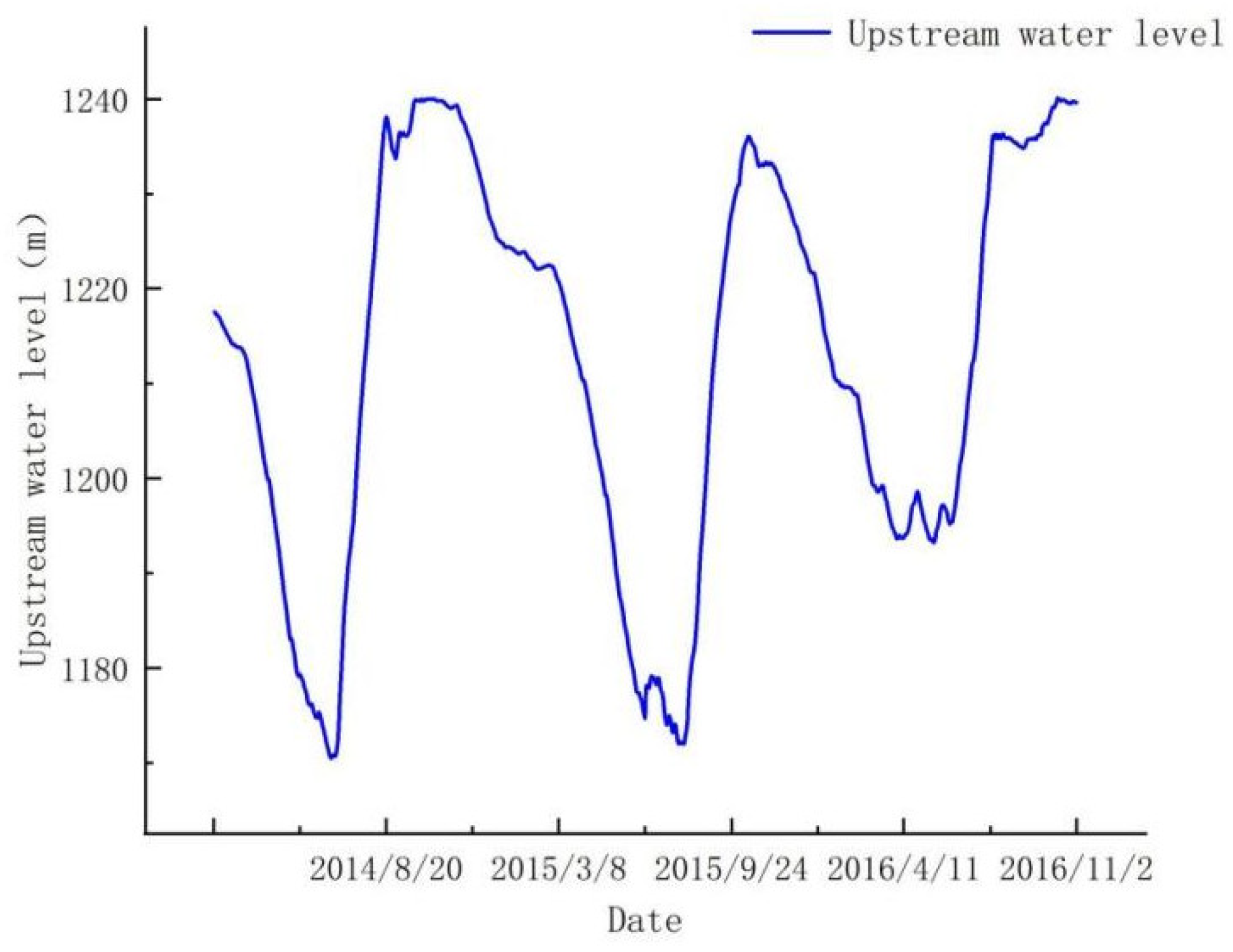
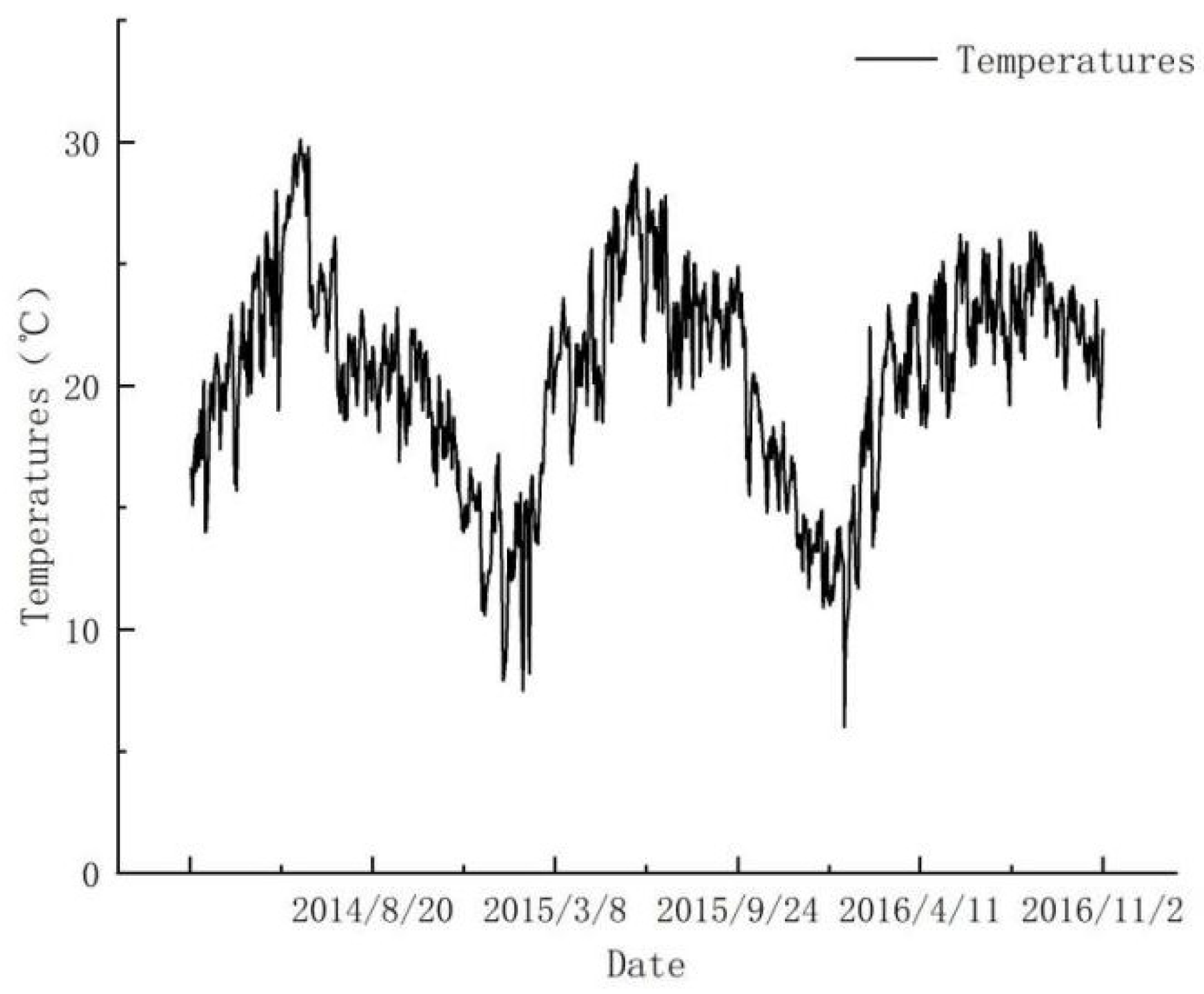
6.1. Factsheet
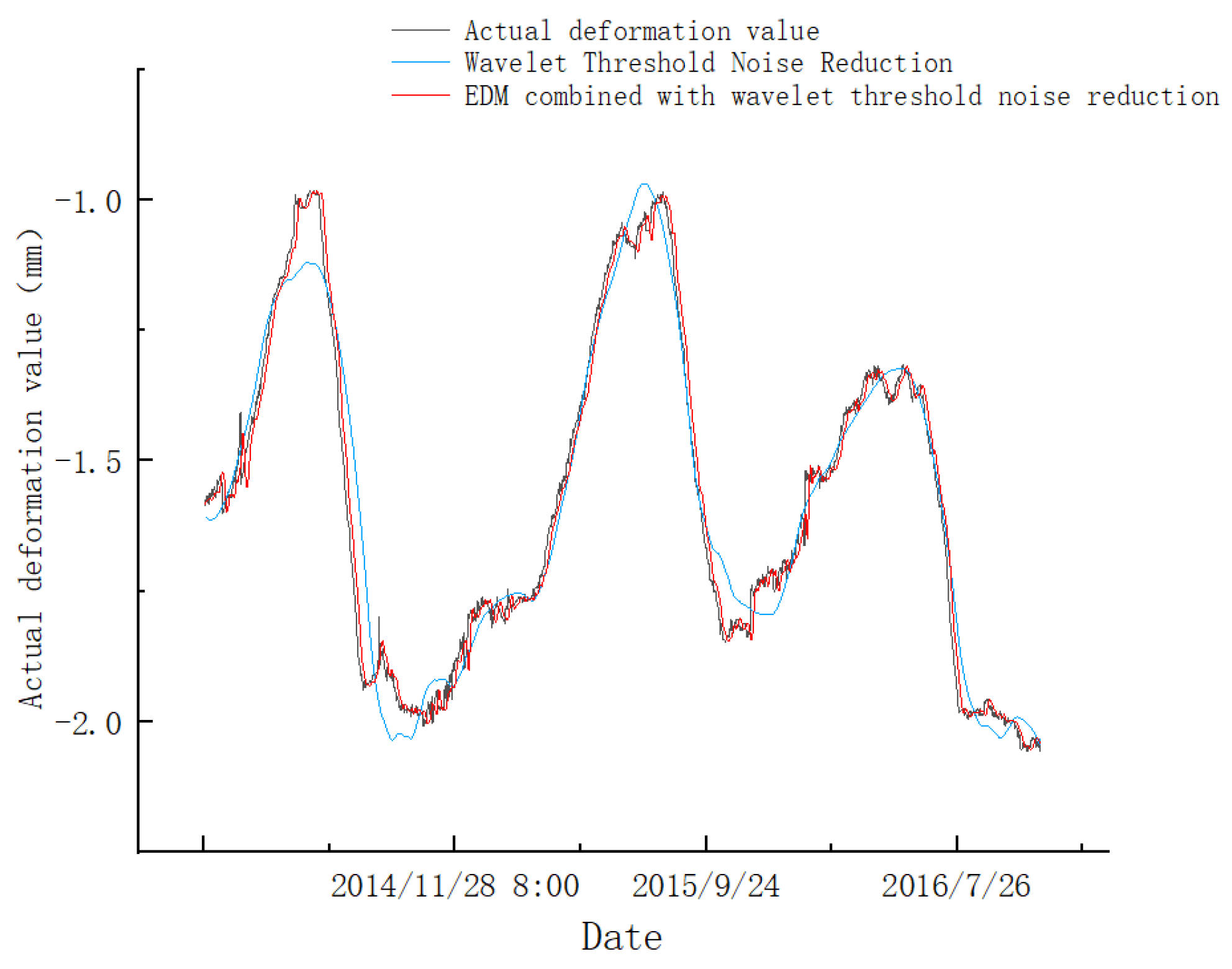
6.2. Data Noise Reduction Based on EMD Combined with Wavelet Threshold
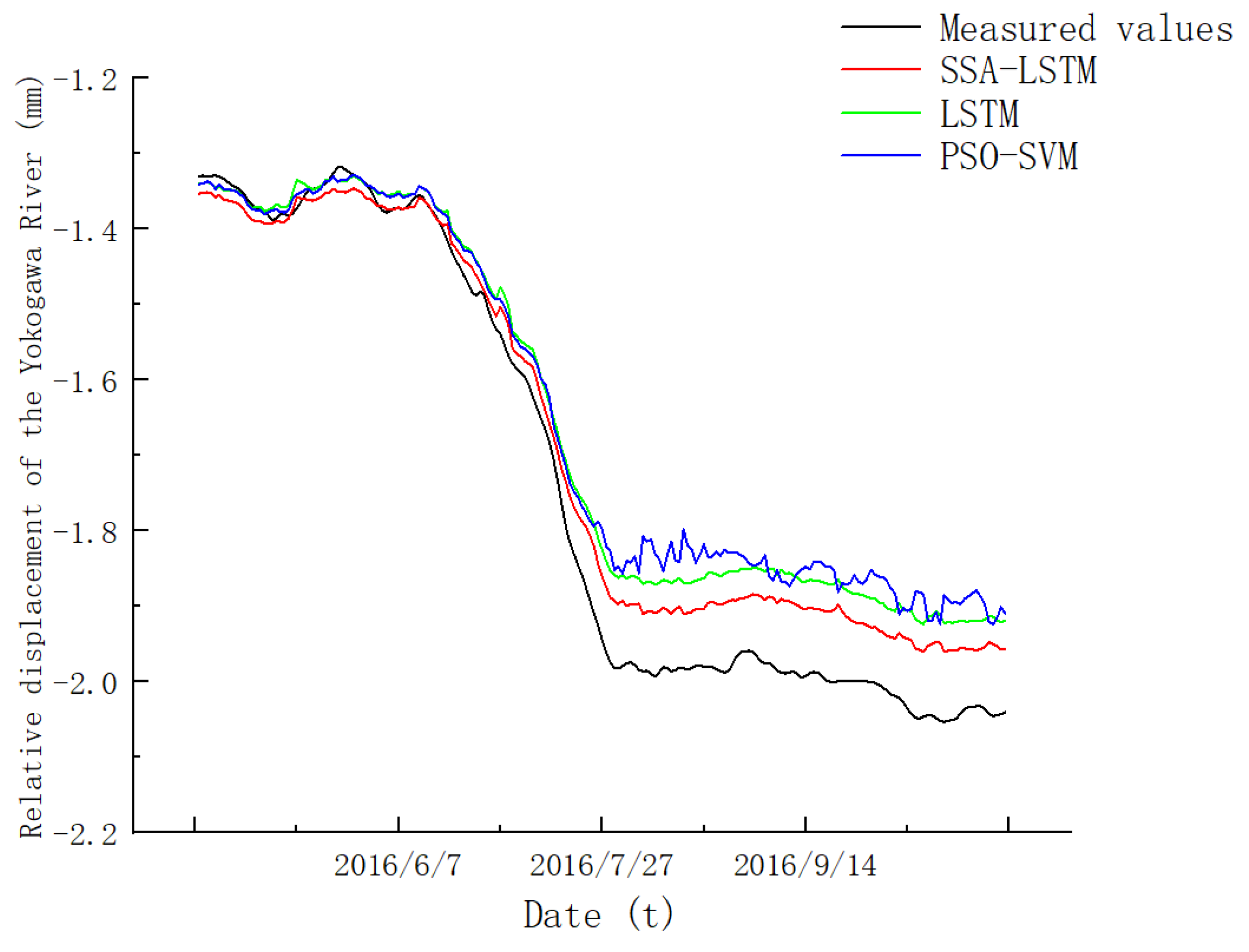
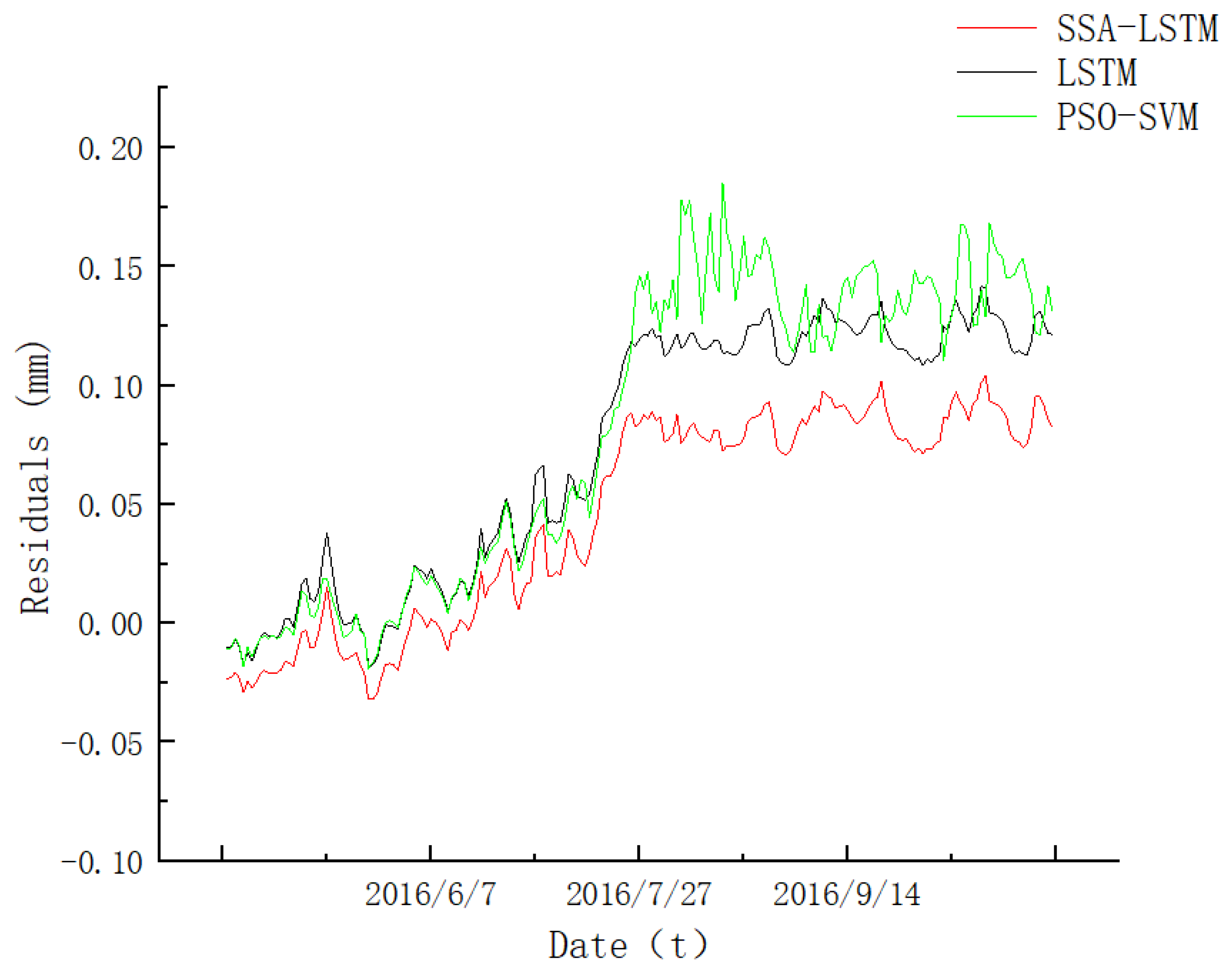
6.3. Model Analysis
7. Conclusions
- This paper proposes a noise reduction method based on EMD combined with wavelet threshold, using the EDM method to decompose the original monitoring data of the dam, and applying wavelet threshold noise reduction to the decomposed high- frequency IMF components. The high-frequency IMF components after noise reduction are obtained, and the low-frequency IMF components obtained by decomposition are combined for reconstruction. A prediction model is constructed from the denoised data, which improves the prediction accuracy of the SAA-LSTM model.
- This paper uses the Sparrow Search Algorithm to optimize the long short-term memory (LSTM), and uses the good stability, convergence speed, scalability, and robustness of the Sparrow Search Algorithm to perform grid training and parameter optimization of the LSTM. The global optimal location and fitness values are updated, and the optimized LSTM model is optimized in terms of the number of hidden layer nodes and learning rate using grid search to effectively mine the complex functional relationship between the dam deformation and its influence factors.
- The two deformation prediction models of LSVM and PSO-SVM are compared by using the example verification analysis. Compared with the other three models, the multiple correlation coefficient R2 of the SSA-LSTM model is 0.9533, which is closer to 1 and has better fitting accuracy. The mean absolute error and root mean square error are 0.05345 and 0.06358, which are smaller than the other two models. It can be seen that the prediction accuracy and convergence speed of the SSA-LSTM model have been significantly improved, which provides a new method for high-precision prediction of dam deformation and is more suitable for practical engineering.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wei, W.; Lou, S.Y.; Xu, F. A combined displacement prediction model for concrete arch dams based on monitoring time-series decomposition and reconfiguration. Eng. Sci. Technol. 2022, 54, 1–13. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Shu, X. A Hybrid Model Integrating Principal Component Analysis, Fuzzy C-Means, and Gaussian Process Regression for Dam Deformation Prediction. Arab. J. Sci. Eng. 2020, 46, 4293–4306. [Google Scholar] [CrossRef]
- Kang, F.; Liu, J.; Li, J. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Struct. Control. Health Monit. 2017, 24, e1997. [Google Scholar] [CrossRef]
- Fan, Z.; Cui, W.; Chen, M. IPSO-RVM based dam safety warning model. J. Chang. Acad. Sci. 2016, 33, 48–51. [Google Scholar] [CrossRef]
- Huang, W.; Fan, Z. Application of Gray Self-Memory Model in Prediction of Ice Flood Water Level of the Yellow River. Yellow River 2013, 35, 3–5. [Google Scholar]
- Yang, S.; Chen, T. Research on electrical main wiring fault monitoring model for water conservancy projects based on grey system theory. Hydropower Technol. 2020, 51, 88–95. [Google Scholar] [CrossRef]
- Lin, Z. Research on Deformation Prediction Model of Earth-rock Dam Based on BP Neural Network. People’s Pearl River 2020, 41, 74–78. [Google Scholar]
- Chen, Z.; Xiong, X.; You, Y. Variational modal decomposition and long-short time neural networks for dam deformation prediction. Mapp. Sci. 2021, 46, 34–42. [Google Scholar] [CrossRef]
- Shao, N.; Yu, Z.W. Application of wavelet neural networks in dam deformation forecasting. Urban Surv. 2018, 4, 156–157. [Google Scholar]
- Wei, B.; Liu, B.; Xu, F. Hybrid model for multi-measurement point deformation monitoring of concrete arch dams incorporating PSO-SVM. J. Wuhan Univ. Inf. Sci. Ed. 2021, 1–14. [Google Scholar]
- Huai, Z.; Zhe, X.; Zhi, P. Performance improvement method of support vector machine-based model monitoring dam safety. Struct. Control. Health Monit. 2016, 23, 252–266. [Google Scholar] [CrossRef]
- Li, M.; Pan, J.; Lui, Y. A Deformation Prediction Model of High Arch Dams in the Initial Operation Period Based on PSR-SVM-IGWO. Math. Probl. Eng. 2021, 2021, 8487997. [Google Scholar] [CrossRef]
- Luo, H.; Guo, S.; Bao, W. Random Forest Model and Application for Arch Dam Deformation Monitoring and Prediction. South-to-North Water Divers. Water Conserv. Technol. 2016, 14, 116–121. [Google Scholar] [CrossRef]
- Li, X.; Wen, Z.; Su, H. An approach using random forest intelligent algorithm to construct a monitoring model for dam safety. Eng. Comput. 2019, 37, 39–56. [Google Scholar] [CrossRef]
- Vadiati, M.; Rajabi Yami, Z.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of artificial intelligence models for prediction of groundwater level fluctuations: Case study (Tehran-Karaj alluvial aquifer). Environ. Monit. Assess. 2022, 194, 619. [Google Scholar] [CrossRef] [PubMed]
- Samani, S.; Vadiati, M.; Azizi, F.; Zamani, E.; Kisi, O. Groundwater Level Simulation Using Soft Computing Methods with Emphasis on Major Meteorological Components. Water Resour. Manag. 2022, 36, 3627–3647. [Google Scholar] [CrossRef]
- Yi, Z.; Su, H.; Yang, L. Combined modeling method of random forest and swordfish optimization for deformation monitoring model of concrete dam. Hydropower Energy Sci. 2021, 39, 106–109. [Google Scholar]
- Wei, B.; Yuan, D.; Bin, X. Deformation prediction model of concrete dam based on optimal correlation vector machine based on chicken swarm algorithm. Water Conserv. Hydropower Technol. 2020, 51, 98–105. [Google Scholar] [CrossRef]
- Zhi, P.; Zen, G.; Hai, D. Self CNN-based time series stream forecasting. Electron. Lett. 2016, 52, 1857–1858. [Google Scholar] [CrossRef]
- Min, K.; Ki, M.; Pa, R.; Huh, K. RNN-Based Path Prediction of Obstacle Vehicles with Deep Ensemble. IEEE Trans. Veh. Technol. 2019, 68, 10252–10256. [Google Scholar] [CrossRef]
- Hu, C.; Pei, H.; Si, X. A Prognostic Model Based on DBN and Diffusion Process for Degrading Bearing. IEEE Trans. Ind. Electron. 2019, 67, 8767–8777. [Google Scholar] [CrossRef]
- Li, Y.; Bao, T.; Gong, J. The prediction of dam displacement time series using STL, extra-trees, and stacked LSTM neural network. IEEE Access 2020, 8, 94440–94452. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, X.; Xie, J. An Improved Long Short-Term Memory Model for Dam Displacement Prediction. Math. Probl. Eng. 2019, 2019, 6792189. [Google Scholar] [CrossRef]
- Wang, S.; Yang, B.; Chen, H.; Fang, W.; Yu, T. LSTM-Based Deformation Prediction Model of the Embankment Dam of the Danjiangkou Hydropower Station. Water 2022, 14, 2464. [Google Scholar] [CrossRef]
- Ou, B.; Wu, B.; Yuan, J. Deformation prediction model of concrete dam based on LSTM. Prog. Water Conserv. Hydropower Sci. Technol. 2022, 42, 21–26. [Google Scholar] [CrossRef]
- Wang, X.; Li, K.; Zhang, Z. Seepage pressure prediction model of earth-rock dam coupled with ALO-LSTM and feature attention mechanism. J. Hydraul. Eng. 2022, 53, 403–412. [Google Scholar] [CrossRef]
- Yang, D.; Gu, C.; Zhu, Y. A Concrete Dam Deformation Prediction Method Based on LSTM With Attention Mechanism. IEEE Access 2020, 8, 185177–185186. [Google Scholar] [CrossRef]
- Liu, W.; Pan, J.; Ren, Y.; Wu, Z.; Wang, J. Coupling prediction model for long-term displacements of arch dams based on long short-term memory network. Struct. Control Health Monit. 2020, 27, e2548. [Google Scholar] [CrossRef]
- Luo, D.; Zheng, D. Wavelet analysis and ARMA prediction model for dam deformation. J. Water Resour. Water Transp. Eng. 2016, 3, 70–75. [Google Scholar] [CrossRef]
- Su, H.; Li, X.; Yang, B.; Wen, Z. Wavelet support vector machine-based prediction model of dam deformation. Mech. Syst. Signal Process. 2018, 110, 412–427. [Google Scholar] [CrossRef]
- Yang, G.; Fan, Z.; Fu, C. Research on outlier identification techniques for dam safety monitoring data based on singular spectrum analysis. Hydroelectricity 2021, 47, 125–129. [Google Scholar] [CrossRef]
- Zhang, J.; Heng, Y. Concrete dam deformation prediction model based on VMD-PE-CNN. Hydropower Technol. 2022, 1–11. (In Chinese) [Google Scholar]
- Hu, H.; Zhang, J.; Li, T. A Novel Hybrid Decompose-Ensemble Strategy with a VMD-BPNN Approach for Daily Streamflow Estimating. Water Resour. Manag. 2021, 35, 5119–5138. [Google Scholar] [CrossRef]
- Liu, S.; Xu, J.; Ju, B. Dam deformation prediction based on EMD and RBF neural networks. Mapp. Bull. 2019, 8, 88–91. [Google Scholar] [CrossRef]
- Chen, Y. Back analysis of permeability coefficient of earth-rock dam based on EMD-RVM. IOP Conf. Ser. Earth Environ. Sci. 2020, 560, 12095. [Google Scholar] [CrossRef]
- Sheng, J.; Teng, F.; Chen, D.; Qian, Q. Dam deformation prediction model and application based on EMD decomposition method. Water Conserv. Hydropower Technol. 2017, 48, 41–44. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, P.; Jian, J. Research on dam deformation prediction based on EMD-PSO-ELM algorithm. Softw. Guide 2020, 19, 1–5. [Google Scholar]
- Xin, D.; Huan, Y.; Cai, Q. Ultra-short-term wind power prediction based on wavelet threshold noise reduction and BP neural network. World Sci. Technol. Res. Dev. 2011, 33, 1006–1010. [Google Scholar] [CrossRef]
- Xue, J. Research and Application of a Novel Swarm Intelligence Optimization Technique; Donghua University: Shanghai, China, 2020. [Google Scholar]
| Measuring Points | Predictive Models | RMSE/mm | MAE/mm2 | MSE/mm | R2 |
|---|---|---|---|---|---|
| C4-A22-PL-05 | SSA-LSTM | 0.06358 | 0.05345 | 0.00404 | 0.9533 |
| LSTM | 0.0913 | 0.07611 | 0.00835 | 0.9036 | |
| PSO-SVM | 0.1293 | 0.09564 | 0.01096 | 0.8852 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Fu, S.; Ou, B.; Liu, Z.; Hu, M. Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction. Water 2022, 14, 3380. https://doi.org/10.3390/w14213380
Zhang C, Fu S, Ou B, Liu Z, Hu M. Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction. Water. 2022; 14(21):3380. https://doi.org/10.3390/w14213380
Chicago/Turabian StyleZhang, Caiyi, Shuyan Fu, Bin Ou, Zhenyu Liu, and Mengfan Hu. 2022. "Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction" Water 14, no. 21: 3380. https://doi.org/10.3390/w14213380
APA StyleZhang, C., Fu, S., Ou, B., Liu, Z., & Hu, M. (2022). Prediction of Dam Deformation Using SSA-LSTM Model Based on Empirical Mode Decomposition Method and Wavelet Threshold Noise Reduction. Water, 14(21), 3380. https://doi.org/10.3390/w14213380






