Synchronization-Enhanced Deep Learning Early Flood Risk Predictions: The Core of Data-Driven City Digital Twins for Climate Resilience Planning
Abstract
:1. Introduction
2. Materials and Methods
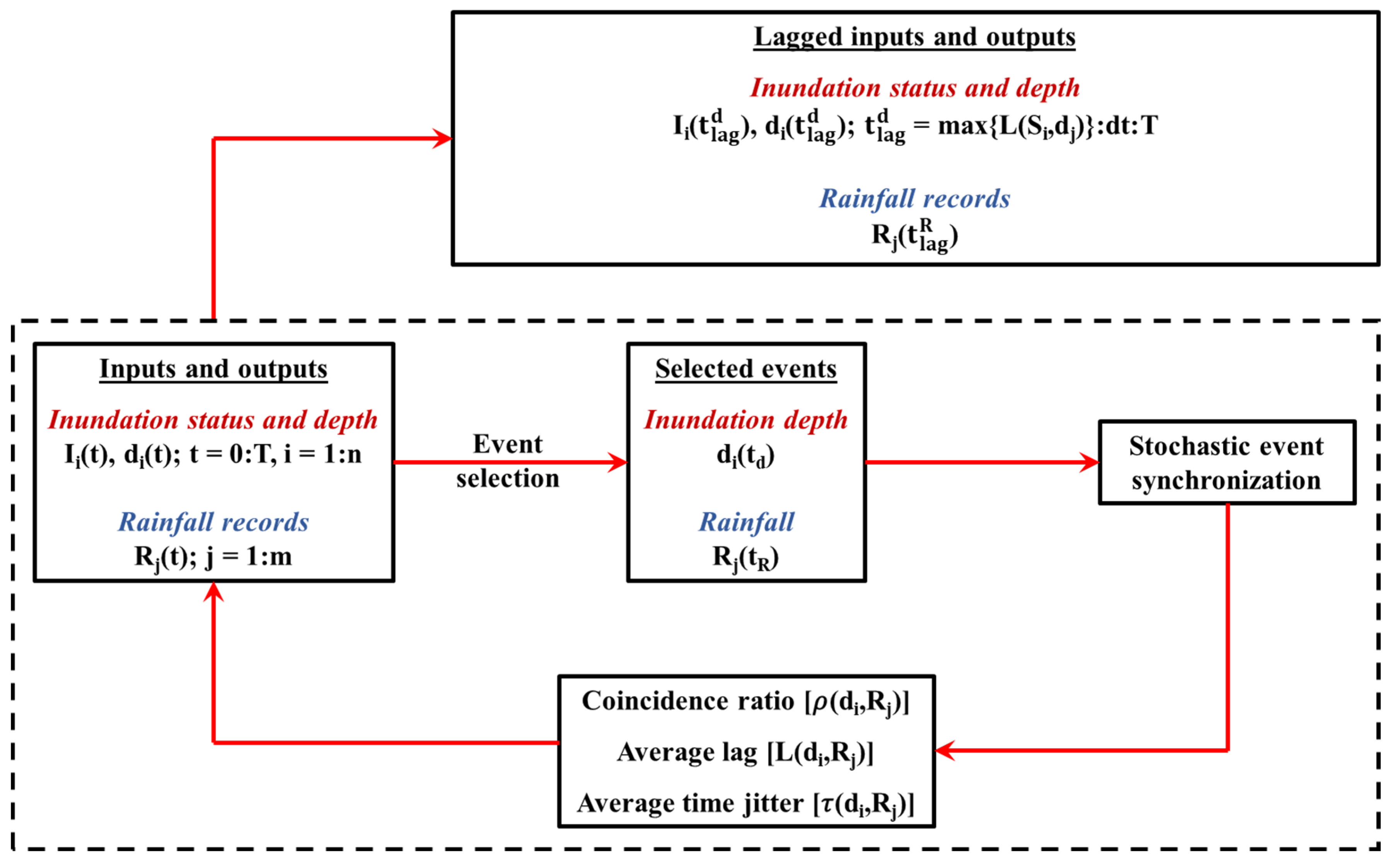
2.1. Synchronization Module
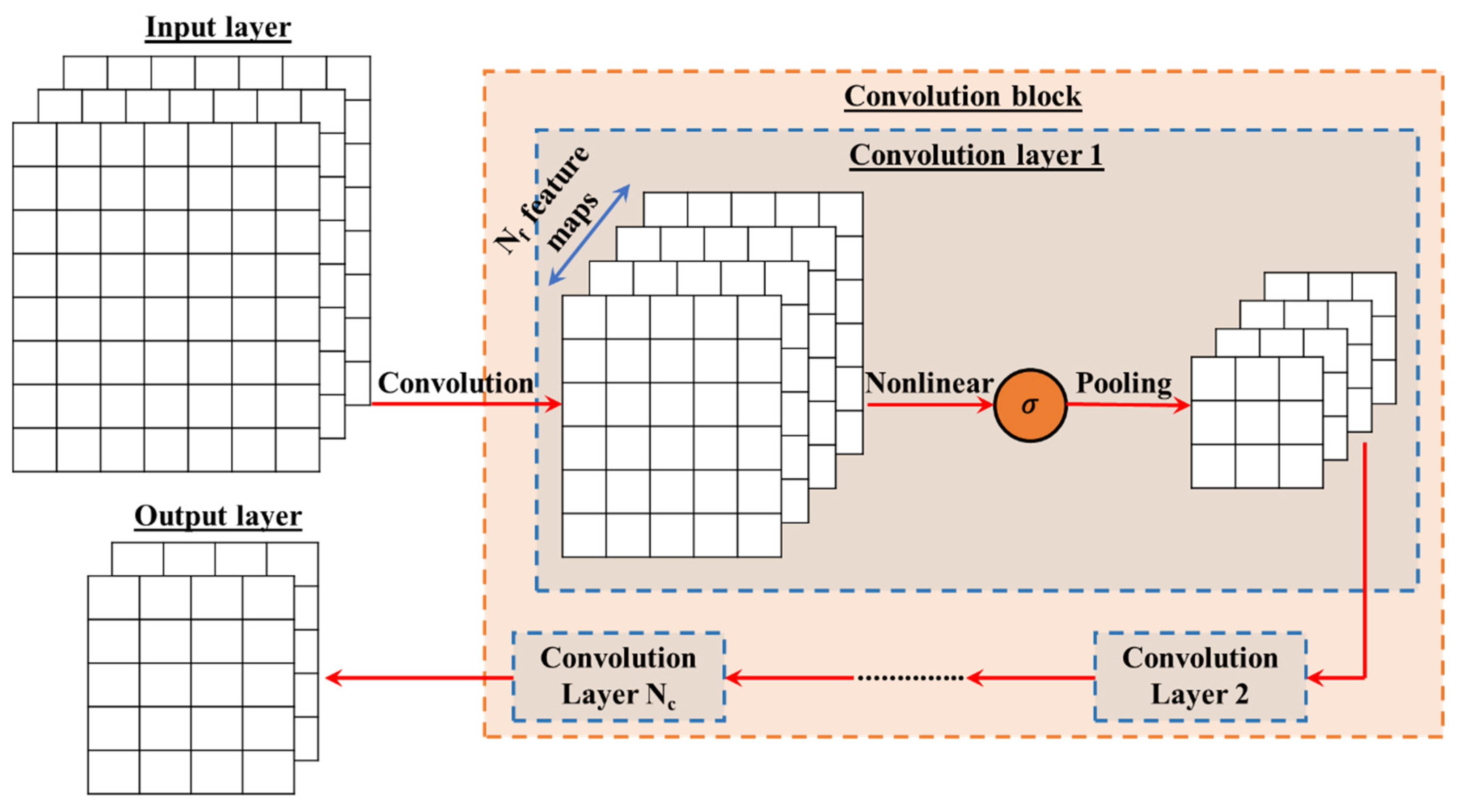
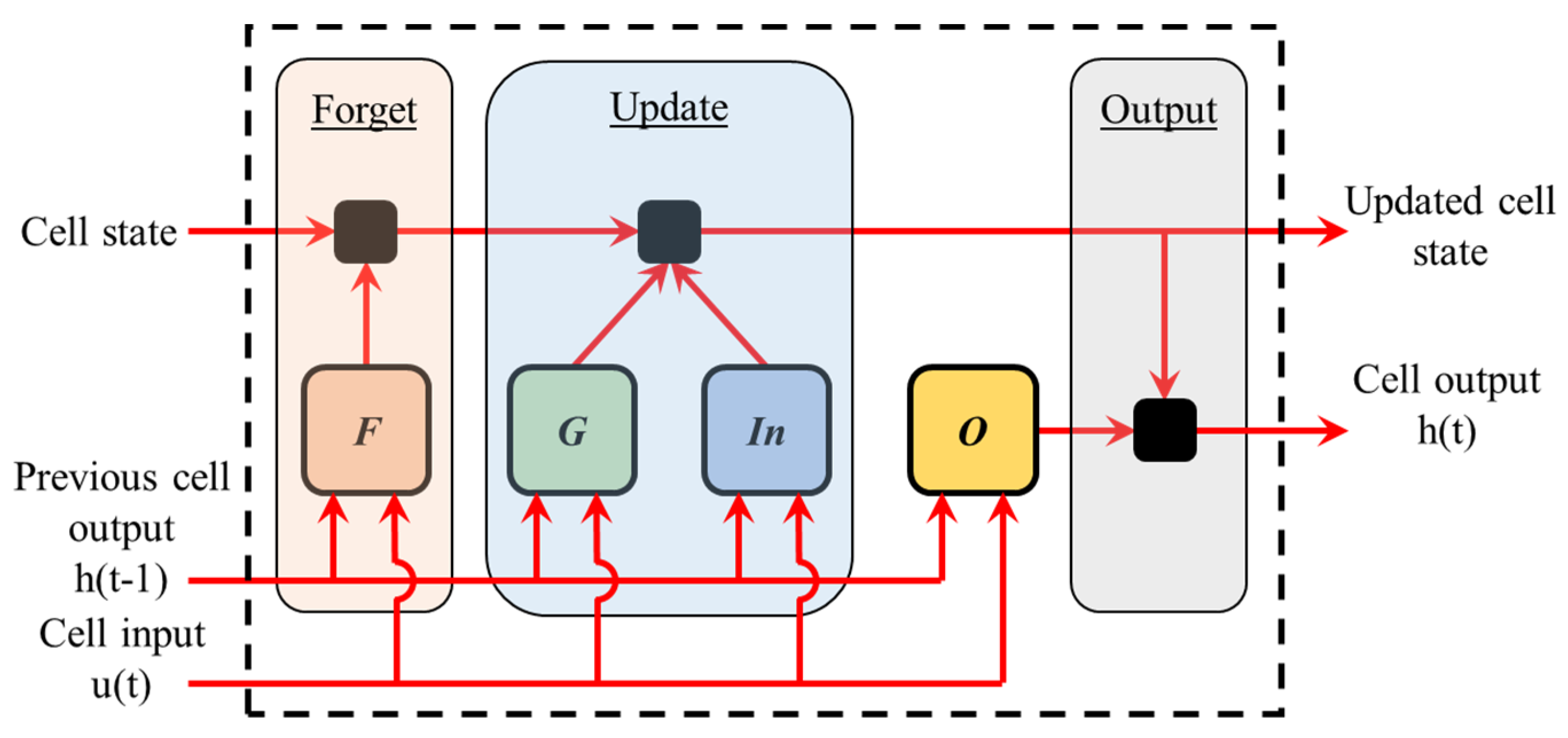
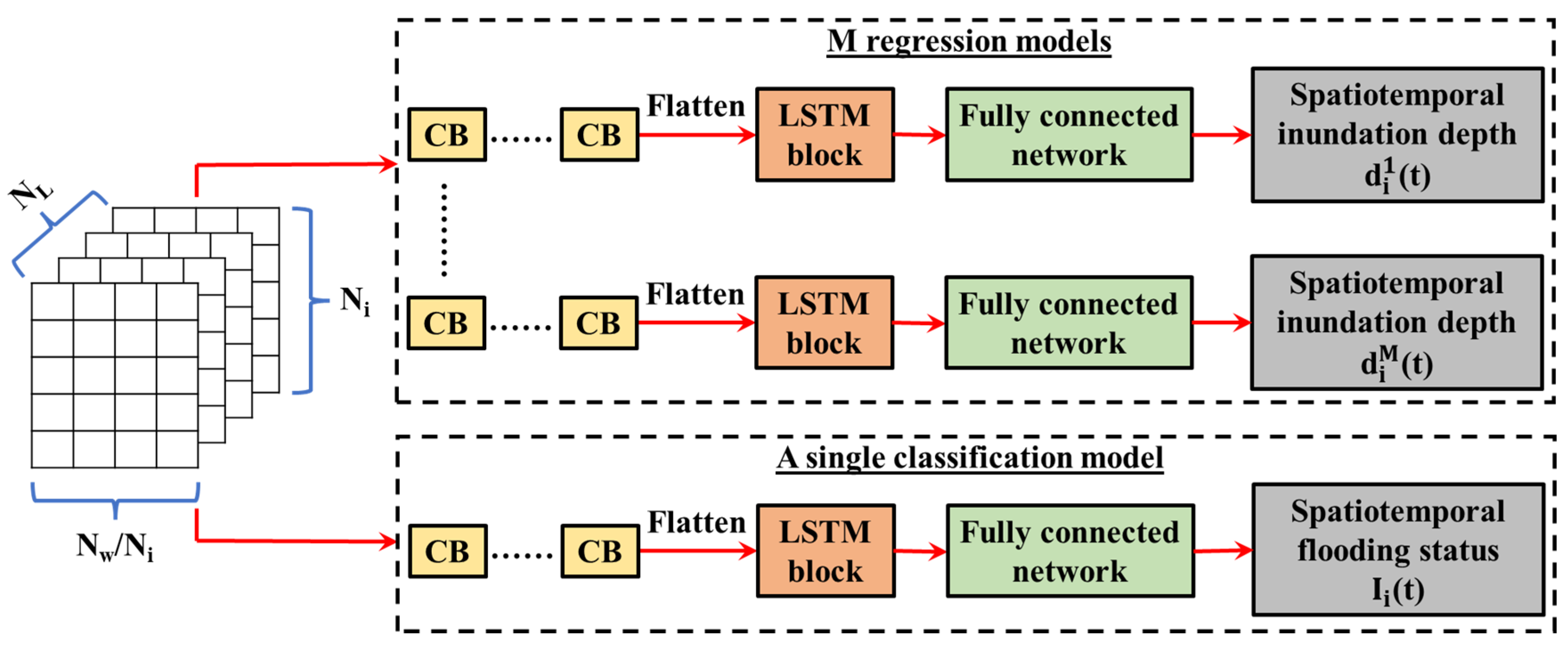
2.2. Deep Learning Module
2.3. Averaging and Testing Module
2.4. Prediction Module
3. Study Area and Data Description
4. Results and Discussion
4.1. Synchronization Analysis Results
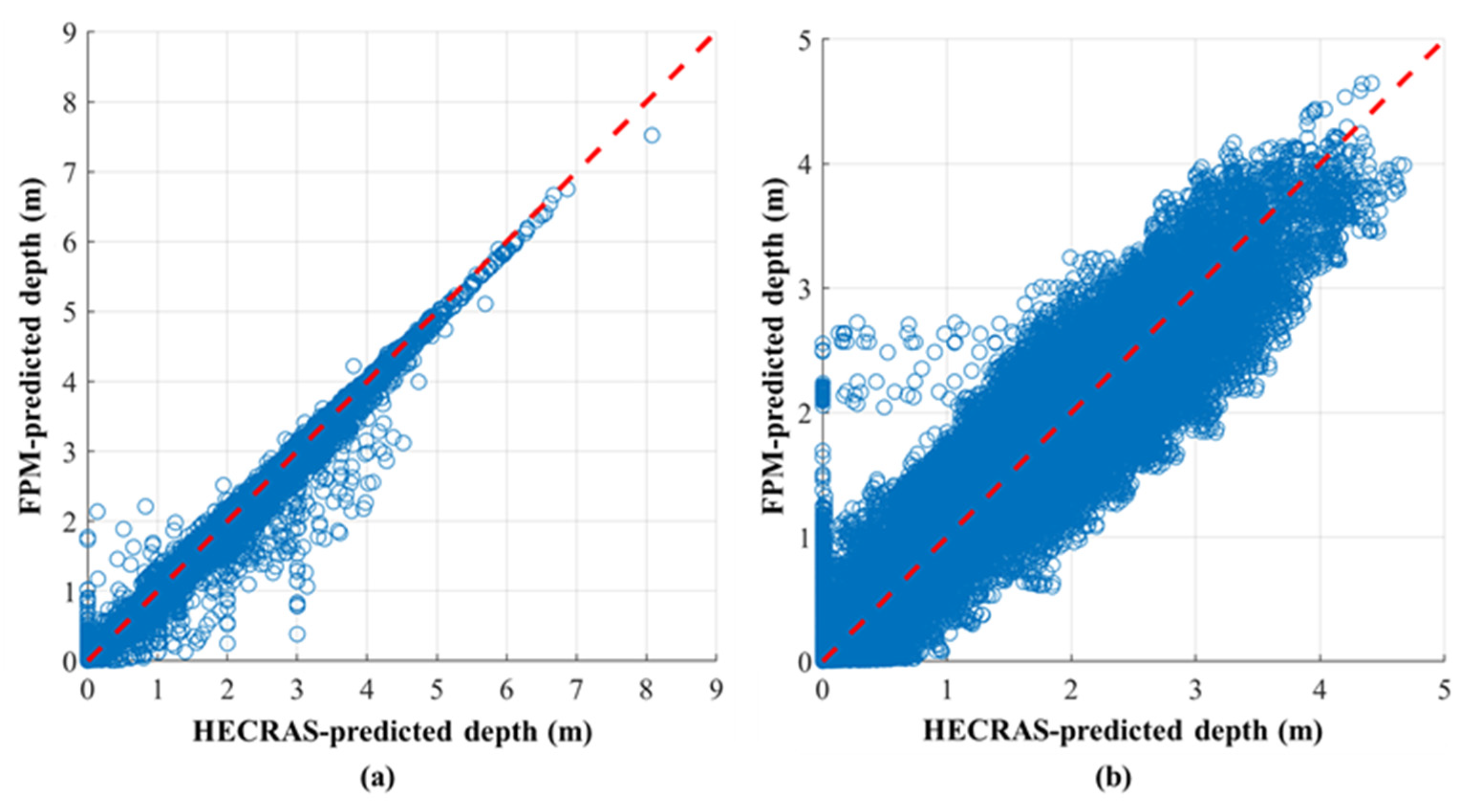
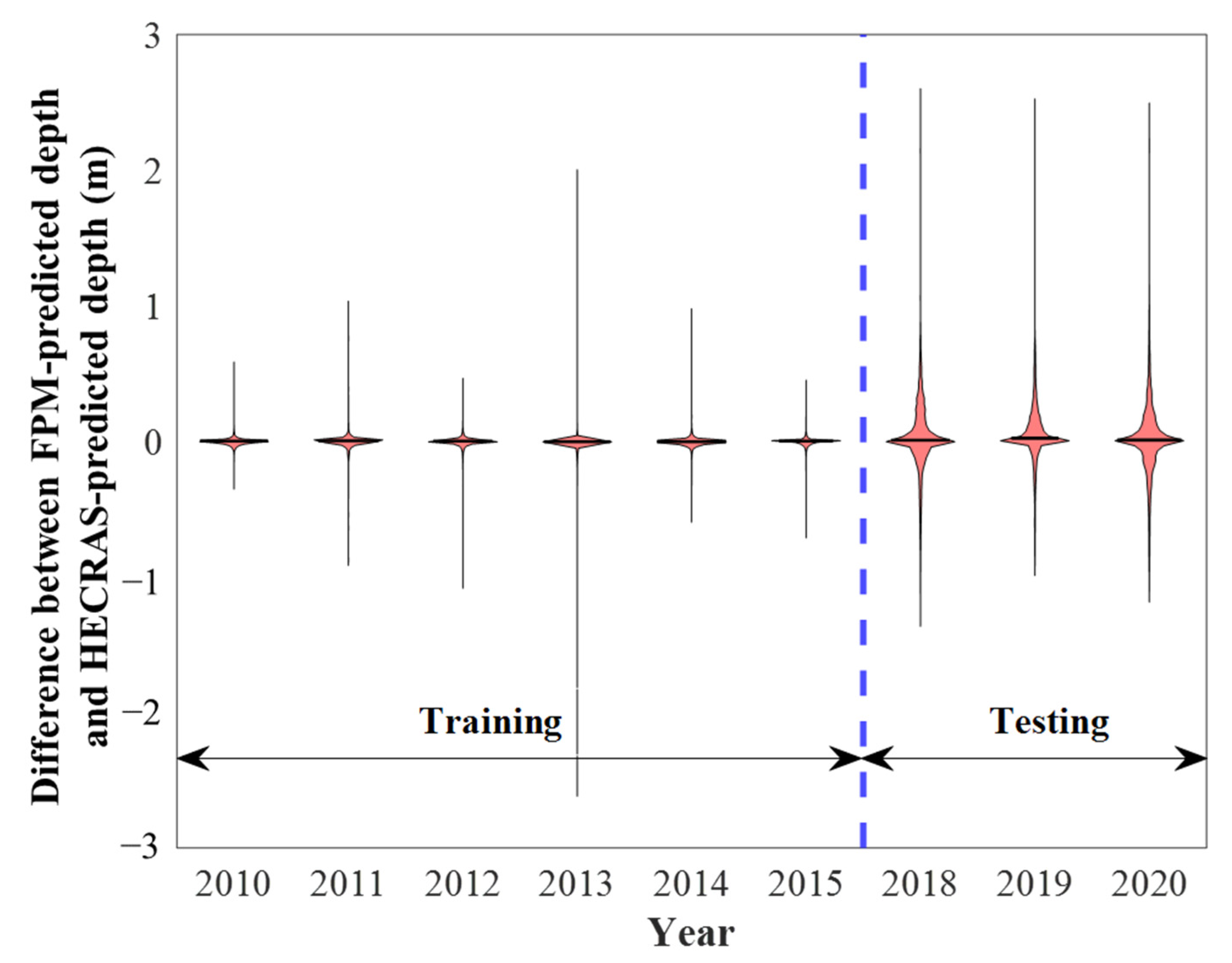
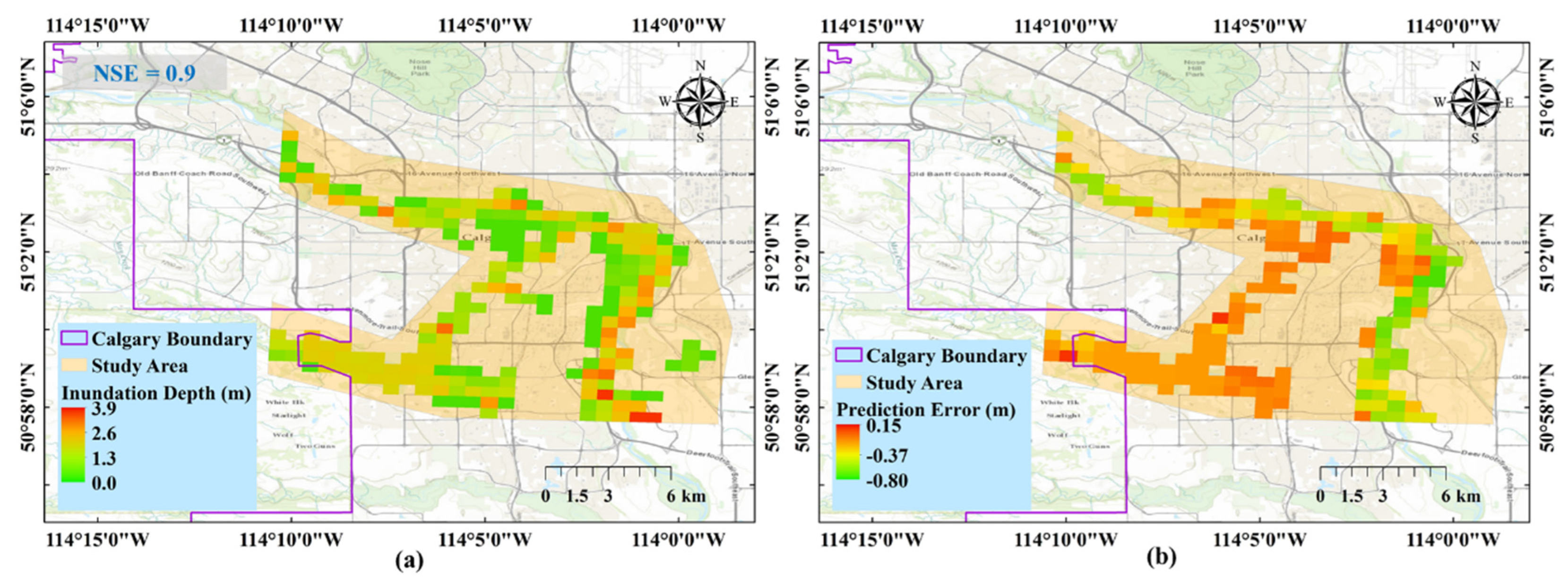
4.2. Deep Learning Model Development and Performance Evaluation
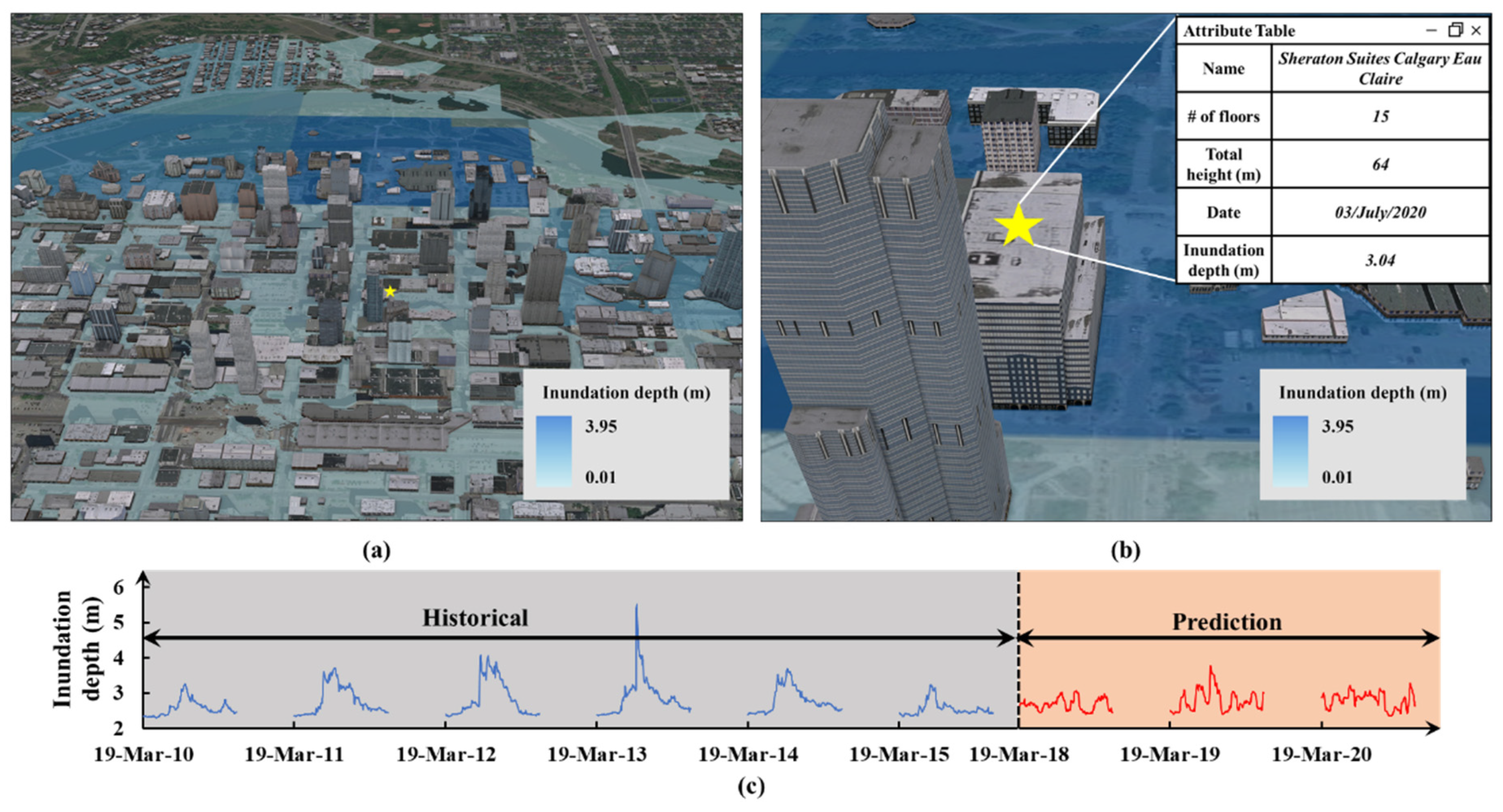
4.3. Example of Model Predictions
5. Insights for City Digital Twin Development and Climate Resilience Planning
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- McLennan, M. The Global Risks Report 2021: 16th Edition; World Economic Forum: Cologny, Switzerland, 2021. [Google Scholar]
- McLennan, M. The Global Risks Report 2022: 17th Edition; World Economic Forum: Cologny, Switzerland, 2022. [Google Scholar]
- Gaur, A.; Gaur, A.; Simonovic, S.P. Future Changes in Flood Hazards across Canada under a Changing Climate. Water 2018, 10, 1441. [Google Scholar] [CrossRef] [Green Version]
- Nofal, O.M.; van de Lindt, J.W. Understanding Flood Risk in the Context of Community Resilience Modeling for the Built Environment: Research Needs and Trends. Sustain. Resilient Infrastruct. 2020, 7, 171–187. [Google Scholar] [CrossRef]
- Gaur, A.; Gaur, A.; Simonovic, S.P. Modelling of Future Flood Risk across Canada Due to Climate Change. In WIT Transactions on Engineering Sciences; WIT Press: Southampton, UK, 2018; Volume 121, pp. 149–159. [Google Scholar]
- Tanaka, T.; Kiyohara, K.; Tachikawa, Y. Comparison of Fluvial and Pluvial Flood Risk Curves in Urban Cities Derived from a Large Ensemble Climate Simulation Dataset: A Case Study in Nagoya, Japan. J. Hydrol. 2020, 584, 124706. [Google Scholar] [CrossRef]
- UN Office for Disaster Risk Reduction. The Human Cost of Disasters—An Overview of the Last 20 Years 2000–2019; UN Office for Disaster Risk Reduction: Geneva, Switzerland, 2020. [Google Scholar]
- Tellman, B.; Sullivan, J.A.; Kuhn, C.; Kettner, A.J.; Doyle, C.S.; Brakenridge, G.R.; Erickson, T.A.; Slayback, D.A. Satellite Imaging Reveals Increased Proportion of Population Exposed to Floods. Nature 2021, 596, 80–86. [Google Scholar] [CrossRef] [PubMed]
- United Nations Office for Disaster Risk Reduction. 2020: The Non-COVID Year in Disasters; United Nations Office for Disaster Risk Reduction: Geneva, Switzerland, 2021. [Google Scholar]
- Pörtner, H.-O.; Roberts, D.C.; Adams, H.; Adelekan, I.; Adler, C.; Adrian, R.; Aldunce, P.; Ali, E.; Ara-Begum, R.; Bednar-Friedl, B.; et al. “Technical Summary” in Climate Change 2022: Impacts, Adaptation, and Vulnerability; Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Ionita, M.; Nagavciuc, V. Extreme Floods in the Eastern Part of Europe: Large-Scale Drivers and Associated Impacts. Water 2021, 13, 1122. [Google Scholar] [CrossRef]
- CRED. Disasters in Africa: 20 Year Review 2000–2019; CRED: Bengaluru, India, 2019. [Google Scholar]
- Tembata, K.; Takeuchi, K. Floods and Exports: An Empirical Study on Natural Disaster Shocks in Southeast Asia. Econ. Disasters Clim. Chang. 2019, 3, 39–60. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Mo, R.; Vitart, F.; Stan, C. Eastern Canada Flooding 2017 and Its Subseasonal Predictions. Atmosphere-Ocean 2019, 57, 195–207. [Google Scholar] [CrossRef] [Green Version]
- Kokas, T.; Simonovic, S.P.; Binns, A. Flood Risk Management in Canadian Urban Environments: A Comprehensive Framework for Water Resources Modeling and Decision-Making; Water Resources Research Report no. 095; Department of Civil and Environmental Engineering: London, ON, Canada, 2016. [Google Scholar]
- Neri, A.; Villarini, G.; Slater, L.J.; Napolitano, F. On the Statistical Attribution of the Frequency of Flood Events across the U.S. Midwest. Adv Water Resour 2019, 127, 225–236. [Google Scholar] [CrossRef]
- Billion-Dollar Weather and Climate Disasters. Available online: https://www.ncei.noaa.gov/access/billions/ (accessed on 20 March 2022).
- Sandink, D. Urban Flooding in Canada; Institute for Catastrophic Loss Reduction: Toronto, ON, Canada, 2013; Volume 52. [Google Scholar]
- Garner, A.J.; Mann, M.E.; Emanuel, K.A.; Kopp, R.E.; Lin, N.; Alley, R.B.; Horton, B.P.; DeConto, R.M.; Donnelly, J.P.; Pollard, D. Impact of Climate Change on New York City’s Coastal Flood Hazard: Increasing Flood Heights from the Preindustrial to 2300 CE. Proc. Natl. Acad. Sci. USA 2017, 114, 11861–11866. [Google Scholar] [CrossRef] [Green Version]
- Paprotny, D.; Vousdoukas, M.I.; Morales-Nápoles, O.; Jonkman, S.N.; Feyen, L. Compound Flood Potential in Europe. Hydrol. Earth Syst. Sci. Discuss. 2018, 132, 1–34. [Google Scholar] [CrossRef]
- Paprotny, D.; Sebastian, A.; Morales-Nápoles, O.; Jonkman, S.N. Trends in Flood Losses in Europe over the Past 150 Years. Nat. Commun. 2018, 9, 1985. [Google Scholar] [CrossRef] [Green Version]
- Berghuijs, W.R.; Aalbers, E.E.; Larsen, J.R.; Trancoso, R.; Woods, R.A. Recent Changes in Extreme Floods across Multiple Continents. Environ. Res. Lett. 2017, 12, 114035. [Google Scholar] [CrossRef]
- Schrotter, G.; Hürzeler, C. The Digital Twin of the City of Zurich for Urban Planning. PFG-J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 99–112. [Google Scholar] [CrossRef] [Green Version]
- Ghaith, M.; Yosri, A.; El-Dakhakhni, W. Digital Twin: A City-Scale Flood Imitation Framework. In Proceedings of the Canadian Society of Civil Engineering Annual Conference, Online, 26–29 May 2021; pp. 577–588. [Google Scholar] [CrossRef]
- Ruohomäki, T.; Airaksinen, E.; Huuska, P.; Kesäniemi, O.; Martikka, M.; Suomisto, J. Smart City Platform Enabling Digital Twin. In Proceedings of the International Conference on Intelligent Systems, Funchal, Portugal, 25–27 September 2018; pp. 155–161. [Google Scholar]
- Ivanov, S.; Nikolskaya, K.; Radchenko, G.; Sokolinsky, L.; Zymbler, M. Digital Twin of City: Concept Overview. In Proceedings of the Global Smart Industry Conference, Chelyabinsk, Russia, 17–19 November 2020; pp. 178–186. [Google Scholar]
- Ford, D.N.; Wolf, C.M. Smart Cities with Digital Twin Systems for Disaster Management. J. Manag. Eng. 2020, 36, 04020027. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Parlikad, A.K.; Woodall, P.; Don Ranasinghe, G.; Xie, X.; Liang, Z.; Konstantinou, E.; Heaton, J.; Schooling, J. Developing a Digital Twin at Building and City Levels: Case Study of West Cambridge Campus. J. Manag. Eng. 2020, 36, 05020004. [Google Scholar] [CrossRef]
- Abdel-Mooty, M.N.; Yosri, A.; El-Dakhakhni, W.; Coulibaly, P. Community Flood Resilience Categorization Framework. Int. J. Disaster Risk Reduct. 2021, 61, 102349. [Google Scholar] [CrossRef]
- Haggag, M.; Yosri, A.; El-Dakhakhni, W.; Hassini, E. Interpretable Data-Driven Model for Climate-Induced Disaster Damage Prediction: The First Step in Community Resilience Planning. Int. J. Disaster Risk Reduct. 2022, 73, 102884. [Google Scholar] [CrossRef]
- Ezzeldin, M.; El-Dakhakhni, W.E. Robustness of Ontario Power Network under Systemic Risks. Sustain. Resilient. Infrastruct. 2021, 6, 252–271. [Google Scholar] [CrossRef]
- Li, X.; Liu, H.; Wang, W.; Zheng, Y.; Lv, H.; Lv, Z. Big Data Analysis of the Internet of Things in the Digital Twins of Smart City Based on Deep Learning. Future Gener. Comput. Syst. 2022, 128, 167–177. [Google Scholar] [CrossRef]
- Papyshev, G.; Yarime, M. Exploring City Digital Twins as Policy Tools: A Task-Based Approach to Generating Synthetic Data on Urban Mobility. Data Policy 2021, 3, e16. [Google Scholar] [CrossRef]
- Lv, Z.; Xie, S. Artificial Intelligence in the Digital Twins: State of the Art, Challenges, and Future Research Topics. Digit. Twin 2021, 1, 12. [Google Scholar] [CrossRef]
- Austin, M.; Delgoshaei, P.; Coelho, M.; Heidarinejad, M. Architecting Smart City Digital Twins: Combined Semantic Model and Machine Learning Approach. J. Manag. Eng. 2020, 36, 04020026. [Google Scholar] [CrossRef]
- Dembski, F.; Wössner, U.; Letzgus, M.; Ruddat, M.; Yamu, C. Urban Digital Twins for Smart Cities and Citizens: The Case Study of Herrenberg, Germany. Sustainability 2020, 12, 2307. [Google Scholar] [CrossRef] [Green Version]
- National Research Foundation: Prime Minister’s Office: Virtual Singapore. Available online: https://www.nrf.gov.sg/ (accessed on 6 November 2022).
- Ham, Y.; Kim, J. Participatory Sensing and Digital Twin City: Updating Virtual City Models for Enhanced Risk-Informed Decision-Making. J. Manag. Eng. 2020, 36, 04020005. [Google Scholar] [CrossRef]
- Chomba, I.C.; Banda, K.E.; Winsemius, H.C.; Chomba, M.J.; Mataa, M.; Ngwenya, V.; Sichingabula, H.M.; Nyambe, I.A.; Ellender, B. A Review of Coupled Hydrologic-Hydraulic Models for Floodplain Assessments in Africa: Opportunities and Challenges for Floodplain Wetland Management. Hydrology 2021, 8, 44. [Google Scholar] [CrossRef]
- Bravo, J.M.; Allasia, D.; Paz, A.R.; Collischonn, W.; Tucci, C.E.M. Coupled Hydrologic-Hydraulic Modeling of the Upper Paraguay River Basin. J. Hydrol. Eng. 2012, 17, 635–646. [Google Scholar] [CrossRef]
- Clilverd, H.M.; Thompson, J.R.; Heppell, C.M.; Sayer, C.D.; Axmacher, J.C. Coupled Hydrological/Hydraulic Modelling of River Restoration Impacts and Floodplain Hydrodynamics. River Res. Appl. 2016, 32, 1927–1948. [Google Scholar] [CrossRef]
- Golmohammadi, G.; Prasher, S.; Madani, A.; Rudra, R. Evaluating Three Hydrological Distributed Watershed Models: MIKE-SHE, APEX, SWAT. Hydrology 2014, 1, 20–39. [Google Scholar] [CrossRef] [Green Version]
- Ghaith, M.; Li, Z. Propagation of Parameter Uncertainty in SWAT: A Probabilistic Forecasting Method Based on Polynomial Chaos Expansion and Machine Learning. J. Hydrol. 2020, 586, 124854. [Google Scholar] [CrossRef]
- Ghaith, M.; Li, Z.; Baetz, B.W. Uncertainty Analysis for Hydrological Models with Interdependent Parameters: An Improved Polynomial Chaos Expansion Approach. Water Resour. Res. 2021, 57, e2020WR029149. [Google Scholar] [CrossRef]
- Hosseiny, H. A Deep Learning Model for Predicting River Flood Depth and Extent. Environ. Model. Softw. 2021, 145, 105186. [Google Scholar] [CrossRef]
- Zanchetta, A.D.L.; Coulibaly, P. Hybrid Surrogate Model for Timely Prediction of Flash Flood Inundation Maps Caused by Rapid River Overflow. Forecasting 2022, 4, 126–148. [Google Scholar] [CrossRef]
- Gunathilake, M.B.; Karunanayake, C.; Gunathilake, A.S.; Marasingha, N.; Samarasinghe, J.T.; Bandara, I.M.; Rathnayake, U. Hydrological Models and Artificial Neural Networks (ANNs) to Simulate Streamflow in a Tropical Catchment of Sri Lanka. Appl. Comput. Intell. Soft Comput. 2021, 2021, 6683389. [Google Scholar] [CrossRef]
- Ghaith, M.; Siam, A.; Li, Z.; El-Dakhakhni, W. Hybrid Hydrological Data-Driven Approach for Daily Streamflow Forecasting. J. Hydrol. Eng. 2020, 25, 04019063. [Google Scholar] [CrossRef]
- Van, S.P.; Le, H.M.; Thanh, D.V.; Dang, T.D.; Loc, H.H.; Anh, D.T. Deep Learning Convolutional Neural Network in Rainfall-Runoff Modelling. J. Hydroinforma. 2020, 22, 541–561. [Google Scholar] [CrossRef] [Green Version]
- Baek, S.S.; Pyo, J.; Chun, J.A. Prediction of Water Level and Water Quality Using a Cnn-Lstm Combined Deep Learning Approach. Water 2020, 12, 3399. [Google Scholar] [CrossRef]
- Elmorsy, M.; El-Dakhakhni, W.; Zhao, B. Generalizable Permeability Prediction of Digital Porous Media via a Novel Multi-scale 3D Convolutional Neural Network. Water Resour. Res. 2022, 58, e2021WR031454. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Hong, H.; Peng, L. Flood Susceptibility Mapping Using Convolutional Neural Network Frameworks. J. Hydrol. 2020, 582, 124482. [Google Scholar] [CrossRef]
- Chang, D.L.; Yang, S.H.; Hsieh, S.L.; Wang, H.J.; Yeh, K.C. Artificial Intelligence Methodologies Applied to Prompt Pluvial Flood Estimation and Prediction. Water 2020, 12, 3552. [Google Scholar] [CrossRef]
- Chen, C.; Hui, Q.; Xie, W.; Wan, S.; Zhou, Y.; Pei, Q. Convolutional Neural Networks for Forecasting Flood Process in Internet-of-Things Enabled Smart City. Comput. Netw. 2021, 186, 107744. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow Prediction Using an Integrated Methodology Based on Convolutional Neural Network and Long Short-Term Memory Networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Jiang, J.; Liao, Z.; Zhou, Y.; Wang, H.; Pei, Q. A Short-Term Flood Prediction Based on Spatial Deep Learning Network: A Case Study for Xi County, China. J. Hydrol. 2022, 607, 127535. [Google Scholar] [CrossRef]
- Guo, Z.; Leitão, J.P.; Simões, N.E.; Moosavi, V. Data-Driven Flood Emulation: Speeding up Urban Flood Predictions by Deep Convolutional Neural Networks. J. Flood Risk. Manag. 2021, 14, e12684. [Google Scholar] [CrossRef]
- Kabir, S.; Patidar, S.; Xia, X.; Liang, Q.; Neal, J.; Pender, G. A Deep Convolutional Neural Network Model for Rapid Prediction of Fluvial Flood Inundation. J. Hydrol. 2020, 590, 125481. [Google Scholar] [CrossRef]
- Bentivoglio, R.; Isufi, E.; Nicolaas Jonkman, S.; Taormina, R. Deep Learning Methods for Flood Mapping: A Review of Existing Applications and Future Research Directions. Hydrol. Earth Syst. Sci. 2021, 614, 4345–4378. [Google Scholar] [CrossRef]
- Boccaletti, S.; Pisarchik, A.N.; del Genio, C.I.; Amann, A. Synchronization: From Coupled Systems to Complex Networks, 1st ed.; Cambridge University Press: Cambridge, UK, 2018; ISBN 978-1-107-05626-8. [Google Scholar]
- Boccaletti, S.; Kurths, J.; Osipov, G.; Valladares, D.L.; Zhou, C.S. Synchronization of Chaotic Systems. Phys. Rep. 2002, 366, 1–101. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Kreuz, T.; Grassberger, P. Event Synchronization: A Simple and Fast Method to Measure Synchronicity and Time Delay Patterns. Phys. Rev. E 2002, 66, 041904. [Google Scholar] [CrossRef] [Green Version]
- Yosri, A.; Dickson-Anderson, S.; Siam, A.; El-Dakhakhni, W. Transport Pathway Identification in Fractured Aquifers: A Stochastic Event Synchrony-Based Framework. Adv. Water Resour. 2021, 147, 103800. [Google Scholar] [CrossRef]
- Dauwels, J.; Vialatte, F.; Weber, T.; Musha, T.; Cichocki, A. Quantifying Statistical Interdependence by Message Passing on Graphs-Part I: One-Dimensional Point Processes. Neural. Comput. 2009, 21, 2152–2202. [Google Scholar] [CrossRef]
- Pelt, D.M.; Sethian, J.A. A Mixed-Scale Dense Convolutional Neural Network for Image Analysis. Proc. Natl. Acad. Sci. USA 2017, 115, 254–259. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yang, S.; Zheng, Y.; Lu, H. Improved Point-Voxel Region Convolutional Neural Network: 3D Object Detectors for Autonomous Driving. IEEE Trans. Intell. Transp. Syst. 2021, 23, 9311–9317. [Google Scholar] [CrossRef]
- Chen, S.; Leng, Y.; Labi, S. A Deep Learning Algorithm for Simulating Autonomous Driving Considering Prior Knowledge and Temporal Information. Comput.-Aided Civ. Infrastruct. Eng. 2020, 35, 305–321. [Google Scholar] [CrossRef]
- Rezk, E.; Eltorki, M.; El-Dakhakhni, W. Leveraging Artificial Intelligence to Improve the Diversity of Dermatological Skin Color Pathology: Protocol for an Algorithm Development and Validation Study. JMIR Res. Protoc. 2022, 11, e34896. [Google Scholar] [CrossRef]
- Muraki, R.; Teramoto, A.; Sugimoto, K.; Sugimoto, K.; Yamada, A.; Watanabe, E. Automated Detection Scheme for Acute Myocardial Infarction Using Convolutional Neural Network and Long Short-Term Memory. PLoS ONE 2022, 17, e0264002. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems; Pereira, F., Burges, C.J., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2012; pp. 1097–1105. ISBN 9781627480031. [Google Scholar]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A Review of Uncertainty Quantification in Deep Learning: Techniques, Applications and Challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Gao, M.; Chen, C.; Shi, J.; Lai, C.S.; Yang, Y.; Dong, Z. A Multiscale Recognition Method for the Optimization of Traffic Signs Using GMM and Category Quality Focal Loss. Sensors 2020, 20, 4850. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. Predicting Flood Susceptibility Using LSTM Neural Networks. J. Hydrol. 2021, 594, 125734. [Google Scholar] [CrossRef]
- Zhou, B.-C.; Han, C.-Y.; Guo, T.-D. Convergence of Stochastic Gradient Descent in Deep Neural Network. Acta Math. Appl. Sin. 2021, 37, 126–136. [Google Scholar] [CrossRef]
- Okewu, E.; Misra, S.; Lius, F.S. Parameter Tuning Using Adaptive Moment Estimation in Deep Learning Neural Networks. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics, Cagliari, Italy, 1–4 July 2020; Volume 12254. [Google Scholar]
- Touvron, H.; Cord, M.; Douze, M.; Massa, F.; Sablayrolles, A.; Jégou, H. Training Data-Efficient Image Transformers & Distillation through Attention. In Proceedings of the 38th International Conference on Machine Learning, Virtual, 18–24 July 2021; pp. 10347–10357. [Google Scholar]
- Sun, C.; Shrivastava, A.; Singh, S.; Gupta, A. Revisiting Unreasonable Effectiveness of Data in Deep Learning Era. In Proceedings of the IEEE International Conference on Computer Vision 2017, Venice, Italy, 22–29 October 29 2017; pp. 843–852. [Google Scholar] [CrossRef]
- Zhu, X.; Vondrick, C.; Fowlkes, C.C.; Ramanan, D. Do We Need More Training Data? Int. J. Comput. Vis. 2016, 119, 76–92. [Google Scholar] [CrossRef] [Green Version]
- Ergen, T.; Pilanci, M. Global Optimality Beyond Two Layers: Training Deep ReLU Networks via Convex Programs. In Proceedings of the 38th International Conference on Machine Learning, Online, 18–24 July 2021; pp. 2993–3003. [Google Scholar]
- Steyvers, M.; Tejeda, H.; Kerrigan, G.; Smyth, P. Bayesian Modeling of Human–AI Complementarity. Proc. Natl. Acad. Sci. USA 2022, 119, e2111547119. [Google Scholar] [CrossRef] [PubMed]
- Duan, K.; Wang, X.; Liu, B.; Zhao, T.; Chen, X. Comparing Bayesian Model Averaging and Reliability Ensemble Averaging in Post-Processing Runoff Projections under Climate Change. Water 2021, 13, 2124. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-Comparison of Different Bayesian Model Averaging Modifications in Streamflow Simulation. Water 2019, 11, 1707. [Google Scholar] [CrossRef] [Green Version]
- Massoud, E.C.; Lee, H.; Gibson, P.B.; Loikith, P.; Waliser, D.E. Bayesian Model Averaging of Climate Model Projections Constrained by Precipitation Observations over the Contiguous United States. J. Hydrometeorol. 2020, 21, 2401–2418. [Google Scholar] [CrossRef]
- Basher, A.; Islam, A.K.M.S.; Stiller-Reeve, M.A.; Chu, P.S. Changes in Future Rainfall Extremes over Northeast Bangladesh: A Bayesian Model Averaging Approach. Int. J. Climatol. 2020, 40, 3232–3249. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, A.K.L. Retrospective Analysis and Bayesian Model Averaging of Cmip6 Precipitation in the Nile River Basin. J. Hydrometeorol. 2020, 22, 217–229. [Google Scholar] [CrossRef]
- Hao, Y.; Baik, J.; Tran, H.; Choi, M. Quantification of the Effect of Hydrological Drivers on Actual Evapotranspiration Using the Bayesian Model Averaging Approach for Various Landscapes over Northeast Asia. J. Hydrol. 2022, 607, 127543. [Google Scholar] [CrossRef]
- Lee, S.; Yen, H.; Yeo, I.Y.; Moglen, G.E.; Rabenhorst, M.C.; McCarty, G.W. Use of Multiple Modules and Bayesian Model Averaging to Assess Structural Uncertainty of Catchment-Scale Wetland Modeling in a Coastal Plain Landscape. J. Hydrol. 2020, 582, 124544. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. HUP-BMA: An Integration of Hydrologic Uncertainty Processor and Bayesian Model Averaging for Streamflow Forecasting. Water Resour. Res. 2021, 57, e2020WR029433. [Google Scholar] [CrossRef]
- Enemark, T.; Peeters, L.; Mallants, D.; Flinchum, B.; Batelaan, O. A Systematic Approach to Hydrogeological Conceptual Model Testing, Combining Remote Sensing and Geophysical Data. Water Resour. Res. 2020, 56, e2020WR027578. [Google Scholar] [CrossRef]
- Gharekhani, M.; Nadiri, A.A.; Khatibi, R.; Sadeghfam, S.; Asghari Moghaddam, A. A Study of Uncertainties in Groundwater Vulnerability Modelling Using Bayesian Model Averaging (BMA). J. Environ. Manag. 2022, 303, 114168. [Google Scholar] [CrossRef]
- Yin, J.; Tsai, F.T.-C.; Kao, S.-C. Accounting for Uncertainty in Complex Alluvial Aquifer Modeling by Bayesian Multi-Model Approach. J. Hydrol. 2021, 601, 126682. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-Model Ensemble Hydrologic Prediction Using Bayesian Model Averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef] [Green Version]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Yang, J.; Reichert, P.; Abbaspour, K.C.; Yang, H. Hydrological Modelling of the Chaohe Basin in China: Statistical Model Formulation and Bayesian Inference. J. Hydrol. 2007, 340, 167–182. [Google Scholar] [CrossRef]
- Jimeno-Sáez, P.; Senent-Aparicio, J.; Pérez-Sánchez, J.; Pulido-Velazquez, D. A Comparison of SWAT and ANN Models for Daily Runoff Simulation in Different Climatic Zones of Peninsular Spain. Water 2018, 10, 192. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Li, Y.; Huang, G.; Chen, X.; Bao, A. Assessment of Parameter Uncertainty in Hydrological Model Using a Markov-Chain-Monte-Carlo-Based Multilevel-Factorial-Analysis Method. J. Hydrol. 2016, 538, 471–486. [Google Scholar] [CrossRef]
- Li, Z.; Shao, Q.; Xu, Z.; Cai, X. Analysis of Parameter Uncertainty in Semi-Distributed Hydrological Models Using Bootstrap Method: A Case Study of SWAT Model Applied to Yingluoxia Watershed in Northwest China. J. Hydrol. 2010, 385, 76–83. [Google Scholar] [CrossRef]




| Time Interval | Precision | Recall | F-Score | |
|---|---|---|---|---|
| Overall | Training | [0.94–1.0] | [0.90–1.0] | [0.92–1.0] |
| Testing | [0.91–1.0] | [0.94–1.0] | [0.93–1.0] | |
| River | Training | [0.86–1.0] | [0.92–1.0] | [0.91–1.0] |
| Testing | [0.92–1.0] | [0.85–1.0] | [0.90–1.0] | |
| Overland flow areas | Training | [0.90–1.0] | [0.79–1.0] | [0.86–1.0] |
| Testing | [0.80–1.0] | [0.87–1.0] | [0.88–1.0] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghaith, M.; Yosri, A.; El-Dakhakhni, W. Synchronization-Enhanced Deep Learning Early Flood Risk Predictions: The Core of Data-Driven City Digital Twins for Climate Resilience Planning. Water 2022, 14, 3619. https://doi.org/10.3390/w14223619
Ghaith M, Yosri A, El-Dakhakhni W. Synchronization-Enhanced Deep Learning Early Flood Risk Predictions: The Core of Data-Driven City Digital Twins for Climate Resilience Planning. Water. 2022; 14(22):3619. https://doi.org/10.3390/w14223619
Chicago/Turabian StyleGhaith, Maysara, Ahmed Yosri, and Wael El-Dakhakhni. 2022. "Synchronization-Enhanced Deep Learning Early Flood Risk Predictions: The Core of Data-Driven City Digital Twins for Climate Resilience Planning" Water 14, no. 22: 3619. https://doi.org/10.3390/w14223619








