Effects of Energy Dissipation Pier Arrangements on the Hydraulic Characteristics of Segmented Pier-Type Step Energy Dissipator Structures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Construction of Numerical Models
2.1.1. Turbulence Model
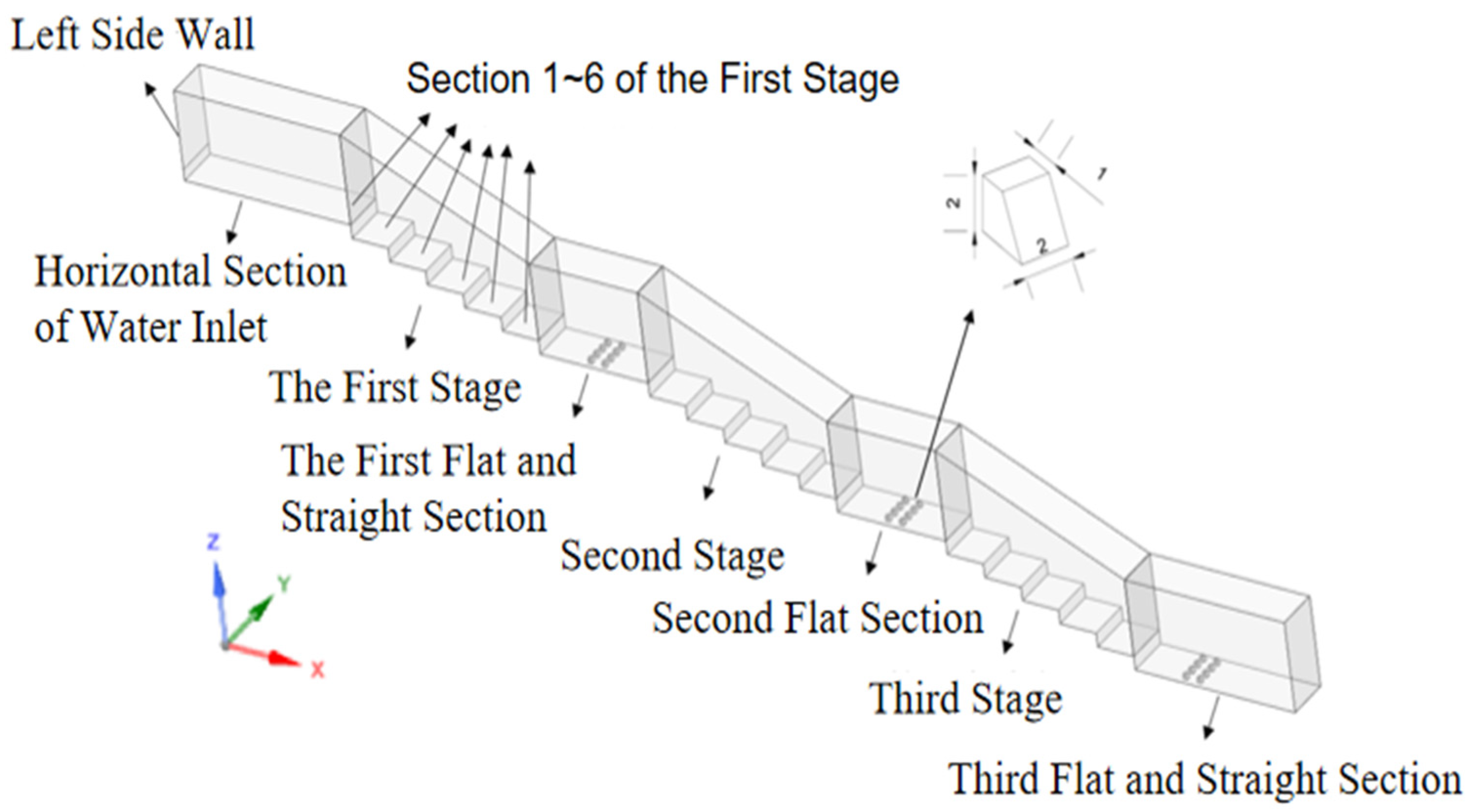
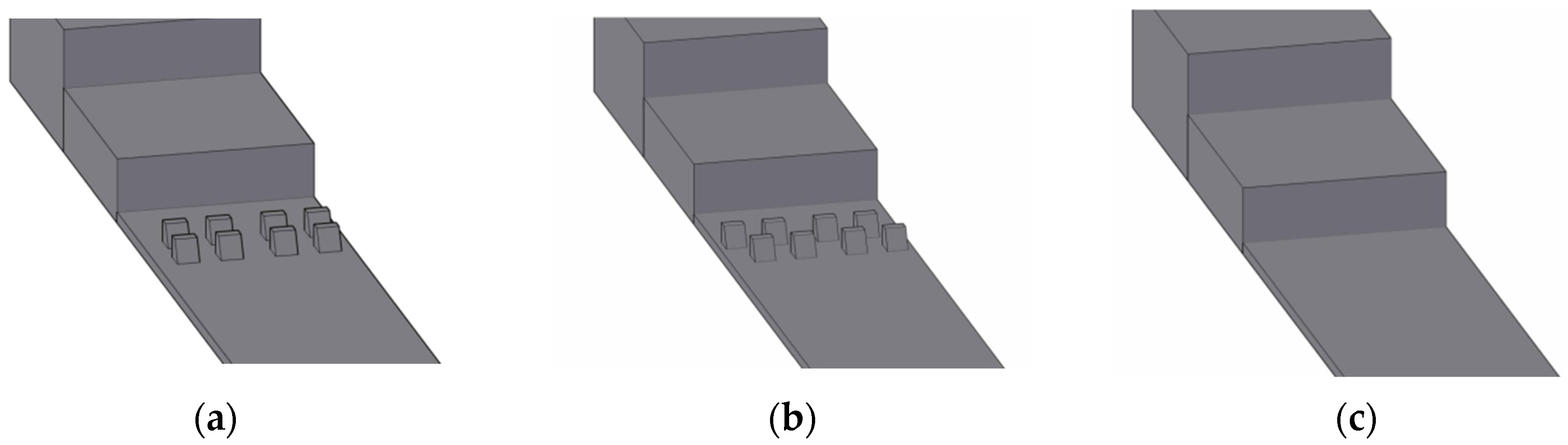
2.1.2. Model Building
2.1.3. Mesh Division and Boundary Setting
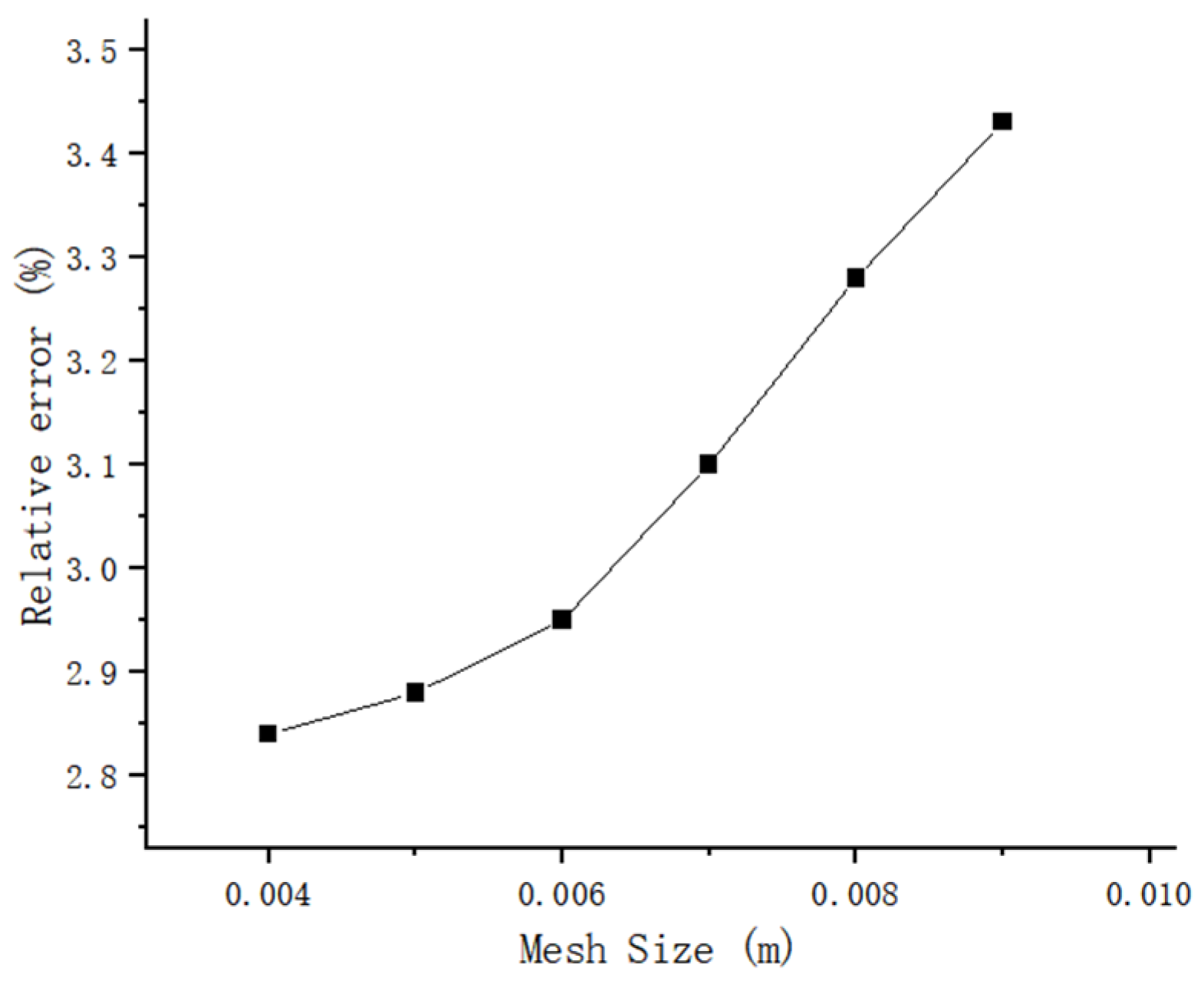
2.1.4. Mesh Sensitivity Analysis
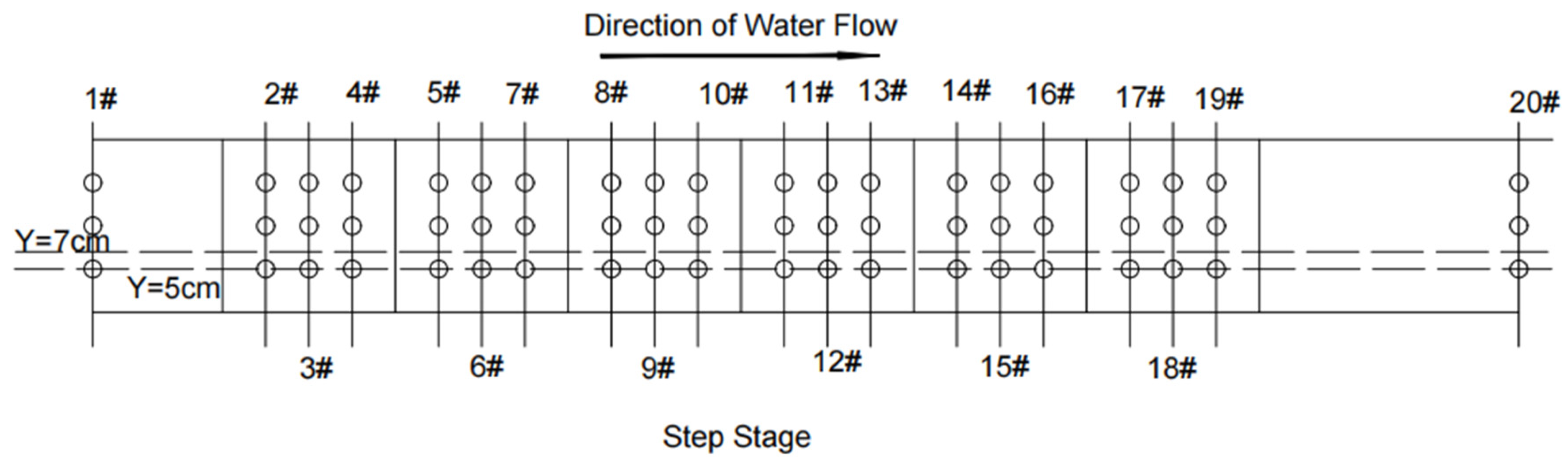
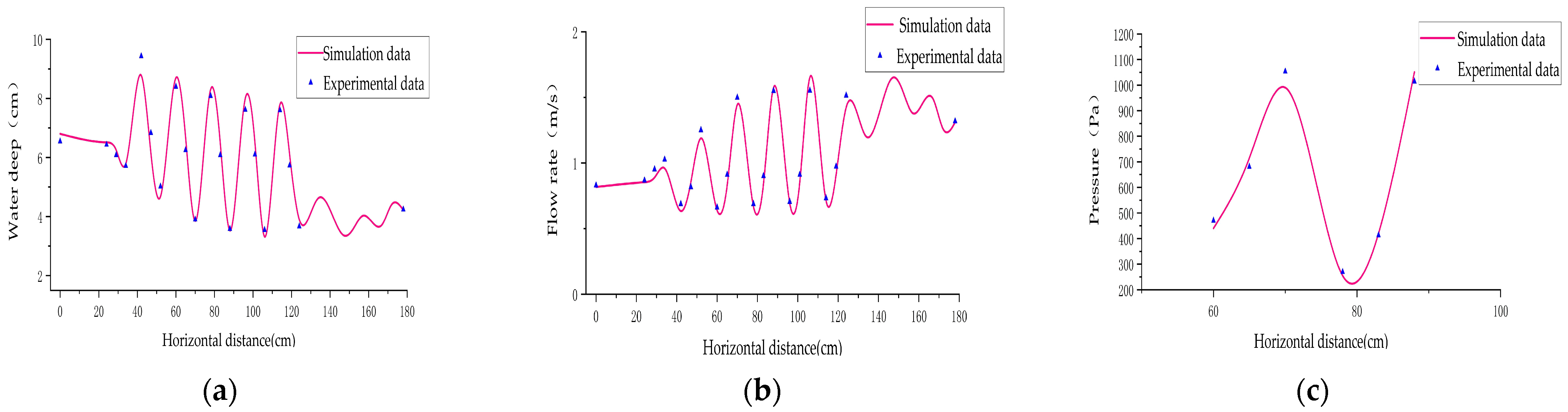
2.2. Experimental Validation of Numerical Model
3. Results and Discussion
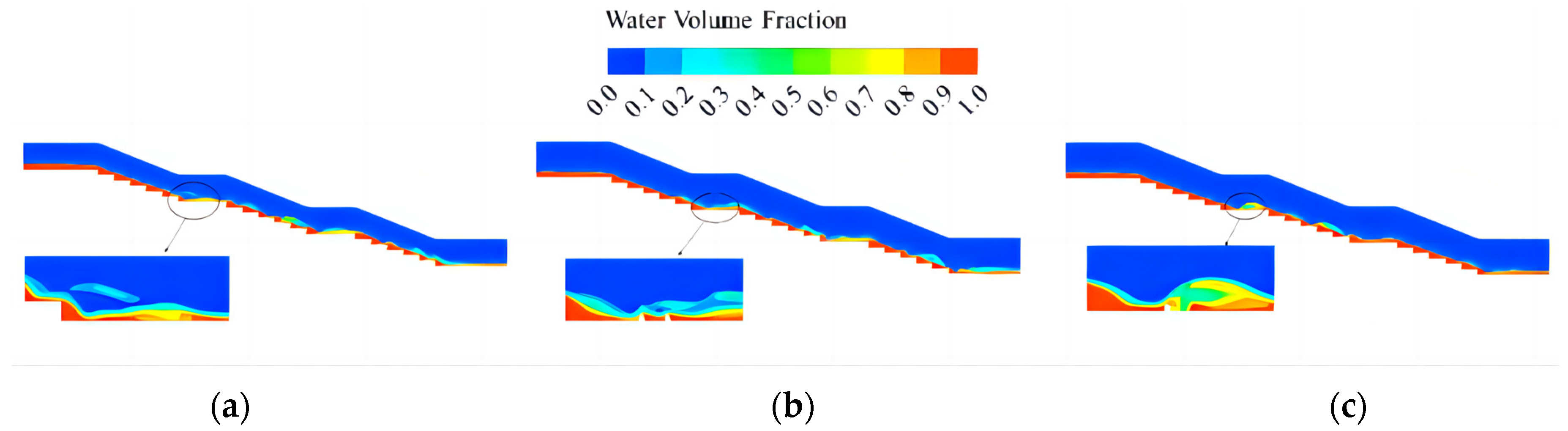
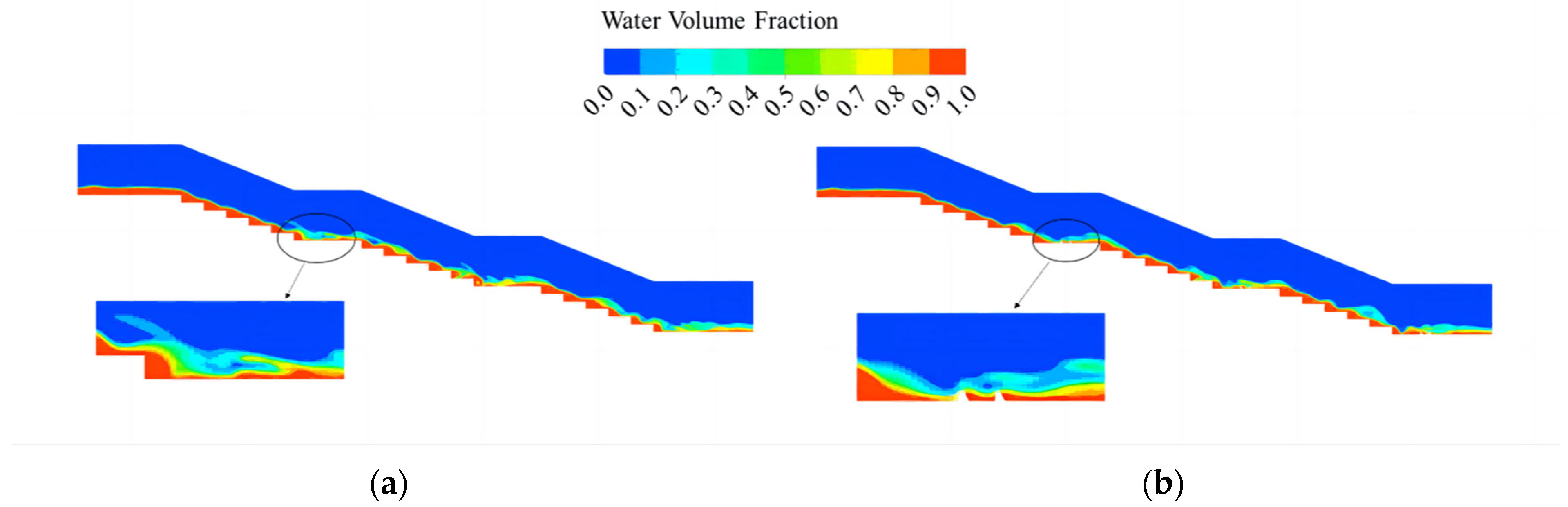
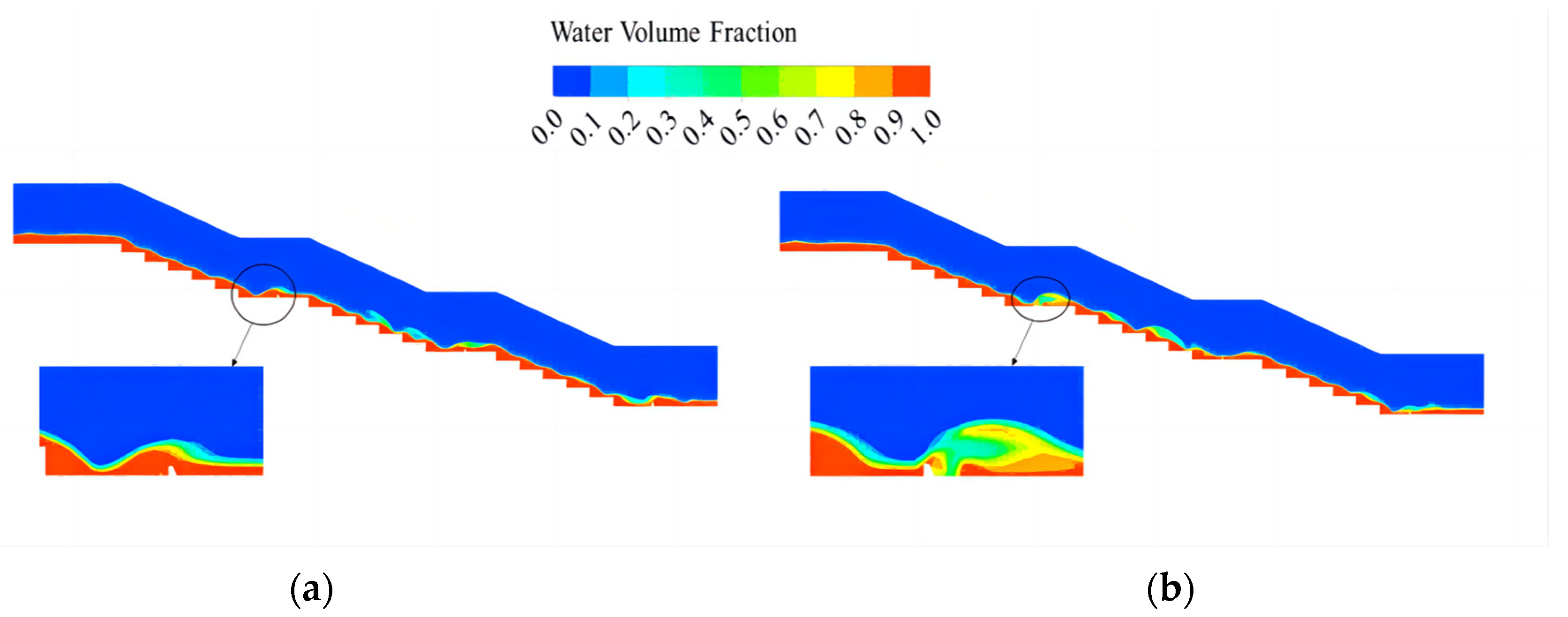
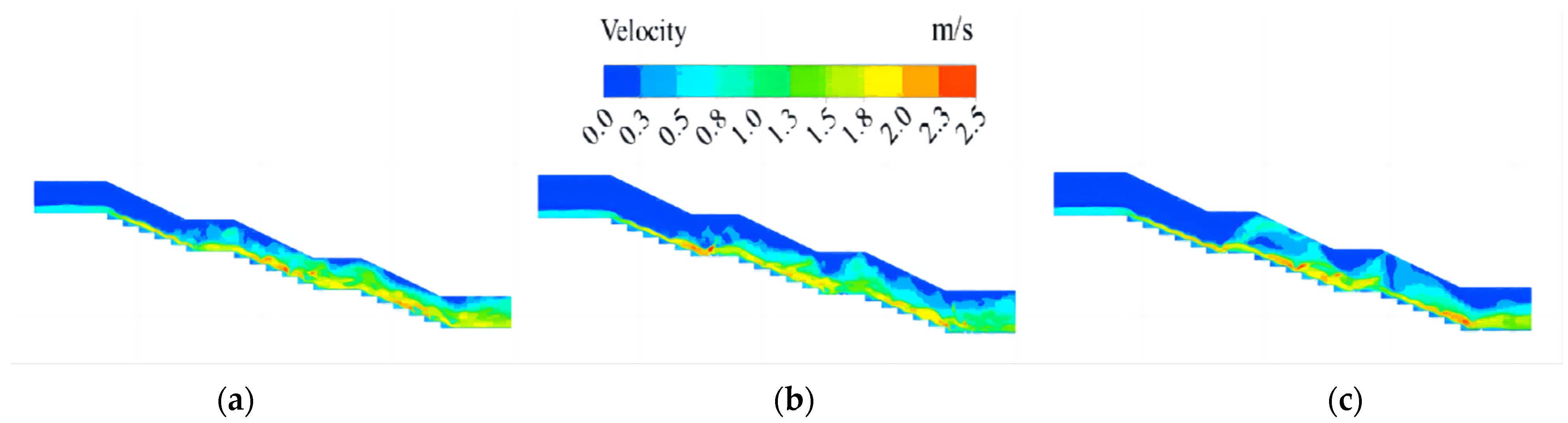
3.1. Flow Analysis
3.2. Flow Rate Analysis
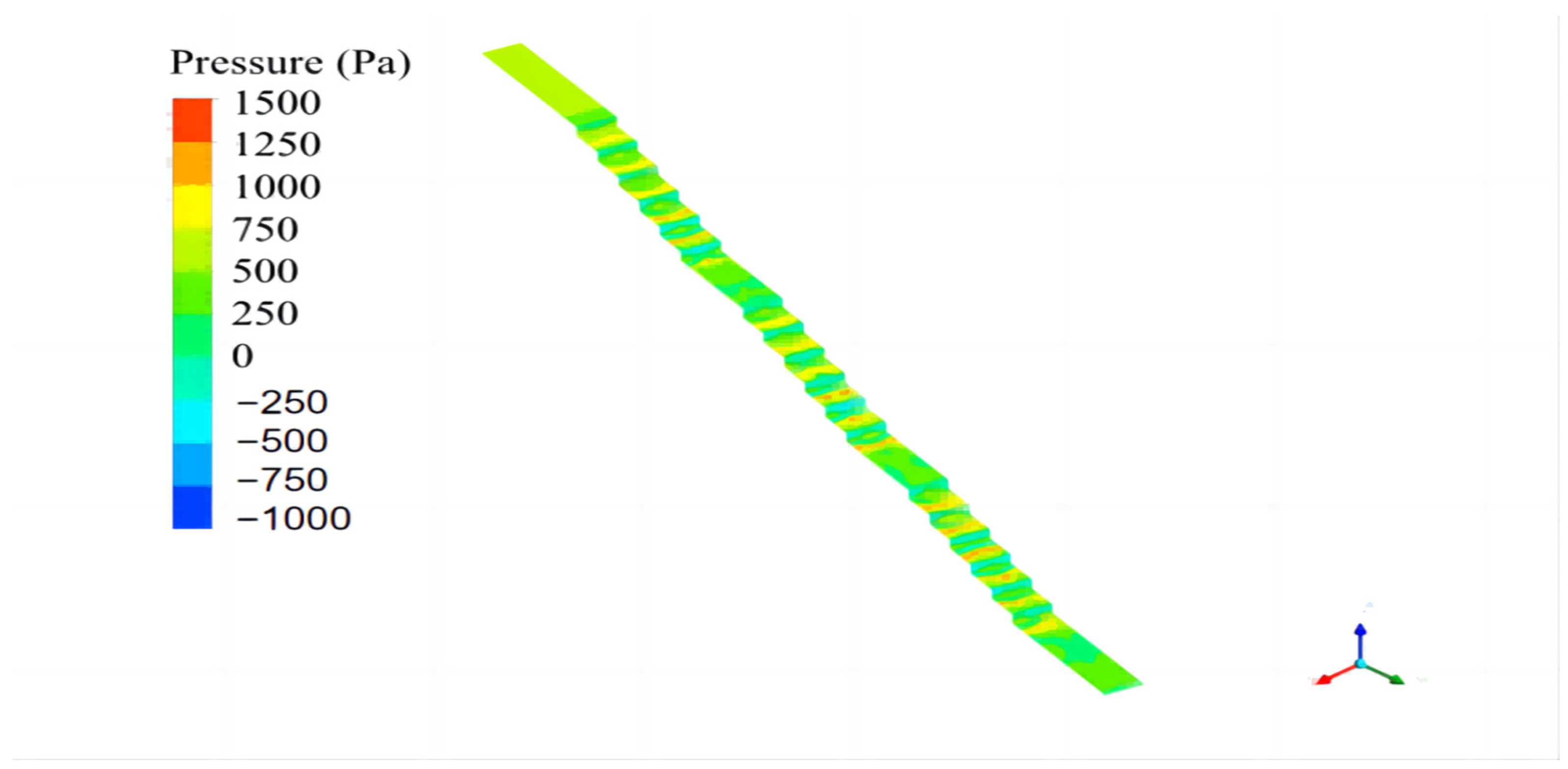
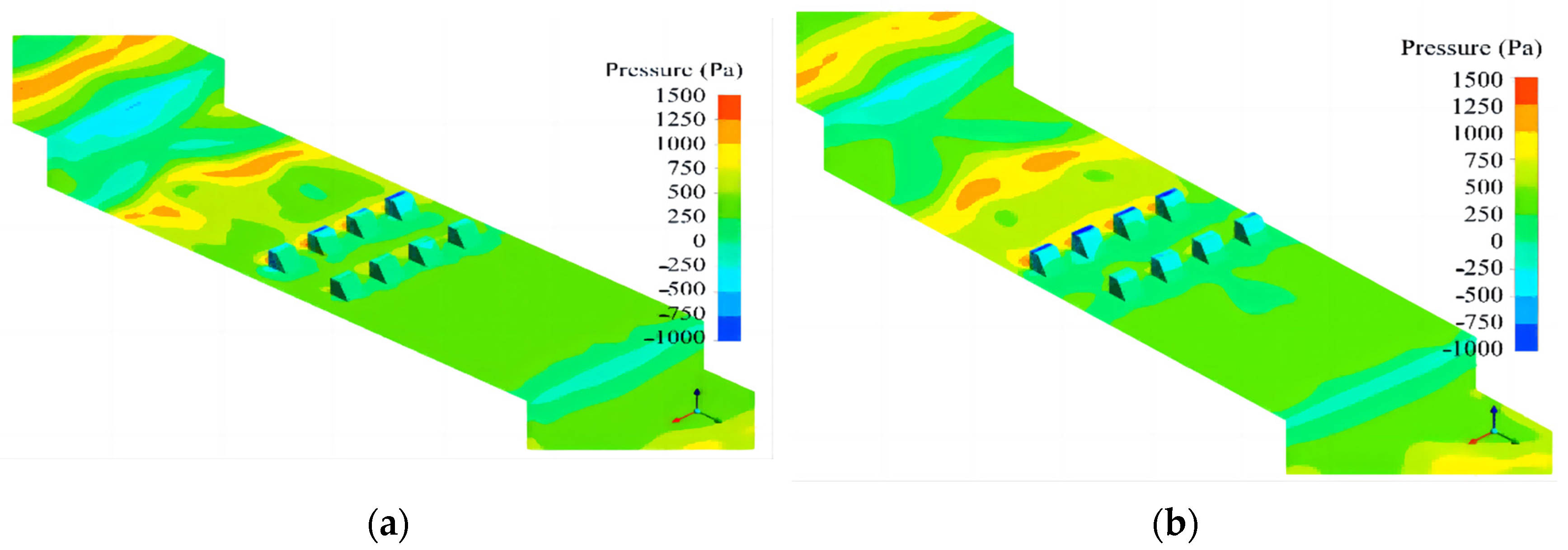
3.3. Pressure Analysis
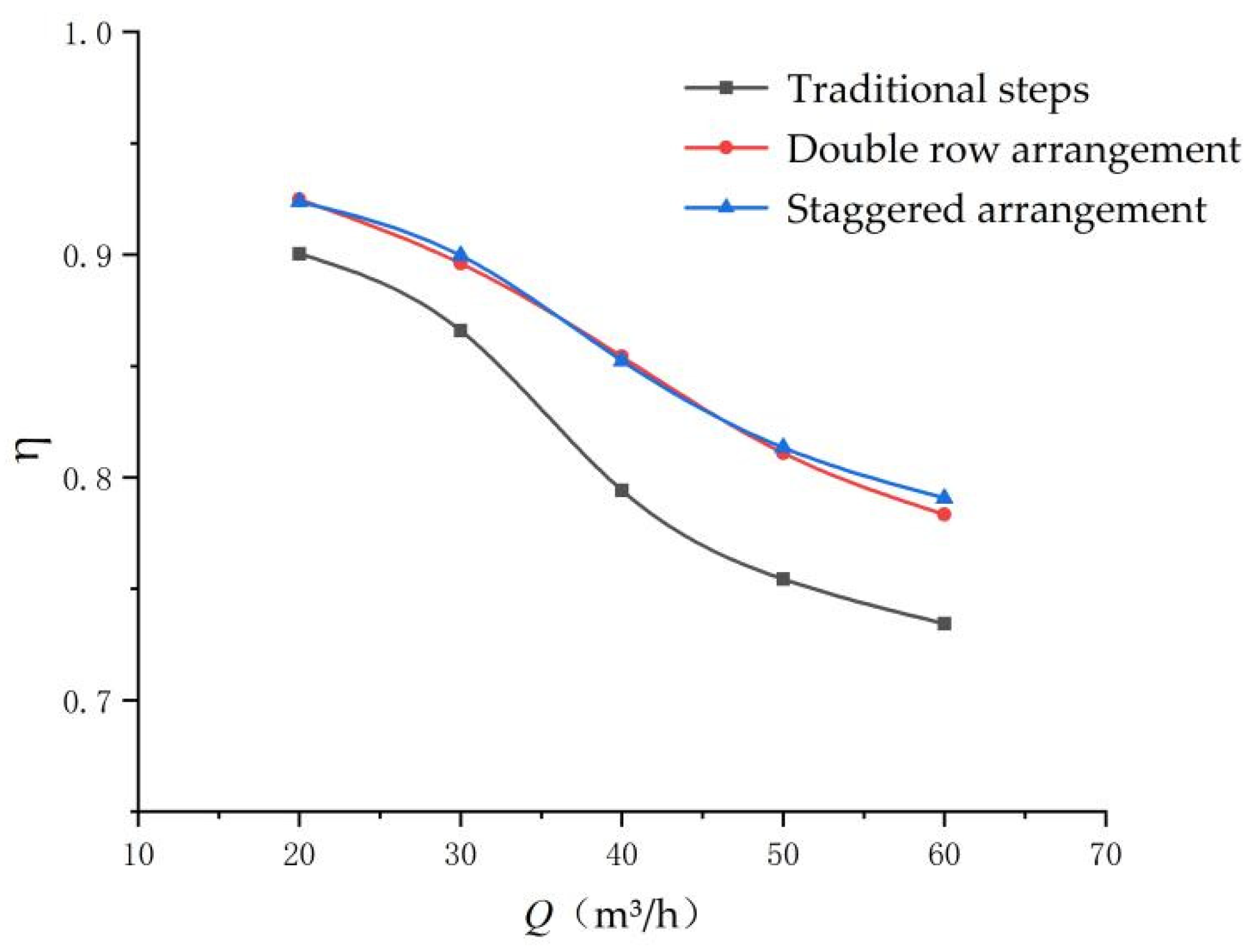
3.4. Energy Dissipation Analysis
4. Conclusions
- (1)
- The staggered arrangement of energy-dissipating piers causes water to jump back. After the jump back, the water depth increases and this improves the air-doping effect of the water flow by increasing the air-doping volume, additionally lowering the risk of cavitation damage in this stage. The staggered arrangement results in a better doping concentration than the double-row arrangement; however, the double-row arrangement is better able to reduce the cavitation hazard. Both arrangements exhibit a full section stage-doping, but the staggered arrangement results in different doping concentrations in different longitudinal sections.
- (2)
- The water flow velocity in the segmented energy dissipation pier structure is high at the surface and lower towards the bottom; the water jump generated by the flat section of the pier reduces the flow velocity along the pier and reduces scour damage downstream. The staggered arrangement improves the flow structure and stabilises the flow; the lower flow velocity at the downstream outlet results in reduced scour damage downstream.
- (3)
- The existence of the flat section of the energy dissipation pier in the segmented pier-type structure means that the piers face the water surface, resulting in high positive water pressure upstream, while high negative pressure builds at the top of the pier and the backwater surface. This negative pressure is higher with the staggered arrangement, and this should be borne in mind by engineers involved with real-world structure projects.
- (4)
- Compared with the traditional no-pier design, the segmented pier-added step energy dissipation structure increases the energy dissipation rate by more than 5% on average and produces an improved energy dissipation effect; however, the choice of a double-row or staggered arrangement has little or no effect on the energy dissipation overall.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ρ | Density factor derived from weighted average of volume fractions (-) |
| μ | Molecular viscosity factor derived from a weighted average of volume fractions (-) |
| Gk | Turbulent energy generation term due to mean flow gradient (-) |
| μt | Turbulent viscosity coefficient (-) |
| μeff | Effective viscosity (-) |
| C1ε, C2ε | Turbulence model coefficients of 1.44 and 1.92, respectively (-) |
| ακ, αε | The inverse of the Planter number for k and ε, taken as 1.0 and 1.3, respectively (-) |
| Cμ | Experience factor, 0.0845 (-) |
| η0, β | Model constants, taking values of 4.38 and 0.015, respectively (-) |
| Q | Flow (m3/h) |
| E1 | 1-1 Total energy of the cross-section (J) |
| E2 | 2-2 Total energy of the cross-section (J) |
| ∆E | Energy difference (J) |
| α1, α2 | Flow coefficient at upstream and downstream sections, generally taken as 1 (-) |
| v1 | Average cross-sectional flow rate upstream (m/s) |
| v2 | Average cross-sectional flow rate downstream (m/s) |
| η | Energy dissipation rate (-) |
References
- Hui, L.Y.; Quan, Z.Y.; Zhen, Z.S.; Zhao, Y.B. Research on stepped section flow field distribution rule of benched dam face energy dissipator. Yunnan Water Power 2002, 18, 82–85. [Google Scholar]
- Guo, X. Numerical Simulation for Stepped Spillway Based on 3D VOF Model. Master’ Thesis, Qinghai University, Xining, China, 2017. [Google Scholar]
- Bentalha, C. Numerical study of turbulent flow for moderate-slope stepped spillways. Malays. J. Civ. Eng. 2018, 30, 57–68. [Google Scholar]
- Tian, J. Hydraulic Characteristics of Stepped Release Structure. Ph.D. Thesis, Polytechnic University, Xi’an, China, 2005. [Google Scholar]
- Tian, J.; Wei, B.; Li, B.; Feng, R.; Liu, J. The characteristics of mean pressure on stepped overflow dam. J. Hydroelectr. Eng. 2007, 6, 67–72. [Google Scholar]
- Sánchez-Juny, M.; Bladé, E.; Dolz, J. Analysis of pressures on a stepped spillway. J. Hydraul. Res. 2008, 46, 410–414. [Google Scholar] [CrossRef]
- Xu, W.; Luo, S.; Zheng, Q.; Luo, J. Experimental study on pressure and aeration characteristics in stepped chute flows. Sci. China Technol. Sci. 2015, 58, 720–726. [Google Scholar] [CrossRef]
- Zou, L. Numerical Simulation of Aeration Flow in Stepped Spillway; Polytechnic University: Xi’an, China, 2016. [Google Scholar]
- Wang, X.; Liu, Y.; Lin, P.; Shao, Y. Numerical simulation study of water depth of aerated water flow in large-slope stepped overflow dam. Shaanxi Water Resour. 2022, 3, 23–25+28. [Google Scholar]
- Gonzalez, C.A.; Chanson, H. Hydraulic design of stepped spillways and downstream energy dissipators for embankment dams. Dam Eng. 2007, 17, 223–244. [Google Scholar]
- Wen, M.; Liu, H.; Fan, L.; Liu, S. Energy characteristics of flow along stepped spillway. J. Yangtze River Sci. Res. Inst. 2016, 33, 60–62+67. [Google Scholar]
- Wu, P.; Wang, B.; Cheng, Y.; Zhou, Q. Energy dissipation of skimming flow over stepped chutes with different slopes. J. Sichuan Univ. 2012, 44, 24–29. [Google Scholar]
- Li, Z.; Kehua, L.; Zhao, Z. Application of the stepped dissipater in low-head overflow dams. Hydro Power New Energy 2015, 1, 26–28. [Google Scholar]
- Hongtao, J. The effects of step configurations on the hydraulic properties of stepped spillways. China Rural Water Hydropower 2019, 10, 148–152+157. [Google Scholar]
- Ma, P.; Hu, Y.; Liu, H. Study on the relative hydraulic characteristics of skimming flow on stepped spillways. Shuili Xuebao 2020, 51, 997–1007. [Google Scholar]
- Ma, S.H.; Liu, H.S. Research on the relative velocity variation law of stepped spillway. China Rural Water Hydropower 2021, 11, 192–197, 208. [Google Scholar]
- Li, S.; Zhang, W.; Wang, J.; Zhao, Z. Hydraulic characteristics of stepped spillway with trapezoidal concave angle. J. Yangtze River Sci. Res. Inst. 2022, 39, 56–63+68. [Google Scholar]
- Hou, X.; Yang, J.; Xiong, C. Study on effects of asymmetrical flaring gate pier Y-shapes on length of aerated cavity and its negative pressure. J. Hydroelectr. Eng. 2015, 34, 80–87. [Google Scholar]
- Dong, Z.; Wang, J.; Vetsch, D.F.; Boes, R.M.; Tan, G. Numerical Simulation of Air–Water Two-Phase Flow on Stepped Spillways behind X-Shaped Flaring Gate Piers under Very High Unit Discharge. Water 2019, 11, 1956. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.-X.; Fu, Z.-M.; Su, H.-Z. A calculation method for water depth in tapered chute of stepped spillway: An improvement to chanson’s formula. J. Yangtze River Sci. Res. Inst. 2019, 36, 59–63. [Google Scholar]
- Ghaderi, A.; Abbasi, S.; Abraham, J.; Azamathulla, H.M. Efficiency of Trapezoidal Labyrinth Shaped stepped spillways. Flow Meas. Instrum. 2020, 72, 101711. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, J.R.; Cheng, Y.Z. Impacts of pre-aerator angles on energy dissipation of stepped spillway. Hydro Sci. Eng. 2016, 4, 118–125. [Google Scholar]
- Gao, Q. Numerical Simulation Study on Hydraulic Characteristics of Asymmetric Spillway Inlet. Master’s Thesis, Dalian University of Technology, Dalian, China, 2019. [Google Scholar]
- Wang, H.; Qi, L.; Shi, Y.; Zeng, Q.; Lin, X. Three-dimensional numerical simulation on energy dissipation hydraulic characteristics of stepped spillway with different shapes. Water Power 2022, 10, 1–9. [Google Scholar]
- Tian, Y.; Li, Y.; Sun, X. Study on the Hydraulic Characteristics of the Trapezoidal Energy Dissipation Baffle Block-Step Combination Energy Dissipator. Water 2022, 14, 2239. [Google Scholar] [CrossRef]

| Parameters | Range of Variations |
|---|---|
| Q | 20 m3/h, 30 m3/h, 40 m3/h, 50 m3/h, 60 m3/h |
| C1ε and C2ε | 1.44 and 1.92 |
| ακ and αε | 1.0 and 1.3 |
| Cμ | 0.0845 |
| η0 and β | 4.38 and 0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Li, Y.; Tian, Y.; Li, Q. Effects of Energy Dissipation Pier Arrangements on the Hydraulic Characteristics of Segmented Pier-Type Step Energy Dissipator Structures. Water 2022, 14, 3590. https://doi.org/10.3390/w14223590
Feng Z, Li Y, Tian Y, Li Q. Effects of Energy Dissipation Pier Arrangements on the Hydraulic Characteristics of Segmented Pier-Type Step Energy Dissipator Structures. Water. 2022; 14(22):3590. https://doi.org/10.3390/w14223590
Chicago/Turabian StyleFeng, Ziwei, Yongye Li, Yu Tian, and Qian Li. 2022. "Effects of Energy Dissipation Pier Arrangements on the Hydraulic Characteristics of Segmented Pier-Type Step Energy Dissipator Structures" Water 14, no. 22: 3590. https://doi.org/10.3390/w14223590




