Abstract
Aquatic submerged vegetation is widespread in rivers. The transverse distribution of flow velocity in rivers is altered because of the vegetation. Based on the vegetation coverage, the cross-section of the ecological channels can be divided into the non-vegetated area and the vegetated area. In the vegetated area, we defined two depth-averaged velocities, which included the water depth-averaged velocity, and the vegetation height-averaged velocity. In this study, we optimized the ratio of these two depth-averaged velocities, and used this velocity ratio in the Navier–Stokes equation to predict the lateral distribution of longitudinal velocity in the open channel that was partially covered by submerged vegetation. Based on the Navier–Stokes equations, the term “vegetation resistance” was introduced in the vegetated area. The equations for the transverse eddy viscosity coefficient ξ, friction coefficient f, drag force coefficient Cd, and porosity α were used for both the non-vegetated area and the vegetated area, and the range of the depth-averaged secondary flow coefficient was investigated. An analytical solution for predicting the transverse distribution of the water depth-averaged streamwise velocity was obtained in channels that were partially covered by submerged vegetation, which was experimentally verified in previous studies. Additionally, the improved ratio proposed here was compared to previous ratios from other studies. Our findings showed that the ratio in this study could perform velocity prediction more effectively in the partially covered vegetated channel, with a maximum average relative error of 4.77%. The improved ratio model reduced the number of parameters, which introduced the diameter of the vegetation, the amount of vegetation per unit area, and the flow depth. This theoretical ratio lays the foundation for analyzing the flow structure of submerged vegetation.
1. Introduction
Aquatic vegetation strongly influences ecosystem functions and improves water quality [1] by filtering nutrients, producing oxygen, and capturing suspended sediments. Aquatic vegetation also provides shelter to organisms in the river, providing them with nutrient-rich foods and spacious habitats, promoting the formation of natural food chains, and improving the ecology of the river [2]. Besides having ecological effects, aquatic vegetation also affects the flow structure owing to its drag force slowing the flow velocity. As a result of the large difference in velocity between vegetated and non-vegetated areas, shear force is generated at the junction of the two areas, and the turbulent flow structure becomes more complicated, ultimately affecting sediment transport and riverbed stability. Therefore, it is essential to study the effect of vegetation on flow velocity.
Several studies have investigated the flow structure in channels with vegetation, and have drawn various and meaningful conclusions. The type of vegetation can be divided into rigid vegetation and flexible vegetation according to its flexibility. Meanwhile, based on the relationship between vegetation height and flow depth, vegetation is divided into submerged and emergent vegetation. The submerged vegetation investigated in this study is similar to emergent vegetation, and the prediction of flow velocity distribution with emergent vegetation provides a reference for our research. Scholle and Aksel [3] presented a clear analytical solution of longitudinal velocity in an inclined channel with visco-capillary flow using the Navier–Stokes equations. White and Nepf [4] presented a method to predict the distribution of velocity and shear stress in shallow channels with a boundary of emergent vegetation. Using the vortex characteristics to predict momentum exchange, the model captured a two-layer structure that consisted of a rapidly varying shear layer across the vegetation interface, and a more gradual boundary layer in the main channel. Terrier [5] improved the Shiono and Knight method (SKM) [6] to account for the increase in turbulence activity due to the presence of vegetation. The researchers found that emergent vegetation significantly increased flow resistance, thus reducing velocity, decreasing boundary shear stress, and causing depth-averaged velocity profiles to converge more rapidly along the flume near the main channel–floodplain interface, compared to vegetation-free areas [7]. Regarding the influence of emergent vegetation on flow velocity, Liu et al. [8] found that near the upstream edge of a patch, lateral flow adjustments led to a decrease in velocity inside the patch, and an increase in velocity in the adjacent bare channel. They proposed a model based on exponential decay, to predict the longitudinal profiles of streamwise velocities upstream of, and inside a patch in the bare channel. Huai et al. [9] preliminarily estimated the secondary flow coefficient K, and proposed a two-dimensional analytical solution to predict the distribution of steady uniform flow velocity. They found that the K-value affected the accuracy of the transverse distribution of the depth-averaged velocity. Later, unlike the traditional emergent vegetation layout, Fu et al. [10] developed an improved analysis model, where the effects of boundary friction, vegetation resistance, lateral shear turbulence, and secondary flow were considered. Then, they predicted the transverse distribution of the water depth-averaged flow velocity in an open-channel flow using floating vegetation islands (FVIs), where the velocity distribution was similar to that of the submerged vegetation.
Concerning submerged vegetation, some researchers first began with rigid vegetation. Devi and Khatua [11] investigated the main channel–floodplain interface in the compound channel when studying the velocity distribution averaged in depth. Based on the friction coefficient calibration, the average absolute deviation of the water depth-averaged streamwise velocity prediction decreased. In order to determine the influence of flow characteristics with submerged vegetation, Sun et al. [12] evaluated the vertical velocity distribution of high and low vegetation on the basis of the height of submerged vegetation. The velocity of low vegetation at the top of the vegetation showed an approximately logarithmic distribution, but not the velocity of high vegetation. The flow velocity below the top of the vegetation was lower than the flow velocity without vegetation, while the flow velocity above the top was higher. This study showed that the transverse distribution of the velocity in the vegetation layer is different at different vegetation heights. Along with the impact of vegetation height on horizontal distribution, Liu et al. [13] also systematically studied the relationship between the secondary flow coefficient and the region. They also applied the model to the compound channel with a fully covered vegetated floodplain, and developed an analytical solution to predict the transverse distribution of the average flow velocity of the water depth. Unlike the artificial cylindrical vegetation previously studied, natural vegetation has a highly inconsistent shape. Yang et al. [14] measured the local flow velocities for different types of submerged vegetation (such as trees, shrubs, and grasses). In the absence of vegetation in the floodplain, all measured flow velocity distributions follow a logarithmic distribution. However, when vegetation is present in the floodplain, the vertical flow velocity has an S-shaped distribution [15,16]. Concerning transverse distribution of velocity with submerged vegetation, more general shapes of velocity profiles could be discussed based on a polynomial expansion, as used in Kowalski et al. [15] and in Koellermeier et al. [16]. Wang et al. [17] investigated the influence of vegetation on the water flow pattern along the vertical direction, and analyzed the dynamic characteristics of water flow passing over submerged vegetation of each subdivided vegetation segment, using the finite analytic method. They obtained the distribution of the water flow velocity within the flow depth range in the vegetation of an arbitrary shape. In addition to dividing the flow region in the transverse direction, Huai et al. [18] proposed a new three-layer model to predict the vertical velocity distribution in an open channel with submerged vegetation. The results showed that the velocity profile is composed of three hydrodynamic regimes (i.e., the upper non-vegetated layer, the outer layer, and the bottom layer within the vegetation). Multi-layer models have gained significant interest in the community of numerical methods for free-surface flows [19]. Based on the equation for the velocity distribution of cylindrical vegetation, some scholars studied the flow characteristics of flexible vegetation. Ghisalberti and Nepf [20] found that submerged flexible vegetation exhibits continuous eddy current oscillations, which can increase the flow velocity in the vegetation layer, and change transverse distribution as a result of the reduction in vegetation resistance. Compared with rigid cylindrical vegetation, the water flow pattern changes more with flexible vegetation. Wang et al. [21] proposed a new vegetation shape function to measure the upstream width. This function helped to obtain an analytical solution for the velocity profile from the momentum equation. The study of the water flow pattern with flexible vegetation led by Sukhodolov and Sukhodolova [22] found that submerged flexible vegetation converted the two-dimensional open-channel flow structure into a complex three-dimensional flow, making it more uneven, or even asymmetric, and improved the two-dimensional transverse velocity distribution. To summarize, the profile of the water depth-averaged streamwise velocity in a vegetated channel has been extensively investigated; moreover, more studies have examined the characteristics of the transverse velocity distribution in open channels that are partially covered by submerged vegetation.
As far as the flow velocity distribution model proposed for a channel with vegetation is concerned, the numerical simulation method has high accuracy. For example, Liu et al. [23] conducted a three-dimensional numerical simulation on the flow field with rigid emergent cylinders based on the hydrodynamic numerical model for free-surface flows, and studied the characteristics of velocity distribution. Yang et al. [24] used ‘Fluent’, a fluid simulation software, to simulate the fine-resolution of open-channel flow with rigid vegetation, and to determine the velocity distribution in channels with suspended and submerged vegetation in the vegetated area. However, numerical simulation with high precision requires high computer performance and more time. In determining the velocity distribution of flow with vegetation, using the analytical solution of velocity distribution is relatively simple. This method can quickly verify the initially developed model, and eliminate the error in the parameter settings. The analytical solution method may be applied in situations where the mathematical model can easily be expressed. Although the analytical solution method could not directly determine the change in the flow velocity, the results for the flow velocity distribution studied in this article were obtained.
In this study, we optimized the ratio of two depth-averaged velocities, and then applied this ratio in the Navier–Stokes equation to predict the lateral distribution of longitudinal velocity for an open channel partially covered by submerged vegetation. Using this method, the analytical solution for the water depth-averaged streamwise velocity was obtained.
2. Theoretical Analysis
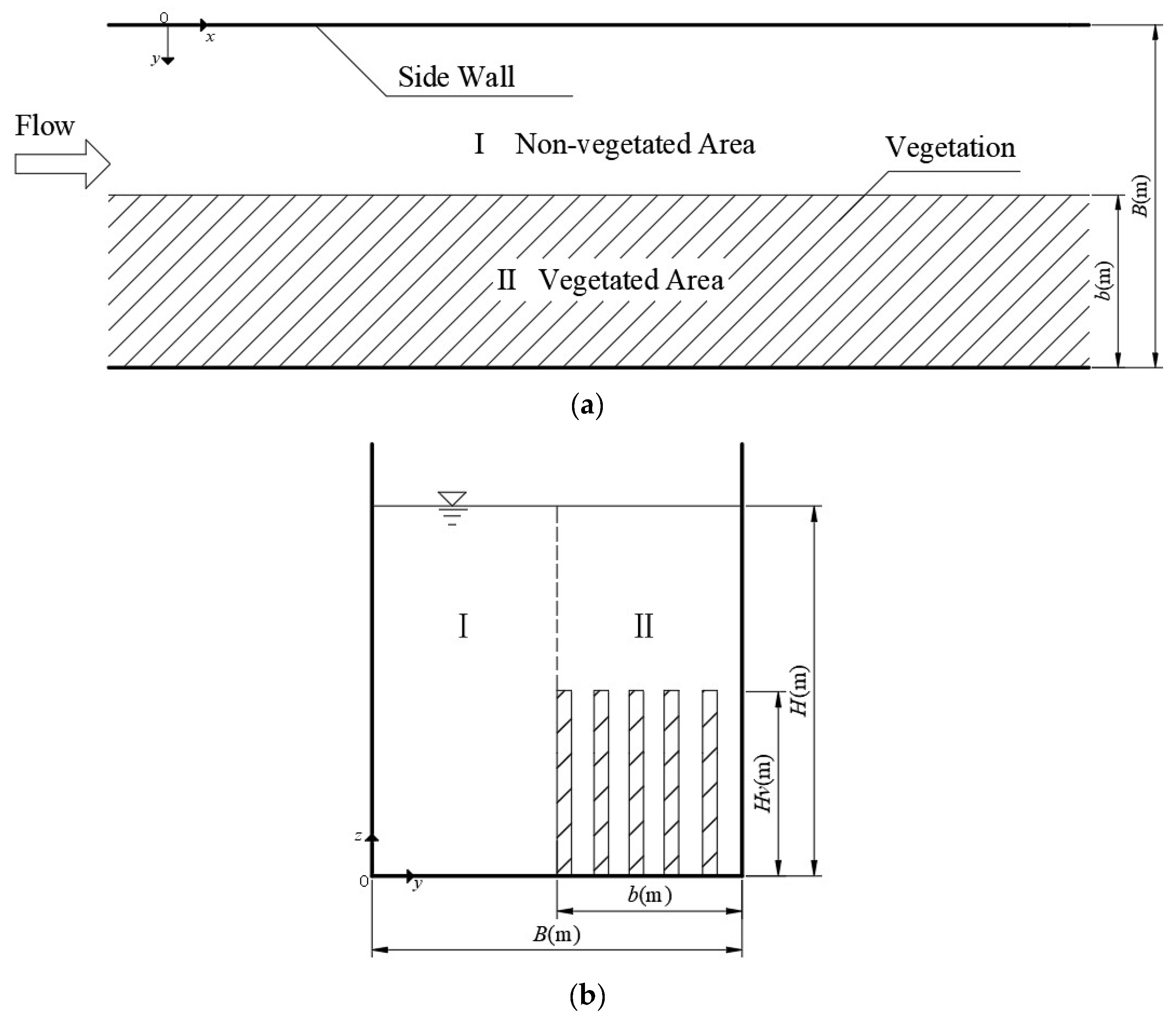
The layout of the submerged vegetation in the open channel flume that we studied is shown in Figure 1. Based on the characteristics of distribution of vegetation, the flume was divided into two sub-areas along the cross-sectional direction, which included the non-vegetated area (I) and the vegetated area (II).
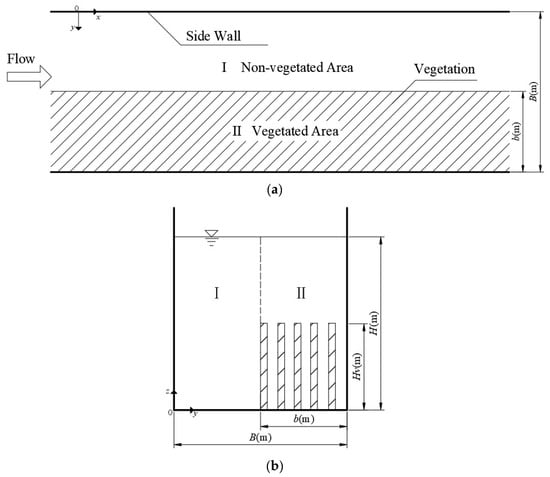
Figure 1.
Layout of the vegetation in the flume. (a) Top view arrangement; (b) arrangement of the cross-section profile. Here, b represents the width of the vegetated area, B represents the width of the flume, Hv represents the height of the vegetation, and H represents the flow depth. I and II represent the non-vegetated area and the vegetated area, respectively.
For open-channel flow with vegetation, to determine the transverse distribution of the water depth-averaged streamwise velocity, a vegetation resistance term was introduced into the Navier–Stokes equation, in order to obtain the governing equation in the x direction, as follows [6]:
where x represents the streamwise coordinate that is parallel to the slope of the bed, y represents the transverse coordinate parallel to the slope of the bed, and z represents the vertical coordinate. U, V, and W represent the time-averaged velocities in the x, y, and z directions. ρ represents the flow density, g represents the gravitational acceleration, and S0 represents the channel bed slope. Along with the constitutive relations for the stresses, the τxx, τyx, and τzx represent forces acting on the surface of the control body in the derivation of the N–S equations [6]. Fv represents the drag force caused by vegetation per unit volume of a fluid, and can be expressed as follows [10]:
where Cd represents the drag force coefficient of vegetation, β represents the shape factor of vegetation, and Av represents the projected area of vegetation per unit volume in the direction toward the downstream flow, Av = mD; m represents the amount of vegetation per unit area, and D represents the stem diameter of the vegetation. Equations (1) and (2) were integrated over the flow depth H. As the water flow was uniform, the water surface in the lateral direction was parallel to the channel bed, indicating that the water depth was constant over the entire cross section [13]. (HU2)/x ≈ 0, /x ≈ 0. Assuming that W(H) = W(0) = 0, Equation (1) can be simplified as follows [6]:
where represents the depth-averaged term, and τb =. The integral depth H for the vegetation resistance term can be divided into two parts: 0~Hv and Hv~H. Hv represents the height of the vegetation. No vegetation occurs in the range of Hv~H, and thus, the resistance is 0. The integral term used in Equation (3) can be presented as follows:
where the depth-averaged streamwise velocity along the vegetation height is defined as follows:
In order to solve the governing equation, determining the relationship between the depth-averaged streamwise velocity along the vegetation height Uv and the water depth-averaged streamwise velocity Ud is necessary. Previous studies obtained different results for the relationship between Uv and Ud.
Stone and Shen [25] stated that for vegetation that covers almost half of the river, the relationship between these two velocities can be expressed as follows:
Here, h* is the relative height coefficient defined as min [Hv, H]/H. Therefore, the value of kv is 1.0 for the emergent vegetation, and less than 1.0 for submerged vegetation.
Cheng [26] developed Equation (8), as follows:
Here,
where λ = mπD2/4, which represents the ratio of the vertical projected area of vegetation to the unit bed area; hs = H − Hv. Regarding flow velocity ratios, in addition to the above-mentioned equations, another equation was presented by Huthoff et al. [27] as follows:
where l is the spacing between adjacent cylindrical vegetation zones.
Using the equations presented by Cheng [26] and Huthoff et al. [27] is a time-consuming process. However, the equation developed by Stone and Shen [25] is simpler than the other formulae. By introducing the diameter of the vegetation, the amount of vegetation per unit area, and the flow depth, the ratio of the depth-averaged streamwise velocity along the vegetation height to the water depth-averaged streamwise velocity for the emergent and submerged vegetation can be obtained. However, the limitation of this formula is that it is more suitable to be calculated on the basis of cylindrical vegetation. Since some parameters are removed, the accuracy of the formula needs to be verified by experiments.
We improved the model for the ratio of two depth-averaged velocities, based on the equation of Stone and Shen [25]. The relationship between the depth-averaged streamwise velocity along the vegetation height Uv and the water depth-averaged streamwise velocity Ud can be determined as follows:
By expressing Uv/Ud as φ, Equation (12) can be substituted into Equation (4) to obtain Equation (13), as follows:
Equation (14) was obtained by substituting Equation (13) into Equation (3), as follows:
The vegetation porosity α [13], was defined as the volume ratio of fluid per unit volume, based on Equation (14) as follows:
Each term at the right side of Equation (15) shows the forces acting on an H-depth water column per unit of vegetated-bed area, and the left side of Equation (15) is the corresponding inertial force. After introducing the vegetation term, the volume of clear water in each term of the equation changes. The corresponding gravity component in the streamwise direction is αρgHS0. When vegetation blockage is considered, the gravity component and other terms in the equation can be obtained by multiplying the terms in Equation (15) by α. However, the drag force due to vegetation is still , indicating that the drag force term remains unchanged [13].
The depth-averaged transverse shear stress is expressed as the transverse gradient of the water depth-averaged streamwise velocity in Equation (15). The depth-averaged eddy viscosity coefficient and the local shear velocity are related to the flow depth H. Local shear velocity is expressed as the relationship between the Darcy–Weisbach friction coefficient f and the water depth-averaged streamwise velocity. These parameters are expressed in Equations (16)–(19) [10]:
Here, ξ denotes the transverse eddy viscosity coefficient, and τb represents the comprehensive shear stress of the boundary. Equations (16)–(19) were substituted into (15) to obtain Equation (20), as follows:
In order to find the secondary flow term on the left side of Equation (20), the expression of proposed by Liu et al. [13] is described as follows:
Here, indicates the depth-averaged value of the secondary flow coefficient, which was obtained by integrating in the direction of flow depth.
For prediction of the distribution of vegetation, the solution of Equation (20) can be obtained as follows:
- For the non-vegetated area, i.e., the area I in Figure 1b, the solutions of Equation (20) for the non-vegetated area and vegetated area are different. This is because, for the non-vegetated area, the drag force coefficient is 0 in Equation (20). Ignoring the vegetation resistance term “”, Ud is expressed as follows:
- 2.
- For the vegetated area, i.e., area II in Figure 1b, Ud is expressed as follows:
Here, A1, C1, A2, and C2 are unknown constants. The superscripts (1) and (2) indicate the non-vegetated area and vegetated area, respectively.
3. Boundary Conditions
In order to obtain the unknown constants A1, C1, A2, and C2 in Equations (22) and (24), four boundary conditions are required, which are described as follows:
- (1)
- On the side wall, the no-slip boundary condition is present, and for the velocity near the side wall, i.e., when y = 0 and y = B, Ud = 0 (two boundary conditions).
- (2)
- The velocity continuity condition exists at the junction between the non-vegetated area and the vegetated area, i.e., when y = B, Ud(i) = Ud(i + 1).
- (3)
- The stress continuity condition is present when the water flow is uniform at the junction between the non-vegetated and vegetated areas. Thus, the flow depth transition is not abrupt at the junction between the areas. The stress continuity condition can be expressed as follows:
Here, i = 1, 2, indicating the non-vegetated area and the vegetated area, respectively.
4. Parameter Determination
In order to obtain the analytical solutions of Equations (22) and (24), finding the model parameters (ξ, f, α, Cd, , and ) is necessary. The values of these parameters are generally different in the non-vegetated and vegetated areas. They can be calculated using the methods described below.
4.1. Transverse Eddy Viscosity Coefficient ξ
The method to calculate the transverse eddy viscosity coefficient was proposed by Abril and Knight [28], and Pasche and Rouvé [29], who presented as follows:
where refers to the transverse eddy viscosity coefficient in the non-vegetated area, and refers to the transverse eddy viscosity coefficient in the vegetated area. Ƙ denotes the Karman constant, and is usually 0.4. Dr is defined as the relative depth ratio, expressed as the ratio of vegetation depth to the water depth.
4.2. Darcy–Weisbach Friction Coefficient f
The friction coefficient was obtained by the formula that was developed by Rameshwaran and Shiono [30], as follows:
where υ represents the kinematic viscosity, and has a value of 1 × 10−6 m2/s, and ϕ = {12.3, 1.2} in the non-vegetated and vegetated areas, respectively; represents the equivalent roughness height, and can be calculated using the equation developed by Ackers [31], as follows:
where n represents Manning’s roughness coefficient. According to Naot et al. [32], n = 0.013 (concrete material), and according to Shi and Huai [33], n = 0.01 (glass material).
4.3. Porosity α
Porosity α is expressed as the volume ratio of fluid per unit volume in the vegetated area, and is calculated as follows:
where refers to the volume occupied by vegetation per unit of the water body. represents the unit of water volume, and is expressed as follows:
4.4. The Drag Force Coefficient Cd
The drag force coefficient Cd, described by Liu et al. [13], is related to the Reynolds number (Re), vegetation shape, and vegetation density. The drag force coefficient Cd decreases with an increase in the Reynolds number of simulated cylindrical vegetation, and increases with an increase in the volume fraction of vegetation [34]. James et al. [35] measured the drag force coefficient of cylindrical vegetation when 200 < Re < 10,000, and found that Cd fluctuated around 1. The Cd value increases significantly with an increase in the number of leaves of cylindrical vegetation. The Reynolds numbers calculated for each case in this study are detailed in Table 1. The drag force coefficient Cd was considered to be 1 in this study.

Table 1.
Summary of the experimental conditions.
4.5. Secondary Flow Coefficients and
As a result of the differences in velocity between the vegetated and non-vegetated areas, a transverse eddy current, called the secondary flow, occurs at the junction between two areas. It is expressed as and for the non-vegetated area and the vegetated area, respectively. The -value is calculated, following the formulae provided by Liu et al. [13]. Generally, the values are negative in the main channel, and positive in the floodplain. In the Discussion, we also explain the effect of the -value to analytical solutions.
5. Experimental Data
In order to validate the applicability and accuracy of the analytical solutions, we used the experimental data that were obtained by Naot et al. [32] and Shi and Huai [33].
5.1. Experimental Data Obtained by Naot et al. [32]
The experiment was conducted by simulating an open channel. The channel was 0.36 m wide, with a slope S0 of 0.0064. The cylindrical diameter D of the simulated rigid vegetation was 0.0036 m. The height of vegetation Hv was 0.03 m, and the flow depth H was 0.06 m. The non-dimensional vegetation density formula, defined as N = mHD, was proposed by Naot et al. [32] and used only in this case. The experiments were conducted with non-dimensional vegetation densities of N = 0.06, N = 0.24, and N = 0.96.
5.2. Experimental Data Obtained by Shi and Huai [33]
The study area had submerged vegetation that covered half of the river. The flume used in the experiment was 18 m long and B was 1 m wide, with an 8-meter-long section made from glass for observation; the vegetated area was 0.475 m wide. The vegetation was simulated using plexiglass rods. In the experiment, acoustic Doppler velocity (ADV) was used to measure a series of velocities at each point on each y-coordinate vertical line; then, the average was calculated as the water depth-averaged streamwise velocity of the y-coordinate. The open channel was equipped with an adjustable tailgate to adjust the water depth, leading to the water depth being parallel to the channel bed in both the longitudinal and lateral directions.
The experimental conditions established by Naot et al. [32] and Shi and Huai [33] are summarized in Table 1.
6. Comparison of Theoretical and Experimental Data
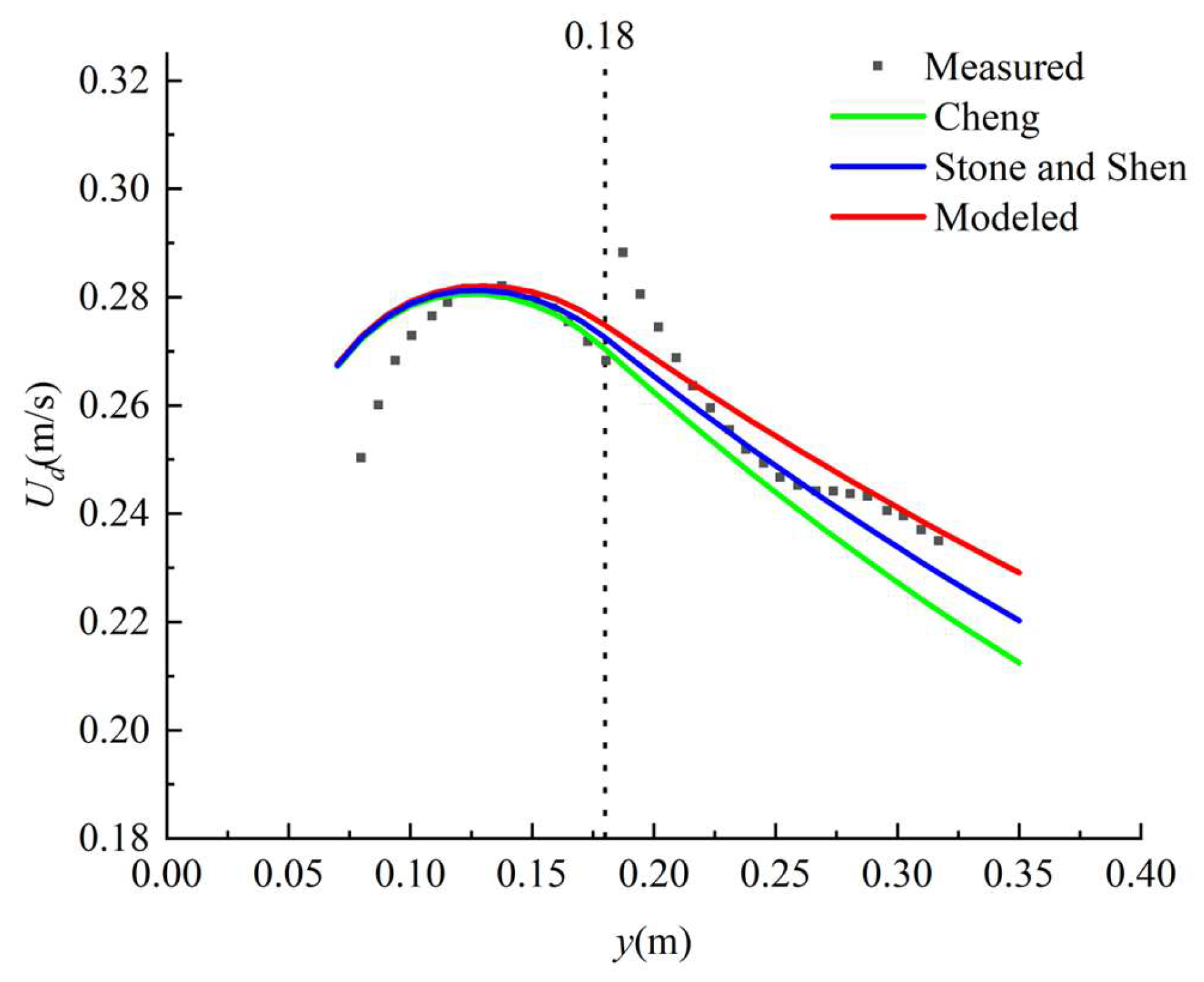
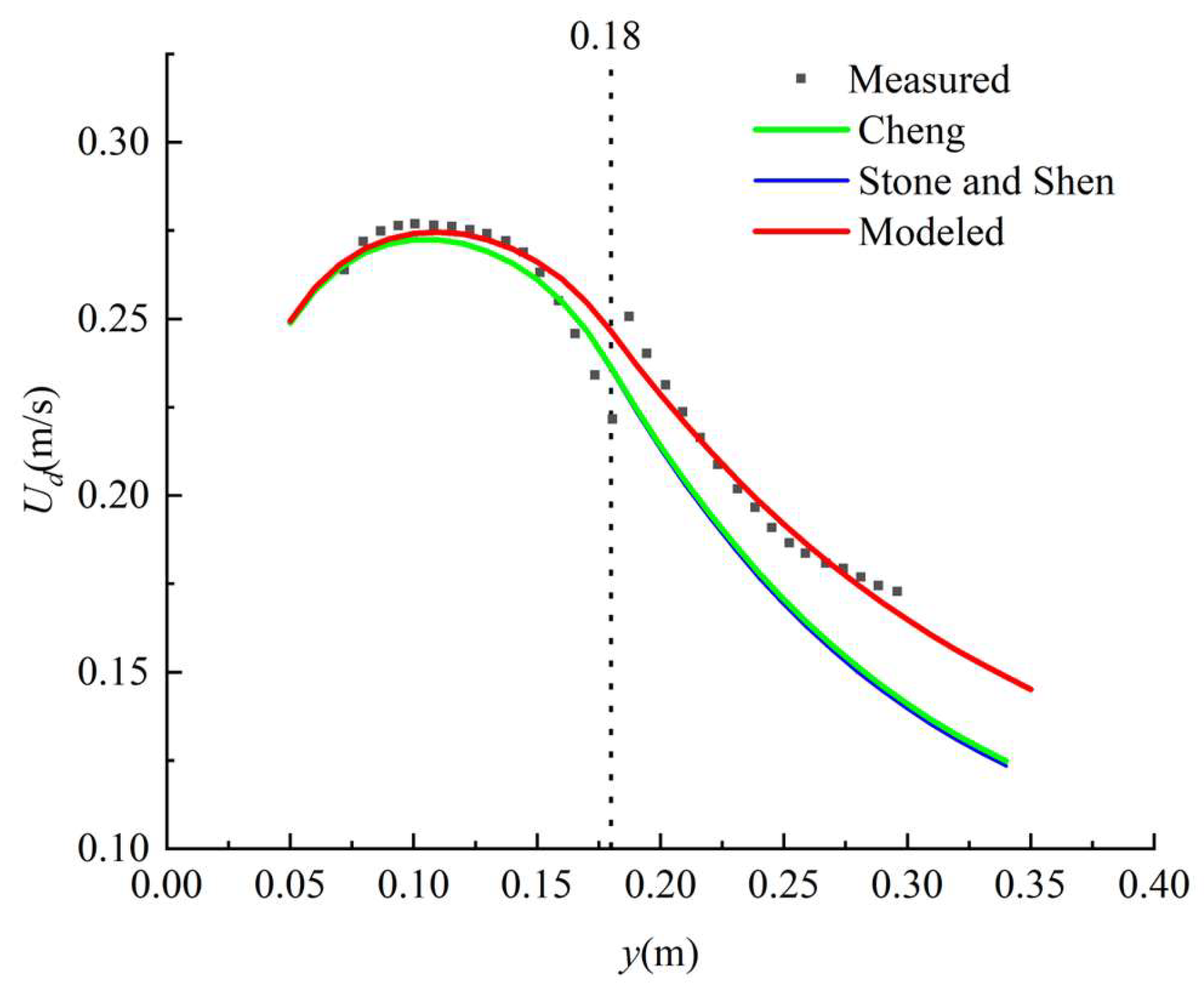
Equation (22) was used to predict the velocity distribution in the non-vegetated area, and Equation (24) was used to predict the velocity distribution in the vegetated area. A comparison was made between the experimental and analytical solutions for the water depth-averaged streamwise velocity under three cases, i.e., N = 0.06, N = 0.24, and N = 0.96, as proposed by Naot et al. [32], which are shown in Figure 2, Figure 3 and Figure 4. The comparison between the experimental and analytical solutions provided by Shi and Huai [33], as calculated in case 4, is shown in Figure 5.
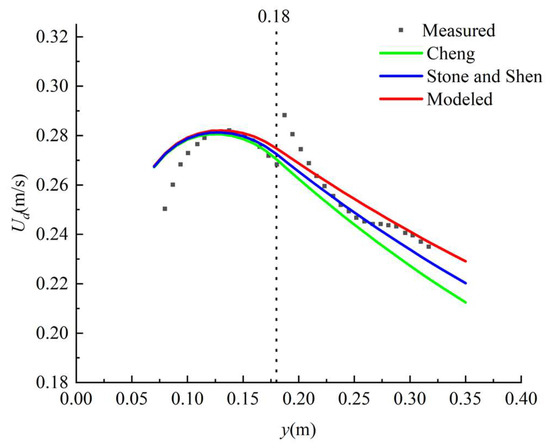
Figure 2.
Water depth-averaged streamwise velocity between the experimental data and analytical solution in case 1. The green line occurs when φ1 = 0.8279 (from Cheng [26]). The blue line occurs when φ2 = 0.6914 (from Stone and Shen [25]). The red line occurs when φ3 = 0.4845 (from the presented model (φ = Uv/Ud)). The dotted line indicates the boundary between the non-vegetated and vegetated areas.
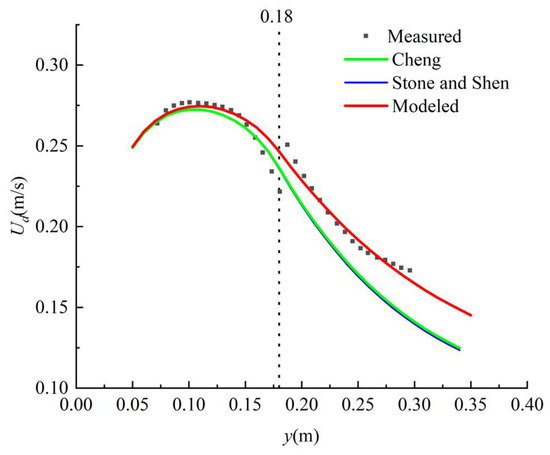
Figure 3.
The water depth-averaged streamwise velocity between the experimental data and analytical solution in case 2. φ1 = 0.6522, φ2 = 0.662, and φ3 = 0.4681.
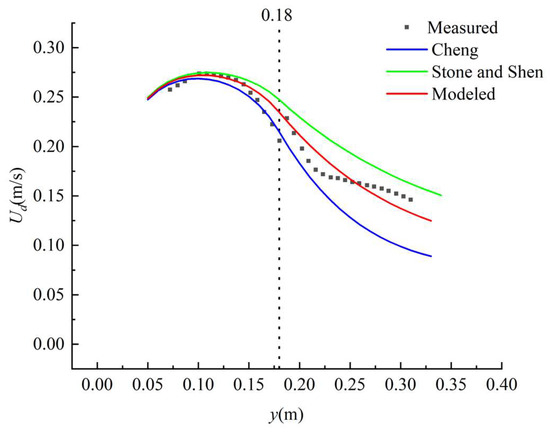
Figure 4.
Water depth-averaged streamwise velocity between the experimental data and analytical solution in case 3. φ1 = 0.3044, φ2 = 0.6107, and φ3 = 0.4318.
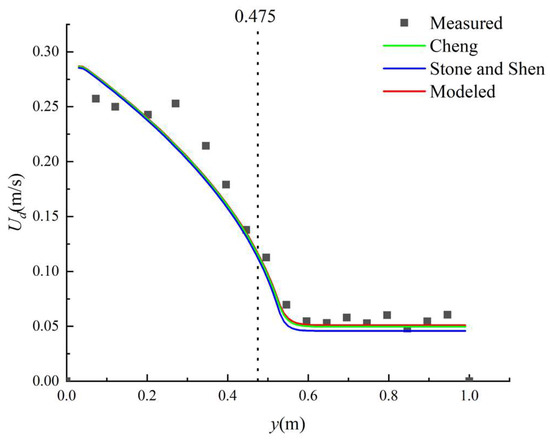
Figure 5.
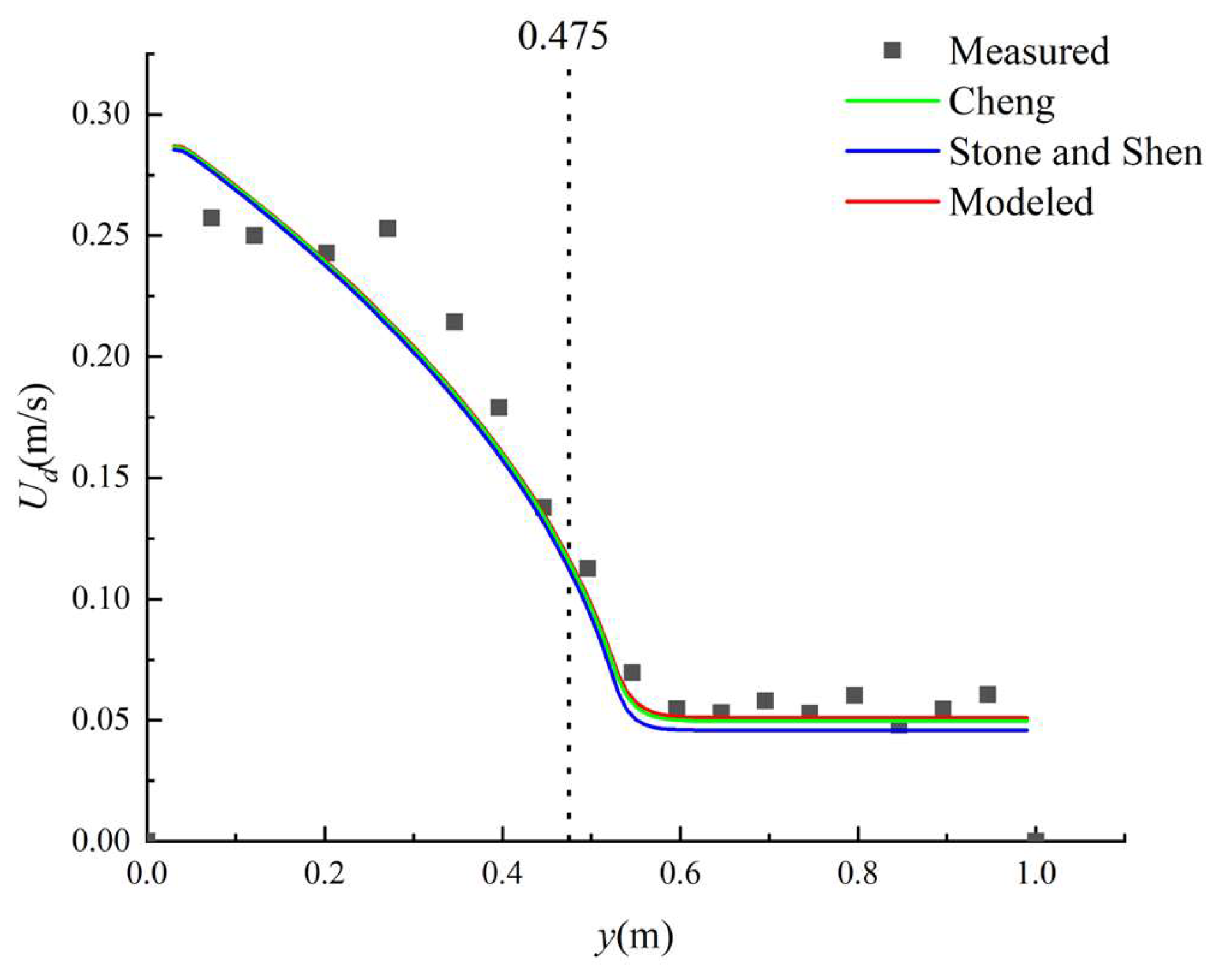
Water depth-averaged streamwise velocity between the experimental data and analytical solution in case 4; φ1 = 0.8013, φ2 = 0.8685, and φ3 = 0.7778.
7. Discussion
The validation of the model using the experimental data obtained by Naot et al. [32] and Shi and Huai [33] showed that when vegetation density is high, the equations proposed by Cheng [26] and Stone and Shen [25] usually yielded relatively larger values. In cases 1 to 3, the analytical solution in the non-vegetated area is relatively consistent with the experimental data. In the vegetated area, there are some deviations between the analytical solution and experimental data, while in case 4, the analytical solution is relatively consistent with the experimental data. Optimizing of the model improved it for the ratio of two depth-averaged velocities, i.e., Uv/Ud. Table 1 shows that in four cases when the flow depth increased from 0.06 m to 0.31 m, the values changed from −0.001 to −0.06, indicating that the absolute value of increased with an increase in flow depth. In order to quantitatively describe the difference between the results of the model and the experimental data, we performed an error analysis from two perspectives: the average values of the absolute error , and the relative error . The absolute error ε is expressed as follows:
where the subscripts “measured” and “calculated” represent the measured values and the analytical solutions, respectively. In order to obtain the average error, it is necessary to calculate the average value of the error for each point along the y direction on the cross section. The average value of the absolute error can be expressed as follows:
Here, Nm represents the number of experimental measurement points. The relative error ε’ is expressed as follows:
The average value of the relative error is expressed as follows:
The average absolute error and relative error values in cases 1–4 are shown in Table 2.

Table 2.
Error statistics of the transverse distribution of the water depth-averaged streamwise velocity calculated by the models.
The average values of the absolute error and the relative error for the presented model were the smallest (Table 2). For cases 1 to 4, the average absolute error in this model was within 0.008. The maximum value of was 0.008 (in case 3). The minimum value of was 0.004 (in case 4). However, the average value of the relative error was less than 5%. The maximum value of was 4.77% (in case 4), and the minimum value of was 1.84% (in case 2).
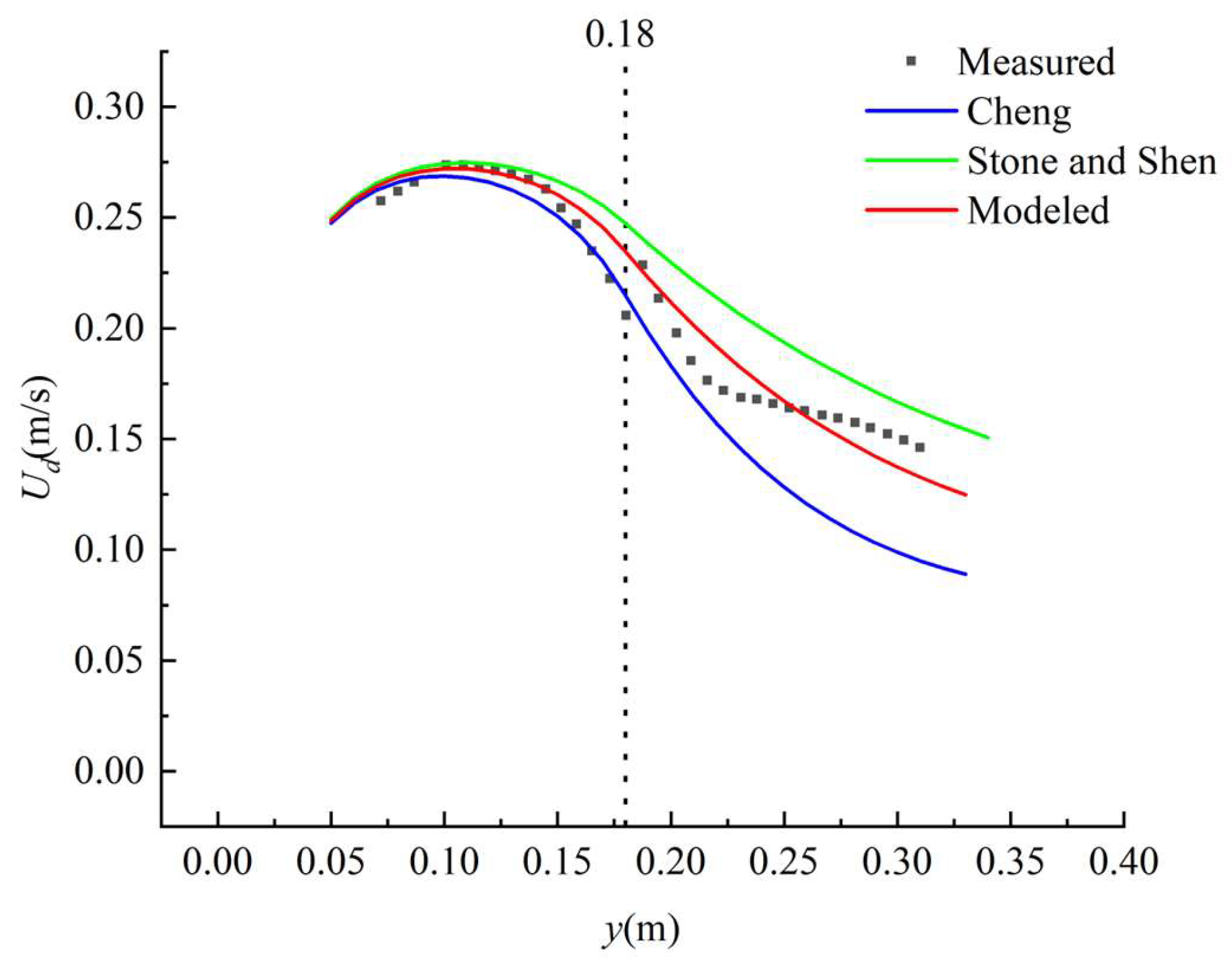
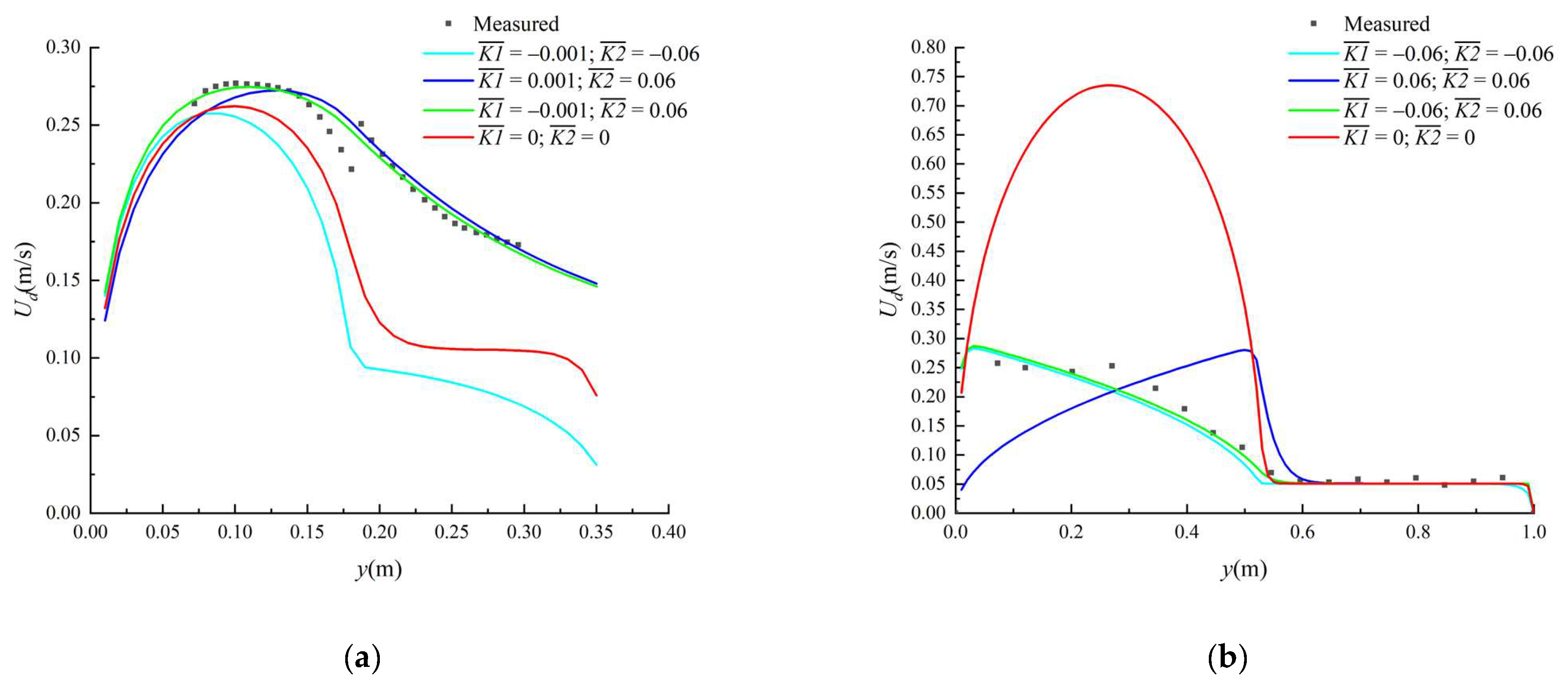
The variation in the values of the secondary flow coefficients and , used for the calculation, are shown in Table 3. In four cases, when the flow depth increased from 0.06 m to 0.31 m, the values changed from −0.001 to −0.06, indicating a positive relationship between the absolute value of and the flow depth; meanwhile, the difference in the absolute value of was small when the flow depth increased in case 4, compared to the value of in cases 1 to 3. When the depth-averaged velocity was calculated, we found that the value of the secondary flow coefficient had a greater effect on the results of analytical solution. Liu et al. [13] proposed that the results of analytical solutions were unsatisfactory, especially in the non-vegetated main channel, when the effect of secondary flow coefficient was ignored or it was considered to be constant. In order to evaluate the importance of the values of and in the calculation model, we considered four cases to modify the sign of one of the coefficients and ignore the coefficient = = 0. We selected cases 2 and 4 for the specific modification methods (Table 3). We found that the secondary flow coefficient greatly influenced the model results, as shown in Figure 6. In case 2, modifying and ignoring the secondary flow coefficient greatly affected the results of analytical solution. In case 4, however, modifying and ignoring the secondary flow coefficient strongly influenced the results of the analytical solution. Therefore, calibrating the secondary flow coefficient in different regions and different cases might affect the calculations in other regions. Additionally, for the floodplain, the intensity and range of secondary flow coefficient increased with an increase in the elevation of the floodplain [36]; thus, it should be considered in the calculation.

Table 3.
Summary of the modification of the -value.
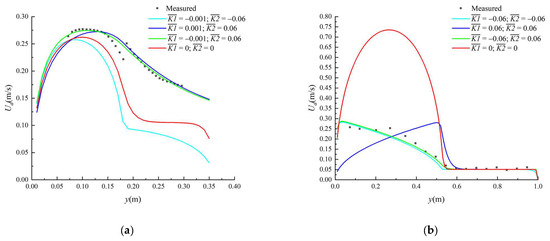
Figure 6.
Effect of the secondary flow coefficient, , on the results of the model for the prediction of the transverse distribution of water depth-averaged streamwise velocity with submerged vegetation. (a) For case 2, in the presented model, = −0.001 and = 0.06. (b) For case 4, in the presented model, = −0.06 and = 0.06.
We found that the experimental data obtained by Naot et al. [32] showed an abrupt change at the junction between the non-vegetated area and the vegetated area, as shown in Figure 2, Figure 3 and Figure 4. The reason for this may be because the flow velocity data in the vegetation layer were not measured, and only the flow velocity data above the vegetation layer were measured. As a result, the velocity inside the vegetation layer is smaller than that outside the vegetation layer, and the depth-averaged streamwise velocity above the vegetation is larger than the water depth-averaged velocity; this leads to a sudden increase at the junction (y = 0.18 m). When the velocity continuity condition was adopted in the present analytical solutions, there was no sudden increase at the junction. The study shows that some deviations between the analytical solution and the experimental data can be easily found in cases 1 to 3. In these three cases, the depth-averaged streamwise velocity above the vegetation was adopted for the vegetated area, and the water depth-averaged streamwise velocity was adopted for the non-vegetated area and the junction (Figure 1b) [37]. For the analysis of the measurement of the experimental data obtained by Shi and Huai [33], the measurement points were arranged in the vegetation layer and above the vegetation layer. Therefore, at the junction between the regions, the water depth-averaged streamwise velocity did not show an abrupt change.
8. Conclusions
This paper optimizes the ratio of the vegetation height-averaged velocity to the water depth-averaged velocity, which can be applied to the N–S equation. The N–S equation with optimized velocity ratio can predict the lateral distribution of the water depth-averaged streamwise velocity in the open channel partially covered by the submerged vegetation. In both the non-vegetated area and submerged vegetation area, different parameters, including the transverse eddy viscosity coefficient ξ, friction coefficient f, porosity α, and the drag force coefficient Cd, were introduced to determine the analytical solution. Additionally, we discussed the methods for calculating the parameters in different zones. Close inspection of the range of the secondary flow coefficient showed that the secondary flow coefficient could not be ignored in different regions. could be determined by the flow depth and the depth of the vegetation layer. According to the error analysis for the velocity data from the analytical solution and experiments, the average relative error is smaller than those from previous studies, revealing that a relative satisfactory prediction of the transverse distribution of water depth-averaged streamwise velocity in the channel flow with submerged vegetation was obtained using the present model. Additionally, when the flow is not assumed to be uniform, the model parameters may be modified, although further experiments are required to verify this. Future studies may put emphasis on the secondary flow coefficient, and extend the model into flows with flexible vegetation.
Author Contributions
All authors made contributions to the conception and design of the study. Material preparation and data collection and analysis were performed by J.Z., Z.M., W.W., Z.L., H.W., Q.W., X.Z. and X.D. The first draft of the paper was completed by J.Z. and Z.M., and all authors commented on previous versions of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study received funding by the National Natural Science Foundation of China [grant numbers U2040208; 52109100], the Postdoctoral Research Foundation of China [grant number 2021M702643], and by AnHui Water Resources Decelopment Co.,Ltd. [grant number KY-2021-13].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors have no relevant financial or non-financial interests to disclose.
Notation
The following main parameters were used in this article:
| Av | projected vegetated area per unit volume in the direction of downstream flow |
| B | width of the flume |
| b | width of the vegetation layer |
| Cd | drag force coefficient for vegetation |
| D | vegetation stem diameter |
| Dr | relative depth ratio |
| Fv | drag force |
| f | Darcy–Weisbach friction coefficient |
| g | gravitational acceleration |
| H | flow depth |
| Hv | height of vegetation |
| secondary flow coefficient | |
| m | number of vegetation per unit of area |
| N | non-dimensional vegetation density |
| S0 | channel bed slope |
| Uv | depth-averaged streamwise velocity along the vegetation height |
| Ud | water depth-averaged streamwise velocity |
| ρ | flow density |
| α | porosity |
| β | shape factor of the vegetation |
| ξ | transverse eddy viscosity coefficient |
| φ | Uv/Ud |
| average value of absolute error | |
| average value of relative error |
References
- Harvey, J.W.; Noe, G.B.; Larsen, L.G.; Nowacki, D.J.; Mcphillips, L.E. Field flume reveals aquatic vegetation’s role in sediment and particulate phosphorus transport in a shallow aquatic ecosystem. Geomorphology 2011, 126, 297–313. [Google Scholar] [CrossRef]
- Cullen-Unsworth, L.; Unsworth, R. Seagrass meadows, ecosystem services, and sustainability. Environ. Sci. Policy Sustain. Dev. 2013, 55, 14–28. [Google Scholar] [CrossRef]
- Scholle, M.; Aksel, N. An exact solution of visco-capillary flow in an inclined channel. Z. Angew. Math. Phys. 2001, 52, 749–769. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2008, 44, W01412. [Google Scholar] [CrossRef]
- Terrier, B. Flow Characteristics in Straight Compound Channels with Vegetation along the Main Channel. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2010. [Google Scholar]
- Shiono, K.; Knight, D.W. Turbulent open-channel flows with variable depth across the channel. J. Fluid Mech. 1991, 222, 617–646. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y. Impact of an emergent model vegetation patch on flow adjustment and velocity. In Proceedings of the Institution of Civil Engineers—Water Management; Thomas Telford Ltd.: London, UK, 2022; Volume 175, pp. 55–66. [Google Scholar] [CrossRef]
- Liu, C.; Shan, Y.; Sun, W.; Yan, C.; Yang, K. An open channel with an emergent vegetation patch: Predicting the longitudinal profiles of velocities based on exponential decay. J. Hydrol. 2020, 582, 124429. [Google Scholar] [CrossRef]
- Huai, W.; Gao, M.; Zeng, Y.; Li, D. Two-dimensional analytical solution for compound channel flows with vegetated floodplains. Appl. Math. Mech. 2009, 30, 1049–1056. [Google Scholar] [CrossRef]
- Fu, X.; Wang, F.; Liu, M.; Huai, W. Transverse distribution of the streamwise velocity for the open-channel flow with floating vegetated islands. Environ. Sci. Pollut. Res. Int. 2021, 28, 51265–51277. [Google Scholar] [CrossRef]
- Devi, K.; Khatua, K.K. Prediction of depth averaged velocity and boundary shear distribution of a compound channel based on the mixing layer theory. Flow Meas. Instrum. 2016, 50, 147–157. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, J.; Zhu, L.; Chong, L.; Liu, J.; Luo, J. Influence of submerged vegetation on flow structure and sediment deposition. J. Zhejiang Univ. (Eng. Sci.) 2021, 55, 71–80. [Google Scholar] [CrossRef]
- Liu, C.; Luo, X.; Liu, X.; Yang, K. Modeling depth-averaged velocity and bed shear stress in compound channels with emergent and submerged vegetation. Adv. Water Resour. 2013, 60, 148–159. [Google Scholar] [CrossRef]
- Yang, K.; Cao, S.; Knight, D.W. Flow patterns in compound channels with vegetated floodplains. J. Hydraul. Eng. 2007, 133, 148–159. [Google Scholar] [CrossRef]
- Kowalski, J.; Torrilhon, M. Moment approximations and model cascades for shallow flow. Commun. Comput. Phys. 2019, 25, 669–702. [Google Scholar] [CrossRef]
- Koellermeier, J.; Rominger, M. Analysis and numerical simulation of hyperbolic shallow water moment equations. Commun. Comput. Phys. 2020, 28, 1038–1084. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.; Chen, Y.; Zhu, D. Vertical profile of horizontal velocity in the flow with submerged vegetation. J. Sichuan Univ. (Eng. Sci. Ed.) 2012, 44, 253–257. [Google Scholar] [CrossRef]
- Huai, W.; Zeng, Y.; Xu, Z.; Yang, Z. Three-layer model for vertical velocity distribution in open channel flow with submerged rigid vegetation. Adv. Water Resour. 2009, 32, 487–492. [Google Scholar] [CrossRef]
- Castro, M.J.; Macias, J.; Pares, C. A q-scheme for a class of systems of coupled conservation laws with source term. application to a two-layer 1-d shallow water system. ESAIM: Math. Model. Numer. Anal. 2001, 35, 107–127. [Google Scholar] [CrossRef]
- Ghisalberti, M.; Nepf, H. Shallow flows over a permeable medium: The hydrodynamics of submerged aquatic canopies. Transp. Porous Media 2009, 78, 309. [Google Scholar] [CrossRef]
- Wang, W.; Huai, W.; Li, S.; Wang, P.; Wang, Y.; Zhang, J. Analytical solutions of velocity profile in flow through submerged vegetation with variable frontal width. J. Hydrol. 2019, 578, 124088. [Google Scholar] [CrossRef]
- Sukhodolov, A.N.; Sukhodolova, T.A. Case study: Effect of submerged aquatic plants on turbulence structure in a Lowland River. J. Hydraul. Eng. 2010, 136, 434–446. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Hu, T. Analysis of local flow field characteristics of non-submerged cylinder group. Shanghai Jiao Tong Univ. 2016, 31, 161–170. [Google Scholar]
- Yang, Y.; Ma, Y.; Zhan, Z.; Fang, S.L.; Zhang, M. Fine numerical simulation of three-dimensional hydrodynamics in vegetation area under submerged and floating vegetation. In Proceedings of the 31st National Symposium on Hydrodynamics; Ocean Press: Lancing, UK, 2020; Volume II. [Google Scholar]
- Stone, B.M.; Shen, H. Hydraulic resistance of flow in channels with cylindrical roughness. J. Hydraul. Eng. 2002, 128, 500–506. [Google Scholar] [CrossRef]
- Cheng, N.S. Representative roughness height of submerged vegetation. Water Resour. Res. 2011, 47, W08517. [Google Scholar] [CrossRef]
- Huthoff, F.; Augustijn, D.C.M.; Hulscher, S.J.M.H. Analytical solution of the depth-averaged flow velocity in case of submerged rigid cylindrical vegetation. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Abril, J.B.; Knight, D.W. Stage-discharge prediction for rivers in flood applying a depth-averaged model. J. Hydraul. Res. 2004, 42, 616–629. [Google Scholar] [CrossRef]
- Pasche, E.; Rouvé, G. Overbank flow with vegetatively roughened flood plains. J. Hydraul. Eng. 1985, 111, 1262–1278. [Google Scholar] [CrossRef]
- Rameshwaran, P.; Shiono, K. Quasi two-dimensional model for straight overbank flows through emergent. J. Hydraul. Res. 2007, 45, 302–315. [Google Scholar] [CrossRef]
- Ackers, P. Hydraulic design of straight compound channels. Detail. Dev. Des. Method 1991, 2, 1–139. [Google Scholar]
- Naot, D. Hydrodynamic behavior of partly vegetated open channels. J. Hydraul. Eng. 1996, 122, 625–633. [Google Scholar] [CrossRef]
- Shi, H.; Huai, W. Two-Dimensional Analytical Solution for a Compound Open Channel Flow with Submerged Vegetation. Sciencepaper Online. 2016. Available online: http://www.paper.edu.cn/releasepaper/content/201612-315 (accessed on 12 September 2022).
- Tanino, Y.; Nepf, H.M. Laboratory investigation of mean drag in a random array of rigid, emergent cylinders. J. Hydraul. Eng. 2008, 134, 34–41. [Google Scholar] [CrossRef]
- James, C.S.; Birkhead, A.L.; Jordanova, A.A.; O’Sullivan, J.J. Flow resistance of emergent vegetation. J. Hydraul. Res. 2004, 42, 390–398. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, H. Hydrodynamic and mixing characteristics of a river confluence with floodplain. J. Hohai Univ. (Nat. Sci.) 2022, 1–13. Available online: http://kns.cnki.net/kcms/detail/32.1117.TV.20220628.1720.008.html (accessed on 12 September 2022).
- Zhang, M. Study on Flow Characteristics of Compound Channel with Vegetation Floodplain. Ph.D. Thesis, Tsinghua University, Beijing, China, 2011. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).