A Continuous Multisite Multivariate Generator for Daily Temperature Conditioned by Precipitation Occurrence
Abstract
:1. Introduction
2. Materials and Methods
2.1. Multivariate Precipitation Occurrence (Dry–Wet)
2.2. Multivariate Maximum and Minimum Temperature
2.3. Evidence for the Goodness of Fit
2.4. Generation of Multivariate Synthetic Series
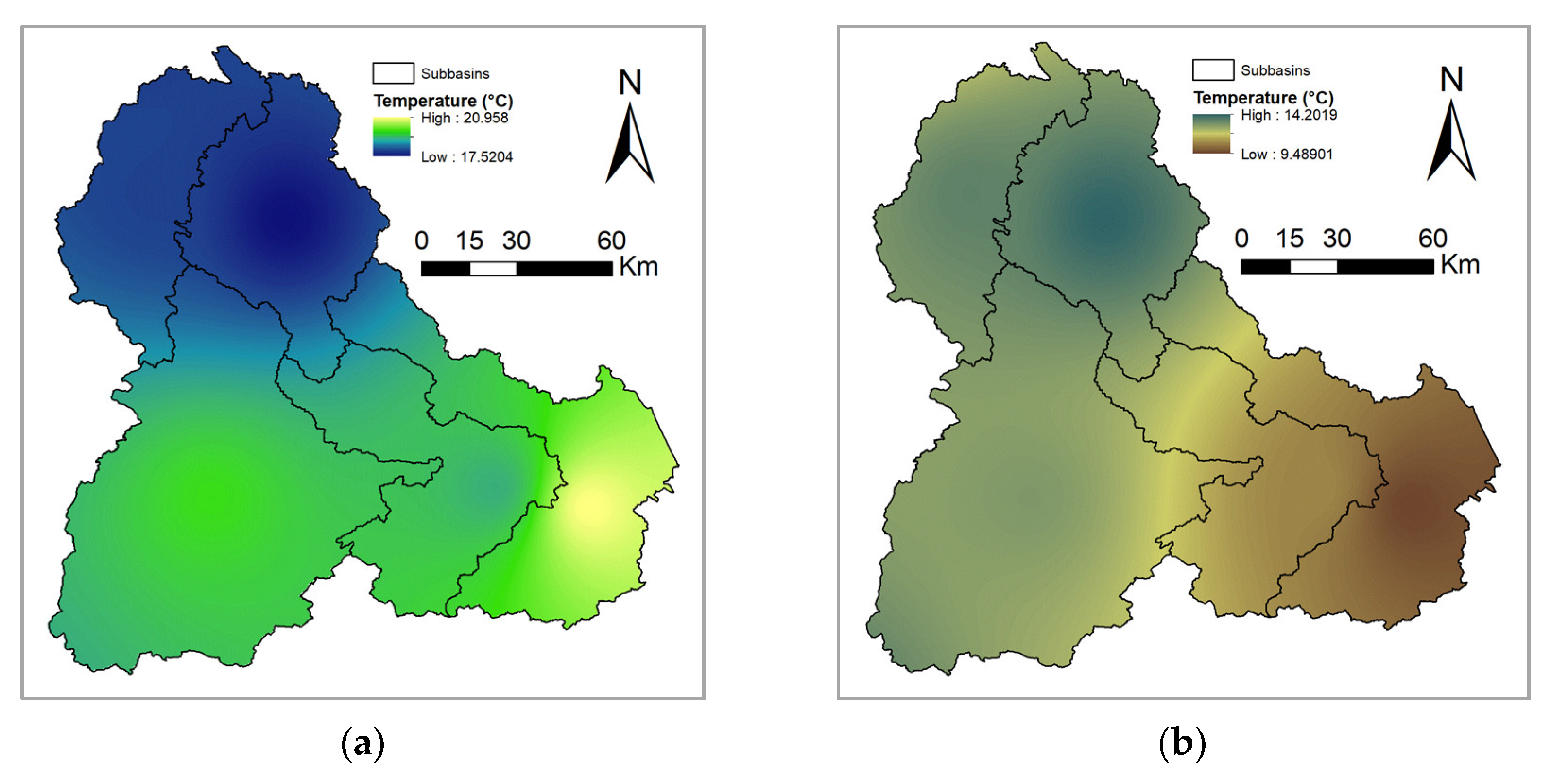
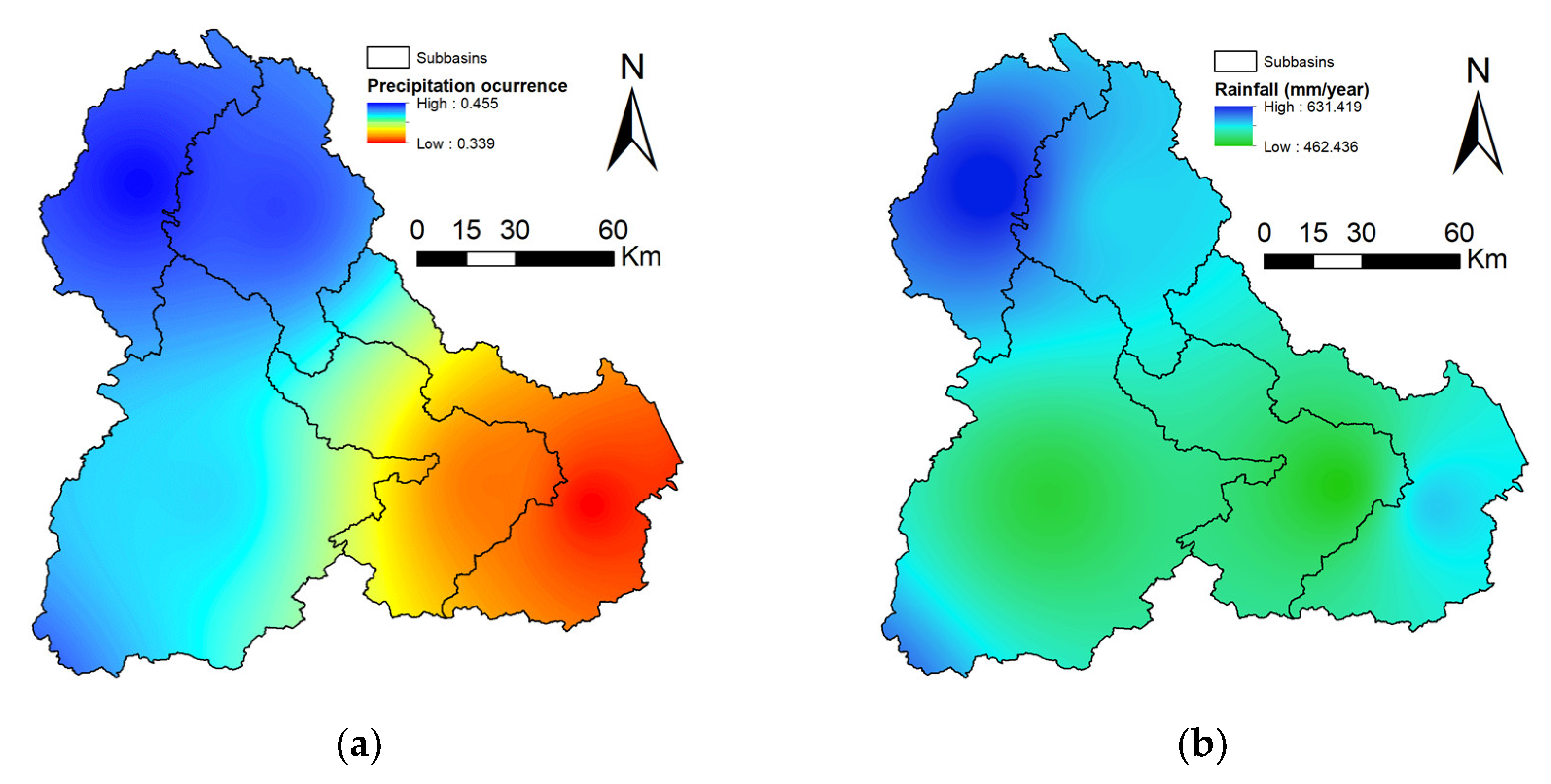
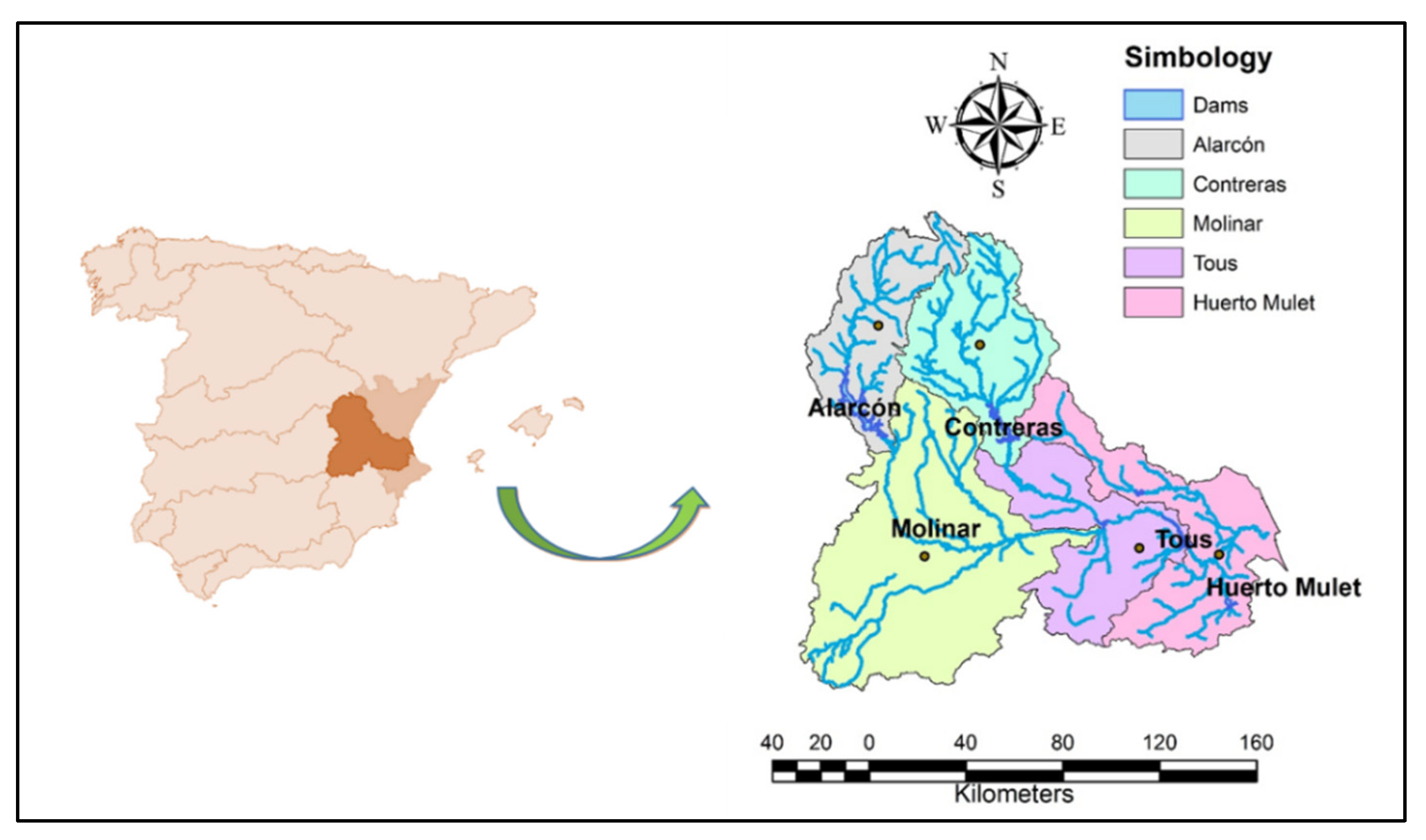
2.5. Study Area
3. Results
3.1. Multivariate Occurrence Synthetic Series
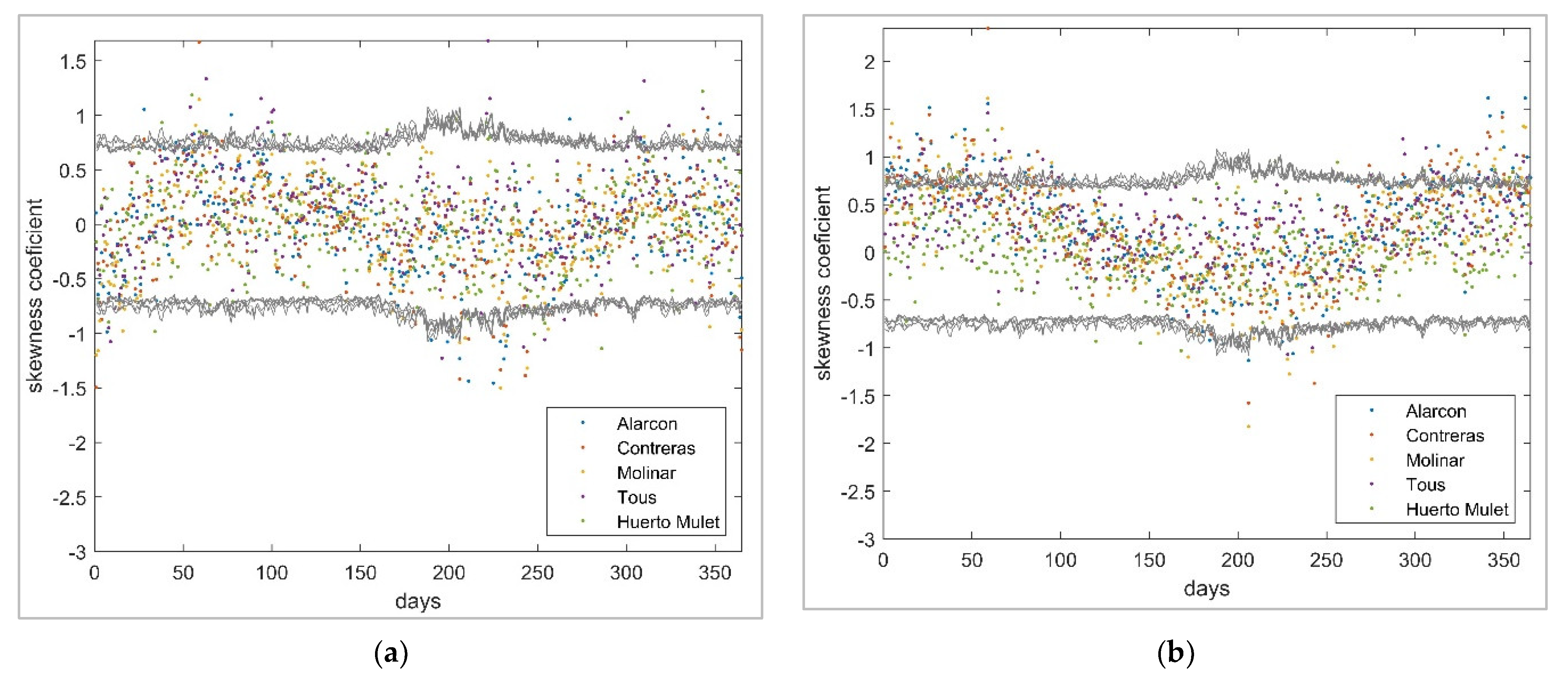
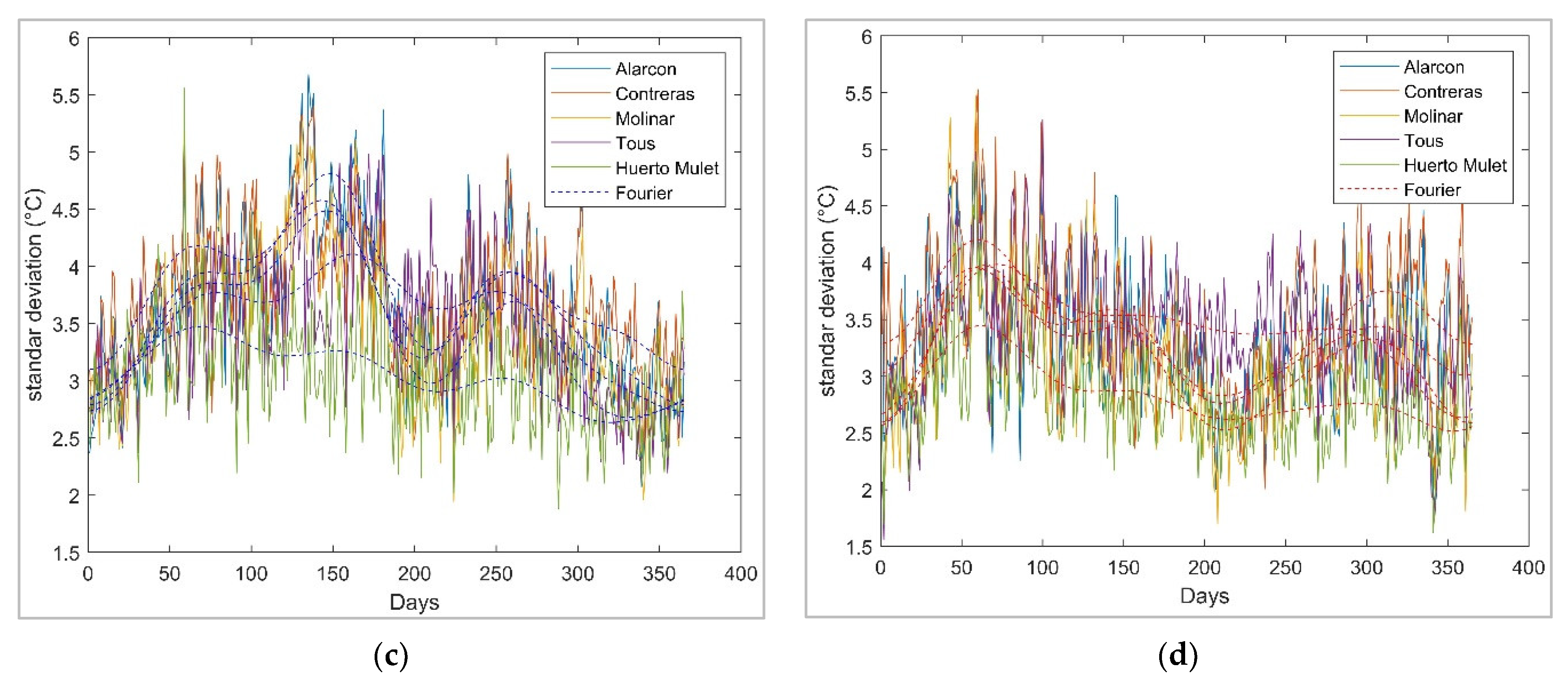
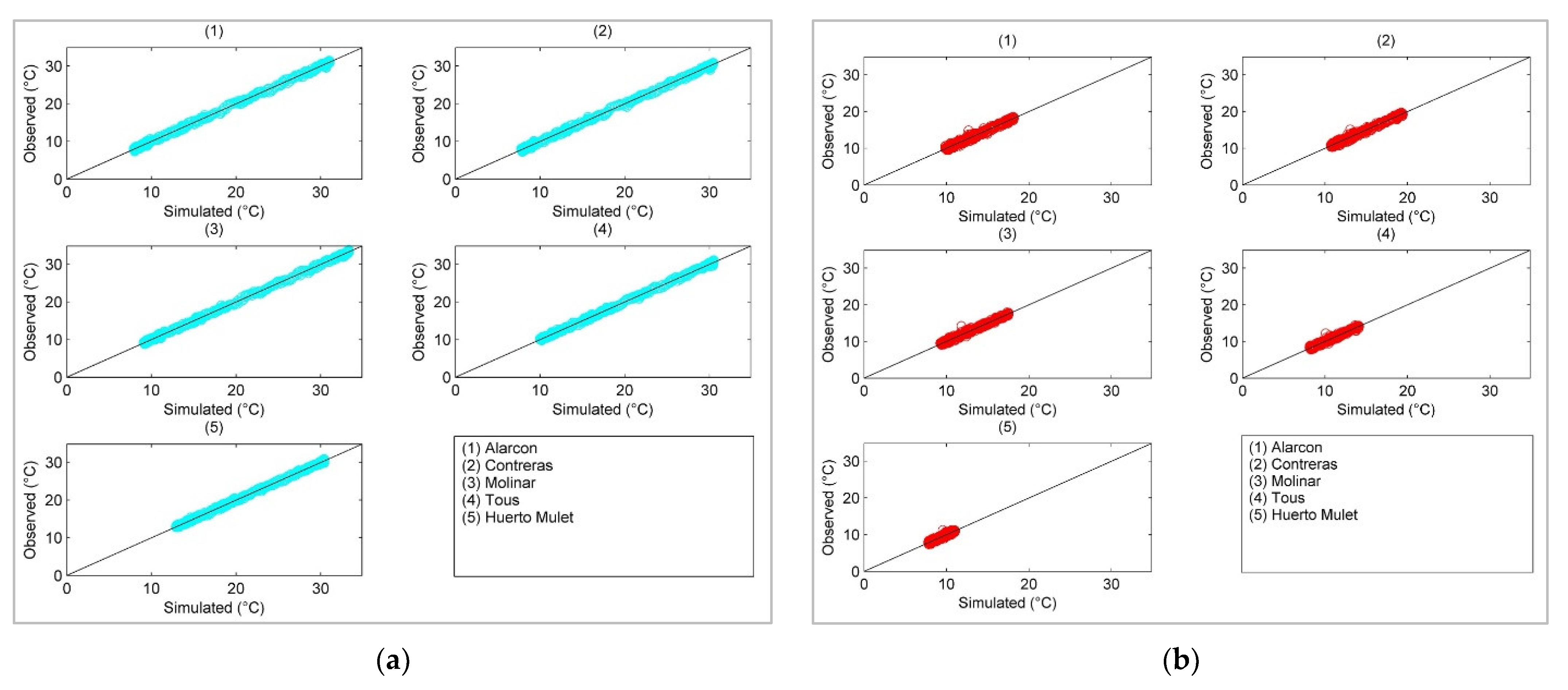
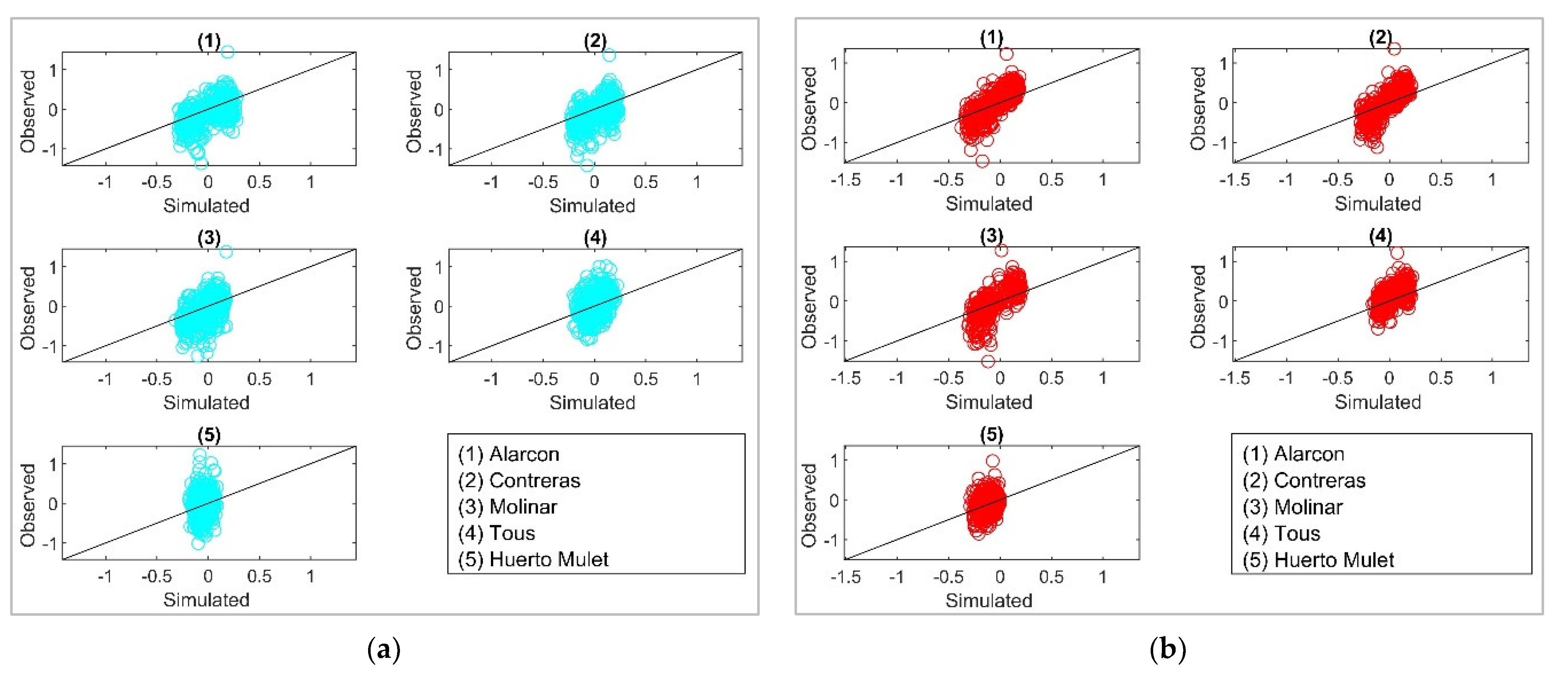
3.2. Stochastic Multisite Multivariate Temperature Series
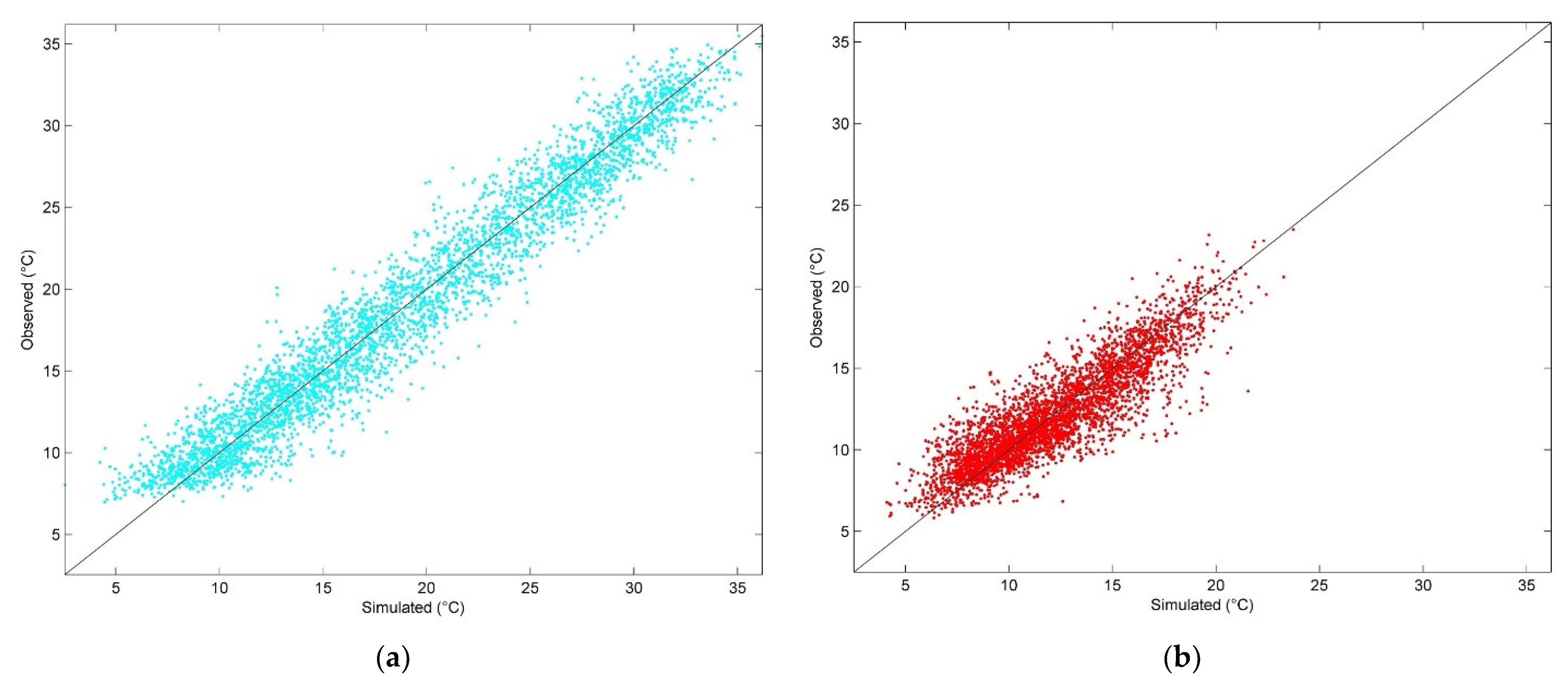
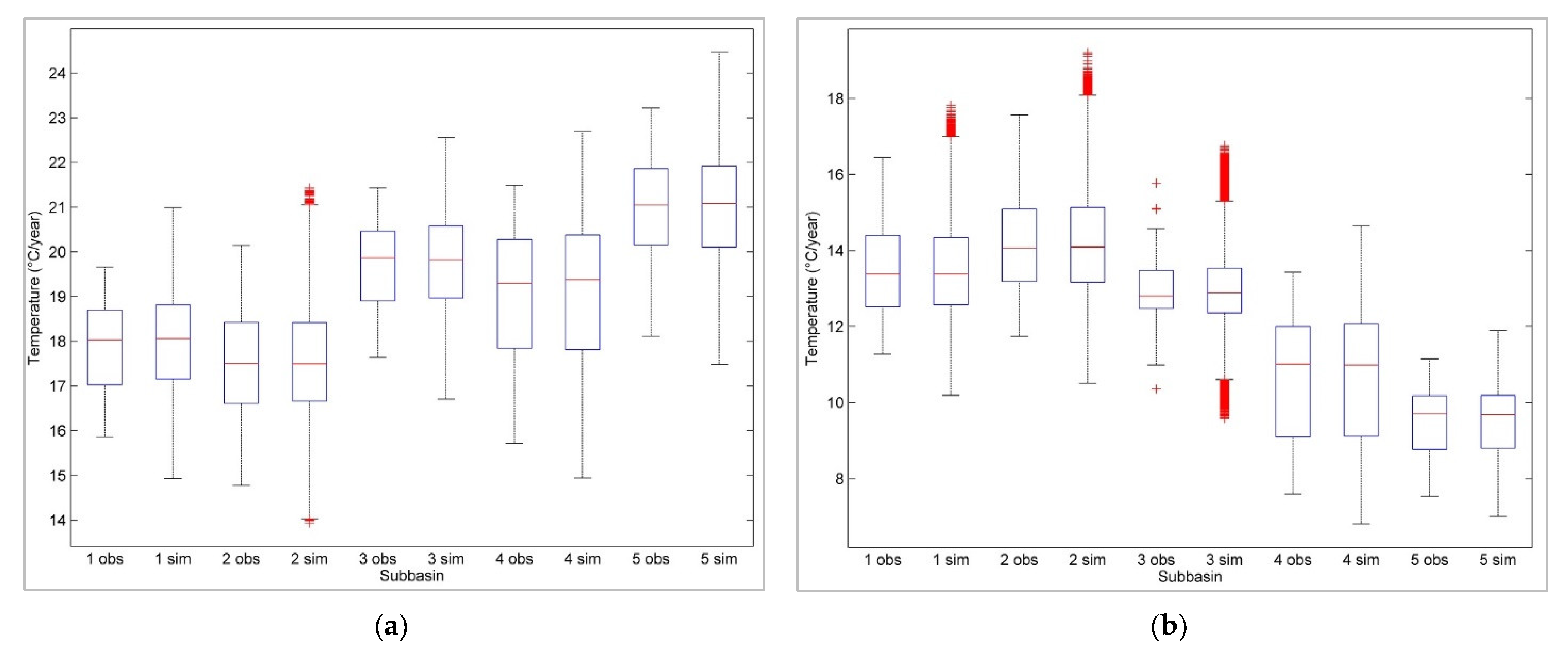
3.3. Generation of Multivariate Synthetic Temperature Series
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A



References
- Sivakumar, B. Chaos in Hydrology: Bridging Determinism and Stochasticity, 1st ed.; Springer Science: Dordrecht, The Netherlands, 2017; pp. 63–111. [Google Scholar]
- Beneyto, C.; Aranda, J.Á.; Benito, G.; Francés, F. New Approach to Estimate Extreme Flooding Using Continuous Synthetic Simulation Supported by Regional Precipitation and Non-Systematic Flood Data. Water 2020, 12, 3174. [Google Scholar] [CrossRef]
- Chang, F.; Hsu, K.; Chang, L. Flood Forecasting Using Machine Learning Methods. Water 2019, 2, 14–53. [Google Scholar] [CrossRef] [Green Version]
- Chang, F.J.; Guo, S. Advances in Hydrologic Forecasts and Water Resources Management. Water 2020, 12, 1819. [Google Scholar] [CrossRef]
- Gabriel, K.R.; Neumann, J. A Markov Chain model for daily rainfall occurrence at tel aviv. Q. J. R. Meteorol. Soc. 1962, 88, 90–95. [Google Scholar] [CrossRef]
- Caskey, E. A Markov Chain model for the probability of precipitation occurrence in intervals of various length. Mon. Weather Rev. 1963, 91, 298–301. [Google Scholar] [CrossRef]
- Matalas, N.C. Time Series Analysis, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1967; Volume 3. [Google Scholar] [CrossRef]
- Todorovic, P.; Woolhiser, D.A. A Stochastic Model of n -Day Precipitation. J. Appl. Meteorol. 1975, 14, 17–24. [Google Scholar] [CrossRef]
- Richardson, C.W. Stochastic Simulation of Daily Precipitation, Temperature, and Solar Radiation. Water Resour. Res. 1981, 17, 182–190. [Google Scholar] [CrossRef]
- Roldán, J. Tendencias Actuales En El Modelado de La Precipitación Diaria. Ing. Agua 1994, I, 89–100. [Google Scholar] [CrossRef] [Green Version]
- Rajagopalan, B.; Lall, U.; Tarboton, D.G. Nonhomogeneous Markov Model for Daily Precipitation. J. Hydrol. Eng. 1996, 1, 33–40. [Google Scholar] [CrossRef]
- Wilks, D.S. Multisite Generalization of a Daily Stochastic Precipitation Generation Model. J. Hydrol. 1998, 210, 178–191. [Google Scholar] [CrossRef]
- Wilks, D.S.S.; Wilby, R.L.L. The Weather Generation Game: A review of stochastic weather models. Prog. Phys. Geogr. 1999, 23, 329–357. [Google Scholar] [CrossRef]
- Harrold, T.I. A Nonparametric Model for Stochastic Generation of Daily Rainfall Amounts. Water Resour. Res. 2003, 39, 1–12. [Google Scholar] [CrossRef]
- Brissette, F.P.; Khalili, M.; Leconte, R. Efficient Stochastic Generation of Multi-Site Synthetic Precipitation Data. J. Hydrol. 2007, 345, 121–133. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, W.; Shao, Y.; Zhang, K. A comparison of four precipitation distribution models used in daily stochastic models. Adv. Atmos. Sci. 2011, 28, 809–820. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. Simulation of the entire range of daily precipitation using a hybrid probability distribution. Water Resour. Res. 2012, 48, 1–17. [Google Scholar] [CrossRef]
- Mehrotra, R.; Li, J.; Westra, S.; Sharma, A. A programming tool to generate multi-site daily rainfall using a two-stage semi parametric model. Environ. Model. Softw. 2015, 63, 230–239. [Google Scholar] [CrossRef]
- So, B.J.; Kwon, H.H.; Kim, D.; Lee, S.O. Modeling of daily rainfall sequence and extremes based on a semiparametric pareto tail approach at multiple locations. J. Hydrol. 2015, 529, 1442–1450. [Google Scholar] [CrossRef]
- Wilks, D.S. Simultaneous stochastic simulation of daily precipitation, temperature and solar radiation at multiple sites in complex terrain. Agric. For. Meteorol. 1999, 96, 85–101. [Google Scholar] [CrossRef]
- Semenov, M.A.; Barrow, E.M. LARS-WG A Stochastic Weather Generator for Use in Climate Impact Studies LARS-WG: Stochastic Weather Generator Contents, Harpenden, Hertfordshire, United Kigdom. Available online: http://resources.rothamsted.ac.uk/sites/default/files/groups/mas-models/download/LARS-WG-Manual.pdf (accessed on 10 December 2021).
- Chen, J.; Brissette, F.P.; Leconte, R. WeaGETS—A Matlab-Based Daily Scale Weather Generator for Generating Precipitation and Temperature. Procedia Environ. Sci. 2012, 13, 2222–2235. [Google Scholar] [CrossRef]
- Salas, J.J.D.; Delleur, J.W.; Yevjevich, V.M.; Lane, W.L. Applied Modeling of Hydrologic Time Series; Water Resources Publication: Littleton, CO, USA, 1980; ISBN 0-918334-37-3. [Google Scholar]
- Srikanthan, R.; McMahon, T.A. Stochastic generation of annual, monthly and daily climate data: A review. Hydrol. Earth Syst. Sci. 2001, 5, 653–670. [Google Scholar] [CrossRef] [Green Version]
- Qian, B.; Gameda, S.; Hayhoe, H.; De Jong, R.; Bootsma, A. Comparison of LARS-WG and AAFC-WG Stochastic Weather Generators for Diverse Canadian Climates. Clim. Res. 2004, 26, 175–191. [Google Scholar] [CrossRef] [Green Version]
- Flecher, C.; Naveau, P.; Allard, D.; Brisson, N. A stochastic daily weather generator for skewed data. Water Resour. Res. 2010, 46, 1–15. [Google Scholar] [CrossRef]
- Hayhoe, H.N. Improvements of stochastic weather data generators for diverse climates. Clim. Res. 2000, 14, 75–87. [Google Scholar] [CrossRef]
- Ailliot, P.; Allard, D.; Monbet, V.; Naveau, P. Stochastic Weather Generators: An Overview of Weather Type Models. J. Société Française Stat. 2015, 156, 101–113. [Google Scholar]
- Richardson, C.W.; Wright, D.A.; Nofziger, D.L.; Hornsby, A.G. WGEN: A Model for Generating Daily Weather Variables. ARS 1984, 8, 1–83. [Google Scholar]
- Carter, T.; Posch, M.; Tuomenvirta, H. SILMUSCEN and CLIGEN User’s Guide: Guidelines for the Construction of Climatic Scenarios and Use of a Stochastic Weather Generator in the Finnish. Available online: https://www.osti.gov/etdeweb/biblio/458148 (accessed on 5 November 2021).
- Stöckle, C.O.; Nelson, R.; Donatelli, M.; Castellvì, F. ClimGen: A flexible weather generation program. In Proceedings of the 2nd International Symposium Modelling Cropping Systems, Florence, Italy, 17 July 2001. [Google Scholar]
- Marcello, D.; Gianni, B.; Ephrem, H.; Simone, B.; Roberto, C.; Bettina, B. CLIMA: A Weather Generator Framework. In Proceedings of the 18th World IMACS/MODSIM Congress, Carins, Australia, 13–17 July 2009; Available online: https://core.ac.uk/download/pdf/38616113.pdf (accessed on 17 July 2009).
- Foufoula-georgiou, E.; Lettenmaier, D.P. A Markov renewal model for rainfall occurrences. Water Resour. Res. 1987, 23, 875–884. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G.G.S. Copula Based Multisite Model for Daily Precipitation Simulation. Hydrol. Earth Syst. Sci. 2009, 13, 2299–2314. [Google Scholar] [CrossRef] [Green Version]
- Sansom, J. A Hidden Markov Model for Rainfall Using Breakpoint Data. J. Clim. 1998, 11, 42–53. [Google Scholar] [CrossRef]
- Ailliot, P.; Thompson, C.; Thomson, P. Space-Time Modelling of Precipitation by Using a Hidden Markov Model and Censored Gaussian Distributions. J. R. Stat. Soc. Ser. C Appl. Stat. 2009, 58, 405–426. [Google Scholar] [CrossRef]
- Racsko, P.; Szeidl, L.; Semenov, M. A serial approach to local stochastic weather models. Ecol. Model. 1991, 57, 27–41. [Google Scholar] [CrossRef]
- Zheng, X.; Katz, R.W. Mixture Model of Generalized Chain-Dependent Processes and Its Application to Simulation of Interannual Variability of Daily Rainfall. J. Hydrol. 2008, 349, 191–199. [Google Scholar] [CrossRef]
- Hannachi, A. Intermittency, Autoregression and Censoring: A First-Order AR Model for Daily Precipitation. Meteorol. Appl. 2014, 21, 384–397. [Google Scholar] [CrossRef]
- Khan, R.S.; Abul, M.; Bhuiyan, E.; Khan, R.S.; Bhuiyan, M.A.E.; García-Ortega, E.; Rigo, T. Artificial Intelligence-Based Techniques for Rainfall Estimation Integrating Multisource Precipitation Datasets. Atmosphere 2021, 12, 1239. [Google Scholar] [CrossRef]
- Chiang, Y.M.; Chang, F.J.; Jou, B.J.D.; Lin, P.F. Dynamic ANN for Precipitation Estimation and Forecasting from Radar Observations. J. Hydrol. 2007, 334, 250–261. [Google Scholar] [CrossRef]
- Cachim, P. ANN Prediction of Fire Temperature in Timber. J. Struct. Fire Eng. 2019, 10, 233–244. [Google Scholar] [CrossRef]
- Li, X.; Li, Z.; Huang, W.; Zhou, P. Performance of Statistical and Machine Learning Ensembles for Daily Temperature Downscaling. Theor. Appl. Climatol. 2020, 140, 571–588. [Google Scholar] [CrossRef]
- Bochenek, B.; Ustrnul, Z. Machine Learning in Weather Prediction and Climate Analyses—Applications and Perspectives. Atmosphere 2022, 13, 180. [Google Scholar] [CrossRef]
- Oses, N.; Azpiroz, I.; Marchi, S.; Guidotti, D.; Quartulli, M.; Olaizola, I.G. Analysis of Copernicus’ Era5 Climate Reanalysis Data as a Replacement for Weather Station Temperature Measurements in Machine Learning Models for Olive Phenology Phase Prediction. Sensors 2020, 20, 6381. [Google Scholar] [CrossRef]
- Hernández-Bedolla, J.; Solera, A.; Paredes-Arquiola, J.; Pedro-Monzonís, M.; Andreu, J.; Sánchez-Quispe, S. The Assessment of Sustainability Indexes and Climate Change Impacts on Integrated Water Resource Management. Water 2017, 9, 213. [Google Scholar] [CrossRef] [Green Version]
- Tang, Y.; Zeng, G.; Yang, X.; Iyakaremye, V.; Li, Z. Intraseasonal Oscillation of Summer Extreme High Temperature in Northeast China and Associated Atmospheric Circulation Anomalies. Atmosphere 2022, 13, 387. [Google Scholar] [CrossRef]
- Yang, Q. Extended-Range Forecast for the Low-Frequency Oscillation of Temperature and Low-Temperature Weather over the Lower Reaches of the Yangtze River in Winter. Chin. J. Atmos. Sci. 2021, 45, 21–36. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. A Daily Stochastic Weather Generator for Preserving Low-Frequency of Climate Variability. J. Hydrol. 2010, 388, 480–490. [Google Scholar] [CrossRef]
- Hansen, J.W.; Mavromatis, T. Correcting Low-Frequency Variability Bias in Stochastic Weather Generators. Agric. For. Meteorol. 2001, 109, 297–310. [Google Scholar] [CrossRef]
- Chen, J.; Arsenault, R.; Brissette, F.P.; Côté, P.; Su, T. Coupling Annual, Monthly and Daily Weather Generators to Simulate Multisite and Multivariate Climate Variables with Low—Frequency Variability for Hydrological Modelling. Clim. Dyn. 2019, 53, 3841–3860. [Google Scholar] [CrossRef]
- Apipattanavis, S.; Podestá, G.; Rajagopalan, B.; Katz, R.W. A Semiparametric Multivariate and Multisite Weather Generator. Water Resour. Res. 2007, 43, W11401. [Google Scholar] [CrossRef]
- Li, X.; Babovic, V. A New Scheme for Multivariate, Multisite Weather Generator with Inter-Variable, Inter-Site Dependence and Inter-Annual Variability Based on Empirical Copula Approach. Clim. Dyn. 2019, 52, 2247–2267. [Google Scholar] [CrossRef]
- Ghosh Dastidar, A.; Ghosh, D.; Dasgupta, S.; De, U.K. Higher Order Markov Chain Models for Monsoon Rainfall over West Bengal, India. Indian J. Radio Space Phys. 2010, 39, 39–44. [Google Scholar]
- Hosseini, R.; Le, N.; Zidek, J. Selecting a Binary Markov Model for a Precipitation Process. Environ. Ecol. Stat. 2011, 18, 795–820. [Google Scholar] [CrossRef]
- Lennartsson, J.; Baxevani, A.; Chen, D. Modelling Precipitation in Sweden Using Multiple Step Markov Chains and a Composite Model. J. Hydrol. 2008, 363, 42–59. [Google Scholar] [CrossRef] [Green Version]
- Otienoongála, J.; Ster, D.; Stern, R. Extending Genstat Capability to Analyze Rainfall Data Using a Markov Chain Model. Eur. Sci. J. August Ed. 2012, 8, 1857–7881. [Google Scholar]
- Chen, J.; Brissette, F.P. Stochastic Generation of Daily Precipitation Amounts: Review and Evaluation of Different Models. Clim. Res. 2014, 59, 189–206. [Google Scholar] [CrossRef] [Green Version]
- Woolhiser, D.A.; Pegram, G.G.S. Maximum Likelihood Estimation of Fourier Coefficients to Describe Seasonal Variations of Parameters in Stochastic Daily Precipitation Models. J. Appl. Meteorol. 1979, 18, 34–42. [Google Scholar] [CrossRef]
- Keller, D.E.; Fischer, A.M.; Frei, C.; Liniger, M.A.; Appenzeller, C.; Knutti, R. Implementation and Validation of a Wilks-Type Multi-Site Daily Precipitation Generator over a Typical Alpine River Catchment. Hydrol. Earth Syst. Sci. 2015, 19, 2163–2177. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P. Comparison of Five Stochastic Weather Generators in Simulating Daily Precipitation and Temperature for the Loess Plateau of China. Int. J. Climatol. 2014, 34, 3089–3105. [Google Scholar] [CrossRef]
- Sakia, R.M. The Box-Cox Transformation Technique: A review. J. R. Stat. Soc. 1992, 41, 169–178. [Google Scholar] [CrossRef]
- Anderson, R.L. Distribution of the Serial Correlation Coefficient. Ann. Math. Stat. 1942, 13, 1–13. [Google Scholar] [CrossRef]
- Moors, D. Stubblebine Chi-Square Tests for multivariate normality with application to common Stock prices. Comun. Stat. -Theory Methods 1981, 10, 713–738. [Google Scholar] [CrossRef]
- Hu, S. Akaike Information Criterion Statistics. Math. Comput. Simul. 1987, 29, 452. [Google Scholar] [CrossRef]
- Pedro-Monzonís, M.; Ferrer, J.; Solera, A.; Estrela, T.; Paredes-Arquiola, J. Key Issues for Determining the Exploitable Water Resources in a Mediterranean River Basin. Sci. Total Environ. 2015, 503–504, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Martín, M.A.; Thurston, W.; Estrela, T.; del Amo, P. Cambio En Las Series Hidrológicas de Los Últimos 30 Años y Sus Causas. El Efecto 80. III Jorn. Ing. Agua (JIA 2013). La Protección Contra Los Riesgos Hídricos 2013, 2, 527–534. [Google Scholar]
- CHJ Plan Hidrológico de La Demarcación Hidrográfica Del Júcar, Memoria-Anejo 2. CJH, Valencia, España. 2015. Available online: https://www.chj.es/es-es/medioambiente/planificacionhidrologica/Paginas/PHC-2015-2021-Plan-Hidrologico-cuenca.aspx (accessed on 10 December 2021).
- Herrera, S.; Fernández, J.; Gutiérrez, J.M. Update of the Spain02 Gridded Observational Dataset for EURO-CORDEX Evaluation: Assessing the Effect of the Interpolation Methodology. Int. J. Climatol. 2016, 36, 900–908. [Google Scholar] [CrossRef] [Green Version]
- Daly, C. Guidelines for Assessing the Suitability of Spatial Climate Data Sets. Int. J. Climatol. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Pérez-Martín, M.A.; Estrela, T.; Andreu, J.; Ferrer, J.; Pérez-Martín, M.A.; Andreu, J.; Estrela, T.; Ferrer, J. Modeling Water Resources and River-Aquifer Interaction in the Júcar River Basin, Spain. Water Resour. Manag. 2014, 28, 4337–4358. [Google Scholar] [CrossRef]
- Melsen, L.; Teuling, A.; Torfs, P.; Zappa, M.; Mizukami, N.; Clark, M.; Uijlenhoet, R. Representation of Spatial and Temporal Variability in Large-Domain Hydrological Models: Case Study for a Mesoscale Pre-Alpine Basin. Hydrol. Earth Syst. Sci. 2016, 20, 2207–2226. [Google Scholar] [CrossRef]
- Parlange, M.B.; Katz, R.W.; Parlange, M.B.; Katz, R.W. An Extended Version of the Richardson Model for Simulating Daily Weather Variables. J. Appl. Meteorol. 2000, 39, 610–622. [Google Scholar] [CrossRef]







| Sub-Basin | Wet Day Threshold (mm) | |||
|---|---|---|---|---|
| 0.001 * | 0.01 | 0.10 | 0.25 | |
| Alarcon | −590.2 | −515.3 | −362.2 | −310.9 |
| Contreras | −681.5 | −551.2 | −459.5 | −421.3 |
| Molinar | −562.3 | −420.7 | −261.2 | −215.1 |
| Tous | −587.4 | −463.6 | −380.5 | −340.0 |
| Huerto Mulet | −610.5 | −554.7 | −467.3 | −427.3 |
| Model | Statistical/Sub-Basin | Alarcon | Contreras | Molinar | Tous | Huerto Mulet |
|---|---|---|---|---|---|---|
| 1 * | Mean | −6.7 × 10−5 | −2.0 × 10−4 | 7.5 × 10−5 | −2.6 × 10−4 | 5.6 × 10−5 |
| Deviation | 0.842 | 0.821 | 0.834 | 0.812 | 0.850 | |
| Skewness coefficient | −0.185 | −0.242 | −0.245 | −0.089 | 0.026 | |
| Lag-one autocorrelation | 0.005 | 0.003 | 0.009 | −0.041 | −0.042 | |
| AIC | −8369 | −9508 | −8814 | −10,152 | −7958 | |
| 2 ** | Mean | −3.09 × 10−4 | −5.98 × 10−4 | −6.83 × 10−5 | −2.70 × 10−4 | −2.65 × 10−4 |
| Deviation | 0.937 | 0.920 | 0.942 | 0.900 | 0.942 | |
| Skewness coefficient | −0.009 | −0.038 | −0.044 | 0.112 | −0.028 | |
| Lag-one autocorrelation | 0.036 | 0.043 | −0.030 | −0.082 | −0.039 | |
| AIC | −6471 | −8233 | −5957 | −10,294 | −5896 |
| Parameter | Model 1 (M1) | Model 2 (M2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | |
| RMSE (°C/day) | 1.881 | 1.107 | 1.392 | 1.156 | 0.767 | 1.786 | 1.019 | 1.290 | 1.078 | 0.780 |
| MAE (°C/day) | 1.503 | 0.820 | 1.092 | 0.896 | 0.572 | 1.455 | 0.773 | 1.021 | 0.852 | 0.582 |
| PE (%) | 0.043 | 0.027 | 0.017 | 0.031 | 0.021 | 0.035 | 0.049 | 0.040 | 0.025 | 0.012 |
| Maximum Temperature Cross-Correlation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Sub-Basin | Alarcon | Contreras | Molinar | Tous | Huerto M | * Alarcon | * Contreras | * Molinar | * Tous | * Huerto M |
| Alarcon | 1.000 | 1.000 | ||||||||
| Contreras | 0.833 | 1.000 | 0.834 | 1.000 | ||||||
| Molinar | 0.760 | 0.797 | 1.000 | 0.765 | 0.819 | 1.000 | ||||
| Tous | 0.239 | 0.492 | 0.598 | 1.000 | 0.243 | 0.489 | 0.610 | 1.000 | ||
| Huerto M | 0.223 | 0.371 | 0.390 | 0.802 | 1.000 | 0.230 | 0.377 | 0.398 | 0.800 | 1.000 |
| Temperature Range Cross-Correlation | ||||||||||
| Sub-Basin | Alarcon | Contreras | Molinar | Tous | Huerto M | * Alarcon | * Contreras | * Molinar | * Tous | * Huerto M |
| Alarcon | 1.000 | 1.000 | ||||||||
| Contreras | 0.719 | 1.000 | 0.718 | 1.000 | ||||||
| Molinar | 0.891 | 0.592 | 1.000 | 0.895 | 0.590 | 1.000 | ||||
| Tous | 0.563 | 0.494 | 0.754 | 1.000 | 0.565 | 0.499 | 0.759 | 1.000 | ||
| Huerto M | 0.504 | 0.331 | 0.710 | 0.918 | 1.000 | 0.502 | 0.333 | 0.708 | 0.917 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hernández-Bedolla, J.; Solera, A.; Paredes-Arquiola, J.; Sanchez-Quispe, S.T.; Domínguez-Sánchez, C. A Continuous Multisite Multivariate Generator for Daily Temperature Conditioned by Precipitation Occurrence. Water 2022, 14, 3494. https://doi.org/10.3390/w14213494
Hernández-Bedolla J, Solera A, Paredes-Arquiola J, Sanchez-Quispe ST, Domínguez-Sánchez C. A Continuous Multisite Multivariate Generator for Daily Temperature Conditioned by Precipitation Occurrence. Water. 2022; 14(21):3494. https://doi.org/10.3390/w14213494
Chicago/Turabian StyleHernández-Bedolla, Joel, Abel Solera, Javier Paredes-Arquiola, Sonia Tatiana Sanchez-Quispe, and Constantino Domínguez-Sánchez. 2022. "A Continuous Multisite Multivariate Generator for Daily Temperature Conditioned by Precipitation Occurrence" Water 14, no. 21: 3494. https://doi.org/10.3390/w14213494






