HYPROP-FIT to Model Rock Water Retention Curves Estimated by Different Methods
Abstract
1. Introduction
2. Materials and Methods
2.1. The Suction Table Method
2.2. The Evaporation Method
2.3. The Quasi-Steady Centrifuge (QSC)
2.4. Dewpoint Potentiometer
2.5. Model
3. Results and Discussion
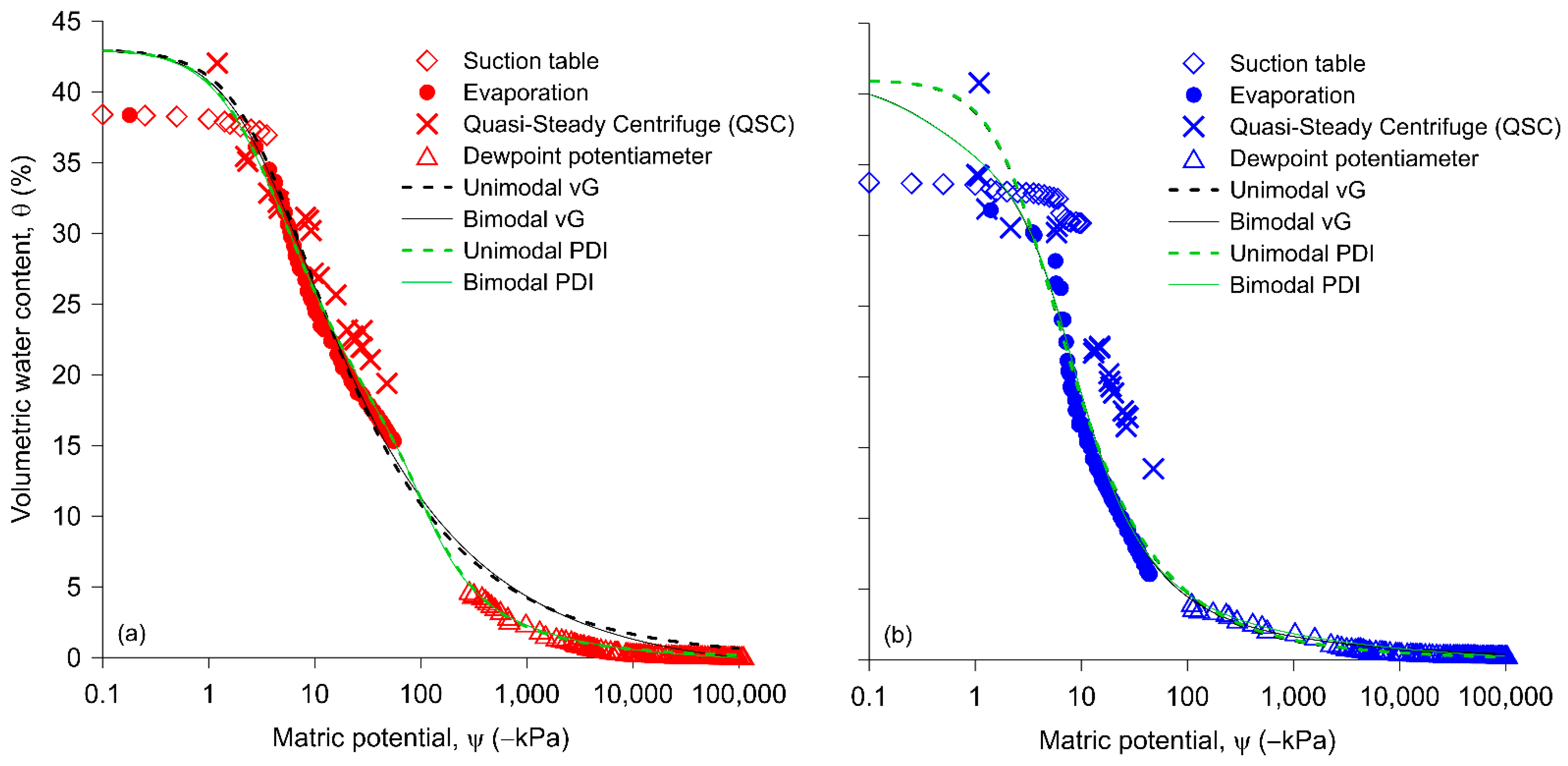
3.1. Rock Water Retention Data
3.2. Fitting Functions and Statistical Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Šimůnek, J.; Nimmo, J.R. Estimating soil hydraulic parameters from transient flow experiments in a centrifuge using parameter optimization technique. Water Resour. Res. 2005, 41, 9. [Google Scholar] [CrossRef]
- Rouxel, M.; Ruiz, L.; Molénat, J.; Hamon, Y.; Chirié, G.; Michot, D. Experimental Determination of Hydrodynamic Properties of Weathered Granite. Vadose Zone J. 2012, 11, vzj2011-0076. [Google Scholar] [CrossRef]
- Luquot, L.; Rötting, T.S.; Carrera, J. Characterization of flow parameters and evidence of pore clogging during limestone dissolution experiments. Water Resour. Res. 2014, 50, 6305–6321. [Google Scholar] [CrossRef]
- Rötting, T.S.; Luquot, L.; Carrera, J.; Casalinuovo, D.J. Changes in porosity, permeability, water retention curve and reactive surface area during carbonate rock dissolution. Chem. Geol. 2015, 403, 86–98. [Google Scholar] [CrossRef]
- Al-Mukhtar, M.; Beck, K.; Van, T.; Vanapalli, S. Water retention characteristics of two limestones. Geotech Spec. Pub. 2006, 147, 1833–1844. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sc. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 517–532. [Google Scholar] [CrossRef]
- Koubaa, Y.; Jamei, M.; Guiras, H. Hydro-mechanical properties of highly porous limestone rock used for historic monuments in North-East Tunisia. J. Civil Environ. Eng. 2018, 8, 11. [Google Scholar] [CrossRef]
- Pirastru, M.; Niedda, M. Field monitoring and dual permeability modelling of water flow through unsaturated calcareous rocks. J. Hydrol. 2010, 392, 40–53. [Google Scholar] [CrossRef]
- Lipovetsky, T.; Zhuang, L.; Teixeira, W.G.; Boyd, A.; Pontedeiro, E.M.; Moriconi, L.; Alves, J.L.D.; Couto, P.; van Genuchten, M.T. HYPROP measurements of the unsaturated hydraulic properties of a carbonate rock sample. J. Hydrol. 2020, 591, 125706. [Google Scholar] [CrossRef]
- Andriani, G.F.; Walsh, N. The effects of wetting and drying, and marine salt crystallization on calcarenite rocks used as building material in historic monuments. Geol. Soc. Lond. Spec. Publ. 2007, 271, 179–188. [Google Scholar] [CrossRef]
- Andriani, G.F.; Walsh, N. Petrophysical and mechanical properties of soft and porous building rocks used in Apulian monuments (south Italy). Geol. Soc. Lond. Spec. Publ. 2010, 333, 129–141. [Google Scholar] [CrossRef]
- Tropeano, M.; Sabato, L. Filling and cannibalization of a foredeep: The Bradanic Trough, Southern Italy. Geol. Soc. London Spec. Pub. 2002, 191, 55–79. [Google Scholar] [CrossRef]
- Turturro, A.C.; Caputo, M.C.; Gerke, H.H. Mercury intrusion porosimetry and centrifuge methods for extended-range retention curves of soil and porous rock samples. Vadose Zone J. 2021, 21, e20176. [Google Scholar] [CrossRef]
- Stakman, W.P.; Valk, G.A.; van der Harst, G.G. Determination of Soil Moisture Retention Curves, I, 3rd ed.; Institute for Land and Water Management Research: Wageningen, The Netherlands, 1969. [Google Scholar]
- Wind, G.P. Capillary conductivity data estimated by a simple method. In Water in Unsaturated Zone, Proceedings of the Wageningen Symposium; Rijtema, P.E., Wassink, H., Eds.; IASH Gentbrugge/UNESCO: Paris, France, 1968; Volume 1, pp. 181–191. [Google Scholar]
- Young, M.H.; Sisson, J. Tensiometry. In Methods of Soil Analysis. Part 4: Physical Methods; Dane, J.H., Topp, C.G., Eds.; SSSA: Madison, WI, USA, 2002; pp. 600–620. [Google Scholar] [CrossRef]
- Caputo, M.C.; Nimmo, J.R. Quasi-steady centrifuge method of unsaturated hydraulic properties. Water Resour. Res. 2005, 41, W11504. [Google Scholar] [CrossRef]
- Campbell, G.S.; Smith, D.M.; Teare, B.L. Application of a dew point method to obtain the soil water characteristic. In Experimental Unsaturated Soil Mechanics; Schanz, T., Ed.; Springer Proceedings in Physics: Berlin, Germany, 2007; Volume 112, pp. 71–77. [Google Scholar] [CrossRef]
- Priesak, E.; Durner, W. Closed-form expression for the multi-modal unsaturated conductivity function. Vadose Zone J. 2006, 5, 121–124. [Google Scholar] [CrossRef]
- Pertassek, T.; Peters, A.; Durner, W. HYPROP-FIT Software User’s Manual, V.3.0; UMS GmbH: München, Germany, 2015; 66p. [Google Scholar]
- Haghverdi, A.; Najarchi, M.; Öztürk, H.S.; Durner, W. Studying unimodal, bimodal, PDI and bimodal-PDI variants of multiple soil water retention models: I. Direct model fit using the extended evaporation and dewpoint methods. Water 2020, 12, 900. [Google Scholar] [CrossRef]
- Schneider, M.; Goss, K.U. Prediction of the water sorption isotherm in air dry soils. Geoderma 2012, 170, 64–69. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Zhang, Q.; Fan, D.; Yao, J. Numerical Investigation of the Effect of Partially Propped Fracture Closure on Gas Production in Fractured Shale Reservoirs. Energies 2020, 13, 5339. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, X.; Li, Z. A mathematical framework for multiphase poromechanics in multiple porosity media. Computers and Geotechnics 2022, 146, 104728. [Google Scholar] [CrossRef]


| Lithotype | C * | M * |
|---|---|---|
| Bulk density, ρb (g/cm3) | 1.50 | 1.56 |
| Particle density, ρp (g/cm3) | 2.65 | 2.65 |
| Porosity, Φ | 0.43 | 0.41 |
| Parameter (Unit) | C | M | ||||||
|---|---|---|---|---|---|---|---|---|
| Unimodal vG | Bimodal vG | Unimodal PDI | Bimodal PDI | Unimodal vG | Bimodal vG | Unimodal PDI | Bimodal PDI | |
| α (1/cm) | 0.028 | - | 0.0298 | - | 0.0329 | - | 0.0329 | - |
| n | 1.41 | - | 1.389 | - | 1.626 | - | 1.635 | - |
| θr (cm3/cm3) | 0.001 | 0.0001 | 0.001 | 0.0001 | 0.003 | 0.0001 | 0.008 | 0.0001 |
| θs (cm3/cm3) | 0.432 * | 0.432 * | 0.432 * | 0.432 * | 0.410 * | 0.410 * | 0.410 * | 0.410 * |
| w2 | - | 0.225 | - | 0.791 | - | 0.655 | - | 0.385 |
| α1 (1/cm) α2 (1/cm) | - | 0.0389 0.00117 | - | 0.00113 0.0391 | - | 0.5 0.0169 | - | 0.0165 0.5 |
| n1 n2 | - | 1.492 2.263 | - | 2.379 1.473 | - | 1.267 1.944 | - | 2.017 1.233 |
| RMSEθ | 0.016 | 0.0118 | 0.016 | 0.0118 | 0.0223 | 0.0207 | 0.0224 | 0.0207 |
| AICc | −1657 | −1773 | −1657 | −1774 | −1553 | −1577 | −1552 | −1578 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caputo, M.C.; De Carlo, L.; Turturro, A.C. HYPROP-FIT to Model Rock Water Retention Curves Estimated by Different Methods. Water 2022, 14, 3443. https://doi.org/10.3390/w14213443
Caputo MC, De Carlo L, Turturro AC. HYPROP-FIT to Model Rock Water Retention Curves Estimated by Different Methods. Water. 2022; 14(21):3443. https://doi.org/10.3390/w14213443
Chicago/Turabian StyleCaputo, Maria Clementina, Lorenzo De Carlo, and Antonietta Celeste Turturro. 2022. "HYPROP-FIT to Model Rock Water Retention Curves Estimated by Different Methods" Water 14, no. 21: 3443. https://doi.org/10.3390/w14213443
APA StyleCaputo, M. C., De Carlo, L., & Turturro, A. C. (2022). HYPROP-FIT to Model Rock Water Retention Curves Estimated by Different Methods. Water, 14(21), 3443. https://doi.org/10.3390/w14213443








