Triggering Rainfall of Large-Scale Landslides in Taiwan: Statistical Analysis of Satellite Imagery for Early Warning Systems
Abstract
:1. Introduction
2. Literature Review
2.1. Occurrence Mechanism-Related Research
2.2. Monitoring-Related Research
- On-site monitoring
- 2.
- Remote Sensing
2.3. Early Warning-Related Research
- Early warning indicators
- comprehensive indicators [59].
- 2.
- Early warning management values
- 3.
- Real-time simulation
3. Materials and Methods
3.1. Case Collection and Screening
3.2. Case Confirmation, Area Size, and Average Slope Identification of LSL
3.3. The Occurrence Time Confirmation of LSL
3.4. The Triggering Rainfall Analysis
- is the triggering rainfall for LSL (mm);
- is the accumulated rainfall from the beginning of the rainfall event that caused the LSL to the moment the landslide occurred (mm);
- is the antecedent rainfall (mm) ;
- is the rainfall on the i-th day (24 h) before the start of the rain field (mm);
- is the number of days to consider the antecedent rainfall (), generally N = 7;
- is the daily (24 h) rainfall triggering landslide decay coefficient (), which can be 0.7 or 0.8. At present, α = 0.7 is used in this study to calculate the antecedent rainfall [62].
3.5. The Linear Regression Analysis
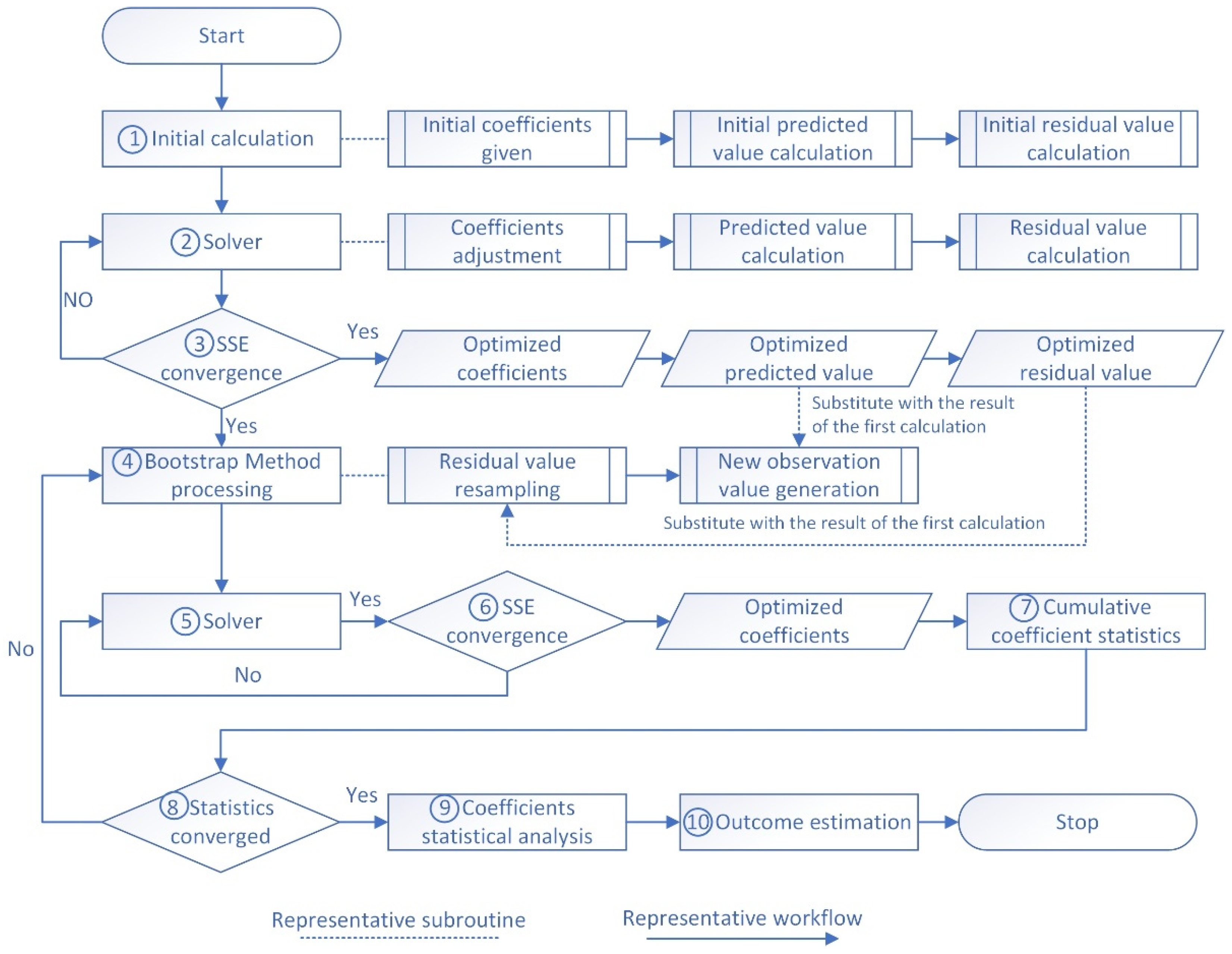
3.6. The Nonlinear Regression Analysis
- Step 1.
- Initial calculation
- is the residual of the i-th data [],
- is the landslide thickness of the i-th prediction (m),
- is the landslide thickness of the i-th observation (m),
- is the total number of observations ().
- Step 2.
- Solver
- Step 3.
- SSE convergence
- Step 4.
- Bootstrap method processing
- Step 5.
- Solver
- Step 6.
- SSE convergence
- Step 7.
- Cumulative coefficient statistics
- is coefficient of variation of the specific coefficient from the 1st to the j-th bootstrap resampling [],
- is the standard deviation of the specific coefficient from the 1st to the j-th bootstrap resampling [],
- is the average value of the specific coefficient from the 1st to the j-th bootstrap resampling [].
- Step 8.
- Statistics converged
- Step 9.
- Coefficient statistical analysis
- Step 10.
- Outcome estimation
4. Results
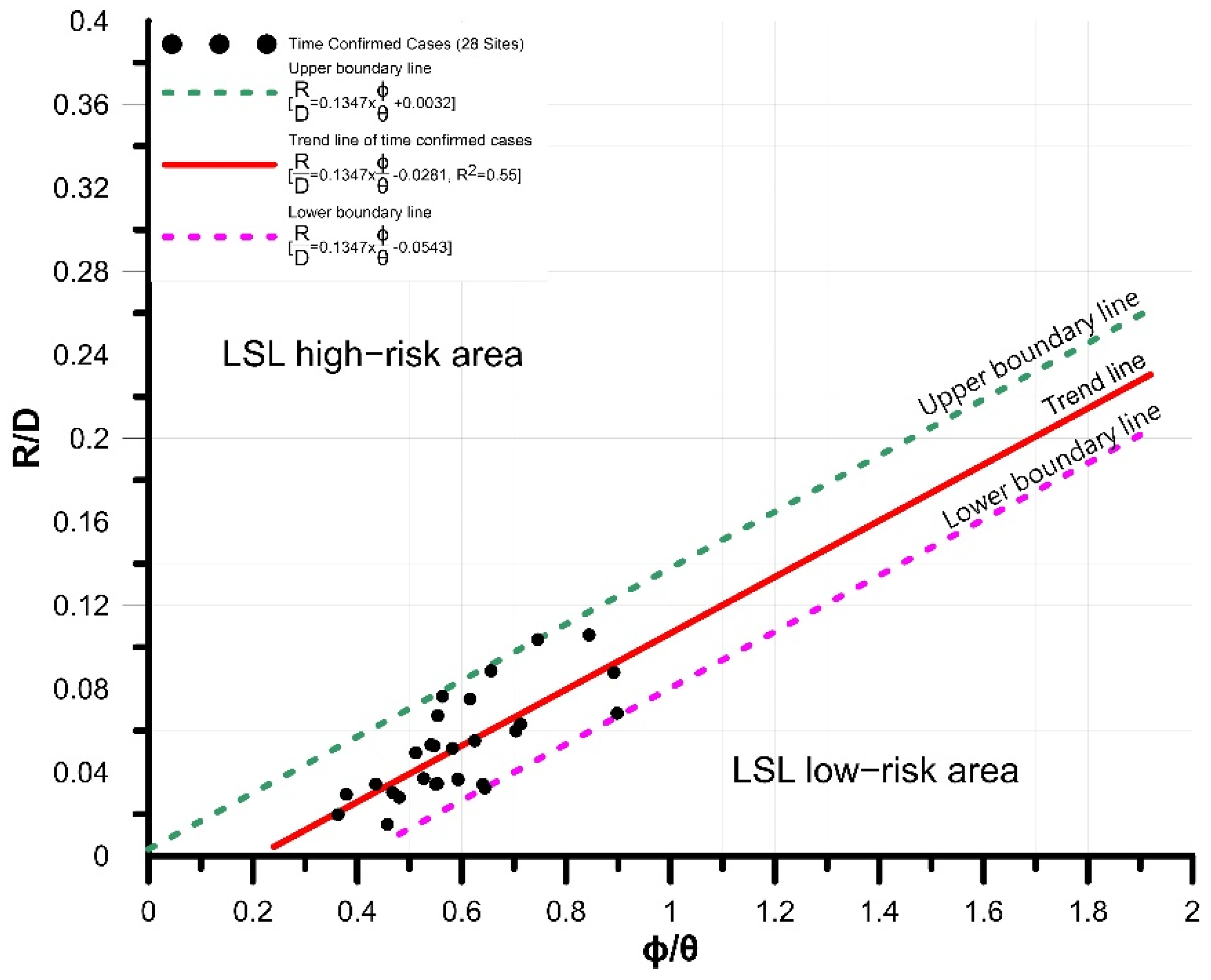
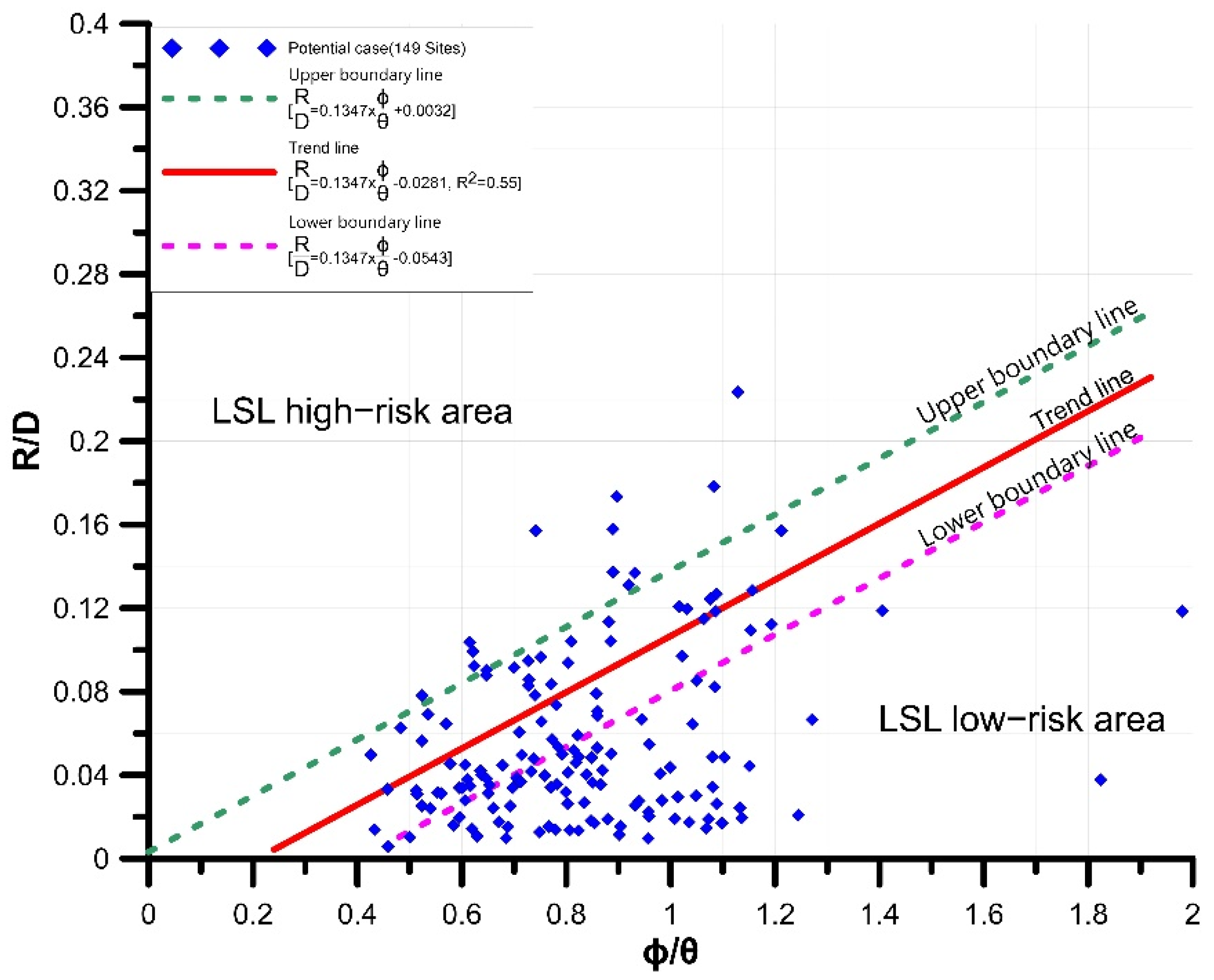
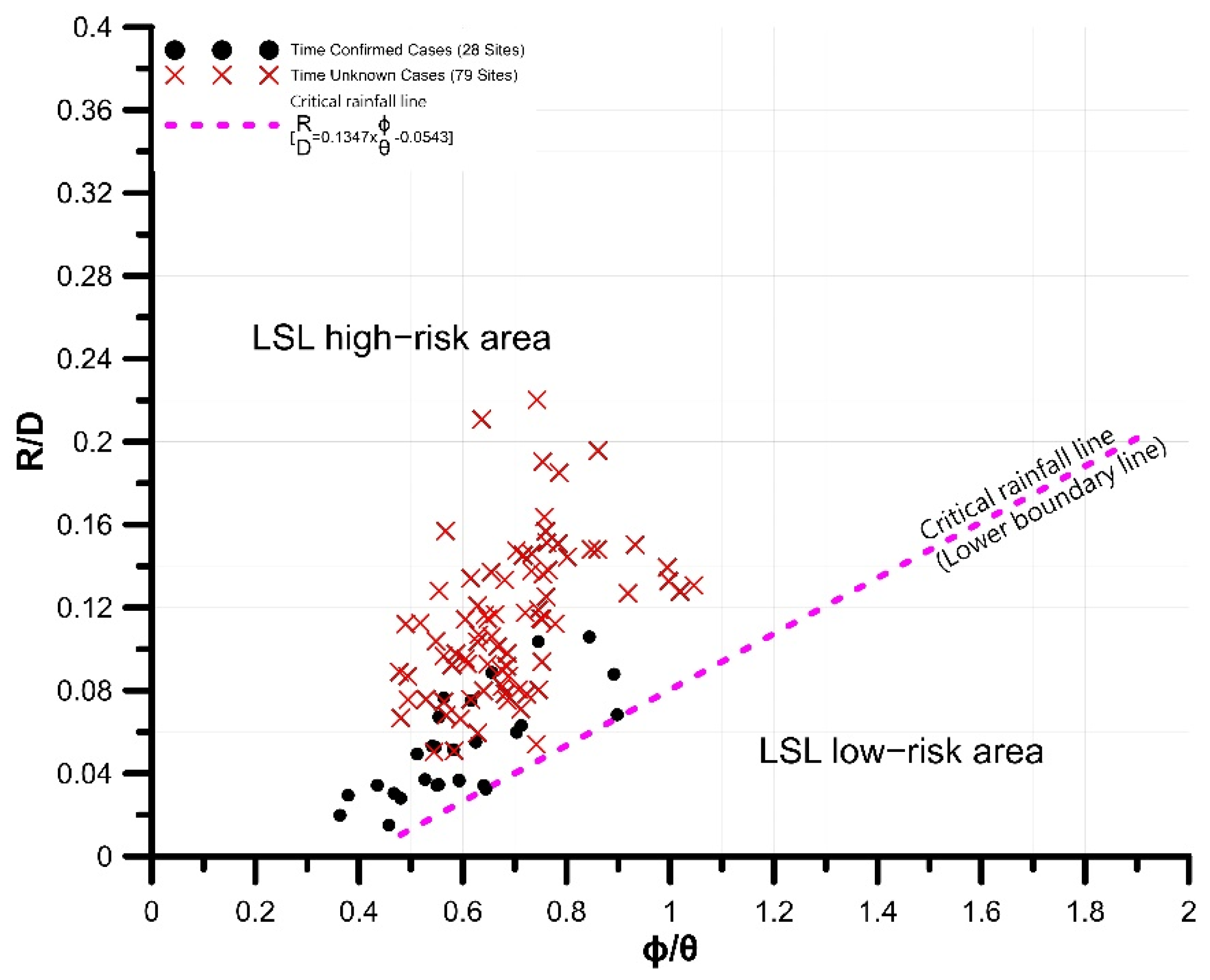
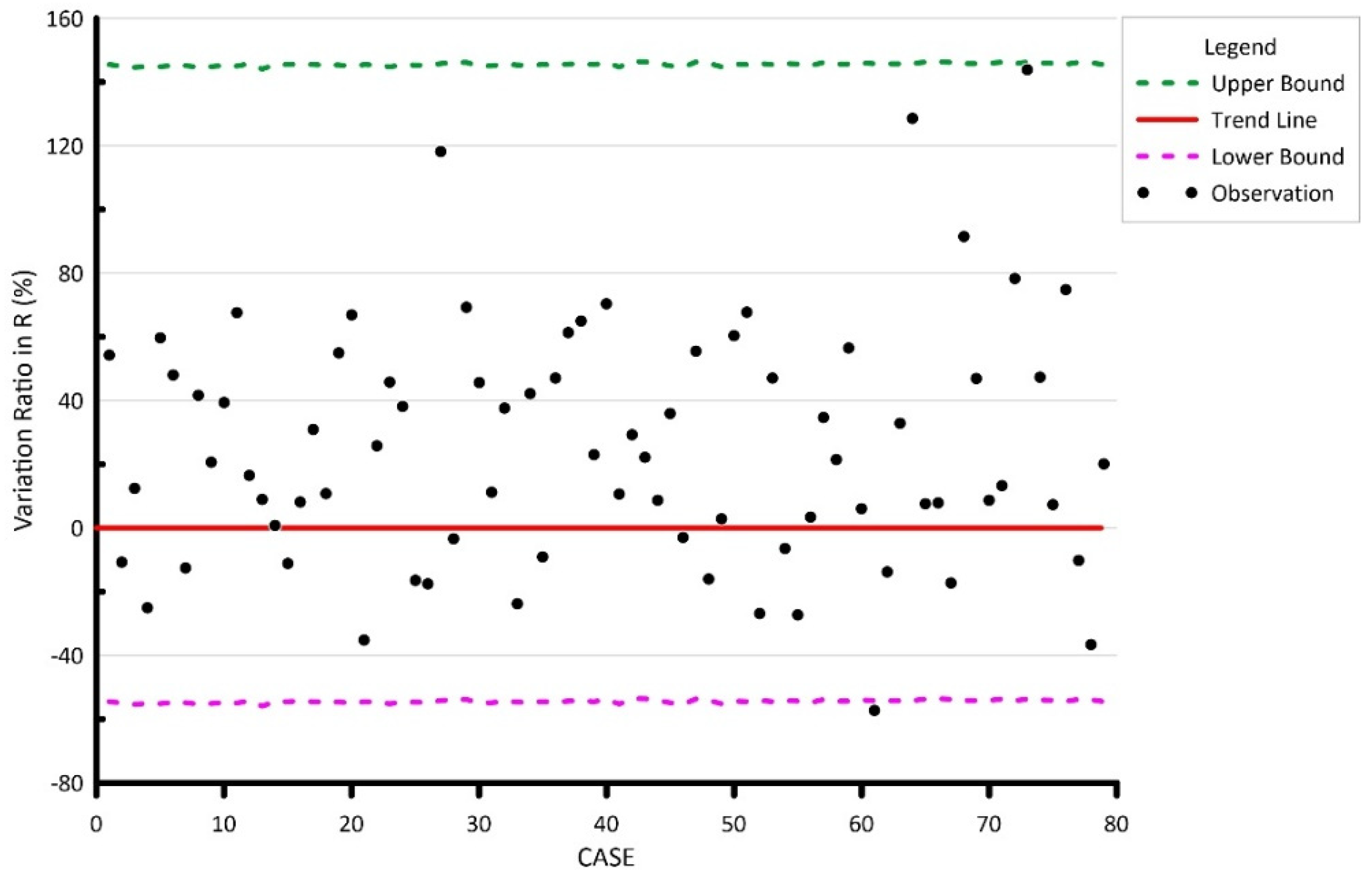
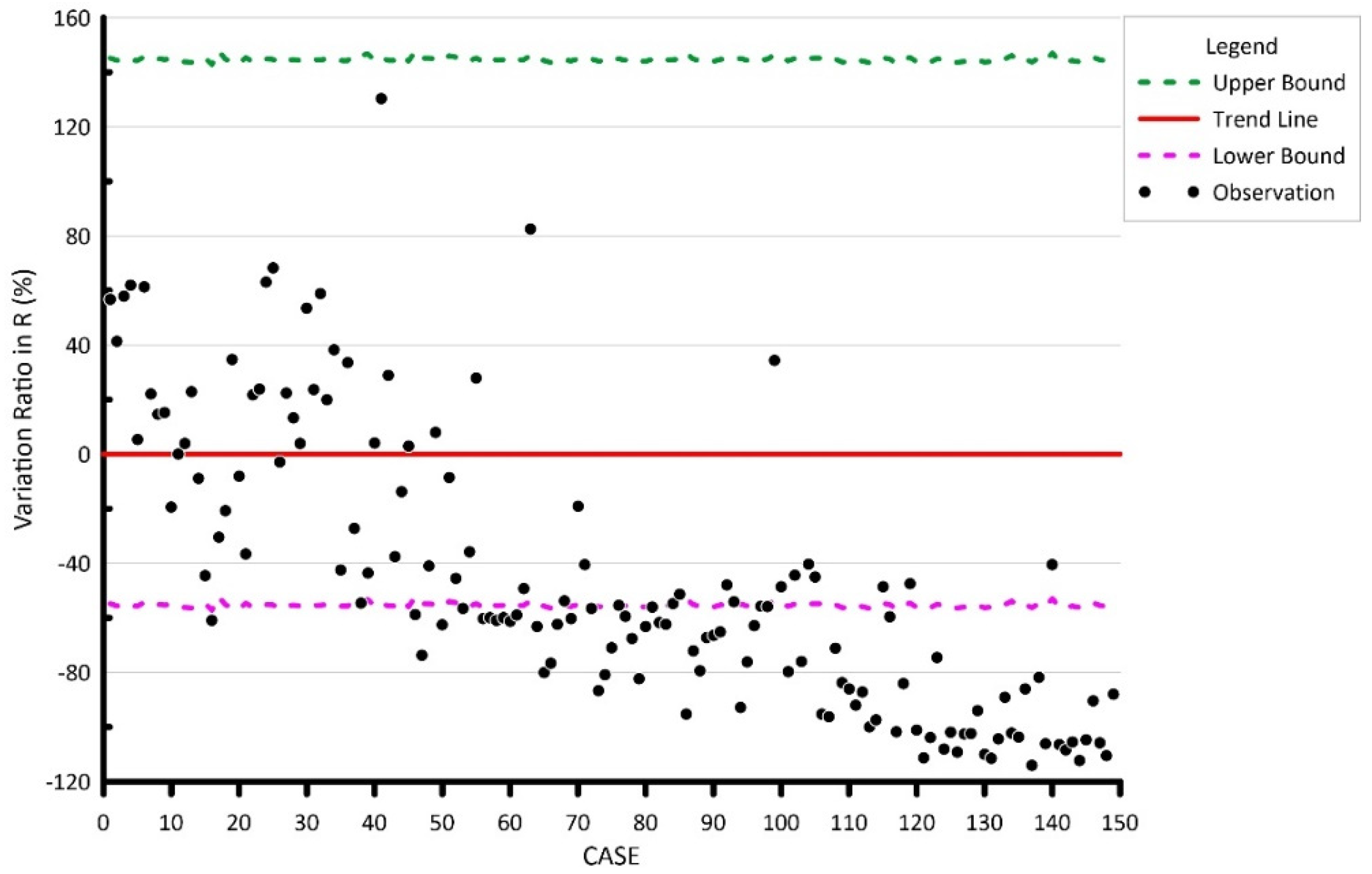
4.1. Linear Regression Analysis Results
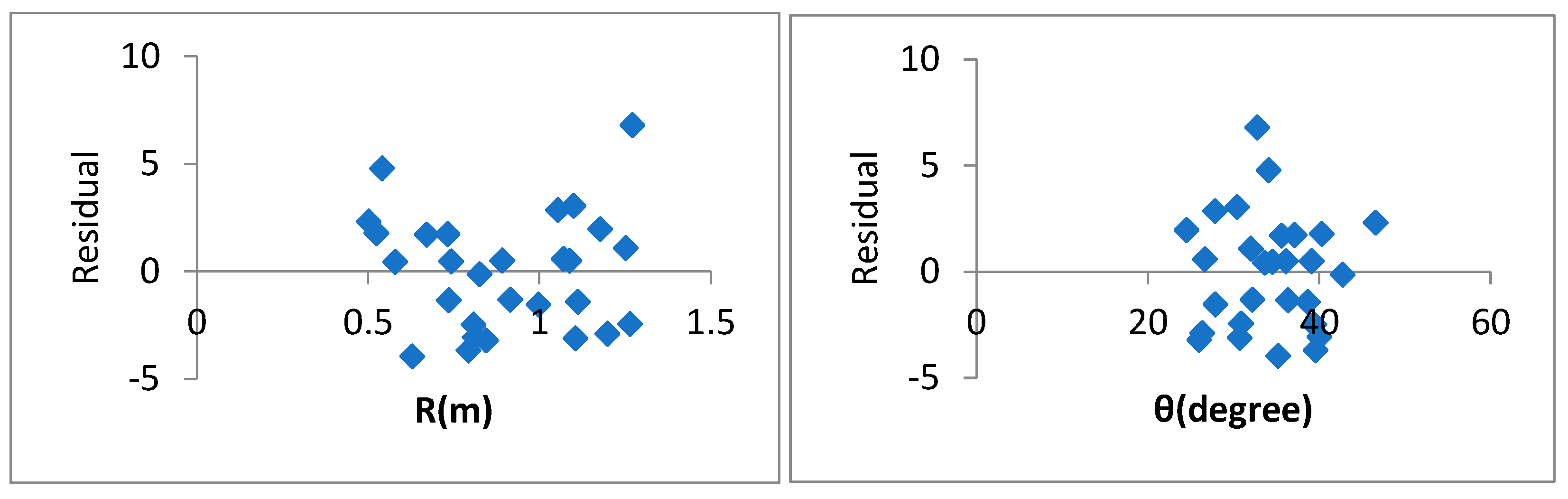
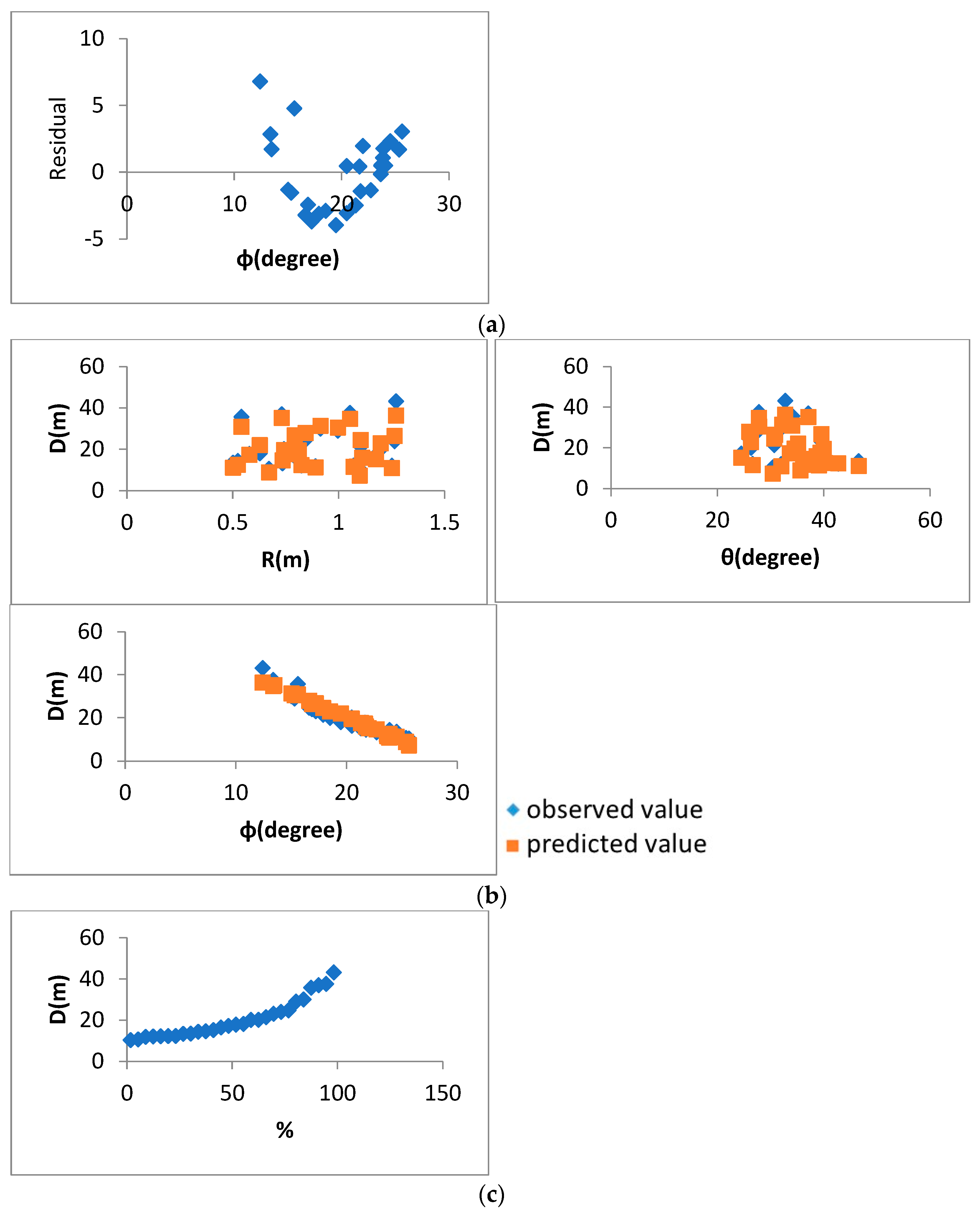
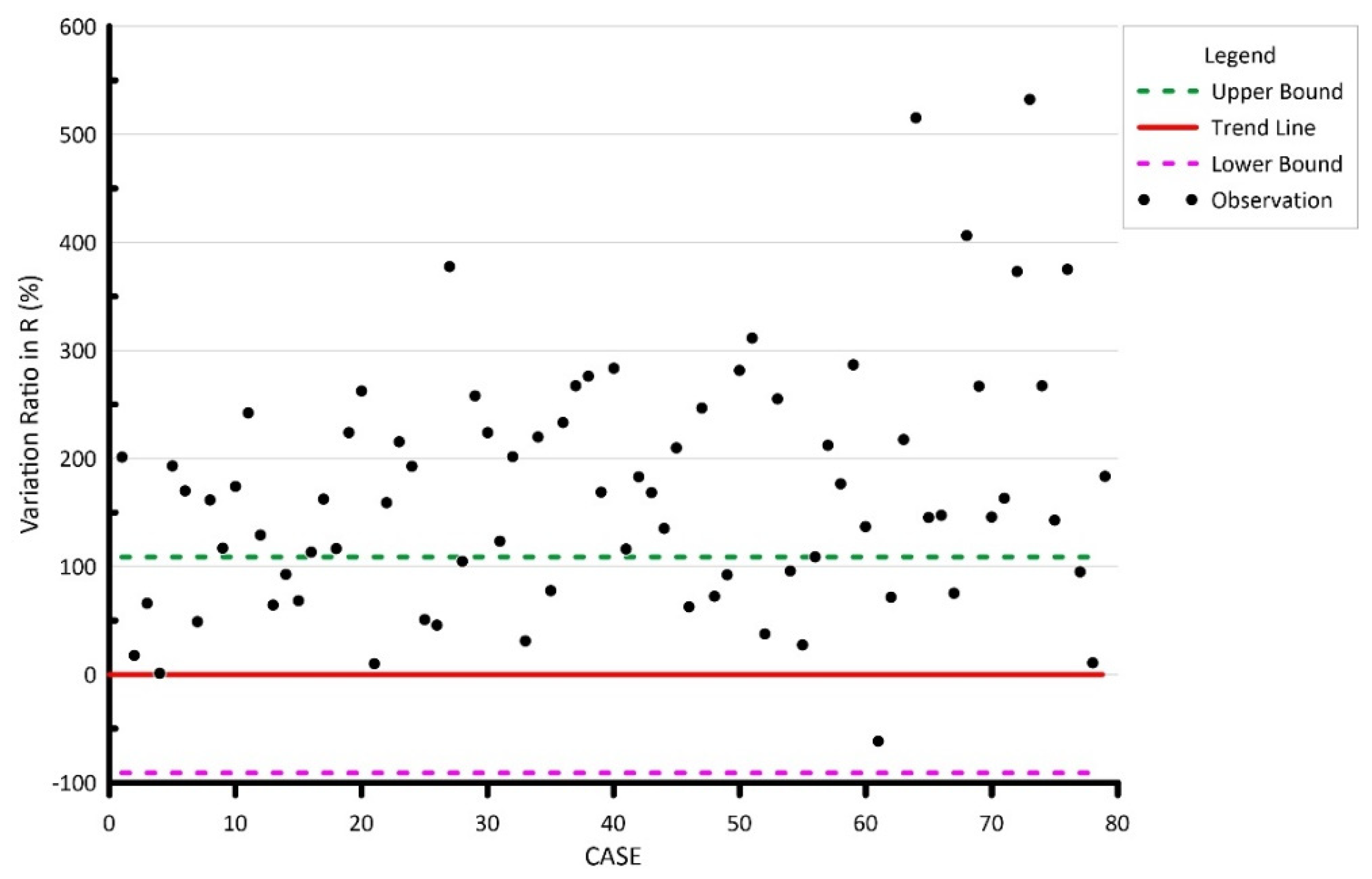
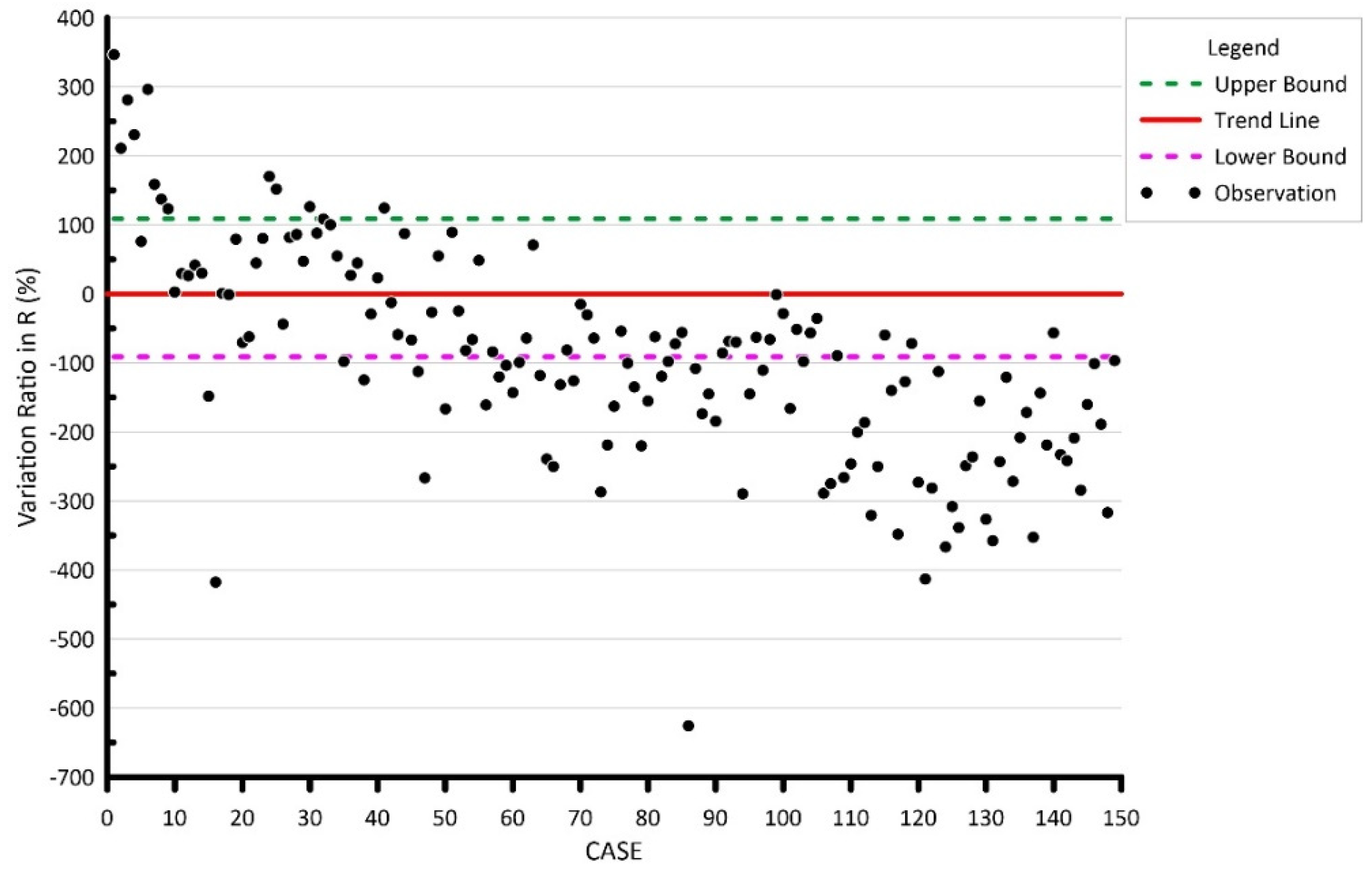
4.2. Nonlinear Regression Analysis Results
5. Discussion
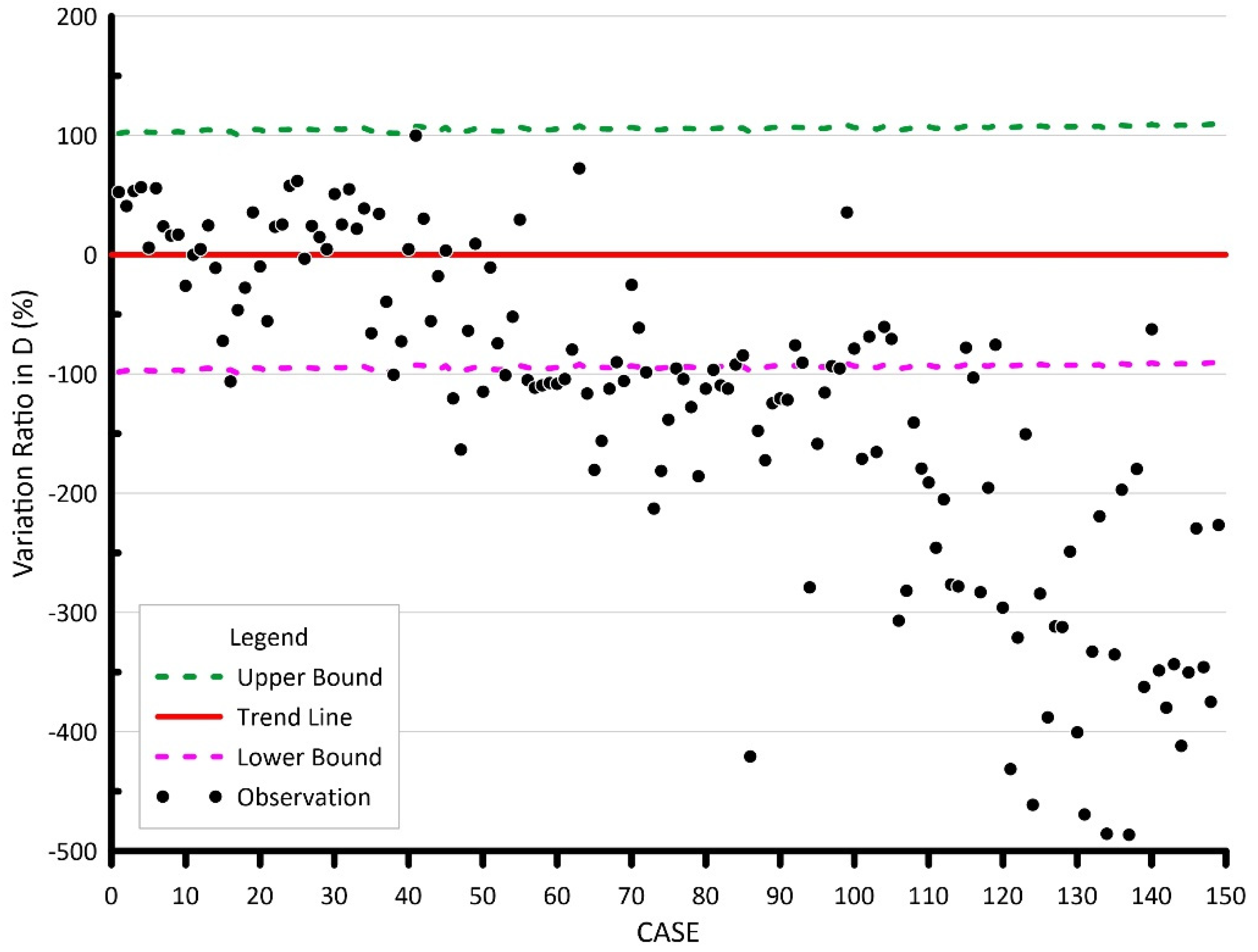
5.1. Prediction Ability
- is the predicted rainfall by the linear regression trend line (m),
- is the predicted rainfall by the linear regression upper boundary line (m),
- is the predicted rainfall by the linear regression lower boundary line (m),
- is the predicted rainfall by the nonlinear regression trend line (m),
- is the predicted rainfall by the nonlinear regression upper boundary line (m),
- is the predicted rainfall by the nonlinear regression lower boundary line (m).
5.2. Limitations
5.3. Early Warning Application
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shieh, C.-L.; Wang, C.-M.; Chen, Y.-S.; Tsai, Y.-J.; Tseng, W.-H. An overview of disasters resulted from Typhoon Morakot in Taiwan. J. Disaster Res. 2010, 5, 236–244. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Kuo, Y.-S.; Lai, W.-C.; Tsai, Y.-J.; Lee, S.-P.; Chen, K.-T.; Shieh, C.-L. Reflection of typhoon morakot—The challenge of compound disaster simulation. J. Mt. Sci. 2011, 8, 571–581. [Google Scholar] [CrossRef]
- Central Weather Bureau. Typhoon Database. Available online: https://rdc28.cwb.gov.tw/TDB/public/typhoon_detail?typhoon_id=200908 (accessed on 7 March 2022).
- Xiaolin Pingpu Cultural Museums. Typhoon Morakot Caused Flood. Available online: https://xiaolin.khcc.gov.tw/index.php?option=module&lang=cht&task=pageinfo&id=4&index=1 (accessed on 8 March 2022).
- National Science and Technology Center for Disaster Reduction. Action Plan for the Prevention and Control of Large-Scale Collapse Disasters; National Science and Technology Center for Disaster Reduction: Taipei, China, 2015. (In Chinese) [Google Scholar]
- Lee, W.-L. Research on Pore Water Pressure Changes during Infiltration and Its Impact on Slope Stability. Ph.D. Thesis, National Cheng Kung University, Tainan, Taiwan, 2020. (In Chinese). [Google Scholar]
- Kalatehjari, R.; Ali, N. A review of three-dimensional slope stability analyses based on limit equilibrium method. Electron. J. Geotech. Eng. 2013, 18, 119–134. [Google Scholar]
- Duncan, J.M.; Wright, S.G.; Brandon, T.L. Soil Strength and Slope Stability; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Lu, N.G.; Jonathan, W. Hillslope Hydrology and Stability; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1975, 15, 139–160. [Google Scholar] [CrossRef] [Green Version]
- Wilson, R.C.; Keefer, D.K. Dynamic analysis of a slope failure from the 6 August 1979 Coyote Lake, California, earthquake. Bull. Seismol. Soc. Am. 1983, 73, 863–877. [Google Scholar] [CrossRef]
- Culmann, K. Die Graphische Statik; Meyer & Zeller (A. Reimann): Zürich, Switzerland, 1875; Volume 1. (In German) [Google Scholar]
- William, E.; Dietrich, D.R.M. Shalstab. Available online: http://calm.geo.berkeley.edu/geomorph/shalstab/index.htm (accessed on 15 March 2022).
- Pack, R.T.; Tarboton, D.G.; Goodwin, C.; Prasad, A. SINMAP 2.0—A Stability Index Approach to Terrain Stability Hazard Mapping, User’s Manual. Available online: https://digitalcommons.usu.edu/cee_facpub/16/ (accessed on 15 September 2022).
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran program for transient rainfall infiltration and grid-based regional slope-stability analysis. In US Geological Survey Open-File Report; US Geological Survey: Reston, VA, USA, 2002. [Google Scholar]
- Survey, U.S.G. Scoops3D. Available online: https://www.usgs.gov/software/scoops3d (accessed on 27 May 2022).
- Brinkgreve, R.B.J. Plaxis Finite Element Code for Soil and Rock Analyses 2D—Version 8; Balkema Rotterdam: Rotterdam, The Netherlands, 2008. [Google Scholar]
- Miyamoto, K. Two dimensional numerical simulation of landslide mass movement. J. Eros. Control Eng. 2002, 55, 5–13. [Google Scholar]
- Itasca Consulting Group, Inc. PFC. Available online: https://www.itascacg.com/software/PFC (accessed on 27 May 2022).
- Itasca Consulting Group, Inc. FLAC. Available online: https://www.itascacg.com/software/FLAC (accessed on 27 May 2022).
- Wang, W.-N. Geological Characteristics of Landslide and Disaster Prevention; Taiwan Disaster Prevention Society: Tainan, China, 2016. (In Chinese) [Google Scholar]
- Coveney, S.; Fotheringham, A.S.; Charlton, M.; McCarthy, T. Dual-scale validation of a medium-resolution coastal DEM with terrestrial LiDAR DSM and GPS. Comput. Geosci. 2010, 36, 489–499. [Google Scholar] [CrossRef]
- Su, M.-B.; Chen, I.-H.; Liao, C.-H. Using TDR cables and GPS for landslide monitoring in high mountain area. J. Geotech. Geoenviron. Eng. 2009, 135, 1113–1121. [Google Scholar] [CrossRef] [Green Version]
- Caviedes-Voullième, D.; Juez, C.; Murillo, J.; García-Navarro, P. 2D dry granular free-surface flow over complex topography with obstacles. Part I: Experimental study using a consumer-grade RGB-D sensor. Comput. Geosci. 2014, 73, 177–197. [Google Scholar] [CrossRef]
- Juez, C.; Caviedes-Voullième, D.; Murillo, J.; García-Navarro, P. 2D dry granular free-surface transient flow over complex topography with obstacles. Part II: Numerical predictions of fluid structures and benchmarking. Comput. Geosci. 2014, 73, 142–163. [Google Scholar] [CrossRef]
- Tsai, W.-N.; Chen, C.-C.; Chiang, C.-W.; Chen, P.-Y.; Kuo, C.-Y.; Wang, K.-L.; Lin, M.-L.; Chen, R.-F. Electrical Resistivity Tomography (ERT) monitoring for landslides: Case study in the Lantai Area, Yilan Taiping Mountain, Northeast Taiwan. Front. Earth Sci. 2021, 9, 737271. [Google Scholar] [CrossRef]
- Broadband Array in Taiwan for Seismology, BATS. Available online: https://gdms.cwb.gov.tw/gdms-broad.php (accessed on 18 May 2022).
- Wang, K.-L.; Lin, J.-T.; Lee, Y.-H.; Chen, T.-W. Study on research on simulation of shallowcollapse behavior with particle flow—Case study of Hongye landslide, Taiwan. In Proceedings of the XIII International Symposium on Landslides, Cartagena, Colombia, 15–19 June 2020. [Google Scholar]
- Lo, C.-M. Evolution of deep-seated landslide at Putanpunas stream, Taiwan. Geomat. Nat. Hazards Risk 2017, 8, 1204–1224. [Google Scholar] [CrossRef]
- Hölbling, D.; Betts, H.; Spiekermann, R.; Phillips, C. Identifying spatio-temporal landslide hotspots on North Island, New Zealand, by analyzing historical and recent aerial photography. Geosciences 2016, 6, 48. [Google Scholar] [CrossRef] [Green Version]
- Lahousse, T.; Chang, K.; Lin, Y.; Günther, A. Landslide mapping with multi-scale object-based image analysis--a case study in the Baichi watershed, Taiwan. Nat. Hazards Earth Syst. Sci. 2011, 11, 2715–2726. [Google Scholar] [CrossRef]
- Wang, K.-L.; Lin, M.-L. Initiation and displacement of landslide induced by earthquake—A study of shaking table model slope test. Eng. Geol. 2011, 122, 106–114. [Google Scholar] [CrossRef]
- Booth, A.M.; Roering, J.J.; Perron, J.T. Automated landslide mapping using spectral analysis and high-resolution topographic data: Puget Sound lowlands, Washington, and Portland Hills, Oregon. Geomorphology 2009, 109, 132–147. [Google Scholar] [CrossRef]
- Dewitte, O.; Jasselette, J.-C.; Cornet, Y.; Van Den Eeckhaut, M.; Collignon, A.; Poesen, J.; Demoulin, A. Tracking landslide displacements by multi-temporal DTMs: A combined aerial stereophotogrammetric and LiDAR approach in western Belgium. Eng. Geol. 2008, 99, 11–22. [Google Scholar] [CrossRef]
- Lee, C.-F.; Lo, C.-M.; Chou, H.-T.; Chi, S.-Y. Landscape evolution analysis of large scale landslides at Don-Ao Peak, Taiwan. Environ. Earth Sci. 2016, 75, 29. [Google Scholar] [CrossRef]
- Lin, M.-L.; Chen, T.-W.; Lin, C.-W.; Ho, D.-J.; Cheng, K.-P.; Yin, H.-Y.; Chen, M.-C. Detecting large-scale landslides using LiDAR data and aerial photos in the Namasha-Liuoguey area, Taiwan. Remote Sens. 2014, 6, 42–63. [Google Scholar] [CrossRef] [Green Version]
- Ventura, G.; Vilardo, G.; Terranova, C.; Sessa, E.B. Tracking and evolution of complex active landslides by multi-temporal airborne LiDAR data: The Montaguto landslide (Southern Italy). Remote Sens. Environ. 2011, 115, 3237–3248. [Google Scholar] [CrossRef]
- Lin, M.-L.; Chen, Y.-C.; Tseng, Y.-H.; Chang, K.-J.; Wang, K.-L. Investigation of geological structures using UAV LiDAR and its effects on the failure mechanism of deep-seated landslide in Lantai Area, Taiwan. Appl. Sci. 2021, 11, 52. [Google Scholar] [CrossRef]
- Wang, K.-L.; Lin, J.-T.; Zhang, J.-W.; Lin, Y.-H.; Hung, J.-S.; Hung, J.-Y.; Ciou, C.-F.; Fu, K.-L. A debris estimation method combining high accuracy UAV, DInSAR and NDSI analysis. J. Taiwan Agric. Eng. 2019, 65, 26–39. [Google Scholar]
- Hung, W.-C.; Hwang, C.; Chen, Y.-A.; Chang, C.-P.; Yen, J.-Y.; Hooper, A.; Yang, C.-Y. Surface deformation from persistent scatterers SAR interferometry and fusion with leveling data: A case study over the Choushui River alluvial fan, Taiwan. Remote Sens. Environ. 2011, 115, 957–967. [Google Scholar] [CrossRef]
- Su, P.-T. A PSInSAR Method with Redundant Observations. Master’s Thesis, National Cheng Kung University, Tainan, China, 2012. [Google Scholar]
- Champenois, J.; Fruneau, B.; Pathier, E.; Deffontaines, B.; Lin, K.-C.; Hu, J.-C. Monitoring of active tectonic deformations in the Longitudinal Valley (Eastern Taiwan) using Persistent Scatterer InSAR method with ALOS PALSAR data. Earth Planet. Sci. Lett. 2012, 337, 144–155. [Google Scholar] [CrossRef]
- Chou, F.-M. Measurement of Surface Deformation in Northern Taiwan by Using PSInSAR Techniques. Master’s Thesis, National Central University, Taoyuan, Taiwan, 2009. (In Chinese). [Google Scholar]
- Greif, V.; Vlcko, J. Monitoring of post-failure landslide deformation by the PS-InSAR technique at Lubietova in Central Slovakia. Environ. Earth Sci. 2011, 66, 1585–1595. [Google Scholar] [CrossRef]
- Lu, P.; Casagli, N.; Catani, F.; Tofani, V. Persistent Scatterers Interferometry Hotspot and Cluster Analysis (PSI-HCA) for detection of extremely slow-moving landslides. Int. J. Remote Sens. 2011, 33, 466–489. [Google Scholar] [CrossRef]
- Lu, C.-H. Faults Activities and Crustal Deformation near Hualien City, Eastern Taiwan Analysed by Persistent Scatterer InSAR; University of Taipei: Taipei, China, 2009. (In Chinese) [Google Scholar]
- Siao, Y.-F. Permanent Scatter Radar Interferometry Applied to Surface Change Detection. Master’s Thesis, National Central University, Taoyuan, China, 2010. (In Chinese). [Google Scholar]
- Tung, H.; Hu, J.-C. Assessments of serious anthropogenic land subsidence in Yunlin County of central Taiwan from 1996 to 1999 by Persistent Scatterers InSAR. Tectonophysics 2012, 578, 126–135. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, Z.; Zhang, Q.; de la Fuente, J. Large-area landslide detection and monitoring with ALOS/PALSAR imagery data over Northern California and Southern Oregon, USA. Remote Sens. Environ. 2012, 124, 348–359. [Google Scholar] [CrossRef]
- Wang, K.-L.; Lin, J.-T.; Wu, C.-C.; Chen, C.-F.; Chiu, T.-W.; Hsieh, M.-H. Study on sliding displacement classification of slope land—An example of NeiHu District, Taipei City. J. Chin. Inst. Civ. Hydraul. Eng. 2021, 33, 139–149. (In Chinese) [Google Scholar] [CrossRef]
- Chen, R.-F.; Lee, C.-Y.; Yin, H.-Y.; Huang, H.-Y.; Cheng, K.-P.; Lin, C.-W. Monitoring the Deep-Seated Landslides by Using ALOS/PALSAR Satellite Imagery in the Disaster Area of 2009 Typhoon Morakot, Taiwan; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Soil and Water Conservation Bureau. Large-Scale Landslide Disaster Prevention and Mitigation under Climate Change; Soil and Water Conservation Bureau: Nantou, China, 2020. (In Chinese) [Google Scholar]
- Del Bene, S.K.; Kilmer, D.; Heck, D.; Smith, A.; Cartwright, M.; Bonamici, S.; Cohen, S. National Landslide Preparedness Act; the U.S. Government Publishing Office: Washington, DC, USA,, 2021. [Google Scholar]
- Kambara, J.; Uchida, T. Technical Guideline for Countermeasures against Deep-Seated Catastrophic (Rapid) Landslide; National Institute for Land and Infrastructure Management: Tsukuba City, Ibaraki Prefecture, Japan, 2014. [Google Scholar]
- National System for Environmental Protection. Linee Guida per il Monitoraggio Delle Frane; National System for Environmental Protection: Roma, Italy, 2021. (In Italian) [Google Scholar]
- Jackson, L.; Bobrowsky, P.; Bichler, A. Identification, Maps and Mapping Canadian Technical Guidelines and Best Practices Related to Landslides: A National Initiative for Loss Reduction; Geological Survery of Canada: Ottawa, ON, Canada, 2012. [Google Scholar] [CrossRef]
- Chae, B.-G.; Choi, J.; Seo, Y.-S. Suggestion of a landslide early warning method using a gradient of volumetric water content. In Landslide Science for a Safer Geoenvironment; Springer: Berlin/Heidelberg, Germany, 2014; pp. 545–550. [Google Scholar]
- Kimura, T.; Yokoyama, N. Monitoring of landslide movement and forecasting of slope failure occurrence. J. Jpn. Landslide Soc. 2006, 43, 172–179. [Google Scholar]
- Wang, J.-S.; Zhong, M.-J.; Ji, S. Discussion on monitoring feedback analysis and early warning application of rainfall-induced landslide. Sinotech Eng. 2011, 110, 27–40. (In Chinese) [Google Scholar] [CrossRef]
- Lin, D.-G.; Chang, K.-C.; Su, M.-B. Numerical assessment of slope stability at Li-San landslide during typhoon rainfall. J. Chin. Soil Water Conserv. 2008, 39, 57–81. (In Chinese) [Google Scholar]
- Gian, Q.A.; Tran, D.-T.; Nguyen, D.C.; Nhu, V.H.; Tien Bui, D. Design and implementation of site-specific rainfall-induced landslide early warning and monitoring system: A case study at Nam Dan landslide (Vietnam). Geomat. Nat. Hazards Risk 2017, 8, 1978–1996. [Google Scholar] [CrossRef]
- Jan, C.-D. Rainfall Warning for Debris Flow Disaster Prevention; Sinotech Foundation for Research & Development of Engineering Sciences & Technologies: Taipei, China, 2016. (In Chinese) [Google Scholar]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Liao, J.-T.; Chen, C.-W.; Chi, C.-C.; Lin, H.-H. Study of slope displacement for management from landslide monitoring cases in Taiwan. Sino-Geotech. 2013, 136, 59–70. (In Chinese) [Google Scholar]
- Martelloni, G.; Segoni, S.; Fanti, R.; Catani, F. Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 2012, 9, 485–495. [Google Scholar] [CrossRef] [Green Version]
- Tsai, T.-T.; Tsai, Y.-J.; Shieh, C.-L. Critical rainfall analysis of large-scale landslide occurrence. In Proceedings of the Interpraenent 2018, Toyama, Japan, 1–4 October 2018; pp. 91–96. [Google Scholar]
- Zêzere, J.; Vaz, T.; Pereira, S.; Oliveira, S.; Marques, R.; Garcia, R.A. Rainfall thresholds for landslide activity in Portugal: A state of the art. Environ. Earth Sci. 2015, 73, 2917–2936. [Google Scholar] [CrossRef]
- Shieh, C.-L.; Luh, Y.-C.; Yu, P.-S.; Chen, L.-J. The critical line of debris flow occurrence. J. Chin. Soil Water Conserv. 1995, 26, 167–172. [Google Scholar]
- Tsai, T.-T.; Li, C.-C.; Tsai, H.-C.; Lin, Y.-F.; Chiu, T.-W.; Lin, C.-W. An Analysis of Slopeland Disasters with Formosat-2 Imagery; Central Geological Survey: Taipei, China, 2010; pp. 18–27. (In Chinese) [Google Scholar]
- Tsai, T.-T. The review of FOMOSAT-II applications in disaster prevention and mitigation. NARL Quart. 2009, 23, 53–60. (In Chinese) [Google Scholar] [CrossRef]
- Sinotech Engineering Consultants Inc. Dynamic Susceptibility Assessment and Warning System of Rainfall Thresholds for Debris Slide; Central Geological Survey: Taipei, China, 2013. (In Chinese) [Google Scholar]
- Soil and Water Conservation Bureau. Majon Disaster Events. Available online: https://246.swcb.gov.tw/Achievement/MajorDisasters (accessed on 22 March 2022).
- Lin, G.-W. Detecting Large Scale Landslides by Taiwan Broadband Seismic Network and the Study of Triggering Rainfall for Landsliding; Soil and Water Conservation Bureau: Nantou, China, 2015. (In Chinese) [Google Scholar]
- Huang, T.-H. Characteristics of Rains Triggering Debris Flows in the Watershed of Chenyoulen Stream. Master’s Thesis, National Cheng Kung University, Tainan, Taiwan, 2002. (In Chinese). [Google Scholar]
- Jan, C.-D.; Lee, M.-H. A debris-flow rainfall-based warning model. J. Chin. Soil Water Conserv. 2004, 35, 275–285. [Google Scholar]
- Soil and Water Conservation Bureau. Soil and Water Conservation Handbook: Debris-Flow Chapter; Soil and Water Conservation Bureau: Taiwan, 2021. [Google Scholar]
- Towhata, I.; Goto, S.; Goto, S.; Akima, T.; Tanaka, J.; Uchimura, T.; Wang, G.; Yamaguchi, H.; Aoyama, S. Mechanism and future risk of slope instability induced by extreme rainfall event in Izu Oshima Island, Japan. Nat. Hazards 2021, 105, 501–530. [Google Scholar] [CrossRef]
- Soil and Water Conservation Bureau. Development and Application of Disaster Prevention and Mitigation Technologies for Large-Scale Landslides; Soil and Water Conservation Bureau: Nantou, China, 2015. (In Chinese) [Google Scholar]
- Scheidegger, A.E. On the prediction of the reach and velocity of catastrophic landslides. Rock Mech. 1973, 5, 231–236. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap methods: Another look at the jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Singh, K.; Xie, M. Bootstrap: A Statistical Method; Department of Statistics, Rutgers University: New Brunswick-Piscataway, NJ, USA, 2008; (unpublished work). [Google Scholar]
- Hu, W.; Xie, J.; Chau, H.W.; Si, B.C. Evaluation of parameter uncertainties in nonlinear regression using Microsoft Excel Spreadsheet. Environ. Syst. Res. 2015, 4, 4. [Google Scholar] [CrossRef]


| Investigation Item | Instruments | Investigation Objects | Accuracy | |
|---|---|---|---|---|
| Surface changes | Surface inclinometer | Tilting direction and amount of ground surface | 1” | |
| Surface extensometer | Fracture displacement and velocity | 0.2 mm | ||
| Surface measurement | Optical measuring instruments | Tilting direction and amount of ground surface | 1~10 mm | |
| GNSS | Displacement of the ground surface | NA | ||
| LiDAR scanner | Terrain 3D variation | NA | ||
| Underground changes | In-place inclinometer | Sliding surface position and variation | 5~10” | |
| Pipe strain gauge | Sliding surface position and variation | 1 × 10−6 | ||
| Borehole extensometer | Sliding surface dislocation rate | 0.2 mm | ||
| Multipoint borehole extensometer | Sliding surface position and dislocation rate | 0.3 mm | ||
| Surface hydrology | Rain gauge | Rainfall amount | 0.5 mm | |
| Underground hydrology | Water level gauge | Variation of water level in the hole | 0.05%FS | |
| Pore pressure gauge | Variation of water pressure of the sliding surface | 0.05%FS | ||
| Soil moisture meter | Variation of soil saturation | NA | ||
| Flowmeter | Variation of discharge | NA | ||
| Structures | Earth pressure gauge | Earth pressure acting on retaining walls, deep foundation piles | 0.1%FS | |
| Load cell | Tension acting on the ground anchor | 0.1%FS | ||
| Strain gauge | Deformation of the structure | 1 × 10−6 | ||
| Rebar gauge | Stress acting on the rebar gauge | 0.1%FS | ||
| Inclinometer | Tilt variation of structure | 1~10” | ||
| In-place inclinometer | Bending deformation of steel pipe piles | 5~10” | ||
| No. | ID | Event | Area Size (ha) | Occurrence Time | Cited From |
|---|---|---|---|---|---|
| 1 | SR-3 | Typhoon Morakot (200908) | 19 | 09 August 2009 17:00 | Interviews with local residents |
| 2 | SR-5 | 238 | 09 August 2009 17:00 | ||
| 3 | SR-6 | 142 | 10 August 2009 12:00 | ||
| 4 | SR-7 | 130 | 09 August 2009 02:00 | ||
| 5 | SR-8 | 88 | 09 August 2009 02:00 | ||
| 6 | SR-9 | 74 | 09 August 2009 04:00 | ||
| 7 | SR-11 | 40 | 08 August 2009 16:00 | ||
| 8 | SR-12 | 32 | 09 August 2009 07:00 | ||
| 9 | SR-16 | 26 | 09 August 2009 07:00 | ||
| 10 | SR-19 | 23 | 08 August 2009 15:00 | ||
| 11 | SR-42 | 15 | 09 August 2009 07:00 | ||
| 12 | SR-43 | 15 | 09 August 2009 07:00 | ||
| 13 | SR-46 | 15 | 09 August 2009 05:00 | ||
| 14 | SR-53 | 14 | 09 August 2009 00:00 | ||
| 15 | SR-94 | 351 | 09 August 2009 10:00 | ||
| 16 | SR-95 | 249 | 09 August 2009 06:00 | ||
| 17 | SR-96 | 81 | 09 August 2009 10:00 | ||
| 18 | SR-97 | 61 | 09 August 2009 09:00 | ||
| 19 | SR-98 | 52 | 09 August 2009 06:00 | ||
| 20 | SR-99 | 15 | 09 August 2009 04:00 | ||
| 21 | SR-100 | 11 | 08 August 2009 10:00 | ||
| 22 | SR-101 | 10 | 09 August 2009 09:00 | ||
| 23 | 2005_002 | Typhoon Haitang (200505) | 18 | 21 July 2005 14:33 | The evaluation results of the LSL occurrence time and location from the BATS |
| 24 | 2006_002 | 0609 Torrential Rain | 12 | 10 Jun 2006 00:53 | |
| 25 | 2008_002 | Typhoon Sinlaku (200813) | 89 | 18 September 2008 02:50 | |
| 26 | 2008_003 | Typhoon Kamaegi (200807) | 10 | 19 July 2008 05:30 | |
| 27 | 2012_002 | Typhoon Saola (201209) | 19 | 03 August 2012 09:02 | |
| 28 | 2012_004 | 25 | 03 August 2012 03:00 |
| Cases | Landslide or Not | Rainfall Type Used | |
|---|---|---|---|
| 107 newborn LSLs | 28 occurrence-time-known cases | Yes | Triggering rainfall |
| 79 occurrence-time-unknown cases | Yes | Total event rainfall | |
| 149 potential LSL areas | No | Total rainfall of Typhoon Morakot | |
| Regression Statistics | ||||||
|---|---|---|---|---|---|---|
| Multiple R | 0.9569 | |||||
| R Square | 0.9157 | |||||
| Adjusted R Square | 0.9052 | |||||
| Standard Error | 2.8447 | |||||
| Observations | 28 | |||||
| ANOVA | ||||||
| df | SS | MS | F | Significance F | ||
| Regression | 3 | 2109.4427 | 703.1476 | 86.8894 | 4.9903 × 10−13 | |
| Residual | 24 | 194.2187 | 8.0924 | |||
| Total | 27 | 2303.6614 | ||||
| Coefficients | Standard Error | t-Test | p-value | Lower 95% | Upper 95% | |
| Intercept | 66.7058 | 6.1858 | 10.7838 | 1.10 × 10−10 | 53.9390 | 79.4725 |
| R(m) | −2.2273 | 2.8034 | −0.7945 | 0.4347 | −8.0133 | 3.5587 |
| θ(degree) | 0.0043 | 0.1279 | 0.0334 | 0.9737 | −0.2597 | 0.2682 |
| (degree) | −2.2251 | 0.1456 | −15.2793 | 7.26 × 10−14 | −2.5257 | −1.9246 |
| Parameter | Max | Min | Mean | Median | 40% | 60% |
|---|---|---|---|---|---|---|
| a | 24,469.2875 | 648.5690 | 6095.1517 | 4438.0571 | 3576.8579 | 5539.8139 |
| b | −0.0229 | −0.3621 | −0.1647 | −0.1604 | −0.1744 | −0.1460 |
| c | 0.1614 | −0.4220 | −0.1339 | −0.1298 | −0.1492 | −0.1089 |
| d | 2.4898 | 0.8831 | 1.6260 | 1.6288 | 1.5488 | 1.7067 |
| e | 5.0123 | −22.1158 | −4.4903 | −3.5814 | −4.7650 | −2.5826 |
| ΔDmax | ΔDmin | ΔDmean | ΔDmedian | ΔD40% | ΔD60% | |
|---|---|---|---|---|---|---|
| Standard deviation | 9.18 (15%) | 6.85 (35%) | 3.52 (9%) | 1.38 (6%) | 1.65 (6%) | 1.77 (7%) |
| Mean of absolute values | 15.03 (72%) | 31.00 (167%) | 8.03 (41%) | 1.07 (5%) | 2.20 (11%) | 2.87 (15%) |
| Maximum value | 42.61 (99%) | −23.20 (−117%) | 16.15 (55%) | 2.38 (12%) | 0.02 (0%) | 6.63 (26%) |
| Mean value | 15.03 (72%) | −31.00 (−167%) | 8.03 (41%) | 0.16 (1%) | −2.20 (−11%) | 2.82 (15%) |
| Median value | 11.38 (76%) | −28.18 (−163%) | 6.94 (43%) | 0.45 (3%) | −1.85 (−10%) | 2.84 (17%) |
| Minimum value | 6.38 (37%) | −50.56 (−231%) | 3.69 (21%) | −4.00 (−13%) | −7.11 (−23%) | −0.36 (−2%) |
| ΔDmax | ΔDmin | ΔDmean | ΔDmedian | ΔD40% | ΔD60% | |
|---|---|---|---|---|---|---|
| Standard deviation | 1.42 (4%) | 1.60 (20%) | 1.20 (8%) | 0.65 (5%) | 0.69 (6%) | 0.67 (5%) |
| Mean of absolute values | 9.26 (75%) | 26.47 (216%) | 4.39 (35%) | 0.63 (5%) | 2.13 (17%) | 1.48 (12%) |
| Maximum value | 16.21 (83%) | −22.69 (−150%) | 8.71 (61%) | 1.62 (15%) | 0.13 (1%) | 3.36 (30%) |
| Mean value | 9.26 (75%) | −26.47 (−216%) | 4.39 (35%) | −0.39 (−3%) | −2.13 (−17%) | 1.48 (12%) |
| Median value | 8.81 (75%) | −26.41 (−219%) | 4.19 (35%) | −0.43 (−3%) | −2.17 (−18%) | 1.42 (12%) |
| Minimum value | 7.46 (62%) | −32.25 (−254%) | 1.85 (17%) | −1.72 (−16%) | −3.55 (−32%) | 0.02 (0%) |
| Maximum value (mm) | 1271.3 | 1599.1 | 1147.8 | 2554.0 | 1425.8 | 804.3 | 3069.4 |
| Minimum value (mm) | 501.6 | 571.4 | −198.5 | 955.9 | 277.0 | 178.7 | 507.4 |
| Error sum of squares (m2) | 2.3922 | 9.0971 | 19.3008 | 2.1096 | 4.3647 | 55.0174 | |
| Normalized error sum of squares | 4.1646 | 9.9850 | 34.2229 | 3.2921 | 4.8297 | 70.8433 | |
| Standard deviation (mm) | 297.7 | 580.5 | 845.5 | 279.5 | 402.1 | 1427.5 | |
| Normalized standard deviation | 0.3927 | 0.6081 | 1.1258 | 0.3492 | 0.4229 | 1.6198 |
| Maximum value (mm) | 1994.4 | 1544.9 | 1174.1 | 1987.9 | 1688.7 | 950.8 | 3589.9 |
| Minimum value (mm) | 779.2 | 464.8 | 132.2 | 862.1 | 872.7 | 470.0 | 1966.4 |
| Error sum of squares (m2) | 11.2251 | 26.5031 | 3.7198 | 4.1568 | 18.3132 | 40.8837 | |
| Normalized error sum of squares | 4.5775 | 12.7829 | 1.9193 | 1.5839 | 7.6505 | 31.4102 | |
| Standard deviation (mm) | 644.8 | 990.8 | 371.2 | 392.4 | 823.6 | 1230.5 | |
| Normalized standard deviation | 0.4117 | 0.6881 | 0.2666 | 0.2422 | 0.5323 | 1.0786 |
| Maximum value (mm) | 2267.9 | 3016.4 | 2685.2 | 3412.0 | 2739.7 | 1575.6 | 5647.8 |
| Minimum value (mm) | 822.3 | 804.5 | 511.1 | 1037.4 | 1144.4 | 591.5 | 2583.9 |
| Error sum of squares (m2) | 10.0854 | 20.0943 | 8.5405 | 6.1552 | 23.6371 | 94.8223 | |
| Normalized error sum of squares | 3.1882 | 5.8767 | 3.4506 | 2.3811 | 6.6163 | 44.9751 | |
| Standard deviation (mm) | 611.2 | 862.7 | 562.4 | 477.5 | 935.7 | 1874.0 | |
| Normalized standard deviation | 0.3436 | 0.4665 | 0.3575 | 0.2970 | 0.4950 | 1.2906 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, T.-T.; Tsai, Y.-J.; Shieh, C.-L.; Wang, J.H.-C. Triggering Rainfall of Large-Scale Landslides in Taiwan: Statistical Analysis of Satellite Imagery for Early Warning Systems. Water 2022, 14, 3358. https://doi.org/10.3390/w14213358
Tsai T-T, Tsai Y-J, Shieh C-L, Wang JH-C. Triggering Rainfall of Large-Scale Landslides in Taiwan: Statistical Analysis of Satellite Imagery for Early Warning Systems. Water. 2022; 14(21):3358. https://doi.org/10.3390/w14213358
Chicago/Turabian StyleTsai, Tsai-Tsung, Yuan-Jung Tsai, Chjeng-Lun Shieh, and John Hsiao-Chung Wang. 2022. "Triggering Rainfall of Large-Scale Landslides in Taiwan: Statistical Analysis of Satellite Imagery for Early Warning Systems" Water 14, no. 21: 3358. https://doi.org/10.3390/w14213358
APA StyleTsai, T.-T., Tsai, Y.-J., Shieh, C.-L., & Wang, J. H.-C. (2022). Triggering Rainfall of Large-Scale Landslides in Taiwan: Statistical Analysis of Satellite Imagery for Early Warning Systems. Water, 14(21), 3358. https://doi.org/10.3390/w14213358







