Using Deep Learning to Formulate the Landslide Rainfall Threshold of the Potential Large-Scale Landslide
Abstract
:1. Introduction
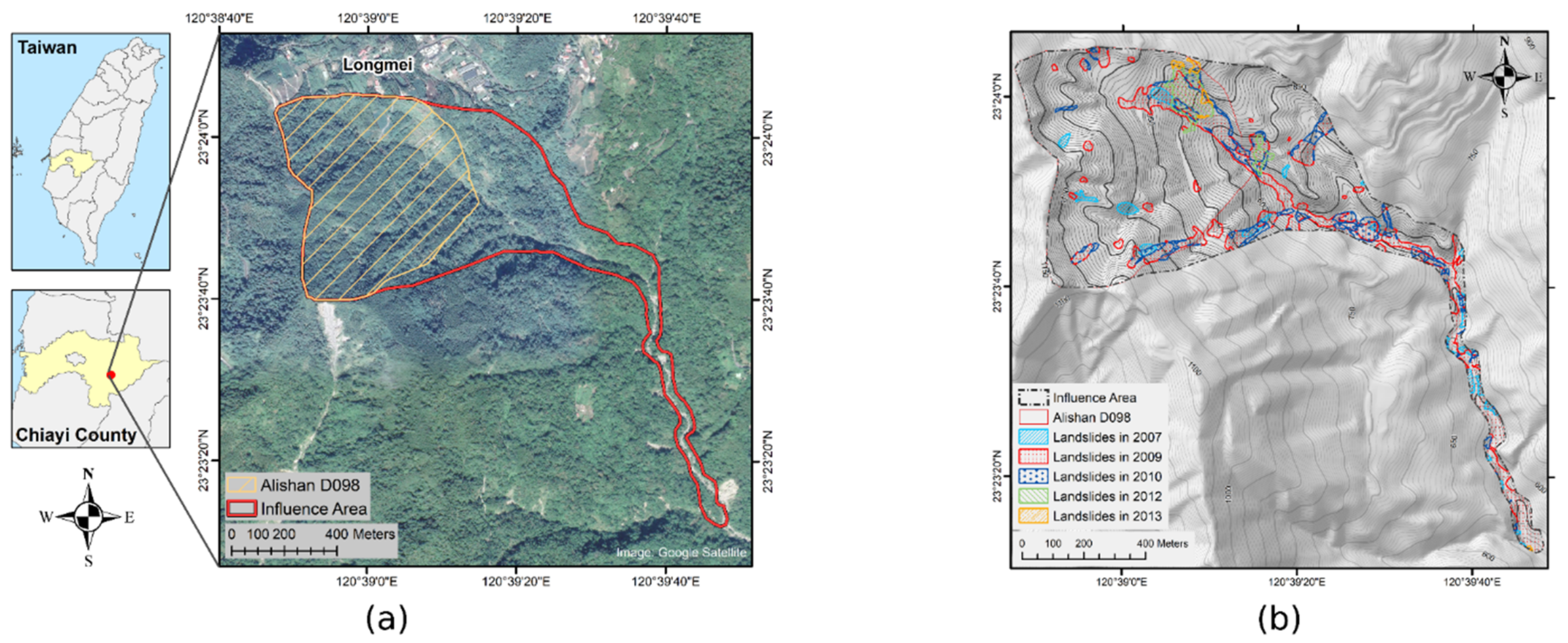
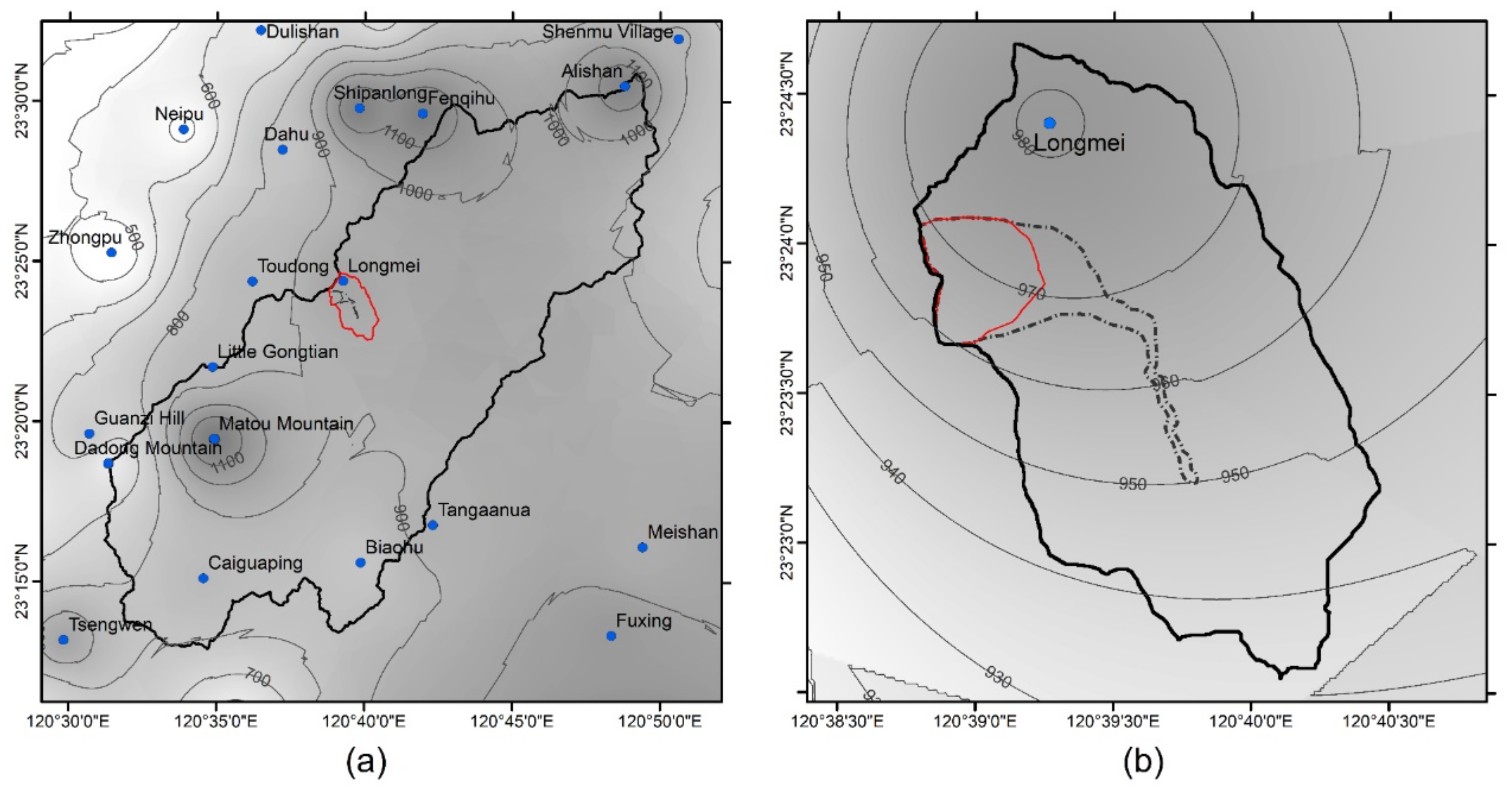
2. Study Area
3. Materials and Methods
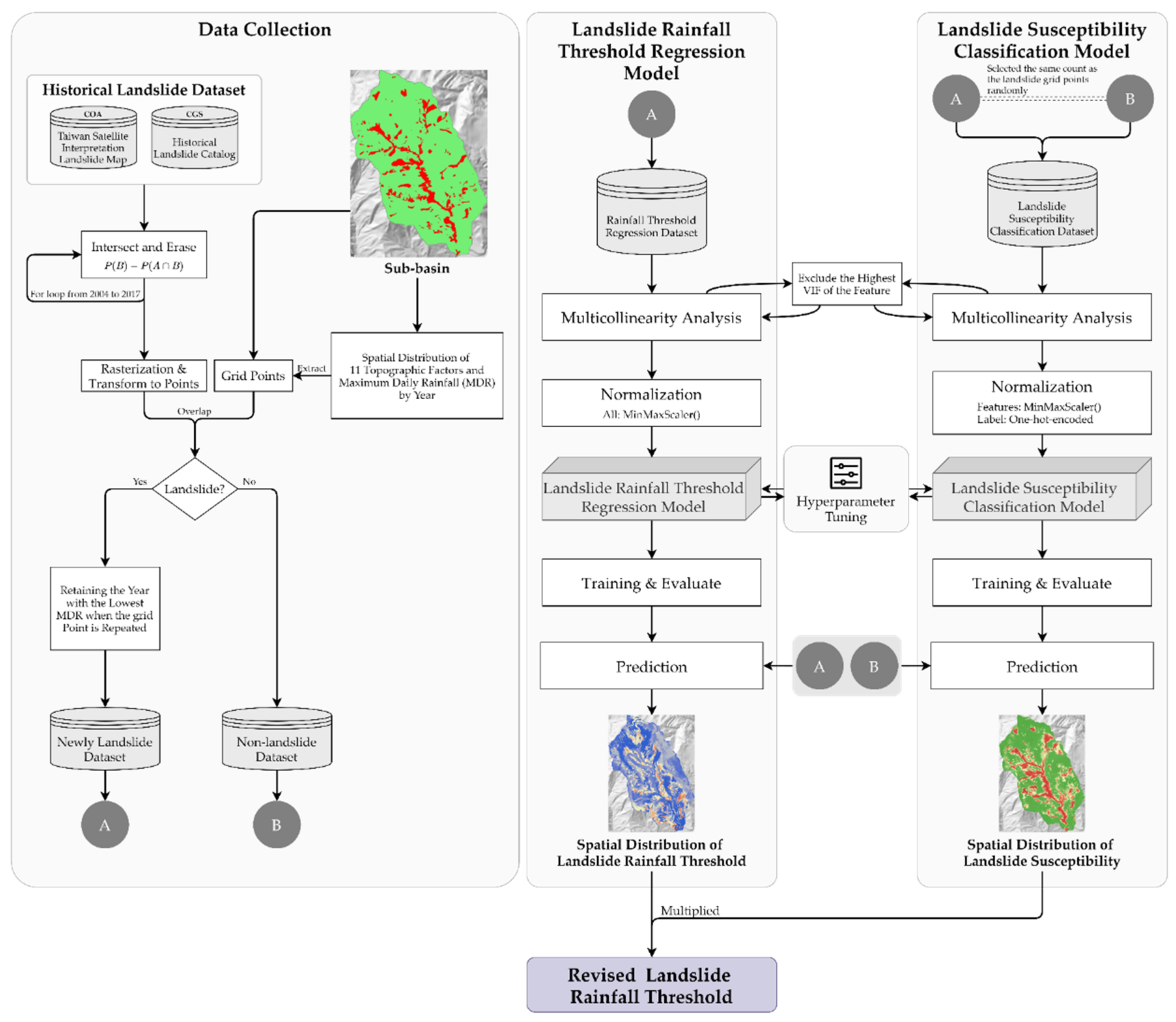
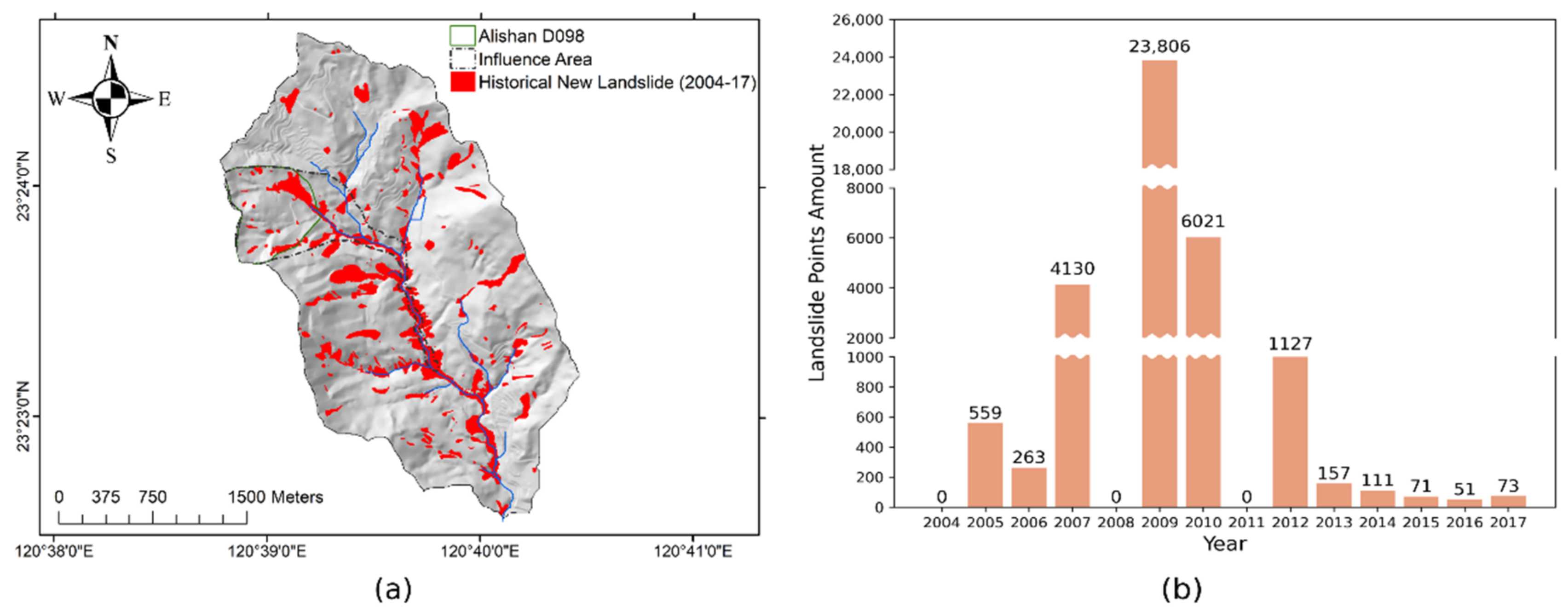
3.1. Data Collection
3.2. Preprocess
3.3. Multicollinearity Analysis
3.4. The Framework of Deep Learning Model
3.5. Hyperparameter Tuning
3.6. Model Evaluate
4. Results and Discussion
4.1. Correlation and Multicollinearity between Factors
4.2. Result of Hyperparameter Tuning
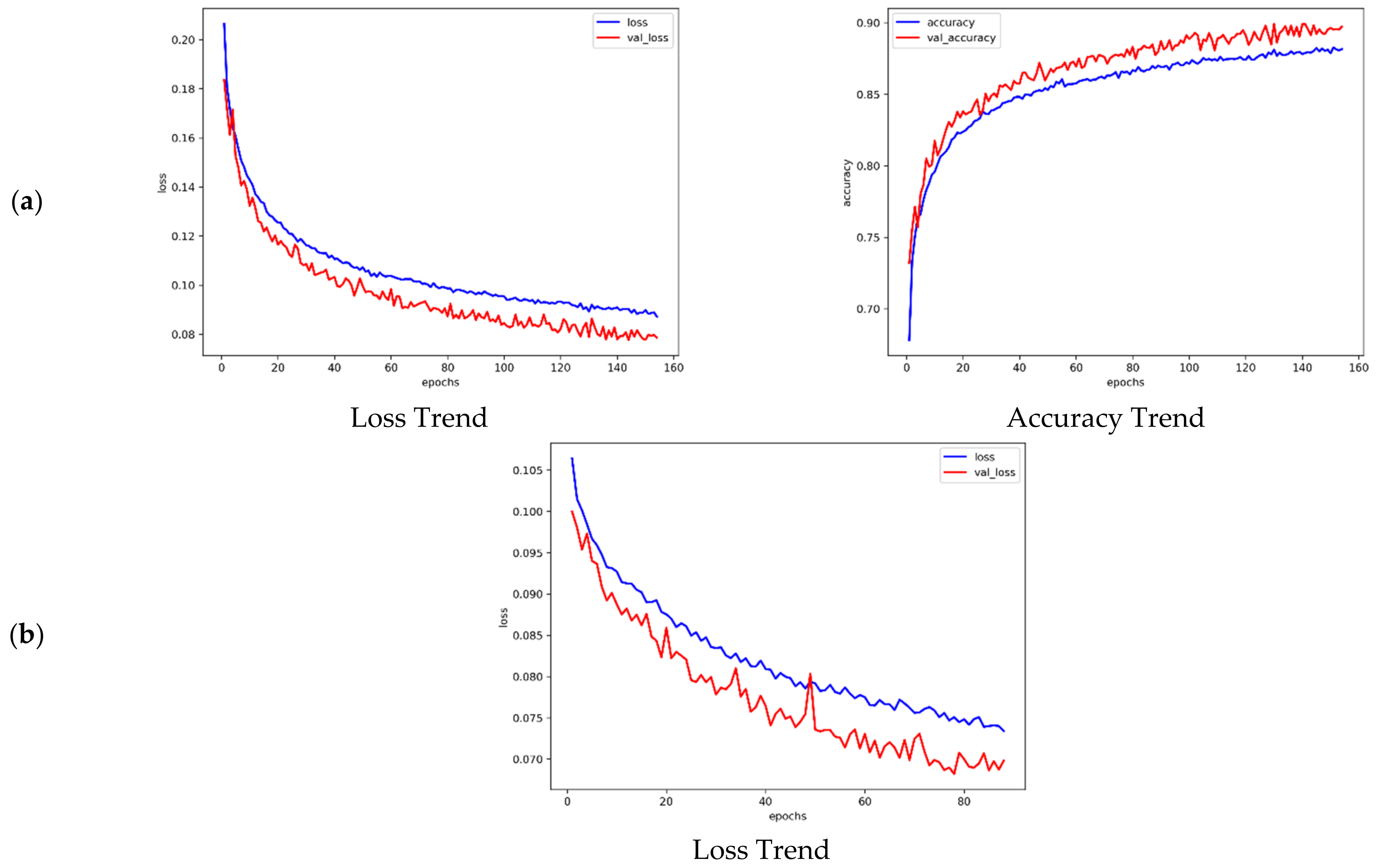
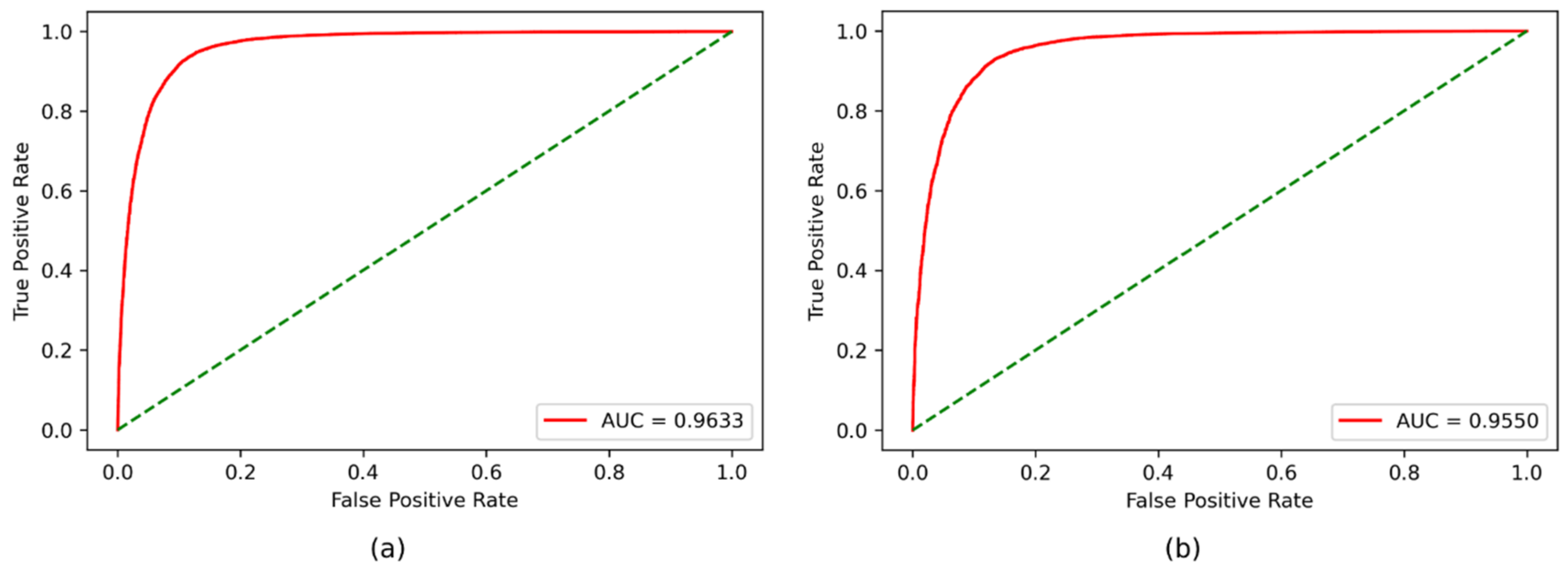
4.3. Training and Evaluated Results
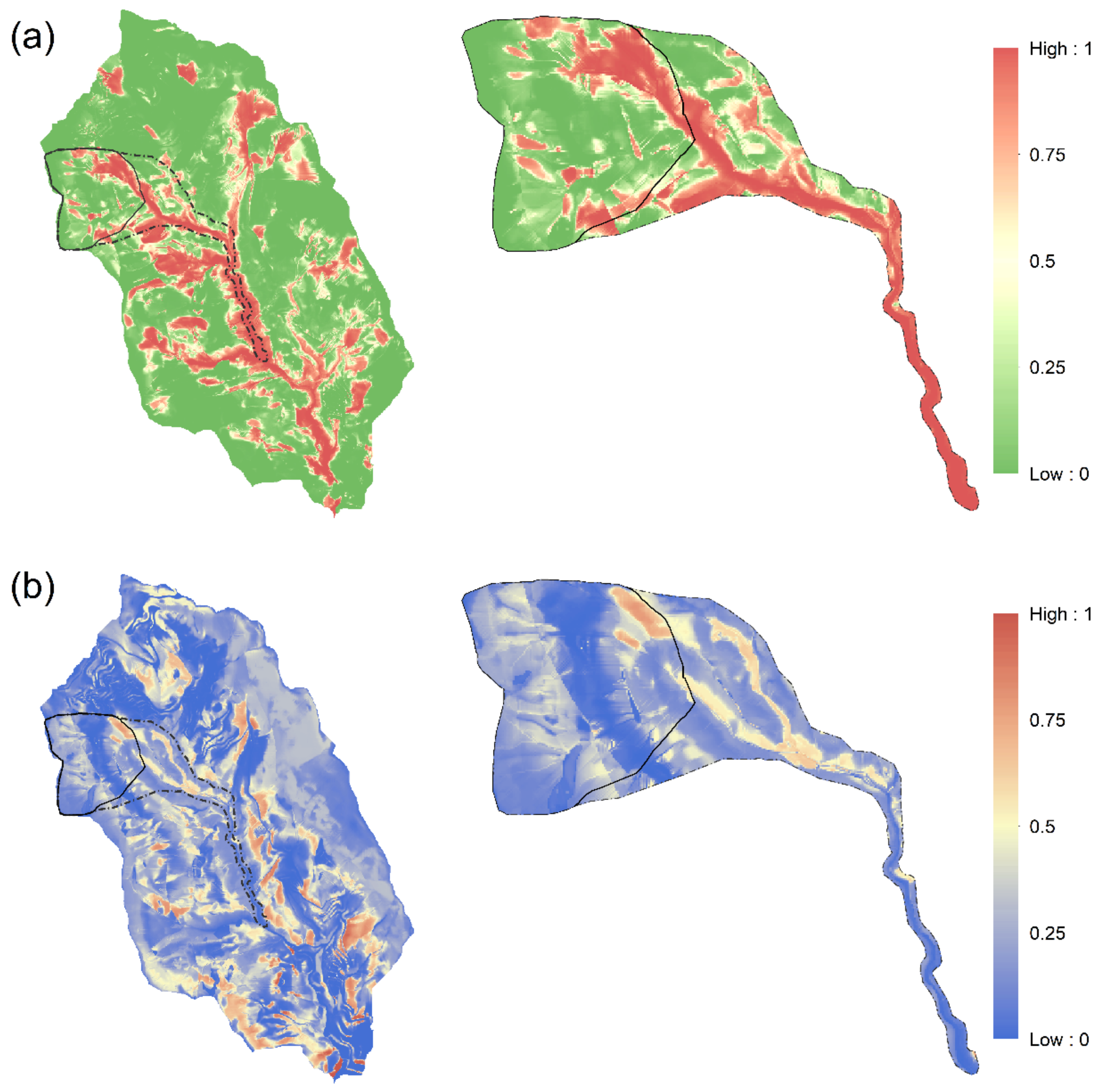
4.4. Predicting and Revising Landslide Rainfall Threshold
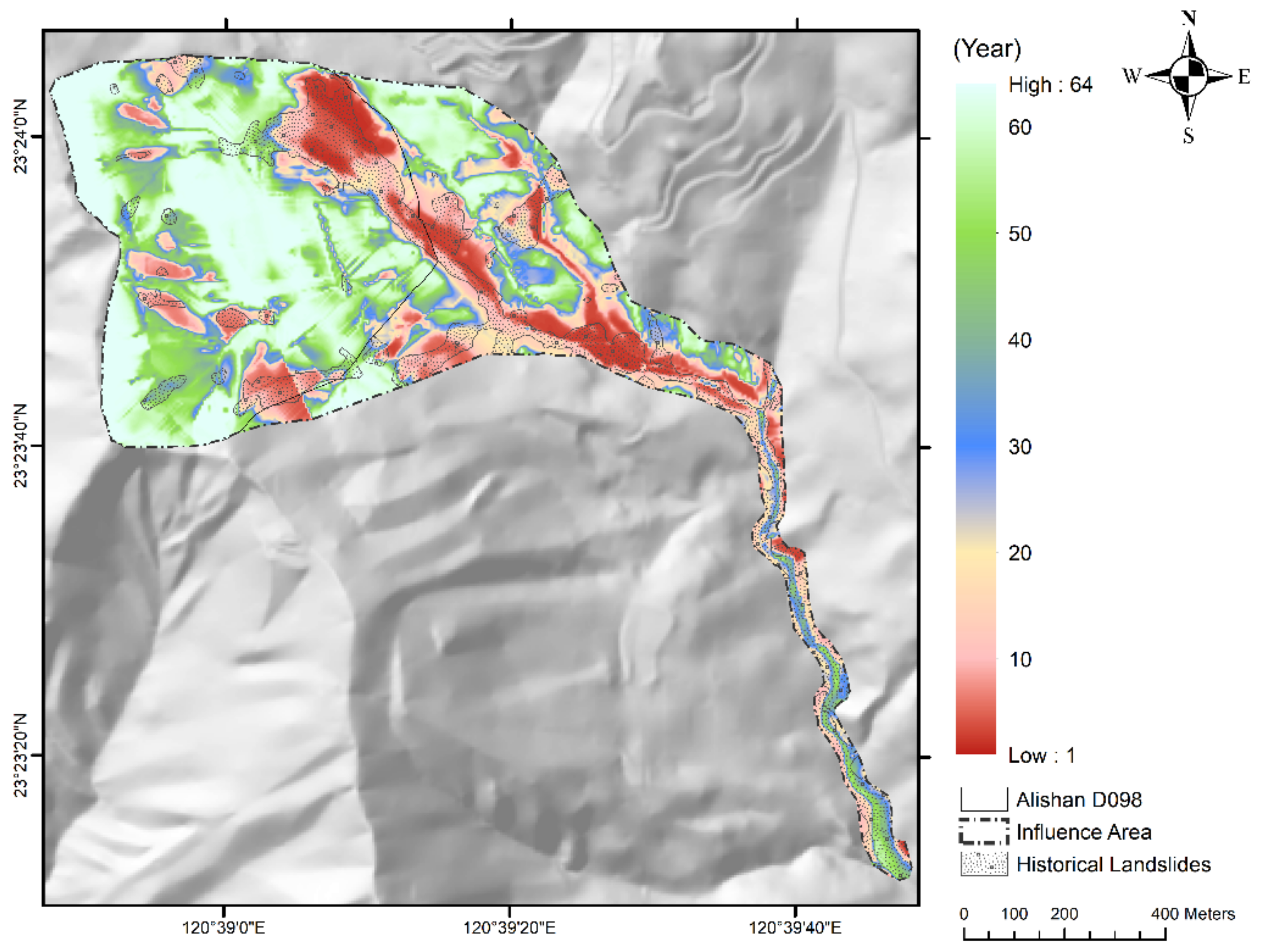
4.5. Establishing Recurrence Interval Distribution of Revised Landslide Rainfall Threshold
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Skilodimou, H.; Bathrellos, G.; Koskeridou, E.; Soukis, K.; Rozos, D. Physical and Anthropogenic Factors Related to Landslide Activity in the Northern Peloponnese, Greece. Land 2018, 7, 85. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, S.; Anand, N.; Sharma, S.; Dhar, S.; Sinha, L.K. Monthly Rainfall Prediction Using Various Machine Learning Algorithms for Early Warning of Landslide Occurrence. In Proceedings of the 2020 International Conference for Emerging Technology (INCET), Belgaum, India, 5–7 June 2020; pp. 1–7. [Google Scholar]
- Distefano, P.; Peres, D.J.; Scandura, P.; Cancelliere, A. Brief communication: Introducing rainfall thresholds for landslide triggering based on artificial neural networks. Nat. Hazards Earth Syst. Sci. 2022, 22, 1151–1157. [Google Scholar] [CrossRef]
- Palladino, M.R.; Viero, A.; Turconi, L.; Brunetti, M.T.; Peruccacci, S.; Melillo, M.; Luino, F.; Deganutti, A.M.; Guzzetti, F. Rainfall thresholds for the activation of shallow landslides in the Italian Alps: The role of environmental conditioning factors. Geomorphology 2018, 303, 53–67. [Google Scholar] [CrossRef]
- Weng, M.-C.; Wu, M.-H.; Ning, S.-K.; Jou, Y.-W. Evaluating triggering and causative factors of landslides in Lawnon River Basin, Taiwan. Eng. Geol. 2011, 123, 72–82. [Google Scholar] [CrossRef]
- Teja, T.S.; Dikshit, A.; Satyam, N. Determination of Rainfall Thresholds for Landslide Prediction Using an Algorithm-Based Approach: Case Study in the Darjeeling Himalayas, India. Geosciences 2019, 9, 302. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Gu, Q.; Wen, H.; Shi, S.; Mi, C.; Zhang, F. A Hybrid Landslide Warning Model Coupling Susceptibility Zoning and Precipitation. Forests 2022, 13, 827. [Google Scholar] [CrossRef]
- Dou, J.; Yamagishi, H.; Pourghasemi, H.R.; Yunus, A.P.; Song, X.; Xu, Y.; Zhu, Z. An integrated artificial neural network model for the landslide susceptibility assessment of Osado Island, Japan. Nat. Hazards 2015, 78, 1749–1776. [Google Scholar] [CrossRef]
- Tehrani, F.; Santinelli, G.; Herrera, M. A framework for predicting rainfall-induced landslides using machine learning methods Un cadre pour prédire les glissements de terrain induits par les précipitations à l’aide d’un apprentissage automatique. In Proceedings of the XVII ECSMGE-2019 Geotechnical Engineering Foundation of the Future, Reykjavik, Iceland, 1–6 September 2019. [Google Scholar]
- Naseer, S.; Haq, T.U.; Khan, A.; Tanoli, J.I.; Khan, N.G.; Qaiser, F.-u.-R.; Shah, S.T.H. GIS-based spatial landslide distribution analysis of district Neelum, AJ&K, Pakistan. Nat. Hazards 2021, 106, 965–989. [Google Scholar] [CrossRef]
- Wu, C.Y.; Yeh, Y.C. A Landslide Probability Model Based on a Long-Term Landslide Inventory and Rainfall Factors. Water 2020, 12, 937. [Google Scholar] [CrossRef] [Green Version]
- Mind’je, R.; Li, L.H.; Nsengiyumva, J.B.; Mupenzi, C.; Nyesheja, E.M.; Kayumba, P.M.; Gasirabo, A.; Hakorimana, E. Landslide susceptibility and influencing factors analysis in Rwanda. Environ. Dev. Sustain. 2020, 22, 7985–8012. [Google Scholar] [CrossRef]
- Nam, K.; Wang, F. An extreme rainfall-induced landslide susceptibility assessment using autoencoder combined with random forest in Shimane Prefecture, Japan. Geoenvironmental Disasters 2020, 7, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Huang, L.; Fan, L.; Huang, J.; Huang, F.; Chen, J.; Zhang, Z.; Wang, Y. Landslide Susceptibility Prediction Modeling Based on Remote Sensing and a Novel Deep Learning Algorithm of a Cascade-Parallel Recurrent Neural Network. Sensors 2020, 20, 1576. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, T.; Li, Y.; Wang, T.; Wang, H.; Chen, T.; Sun, Z.; Luo, D.; Li, C.; Han, L. Evaluation of different machine learning models and novel deep learning-based algorithm for landslide susceptibility mapping. Geosci. Lett. 2022, 9, 26. [Google Scholar] [CrossRef]
- Yang, R.; Zhang, F.; Xia, J.; Wu, C. Landslide Extraction Using Mask R-CNN with Background-Enhancement Method. Remote Sens. 2022, 14, 2206. [Google Scholar] [CrossRef]
- Lu, H.; Ma, L.; Fu, X.; Liu, C.; Wang, Z.; Tang, M.; Li, N. Landslides Information Extraction Using Object-Oriented Image Analysis Paradigm Based on Deep Learning and Transfer Learning. Remote Sens. 2020, 12, 752. [Google Scholar] [CrossRef] [Green Version]
- Prakash, N.; Manconi, A.; Loew, S. Mapping Landslides on EO Data: Performance of Deep Learning Models vs. Traditional Machine Learning Models. Remote Sens. 2020, 12, 346. [Google Scholar] [CrossRef] [Green Version]
- Park, S.-J.; Lee, D.-k. Predicting susceptibility to landslides under climate change impacts in metropolitan areas of South Korea using machine learning. Geomat. Nat. Hazards Risk 2021, 12, 2462–2476. [Google Scholar] [CrossRef]
- Saha, S.; Sarkar, R.; Roy, J.; Hembram, T.K.; Acharya, S.; Thapa, G.; Drukpa, D. Measuring landslide vulnerability status of Chukha, Bhutan using deep learning algorithms. Sci. Rep. 2021, 11, 16374. [Google Scholar] [CrossRef] [PubMed]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep learning-based landslide susceptibility mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef] [PubMed]
- Nhu, V.-H.; Hoang, N.-D.; Nguyen, H.; Ngo, P.T.T.; Thanh Bui, T.; Hoa, P.V.; Samui, P.; Tien Bui, D. Effectiveness assessment of Keras based deep learning with different robust optimization algorithms for shallow landslide susceptibility mapping at tropical area. Catena 2020, 188, 104458. [Google Scholar] [CrossRef]
- Li, X.; Li, S. Large-Scale Landslide Displacement Rate Prediction Based on Multi-Factor Support Vector Regression Machine. Appl. Sci. 2021, 11, 1381. [Google Scholar] [CrossRef]
- Meng, Q.X.; Wang, H.L.; He, M.J.; Gu, J.J.; Qi, J.; Yang, L.L. Displacement prediction of water-induced landslides using a recurrent deep learning model. Eur. J. Environ. Civ. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Orland, E.; Roering, J.J.; Thomas, M.A.; Mirus, B.B. Deep Learning as a Tool to Forecast Hydrologic Response for Landslide-Prone Hillslopes. Geophys. Res. Lett. 2020, 47, e2020GL088731. [Google Scholar] [CrossRef]
- Ma, J.; Xia, D.; Wang, Y.; Niu, X.; Jiang, S.; Liu, Z.; Guo, H. A comprehensive comparison among metaheuristics (MHs) for geohazard modeling using machine learning: Insights from a case study of landslide displacement prediction. Eng. Appl. Artif. Intell. 2022, 114, 105150. [Google Scholar] [CrossRef]
- Ma, J.; Xia, D.; Guo, H.; Wang, Y.; Niu, X.; Liu, Z.; Jiang, S. Metaheuristic-based support vector regression for landslide displacement prediction: A comparative study. Landslides 2022, 19, 2489–2511. [Google Scholar] [CrossRef]
- Li, S.H.; Wu, L.Z.; Huang, J. A novel mathematical model for predicting landslide displacement. Soft Comput. 2020, 25, 2453–2466. [Google Scholar] [CrossRef]
- Shihabudheen, K.V.; Peethambaran, B. Landslide displacement prediction technique using improved neuro-fuzzy system. Arab. J. Geosci. 2017, 10, 502. [Google Scholar] [CrossRef]
- Ma, J.; Tang, H.; Liu, X.; Wen, T.; Zhang, J.; Tan, Q.; Fan, Z. Probabilistic forecasting of landslide displacement accounting for epistemic uncertainty: A case study in the Three Gorges Reservoir area, China. Landslides 2018, 15, 1145–1153. [Google Scholar] [CrossRef]
- Li, H.; Xu, Q.; He, Y.; Deng, J. Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models. Landslides 2018, 15, 2047–2059. [Google Scholar] [CrossRef]
- Krkač, M.; Špoljarić, D.; Bernat, S.; Arbanas, S.M. Method for prediction of landslide movements based on random forests. Landslides 2016, 14, 947–960. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Y.; Huang, X.; Zhang, L.; Li, X.; Wang, S. Displacement prediction method of rainfall-induced landslide considering multiple influencing factors. Nat. Hazards 2022. [Google Scholar] [CrossRef]
- Council of Agriculture. 36 Potential Large-Scale Landslide Areas in 2022. Available online: https://data.coa.gov.tw/open_detail.aspx?id=I20 (accessed on 4 July 2022).
- Tsai, Y.-J.; Syu, F.-T.; Shieh, C.-L.; Chung, C.-R.; Lin, S.-S.; Yin, H.-Y. Framework of Emergency Response System for Potential Large-Scale Landslide in Taiwan. Water 2021, 13, 712. [Google Scholar] [CrossRef]
- Shao, P.-H.; Kao, M.-C. Explanatory Text for the Geological Map of TAIWAN Scale 1:50,000—Zhongpu; Central Geological Survey: Taipei, 2009. [Google Scholar]
- Feng, Z.-Y.; Huang, H.-C.; Huang, J.-J.; Lai, H.-Y. Preliminary Discussion of the Factors Causing Laitou Landslide in Jiayi. J. Soil Water Conserv. 2012, 44, 177–188. [Google Scholar]
- Chen, C.-K.; Lin, B.-S.; Chi, S.-Y.; Chien, Y.-D.; Tsai, M.-F. Sediment Stability Assessment for Large-Scale Landslides Induced by Typhoon Morakot After Remediation in an Upstream Reservoir Watershed. Sinotech Eng. 2015, 182, 25–37. [Google Scholar]
- Wang, H.J.; Zhang, L.M.; Yin, K.S.; Luo, H.Y.; Li, J.H. Landslide identification using machine learning. Geosci. Front. 2021, 12, 351–364. [Google Scholar] [CrossRef]
- Vojtek, M.; Vojteková, J.; Pham, Q.B. GIS-Based Spatial and Multi-Criteria Assessment of Riverine Flood Potential: A Case Study of the Nitra River Basin, Slovakia. ISPRS Int. J. Geo-Inf. 2021, 10, 578. [Google Scholar] [CrossRef]
- Nguyen, K.; Chen, W. DEM- and GIS-Based Analysis of Soil Erosion Depth Using Machine Learning. ISPRS Int. J. Geo-Inf. 2021, 10, 452. [Google Scholar] [CrossRef]
- Chen, S.-C.; Wu, C.-Y. Establishment of Landslide Susceptibility Early Warning Model in National Forest Areas Based on Geo-intrinsic and Hydro-extrinsic Factors. J. Chin. Soil Water Conserv. 2018, 49, 89–97. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill/Irwin: New York, NY, USA, 2004. [Google Scholar]
- O’brien, R.M. A Caution Regarding Rules of Thumb for Variance Inflation Factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar]
- Chollet, F. Keras: The Python deep learning API. Available online: https://keras.io/ (accessed on 20 December 2021).
- Hale, J. Deep Learning Framework Power Scores 2018. Available online: https://www.kaggle.com/discdiver/deep-learning-framework-power-scores-2018 (accessed on 22 December 2021).
- Kaggle. State of Machine Learning and Data Science 2021. Available online: https://www.kaggle.com/kaggle-survey-2021 (accessed on 23 August 2022).
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. In Proceedings of the ICLR 2015, San Diego, CA, USA, 7–9 May 2015; 2015. [Google Scholar]
- O’Malley, T.; Bursztein, E.; Long, J.; Chollet, F.; Jin, H.; Invernizzi, L. KerasTuner. Available online: https://github.com/keras-team/keras-tuner (accessed on 4 May 2022).
- Chinchor, N. MUC-4 Evaluation Metrics. In Proceedings of the MUC4 92: Conference on Message Understanding, Stroudsburg, PA, USA, 16–18 June 1992; pp. 22–29. [Google Scholar]
- Taha, A.A.; Hanbury, A. Metrics for evaluating 3D medical image segmentation: Analysis, selection, and tool. BMC Med. Imaging 2015, 15, 29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chicco, D.; Warrens, M.J.; Jurman, G. The Matthews Correlation Coefficient (MCC) is More Informative Than Cohen’s Kappa and Brier Score in Binary Classification Assessment. IEEE Access 2021, 9, 78368–78381. [Google Scholar] [CrossRef]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library. Available online: https://gdal.org (accessed on 30 August 2022).





| Topography Factors | Data Source | Data Type | Value Range |
|---|---|---|---|
| Elevation | DEM | Continuous | 384.70–1238.10 |
| Slope | DEM | Continuous | 0.00–64.89 |
| Aspect | DEM | Continuous | −1.00–360.00 |
| Plan curvature | DEM | Continuous | −27.07–25.72 |
| Profile curvature | DEM | Continuous | −31.32–30.42 |
| Topographic Wetness Index (TWI) | DEM | Continuous | 2.65–20.51 |
| Stream Power Index (SPI) | DEM | Continuous | 0–4,388,483 |
| Distance to fault | CGS | Continuous | 0.00–1646.15 |
| Distance to river | DEM | Continuous | 0.00–680.66 |
| Distance to road | OpenStreetMap | Continuous | 0.00–610.98 |
| Lithology | CGS | Categorical | n/a |
| Hyperparameters | Type | Defined Parameters |
|---|---|---|
| Counts of Hidden Layer | Integer | 2–10 |
| Neurons of Hidden Layer | Integer | 4, 8, 12, …, 124, 128 |
| Dropout Rate | Real | 0.00, 0.05, 0.10, …, 0.85, 0.90 |
| Stepsize of Adam Optimizer | Float | 0.0001–0.1 |
| Features | Landslide Susceptibility (n = 62,252) | Rainfall Threshold (n = 31,126) |
|---|---|---|
| Elevation | 2.916 | 3.330 |
| Slope | 1.359 | 1.502 |
| Aspect | 1.435 | 1.381 |
| Plan Curvature | 1.548 | 1.548 |
| Profile Curvature | 1.246 | 1.252 |
| TWI | 1.963 | 2.293 |
| SPI | 1.279 | 1.447 |
| Distance to fault | 2.444 | 2.492 |
| Distance to river | 2.094 | 2.491 |
| Distance to road | 1.060 | 1.041 |
| Lithology | 1.346 | 1.423 |
| Hyperparameters | Landslide Susceptibility Classification | Rainfall Threshold Regression | ||||
|---|---|---|---|---|---|---|
| 1st | 2nd | 3rd | 1st | 2nd | 3rd | |
| Counts of hidden layer | 4 | 4 | 3 | 4 | 4 | 3 |
| Neurons of hidden layer 1 | 108 | 108 | 108 | 124 | 120 | 120 |
| Rate of dropout layer 1 | 0.05 | 0.05 | 0.30 | 0.20 | 0.20 | 0.45 |
| Neurons of hidden layer 2 | 84 | 84 | 96 | 128 | 108 | 84 |
| Rate of dropout layer 2 | 0.25 | 0.25 | 0.45 | 0.20 | 0.70 | 0.05 |
| Neurons of hidden layer 3 | 100 | 100 | 60 | 36 | 28 | 88 |
| Rate of dropout layer 3 | 0.45 | 0.45 | 0.10 | 0.25 | 0.05 | 0.00 |
| Neurons of hidden layer 4 | 112 | 112 | - | 72 | 28 | - |
| Rate of dropout layer 4 | 0.30 | 0.30 | - | 0.10 | 0.40 | - |
| Stepsize of Adam Optimizer | 0.000874 | 0.000874 | 0.000383 | 0.001889 | 0.000669 | 0.000507 |
| Initial epoch | 67 | 23 | 67 | 67 | 67 | 67 |
| Epochs | 200 | 67 | 200 | 200 | 200 | 200 |
| Best step | 91 | 41 | 127 | 83 | 120 | 99 |
| Validation accuracy | 0.8916 | 0.8683 | 0.8652 | n/a | n/a | n/a |
| Score (Validation loss) | 0.0801 | 0.0977 | 0.0998 | 0.0675 | 0.0704 | 0.0710 |
| Models | Evaluate | Train Dataset | Test Dataset |
|---|---|---|---|
| Landslide Susceptibility Classification | Overall accuracy | 0.9094 | 0.8959 |
| Precision | 0.9118 | 0.8985 | |
| Recall | 0.9094 | 0.8959 | |
| ROC AUC | 0.9633 | 0.9550 | |
| F1 score | 0.9092 | 0.8957 | |
| Cohen’s kappa | 0.8187 | 0.7918 | |
| MCC | 0.8211 | 0.7944 | |
| Rainfall Threshold Regression | MAE | 180.09 | 185.98 |
| RMSE | 228.03 | 233.97 | |
| MAPE | 0.2631 | 0.2716 |
| Recurrence Interval | p-Value | RMSE |
|---|---|---|
| Extreme-value Type I Distribution | 0.9995 | 0.0424 |
| Normal Distribution | 0.8510 | 0.0555 |
| Pearson Type III Distribution | 0.9725 | 0.0441 |
| Log-Normal Distribution | 0.9725 | 0.0437 |
| Log-Pearson Type III Distribution | 0.8510 | 0.0840 |
| Regions | Condition | Rainfall Threshold (mm/day) | Recurrence Interval (Year) |
|---|---|---|---|
| Northeast Alishan D098 Downstream of Alishan D098 Longmei Settlement | Non-managed | 780 | 20 |
| Has been managed | 820 | 25 | |
| Whole Area | n/a | 980 | 64 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiang, J.-L.; Kuo, C.-M.; Fazeldehkordi, L. Using Deep Learning to Formulate the Landslide Rainfall Threshold of the Potential Large-Scale Landslide. Water 2022, 14, 3320. https://doi.org/10.3390/w14203320
Chiang J-L, Kuo C-M, Fazeldehkordi L. Using Deep Learning to Formulate the Landslide Rainfall Threshold of the Potential Large-Scale Landslide. Water. 2022; 14(20):3320. https://doi.org/10.3390/w14203320
Chicago/Turabian StyleChiang, Jie-Lun, Chia-Ming Kuo, and Leila Fazeldehkordi. 2022. "Using Deep Learning to Formulate the Landslide Rainfall Threshold of the Potential Large-Scale Landslide" Water 14, no. 20: 3320. https://doi.org/10.3390/w14203320





