Effect of Attached Growth on Treatment Performance in Waste Stabilization Ponds
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
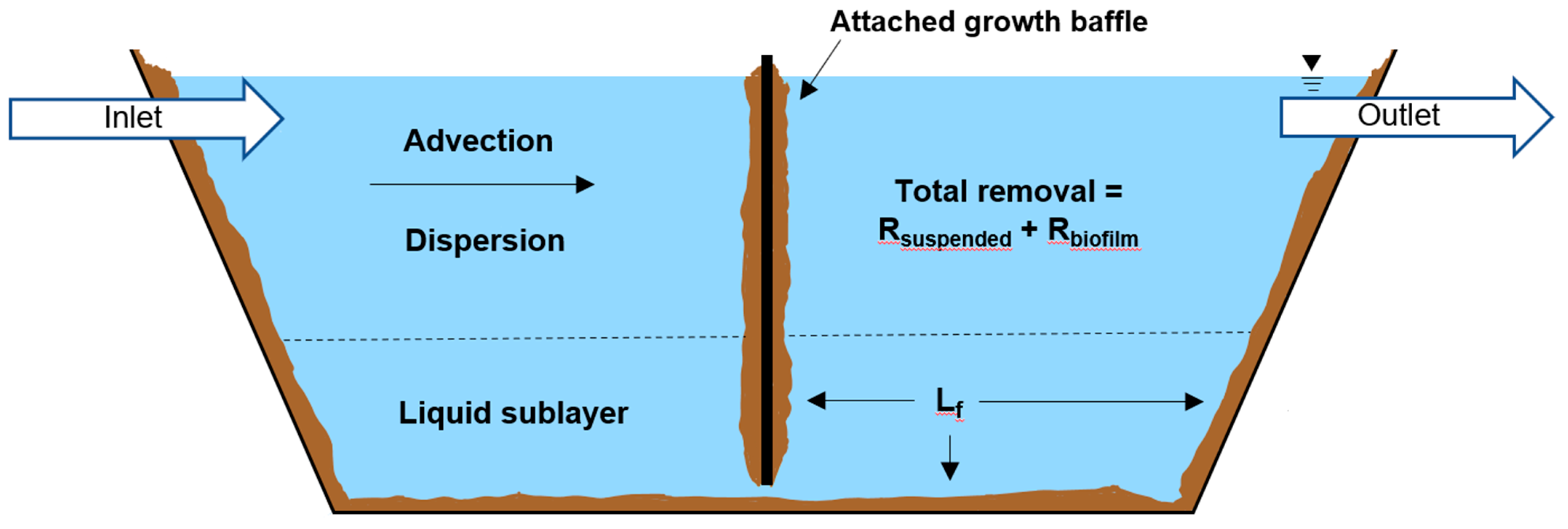
2.2. Attached Growth Baffle Selection and Installation
2.3. Application of First-Order Kinetics to Determine the Contribution of Baffles on Pond Performance
2.4. Baffle Impacts Analysis and Generalization of Kinetic Model
2.5. Statistical Analysis
3. Results
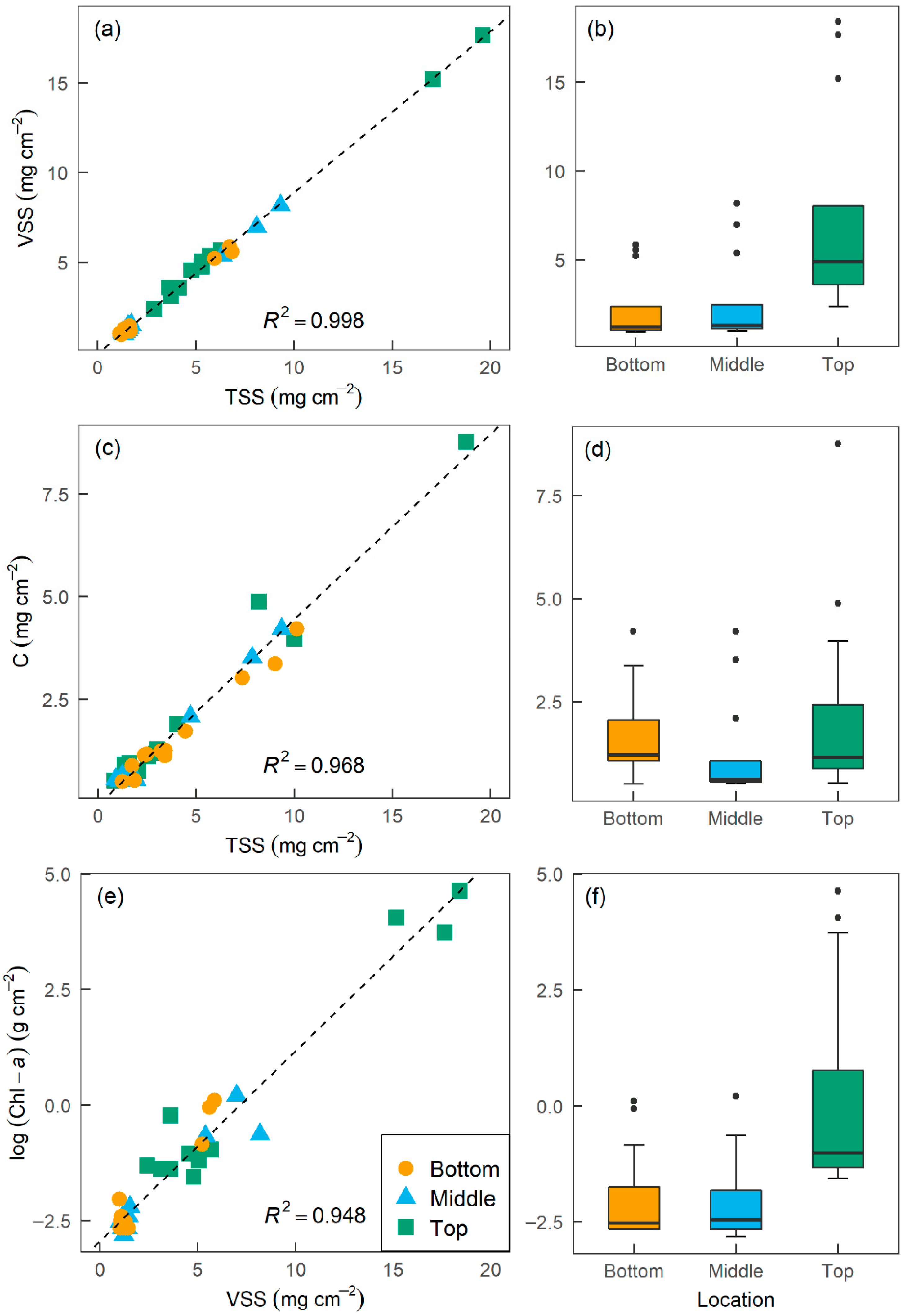
3.1. Hydraulics and Attached Growth
3.2. Application of Kinetic Model
3.2.1. Model Validation
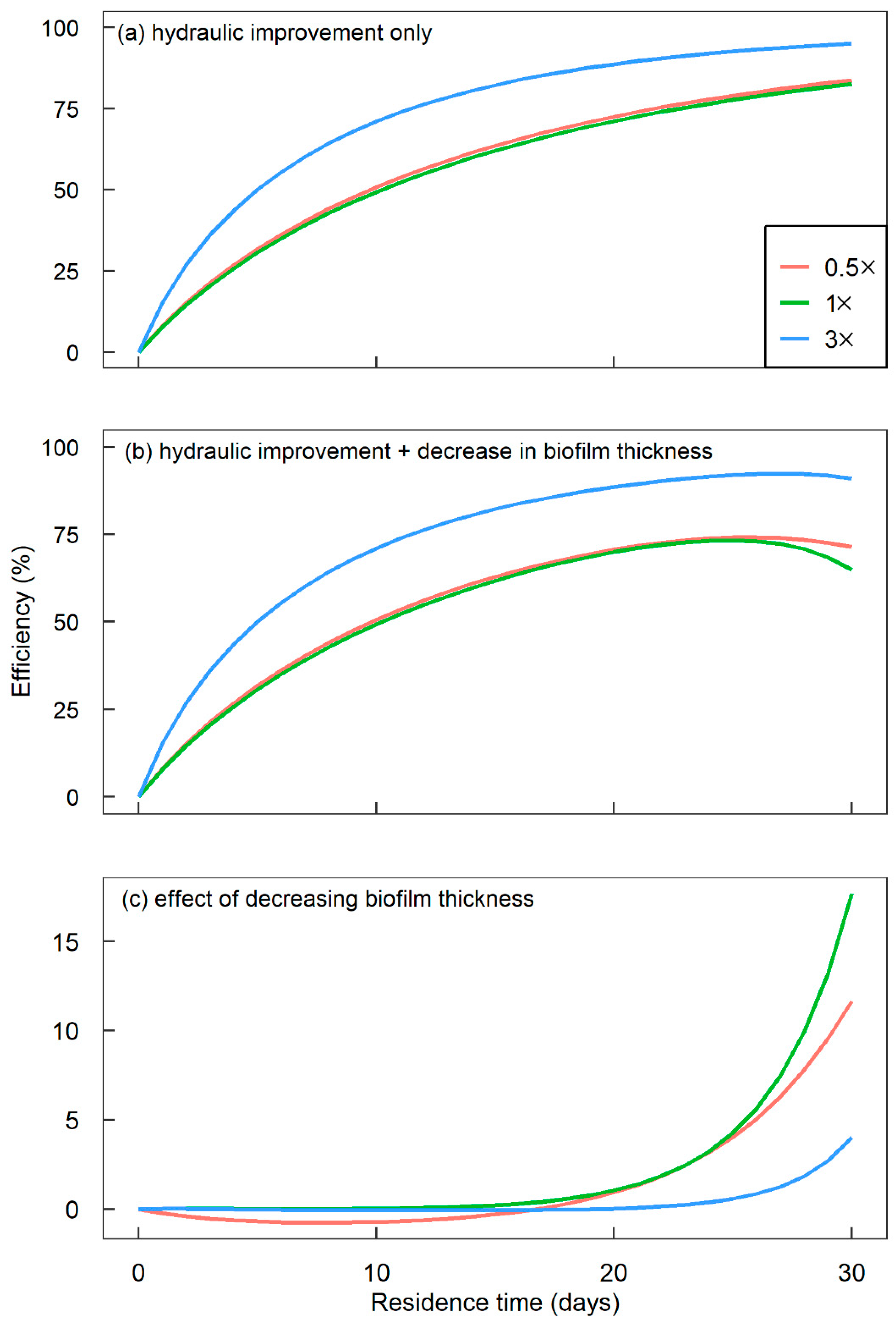
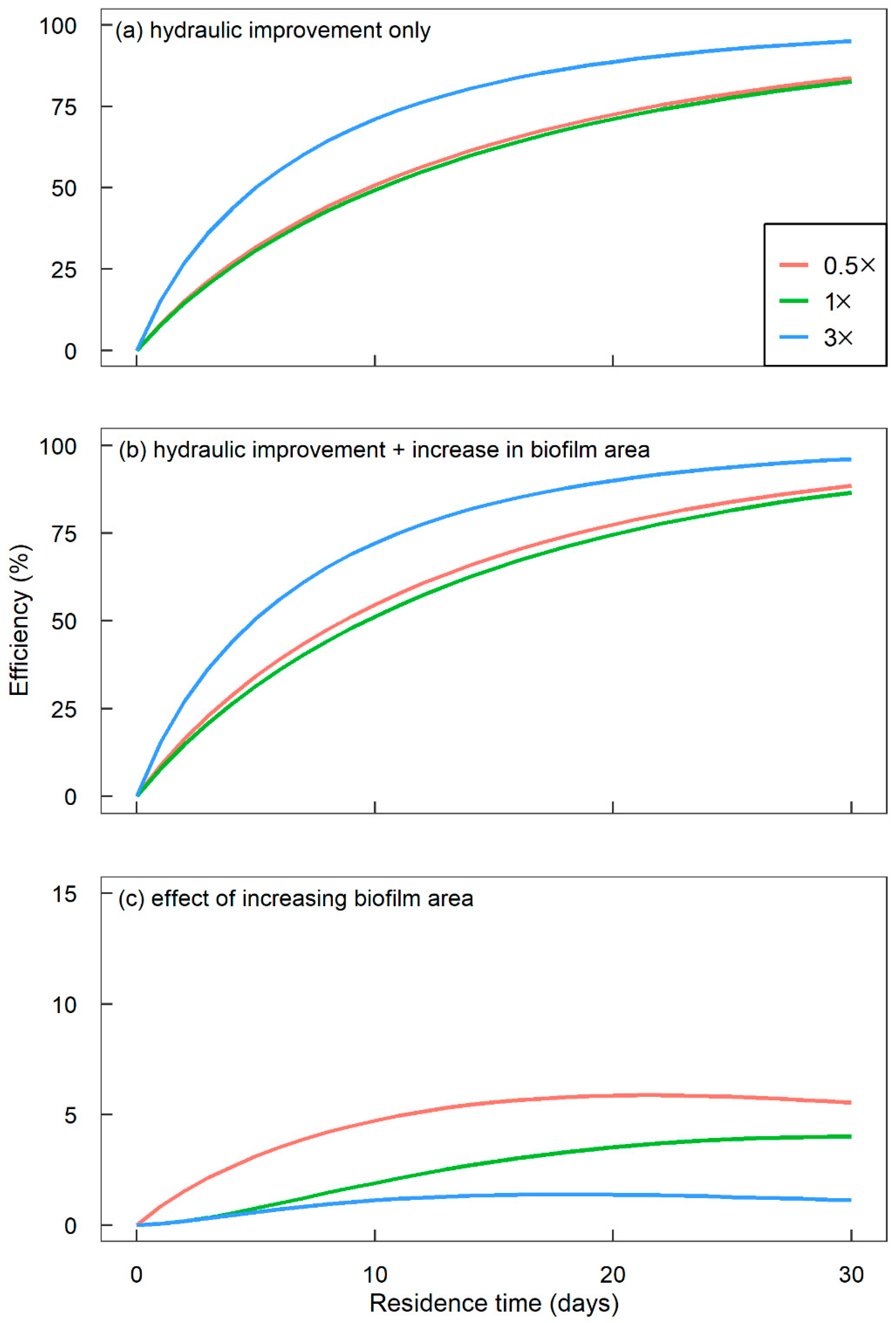
3.2.2. Calculating BOD Reduction of Different Scenarios
3.2.3. Generalisation of Kinetic Model
3.3. Water Quality
4. Discussion
4.1. Hydraulic Improvement and Attached Growth
4.2. Analysis of the Improvement of Pond Performance
4.3. The Influence of Biofilm Thickness Changes on Pond Performance
4.4. The Influence of Increasing Biofilm Area on Pond Performance
4.5. The Analysis of First-Order Kinetic Model Formula
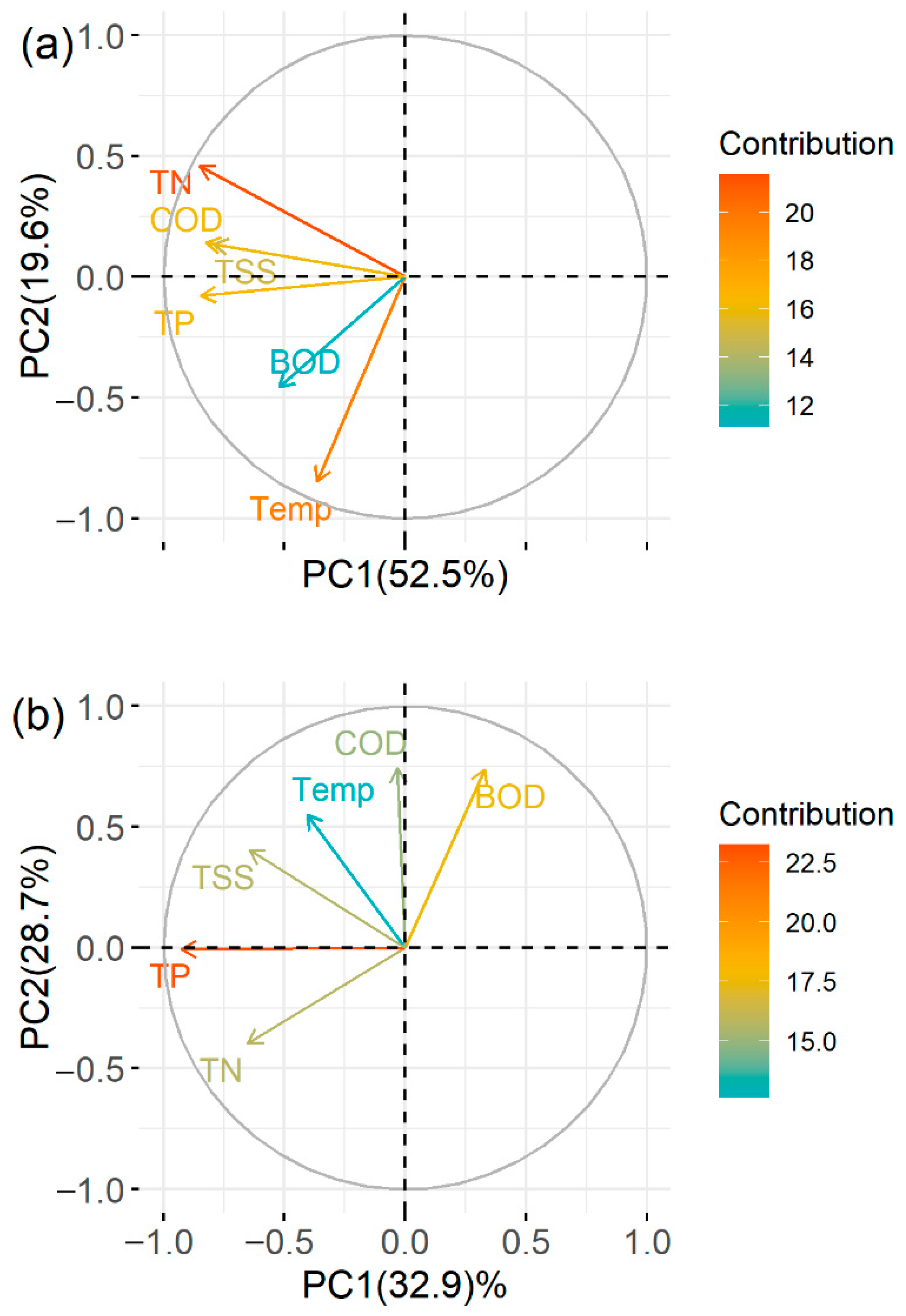
4.6. The Relationship among Water Quality Indicators
4.7. Recommendations
- Exploring and considering the interplay between hydraulics and suspended biomass in the kinetic model.
- Including the correlation between biofilm structure and development in the model formula.
- Performing longer field experiments and increasing the frequency of water quality data collection. In this study, the attached growth baffles were installed in Pond 2 at the study site for 13 months, however, the water quality data was limited after removing the outliers.
- Measuring all the result-sensitive values in the first-order kinetic model formula (e.g., kfa).
- The choice of baffle material would be more flexible: choosing baffles without the ability of attached growth, which will lower their cost.
- Exploring methods and materials to greatly increase attached growth area to maximize the effect of both hydraulics improvement and attached growth.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mara, D. Domestic Wastewater Treatment in Developing Countries; Routledge: London, UK, 2013. [Google Scholar]
- Coggins, L.X.; Crosbie, N.D.; Ghadouani, A. The small, the big, and the beautiful: Emerging challenges and opportunities for waste stabilization ponds in Australia. Wiley Interdiscip. Rev. Water 2019, 6, e1383. [Google Scholar] [CrossRef] [Green Version]
- Peña, M.; Mara, D. Waste Stabilisation Ponds; IRC International Water and Sanitation Centre: Delft, The Netherlands, 2004. [Google Scholar]
- Passos, R.; Dias, D.; Von Sperling, M. Review of practical aspects for modelling of stabilization ponds using Computational Fluid Dynamics. Environ. Technol. Rev. 2016, 5, 78–102. [Google Scholar] [CrossRef]
- Persson, J.; Wittgren, H.B. How hydrological and hydraulic conditions affect performance of ponds. Ecol. Eng. 2003, 21, 259–269. [Google Scholar] [CrossRef] [Green Version]
- Sah, L.; Rousseau, D.P.; Hooijmans, C.M. Numerical modelling of waste stabilization ponds: Where do we stand? Water Air Soil Pollut. 2012, 223, 3155–3171. [Google Scholar] [CrossRef]
- Passos, R.G.; Dias, D.F.C.; von Sperling, M. Simple mid-depth transverse baffles to improve bacterial disinfection in a shallow maturation pond–performance evaluation and CFD simulation. Environ. Technol. 2020, 43, 1437–1445. [Google Scholar] [CrossRef] [PubMed]
- Dahl, N.W.; Woodfield, P.L.; Simpson, B.A.; Stratton, H.M.; Lemckert, C.J. Effect of turbulence, dispersion, and stratification on Escherichia coli disinfection in a subtropical maturation pond. J. Environ. Manag. 2021, 288, 112470. [Google Scholar] [CrossRef]
- Farjood, A.; Melville, B.W.; Shamseldin, A.Y. The effect of different baffles on hydraulic performance of a sediment retention pond. Ecol. Eng. 2015, 81, 228–232. [Google Scholar] [CrossRef]
- Martyniuk, N.; Souza, M.S.; Navarro, M.B.; Balseiro, E.; Modenutti, B. Nutrient limitation affects biofilm enzymatic activities in a glacier-fed river. Hydrobiologia 2022, 849, 2877–2894. [Google Scholar] [CrossRef]
- Li, N.; Li, X.; Fan, X.-Y. Storage tank as a pretreatment unit for rainwater cleaner production: Role of biofilm bacterial communities and functional genera in water quality improvement. J. Environ. Manag. 2021, 303, 114118. [Google Scholar] [CrossRef]
- Mahapatra, S.; Samal, K.; Dash, R.R. Waste Stabilization Pond (WSP) for wastewater treatment: A review on factors, modelling and cost analysis. J. Environ. Manag. 2022, 308, 114668. [Google Scholar] [CrossRef]
- Salter, H.E.; Ta, C.T.; Ouki, S.K.; Williams, S.C. Three-dimensional computational fluid dynamic modelling of a facultative lagoon. Water Sci. Technol. 2000, 42, 335–342. [Google Scholar] [CrossRef]
- Shilton, A. Potential application of computational fluid dynamics to pond design. Water Sci. Technol. 2000, 42, 327–334. [Google Scholar] [CrossRef]
- Shilton, A.; Harrison, J. Integration of coliform decay within a CFD (computational fluid dynamic) model of a waste stabilisation pond. Water Sci. Technol. 2003, 48, 205–210. [Google Scholar] [CrossRef] [PubMed]
- Vega, G.; Peña, M.R.; Ramírez, C.; Mara, D. Application of CFD modelling to study the hydrodynamics of various anaerobic pond configurations. Water Sci. Technol. 2003, 48, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Shilton, A.; Mara, D. CFD (computational fluid dynamics) modelling of baffles for optimizing tropical waste stabilization pond systems. Water Sci. Technol. 2005, 51, 103–106. [Google Scholar] [CrossRef]
- Abbas, H.; Nasr, R.; Seif, H. Study of waste stabilization pond geometry for the wastewater treatment efficiency. Ecol. Eng. 2006, 28, 25–34. [Google Scholar] [CrossRef]
- Banda, C.G.; Sleigh, P.A.; Mara, D.D. 3D-CFD modelling of E. coli removal in baffled primary facultative ponds: Classical design optimization. In Proceedings of the 7th IWA Specialist Group Conference on Waste Stabilization Ponds, Bangkok, Thailand, 25–27 September 2006. [Google Scholar]
- Banda, C.G.; Sleigh, P.A.; Mara, D.D. CFD-based design of waste stabilization ponds: Significance of wind velocity. In Proceedings of the 7th IWA Specialist Group Conference on Waste Stabilization Ponds, Bangkok, Thailand, 25–27 September 2006; pp. 25–27. [Google Scholar]
- Polprasert, C.; Agarwalla, B.K. A facultative pond model incorporating biofilm activity. Water Environ. Res. 1994, 66, 725–732. [Google Scholar] [CrossRef]
- Muttamara, S.; Puetpaiboon, U. Roles of baffles in waste stabilization ponds. Water Sci. Technol. 1997, 35, 275–284. [Google Scholar] [CrossRef]
- Polprasert, C.; Agarwalla, B.K. Significance of biofilm activity in facultative pond design and performance. Water Sci. Technol. 1995, 31, 119–128. [Google Scholar] [CrossRef]
- Shin, H.K.; Polprasert, C. Attached growth Waste Stabilization Pond Treatment Evaluation. Water Sci. Technol. 1987, 19, 229–235. [Google Scholar] [CrossRef]
- Muttamara, S.; Puetpaiboon, U. Nitrogen removal in Baffled waste stabilization ponds. Water Sci. Technol. 1996, 33, 173–181. [Google Scholar] [CrossRef]
- Coggins, L.X.; Sounness, J.; Zheng, L.; Ghisalberti, M.; Ghadouani, A. Impact of Hydrodynamic Reconfiguration with Baffles on Treatment Performance in Waste Stabilisation Ponds: A Full-Scale Experiment. Water 2018, 10, 109. [Google Scholar] [CrossRef] [Green Version]
- Bureau of Meteorology (BOM). Climate Data. Available online: http://www.bom.gov.au/climate/data/ (accessed on 19 July 2016).
- Burns, A.; Ryder, D.S. Potential for biofilms as biological indicators in Australian riverine systems. Ecol. Manag. Restor. 2001, 2, 53–64. [Google Scholar] [CrossRef]
- Polprasert, C.; Bhattarai, K.K. Dispersion Model for Waste Stabilization Ponds. J. Environ. Eng. 1985, 111, 45–59. [Google Scholar] [CrossRef]
- von Sperling, M. Performance evaluation and mathematical modelling of coliform die-off in tropical and subtropical waste stabilization ponds. Water Res. 1999, 33, 1435–1448. [Google Scholar] [CrossRef]
- Ro, K.S.; Neethling, J.B. Biofilm density for biological fluidized beds. Res. J. Water Pollut. Control Fed. 1991, 63, 815–818. [Google Scholar]
- Mara, D. Sewage Treatment in Hot Climates; John Wiley & Sons Ltd.: Chichester, UK, 1976. [Google Scholar]
- Thirumurthi, D. Design criteria for waste stabilization ponds. J. (Water Pollut. Control Fed.) 1974, 46, 2094–2106. [Google Scholar]
- Melloul, A.; Collin, M. The ‘principal components’ statistical method as a complementary approach to geochemical methods in water quality factor identification; application to the Coastal Plain aquifer of Israel. J. Hydrol. 1992, 140, 49–73. [Google Scholar] [CrossRef]
- Bengraïne, K.; Marhaba, T.F. Using principal component analysis to monitor spatial and temporal changes in water quality. J. Hazard. Mater. 2003, 100, 179–195. [Google Scholar] [CrossRef]
- Ni, M.; Yuan, J.-L.; Liu, M.; Gu, Z.-M. Assessment of water quality and phytoplankton community of Limpenaeus vannamei pond in intertidal zone of Hangzhou Bay, China. Aquac. Rep. 2018, 11, 53–58. [Google Scholar] [CrossRef]
- Laspidou, C.S.; Rittmann, B.E. A unified theory for extracellular polymeric substances, soluble microbial products, and active and inert biomass. Water Res. 2002, 36, 2711–2720. [Google Scholar] [CrossRef]
- Evans, E.; Brown, M.R.W.; Gilbert, P. Iron chelator, exopolysaccharide and protease production in Staphylococcus epidermidis: A comparative study of the effects of specific growth rate in biofilm and planktonic culture. Microbiology 1994, 140, 153–157. [Google Scholar] [CrossRef] [PubMed]
- Robinson, J.A.; Trulear, M.G.; Characklis, W.G. Cellular reporoduction and extracellular polymer formation byPseudomonas aeruginosa in continuous culture. Biotechnol. Bioeng. 1984, 26, 1409–1417. [Google Scholar] [CrossRef] [PubMed]
- Van Loosdrecht, M.C.M.; Eikelboom, D.; Gjaltema, A.; Mulder, A.; Tijhuis, L.; Heijnen, J.J. Biofilm structures. Water Sci. Technol. 1995, 32, 35–43. [Google Scholar] [CrossRef]
- Celmer, D.; Oleszkiewicz, J.; Cicek, N. Impact of shear force on the biofilm structure and performance of a membrane biofilm reactor for tertiary hydrogen-driven denitrification of municipal wastewater. Water Res. 2008, 42, 3057–3065. [Google Scholar] [CrossRef]
- Kesaano, M.; Sims, R.C. Algal biofilm based technology for wastewater treatment. Algal Res. 2014, 5, 231–240. [Google Scholar] [CrossRef]
- Corcoll, N.; Bonet, B.; Leira, M.; Montuelle, B.; Tlili, A.; Guasch, H. Light History Influences the Response of Fluvial Biofilms to Zn Exposure. J. Phycol. 2012, 48, 1411–1423. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Li, X.L.; Ji, M.; Liu, J. Performance and microbial characteristics of integrated fixed-film activated sludge system treating industrial wastewater. Water Sci. Technol. 2012, 66, 2785–2792. [Google Scholar] [CrossRef] [PubMed]
- Lazarova, V.; Pierzo, V.; Fontvielle, D.; Manem, J. Integrated Approach for Biofilm Characterisation and Biomass Activity Control. Water Sci. Technol. 1994, 29, 345–354. [Google Scholar] [CrossRef]
- Liu, Y. Estimating Minimum Fixed Biomass Concentration and Active Thickness of Nitrifying Biofilm. J. Environ. Eng. 1997, 123, 198–202. [Google Scholar] [CrossRef]
- Christensen, F.R.; Kristensen, G.H.; Jansen, J.L.C. Biofilm Structure–An Important and Neglected Parameter in Waste Water Treatment. Water Sci. Technol. 1989, 21, 805–814. [Google Scholar] [CrossRef]
- Harremoës, P. Half-order reactions in biofilm and filter kinetics. Vatten 1977, 2, 122–143. [Google Scholar]
- La Motta, E.J. Kinetics of Growth and Substrate Uptake in a Biological Film System. Appl. Environ. Microbiol. 1976, 31, 286–293. [Google Scholar] [CrossRef] [PubMed]
- Williamson, K.; McCarty, P.L. Verification studies of the biofilm model for bacterial substrate utilization. J. (Water Pollut. Control Fed.) 1976, 48, 281–296. [Google Scholar]
- Polprasert, C.; Khatiwada, N.R. An integrated kinetic model for water hyacinth ponds used for wastewater treatment. Water Res. 1998, 32, 179–185. [Google Scholar] [CrossRef]
- Tee, P.-F.; Abdullah, M.O.; Tan, I.A.; Amin, M.A.; Nolasco-Hipolito, C.; Bujang, K. Effects of temperature on wastewater treatment in an affordable microbial fuel cell-adsorption hybrid system. J. Environ. Chem. Eng. 2017, 5, 178–188. [Google Scholar] [CrossRef] [Green Version]
- Tejaswini, E.; Babu, G.U.B.; Rao, A.S. Effect of Temperature on Effluent Quality in a Biological Wastewater Treatment Process. Chem. Prod. Process Model. 2019, 15, 18. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Yu, S.; Rhew, D. Relationships between water quality parameters in rivers and lakes: BOD5, COD, NBOPs, and TOC. Environ. Monit. Assess. 2016, 188, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Meili, M. Sources, concentrations and characteristics of organic matter in softwater lakes and streams of the Swedish forest region. Hydrobiologia 1992, 229, 23–41. [Google Scholar] [CrossRef]
- Lever, J.; Krzywinski, M.; Altman, N. Points of Significance: Principal component analysis. Nat. Methods 2017, 14, 641–642. [Google Scholar] [CrossRef]





| Scenario | Characteristics |
|---|---|
| 1 | No baffles (control pond) |
| 2 | Three perpendicular baffles, no attached growth |
| 3 | Three perpendicular baffles with attached growth |
| 4 | One island + three perpendicular baffles, no attached growth |
| 5 | One island + three perpendicular baffles with attached growth |
| Organic Loading Rate | Characteristics |
|---|---|
| As in the experiment (1×) | With hydraulic improvement but no attached growth. |
| Three times that of the experiment (3×) | With hydraulic improvement and change in biofilm thickness. |
| Half that of the experiment (0.5×) | With hydraulic improvement and increased in biofilm area. |
| Parameter | Pond 1 | Pond 2 (Baffle) |
|---|---|---|
| Raw water | 200 | 200 |
| Observed | 89 | 64 |
| Estimated | 89.68 | 65.48 |
| Suspended biomass only | 134 | 116 |
| Actual treatment efficiency | 55.5% | 68% |
| Estimated treatment efficiency | 55.16% | 67.3% |
| BOD reduction by suspended biomass only | 34% | 42% |
| Parameters | Unit | Pond 1 | Pond 2 (Baffled) | Comment |
|---|---|---|---|---|
| d | - | 0.35 | 0.39 | Equations (5) and (6) give the range of 0.336–0.445 for Pond 1 and 0.383–0.400 for Pond 2. |
| as | m2 m−3 | 0.822 | 0.858 | Equations (9) and (10) |
| kfs | day−1 | 0.0366 | 0.0366 | Equation (8) |
| kfa | day−1 | 199 | 199 | Adjusted based on the assumed biofilm density 0.03 g cm−3. |
| Df | m2 day−1 | 24.45 × 10−6 | 24.45 × 10−6 | Assumed based on reasonable principle. |
| Dw | m2 day−1 | 48.9 × 10−6 | 48.9 × 10−6 | Assumed based on reasonable principle. |
| Lf | m | 1.54 × 10−3 | 1.386 × 10−3 | Assumed based on reasonable principle. |
| Ls | m | 200 × 10−6 | 200 × 10−6 | Assumed based on reasonable principle. |
| Scenario | Residence Time (days) | Specific Surface Area (m2/m3) | BOD Removal Efficiency | Compared to Control Pond | Comparison of with and without Attached Growth |
|---|---|---|---|---|---|
| No baffles | 14 | 0.822 | 60.4% | 0 | ---- |
| Three perpendicular baffles, no attached growth | 17 | 0.822 | 65.6% | +5.3% | 0 |
| Three perpendicular baffles with attached growth | 17 | 0.858 | 67.3% | +6.9% | +1.6% |
| One island + three perpendicular baffles, no attached growth | 22.4 | 0.822 | 74.4% | +14.1% | 0 |
| One island + three perpendicular baffles with attached growth | 22.4 | 0.882 | 75.7% | +15.3% | +1.2% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, Y.; Coggins, L.X.; Hay, J.; van de Ven, A.; Ghadouani, A. Effect of Attached Growth on Treatment Performance in Waste Stabilization Ponds. Water 2022, 14, 3245. https://doi.org/10.3390/w14203245
Lian Y, Coggins LX, Hay J, van de Ven A, Ghadouani A. Effect of Attached Growth on Treatment Performance in Waste Stabilization Ponds. Water. 2022; 14(20):3245. https://doi.org/10.3390/w14203245
Chicago/Turabian StyleLian, Yirui, Liah X. Coggins, Jessica Hay, Andrew van de Ven, and Anas Ghadouani. 2022. "Effect of Attached Growth on Treatment Performance in Waste Stabilization Ponds" Water 14, no. 20: 3245. https://doi.org/10.3390/w14203245








