Review of Nonpoint Source Pollution Models: Current Status and Future Direction
Abstract
:1. Introduction
2. Overview of NPS Model
2.1. Basic NPS Pollution Processes and Model Framework
2.2. NPS Model Development
2.3. Model Classification
2.3.1. Statistical Model and Mechanism Model
2.3.2. Lumped, Semi-Distributed and Distributed Model
2.3.3. Field-Scale, Catchment-Scale and Watershed-Scale Model
2.4. Classical NPS Models
2.4.1. The Export Coefficient Model
2.4.2. Soil and Water Assessment Tool (SWAT) Model
2.4.3. Hydrological Simulation Programs Fortran (HSPF) Model
2.5. Trends of NPS Model Research
3. Challenges in NPS Model Research
3.1. Challenges in Model Construction
3.1.1. Specific Process Incorporation
3.1.2. Model Expansion to Different Scales
3.2. Challenges in Model Application
3.2.1. Data Are Still a Problem
3.2.2. Prediction Uncertainty Puzzles Modelers
Data Uncertainty
Structural Uncertainty
Parameter Uncertainty
3.2.3. Insufficient Accuracy for Decision-Making
4. Future Prospects for NPS Model Development
4.1. The “Source–Flow–Sink” Framework for Model Development
4.2. Standardization for Model Input and Parameter
4.3. Make Reliable Decision Support
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kast, J.B.; Apostel, A.M.; Kalcic, M.M.; Muenich, R.L.; Dagnew, A.; Long, C.M.; Evenson, G.; Martin, J.F. Source contribution to phosphorus loads from the Maumee River watershed to Lake Erie. J. Environ. Manag. 2021, 279, 111803. [Google Scholar] [CrossRef] [PubMed]
- Driscoll, C.T.; Whitall, D.; Aber, J.; Boyer, E.; Castro, M.; Cronan, C.; Goodale, C.L.; Groffman, P.; Hopkinson, C.; Lambert, K.; et al. Nitrogen pollution in the northeastern United States: Sources, effects, and management options. Bioscience 2003, 53, 357–374. [Google Scholar] [CrossRef]
- Sun, C.; Chen, L.; Zhai, L.M.; Liu, H.B.; Zhou, H.Z.; Wang, Q.R.; Wang, K.; Shen, Z.Y. National-scale evaluation of phosphorus emissions and the related water-quality risk hotspots accompanied by increased agricultural production. Agric. Ecosyst. Environ. 2018, 267, 33–41. [Google Scholar] [CrossRef]
- Xie, H.; Chen, L.; Shen, Z.Y. Assessment of Agricultural Best Management Practices Using Models: Current Issues and Future Perspectives. Water 2015, 7, 1088–1108. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.M.; Wu, Y.Y.; Liu, X.J.; Reis, S.; Jin, J.X.; Dragosits, U.; Van Damme, M.; Clarisse, L.; Whitburn, S.; Coheur, P.F.; et al. Ammonia Emissions May Be Substantially Underestimated in China. Environ. Sci. Technol. 2017, 51, 12089–12096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, S.; Chen, L.; Liu, X.; Pan, Y.; Zhou, F.; Guo, J.; Huang, T.; Chen, F.; Shen, Z. Unexpected nitrogen flow and water quality change due to varying atmospheric deposition. J. Hydrol. 2022, 609, 127679. [Google Scholar] [CrossRef]
- Zhou, L.; Geng, R. Development and Assessment of a New Framework for Agricultural Nonpoint Source Pollution Control. Water 2021, 13, 3156. [Google Scholar] [CrossRef]
- Yuan, L.F.; Sinshaw, T.; Forshay, K.J. Review of Watershed-Scale Water Quality and Nonpoint Source Pollution Models. Geosciences 2020, 10, 25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, B.; Merritt, W.S.; Croke, B.F.W.; Weber, T.R.; Jakeman, A.J. A review of catchment-scale water quality and erosion models and a synthesis of future prospects. Environ. Model. Softw. 2019, 114, 75–97. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Yang, X.Y.; Haywood, J. A review of SWAT applications, performance and future needs for simulation of hydro-climatic extremes. Adv. Water Resour. 2020, 143, 103662. [Google Scholar] [CrossRef]
- Ly, K.; Metternicht, G.; Marshall, L. Transboundary river catchment areas of developing countries: Potential and limitations of watershed models for the simulation of sediment and nutrient loads. A review. J. Hydrol. Reg. Stud. 2019, 24, 100605. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Zhang, T.Q.; Tan, C.S.; Qi, Z.M. Modeling of phosphorus loss from field to watershed: A review. J. Environ. Qual. 2020, 49, 1203–1224. [Google Scholar] [CrossRef] [PubMed]
- Arnillas, C.A.; Yang, C.; Zamaria, S.A.; Neumann, A.; Javed, A.; Shimoda, Y.; Feisthauer, N.; Crolla, A.; Dong, F.F.; Blukacz, A.R.; et al. Integrating watershed and ecosystem service models to assess best management practice efficiency: Guidelines for Lake Erie managers and watershed modellers. Environ. Rev. 2021, 29, 31–63. [Google Scholar] [CrossRef]
- Gu, B.J.; Ju, X.T.; Chang, J.; Ge, Y.; Vitousek, P.M. Integrated reactive nitrogen budgets and future trends in China. Proc. Natl. Acad. Sci. USA 2015, 112, 8792–8797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, H.C.; Zhang, L.; Wang, S.R.; Jiao, L.X. Features and influencing factors of nitrogen and phosphorus diffusive fluxes at the sediment-water interface of Erhai Lake. Environ. Sci. Pollut. Res. 2018, 25, 1933–1942. [Google Scholar] [CrossRef]
- Morbidelli, R.; Corradini, C.; Saltalippi, C.; Flammini, A.; Dari, J.; Govindaraju, R.S. Rainfall Infiltration Modeling: A Review. Water 2018, 10, 1873. [Google Scholar] [CrossRef] [Green Version]
- Shi, W.H.; Huang, M.B.; Wu, L.H. Prediction of storm-based nutrient loss incorporating the estimated runoff and soil loss at a slope scale on the Loess Plateau. Land Degrad. Dev. 2018, 29, 2899–2910. [Google Scholar] [CrossRef]
- Alewell, C.; Borrelli, P.; Meusburger, K.; Panagos, P. Using the USLE: Chances, challenges and limitations of soil erosion modelling. Int. Soil Water Conserv. Res. 2019, 7, 203–225. [Google Scholar] [CrossRef]
- Chen, C.; Song, M. Visualizing a field of research: A methodology of systematic scientometric reviews. PLoS ONE 2019, 14, e0223994. [Google Scholar] [CrossRef] [Green Version]
- Knisel, W.G.; Douglas-Mankin, K.R. CREAMS/GLEAMS: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1291–1302. [Google Scholar] [CrossRef]
- Young, R.A.; Onstad, C.A.; Bosch, D.D.; Anderson, W.P. AGNPS—A nonpoint-source pollution model for evaluating agricultural watersheds. J. Soil Water Conserv. 1989, 44, 168–173. [Google Scholar]
- Duda, P.B.; Hummel, P.R.; Donigian, A.S.; Imhoff, J.C. BASINS/HSPF: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1523–1547. [Google Scholar] [CrossRef]
- Yuan, Y.P.; Bingner, R.L.; Rebich, R.A. Evaluation of AnnaGNPS on Mississippi Delta MSEA watersheds. Trans. ASABE 2001, 44, 1183–1190. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Kim, S.; Kim, M.; Kim, H.; Baek, S.S.; Kim, W.; Kim, S.D.; Cho, K.H. Chemical accidents in freshwater: Development of forecasting system for drinking water resources. J. Hazard. Mater. 2022, 432, 128714. [Google Scholar] [CrossRef] [PubMed]
- Shultz, C.D.; Bailey, R.T.; Gates, T.K.; Heesemann, B.E.; Morway, E.D. Simulating selenium and nitrogen fate and transport in coupled stream-aquifer systems of irrigated regions. J. Hydrol. 2018, 560, 512–529. [Google Scholar] [CrossRef]
- Borah, D.K.; Ahmadisharaf, E.; Padmanabhan, G.; Imen, S.; Mohamoud, Y.M. Watershed Models for Development and Implementation of Total Maximum Daily Loads. J. Hydrol. Eng. 2019, 24, 03118001. [Google Scholar] [CrossRef]
- Gilhespy, S.L.; Anthony, S.; Cardenas, L.; Chadwick, D.; del Prado, A.; Li, C.; Misselbrook, T.; Rees, R.M.; Salas, W.; Sanz-Cobena, A.; et al. First 20 years of DNDC (DeNitrification DeComposition): Model evolution. Ecol. Model. 2014, 292, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.; Grant, B.; Qi, Z.; He, W.; VanderZaag, A.; Drury, C.F.; Helmers, M. Development of the DNDC model to improve soil hydrology and incorporate mechanistic tile drainage: A comparative analysis with RZWQM2. Environ. Model. Softw. 2020, 123, 104577. [Google Scholar] [CrossRef]
- Gassman, P.W.; Williams, J.R.; Wang, X.; Saleh, A.; Osei, E.; Hauck, L.M.; Izaurralde, R.C.; Flowers, J.D. The Agricultural Policy/environmental Extender (apex) Model: An Emerging Tool For Landscape And Watershed Environmental Analyses. Trans. ASABE 2010, 53, 711–740. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, A.; Lee, S.; McCarty, G.W.; Lang, M.W.; Jeong, J.; Sadeghi, A.M.; Rabenhorst, M.C. Enhancement of Agricultural Policy/Environment eXtender (APEX) Model to Assess Effectiveness of Wetland Water Quality Functions. Water 2019, 11, 606. [Google Scholar] [CrossRef]
- Zhu, Z.; Chen, Z.; Chen, X.; Yu, G. An assessment of the hydrologic effectiveness of low impact development (LID) practices for managing runoff with different objectives. J. Environ. Manag. 2019, 231, 504–514. [Google Scholar] [CrossRef] [PubMed]
- Neumann, A.; Blukacz-Richards, E.A.; Yao, H.X.; James, A.L.; Arhonditsis, G.B. An ensemble of Bayesian SPARROW models for the Precambrian Shield in the eastern Georgian Bay drainage basin, Ontario, Canada. J. Great Lakes Res. 2021, 47, 1671–1688. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Hong, Q.; Chu, Z.; Gong, Y.W. A framework for priority non-point source area identification and load estimation integrated with APPI and PLOAD model in Fujiang Watershed, China. Agric. Water Manag. 2011, 98, 977–989. [Google Scholar] [CrossRef]
- Lin, C.; Wu, Z.P.; Ma, R.H.; Su, Z.H. Detection of sensitive soil properties related to non-point phosphorus pollution by integrated models of SEDD and PLOAD. Ecol. Indic. 2016, 60, 483–494. [Google Scholar] [CrossRef]
- Xin, Z.H.; Ye, L.; Zhang, C. Application of Export Coefficient Model and QUAL2K for Water Environmental Management in a Rural Watershed. Sustainability 2019, 11, 6022. [Google Scholar] [CrossRef] [Green Version]
- Ding, X.W.; Shen, Z.Y.; Hong, Q.; Yang, Z.F.; Wu, X.; Liu, R.M. Development and test of the Export Coefficient Model in the Upper Reach of the Yangtze River. J. Hydrol. 2010, 383, 233–244. [Google Scholar] [CrossRef]
- Lambrecht, N.; Katsev, S.; Wittkop, C.; Hall, S.J.; Sheik, C.S.; Picard, A.; Fakhraee, M.; Swanner, E.D. Biogeochemical and physical controls on methane fluxes from two ferruginous meromictic lakes. Geobiology 2020, 18, 54–69. [Google Scholar] [CrossRef]
- Ning, L.K.; Zhan, C.S.; Luo, Y.; Wang, Y.L.; Liu, L.M.Z. A review of fully coupled atmosphere-hydrology simulations. J. Geogr. Sci. 2019, 29, 465–479. [Google Scholar] [CrossRef] [Green Version]
- Benavidez, R.; Jackson, B.; Maxwell, D.; Norton, K. A review of the (Revised) Universal Soil Loss Equation ((R)USLE): With a view to increasing its global applicability and improving soil loss estimates. Hydrol. Earth Syst. Sci. 2018, 22, 6059–6086. [Google Scholar] [CrossRef] [Green Version]
- Karki, R.; Srivastava, P.; Veith, T.L. Application of the Soil and Water Assessment Tool (SWAT) at Field Scale: Categorizing Methods and Review of Applications. Trans. ASABE 2020, 63, 513–522. [Google Scholar] [CrossRef]
- El-Sadek, A. Upscaling Field Scale Hydrology and Water Quality Modelling to Catchment Scale. Water Resour. Manag. 2007, 21, 149–169. [Google Scholar] [CrossRef]
- Wellen, C.; Kamran-Disfani, A.R.; Arhonditsis, G.B. Evaluation of the Current State of Distributed Watershed Nutrient Water Quality Modeling. Environ. Sci. Technol. 2015, 49, 3278–3290. [Google Scholar] [CrossRef] [PubMed]
- Spruill, C.A.; Workman, S.R.; Taraba, J.L. Simulation of daily and monthly stream discharge from small watersheds using the SWAT model. Trans. ASABE 2000, 43, 1431–1439. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of base flow and groundwater recharge in the Upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Worrall, F.; Burt, T.P. The impact of land-use change on water quality at the catchment scale: The use of export coefficient and structural models. J. Hydrol. 1999, 221, 75–90. [Google Scholar] [CrossRef]
- Angello, Z.A.; Behailu, B.M.; Tranckner, J. Integral Application of Chemical Mass Balance and Watershed Model to Estimate Point and Nonpoint Source Pollutant Loads in Data-Scarce Little Akaki River, Ethiopia. Sustainability 2020, 12, 7084. [Google Scholar] [CrossRef]
- Bhatta, B.; Shrestha, S.; Shrestha, P.K.; Talchabhadel, R. Evaluation and application of a SWAT model to assess the climate change impact on the hydrology of the Himalayan River Basin. Catena 2019, 181, 104082. [Google Scholar] [CrossRef]
- Frederiksen, R.R.; Molina-Navarro, E. The importance of subsurface drainage on model performance and water balance in an agricultural catchment using SWAT and SWAT-MODFLOW. Agric. Water Manag. 2021, 255, 107058. [Google Scholar] [CrossRef]
- Wu, L.; Liu, X.; Chen, J.; Yu, Y.; Ma, X. Overcoming equifinality: Time-varying analysis of sensitivity and identifiability of SWAT runoff and sediment parameters in an arid and semiarid watershed. Environ. Sci. Pollut. Res. 2022, 29, 31631–31645. [Google Scholar] [CrossRef] [PubMed]
- Borah, D.K.; Bera, M. Watershed-scale hydrologic and nonpoint-source pollution models: Review of mathematical bases. Trans. ASABE 2003, 46, 1553–1566. [Google Scholar] [CrossRef]
- Yazdi, M.N.; Ketabchy, M.; Sample, D.J.; Scott, D.; Liao, H.H. An evaluation of HSPF and SWMM for simulating streamflow regimes in an urban watershed. Environ. Model. Softw. 2019, 118, 211–225. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, C.Y.; Chen, X.W.; Xu, Y.P.; Yin, Y.X.; Gao, L.; Liu, M.B. Uncertainty in simulation of land-use change impacts on catchment runoff with multi-timescales based on the comparison of the HSPF and SWAT models. J. Hydrol. 2019, 573, 486–500. [Google Scholar] [CrossRef]
- Xie, H.; Dong, J.W.; Shen, Z.Y.; Chen, L.; Lai, X.J.; Qiu, J.L.; Wei, G.Y.; Peng, Y.X.; Chen, X.Q. Intra- and inter-event characteristics and controlling factors of agricultural nonpoint source pollution under different types of rainfall-runoff events. Catena 2019, 182, 104105. [Google Scholar] [CrossRef]
- Kumwimba, M.N.; Meng, F.; Iseyemi, O.; Moore, M.T.; Bo, Z.; Tao, W.; Liang, T.J.; Ilunga, L. Removal of non-point source pollutants from domestic sewage and agricultural runoff by vegetated drainage ditches (VDDs): Design, mechanism, management strategies, and future directions. Sci. Total Environ. 2018, 639, 742–759. [Google Scholar] [CrossRef]
- Hill, M.J.; Hassall, C.; Oertli, B.; Fahrig, L.; Robson, B.J.; Biggs, J.; Samways, M.J.; Usio, N.; Takamura, N.; Krishnaswamy, J.; et al. New policy directions for global pond conservation. Conserv. Lett. 2018, 11, e12447. [Google Scholar] [CrossRef] [Green Version]
- Holgerson, M.A.; Raymond, P.A. Large contribution to inland water CO2 and CH4 emissions from very small ponds. Nat. Geosci. 2016, 9, 222–226. [Google Scholar] [CrossRef]
- Sun, C.; Chen, L.; Liu, H.B.; Zhu, H.; Lu, M.Q.; Chen, S.B.; Wang, Y.W.; Shen, Z.Y. New Modeling Framework for Describing the Pollutant Transport and Removal of Ditch-Pond System in an Agricultural Catchment. Water Resour. Res. 2021, 57, e2021WR031077. [Google Scholar] [CrossRef]
- Dong, Z.; Hu, L.; Li, J.; Kumwimba, M.N.; Tang, J.; Zhu, B. Nitrogen Retention in Mesocosm Sediments Received Rural Wastewater Associated with Microbial Community Response to Plant Species. Water 2020, 12, 3035. [Google Scholar] [CrossRef]
- Pan, Y.P.; Tian, S.L.; Zhao, Y.H.; Zhang, L.; Zhu, X.Y.; Gao, J.; Huang, W.; Zhou, Y.B.; Song, Y.; Zhang, Q.; et al. Identifying Ammonia Hotspots in China Using a National Observation Network. Environ. Sci. Technol. 2018, 52, 3926–3934. [Google Scholar] [CrossRef] [Green Version]
- Zhang, P.; Chen, L.; Yan, T.Z.; Liu, J.; Shen, Z.Y. Sources of nitrate-nitrogen in urban runoff over and during rainfall events with different grades. Sci. Total Environ. 2022, 808, 152069. [Google Scholar] [CrossRef] [PubMed]
- Tian, H.; Xu, R.; Canadell, J.G.; Thompson, R.L.; Winiwarter, W.; Suntharalingam, P.; Davidson, E.A.; Ciais, P.; Jackson, R.B.; Janssens-Maenhout, G.; et al. A comprehensive quantification of global nitrous oxide sources and sinks. Nature 2020, 586, 248–256. [Google Scholar] [CrossRef] [PubMed]
- Zhan, X.; Bo, Y.; Zhou, F.; Liu, X.; Paerl, H.W.; Shen, J.; Wang, R.; Li, F.; Tao, S.; Dong, Y.; et al. Evidence for the Importance of Atmospheric Nitrogen Deposition to Eutrophic Lake Dianchi, China. Environ. Sci. Technol. 2017, 51, 6699–6708. [Google Scholar] [CrossRef] [PubMed]
- Tosha, T.; Yamagiwa, R.; Sawai, H.; Shiro, Y. NO Dynamics in Microbial Denitrification System. Chem. Lett. 2021, 50, 280–288. [Google Scholar] [CrossRef]
- Dai, Z.M.; Yu, M.J.; Chen, H.H.; Zhao, H.C.; Huang, Y.L.; Su, W.Q.; Xia, F.; Chang, S.X.; Brookes, P.C.; Dahlgren, R.A.; et al. Elevated temperature shifts soil N cycling from microbial immobilization to enhanced mineralization, nitrification and denitrification across global terrestrial ecosystems. Glob. Chang. Biol. 2020, 26, 5267–5276. [Google Scholar] [CrossRef]
- Tong, Y.D.; Xu, X.W.; Qi, M.; Sun, J.J.; Zhang, Y.Y.; Zhang, W.; Wang, M.Z.; Wang, X.J.; Zhang, Y. Lake warming intensifies the seasonal pattern of internal nutrient cycling in the eutrophic lake and potential impacts on algal blooms. Water Res. 2021, 188, 116570. [Google Scholar] [CrossRef]
- Yan, R.H.; Li, L.L.; Gao, J.F. Framework for quantifying rural NPS pollution of a humid lowland catchment in Taihu Basin, Eastern China. Sci. Total Environ. 2019, 688, 983–993. [Google Scholar] [CrossRef]
- Musafiri, C.M.; Macharia, J.M.; Kiboi, M.N.; Ng’etich, O.K.; Shisanya, C.A.; Okeyo, J.M.; Okwuosa, E.A.; Ngetich, F.K. Comparison between observed and DeNitrification-DeComposition model-based nitrous oxide fluxes and maize yields under selected soil fertility management technologies in Kenya. Plant Soil 2021, 463, 395–413. [Google Scholar] [CrossRef]
- Han, J.X.; Xin, Z.H.; Han, F.; Xu, B.; Wang, L.F.; Zhang, C.; Zheng, Y. Source contribution analysis of nutrient pollution in a P-rich watershed: Implications for integrated water quality management. Environ. Pollut. 2021, 279, 116885. [Google Scholar] [CrossRef] [PubMed]
- Samimi, M.; Mirchi, A.; Moriasi, D.; Ahn, S.; Alian, S.; Taghvaeian, S.; Sheng, Z.P. Modeling arid/semi-arid irrigated agricultural watersheds with SWAT: Applications, challenges, and solution strategies. J. Hydrol. 2020, 590, 125418. [Google Scholar] [CrossRef]
- Kim, D.K.; Kaluskar, S.; Mugalingam, S.; Blukacz-Richards, A.; Long, T.Y.; Morley, A.; Arhonditsis, G.B. A Bayesian approach for estimating phosphorus export and delivery rates with the SPAtially Referenced Regression On Watershed attributes (SPARROW) model. Ecol. Inform. 2017, 37, 77–91. [Google Scholar] [CrossRef]
- Gustafsson, N.; Janjic, T.; Schraff, C.; Leuenberger, D.; Weissmann, M.; Reich, H.; Brousseau, P.; Montmerle, T.; Wattrelot, E.; Bucanek, A.; et al. Survey of data assimilation methods for convective-scale numerical weather prediction at operational centres. Q. J. R. Meteorol. Soc. 2018, 144, 1218–1256. [Google Scholar] [CrossRef] [Green Version]
- Piniewski, M.; Marcinkowski, P.; Koskiaho, J.; Tattari, S. The effect of sampling frequency and strategy on water quality modelling driven by high-frequency monitoring data in a boreal catchment. J. Hydrol. 2019, 579, 124186. [Google Scholar] [CrossRef]
- Dai, Y.; Chen, L.; Hou, X.S.; Shen, Z.Y. Effects of the spatial resolution of urban drainage data on nonpoint source pollution prediction. Environ. Sci. Pollut. Res. 2018, 25, 14799–14812. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.S.; Engel, B.A. Use of Pollutant Load Regression Models with Various Sampling Frequencies for Annual Load Estimation. Water 2014, 6, 1685–1697. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yen, H.; Daren Harmel, R.; Lei, Q.; Zhou, J.; Hu, W.; Li, W.; Lian, H.; Zhu, A.X.; Zhai, L.; et al. Effects of sampling strategies and estimation algorithms on total nitrogen load determination in a small agricultural headwater watershed. J. Hydrol. 2019, 579, 124114. [Google Scholar] [CrossRef]
- Littlewood, I.G.; Marsh, T.J. Annual freshwater river mass loads from Great Britain, 1975–1994: Estimation algorithm, database and monitoring network issues. J. Hydrol. 2005, 304, 221–237. [Google Scholar] [CrossRef]
- Lu, Y.; Gao, Y.; Yang, T.T. A review of mass flux monitoring and estimation methods for biogeochemical interface processes in watersheds. J. Geogr. Sci. 2020, 30, 881–907. [Google Scholar] [CrossRef]
- Chen, L.; Sun, C.; Wang, G.B.; Xie, H.; Shen, Z.Y. Event-based nonpoint source pollution prediction in a scarce data catchment. J. Hydrol. 2017, 552, 13–27. [Google Scholar] [CrossRef]
- Chen, L.; Xu, J.J.; Wang, G.B.; Liu, H.B.; Zhai, L.M.; Li, S.; Sun, C.; Shen, Z.Y. Influence of rainfall data scarcity on non-point source pollution prediction: Implications for physically based models. J. Hydrol. 2018, 562, 1–16. [Google Scholar] [CrossRef]
- Lin, Y.; Li, L.; Yu, J.; Hu, Y.; Zhang, T.H.; Ye, Z.L.; Syed, A.; Li, J. An optimized machine learning approach to water pollution variation monitoring with time-series Landsat images. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102370. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G. An evaluation of grid size uncertainty in empirical soil loss modeling with digital elevation models. Environ. Model. Assess. 2005, 10, 33–42. [Google Scholar] [CrossRef]
- Duncan, M.R.; Austin, B.; Fabry, F.; Austin, G.L. The effect of gauge sampling density on the accuracy of streamflow prediction for rural catchments. J. Hydrol. 1993, 142, 445–476. [Google Scholar] [CrossRef]
- Strauch, M.; Bernhofer, C.; Koide, S.; Volk, M.; Lorz, C.; Makeschin, F. Using precipitation data ensemble for uncertainty analysis in SWAT streamflow simulation. J. Hydrol. 2012, 414, 413–424. [Google Scholar] [CrossRef]
- Shen, Z.Y.; Chen, L.; Liao, Q.; Liu, R.M.; Huang, Q. A comprehensive study of the effect of GIS data on hydrology and non-point source pollution modeling. Agric. Water Manag. 2013, 118, 93–102. [Google Scholar] [CrossRef]
- Wang, H.; Jia, Y.W.; Yang, G.Y.; Zhou, Z.H.; Qiu, Y.Q.; Niu, C.W.; Peng, H. Integrated simulation of the dualistic water cycle and its associated processes in the Haihe River Basin. Chin. Sci. Bull. 2013, 58, 3297–3311. [Google Scholar] [CrossRef] [Green Version]
- Van Meter, K.J.; Basu, N.B. Time lags in watershed-scale nutrient transport: An exploration of dominant controls. Environ. Res. Lett. 2017, 12, 084017. [Google Scholar] [CrossRef]
- Basu, N.B.; Van Meter, K.J.; Byrnes, D.K.; Van Cappellen, P.; Brouwer, R.; Jacobsen, B.H.; Jarsjö, J.; Rudolph, D.L.; Cunha, M.C.; Nelson, N.; et al. Managing nitrogen legacies to accelerate water quality improvement. Nat. Geosci. 2022, 15, 97–105. [Google Scholar] [CrossRef]
- Chen, D.J.; Zhang, Y.F.; Shen, H.; Yao, M.Y.; Hu, M.P.; Dahlgren, R.A. Decreased buffering capacity and increased recovery time for legacy phosphorus in a typical watershed in eastern China between 1960 and 2010. Biogeochemistry 2019, 144, 273–290. [Google Scholar] [CrossRef] [Green Version]
- Ilampooranan, I.; Van Meter, K.J.; Basu, N.B. A Race Against Time: Modeling Time Lags in Watershed Response. Water Resour. Res. 2019, 55, 3941–3959. [Google Scholar] [CrossRef]
- Zhu, A.X.; Mackay, D.S. Effects of spatial detail of soil information on watershed modeling. J. Hydrol. 2001, 248, 54–77. [Google Scholar] [CrossRef]
- Fernandez, G.P.; Chescheir, G.M.; Skaggs, R.W.; Amatya, D.M. DRAINMOD-GIS: A lumped parameter watershed scale drainage and water quality model. Agric. Water Manag. 2006, 81, 77–97. [Google Scholar] [CrossRef]
- Sorensen, R.; Seibert, J. Effects of DEM resolution on the calculation of topographical indices: TWI and its components. J. Hydrol. 2007, 347, 79–89. [Google Scholar] [CrossRef]
- Butts, M.B.; Payne, J.T.; Kristensen, M.; Madsen, H. An evaluation of the impact of model structure on hydrological modelling uncertainty for streamflow simulation. J. Hydrol. 2004, 298, 242–266. [Google Scholar] [CrossRef]
- Hollering, S.; Wienhofer, J.; Ihringer, J.; Samaniego, L.; Zehe, E. Regional analysis of parameter sensitivity for simulation of streamflow and hydrological fingerprints. Hydrol. Earth Syst. Sci. 2018, 22, 203–220. [Google Scholar] [CrossRef] [Green Version]
- Norton, J. An introduction to sensitivity assessment of simulation models. Environ. Model. Softw. 2015, 69, 166–174. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. Understanding the time-varying importance of different uncertainty sources in hydrological modelling using global sensitivity analysis. Hydrol. Process. 2016, 30, 3991–4003. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Chen, S.B.; Li, S.; Shen, Z.Y. Temporal and spatial scaling effects of parameter sensitivity in relation to non-point source pollution simulation. J. Hydrol. 2019, 571, 36–49. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Westerberg, I.K.; Guerrero, J.L.; Younger, P.M.; Beven, K.J.; Seibert, J.; Halldin, S.; Freer, J.E.; Xu, C.Y. Calibration of hydrological models using flow-duration curves. Hydrol. Earth Syst. Sci. 2011, 15, 2205–2227. [Google Scholar] [CrossRef] [Green Version]
- Franz, K.J.; Hogue, T.S. Evaluating uncertainty estimates in hydrologic models: Borrowing measures from the forecast verification community. Hydrol. Earth Syst. Sci. 2011, 15, 3367–3382. [Google Scholar] [CrossRef]
- Chen, L.; Shen, Z.Y.; Yang, X.H.; Liao, Q.; Yu, S.L. An Interval-Deviation Approach for hydrology and water quality model evaluation within an uncertainty framework. J. Hydrol. 2014, 509, 207–214. [Google Scholar] [CrossRef]
- Chen, L.; Li, S.; Zhong, Y.; Shen, Z. Improvement of model evaluation by incorporating prediction and measurement uncertainty. Hydrol. Earth Syst. Sci. 2018, 22, 4145–4154. [Google Scholar] [CrossRef] [Green Version]
- Lintern, A.; McPhillips, L.; Winfrey, B.; Duncan, J.; Grady, C. Best Management Practices for Diffuse Nutrient Pollution: Wicked Problems Across Urban and Agricultural Watersheds. Environ. Sci. Technol. 2020, 54, 9159–9174. [Google Scholar] [CrossRef] [PubMed]
- Munoz-Carpena, R.; Parsons, J.E.; Gilliam, J.W. Modeling hydrology and sediment transport in vegetative filter strips. J. Hydrol. 1999, 214, 111–129. [Google Scholar] [CrossRef]
- Lowrance, R.; Altier, L.S.; Williams, R.G.; Inamdar, S.P.; Sheridan, J.M.; Bosch, D.D.; Hubbard, R.K.; Thomas, D.L. REMM: The Riparian Ecosystem Management Model. J. Soil Water Conserv. 2000, 55, 27–34. [Google Scholar]
- White, M.J.; Storm, D.E.; Busteed, P.R.; Smolen, M.D.; Zhang, H.; Fox, G.A. A quantitative phosphorus loss assessment tool for agricultural fields. Environ. Model. Softw. 2010, 25, 1121–1129. [Google Scholar] [CrossRef] [Green Version]
- White, M.W.; Harmel, R.D.; Haney, R.L. Development and validation of the Texas Best Management Practice Evaluation Tool (TBET). J. Soil Water Conserv. 2012, 67, 525–535. [Google Scholar] [CrossRef]
- Bracmort, K.S.; Arabi, M.; Frankenberger, J.; Engel, B.A.; Arnold, J. Modeling Long-Term Water Quality Impacts of Structural BMPs. Trans. ASABE 2006, 49, 367–374. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Tian, D.; Lowe, L.; Kalin, L.; Lehrter, J. Deep Learning for Daily Precipitation and Temperature Downscaling. Water Resour. Res. 2021, 57, e2020WR029308. [Google Scholar] [CrossRef]
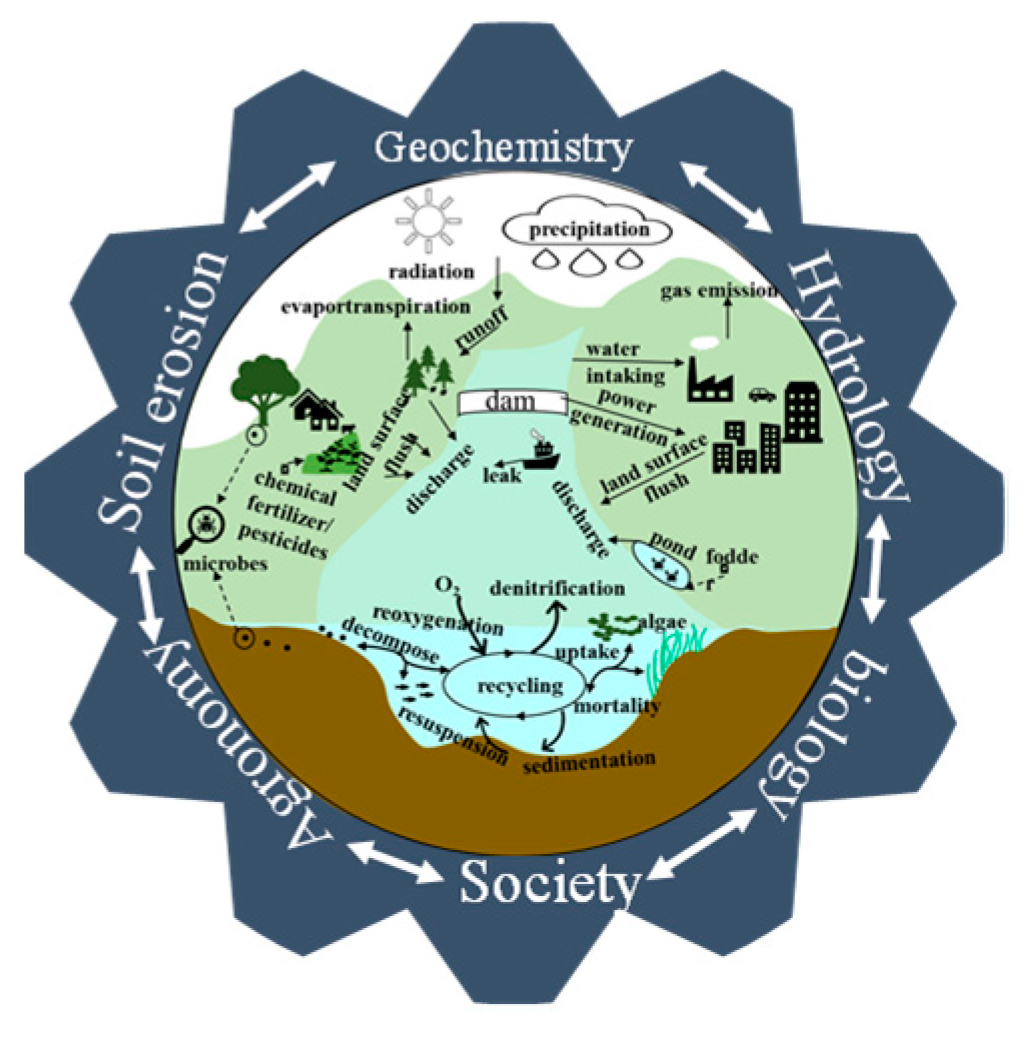
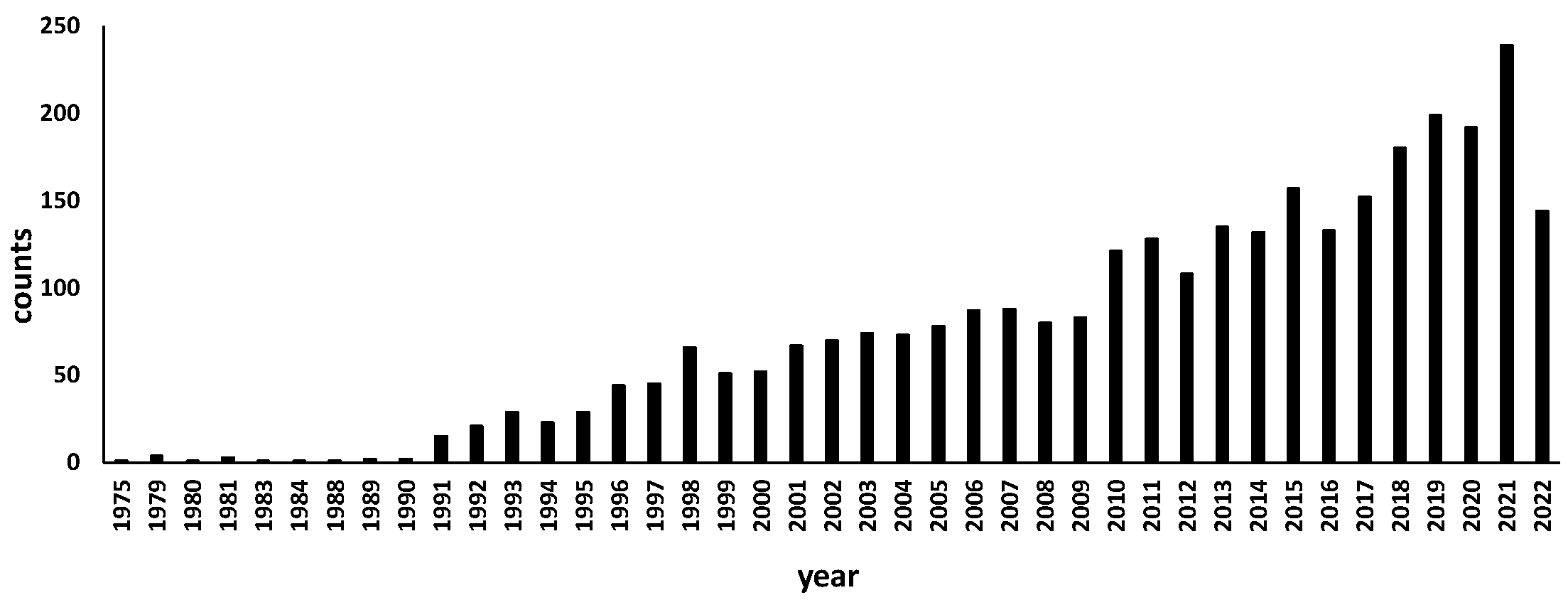
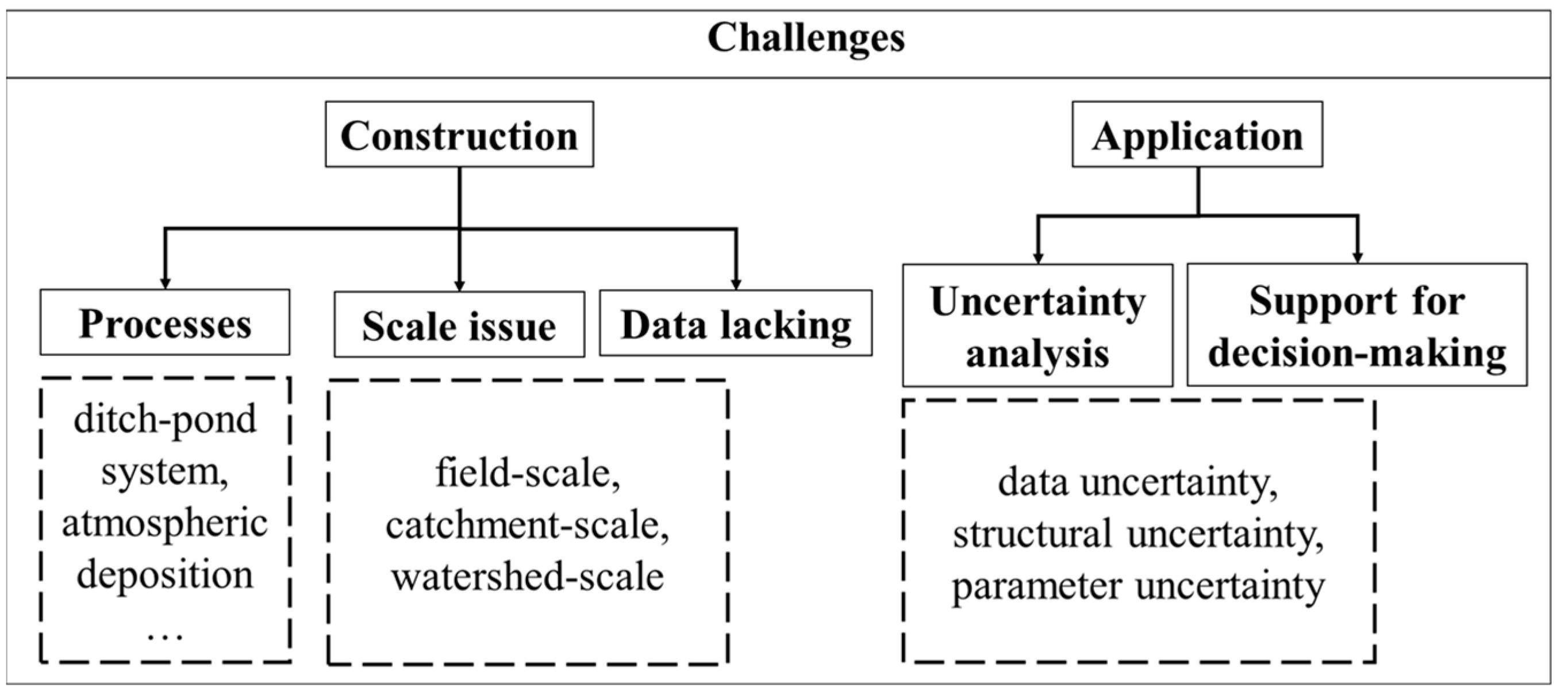
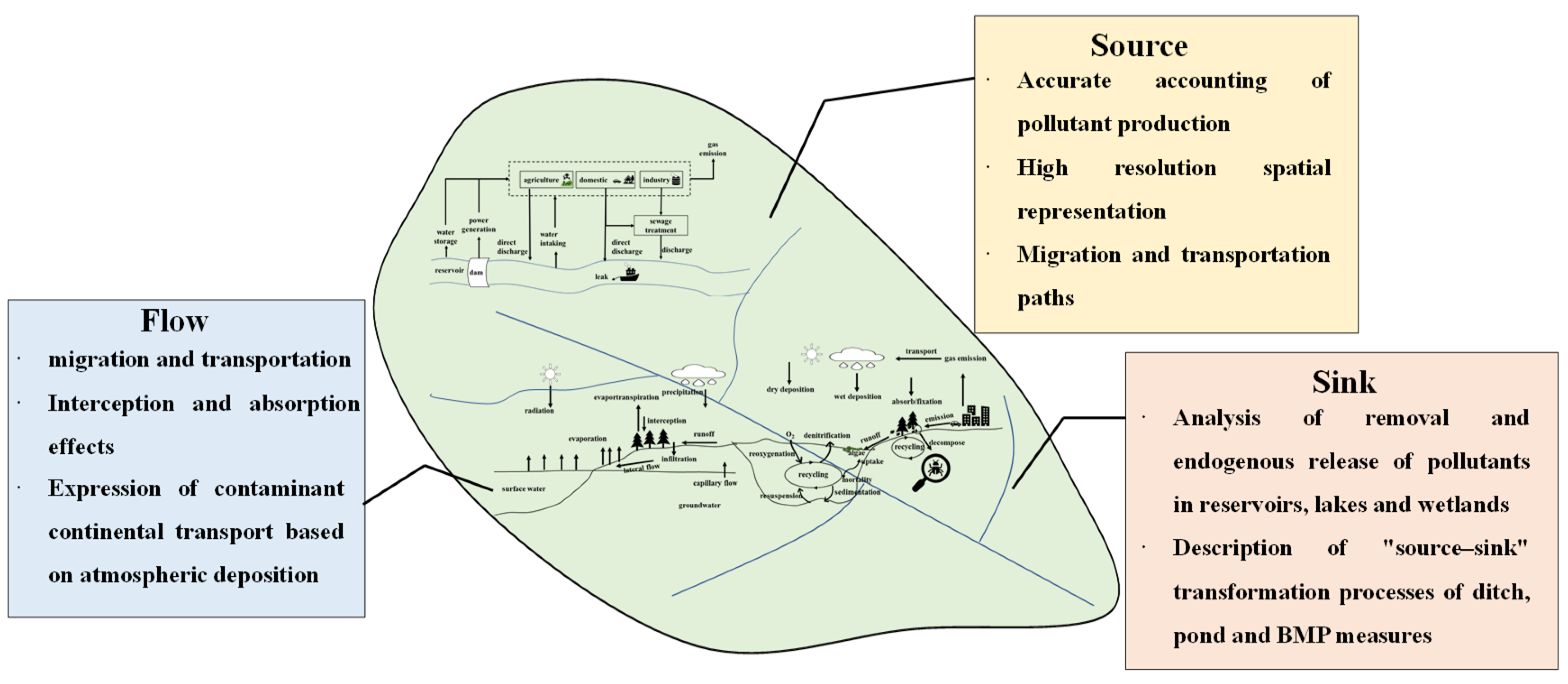
| Model | Materials | Spatial Scales | Application |
|---|---|---|---|
| SWAT [24] | sediment, nutrients, pesticide, heavy metal, etc. | watershed | A semi-distributed model that can effectively simulate the spatial and temporal characteristics of runoff and pollutants, and analyze the influence of topographic features, substrate features, land management features, climatic features, hydrological features and other factors on runoff, soil erosion, pollutant leaching and groundwater environment. |
| HSPF [22] | sediment, nutrients, pesticide, salts, pathogens, etc. | watershed | A lumped model that can simulate the runoff and water quality for each subbasin individually, and the migration and transformation process of river pollutants can also be simulated according to the upstream and downstream relationships of the basin. |
| AGNPS [21] | COD, nutrients, etc. | catchment | An event-oriented distributed model that mainly used for agricultural NPS pollution estimation and prediction. It requires less data than other distributed models. |
| AnnAGNPS [8] | COD, nutrients, etc. | watershed | A continuous distributed model that developed from the AGNPS model, inherits the advantages of the AGNPS model except for the simulation of single rainfall event. |
| GWLF [27] | sediment, nutrients | catchment/watershed | A semi-distributed and semiempirical watershed load model; it can be applied to an ungauged watershed, used in estimation of nutrient loads from multiple sources (including point source, rural runoff, urban runoff, groundwater, saprophytic drainage system, etc.). |
| DNDC [28,29] | carbon (C) and N cycles | field | A plot model for simulating C and N cycles in terrestrial ecosystems; it has a good performance in paddy ecosystem; different farm management scenarios can be simulated and analyzed. |
| CREAMS [20] | nutrients, pesticide, etc. | field | A field model to simulate NPS pollution and to simulate the effects of different management practices on pesticide loads in groundwater. |
| GLEAMS [20] | nutrients, pesticide, etc. | field | A field model to evaluate the effect of agricultural management practices on soil erosion, nutrients and pesticide leaching, and runoff with a layering system. |
| APEX [30,31] | sediment, nutrients, pesticide, etc. | catchment/watershed | A spatially distributed model that can divide the field or small watershed area into relatively uniform spatial units according to soil type, landscape location, surface hydrological elements, and management practices; the units are interconnected by river channels. Additionally, it can simulate the contaminants at each subdivision outlet or at the entire watershed outlet. |
| SWMM [27,32] | nutrients, pesticide, TSS, oil/grease, etc. | catchment/watershed | An urban NPS model mainly used for water quality simulation, scenario prediction and pollutant management assessment for single rainfall events or long-term continuous rainfall-runoff processes from primarily urban areas. |
| SPARROW [33] | nutrients, pesticide, heavy metal, etc. | watershed | A regression statistical model of watershed spatial attributes combining empirical statistics and mechanisms; the statistical estimation of land and water parameters separately to quantitatively describe the migration rate of pollutants from source to river and the transport between upstream and downstream of the river network, which is advantageous in terms of data requirement and is also feasible for simulation in areas with uneven distribution of monitoring points. |
| PLOAD [34,35] | nutrients, pesticide, heavy metal, etc. | watershed | A GIS-based model for calculating NPS pollutant loads from different sub-watersheds based on annual or seasonal precipitation and land use. |
| Export coefficient model [36,37] | nutrients, pesticide, heavy metal, etc. | watershed | A typical statistical NPS model that mainly estimates pollution loads based on export coefficients, without considering the influence of subsurface conditions, provides good applicability to areas with scarce data. |
| EFDC [25] | DO, COD, algae, nutrients, active metal, etc. | river, lake, reservoir, estuaries, ocean and wetland | EFDC is a 3D environmental fluid dynamics model, which is widely used in the dispersion process of pollutants in lakes, reservoirs, rivers, etc. This model is often used in the assessment of environmental response to NPS pollution and in the simulation of algal outbreaks. |
| OTIS [26] | water-borne solutes, e.g., chloride, phosphate, nitrate, dissolved metals, etc. | river, stream | A model that focuses primarily on the fate and transport processes of solutes in a river or stream. The model is good at pollutant longitudinal transport simulation but lacks consideration of vertical deposition. Two conceptual areas are defined in the model: the main channel for advection and dispersion processes, and the storage area (the porous area of the dead pool and the riverbed) for transient storage process. |
| Counts | Year | Keywords |
|---|---|---|
| 1186 | 2003 | nonpoint source pollution |
| 519 | 2003 | water quality |
| 339 | 2003 | land use |
| 319 | 2003 | runoff |
| 316 | 2003 | nitrogen pollution |
| 306 | 2003 | swat model |
| 305 | 2003 | soil |
| 299 | 2003 | phosphorus |
| 267 | 2003 | best management practice (bmp) |
| 216 | 2003 | sediment |
| 199 | 2003 | river basin |
| 199 | 2003 | uncertainty analysis |
| 183 | 2003 | climate change |
| 177 | 2003 | catchment |
| 176 | 2003 | simulation |
| 163 | 2004 | river |
| 156 | 2003 | land use change |
| 127 | 2003 | soil erosion |
| 119 | 2007 | nutrient |
| 116 | 2005 | basin |
| 116 | 2005 | calibration |
| 112 | 2003 | flow |
| 111 | 2003 | scale |
| 108 | 2003 | sensitivity analysis |
| 103 | 2003 | watershed management |
| Keywords | Strength | Begin | End |
|---|---|---|---|
| geographic information system | 14.32 | 2003 | 2008 |
| watershed management | 13.49 | 2003 | 2008 |
| agnps model | 10.1 | 2003 | 2008 |
| flow | 9.01 | 2003 | 2010 |
| water quality | 7.32 | 2003 | 2004 |
| prediction | 5.61 | 2003 | 2012 |
| spatial variability | 5.24 | 2003 | 2010 |
| sediment transport | 5.12 | 2003 | 2012 |
| hydrological modeling | 5.04 | 2003 | 2008 |
| watershed modeling | 4.95 | 2003 | 2012 |
| watershed model | 4.76 | 2003 | 2010 |
| nonpoint source pollution model | 4.42 | 2003 | 2014 |
| watershed | 4.98 | 2005 | 2008 |
| runoff | 4.58 | 2005 | 2006 |
| total maximum daily load | 6.44 | 2007 | 2014 |
| validation | 5.06 | 2007 | 2016 |
| constructed wetland | 4.52 | 2009 | 2014 |
| gulf of mexico | 6.76 | 2011 | 2016 |
| china | 7.59 | 2017 | 2018 |
| landscape pattern | 5.53 | 2017 | 2022 |
| emission | 4.91 | 2017 | 2020 |
| conservation practice | 4.57 | 2017 | 2020 |
| climate change | 9.11 | 2019 | 2022 |
| ecosystem service | 5.23 | 2019 | 2022 |
| performance | 5.02 | 2019 | 2022 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Chen, L.; Wu, L.; Zhang, L.; Xie, H.; Shen, Z. Review of Nonpoint Source Pollution Models: Current Status and Future Direction. Water 2022, 14, 3217. https://doi.org/10.3390/w14203217
Wang M, Chen L, Wu L, Zhang L, Xie H, Shen Z. Review of Nonpoint Source Pollution Models: Current Status and Future Direction. Water. 2022; 14(20):3217. https://doi.org/10.3390/w14203217
Chicago/Turabian StyleWang, Mingjing, Lei Chen, Lei Wu, Liang Zhang, Hui Xie, and Zhenyao Shen. 2022. "Review of Nonpoint Source Pollution Models: Current Status and Future Direction" Water 14, no. 20: 3217. https://doi.org/10.3390/w14203217






