Scaling Up from Leaf to Whole-Plant Level for Water Use Efficiency Estimates Based on Stomatal and Mesophyll Behaviour in Platycladus orientalis
Abstract
:1. Introduction
2. Theoretical Background
2.1. Coupled gsw-Pn,L Model
2.2. Coupled gm-Pn Model
2.3. Leaf and Whole-Plant WUE Model
3. Material and Methods
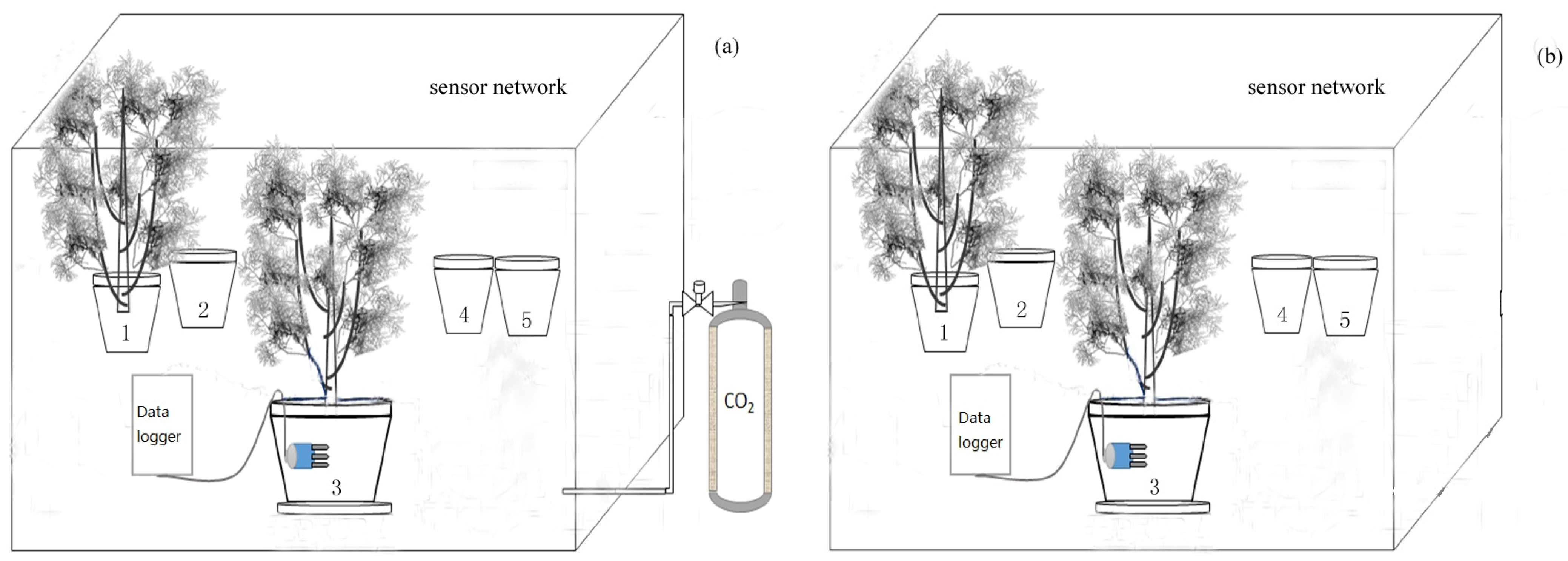
3.1. Experimental Design and Management
3.2. Measurements
3.2.1. Whole-Plant Carbon Balance and Measurement
3.2.2. Whole-Plant Transpiration Measurements
3.2.3. Leaf Gas Exchange and Stable Isotope Analysis
3.2.4. Whole-Plant Total Leaf Area Measurement
3.3. Data Analysis
4. Results
4.1. Measured and Modelled Responses of gsw to SWC and Ca
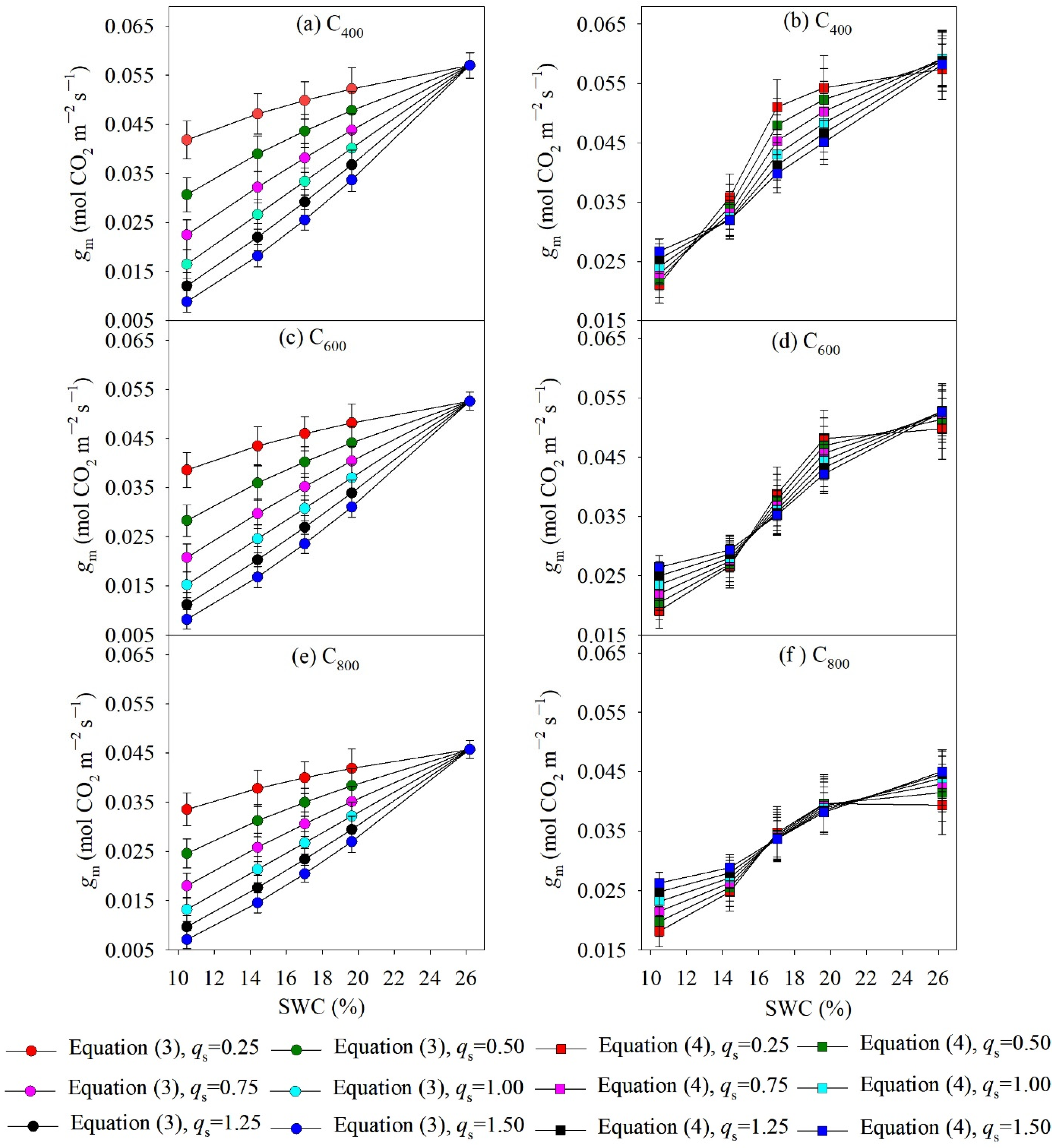
4.2. Measured and Modelled Responses of gm to SWC and Ca
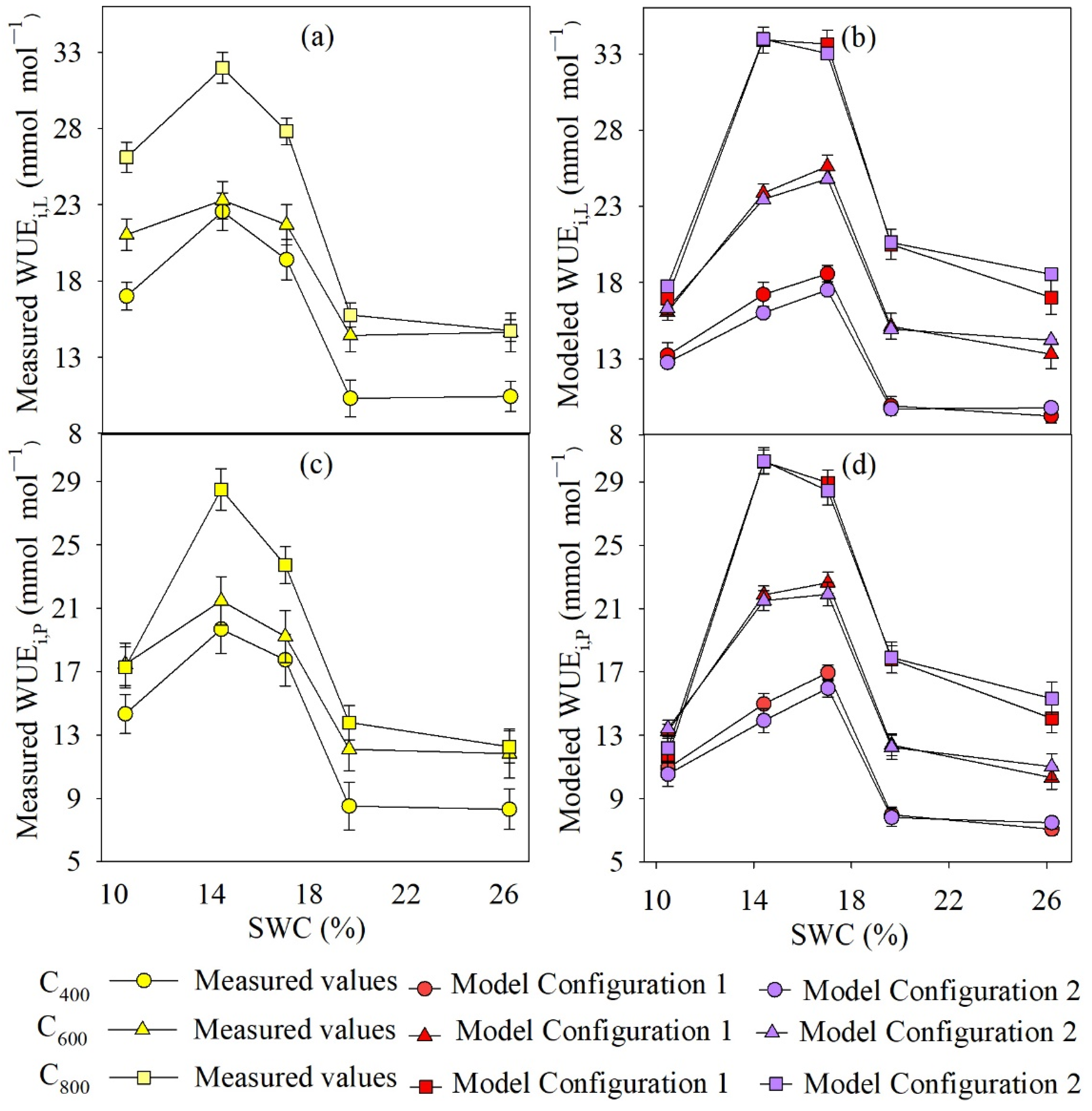
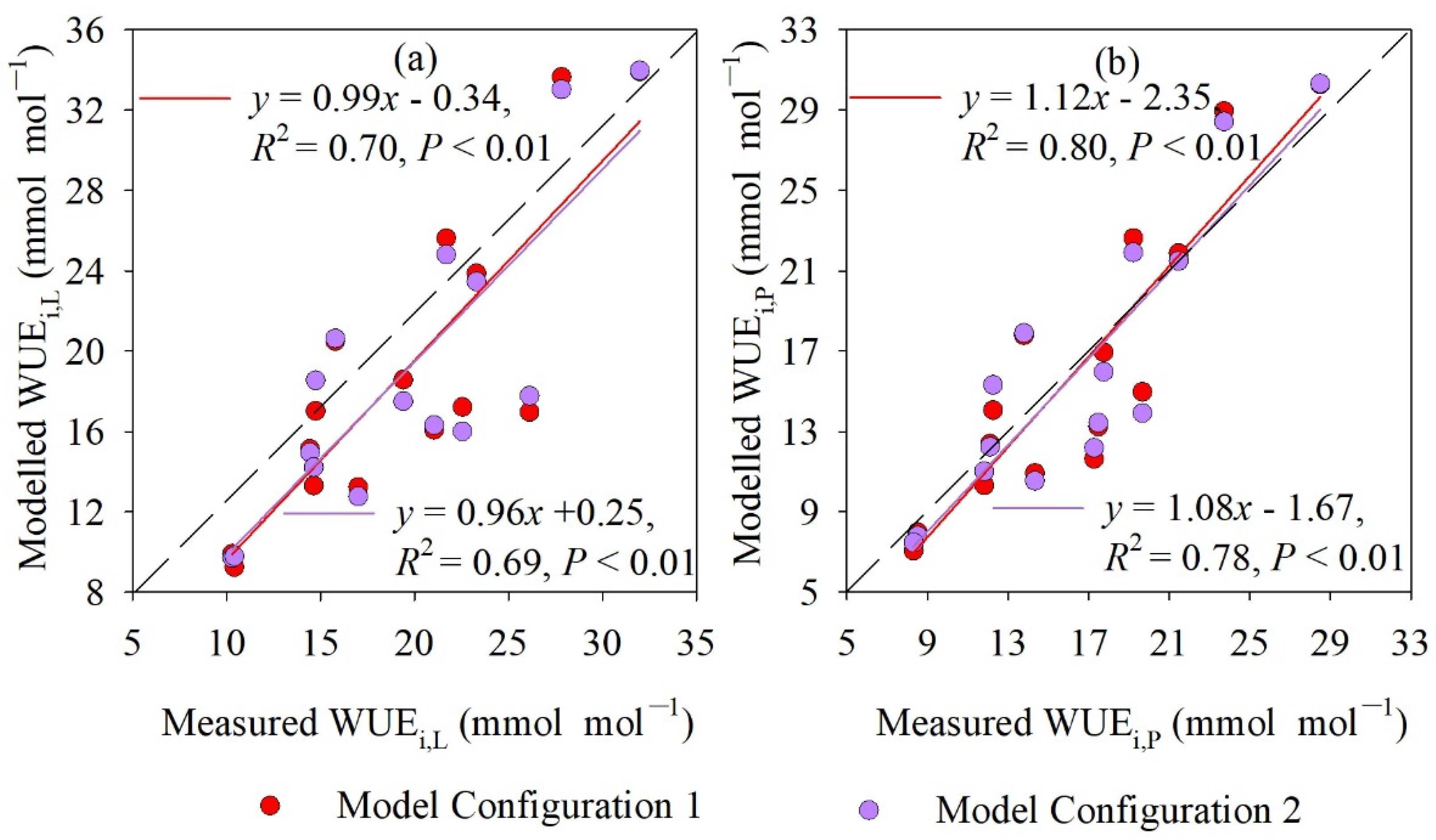
4.3. Measured and Modeled Instantaneous WUE at Leaf and Whole-Plant Level
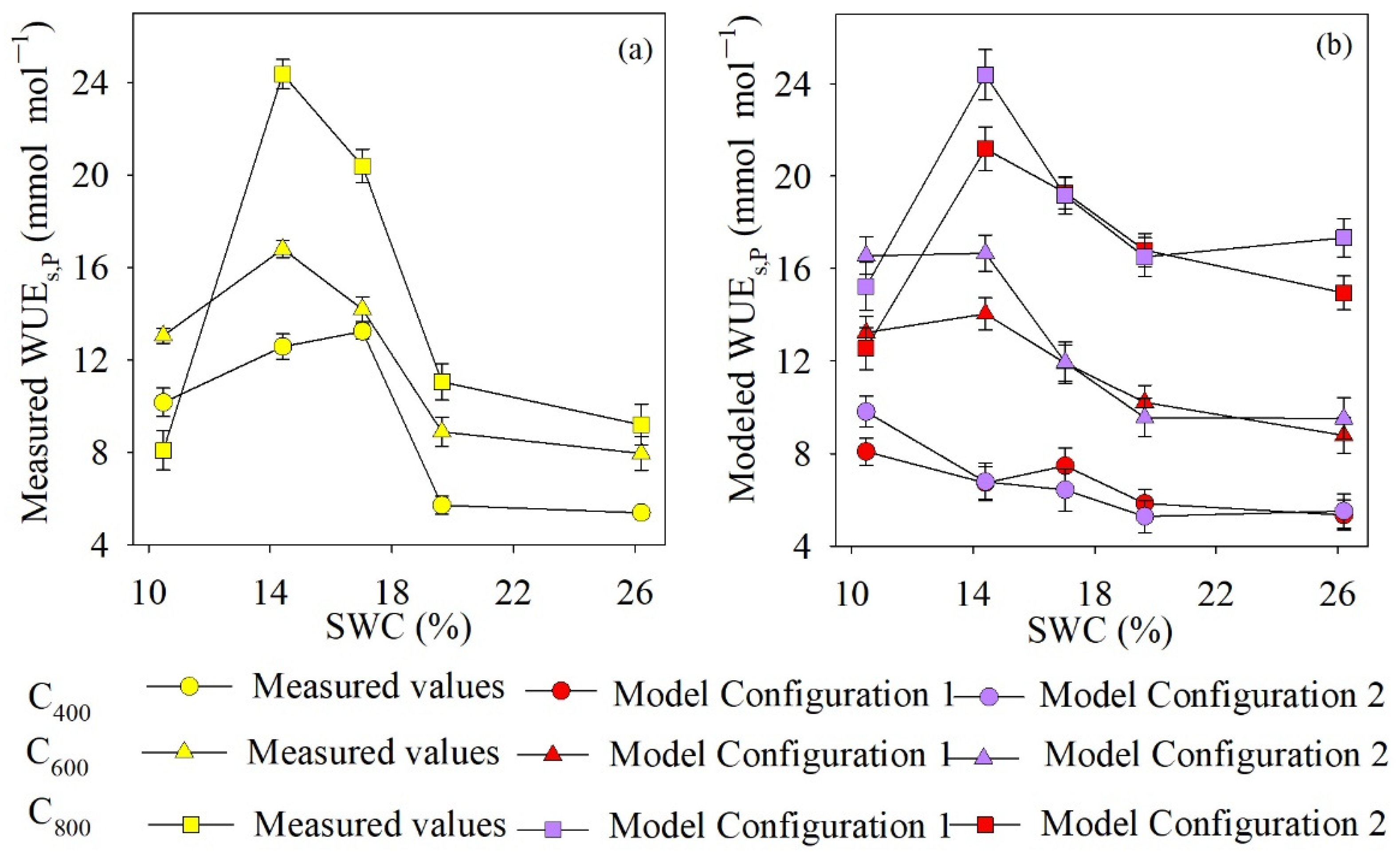
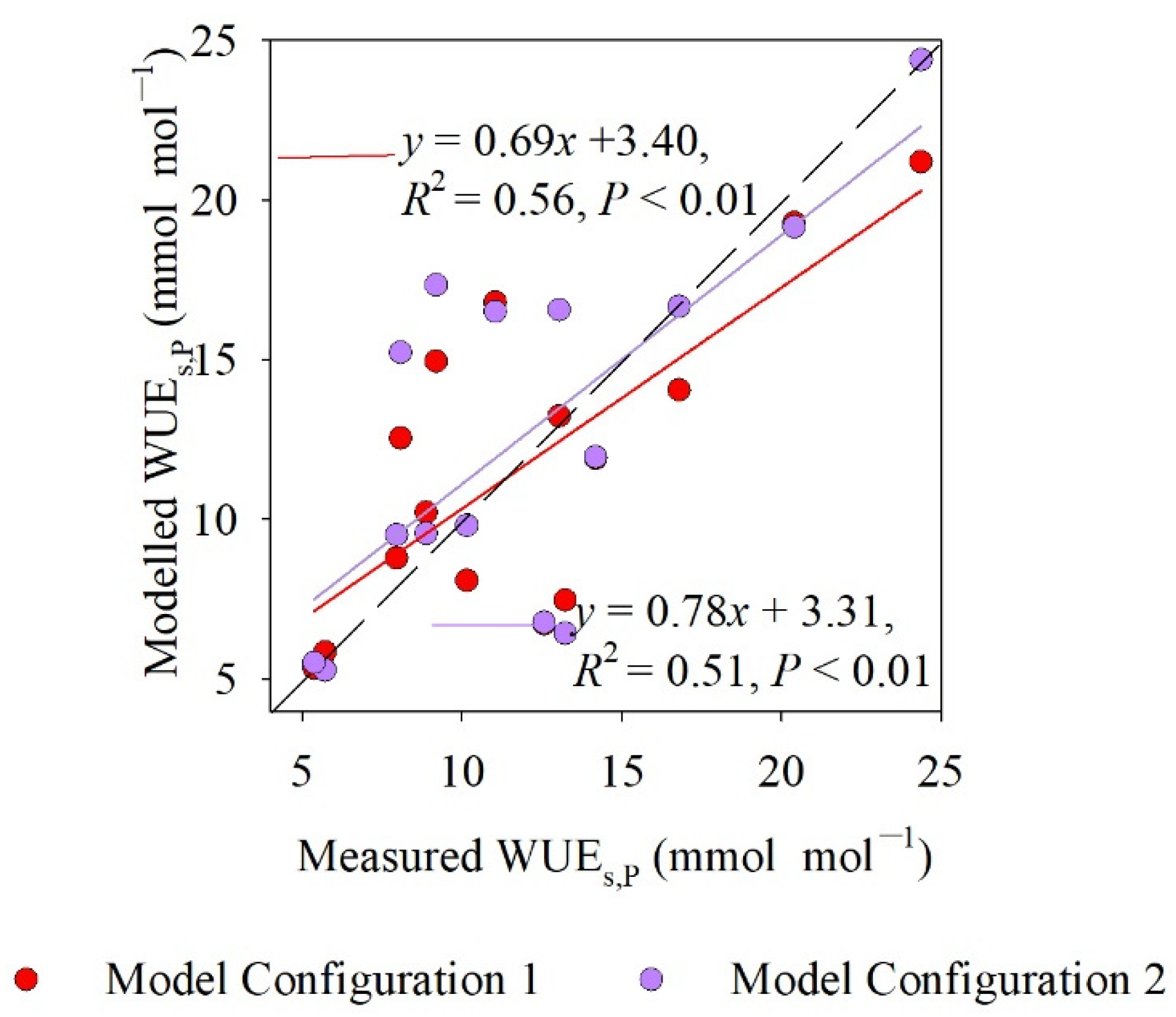
4.4. Comparison of Measured and Modeled WUEs,P Values
5. Discussion
5.1. Model Performance for Estimating gsw and gm
5.2. Different Model Configurations for Estimating WUEs,P
5.3. Uncertainties of WUEs,P Introduced by gsw and gm
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SSWC | Soil water content |
| θ (SWC) | Actual soil water content |
| θc | Soil water content at field capacity (26.20%) |
| θw | Soil water content at permanent wilting point (4.08%) |
| Ca | Atmosphere CO2 concentration (µmol·mol−1). The C600 and C800 are Ca levels of 600 μmol·mol−1 and 800 μmol mol−1, and the C400 is Ca level of 400 μmol·mol−1. |
| WUE | Water use efficiency (mmol·mol−1) |
| WUEi-L | Leaf instantaneous water use efficiency (mmol·mol−1) |
| WUEi-P | Whole-plant instantaneous water use efficiency (mmol·mol−1) |
| WUEs-P | Whole-plant short-term water use efficiency (mmol·mol−1) |
| Pn,L | Leaf daytime net photosynthetic rate (µmol·m−2·s−1) |
| EL | Leaf daytime transpiration rate (mmol·m−2·s−1) |
| Pn,P | Whole-plant daytime net photosynthetic rate (mmol·h−1) |
| ∫Pn,P | Whole-plant cumulative net carbon sequestration over a day-night cycle (mmol−1) |
| EP | Whole-plant daytime transpiration rate (mol·h−1) |
| Ed | Whole-plant nighttime transpiration rate (mol·h −1) |
| ∫EP | Whole-plant cumulative transpiration over a day-night cycle (mol−1) |
| RP | Whole-plant nighttime respiration rate (mmol·h −1) |
| Cs | Leaf surface CO2 concentration (µmol·mol −1) |
| Ci | Leaf intercellular CO2 concentration (µmol·mol −1) |
| gb | Leaf boundary layer conductance (mol CO2·m−2·s−1) |
| gsw | Leaf stomatal conductance (mol H2O·m−2·s−1) |
| gsc | Leaf stomatal conductance for CO2 (mol CO2·m−2·s−1) |
| g1 | Fitted parameter associated with the photosynthesis–stomatal conductance model |
| g0,sw | Fitted parameter, and g0,sw is considered to represent the residual stomatal conductance (mol H2O·m−2·s−1) |
| f(θs) | Stomatal conductance limitation function that depends on soil water stress |
| qs | The exponents involved in the stomatal conductance limitation function |
| gm | Leaf mesophyll conductance (mmol CO2·m−2·s−1) |
| gm,p | Potential (unstressed) gm (mmol CO2·m−2·s−1) |
| g2 | Fitted parameter associated with the photosynthesis–mesophyll conductance model |
| gm,0 | Fitted parameter, and g0,m is considered to represent the residual mesophyll conductance (mol CO2·m−2·s−1) |
| f(θm) | Mesophyll conductance limitation function that depends on soil water stress |
| qm | The exponents involved in the mesophyll conductance limitation function |
| Δmea | Measured short-term photosynthetic 13C discrimination (‰) |
| Δlin | The 13C discrimination calculated by the linear model (‰) |
| δ13Ca | The δ13C of atmosphere CO2 (‰) |
| δ13Cl | The δ13C of leaf water-soluble organic materials (WSOM) (‰) |
| a | Fractionation associated with the CO2 diffusion in air (4.4‰) |
| b′ | Fractionation relevant to the reactions of Rubisco and PEP carboxylase (27‰) |
| am | Fractionation of CO2 diffusion and dissolution in the liquid phase (1.8‰) |
| ai | Fractionation of CO2 diffusion and dissolution in the liquid phase (1.8‰) |
| b | Fractionation during carboxylation (29‰) |
| e | Discrimination value for the mitochondrial respiration (dark respiration) |
| f | Discrimination value for photorespiration |
| Γ | CO2 compensation point with dark respiration |
| k | Carboxylation efficiency |
| D | Water vapor pressure difference between the intercellular spaces of the leaf and the leaf external air (mbar) |
| ϕw,i | Instantaneous proportion of “unproductive” water loss, that is, water lost by transpiration from twigs and stems during the day |
| ϕc,i | Instantaneous proportion of carbon fixed during photosynthesis, that is, subsequently lost by respiration from twigs and stems during the day |
| ϕw,s | Proportion of “unproductive” water loss at short time scale (over a day–night cycle), that is, water lost by transpiration from twigs and stems during the day, and from twigs, stems, and leaves at night |
| ϕc,s | Proportion of carbon fixed during photosynthesis at short time scale (over a day–night cycle), that is, subsequently lost by respiration from twigs and stems over the whole period, and from leaves during the night |
| LA | Total leaf area (m2) |
| DW | Dry weight (g) |
References
- Medrano, H.; Tomás, M.; Martorell, S.; Flexas, J.; Hernández, E.; Rosselló, J.; Pou, A.; Escalona, J.-M.; Bota, J. From leaf to whole–plant water use efficiency WUE in complex canopies: Limitations of leaf WUE as a selection target. Crop J. 2015, 3, 220–228. [Google Scholar] [CrossRef] [Green Version]
- Flexas, J.; Ribas-Carbó, M.; Bota, J.; Galmés, J.; Henkle, M.; Martínez-Cañellas, S.; Medrano, H. Decreased Rubisco activity during water stress is not induced by decreased relative water content but related to conditions of low stomatal conductance and chloroplast CO2 concentration. New Phytol. 2006, 172, 73–82. [Google Scholar] [CrossRef]
- Warren, C.R.; Adams, M.A. Internal conductance does not scale with photosynthetic capacity, implications for carbon isotope discrimination and the economics of water and nitrogen use in photosynthesis. Plant Cell Environ. 2006, 29, 192–201. [Google Scholar] [CrossRef] [PubMed]
- Perez-Martin, A.; Flexas, J.; Ribas-Carbo, M.; Bota, J.; Tomas, M.S.; Infante, J.M.; Diaz-Espejo, A. Interactive effects of soil water deficit and air vapour pressure deficit on mesophyll conductance to CO2 in Vitis vinifera and Olea europaea. J. Exp. Bot. 2009, 60, 2391–2405. [Google Scholar] [CrossRef]
- Hu, J.; Moore DJ, P.; Riveros-Iregui, D.A.; Burns, S.P.; Monson, R.K. Modeling whole–tree carbon assimilation rate using observed transpiration rates and needle sugar carbon isotope ratios. New Phytol. 2010, 1854, 1000–1015. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farquhar, G.D.; Richards, R.A. Isotopic composition of plant carbon correlates with water–use efficiency in wheat genotypes. Aust. J. Plant Physiol. 1984, 11, 539–552. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Ehleringer, J.R.; Hubick, K.T. Carbon isotope discrimination and photosynthesis. Annu. Rev. Plant Physiol. Plant Mol. Biol. 1989, 40, 503–537. [Google Scholar] [CrossRef]
- Hubick, K.T.; Farquhar, G.D. Carbon isotope discrimination and the ratio of carbon gained to water lost in barley cultivars. Plant Cell Environ. 1989, 12, 795–804. [Google Scholar] [CrossRef]
- Seibt, U.; Rajabi, A.; Griffiths, H.; Berry, J.A. Carbon isotopes and water–use efficiency, sense and sensitivity. Oecologia 2008, 155, 441–454. [Google Scholar] [CrossRef]
- Zhang, Y.E.; Yu, X.; Chen, L.; Jia, G. Whole–plant instantaneous and short–term water–use efficiency in response to soil water content and CO2 concentration. Plant Soil 2019, 444, 281–298. [Google Scholar] [CrossRef]
- Pons, T.L.; Flexas, J.; Von Caemmerer, S.; Evans, J.R.; Genty, B.; Ribas-Carbo, M.; Brugnoli, E. Estimating mesophyll conductance to CO2, methodology potential errors and recommendations. J. Exp. Bot. 2009, 608, 2217–2234. [Google Scholar] [CrossRef] [Green Version]
- Keenan, T.; Sabate, S.; Gracia, C. Soil water stress and coupled photosynthesis conductance models: Bridging the gap between conflicting reports on the relative roles of stomatal, mesophyll conductance and biochemical limitations to photosynthesis. Agric. For. Meteorol. 2010, 150, 443–453. [Google Scholar] [CrossRef]
- WMO Greenhouse Gas Bulletin The State of Greenhouse Gases in the Atmosphere Based on Global Observations through 2020; World Meteorological Organization: Geneva, Switzerland, 2021.
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions. In Progress in Photosynthesis Research; Martinus Nijhoff Publishers: Leiden, The Netherlands, 1987. [Google Scholar]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. B Biol. Sci. 1976, 273, 593–610. [Google Scholar]
- Leuning, R. Modelling Stomatal Behaviour and and Photosynthesis of Eucalyptus grandis. Funct. Plant Biol. 1990, 17, 159–175. [Google Scholar] [CrossRef]
- Leuning, R. A critical appraisal of a combined stomatal–photosynthesis model for C3 plants. Plant Cell Environ. 1995, 18, 339–355. [Google Scholar] [CrossRef]
- Collatz, G.J.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
- Lloyd, J. Modelling Stomatal Responses to Environment in Macadamia integrifolia. Funct. Plant Biol. 1991, 18, 649–660. [Google Scholar] [CrossRef]
- Lohammar, T.; Larsson, S.; Linder, S.; Falk, S.O. FAST: Simulation Models of Gaseous Exchange in Scots Pine. Ecol. Bull. 1980, 32, 505–523. [Google Scholar]
- Yu, G.R.; Zhuang, J.; Yu, Z.L. An attempt to establish a synthetic model of photosynthesis–transpiration based on stomatal behavior for maize and soybean plants grown in field. Plant Physiol. 2001, 158, 861–874. [Google Scholar] [CrossRef]
- Egea, G.; Verhoef, A.; González–Real, M.M.; Baille, A.; Nortes, P.A.; Domingo, R. Comparison of several approaches to modelling stomatal conductance in well–watered and drought–stressed almond trees. Acta Hortic. 2011, 922, 285–293. [Google Scholar] [CrossRef]
- Egea, G.; Verhoef, A.; Vidale, P.L. Towards an improved and more flexible representation of water stress in coupled photosynthesis–stomatal conductance models. Agric. For. Meteorol. 2011, 151, 1370–1384. [Google Scholar] [CrossRef]
- Flexas, J.; Diaz-Espejo, A.; Galmés, J.; Kaldenhoff, R.; Medrano, H.; Ribas-Carbo, M. Rapid variations of mesophyll conductance in response to changes in CO2 concentration around leaves. Plant Cell Environ. 2007, 30, 1284–1298. [Google Scholar] [CrossRef] [PubMed]
- Douthe, C.; Dreyer, E.; Brendel, O.; Warren, C.R. Is mesophyll conductance to CO2 in leaves of three Eucalyptus species sensitive to short–term changes of irradiance under ambient as well as low O2? Funct. Plant Biol. 2012, 38, 434–447. [Google Scholar] [CrossRef]
- Misson, L.; Limousin, J.M.; Rodriguez, R.; Letts, M.G. Leaf physiological responses to extreme droughts in Mediterranean Quercus ilex forest. Plant Cell Environ. 2010, 33, 1898–1910. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Zhou, G. Responses of photosynthetic capacity to soil moisture gradient in perennial rhizome grass and perennial bunchgrass. BMC Plant Biol. 2011, 11, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Porporato, A.; Laio, F.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water–controlled ecosystems: Active role in hydrologic processes and response to water stress Ⅲ. Vegetation water stress. Adv. Water Resour. 2001, 24, 725–744. [Google Scholar] [CrossRef]
- Gessler, A.; Rennenberg, H.; Keitel, C. Stable isotope composition of organic compounds transported in the phloem of European beech–evaluation of different methods of phloem sap collection and assessment of gradients in carbon isotope composition during leaf–to–stem transport. Plant Biol. 2004, 6, 721–729. [Google Scholar] [CrossRef]
- Hu, J.; Moore DJ, P.; Monson, R.K. Weather and climate controls over the seasonal carbon isotope dynamics of sugars from subalpine forest trees. Plant Cell Environ. 2009, 33, 35–47. [Google Scholar] [CrossRef]
- Kodama, N.; Barnard, R.L.; Salmon, Y.; Weston, C.; Ferrio, J.P.; Holst, J.; Gessler, A. Temporal dynamics of the carbon isotope composition in a Pinus sylvestris stand: From newly assimilated organic carbon to respired carbon dioxide. Oecologia 2008, 156, 737–750. [Google Scholar] [CrossRef] [PubMed]
- Jasoni, R.; Kane, C.; Green, C.; Peffley, E.; Tissue, D.; Thompson, L.; Payton, P.; Paré, P.W. Altered leaf and root emissions from onion (Allium cepa L.) grown under elevated CO2 conditions. Environ. Exp. Bot. 2004, 51, 273–280. [Google Scholar] [CrossRef]
- Escalona, J.M.; Fuentes, S.; Tomás, M.; Martorell, S.; Flexas, J.; Medrano, H. Responses of leaf night transpiration to drought stress in Vitis vinifera L. Agric. Water Manag. 2013, 118, 50–58. [Google Scholar] [CrossRef]
- Farquhar, G.D.; O’Leary, M.H.; Berry, J.A. On the relationship between carbon isotope discrimination and the intercellular carbon dioxide concentration in leaves. Aust. J. Plant Physiol. 1982, 9, 121–137. [Google Scholar] [CrossRef]
- Sala, A.; Tenhunen, J.D. Simulations of canopy net photosynthesis and transpiration in Quercus ilex L under the influence of seasonal drought. Agric. For. Meteorol. 1996, 78, 203–222. [Google Scholar] [CrossRef]
- Galmés, J.; Medrano, H.; Flexas, J. Photosynthetic limitations in response to water stress and recovery in Mediterranean plants with different growth forms. New Phytol. 2007, 175, 81–93. [Google Scholar] [CrossRef] [PubMed]
- Grassi, G.; Magnani, F. Stomatal, mesophyll conductance and biochemical limitations to photosynthesis as affected by drought and leaf ontogeny in ash and oak trees. Plant Cell Environ. 2005, 28, 834–849. [Google Scholar] [CrossRef]
- Centritto, M.; Lucas, M.E.; Jarvis, P.G. Gas exchange, biomass, whole-plant water-use efficiency and water uptake of peach (Prunus persica) seedlings in response to elevated carbon dioxide concentration and water availability. Tree Physiol. 2002, 22, 699–706. [Google Scholar] [CrossRef] [PubMed]
- Jones, H.G. Plants and Microclimate, 2nd ed.; Cambridge University Press: New York, NY, USA, 1992; pp. 163–214. [Google Scholar]
- Tcherkez, G.; Cornic, G.; Bligny, R.; Gout, E.; Ghashghaie, J. In Vivo Respiratory Metabolism of Illuminated Leaves. Plant Physiol. 2005, 138, 1596–1606. [Google Scholar] [CrossRef] [Green Version]
- Wingate, L.; Seibt, U.; Moncrieff, J.B.; Jarvis, P.G.; Lloyd, J. Variations in 13C discrimination during CO2 exchange by Picea sitchensis branches in the field. Plant Cell Environ. 2007, 30, 600–616. [Google Scholar] [CrossRef]
- Zhao, N.; Meng, P.; He, Y.B.; Yu, X. Interaction of CO2 concentrations and water stress in semiarid plants causes diverging response in instantaneous win instantaneous water use efficiency and carbon isotope composition. Biogeoscience 2017, 14, 3431–3444. [Google Scholar] [CrossRef] [Green Version]
- McCutchan, H.; Shackel, K.A. Stem-water Potential as a Sensitive Indicator of Water Stress in Prune Trees (Prunus domestica L. cv. French). J. Am. Soc. Hortic. Sci. 1992, 117, 607–611. [Google Scholar] [CrossRef] [Green Version]
- Bögelein, R.; Hassdenteufel, M.; Thomas, F.M.; Werner, W. Comparison of leaf gas exchange and stable isotope signature of water-soluble compounds along canopy gradients of co-occurring Douglas-fir and European beech. Plant Cell Environ. 2012, 35, 1245–1257. [Google Scholar] [CrossRef] [PubMed]
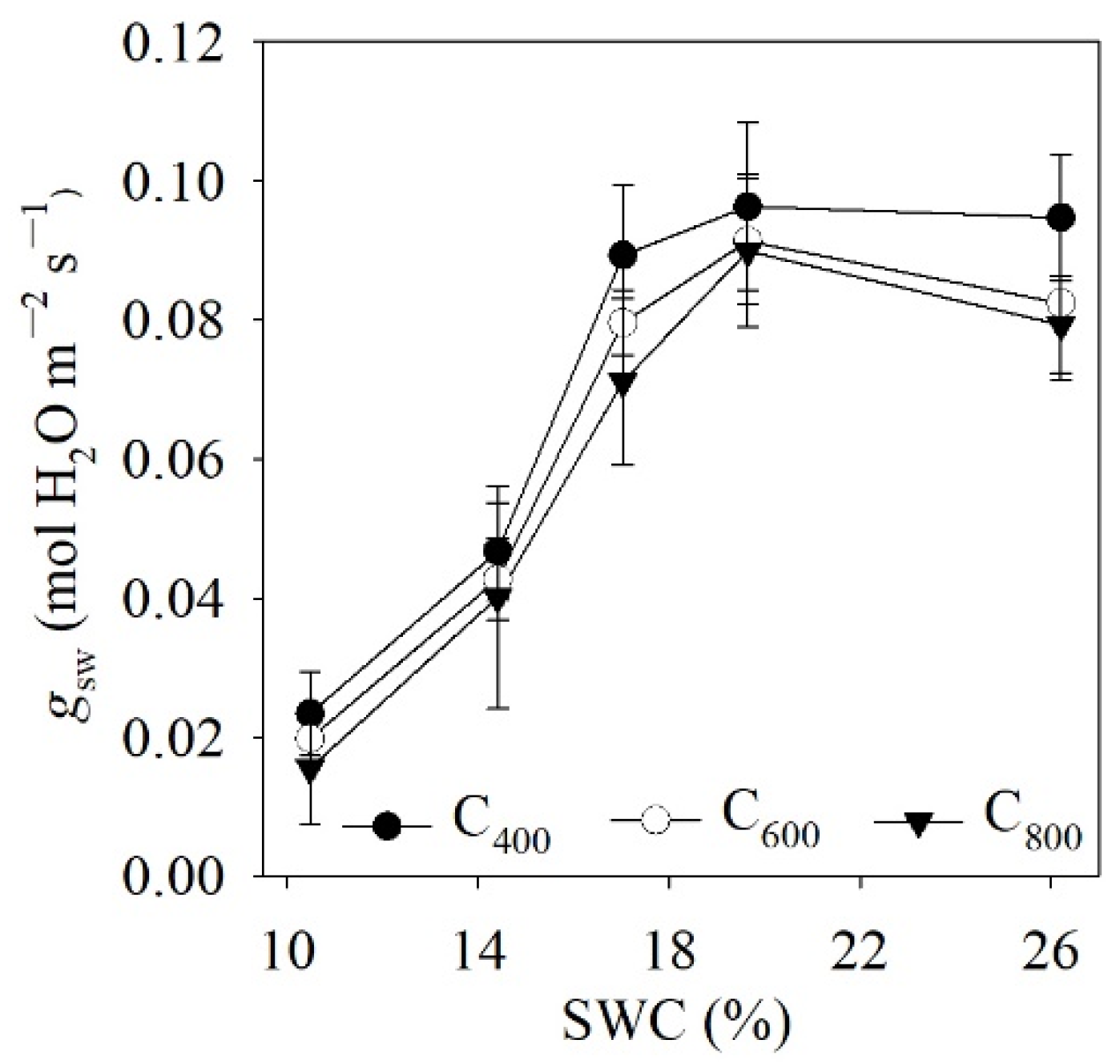
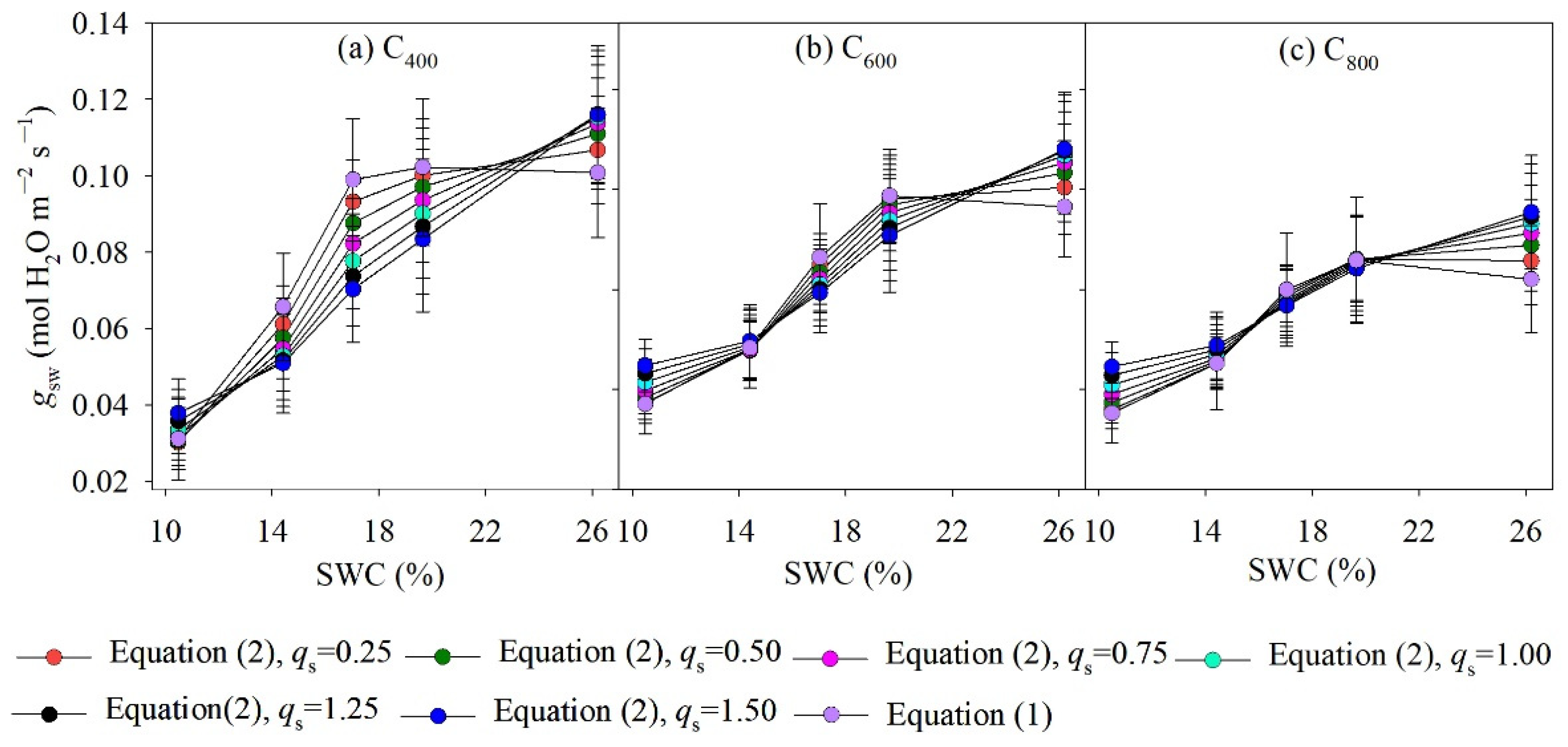
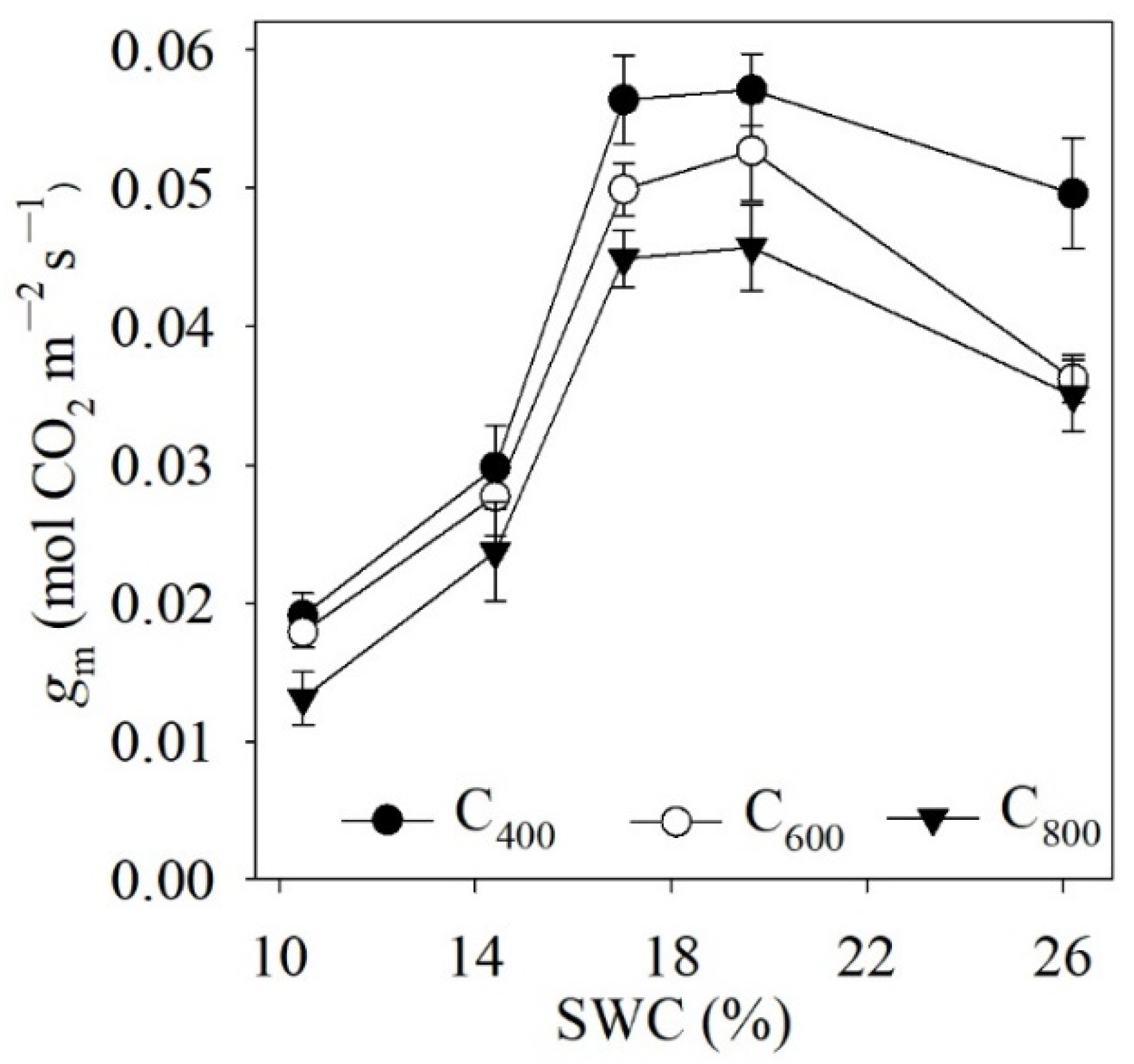
| Model | Regression of Measured and Modelled Leaf gsw | ||
|---|---|---|---|
| Linear Regression Equation | R2 | p | |
| Equation (2), qs = 0.25 | y = 0.88x + 0.01 | 0.88 | <0.01 |
| Equation (2), qs = 0.50 | y = 0.86x + 0.01 | 0.86 | <0.01 |
| Equation (2), qs = 0.75 | y = 0.83x + 0.01 | 0.83 | <0.01 |
| Equation (2), qs = 1.00 | y = 0.79x + 0.01 | 0.79 | <0.01 |
| Equation (2), qs = 1.25 | y = 0.74x + 0.02 | 0.74 | <0.01 |
| Equation (2), qs = 1.50 | y = 0.68x + 0.02 | 0.68 | <0.01 |
| Equation (1) | y = 0.87x + 0.01 | 0.87 | <0.01 |
| Model | Regression of Measured and Modeled Leaf gsw | ||
|---|---|---|---|
| Linear Regression Equation | R2 | p | |
| Equation (3), qm = 0.25 | y = 0.30x + 0.03 | 0.50 | <0.01 |
| Equation (3), qm = 0.50 | y = 0.44x + 0.02 | 0.52 | <0.01 |
| Equation (3), qm = 0.75 | y = 0.53x + 0.02 | 0.48 | <0.05 |
| Equation (3), qm = 1.00 | y = 0.58x + 0.01 | 0.43 | <0.05 |
| Equation (3), qm = 1.25 | y = 0.61x + 0.01 | 0.38 | <0.05 |
| Equation (3), qm = 1.50 | y = 0.61x + 0.03 | 0.34 | <0.05 |
| Equation (3), qm = 0.25 | y = 0.79x + 0.01 | 0.79 | <0.01 |
| Equation (3), qm = 0.50 | y = 0.72x + 0.01 | 0.72 | <0.01 |
| Equation (3), qm = 0.75 | y = 0.65x + 0.01 | 0.65 | <0.01 |
| Equation (3), qm = 1.00 | y = 0.57x + 0.02 | 0.57 | <0.01 |
| Equation (3), qm = 1.25 | y = 0.51x + 0.02 | 0.51 | <0.01 |
| Equation (3), qm = 1.50 | y = 0.44x + 0.02 | 0.44 | <0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, B.; Jia, G.; Yu, X.; Zhang, X.; Yin, X.; Zhao, Y.; Wang, Z.; Cheng, C.; Wang, Y.; et al. Scaling Up from Leaf to Whole-Plant Level for Water Use Efficiency Estimates Based on Stomatal and Mesophyll Behaviour in Platycladus orientalis. Water 2022, 14, 263. https://doi.org/10.3390/w14020263
Zhang Y, Liu B, Jia G, Yu X, Zhang X, Yin X, Zhao Y, Wang Z, Cheng C, Wang Y, et al. Scaling Up from Leaf to Whole-Plant Level for Water Use Efficiency Estimates Based on Stomatal and Mesophyll Behaviour in Platycladus orientalis. Water. 2022; 14(2):263. https://doi.org/10.3390/w14020263
Chicago/Turabian StyleZhang, Yonge, Bing Liu, Guodong Jia, Xinxiao Yu, Xiaoming Zhang, Xiaolin Yin, Yang Zhao, Zhaoyan Wang, Chen Cheng, Yousheng Wang, and et al. 2022. "Scaling Up from Leaf to Whole-Plant Level for Water Use Efficiency Estimates Based on Stomatal and Mesophyll Behaviour in Platycladus orientalis" Water 14, no. 2: 263. https://doi.org/10.3390/w14020263
APA StyleZhang, Y., Liu, B., Jia, G., Yu, X., Zhang, X., Yin, X., Zhao, Y., Wang, Z., Cheng, C., Wang, Y., & Xin, Y. (2022). Scaling Up from Leaf to Whole-Plant Level for Water Use Efficiency Estimates Based on Stomatal and Mesophyll Behaviour in Platycladus orientalis. Water, 14(2), 263. https://doi.org/10.3390/w14020263





