Evaluation of Soil Water Content Using SWAT for Southern Saskatchewan, Canada
Abstract
:1. Introduction
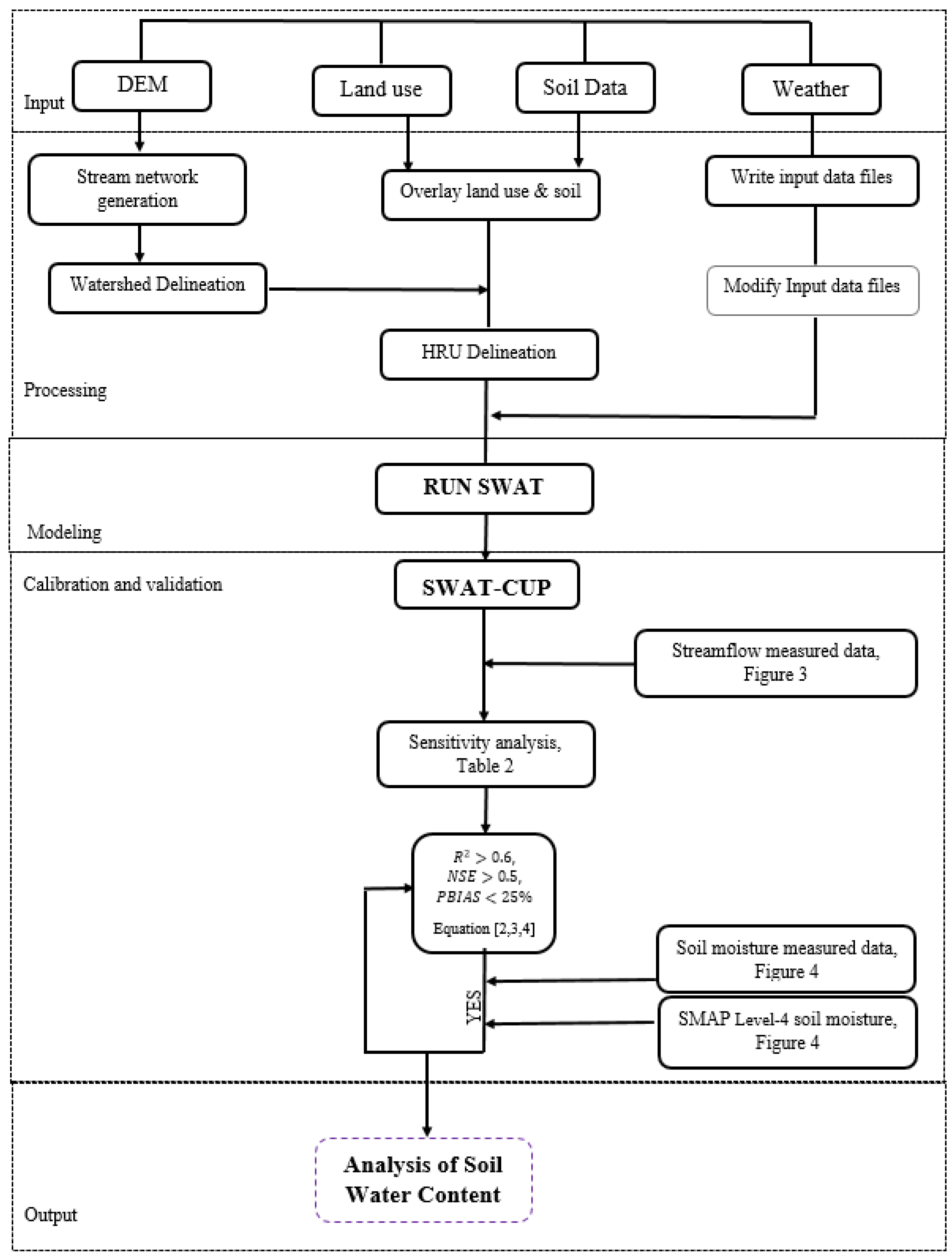
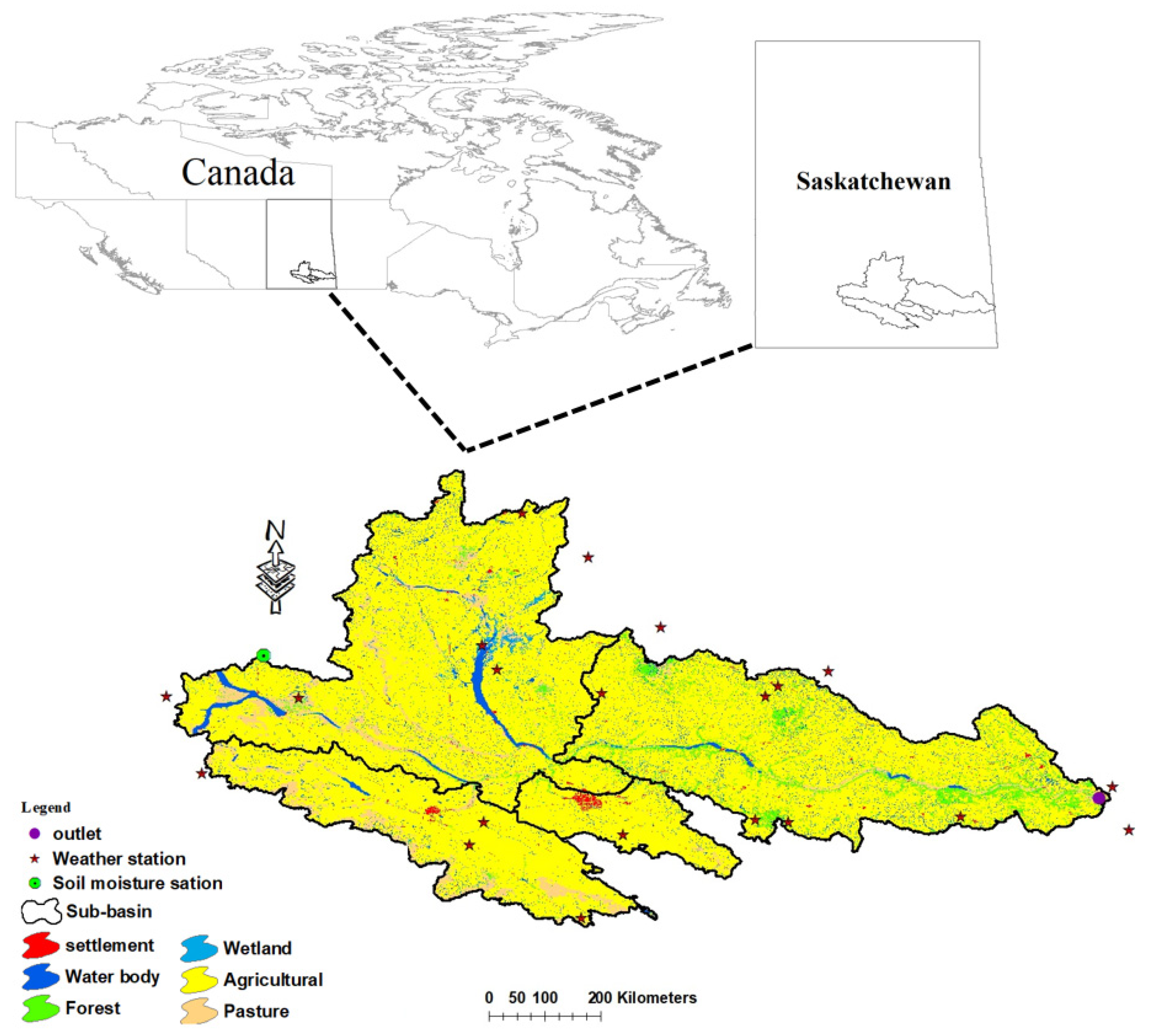
2. Research Methodology
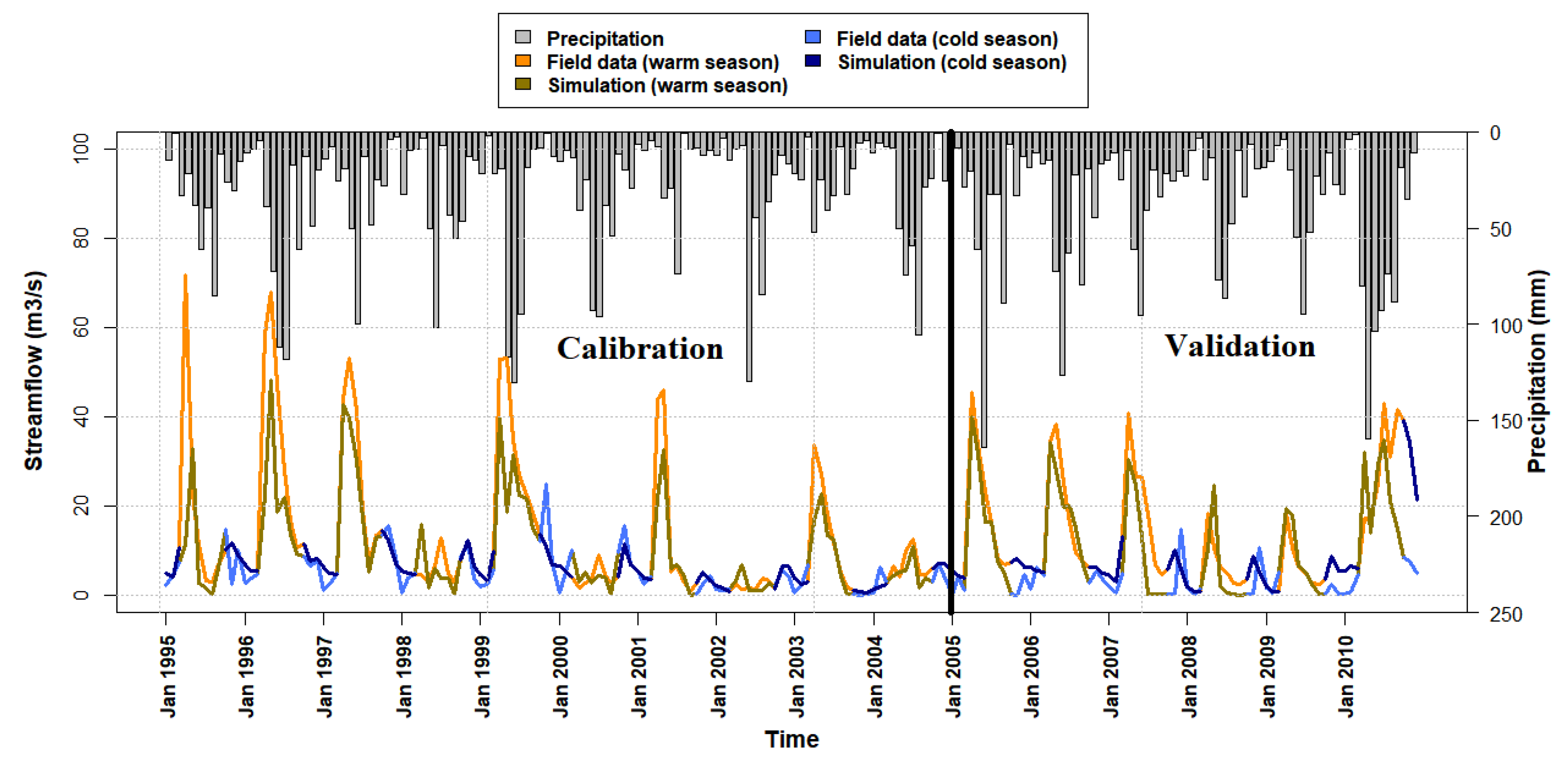
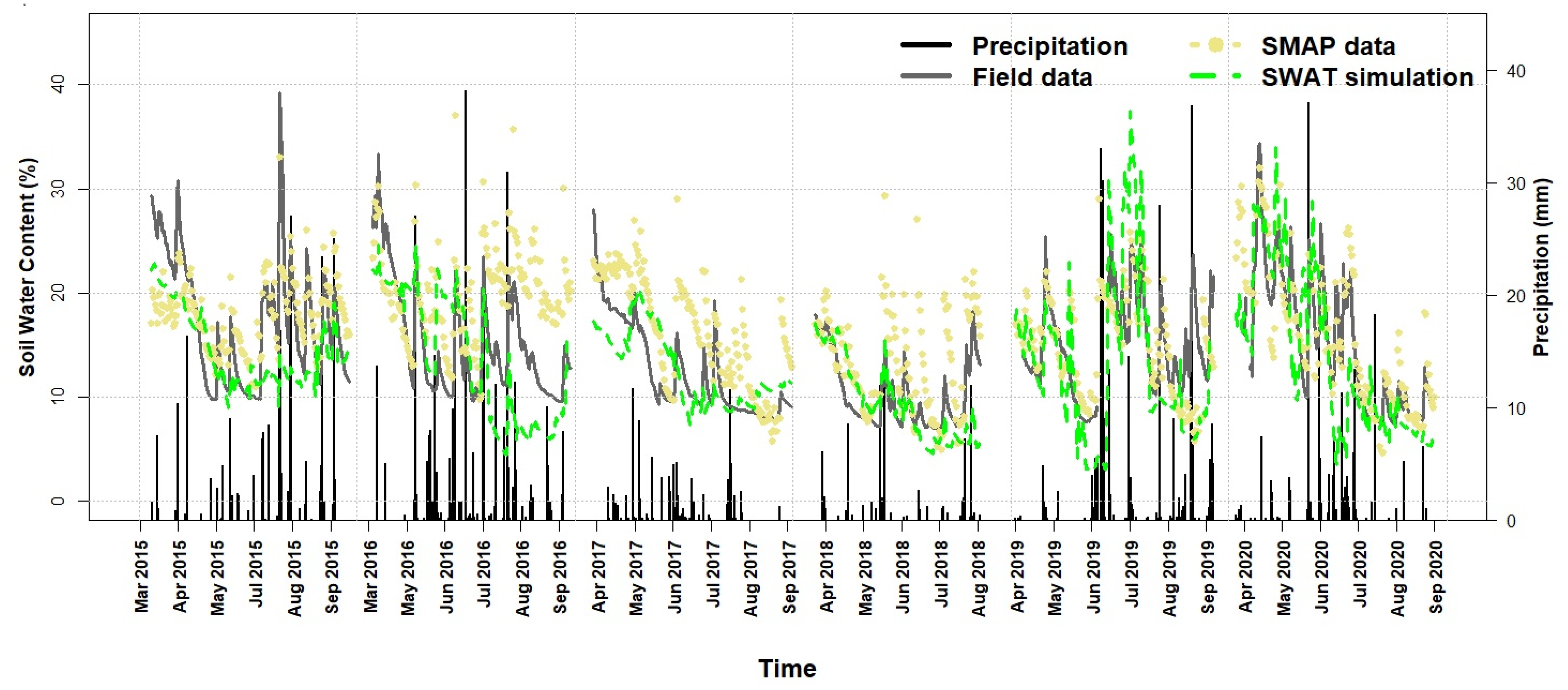
3. Results and Discussion
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hong, W.; Park, M.; Park, J.; Park, G.; Kim, S. The spatial and temporal correlation analysis between MODIS NDVI and SWAT predicted soil moisture during forest NDVI increasing and decreasing periods. KSCE J. Civ. Eng. 2010, 14, 931–939. [Google Scholar] [CrossRef]
- Uniyal, B.; Dietrich, J.; Vasilakos, C.; Tzoraki, O. Evaluation of SWAT simulated soil moisture at catchment scale by field measurements and Landsat derived indices. Agric. Water Manag. 2017, 193, 55–70. [Google Scholar] [CrossRef]
- Champagne, C.; Berg, A.; McNairn, H.; Drewitt, G.; Huffman, T. Evaluation of soil moisture extremes for agricultural productivity in the Canadian prairies. Agric. For. Meteorol. 2012, 165, 1–11. [Google Scholar] [CrossRef]
- McGinn, S.M.; Shepherd, A. Impact of climate change scenarios on the agroclimate of the Canadian prairies. Can. J. Soil Sci. 2003, 83, 623–630. [Google Scholar] [CrossRef]
- Akhter, A.; Azam, S. Flood-drought hazard assessment for a flat clayey deposit in the Canadian Prairies. J. Environ. Inform. Lett. 2019, 1, 8–19. [Google Scholar] [CrossRef]
- Saskatchewan Ministry of Agriculture. 2012. Available online: http://www.agriculture.gov.sk.ca/ (accessed on 28 August 2021).
- Pomeroy, J.; De Boer, D.; Martz, L. Hydrology and Water Resources of Saskatchewan; Report no. 1; Center for Hydrology: Saskatoon, SK, Canada, 2005. [Google Scholar]
- Bressiani, D.A.; Gassman, P.W.; Fernandes, J.G.; Garbossa, L.H.; Srinivasan, R.; Bonumá, N.B.; Mendiondo, E.M. A review of SWAT (Soil and Water Application Tool) applications in Brazil: Challenges and prospects. Int. J. Agric. Biol. Eng. 2015, 8, 9–35. [Google Scholar]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) model: Current developments and applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Gassman, P.W.; Reyes, M.R.; Green, C.H.; Arnold, J.G. The Soil and Water Assessment Tool: Historical development, applications, and future research directions. Trans. ASABE 2007, 50, 1211–1240. [Google Scholar] [CrossRef] [Green Version]
- Krysanova, V.; White, M. Advances in water resources assessment with SWAT—An overview. Hydrol. Sci. J. 2015, 60, 771–783. [Google Scholar] [CrossRef] [Green Version]
- Tuppad, P.; Douglas-Mankin, K.R.; Lee, T.; Srinivasan, R.; Arnold, J. Soil and Water Assessment Tool (SWAT) hydrologic/water quality model: Extended capability and wider adoption. Am. Soc. Agric. Biol. Eng. 2011, 54, 1677–1684. [Google Scholar] [CrossRef]
- Arnold, J.G.; Moriasi, D.N.; Gassman, P.W.; Abbaspour, K.C.; White, M.J.; Srinivasan, R.; Santhi, C.; Harmel, R.D.; Van Griensven, A.; Van Liew, M.W.; et al. SWAT: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1491–1508. [Google Scholar] [CrossRef]
- Mapfumo, E.; Chanasyk, D.S.; Willms, W.D. Simulating daily soil water under foothills fescue grazing with the Soil and Water Assessment Tool model (Alberta, Canada). Hydrol. Process. 2004, 18, 2787–2800. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Storm, B. MIKE-SHE. In Computer Models of Watershed Hydrology; Singh, V.J., Ed.; Water Resources Pub.: Englandwood, CO, USA, 1995; pp. 809–846. [Google Scholar]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Park, J.Y.; Ahn, S.R.; Hwang, S.J.; Jang, C.H.; Park, G.A.; Kim, S.J. Evaluation of MODIS NDVI and LST for indicating soil moisture of forest areas based on SWAT modeling. Int. Soc. Pad. Water. Environ. Eng. 2014, 121, 77–88. [Google Scholar] [CrossRef]
- Havrylenko, S.B.; Bodoque, J.M.; Srinivasan, R.; Zucarelli, G.V.; Mercuri, P. Assessment of the soil water content in the Pampas region using SWAT. Catena 2016, 137, 298–309. [Google Scholar] [CrossRef]
- Nilawar, A.P.; Calderella, C.P.; Lakhankar, T.Y. Satellite soil moisture validation using hydrological SWAT model: A case study of Puerto Rico, USA. Hydrology 2017, 4, 45. [Google Scholar] [CrossRef] [Green Version]
- Rajib, A.; Merwade, V.; Kim, I.L.; Zhao, L.; Song, C.; Zhe, S. SWATShare—A web platform for collaborative research and education through online sharing, simulation and visualization of SWAT models. Environ. Model. Softw. 2016, 75, 498–512. [Google Scholar] [CrossRef] [Green Version]
- Azimi, S.; Dariane, A.; Modanesi, S.; Bauer-Marschallinger, B.; Bindlish, R.; Wagner, W.; Massari, C. Assimilation of Sentinel 1 and SMAP–based satellite soil moisture retrievals into SWAT hydrological model: The impact of satellite revisit time and product spatial resolution on flood simulations in small basins. J. Hydrol. 2020, 581, 1–16. [Google Scholar] [CrossRef]
- Breen, K.; James, S.; White, J.; Allan, P.; Arnold, J. A Hybrid Artificial Neural Network to Estimate Soil Moisture Using SWAT+ and SMAP Data, Mach. Learn. Knowl. Extr. 2020, 2, 283–306. [Google Scholar]
- Li, D.; Liang, Z.; Li, B.; Lei, X.; Zhou, Y. Multi-objective calibration of MIKE SHE with SMAP soil moisture datasets. Hydrol. Curr. Res. 2019, 50, 644–654. [Google Scholar] [CrossRef] [Green Version]
- Yi, L.; Zhang, Q.; Li, X. Assessing hydrological modelling driven by different precipitation datasets via the SMAP soil moisture product and gauged streamflow data. Remote Sens. 2018, 10, 1872. [Google Scholar] [CrossRef] [Green Version]
- Tavakol, A.; Rahmani, V.; Quiring, S.M.; Kumar, S.V. Evaluation analysis of NASA SMAP L3 and L4 and SPoRT-LIS soil moisture data in the United States. Remote Sens. Environ. 2019, 229, 234–246. [Google Scholar] [CrossRef]
- Reichle, R.H.; de Lannoy, G.; Koster, R.D.; Crow, W.T.; Kimball, J.S. Assessment of the SMAP Level-4 Surface and Root-Zone Soil Moisture Product Using In Situ Measurements. J. Hydrometeorol. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual; Open File Rep.; Eawag, Swiss Federal Institute of Aquatic Science and Technology: Dübendorf, Switzerland, 2015; 100p. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Musyoka, F.K.; Strauss, P.; Zhao, G.; Srinivasan, R.; Klik, A. Multi-Step calibration approach for SWAT model using soil moisture and crop yields in a small agricultural catchment. Water 2021, 13, 2238. [Google Scholar] [CrossRef]
- Perez-Valdivia, C.; Cade, B.; McMartin, D. Hydrological modeling of the pipestone creek watershed using the Soil Water Assessment Tool (SWAT): Assessing impacts of wetland drainage on hydrology. J. Hydrol. 2017, 14, 109–129. [Google Scholar] [CrossRef]
- Mekonnen, B.; Mazurek, K.; Putz, G. Incorporating landscape depression heterogeneity into the Soil and Water Assessment Tool (SWAT) using a probability distribution. Hydrol. Process. 2016, 30, 2373–2389. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, Y.; Qiu, L.; Sun, Y.; Sun, L.; Li, Q.; Niu, J.; Wang, G. Parameter uncertainty analysis of the SWAT model in a Mountain-Loess Transitional watershed on the Chinese Loess Plateau. Water 2018, 10, 690. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Wang, Q.; Zhou, L.; Sun, Q.; Li, Q. Predictive Contributions of Snowmelt and Rainfall to Streamflow Variations in the Western United States. Adv. Meteorol. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- Due, X.; Goss, G.; Faramarzi, M. Impacts of Hydrological Processes on Stream Temperature in a Cold Region Watershed Based on the SWAT Equilibrium Temperature Model. Water 2020, 12, 1112. [Google Scholar] [CrossRef] [Green Version]
- Sun, N.; Yearsley, J.; Baptiste, M.; Cao, Q.; Lettenmaier, D.P.; Nijssen, B. A spatial distributed model for assessment of the effects of changing land use and climate on urban stream quality. Hydrol. Process. 2016, 30, 4779–4798. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Crow, W.T.; De Lannoy, G.J.M.; Kimball, J.S.; Ardizzone, J.V.; Bosch, D.; Colliander, A.; Cosh, M.; et al. Version 4 of the SMAP level-4 soil moisture algorithm and data product. J. Adv. Model. Earth Syst. 2019, 11, 3106–3130. [Google Scholar] [CrossRef] [Green Version]
- Crow, W.T.; Chen, F.; Reichle, R.H.; Xia, Y. Diagnosing bias in modeled soil moisture/runoff coefficient correlation using the SMAP Level 4 soil moisture product. Water Resour. Res. 2019, 55, 7010–7026. [Google Scholar] [CrossRef]
- Dong, J.; Crow, W.T.; Reichle, R.H.; Liu, Q.; Lei, F.; Cosh, M. A global assessment of added value in the SMAP Level-4 Soil Moisture product relative to its baseline land surface model. Geophys. Res. Lett. 2019, 46, 6604–6613. [Google Scholar] [CrossRef]
- Richard, J.; Madramootoo, C.; Trotman, A. Application of the Standardized Precipitation Index and Normalized Difference Vegetation Index for Evaluation of Irrigation Demands at Three Sites in Jamaica. J. Irrig. Drain. Eng. 2013, 139, 922–932. [Google Scholar] [CrossRef]
- Milzow, C.; Krogh, P.E.; Bauer-Gottwein, P. Combining satellite radar altimetry, SAR surface soil moisture and GRACE total storage changes for hydrological model calibration in a large poorly gauged catchment. Hydrol. Earth Syst. Sci. 2016, 15, 1729–1743. [Google Scholar] [CrossRef] [Green Version]
- Wanders, N.; Bierkens, M.F.P.; De Jong, S.M.; de Roo, A.; Karssenberg, D. The benefits of using remotely sensed soilmoisture in parameter identification of large-scale hydrologicalmodels. Water Resour. Res. 2014, 50, 6874–6891. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Luo, Y.; Zhang, D.; Zhang, M.; Liu, C. Recent changes in pan-evaporation dynamics in China. Geophys. Res. Lett. 2011, 38, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Purdy, A.J.; Fisher, J.B.; Goulden, M.L.; Colliander, A.; Halverson, G.; Tu, K.; Famiglietti, J.S. SMAP soil moisture improves global evapotranspiration. Remote Sens. Environ. 2018, 219, 1–14. [Google Scholar] [CrossRef]
- Verstraeten, W.; Veroustraete, F.; Feyen, J. Assessment of evapotranspi-ration and soil moisture content across different scales of observation. Sensors 2008, 8, 70–117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, T.; Franz, T.E. Field observations of regional controls of soil hydraulic properties on soil moisture spatial variability in different climate zones. Vadose Zone J. 2015, 14, 1–8. [Google Scholar] [CrossRef]

| Data Type | Description | Information | Source |
|---|---|---|---|
| Digital Elevation Model | Watershed delineation | Raster, 20 m-resolution | http://geogratis.gc.ca accessed on 28 September 2020 |
| Land use | Land-use classification | Raster, 30 m-resolution | http://geogratis.gc.ca accessed on 30 September 2020 |
| Soil type | Soil properties | Vector | http://www.agr.gc.ca accessed on 2 October 2020 |
| Weather | Precipitation and temperature | Daily | https://weather.gc.ca accessed on 15 November 2020 |
| Streamflow | Calibration and validation model | Daily | https://wateroffice.ec.gc.ca accessed on 16 December 2020 |
| Parameter | Description | Type | Initial Range | Optimal Value | p-Value | t-State | Rank |
|---|---|---|---|---|---|---|---|
| ALPHA_BF | Base flow alpha factor | v | 0.0–1.0 | 0.1–0.241 | 0.000 | −36.26 | 1 |
| GW_REVAP | Ground water re-evaporation coefficient | v | −0.2–0.2 | 0.1–0.17 | 0.000 | 16.89 | 2 |
| CH_K2 | Effective hydraulic conductivity in main channel alluvium (mm/h) | v | 0.0–500 | 154–642 | 0.001 | 14.73 | 3 |
| CN2 | Curve number at moisture condition II | r | −0.2–0.2 | −0.13–0.038 | 0.008 | 13.21 | 4 |
| GWQMN | Threshold depth of water in the shallow aquifer required for return flow (mm) | r | 0.0–0.2 | 0.64–1.94 | 0.074 | 10.9 | 5 |
| SOL_ALB | Moist soil albedo | r | 0–0.25 | 0.08–0.139 | 0.08 | −10.7 | 6 |
| ESCO | Soil evaporation compensation factor | v | 0.0–1.0 | 0.241–0.832 | 0.354 | 9.26 | 7 |
| CH_N2 | Manning’s ‘‘n’’ value for the channel | v | 0.0–0.3 | 0.09–0.272 | 0.382 | −8.74 | 8 |
| GW_DELAY | Groundwater delay (days) | v | 0–500 | 181–272 | 0.533 | −0.623 | 9 |
| SOL_BD | Saturated hydraulic conductivity of first layer | r | −0.1–1.0 | −0.005–0.183 | 0.551 | 0.596 | 10 |
| SURLAG | Surface runoff lag coefficient (day) | v | 0.0–24 | 2.68–23.04 | 0.787 | 0.272 | 11 |
| SOL_AWC | Soil water available capacity | r | −0.1–1.0 | −0.061–0.357 | 0.796 | 0.257 | 12 |
| SOL_K | Saturated hydraulic conductivity (mm/h) | r | −0.1–1.0 | −0.011–0.027 | 0.803 | −0.248 | 13 |
| SOL_Z | Depth from the soil surface to layer bottom | r | −0.1–1.0 | −0.03–0.021 | 0.842 | −0.198 | 14 |
| Data | RMSE | Bias | R | p-Value | N | |
|---|---|---|---|---|---|---|
| Measurement | SWAT | 0.046 | 0.012 | 0.633 | 0.000 | 703 |
| SMAP | 0.052 | −0.035 | 0.698 | 0.000 | 703 | |
| SWAT | SMAP | 0.106 | −0.096 | 0.373 | 0.000 | 703 |
| Statistical Indices | Data | April | May | June | July | August | September | |
|---|---|---|---|---|---|---|---|---|
| R | Measurement | SWAT | −0.055 | 0.063 | 0.725 | 0.864 | 0.6 | 0.605 |
| SMAP | 0.091 | 0.02 | 0.966 | 0.877 | 0.782 | 0.762 | ||
| SWAT | SMAP | −0.036 | 0.107 | 0.748 | 0.152 | 0.306 | 0.247 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, M.; Azam, S.; Sauchyn, D. Evaluation of Soil Water Content Using SWAT for Southern Saskatchewan, Canada. Water 2022, 14, 249. https://doi.org/10.3390/w14020249
Zare M, Azam S, Sauchyn D. Evaluation of Soil Water Content Using SWAT for Southern Saskatchewan, Canada. Water. 2022; 14(2):249. https://doi.org/10.3390/w14020249
Chicago/Turabian StyleZare, Mohammad, Shahid Azam, and David Sauchyn. 2022. "Evaluation of Soil Water Content Using SWAT for Southern Saskatchewan, Canada" Water 14, no. 2: 249. https://doi.org/10.3390/w14020249
APA StyleZare, M., Azam, S., & Sauchyn, D. (2022). Evaluation of Soil Water Content Using SWAT for Southern Saskatchewan, Canada. Water, 14(2), 249. https://doi.org/10.3390/w14020249








