Determination of Pipeline Leaks Based on the Analysis the Hurst Exponent of Acoustic Signals
Abstract
1. Introduction
2. Materials and Methods
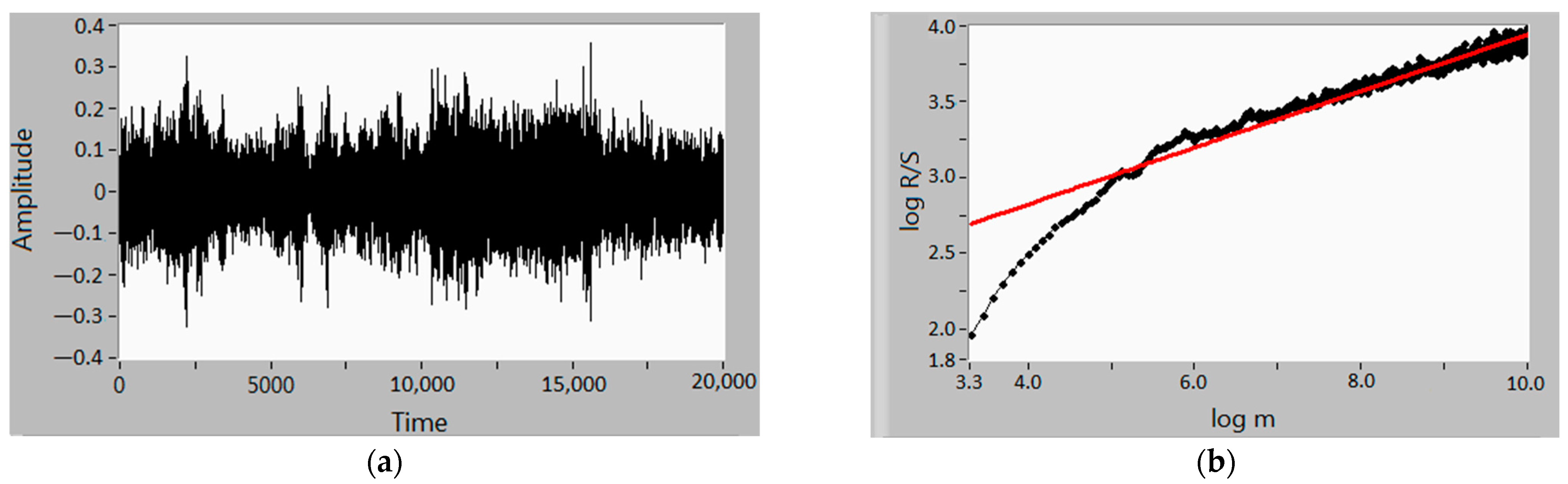
2.1. R/S Analysis Algorithm
- 1.
- The smallest own divisor m of the sample n is determined. Sample n is divided into k = n/m groups.
- 2.
- For each group, the average is calculatedand accumulated deviations from the mean Xi
- 3.
- Calculate the normalized diaposon for each group
- 4.
- For each group, the standard deviation Sk calculated according to the standard formula
- 5.
- The R/S index for each group is defined as Rk/Sk. Then, the average range of the variation is found
- 6.
- The procedure described above is repeated for all possible proper divisors as m. At the last step, m = n/2.Thus, a selection is obtainedThe number of elements in the sample match the number of proper divisors.
- 7.
- A graph of dependences of log R/S on log m is being built and using the method of least squares a regression equation of the formwhere H is the Hurst exponent.
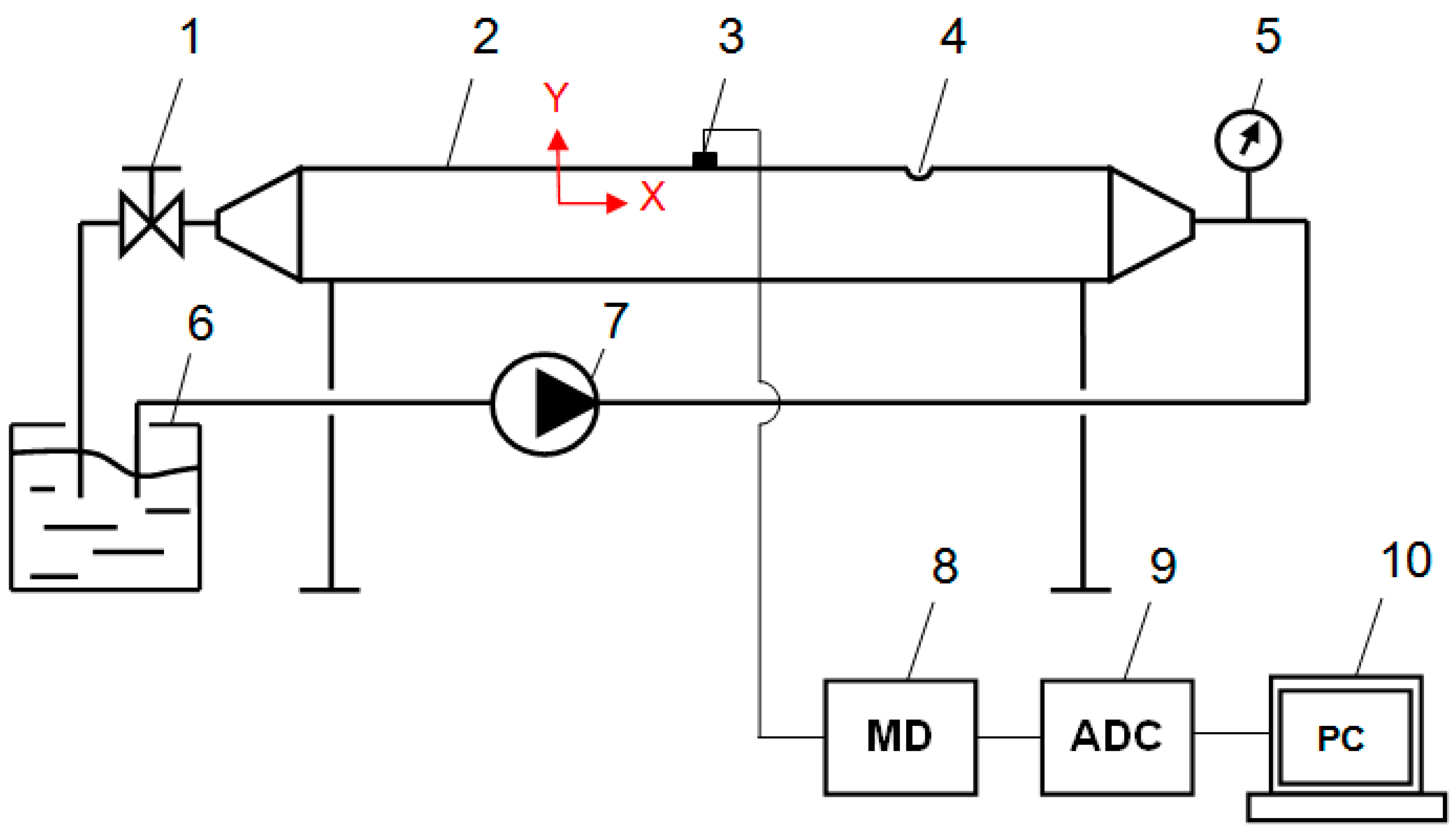
2.2. Experimental Stand
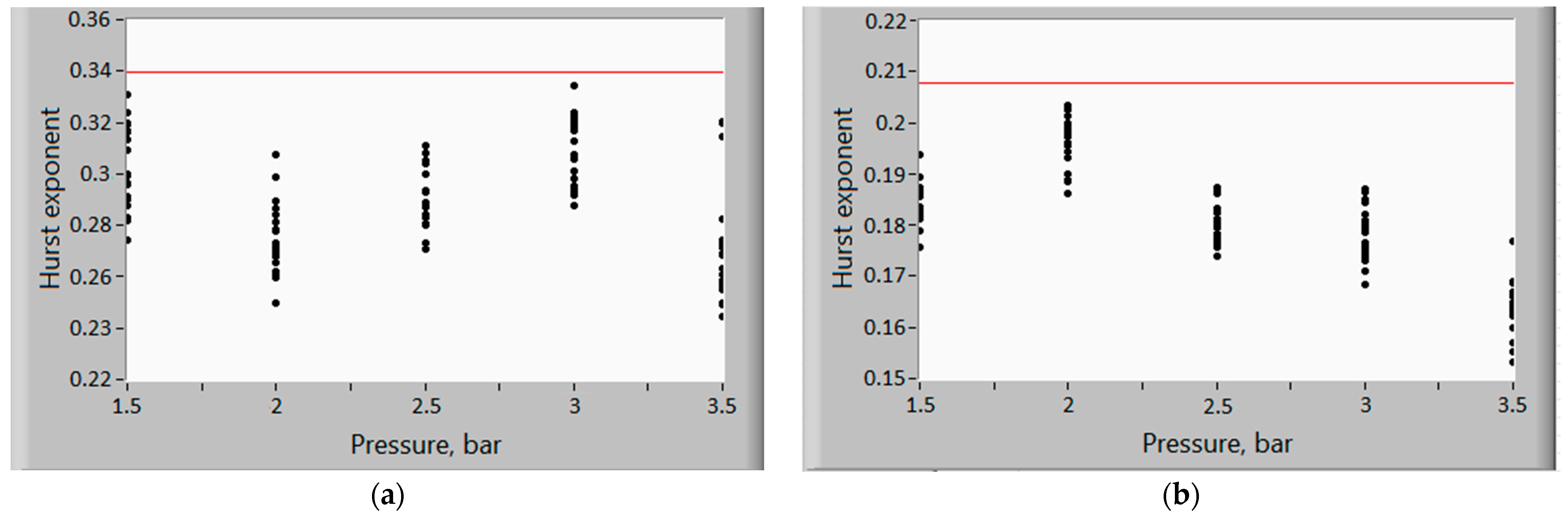
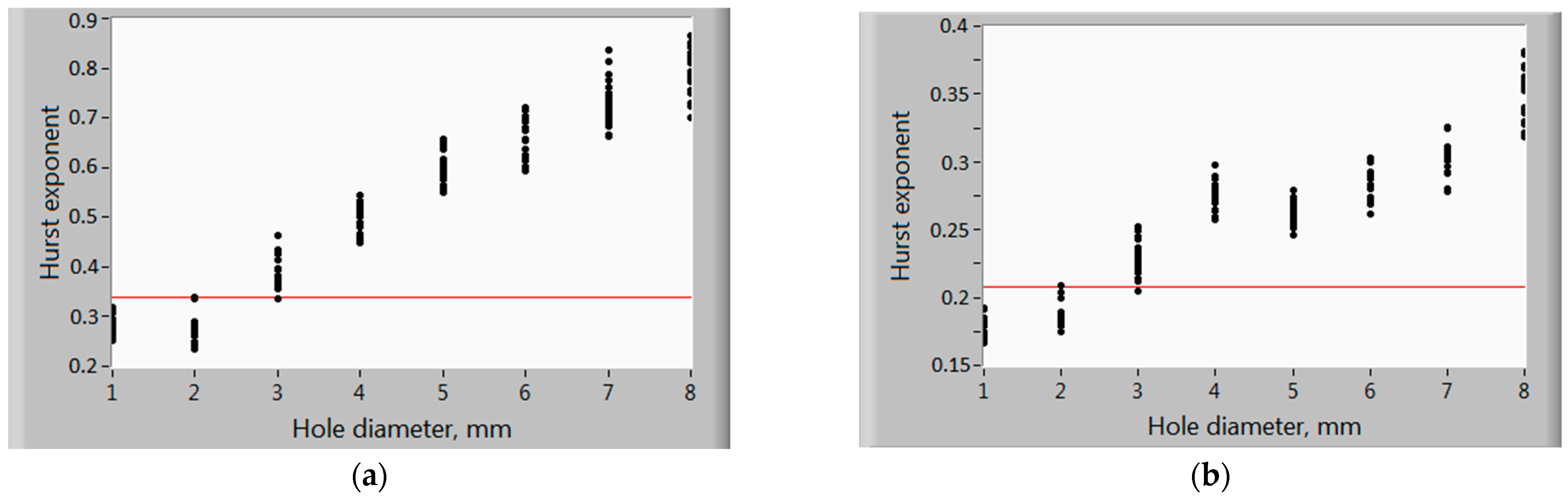
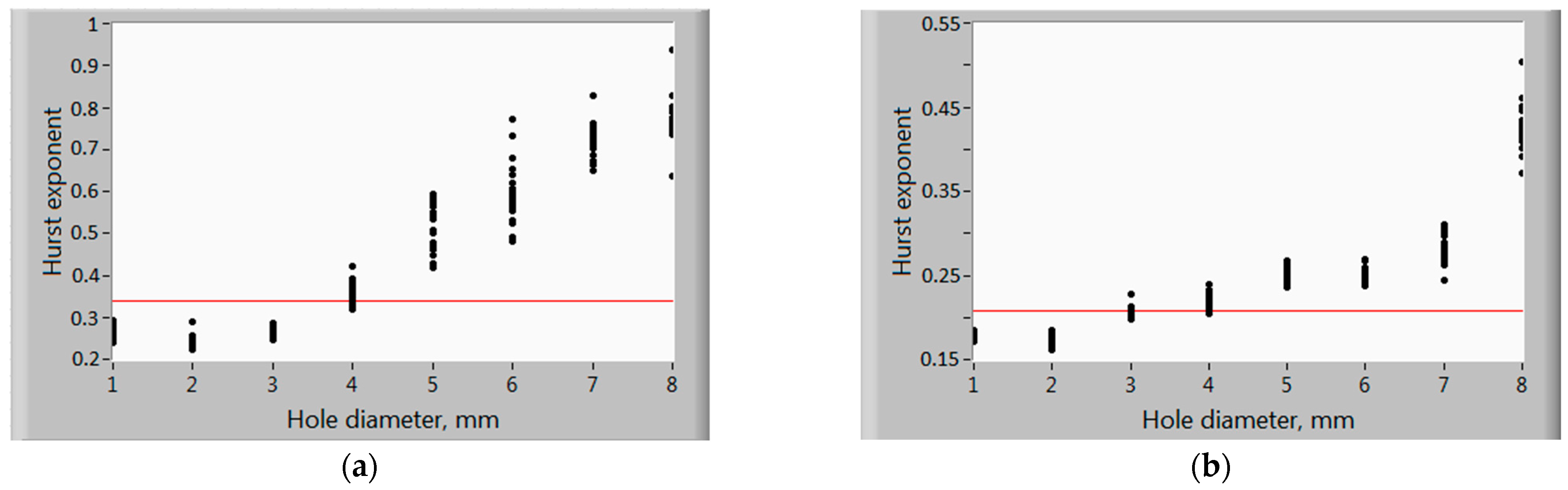
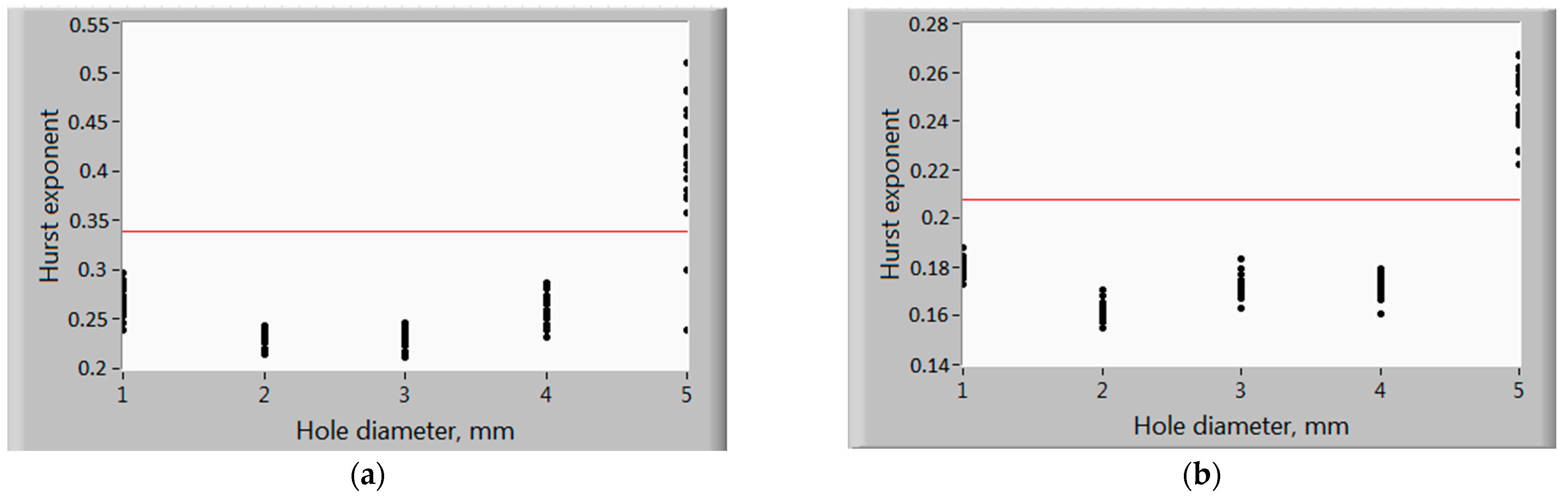
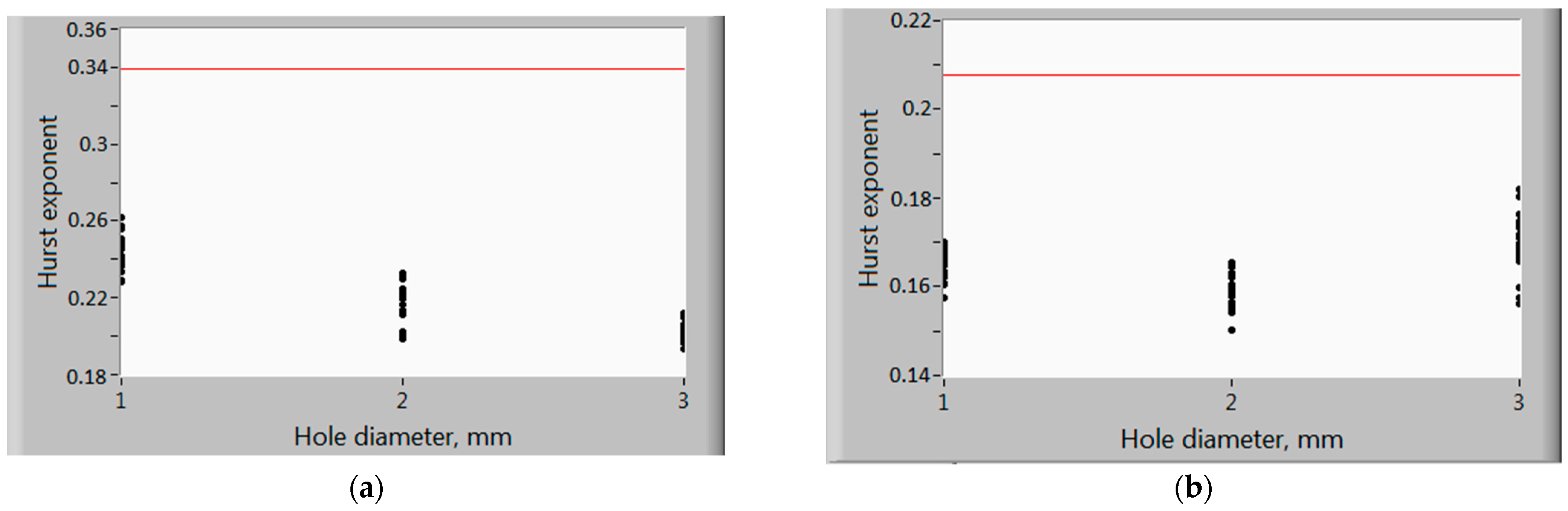
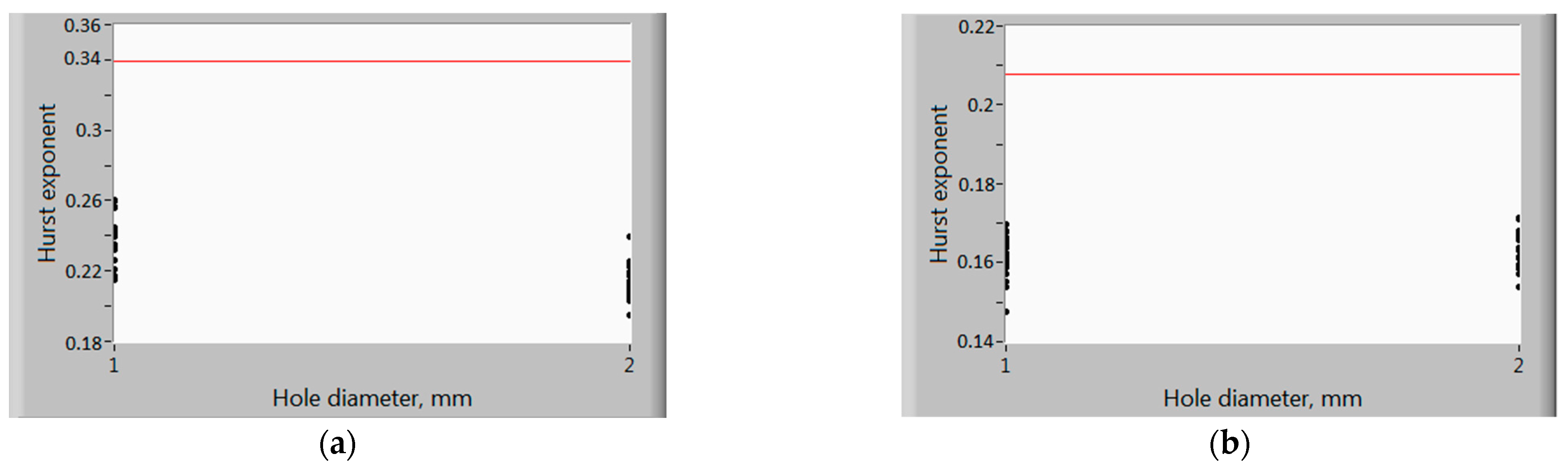
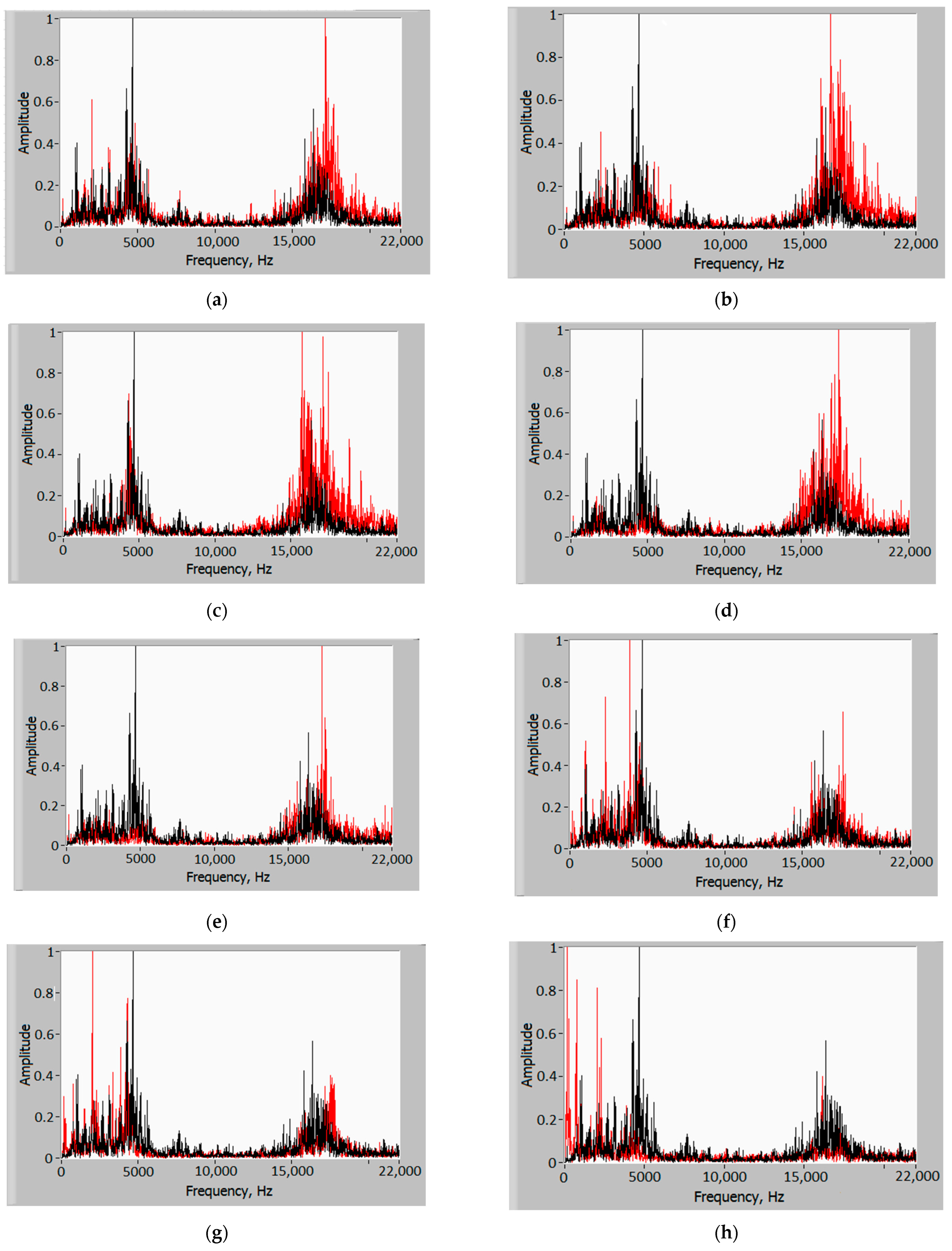
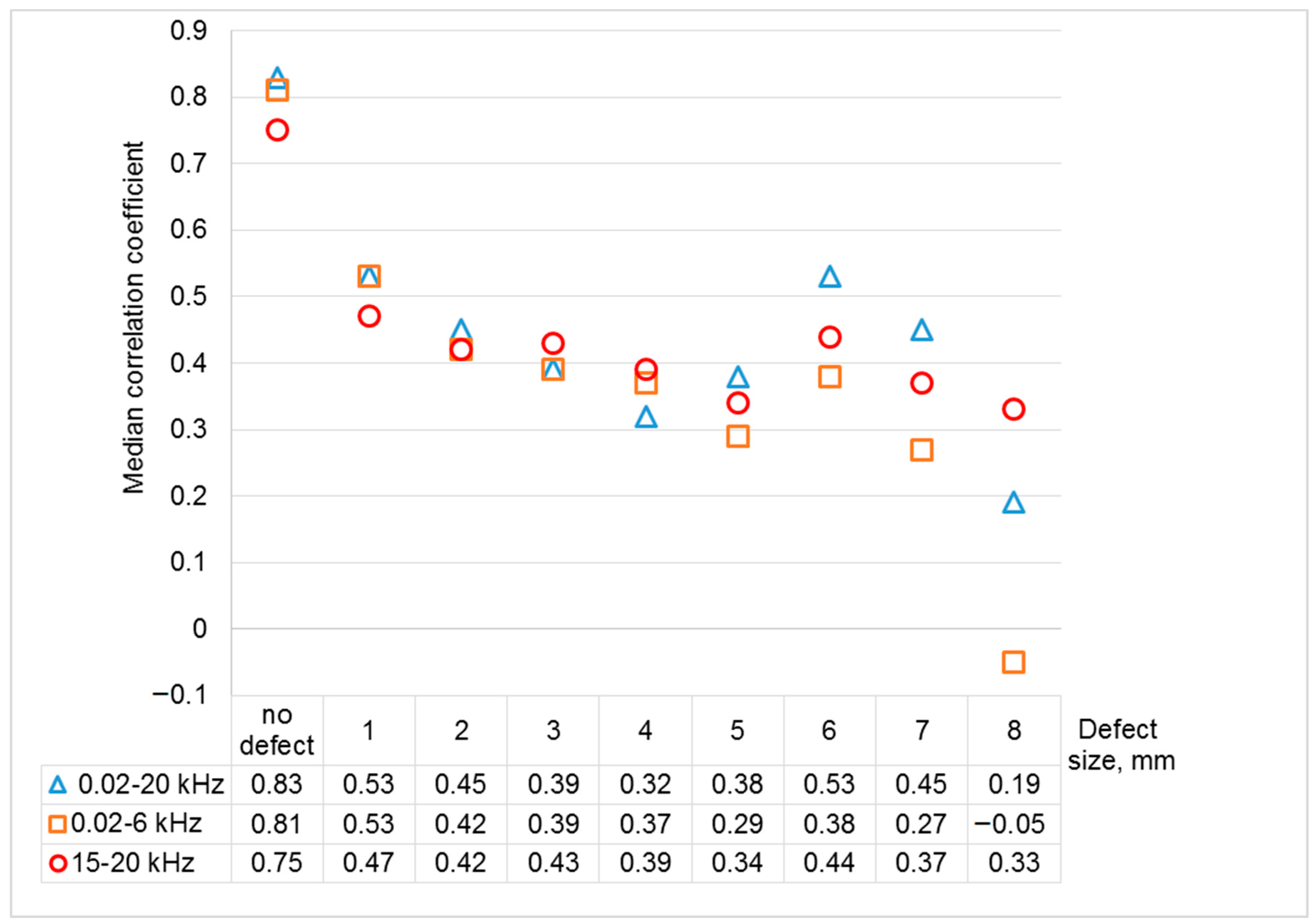
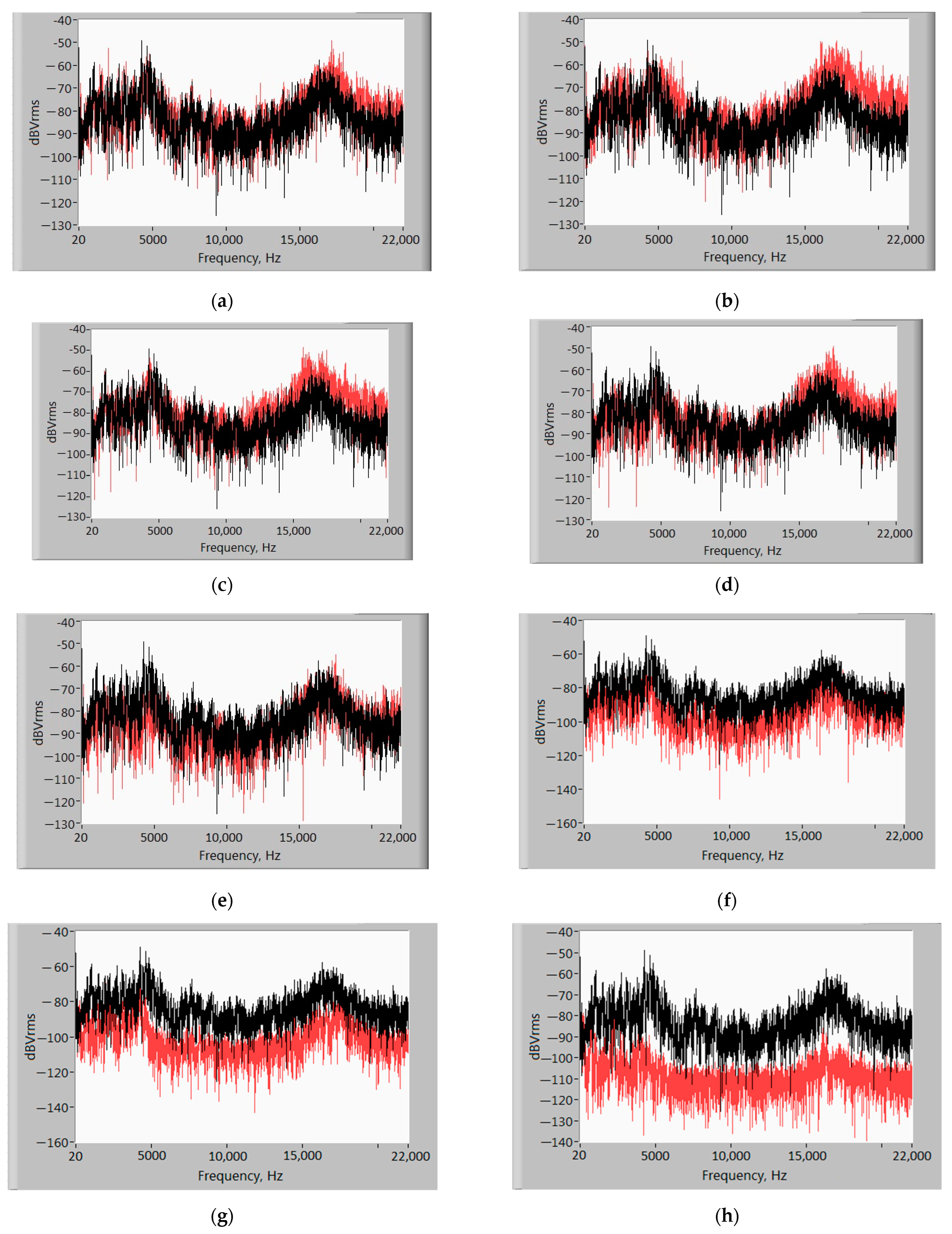
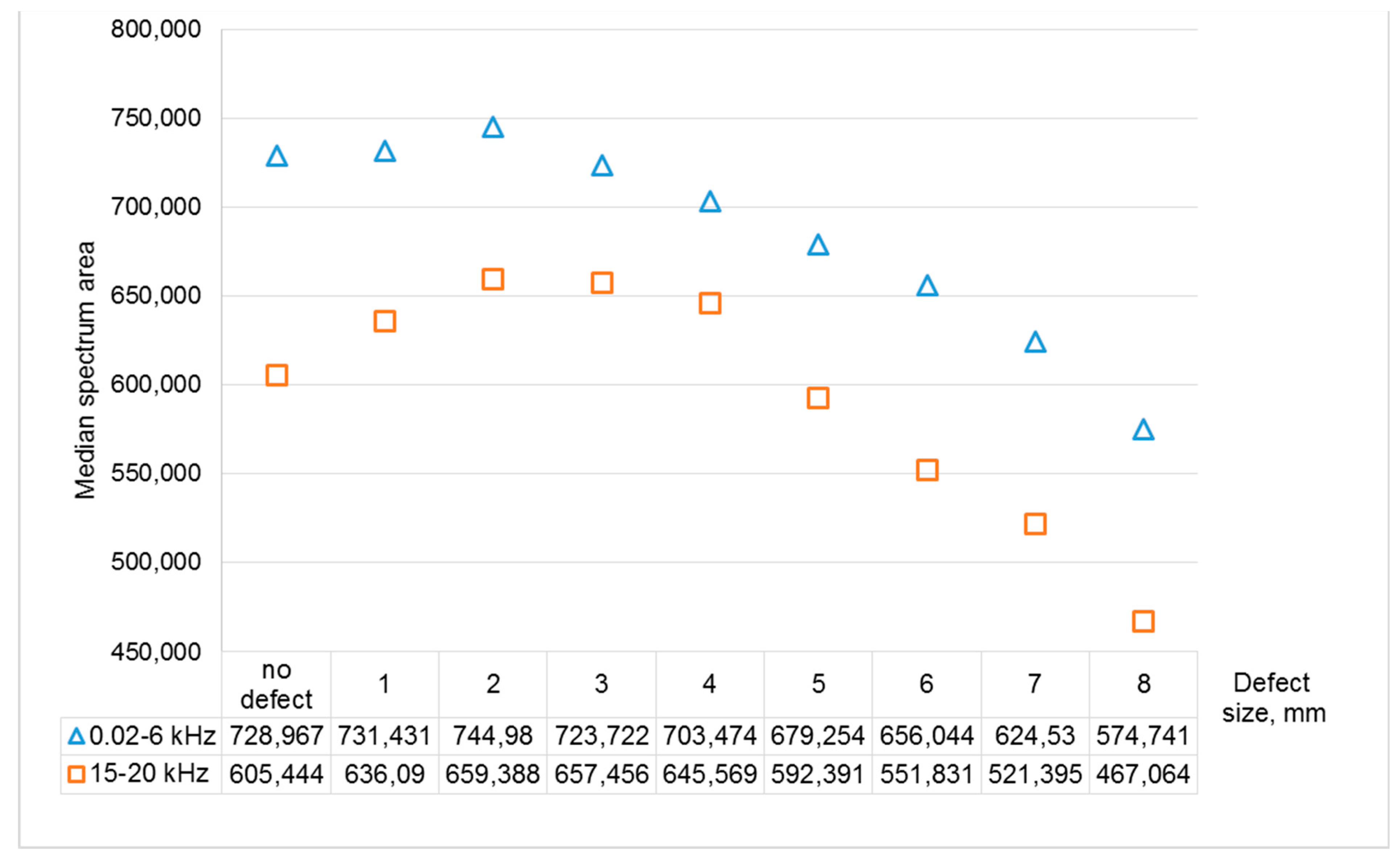
3. Results and Discussion
- The position estimate is calculated .
- The spread estimate S is calculated as a standard deviation.
- For a given significance level α confidence interval is constructed:where t (α, m) is the α-quantile of the Student’s distribution with m degrees of freedom.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pan, B.; Duan, H.F.; Meniconi, S.; Brunone, B. FRF-based transient wave analysis for the viscoelastic parameters identification and leak detection in water-filled plastic pipes. Mech. Syst. Signal Process. 2021, 146, 107056. [Google Scholar] [CrossRef]
- Cao, X.Q.; Ruan, C.M. Compilation of investigation on water loss rate of water supply pipelines in global major cities. Water Purificat. Technol. 2017, 36, 6–14. [Google Scholar]
- Dindorf, R.; Wos, P. Universal programmable portable measurement device for diagnostics and monitoring of industrial fluid power systems. Sensors 2021, 21, 3440. [Google Scholar] [CrossRef] [PubMed]
- Vankov, Y.; Rumyantsev, A.; Ziganshin, S.; Politova, T.; Minyazev, R.; Zagretdinov, A. Assessment of the condition of pipelines using convolutional neural networks. Energies 2020, 13, 618. [Google Scholar] [CrossRef]
- Hawari, A.; Alkadour, F.; Elmasry, M.; Zayed, T. A state of the art review on condition assessment models developed for sewer pipelines. Eng. Appl. Artif. Intell. 2020, 93, 103721. [Google Scholar] [CrossRef]
- Siow, P.Y.; Ong, Z.C.; Khoo, S.Y.; Lim, K. Damage sensitive PCA-FRF feature in unsupervised machine learning for damage detection of plate-like structures. Int. J. Struct. Stab. Dyn. 2021, 21, 2150028. [Google Scholar] [CrossRef]
- Pesinis, K.; Tee, K.F. Statistical model and structural reliability analysis for onshore gas transmission pipelines. Eng. Fail. Anal. 2017, 82, 1–15. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y.; Yu, X. Reliability analysis of water distribution systems using physical probabilistic pipe failure method. J. Water Resour. Plan. Manag. 2019, 145, 04018097. [Google Scholar] [CrossRef]
- Valor, A.; Caleyo, F.; Hallen, J.M.; Velázquez, J.C. Reliability assessment of buried pipelines based on different corrosion rate models. Corros. Sci. 2013, 66, 78–87. [Google Scholar] [CrossRef]
- Heidary, R.; Gabriel, S.A.; Modarres, M.; Groth, K.M.; Vahdati, N. A review of data-driven oil and gas pipeline pitting corrosion growth models applicable for prognostic and health management. Int. J. Progn. Health Manag. 2018, 9, 1–13. [Google Scholar] [CrossRef]
- Ji, J.; Robert, D.; Zhang, C.; Zhang, D.; Kodikara, J. Probabilistic physical modelling of corroded cast iron pipes for lifetime prediction. Struct. Saf. 2017, 64, 62–75. [Google Scholar] [CrossRef]
- Liu, W.; Wang, Z.; Liu, X.; Zeng, N.; Liu, Y.; Alsaadi, F.E. A survey of deep neural network architectures and their applications. Neurocomputing 2017, 234, 11–26. [Google Scholar] [CrossRef]
- el Abbasy, M.S.; Senouci, A.; Zayed, T.; Mirahadi, F.; Parvizsedghy, L. Artificial neural network models for predicting condition of offshore oil and gas pipelines. Autom. Constr. 2014, 45, 50–65. [Google Scholar] [CrossRef]
- Peng, S.; Zhang, Z.; Liu, E.; Liu, W.; Qiao, W. A new hybrid algorithm model for prediction of internal corrosion rate of multiphase pipeline. J. Nat. Gas Sci. Eng. 2021, 85, 103716. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Keshtegar, B.; Taleb-Berrouane, M.; Abbassi, R.; Trung, N.-T. Advanced intelligence frameworks for predicting maximum pitting corrosion depth in oil and gas pipelines. Process Saf. Environ. Prot. 2021, 147, 818–833. [Google Scholar] [CrossRef]
- Mazumder, R.K.; Salman, A.M.; Li, Y. Failure risk analysis of pipelines using data-driven machine learning algorithms. Struct. Saf. 2021, 89, 102047. [Google Scholar] [CrossRef]
- Ossai, C.I. Corrosion defect modelling of aged pipelines with a feed-forward multi-layer neural network for leak and burst failure estimation. Eng. Fail. Anal. 2020, 110, 104397. [Google Scholar] [CrossRef]
- Liu, Z.; Kleiner, Y. State of the art review of inspection technologies for condition assessment of water pipes. Measurement 2013, 46, 1–15. [Google Scholar] [CrossRef]
- Hu, Z.; Tariq, S.; Zayed, T. A comprehensive review of acoustic based leak localization method in pressurized pipelines. Mech. Syst. Signal Process. 2021, 161, 107994. [Google Scholar] [CrossRef]
- Bobrov, A.; Kuten, M. Intellectual innovations in acoustic emission control in the safety system of pipeline transport. Transp. Res. Procedia 2021, 54, 340–345. [Google Scholar] [CrossRef]
- Li, S.; Wen, Y.; Li, P.; Yang, J.; Yang, L. Leak detection and location for gas pipelines using acoustic emission sensors. In Proceedings of the IEEE International Ultrasonics Symposium, Dresden, Germany, 7–10 October 2012; pp. 957–960. [Google Scholar] [CrossRef]
- Smith, A.; Dixon, N.; Fowmes, G. Monitoring buried pipe deformation using acoustic emission: Quantification of attenuation. Int. J. Geotech. Eng. 2017, 11, 418–430. [Google Scholar] [CrossRef]
- Bang, S.S.; Lee, Y.H.; Shin, Y. Defect detection in pipelines via guided wave-based time-frequency-domain reflectometry. IEEE Trans. Instrum. Meas. 2021, 70. [Google Scholar] [CrossRef]
- Lowe, M.J.S.; Alleyne, D.N.; Cawley, P. Defect detection in pipes using guided waves. Ultrasonics 1998, 36, 147–154. [Google Scholar] [CrossRef]
- Mohr, W.; Holler, P. On Inspection of Thin-Walled Tubes for Transverse and Longitudinal Flaws by Guided Ultrasonic Waves. IEEE Trans. Sonics Ultrason. 1976, 23, 369–373. [Google Scholar] [CrossRef]
- Lowe, M.; Alleyne, D.; Cawley, P. Mode Conversion of Guided Waves by Defects in Pipes. In Review of Progress in Quantitative Nondestructive Evaluation; Springer: Boston, MA, USA, 1997; Volume 16. [Google Scholar] [CrossRef]
- Hunaidi, O.; Chu, W.T. Acoustical characteristics of leak signals in plastic water distribution pipes. Appl. Acoust. 1999, 58, 235–254. [Google Scholar] [CrossRef]
- Martini, A.; Rivola, A.; Troncossi, M. Autocorrelation analysis of vibro-acoustic signals measured in a test field for water leak detection. Appl. Sci. 2018, 8, 2450. [Google Scholar] [CrossRef]
- Ghazali, M.F.; Beck, S.B.M.; Shucksmith, J.D.; Boxall, J.B.; Staszewski, W.J. Comparative study of instantaneous frequency based methods for leak detection in pipeline networks. Mech. Syst. Signal Process. 2012, 29, 187–200. [Google Scholar] [CrossRef]
- Yang, M.D.; Su, N.C.; Pan, N.F.; Liu, P. Feature extraction of sewer pipe failures by wavelet transform and co-occurrence matrix. In Proceedings of the 2008 International Conference on Wavelet Analysis and Pattern Recognition, ICWAPR 2, Hong Kong, China, 30–31 August 2008. [Google Scholar] [CrossRef]
- Cheraghi, N.; Taheri, F. A damage index for structural health monitoring based on the empirical mode decomposition. J. Mech. Mater. Struct. 2007, 2, 43–62. [Google Scholar] [CrossRef]
- Moselhi, O.; Shehab-Eldeen, T. Classification of defects in sewer pipes using neural networks. J. Infrastruct. Syst. 2000, 6, 97–104. [Google Scholar] [CrossRef]
- Carvalho, A.A.; Rebello, J.M.A.; Souza, M.P.V.; Sagrilo, L.V.S.; Soares, S.D. Reliability of non-destructive test techniques in the inspection of pipelines used in the oil industry. Int. J. Press. Vessel. Pip. 2008, 85, 745–751. [Google Scholar] [CrossRef]
- Datta, D.; Sathish, S. Application of fractals to detect breast cancer. J. Phys. Conf. Ser. 2019, 1377, 012030. [Google Scholar] [CrossRef]
- Hart, M.G.; Romero-Garcia, R.; Price, S.J.; Suckling, J. Global effects of focal brain tumors on functional complexity and network robustness: A prospective cohort study. Clin. Neurosurg. 2019, 84, 1201–1213. [Google Scholar] [CrossRef] [PubMed]
- Dona, O.; Hall, G.B.; Noseworthy, M.D. Temporal fractal analysis of the rs-BOLD signal identifies brain abnormalities in autism spectrum disorder. PLoS ONE 2017, 12, e0190081. [Google Scholar] [CrossRef] [PubMed]
- Babanin, O.; Bulba, V. Designing the technology of express diagnostics of electric train’s traction drive by means of fractal analysis. East.-Eur. J. Enterp. Technol. 2016, 4, 45–54. [Google Scholar] [CrossRef][Green Version]
- Chandrasekaran, S.; Poomalai, S.; Saminathan, B.; Suthanthiravel, S.; Sundaram, K.; Hakkim, F.F.A. An investigation on the relationship between the hurst exponent and the predictability of a rainfall time series. Meteorol. Appl. 2019, 26, 511–519. [Google Scholar] [CrossRef]
- Li, Q.; Liang, S.Y. Degradation trend prognostics for rolling bearing using improved R/S statistic model and fractional brownian motion approach. IEEE Access 2017, 6, 21103–21114. [Google Scholar] [CrossRef]
- Hurst, H. Long Term Storage Capacity of Reservoirs. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar] [CrossRef]
- Nazarychev, S.A.; Zagretdinov, A.R.; Ziganshin, S.G.; Vankov, Y.V. Classification of time series using the Hurst exponent. J. Phys. Conf. Ser. 2019, 1328, 012056. [Google Scholar] [CrossRef]
- Khulief, Y.A.; Khalifa, A.; Mansour, R.B.; Habib, M.A. Acoustic detection of leaks in water pipelines using measurements inside pipe. J. Pipeline Syst. Eng. Pract. 2012, 3, 47–54. [Google Scholar] [CrossRef]
- Martini, A.; Troncossi, M.; Rivola, A. Automatic leak detection in buried plastic pipes of water supply networks by means of vibration measurements. Shock. Vib. 2015, 2015, 165304. [Google Scholar] [CrossRef]


| Pressure, Bar | Consumption, L/Min |
|---|---|
| 1.5 | 45 |
| 2 | 38 |
| 2.5 | 31 |
| 3 | 24 |
| 3.5 | 16 |
| Hole Diameter, Mm | Maximum Pressure, Bar |
|---|---|
| 1 | 3.5 |
| 2 | 3.5 |
| 3 | 3 |
| 4 | 2.5 |
| 5 | 2.5 |
| 6 | 2 |
| 7 | 2 |
| 8 | 2 |
| Pressure, Bar | Reynolds Number |
|---|---|
| 1.5 | 6461 |
| 2 | 5456 |
| 2.5 | 4451 |
| 3 | 3446 |
| 3.5 | 2441 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zagretdinov, A.; Ziganshin, S.; Vankov, Y.; Izmailova, E.; Kondratiev, A. Determination of Pipeline Leaks Based on the Analysis the Hurst Exponent of Acoustic Signals. Water 2022, 14, 3190. https://doi.org/10.3390/w14193190
Zagretdinov A, Ziganshin S, Vankov Y, Izmailova E, Kondratiev A. Determination of Pipeline Leaks Based on the Analysis the Hurst Exponent of Acoustic Signals. Water. 2022; 14(19):3190. https://doi.org/10.3390/w14193190
Chicago/Turabian StyleZagretdinov, Ayrat, Shamil Ziganshin, Yuri Vankov, Eugenia Izmailova, and Alexander Kondratiev. 2022. "Determination of Pipeline Leaks Based on the Analysis the Hurst Exponent of Acoustic Signals" Water 14, no. 19: 3190. https://doi.org/10.3390/w14193190
APA StyleZagretdinov, A., Ziganshin, S., Vankov, Y., Izmailova, E., & Kondratiev, A. (2022). Determination of Pipeline Leaks Based on the Analysis the Hurst Exponent of Acoustic Signals. Water, 14(19), 3190. https://doi.org/10.3390/w14193190








