Uncertainty Analysis of Numerical Simulation of Seawater Intrusion Using Deep Learning-Based Surrogate Model
Abstract
:1. Introduction
2. Factors Influencing Uncertainty in Numerical Models
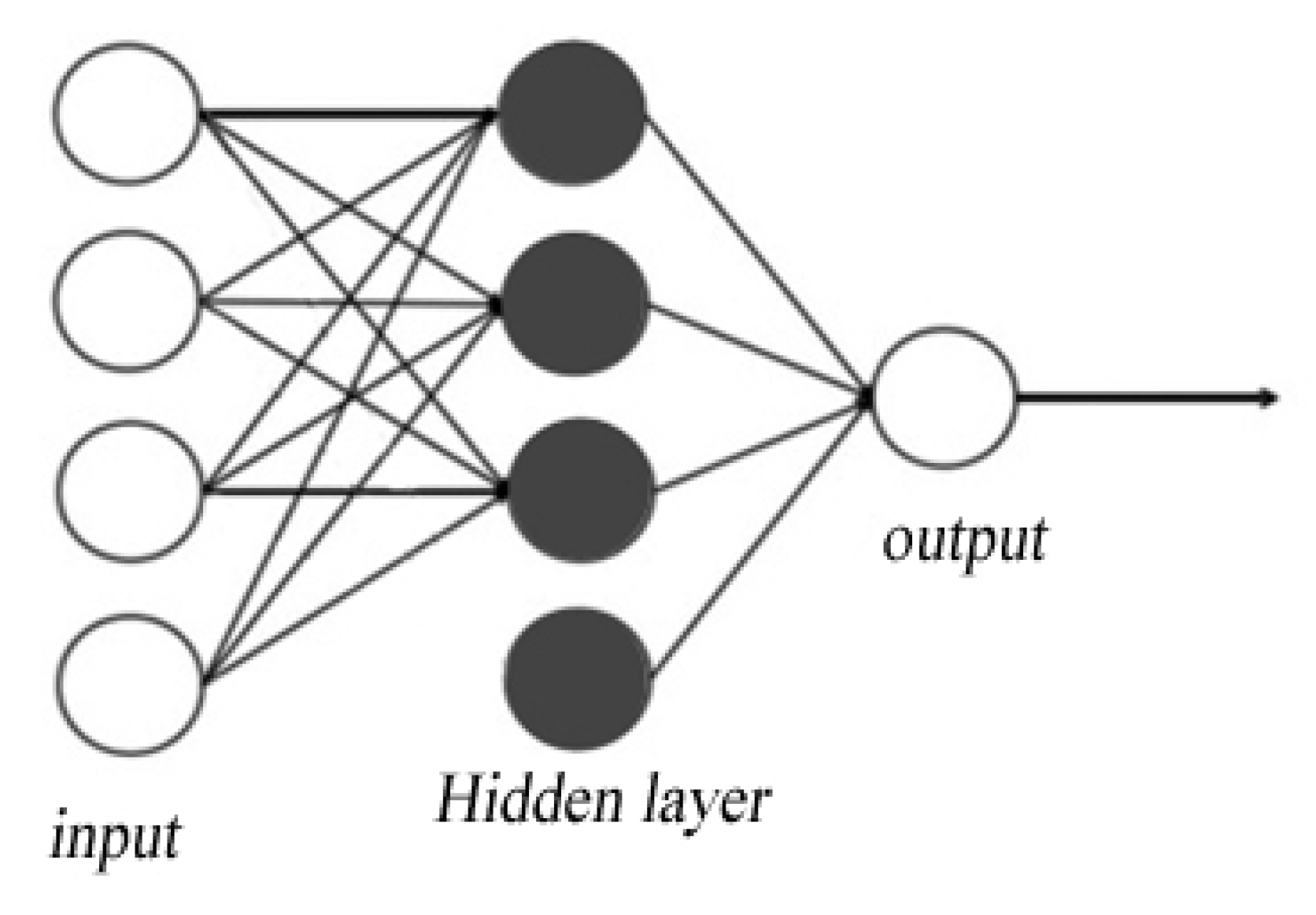
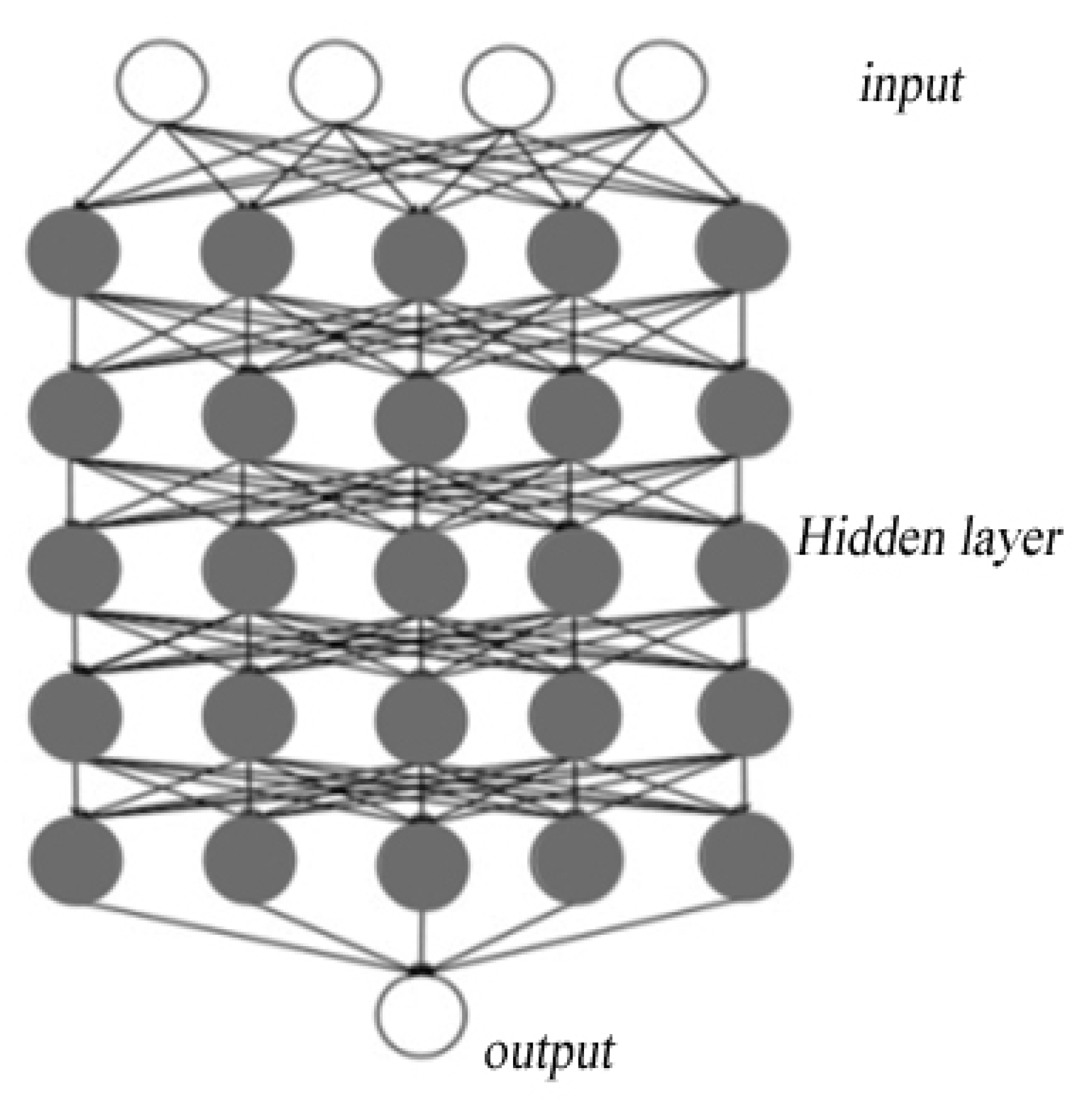
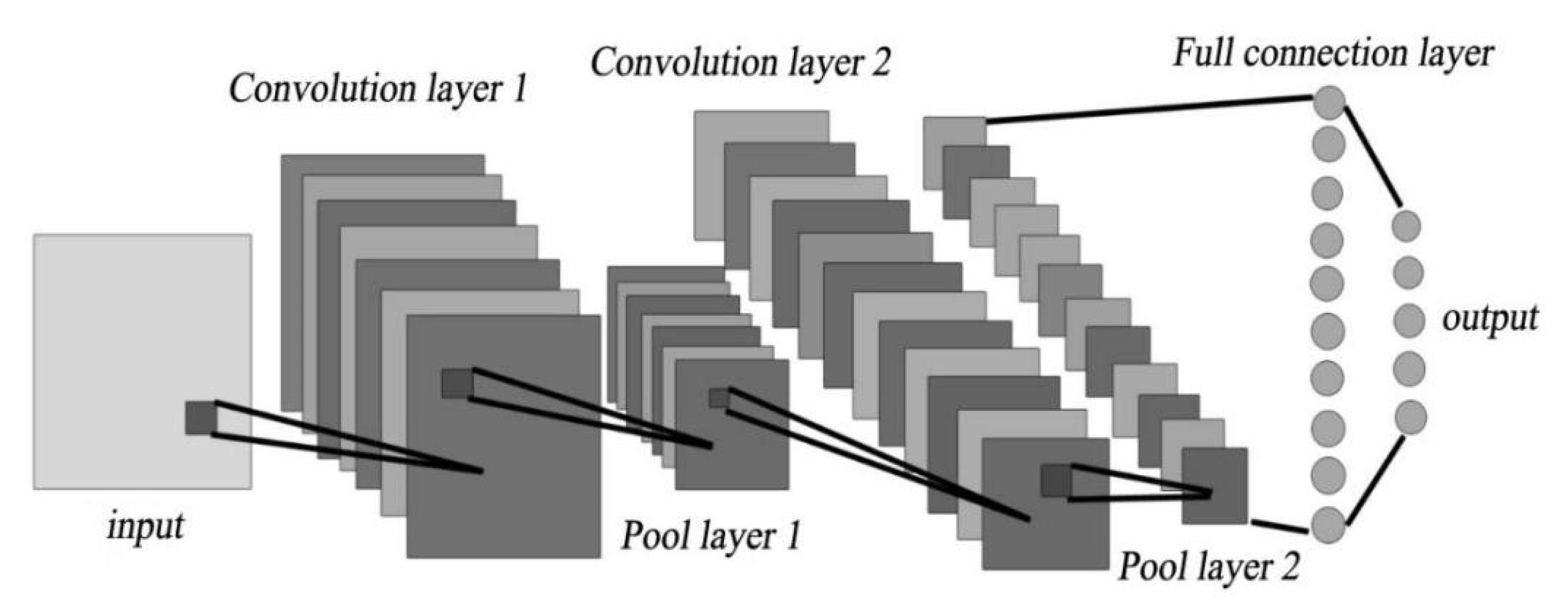
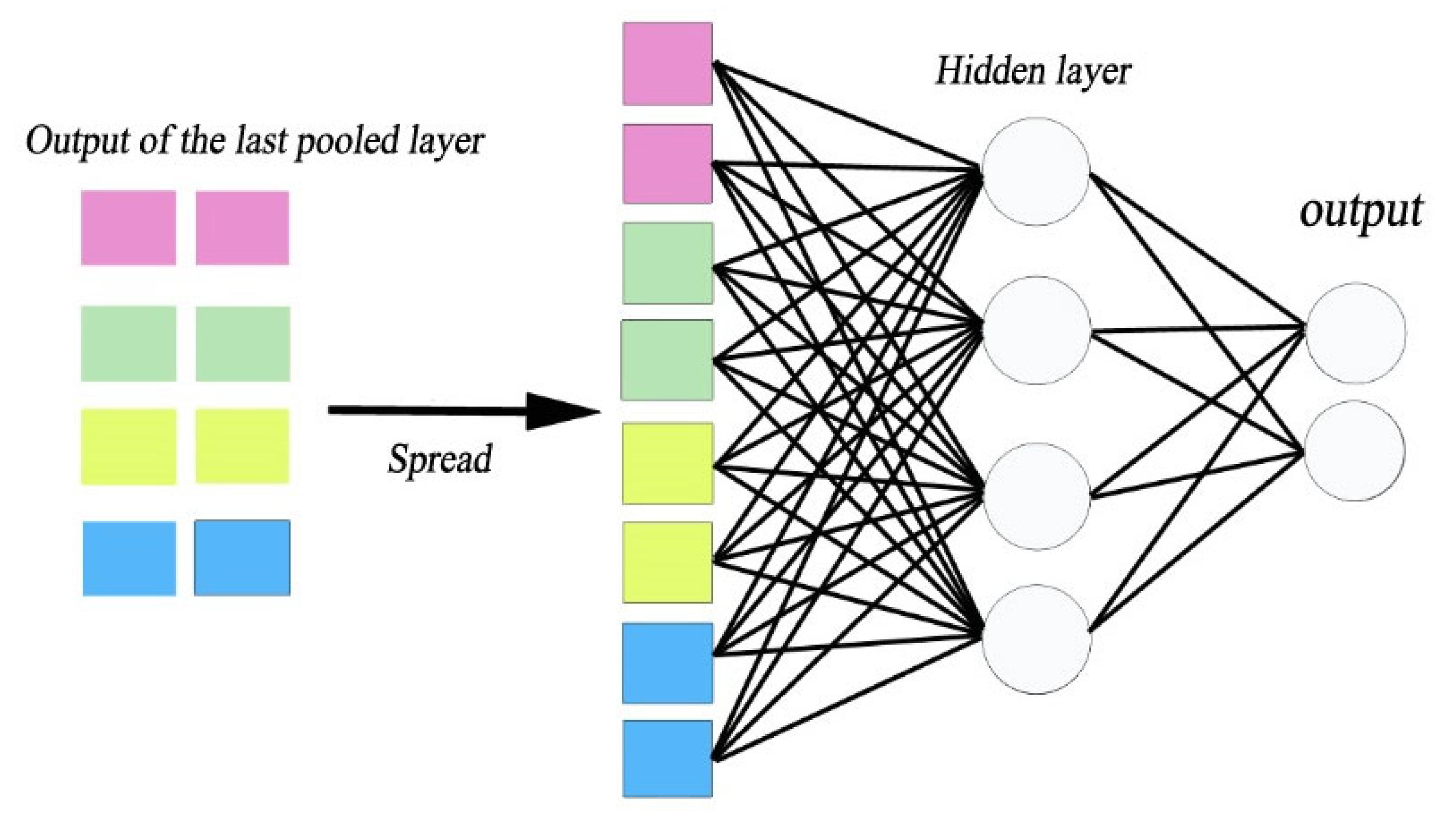
3. Methods of Surrogate Model-Artificial Intelligence-Based Deep Learning
- (1)
- Normalizing the target:
- (2)
- Using DBNN to replace the setting of the model parameters:
- ①
- Parameter Initialization
- ②
- Numbers of Hidden Layers
- ③
- Determining the Number of odes in the Hidden Layers
- (3)
- Unsupervised learning:
- (4)
- Fine-tuning the learning process:
- (5)
- Reverse data normalization:
- (1)
- Principle of forward conduction:
- (2)
- Principle of back-propagation:
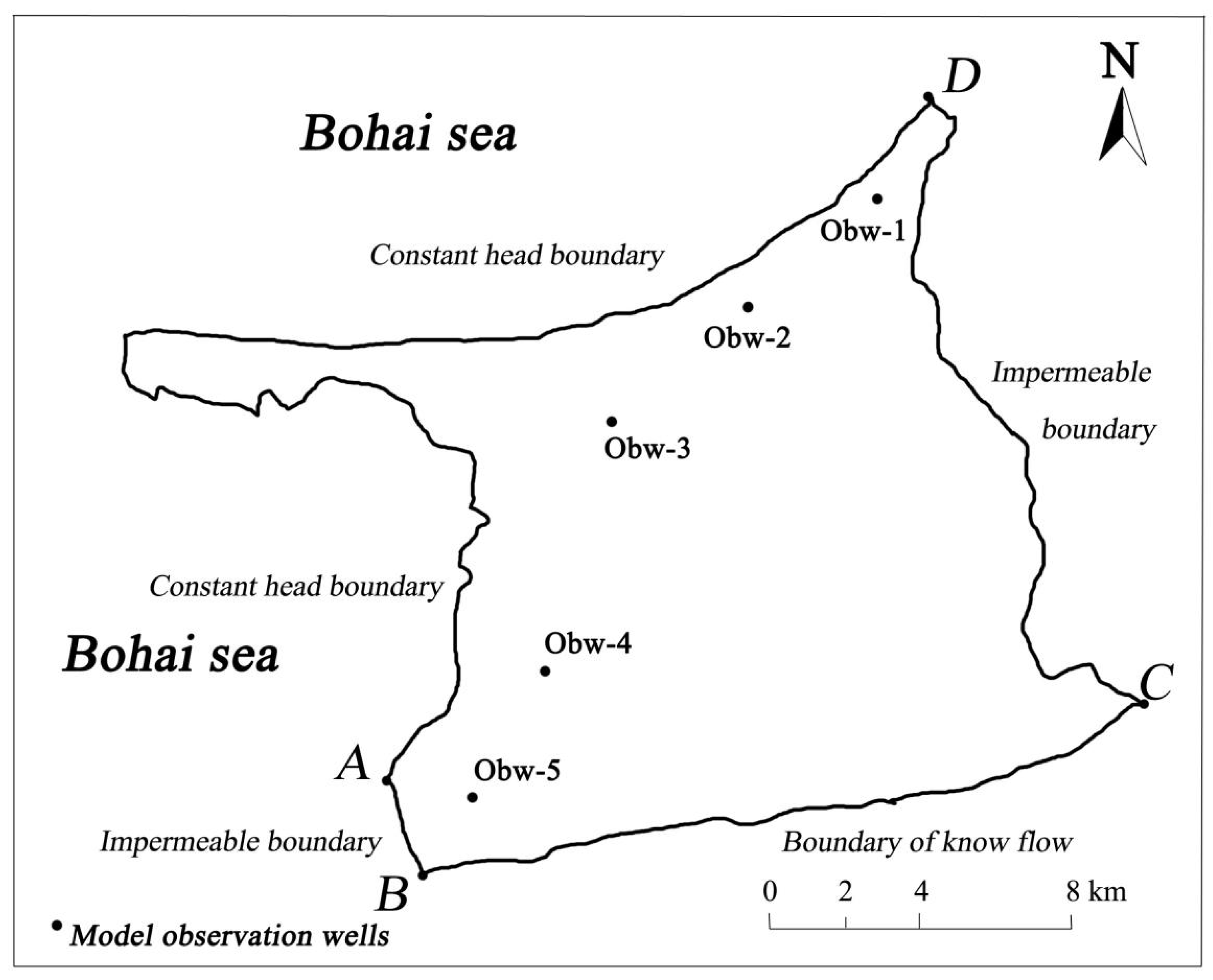
4. Establishing a Seawater Intrusion Simulation Model
5. Establishment of the Surrogate Model
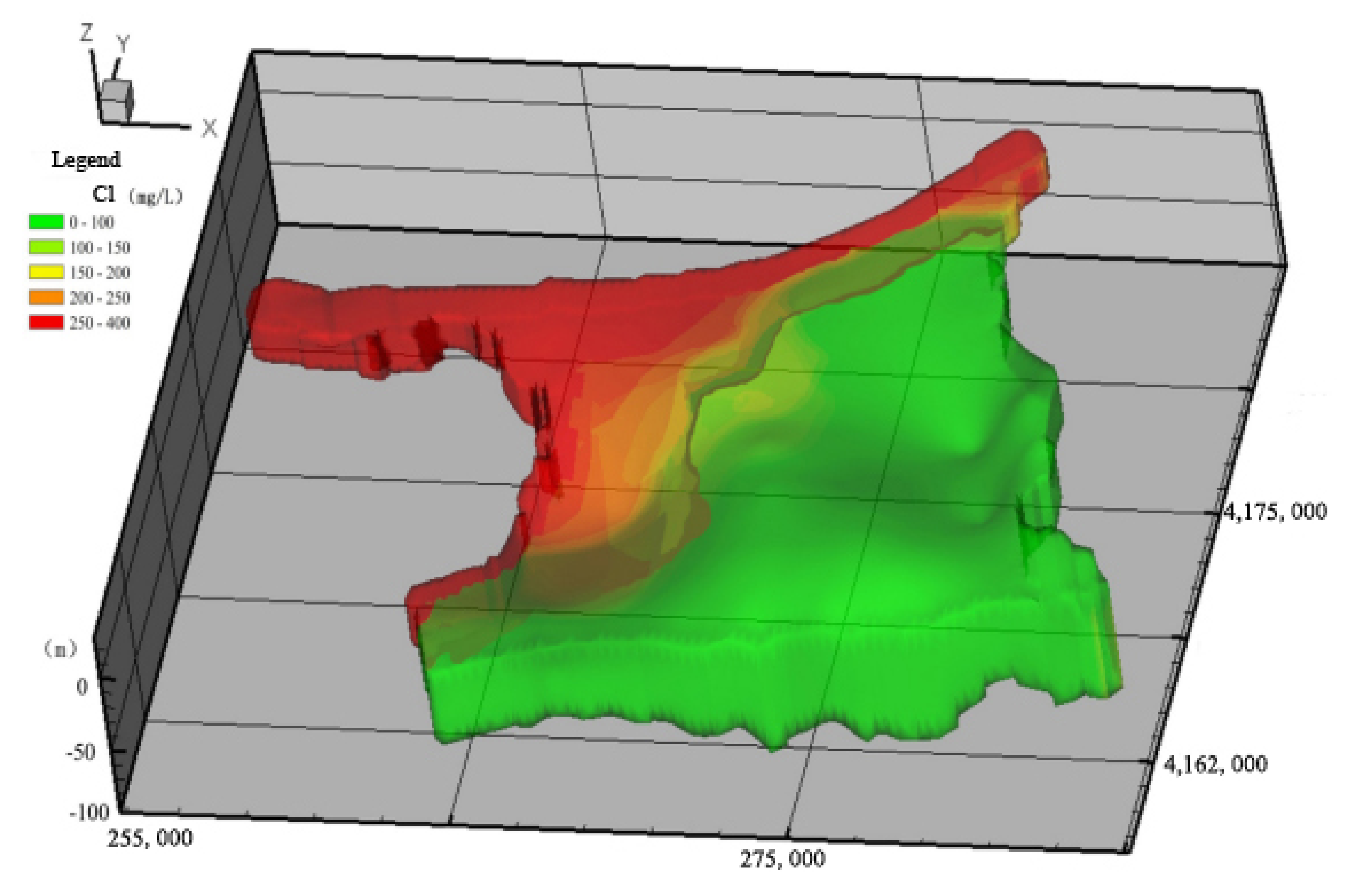
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, J.; Snodsmith, J.B.; Zheng, C.; Wu, J. A modeling study of seawater intrusion in Alabama Gulf Coast, USA. Environ. Geol. 2009, 57, 119–130. [Google Scholar] [CrossRef]
- Kaleris, Vassilios K.;Ziogas, Alexandros I..Using electrical resistivity logs and short duration pumping tests to estimate hydraulic conductivity profiles. J. Hydrol. 2020, 590, 125277. [CrossRef]
- Ketabchi, H.; Mahmoodzadeh, D.; Ataie-Ashtiani, B.; Simmons, C.T. Sea-level rise impacts on seawater intrusion in coastal aquifers: Review and integration. J. Hydrol. 2016, 535, 235–255. [Google Scholar] [CrossRef]
- Larsen, F.; Tran, L.V.; Van Hoang, H.; Tran, L.T.; Christiansen, A.V.; Pham, N.Q. Groundwater salinity influe.nced by Holocene seawater trapped in incised valleys in the Red River delta plain. Nat. Geosci. 2017, 10, 376–381. [Google Scholar] [CrossRef]
- Fan, Y.; Lu, W.; Miao, T.; Li, J.; Lin, J. Multiobjective optimization of the groundwater exploitation layout in coastal areas based on multiple surrogate models. Environ. Sci. Pollut. Res. 2020, 27, 19561–19576. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, A.; Brouziyne, Y. Comparing four machine learning model performances in forecasting the alluvial aquifer level in a semi-arid region. J. Afr. Earth Sci. 2021, 181, 104244. [Google Scholar] [CrossRef]
- Miao, T.; Lu, W.; Lin, J.; Guo, J.; Liu, T. Modeling and uncertainty analysis of seawater intrusion in coastal aquifers using a surrogate model: A case study in Longkou, China. Arab. J. Geosci. 2019, 12, 1. [Google Scholar] [CrossRef]
- Singh, A.; Hauffpauir, R.; Mishra, S.; Lavenue, M.; Valocchi, A. Analyzing Uncertainty and Risk in the Management of Water Resources for the Texas Water Development Board. In Proceedings of the World Environmental & Water Resources Congress, Providence, RI, USA, 16–20 May 2010. [Google Scholar]
- Allgeier, J.; González-Nicolás, A.; Erdal, D.; Nowak, W.; Cirpka, O.A. A Stochastic Framework to Optimize Monitoring Strategies for Delineating Groundwater Divides. Front. Earth Sci. 2020, 8, 554845. [Google Scholar] [CrossRef]
- Gallagher, M.; Doherty, J. Parameter estimation and uncertainty analysis for a watershed model. Environ. Model. Softw. 2007, 22, 1000–1020. [Google Scholar] [CrossRef]
- Wu, J.C.; Lu, L.; Tang, T. Bayesian analysis for uncertainty and risk in a groundwater numerical model’s predictions. Hum. Ecol. Risk Assess. Int. J. 2011, 17, 1310–1331. [Google Scholar] [CrossRef]
- Neufeld, D.; Behdinan, K.; Chung, J. Aircraft wing box optimization considering uncertainty in surrogate models. Struct. Multidiscip. Optim. 2010, 42, 745–753. [Google Scholar] [CrossRef]
- Miao, T.S.; Lu, W.X.; Ouyang, Q. Application of Uncertainty Analysis of Groundwater Numerical Simulation in Water Quality Prediction. Water Resour. Power 2016, 34, 20–23. [Google Scholar]
- Koohbor, B.; Fahs, M.; Ataie-Ashtiani, B.; Belfort, B.; Simmons, C.T.; Younes, A. Uncertainty analysis for seawater intrusion in fractured coastal aquifers: Effects of fracture location, aperture, density and hydrodynamic parameters. J. Hydrol. 2019, 571, 159–177. [Google Scholar] [CrossRef]
- Abd-Elhamid, H.F.; Javadi, A.A. Impact of sea level rise and over-pumping on seawater intrusion in coastal aquifers. J. Water Clim. Chang. 2011, 2, 19. [Google Scholar] [CrossRef]
- Bohorquez, P.; Ancey, C. Stochastic-deterministic modeling of bed load transport in shallow water flow over erodible slope: Linear stability analysis and numerical simulation. Adv. Water Resour. 2015, 83, 36–54. [Google Scholar] [CrossRef]
- Lee, J.; Kang, S. GA based meta-modeling of BPN architecture for constrained approximate optimization. Int. J. Solids Struct. 2007, 44, 5980–5993. [Google Scholar] [CrossRef]
- Hou, Z.; Lu, W. Stochastic nonlinear programming based on uncertainty analysis for DNAPL-contaminated aquifer remediation strategy optimization. J. Water Resour. Plan. Manag. 2018, 144, 04017076. [Google Scholar] [CrossRef]
- Won, K.S.; Ray, T. A framework for design optimization using surrogates. Eng. Optim. 2005, 37, 685–703. [Google Scholar] [CrossRef]
- Sreekanth, J.; Datta, B. Multi-objective management of saltwater intrusion in coastal aquifers using genetic programming and modular neural network based surrogate models. J. Hydrol. 2010, 393, 245–256. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Unsupervised Feature Learning and Deep Learning: A Review and New Perspectives. arXiv 2012, arXiv: 1206.5538. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Li, Z.; Gong, B.; Yang, T. Improved Dropout for Shallow and Deep Learning. In Proceedings of the Advances in Neural Information Processing Systems 29: Annual Conference on Neural Information Processing Systems 2016, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Luger, G. Artificial Intelligence: Structures and Strategies for Complex Problem Solving, 5th ed.; Pearson Addison Wesley: San Francisco, CA, USA, 2004. [Google Scholar]
- Xiao, T.; Xu, Y.; Yang, K.; Zhang, J.; Peng, Y.; Zhang, Z. The Application of Two-level Attention Models in Deep Convolutional Neural Network for Fine-grained Image Classification. In Proceedings of the Proceedings of the IEEE conference on computer vision and pattern recognition, Washington, DC, USA, 23–28 June 2014. [Google Scholar]
- Xu, L.; Ren, J.S.; Liu, C.; Jia, J. Deep Convolutional Neural Network for Image Deconvolution. In International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; pp. 1790–1798. [Google Scholar]
- Ferrag, M.A.; Maglaras, L.; Moschoyiannis, S.; Janicke, H. Deep learning for cyber security intrusion detection: Approaches, datasets, and comparative study. Inf. Secur. Technol. Rep. 2020, 50, 102419.1–102419.19. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.; Hofmann, T. Greedy layer-wise training of deep networks. In Advances in Neural Information Processing Systems 19: Proceedings of the 2006 Conference; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Vedaldi, A.; Lenc, K. MatConvNet—Convolutional Neural Networks for MATLAB. In Proceedings of the 23rd ACM International Conference, ACM, Brisbane, Australia, 26–30 October 2015. [Google Scholar]
- Allen, C.D.; Macalady, A.K.; Chenchouni, H.; Bachelet, D.; McDowell, N.; Vennetier, M.; Kitzberger, T.; Rigling, A.; Breshears, D.D.; Hogg, E.H. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. For. Ecol. Manag. 2010, 259, 660–684. [Google Scholar] [CrossRef]
- Praveena, S.M.; Lin, C.Y.; Aris, A.Z.; Abdullah, M.H. Groundwater assessment at Manukan Island, Sabah: Multidisciplinary approaches. Nat. Resour. Res. 2010, 19, 279–291. [Google Scholar] [CrossRef]
- Langevin, C.D. SEAWAT: A Computer Program for Simulation of Variable-Density Groundwater Flow and Multi-Species Solute and Heat Transport; US Geological Survey: Menlo Park, CA, USA, 2009. [Google Scholar]
- Wagner, M.; Wilson, J.R. Using Univariate Bezier Distributions to Model Simulation Input Processes. A I I E Trans. 1994, 28, 699–711. [Google Scholar] [CrossRef]
- Park, J.; Sandberg, I. Universal Approximation Using Radial-Basis-Function Networks. Neural Comput. 2014, 3, 246–257. [Google Scholar] [CrossRef]
- Slpponen, P.; Kekki, M.; Haapakoski, J.; Ihamäki, T.; Siurala, M. Gastric cancer risk in chronic atrophic gastritis: Statistical calculations of cross-sectional data. Int. J. Cancer 1985, 35, 173–177. [Google Scholar] [CrossRef]
- Papadopoulos, C.E.; Yeung, H. Uncertainty estimation and Monte Carlo simulation method. Flow Meas. Instrum. 2002, 12, 291–298. [Google Scholar] [CrossRef]
- Lo, S.C.; Ma, H.W.; Lo, S.L. Quantifying and reducing uncertainty in life cycle assessment using the Bayesian Monte Carlo method. Sci. Total Environ. 2005, 340, 23–33. [Google Scholar] [CrossRef]
- Miao, T.; Guo, J. Application of artificial intelligence deep learning in numerical simulation of seawater intrusion. Environ. Sci. Pollut. Res. 2021, 28, 54096–54104. [Google Scholar] [CrossRef]
- Olsson, A.; Sandberg, G.; Dahlblom, O. On Latin hypercube sampling for structural reliability analysis. Struct. Saf. 2003, 25, 47–68. [Google Scholar] [CrossRef]
- Iman, R.L. Latin Hypercube Sampling; American Cancer Society: Atlanta, GA, USA, 2008. [Google Scholar]


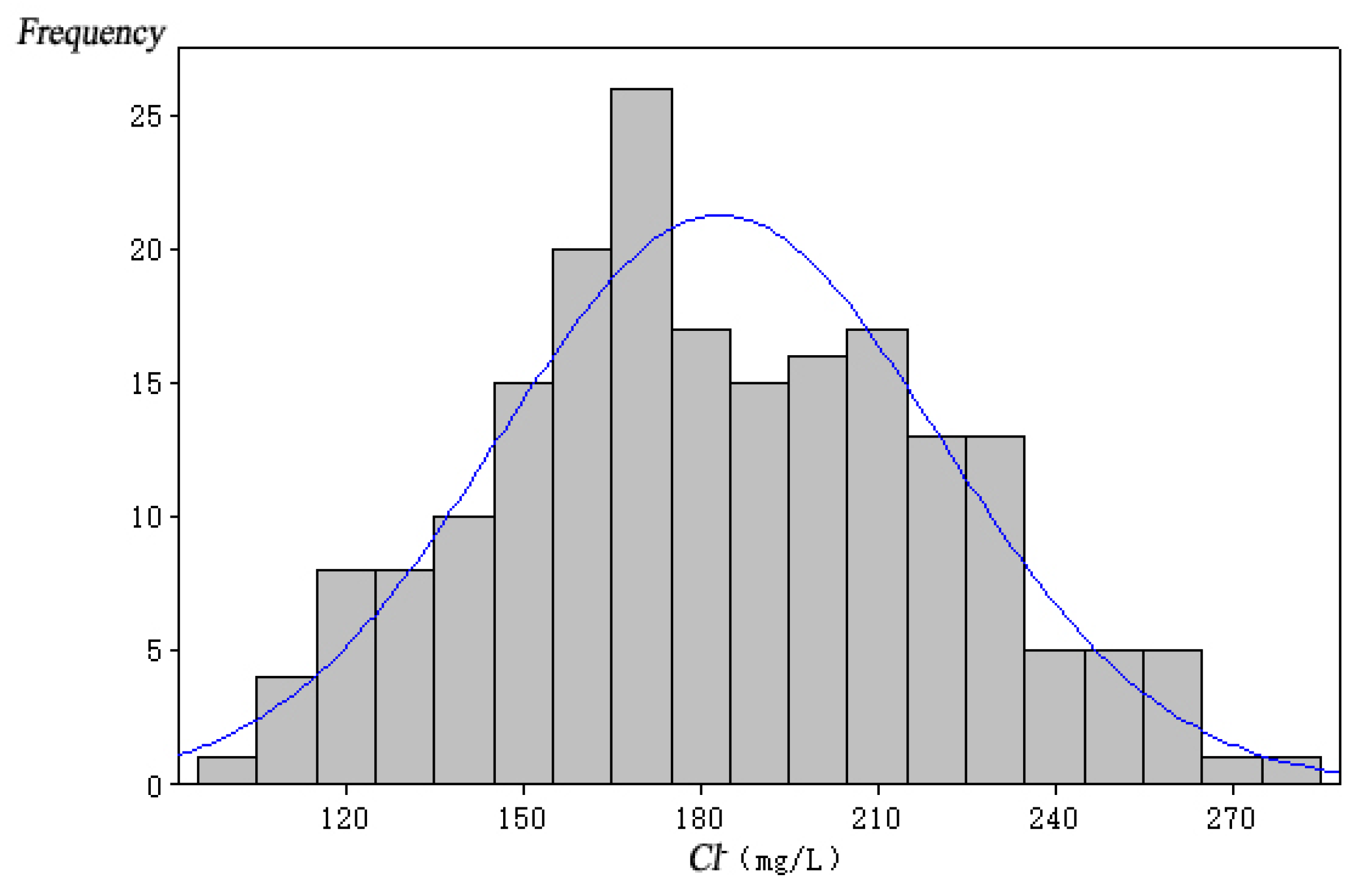
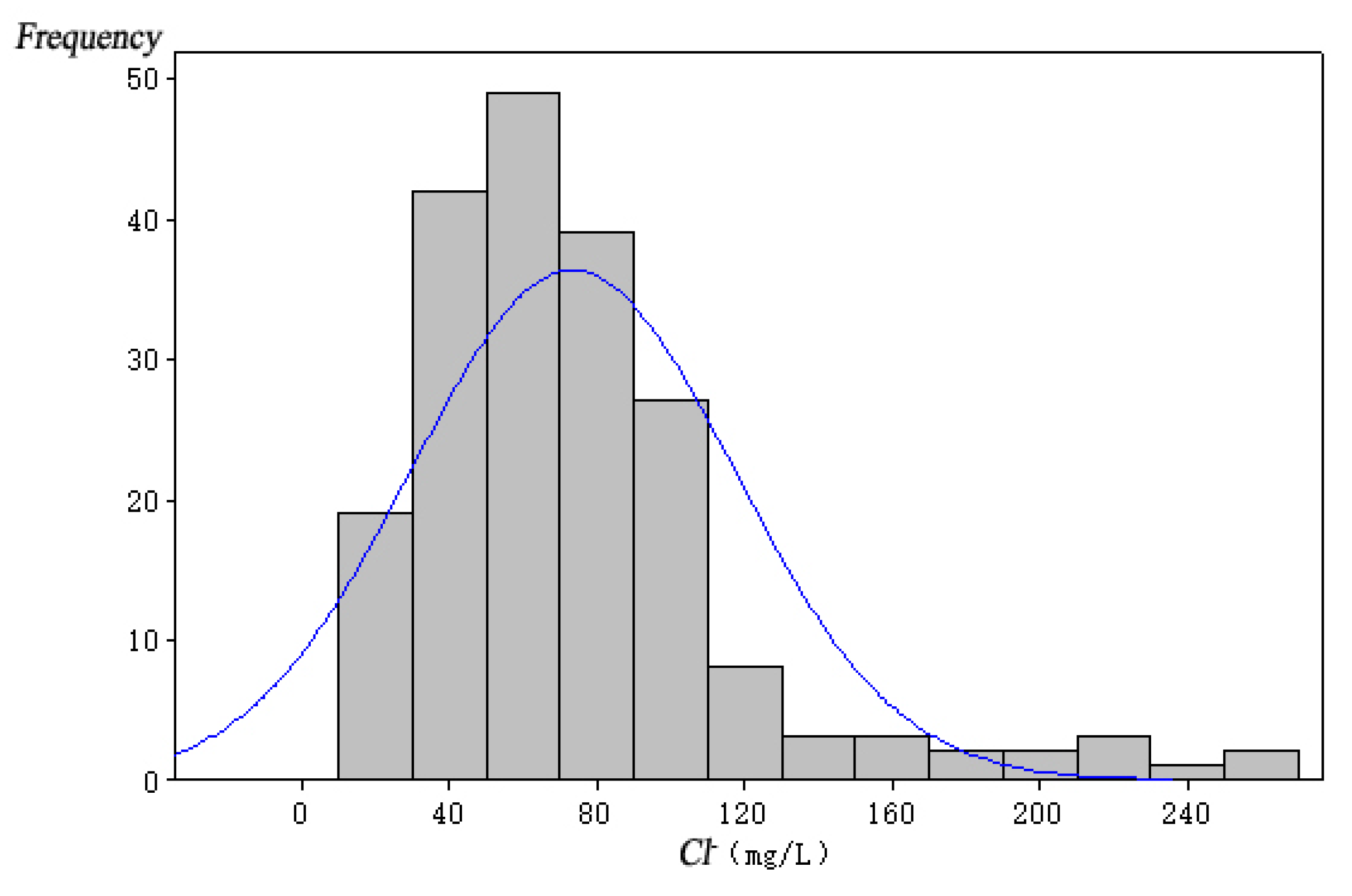
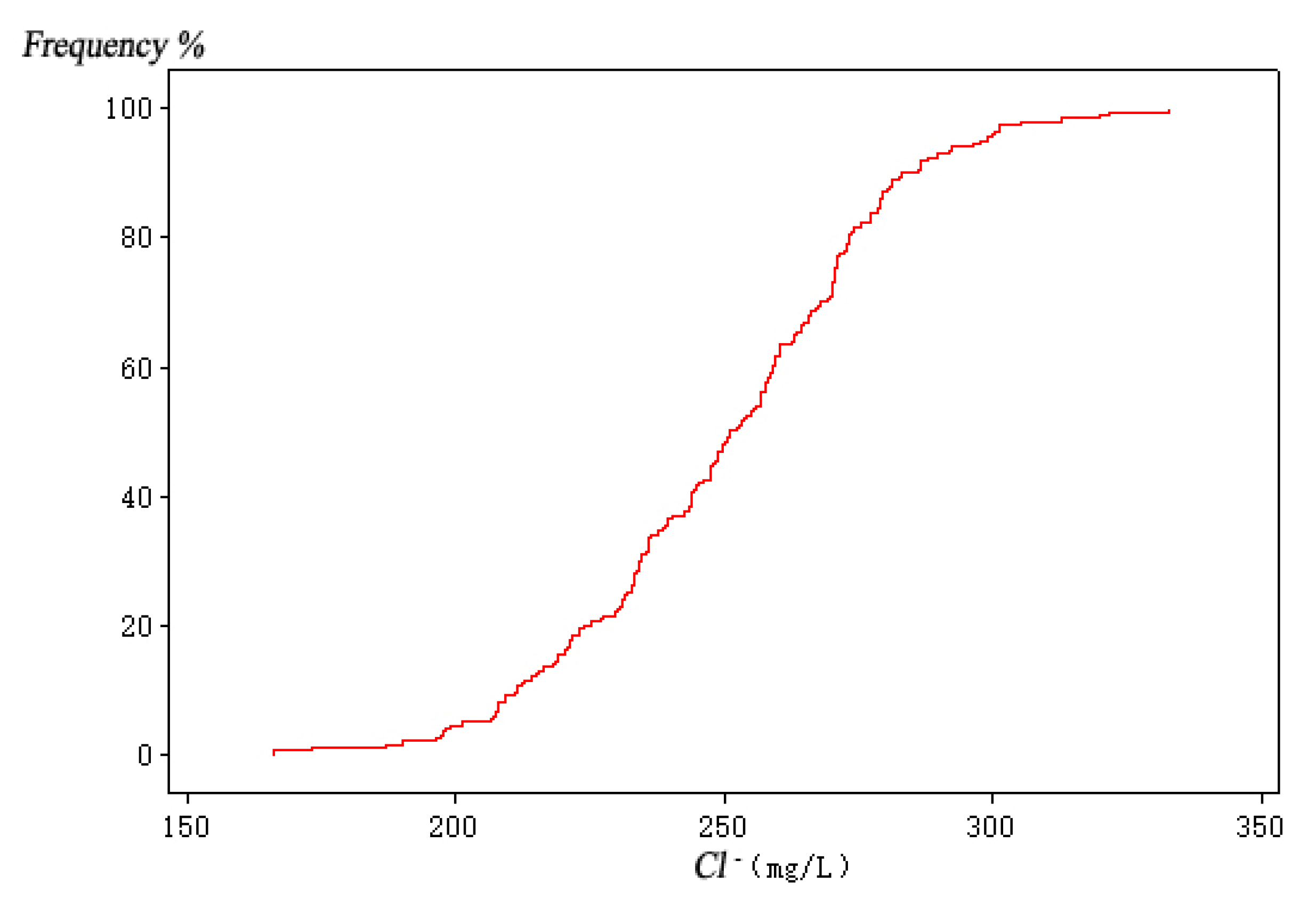
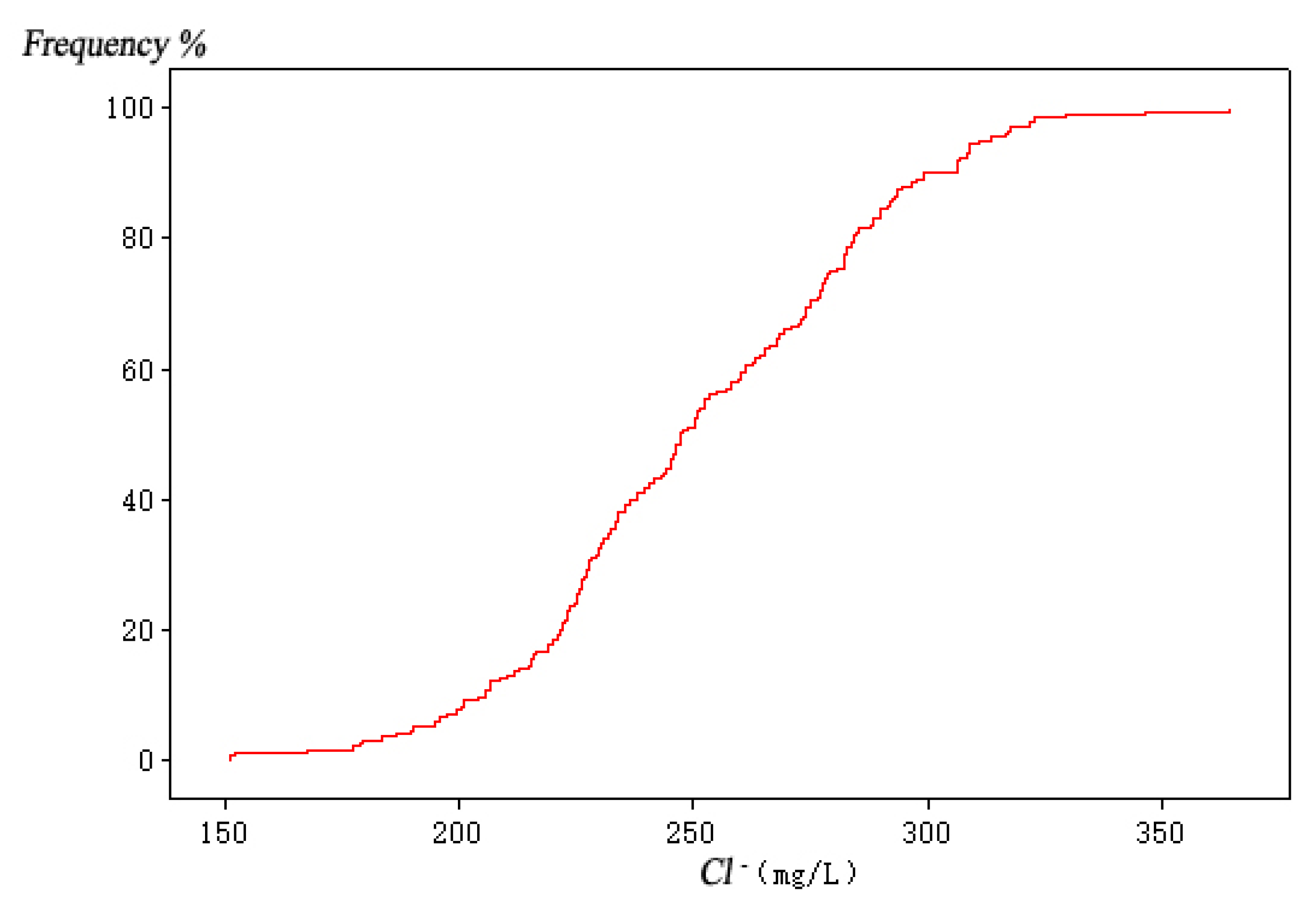


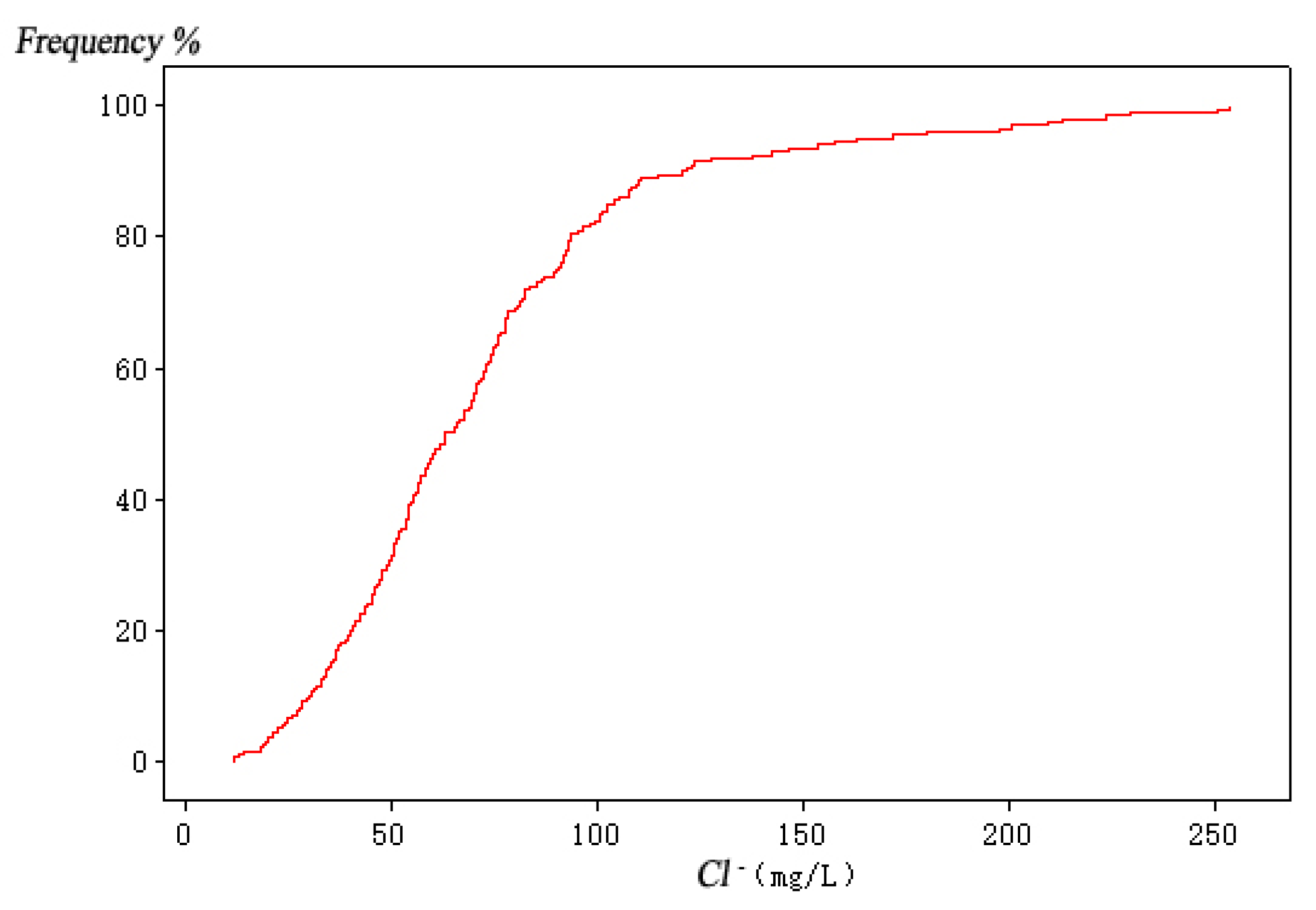
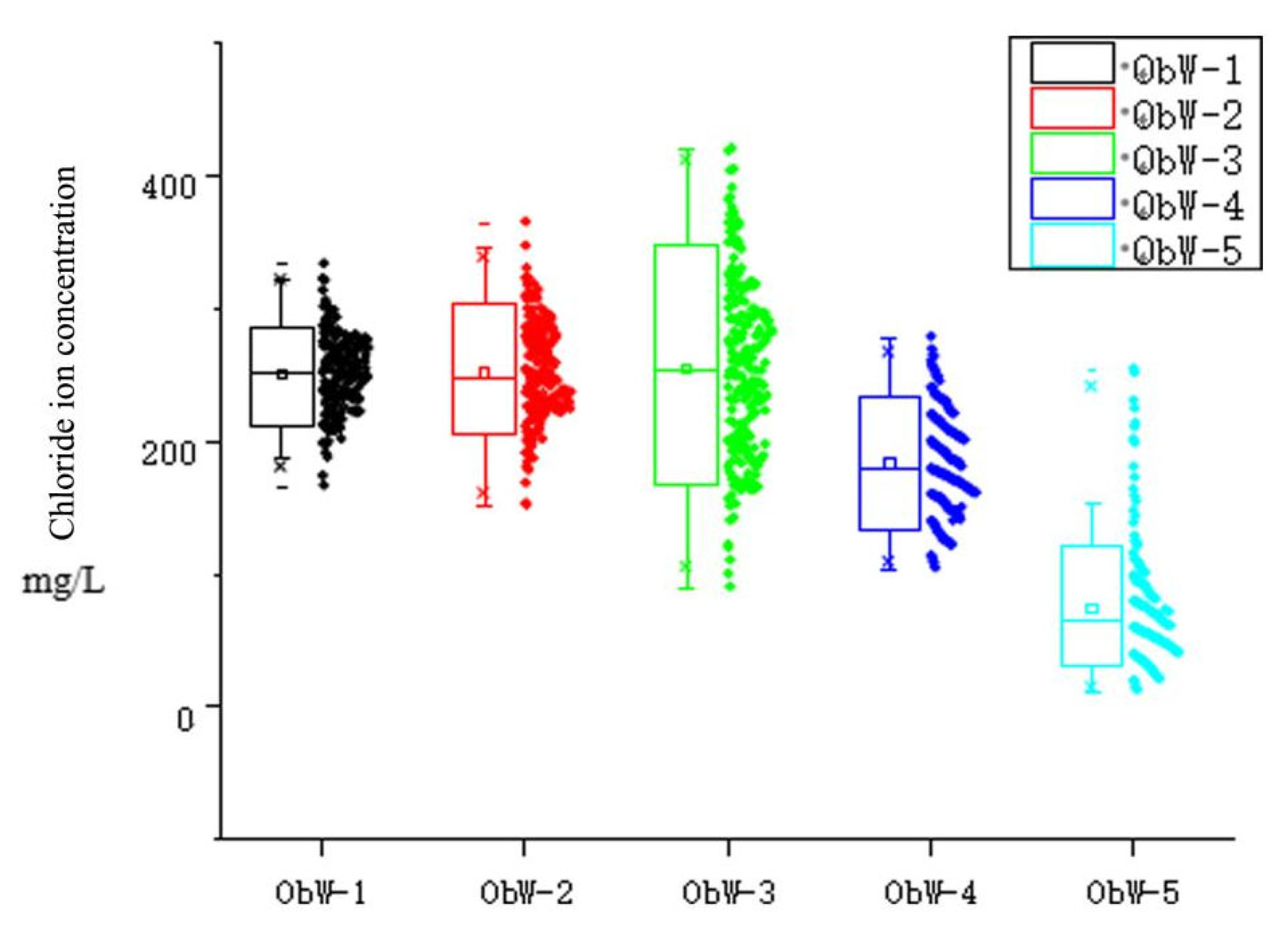
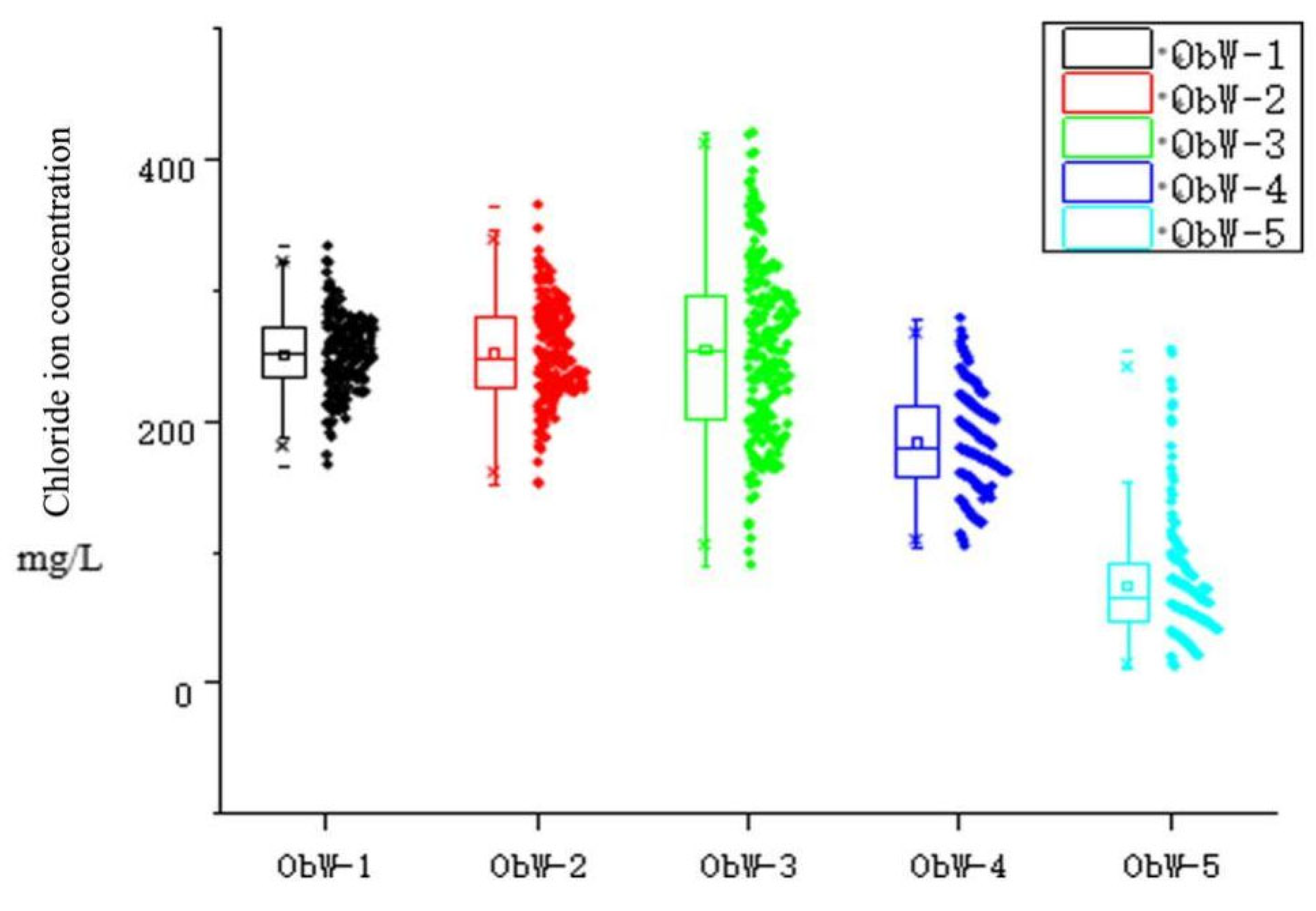
| Variable Name | Sea Level Rise (mm) | Pumping Capacity of Well Group 1 (104 m3/a) | Pumping Capacity of Well Group 2 (104 m3/a) | Pumping Capacity of Well Group 3 (104 m3/a) |
|---|---|---|---|---|
| Distribution characteristics | Random variable (normal distribution) | Deterministic variable | ||
| Value range | 80.00–170.00 | 273.00 | 161.00 | 230.00 |
| Name | DBNN | RBF | DCNN |
|---|---|---|---|
| Max relative error (%) | 3.961 | 6.720 | 4.114 |
| Mean relative error (%) | 1.658 | 4.009 | 4.013 |
| Root mean-squared error | 3.707 | 8.162 | 5.179 |
| Coefficient of determination | 0.989 | 0.804 | 0.920 |
| Wells | ObW-1 | ObW-2 | ObW-3 | ObW-4 | ObW-5 | |
|---|---|---|---|---|---|---|
| Value (mg/L) | ||||||
| Max. value | 332.92 | 364.44 | 419.71 | 278.02 | 254.00 | |
| Min. value | 166.04 | 151.38 | 89.57 | 104.02 | 11.96 | |
| Average value | 250.63 | 251.65 | 253.95 | 183.26 | 73.38 | |
| Standard deviation | 28.29 | 37.77 | 66.45 | 37.49 | 43.90 | |
| Well Name | ObW-1 | ObW-2 | ObW-3 | ObW-4 | ObW-5 |
|---|---|---|---|---|---|
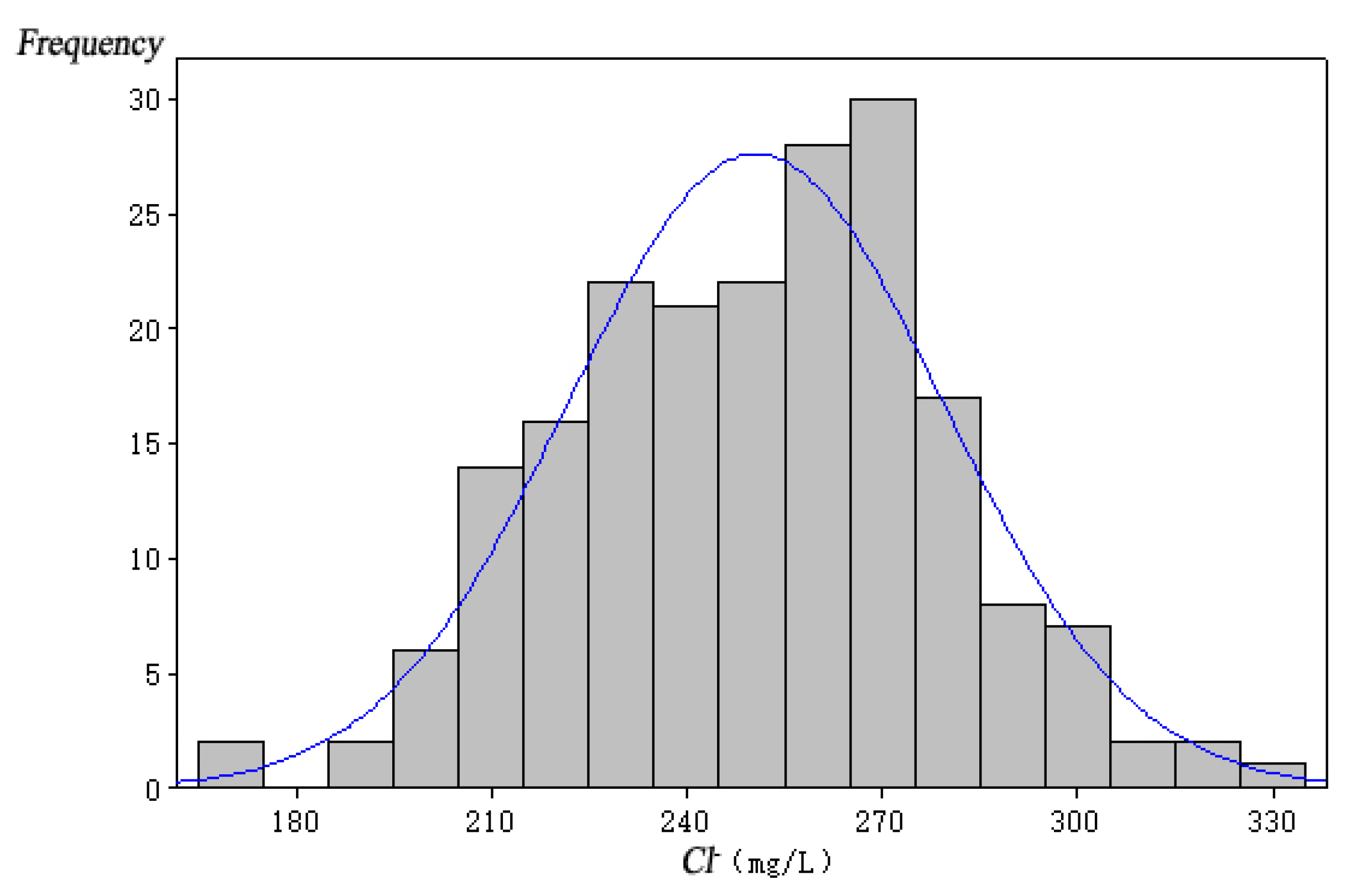
| Risk of seawater intrusion (Cl− > 250 mg/L) | 52.00% | 49.50% | 58.00% | 5.50% | 1.00% |
| Well | Confidence Level (%) | Confidence Interval (mg/L) | Confidence Level (%) | Confidence Interval (mg/L) |
|---|---|---|---|---|
| ObW-1 | 80 | 211.55−284.77 | 50 | 232.42−270.73 |
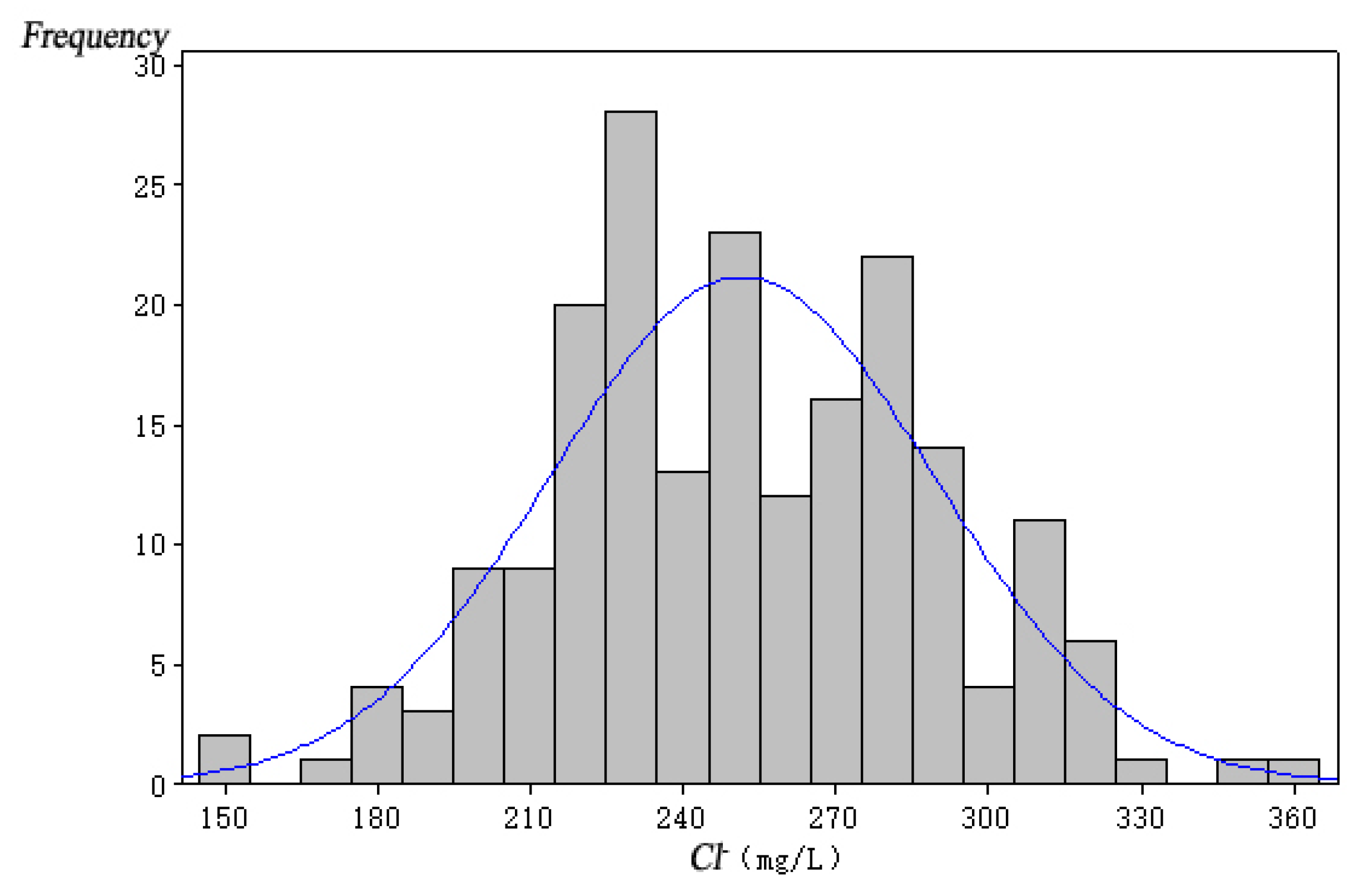
| ObW-2 | 80 | 205.65−302.82 | 50 | 225.33−279.90 |
| ObW-3 | 80 | 167.26−346.96 | 50 | 200.65−295.49 |
| ObW-4 | 80 | 132.79−233.51 | 50 | 157.49−210.38 |
| ObW-5 | 80 | 30.71−121.56 | 50 | 45.98−90.67 |
| Median km2 | Standard Deviation km2 | Average km2 | Coefficient of Variation | Confidence Interval (km2) | |
|---|---|---|---|---|---|
| 80% | 50% | ||||
| 70.27 | 7.31 | 69.39 | 10.40 | 68.01−72.55 | 69.16−71.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, T.; Huang, H.; Guo, J.; Li, G.; Zhang, Y.; Chen, N. Uncertainty Analysis of Numerical Simulation of Seawater Intrusion Using Deep Learning-Based Surrogate Model. Water 2022, 14, 2933. https://doi.org/10.3390/w14182933
Miao T, Huang H, Guo J, Li G, Zhang Y, Chen N. Uncertainty Analysis of Numerical Simulation of Seawater Intrusion Using Deep Learning-Based Surrogate Model. Water. 2022; 14(18):2933. https://doi.org/10.3390/w14182933
Chicago/Turabian StyleMiao, Tiansheng, He Huang, Jiayuan Guo, Guanghua Li, Yu Zhang, and Naijia Chen. 2022. "Uncertainty Analysis of Numerical Simulation of Seawater Intrusion Using Deep Learning-Based Surrogate Model" Water 14, no. 18: 2933. https://doi.org/10.3390/w14182933
APA StyleMiao, T., Huang, H., Guo, J., Li, G., Zhang, Y., & Chen, N. (2022). Uncertainty Analysis of Numerical Simulation of Seawater Intrusion Using Deep Learning-Based Surrogate Model. Water, 14(18), 2933. https://doi.org/10.3390/w14182933






