Artificial Neural Networks and Multiple Linear Regression for Filling in Missing Daily Rainfall Data
Abstract
:1. Introduction
2. Materials and Methods
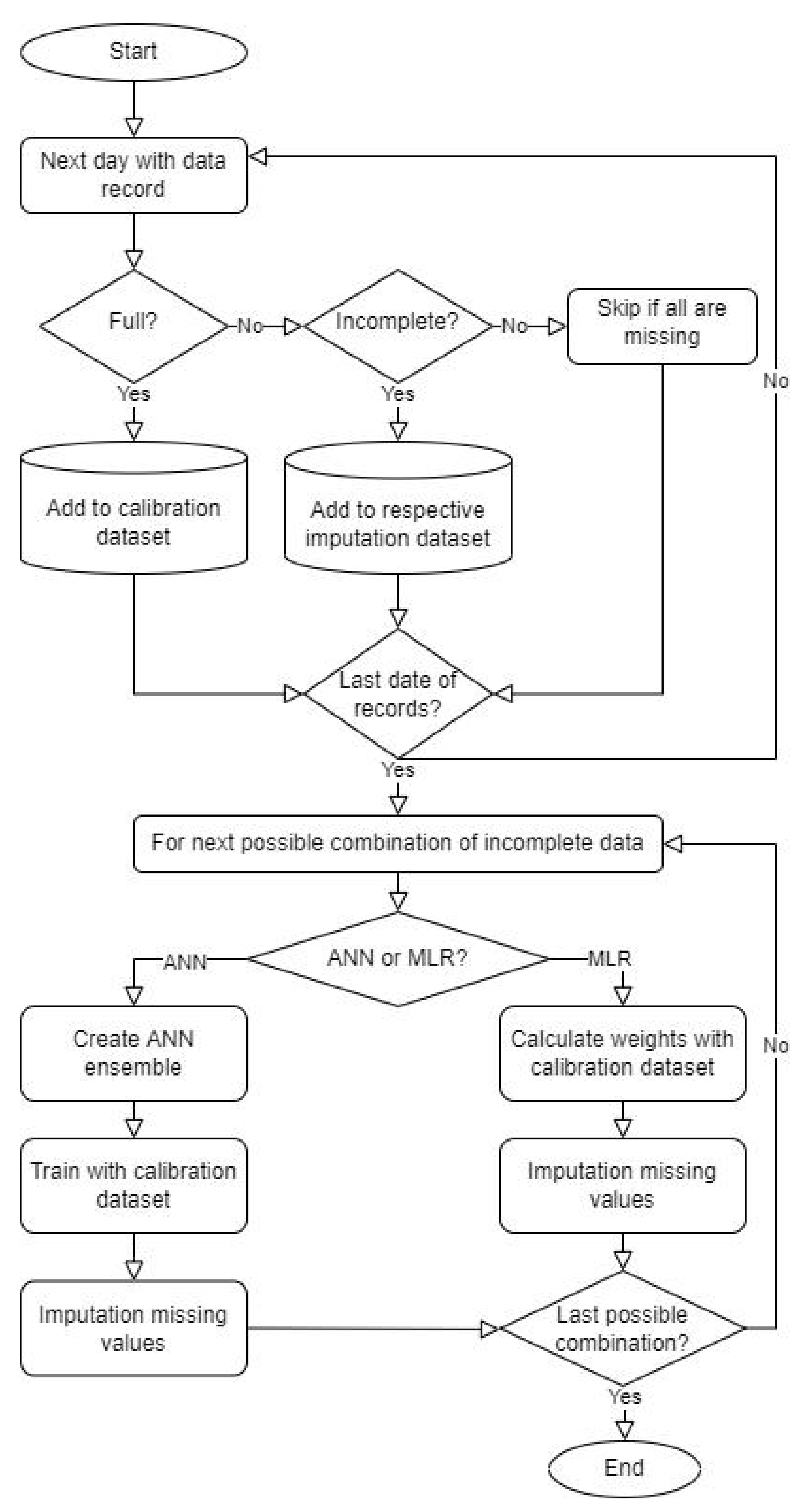
2.1. ANN and MLR Creation
2.2. Model Evaluation
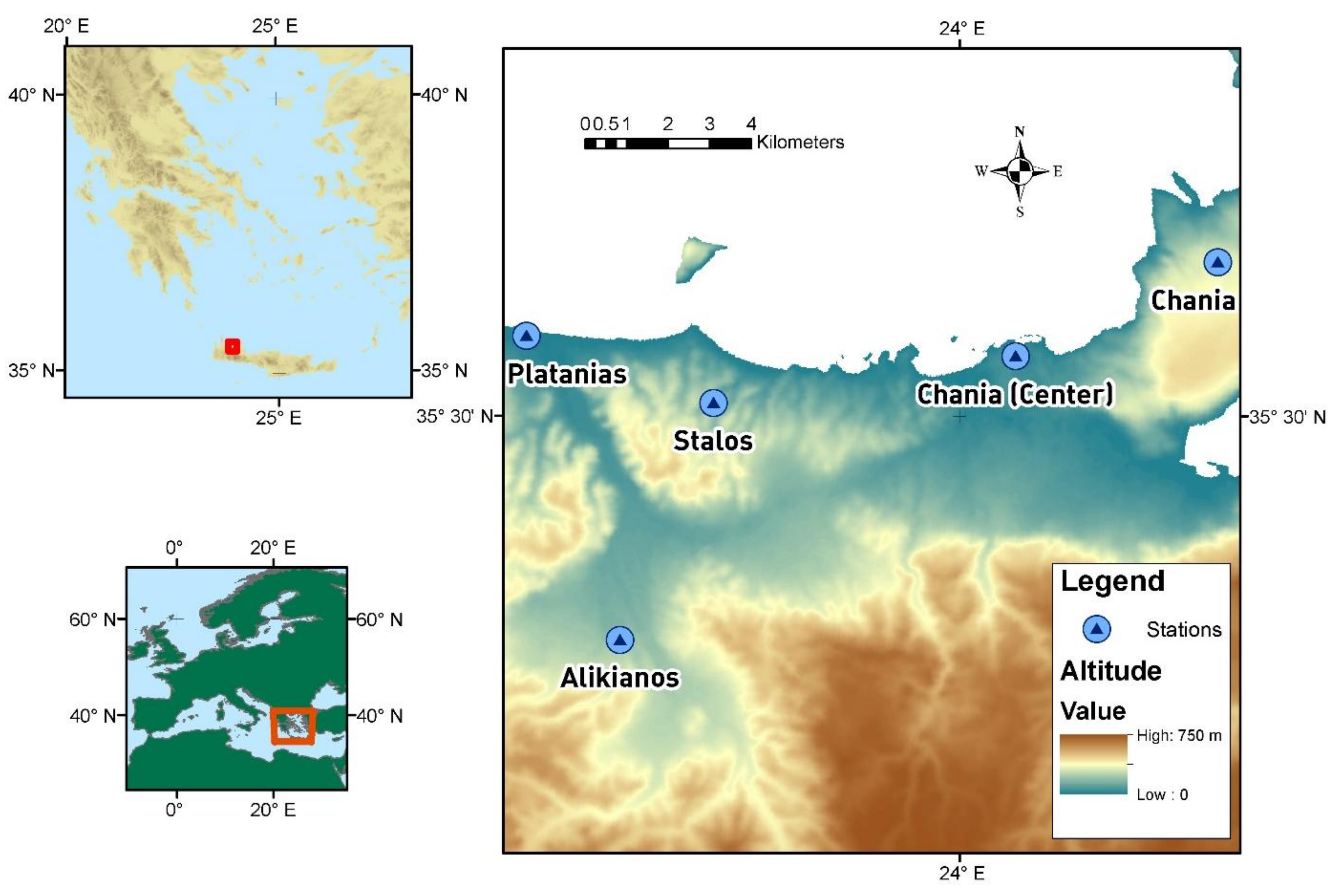
2.3. Case Study
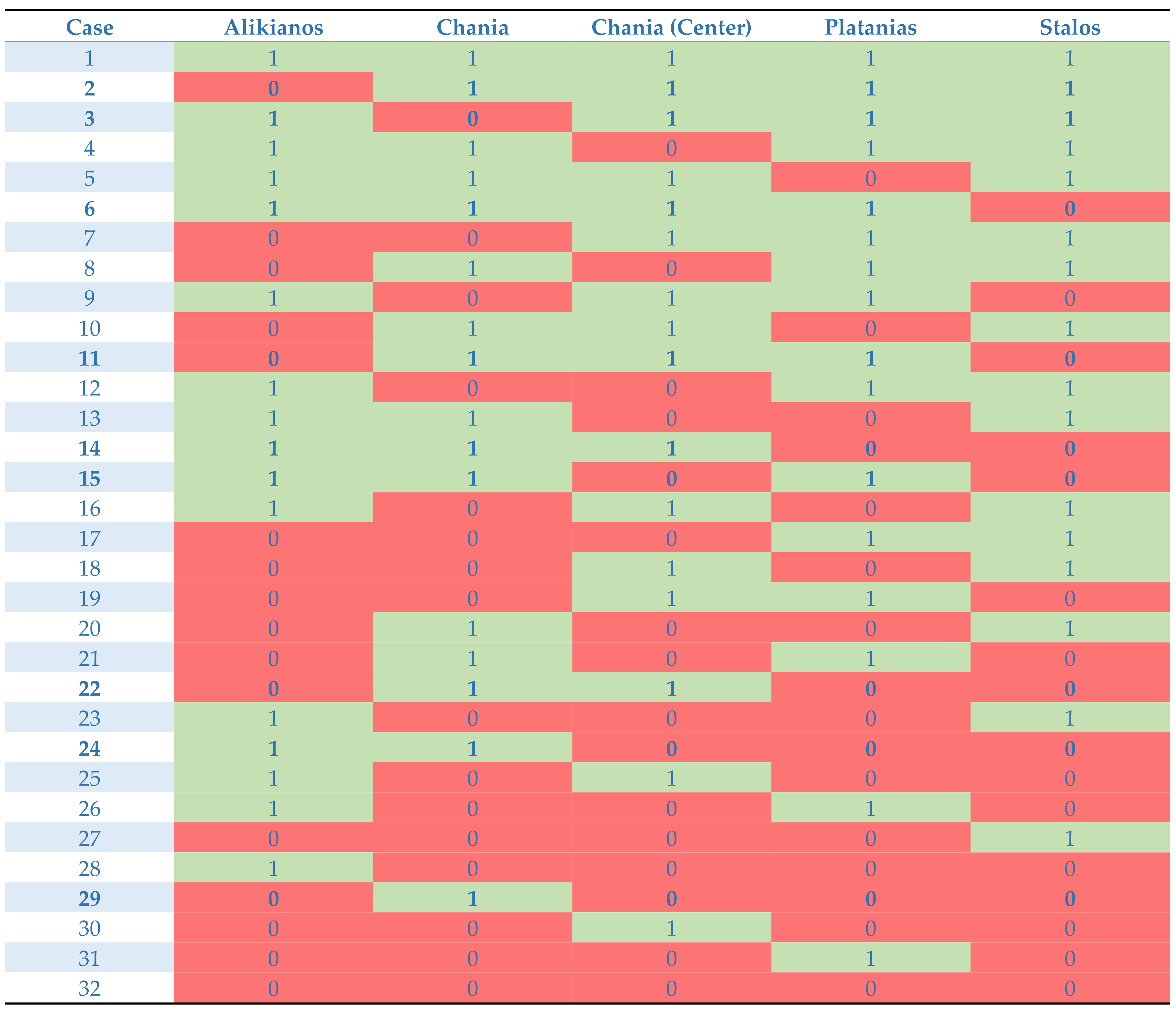
2.4. Different Combinations of Stations Missing Data (Cases)
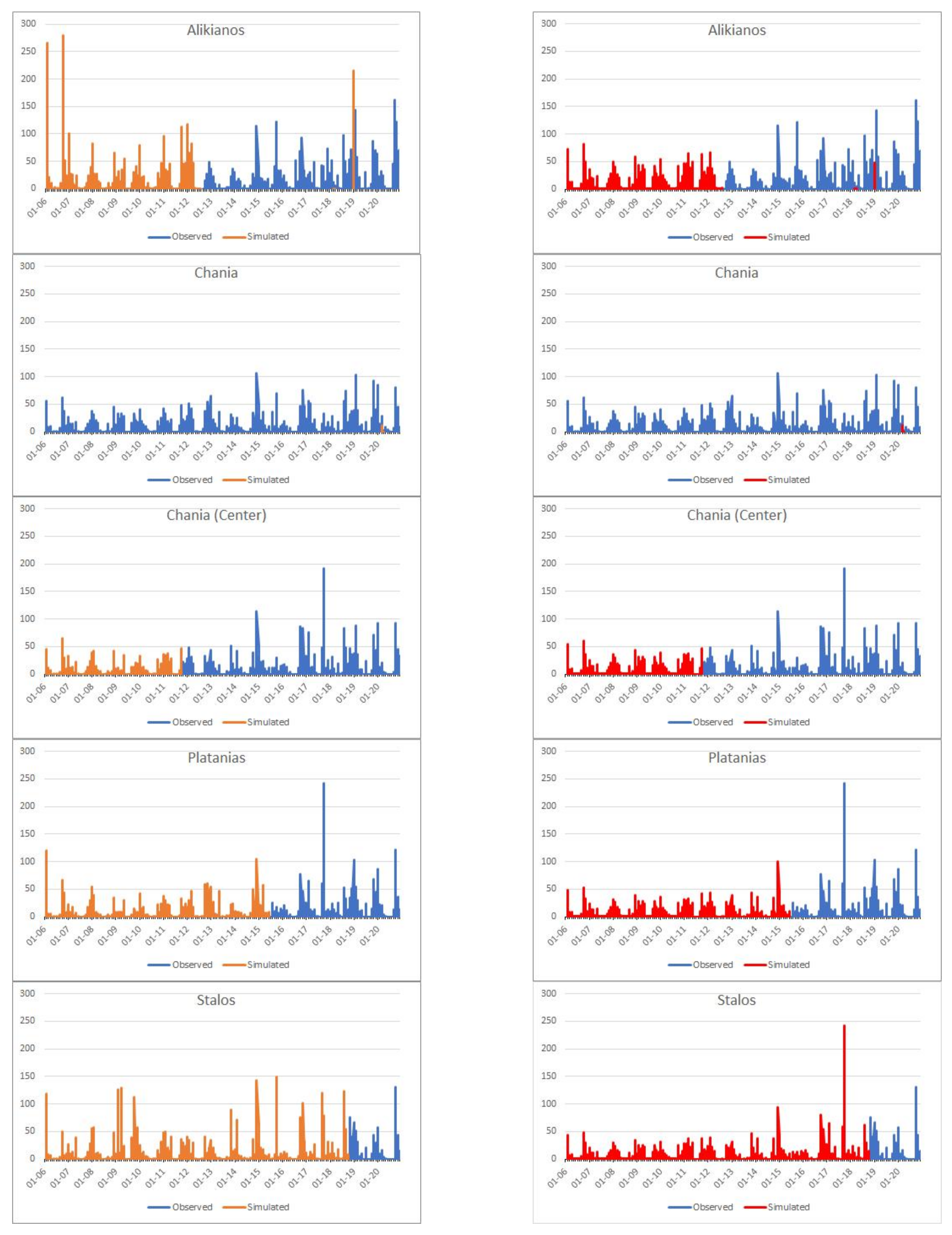
3. Results
3.1. Root Mean Square Error (RMSE)
3.2. Nash–Sutcliffe Efficiency
- If NSE = 1, then there is a complete match between the simulated values given by the model and those observed by the stations;
- If NSE = 0, then the values simulated by the model give the same result as if the average of the observed values of the stations were used as the forecast model for each time point;
- If NSE < 0, then the model is practically unusable, as the values simulated by it give a less accurate result than if the average of the observed values of the stations were used as a predictive model for each time point.
3.3. Coefficient of Correlation (R)
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Canchala-Nastar, T.; Carvajal-Escobar, Y.; Alfonso-Morales, W.; Loaiza Cerón, W.; Caicedo, E. Estimation of Missing Data of Monthly Rainfall in Southwestern Colombia Using Artificial Neural Networks. Data Brief 2019, 26, 104517. [Google Scholar] [CrossRef] [PubMed]
- Nkuna, T.R.; Odiyo, J.O. Filling of Missing Rainfall Data in Luvuvhu River Catchment Using Artificial Neural Networks. Phys. Chem. Earth Parts A/B/C 2011, 36, 830–835. [Google Scholar] [CrossRef]
- Tran Anh, D.; Van, S.P.; Dang, T.D.; Hoang, L.P. Downscaling Rainfall Using Deep Learning Long Short-term Memory and Feedforward Neural Network. Int. J. Climatol. 2019, 39, 4170–4188. [Google Scholar] [CrossRef]
- Ben Aissia, M.-A.; Chebana, F.; Ouarda, T.B. Multivariate Missing Data in Hydrology—Review and Applications. Adv. Water Resour. 2017, 110, 299–309. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V.; Aly, A.; Pathak, C.S.; Ahlquist, J.; Fuelberg, H.; Hood, J. Infilling Missing Precipitation Records Using Variants of Spatial Interpolation and Data-Driven Methods: Use of Optimal Weighting Parameters and Nearest Neighbour-Based Corrections: INFILLING MISSING PRECIPITATION RECORDS. Int. J. Climatol. 2018, 38, 776–793. [Google Scholar] [CrossRef]
- Elshaboury, N.; Elshourbagy, M.; Al-Sakkaf, A.; Abdelkader, E.M. Rainfall Forecasting in Arid Regions Using an Ensemble of Artificial Neural Networks. J. Phys. Conf. Ser. 2021, 1900, 012015. [Google Scholar] [CrossRef]
- Mishra, N.; Soni, H.K.; Sharma, S.; Upadhyay, A.K. A Comprehensive Survey of Data Mining Techniques on Time Series Data for Rainfall Prediction. J. ICT Res. Appl. 2017, 11, 167–183. [Google Scholar] [CrossRef]
- Kashiwao, T.; Nakayama, K.; Ando, S.; Ikeda, K.; Lee, M.; Bahadori, A. A Neural Network-Based Local Rainfall Prediction System Using Meteorological Data on the Internet: A Case Study Using Data from the Japan Meteorological Agency. Appl. Soft Comput. 2017, 56, 317–330. [Google Scholar] [CrossRef]
- Ridwan, W.M.; Sapitang, M.; Aziz, A.; Kushiar, K.F.; Ahmed, A.N.; El-Shafie, A. Rainfall Forecasting Model Using Machine Learning Methods: Case Study Terengganu, Malaysia. Ain Shams Eng. J. 2021, 12, 1651–1663. [Google Scholar] [CrossRef]
- Goyal, M.K. Monthly Rainfall Prediction Using Wavelet Regression and Neural Network: An Analysis of 1901–2002 Data, Assam, India. Theor. Appl. Climatol. 2014, 118, 25–34. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef]
- Qin, Y.; Lou, Y. Hydrological Time Series Anomaly Pattern Detection Based on Isolation Forest. In Proceedings of the 2019 IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019; pp. 1706–1710. [Google Scholar]
- Khazaee Poul, A.; Shourian, M.; Ebrahimi, H. A Comparative Study of MLR, KNN, ANN and ANFIS Models with Wavelet Transform in Monthly Stream Flow Prediction. Water Resour. Manag. 2019, 33, 2907–2923. [Google Scholar] [CrossRef]
- Desai, S.; Ouarda, T.B. Regional Hydrological Frequency Analysis at Ungauged Sites with Random Forest Regression. J. Hydrol. 2021, 594, 125861. [Google Scholar] [CrossRef]
- Haidar, A.; Verma, B. A Novel Approach for Optimizing Climate Features and Network Parameters in Rainfall Forecasting. Soft Comput. 2018, 22, 8119–8130. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S. Optimization of Neural Network Using Kidney-Inspired Algorithm with Control of Filtration Rate and Chaotic Map for Real-World Rainfall Forecasting. Eng. Appl. Artif. Intell. 2018, 67, 246–259. [Google Scholar] [CrossRef]
- Cheng, S.; Lu, F. A Two-Step Method for Missing Spatio-Temporal Data Reconstruction. ISPRS Int. J. Geo-Inf. 2017, 6, 187. [Google Scholar] [CrossRef]
- Yen, M.-H.; Liu, D.-W.; Hsin, Y.-C.; Lin, C.-E.; Chen, C.-C. Application of the Deep Learning for the Prediction of Rainfall in Southern Taiwan. Sci. Rep. 2019, 9, 12774. [Google Scholar] [CrossRef]
- Lee, J.; Kim, C.-G.; Lee, J.; Kim, N.; Kim, H. Application of Artificial Neural Networks to Rainfall Forecasting in the Geum River Basin, Korea. Water 2018, 10, 1448. [Google Scholar] [CrossRef]
- Goumas, C.; Trichakis, I.; Vozinaki, A.-I.; Karatzas, G.P. Flood Risk Assessment and Flow Modeling of the Stalos Stream Area. J. Hydroinform. 2022, 24, 677–696. [Google Scholar] [CrossRef]
- Praveen, B.; Talukdar, S.; Shahfahad, M.S.; Mondal, J.; Sharma, P.; Islam, A.R.M.D.T.; Rahman, A. Analyzing Trend and Forecasting of Rainfall Changes in India Using Non-Parametrical and Machine Learning Approaches. Sci. Rep. 2020, 10, 10342. [Google Scholar] [CrossRef]
- Beritelli, F.; Capizzi, G.; Lo Sciuto, G.; Napoli, C.; Scaglione, F. Rainfall Estimation Based on the Intensity of the Received Signal in a LTE/4G Mobile Terminal by Using a Probabilistic Neural Network. IEEE Access 2018, 6, 30865–30873. [Google Scholar] [CrossRef]
- Jhong, Y.-D.; Chen, C.-S.; Lin, H.-P.; Chen, S.-T. Physical Hybrid Neural Network Model to Forecast Typhoon Floods. Water 2018, 10, 632. [Google Scholar] [CrossRef]
- Alam, K.M.R.; Siddique, N.; Adeli, H. A Dynamic Ensemble Learning Algorithm for Neural Networks. Neural Comput. Appl. 2020, 32, 8675–8690. [Google Scholar] [CrossRef]
- Zhou, J.; Peng, T.; Zhang, C.; Sun, N. Data Pre-Analysis and Ensemble of Various Artificial Neural Networks for Monthly Streamflow Forecasting. Water 2018, 10, 628. [Google Scholar] [CrossRef]
- Haidar, A.; Verma, B.; Sinha, T. A Novel Approach for Optimizing Ensemble Components in Rainfall Prediction. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Kim, T.; Shin, J.; Kim, H.; Heo, J. Ensemble-Based Neural Network Modeling for Hydrologic Forecasts: Addressing Uncertainty in the Model Structure and Input Variable Selection. Water Resour. Res. 2020, 56, e2019WR026262. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting Evapotranspiration in Different Climates Using Ensembles of Recurrent Neural Networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Althoff, D.; Rodrigues, L.N.; Bazame, H.C. Uncertainty Quantification for Hydrological Models Based on Neural Networks: The Dropout Ensemble. Stoch. Environ. Res. Risk Assess. 2021, 35, 1051–1067. [Google Scholar] [CrossRef]
- Bandyopadhyay, G.; Chattopadhyay, S. Single Hidden Layer Artificial Neural Network Models versus Multiple Linear Regression Model in Forecasting the Time Series of Total Ozone. Int. J. Environ. Sci. Technol. 2007, 4, 141–149. [Google Scholar] [CrossRef]
- Zhong, K.; Song, Z.; Jain, P.; Bartlett, P.L.; Dhillon, I.S. Recovery Guarantees for One-Hidden-Layer Neural Networks. arXiv 2017, arXiv:1706.03175. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Veith Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Lagouvardos, K.; Kotroni, V.; Bezes, A.; Koletsis, I.; Kopania, T.; Lykoudis, S.; Mazarakis, N.; Papagiannaki, K.; Vougioukas, S. The Automatic Weather Stations NOANN Network of the National Observatory of Athens: Operation and Database. Geosci. Data J. 2017, 4, 4–16. [Google Scholar] [CrossRef]
- Shen, S.-L.; Zhang, N.; Zhou, A.; Yin, Z.-Y. Enhancement of Neural Networks with an Alternative Activation Function TanhLU. Expert Syst. Appl. 2022, 199, 117181. [Google Scholar] [CrossRef]
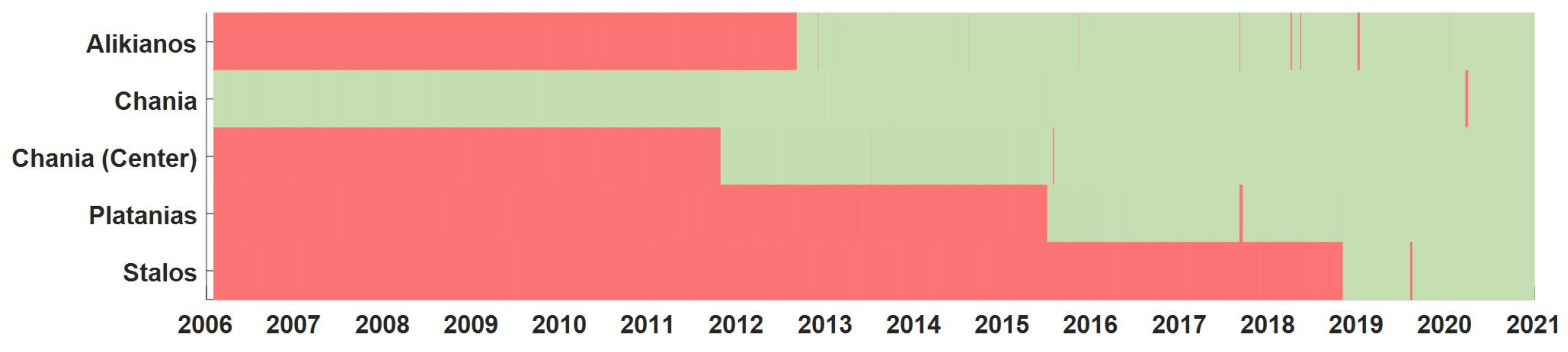
| Station | Altitude (m) | Number of Data | Start of Data |
|---|---|---|---|
| Alikianos | 95 | 3044 | 1 September 2012 |
| Chania | 137 | 5448 | 1 February 2006 |
| Chania (Center) | 7 | 3745 | 1 October 2010 |
| Platanias | 12 | 2011 | 1 July 2015 |
| Stalos | 93 | 792 | 1 November 2018 |
| Case | RMSE [mm] | |
|---|---|---|
| ANN | MLR | |
| Case 2 | 1.76 | 6.43 |
| Case 3 | 1.22 | 2.37 |
| Case 6 | 1.22 | 2.92 |
| Case 11 | 2.30 | 4.99 |
| Case 14 | 1.24 | 3.03 |
| Case 15 | 1.16 | 2.46 |
| Case 22 | 2.19 | 4.47 |
| Case 24 | 1.83 | 3.16 |
| Case 29 | 2.42 | 4.94 |
| Case | Nash–Sutcliffe Efficiency | Simulated Precipitation Value Station(s) | |
|---|---|---|---|
| ANN | MLR | ||
| Case 2 | 0.967 | 0.803 | Alikianos |
| Case 3 | 0.975 | 0.937 | Chania |
| Case 6 | 0.981 | 0.882 | Stalos |
| Case 11 | 0.954 | 0.803 | Alikianos |
| 0.957 | 0.882 | Stalos | |
| Case 14 | 0.976 | 0.908 | Platanias |
| 0.969 | 0.845 | Stalos | |
| Case 15 | 0.989 | 0.968 | Chania (Center) |
| 0.973 | 0.871 | Stalos | |
| Case 22 | 0.934 | 0.802 | Alikianos |
| 0.957 | 0.908 | Platanias | |
| 0.927 | 0.844 | Stalos | |
| Case 24 | 0.975 | 0.954 | Chania (Center) |
| 0.957 | 0.869 | Platanias | |
| 0.943 | 0.781 | Stalos | |
| Case 29 | 0.911 | 0.708 | Alikianos |
| 0.971 | 0.933 | Chania (Center) | |
| 0.968 | 0.843 | Platanias | |
| 0.959 | 0.748 | Stalos | |
| Case | Coefficient of Correlation (R) | |
|---|---|---|
| ANN | MLR | |
| Case 2 | 0.98353 | 0.80337 |
| Case 3 | 0.98777 | 0.93740 |
| Case 6 | 0.99066 | 0.88198 |
| Case 11 | 0.97737 | 0.76844 |
| Case 14 | 0.98639 | 0.87493 |
| Case 15 | 0.99101 | 0.90800 |
| Case 22 | 0.96842 | 0.78287 |
| Case 24 | 0.97975 | 0.86749 |
| Case 29 | 0.96998 | 0.74782 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papailiou, I.; Spyropoulos, F.; Trichakis, I.; Karatzas, G.P. Artificial Neural Networks and Multiple Linear Regression for Filling in Missing Daily Rainfall Data. Water 2022, 14, 2892. https://doi.org/10.3390/w14182892
Papailiou I, Spyropoulos F, Trichakis I, Karatzas GP. Artificial Neural Networks and Multiple Linear Regression for Filling in Missing Daily Rainfall Data. Water. 2022; 14(18):2892. https://doi.org/10.3390/w14182892
Chicago/Turabian StylePapailiou, Ioannis, Fotios Spyropoulos, Ioannis Trichakis, and George P. Karatzas. 2022. "Artificial Neural Networks and Multiple Linear Regression for Filling in Missing Daily Rainfall Data" Water 14, no. 18: 2892. https://doi.org/10.3390/w14182892







