1. Introduction
The proper determination of a ‘fair’ or ‘just’ sharing of joint costs has been identified as a growing concern in public service [
1,
2]. This issue becomes more intractable when concerning water supply projects [
3], which are an essential field of public service. The inter-basin water diversion project (IWDP) is a typical water supply project, involving multiple municipalities and stakeholders; therefore, it requires a proper and reasonable pricing approach towards determining the sharing costs.
With the water transmission of the IWDP, the downstream users need to share the costs of engineering construction and maintenance with the upstream users, because the facilities, such as pumping stations and the diversion dam, built by the upstream users, not only serve themselves, but also serve the downstream users, in the process of water withdrawal [
4]. The existing research has studied the competition and cooperation among users, such as: the water-transfer project from the Tajo basin to the Lorca irrigated valley, Spain [
5]; the Flumendosa-Campidano water system, Italy [
6]; and the South to North Water Diversion Project, China [
7]. Although the establishment of joint water supply facilities can save more money for municipal facilities than the establishment of their own water supply facilities [
8], this practice may conflict with participants’ perceptions of self-interest, since it fails to provide the users with sufficient incentives to participate and cooperate in such joint projects [
9,
10].
There are various pricing models focusing on sharing the costs between upstream users and downstream users, which attempt to coordinate the relationship between them. Current studies on cost-sharing methods of water supply are dominated by three types of models. The first type of model is the proportional sharing method (PSM), which has been widely used. PSM is based on the proportion of some single numerical criterion, such as water quantity, population, or the level of benefit [
8]. The second model is characterized by using the multi-objective optimization method. Some examples include: the separable costs-remaining benefits (SCRB) model [
11,
12]; adjusted winner mechanism [
13]; multivariate analysis biplot [
14]; and fuzzy cognitive maps [
15]. These models assume that the cost of a comprehensive project is less than the cost of establishing separate sub-projects, while all users tend to maximize the sharing of the costs saved by the comprehensive project. The third one is based on the game theory, an increasingly popular method for decision-making by pricing the water resources in terms of computational and informational demands [
1,
16].
However, each of these three types of models has its advantages and limitations when applied to different site-specific projects. For example, Young et al. (1982) proposed that the PSM may be preferable to the SCRB, although the SCRB is a more complicated method. This is because the SCRB considers more factors, but this may result in index redundancy and may also affect the accuracy. PSM cannot provide a comprehensive sharing scheme, due to its simplified indicators and mechanism. The game theory-based method requires a host of information on water rights trading, based on the market mechanism, which is difficult to obtain in the regions with underdeveloped water markets, taking China as an example thereof. Therefore, the justification of a cost-sharing strategy lies not only in the calculation method, but also in the applicable environment, such as the establishment and management of the water market.
China’s South to North Water Diversion Project (SNWDP), the largest and most expensive IWDP in the world [
17], attempts to change the uneven spatial distribution of water resources in China by transferring water from the Yangtze River to North China [
18]. The eastern route of SNWDP (ER-SNWDP) requires a large number of pumping stations to transfer the water because the elevation of the water-receiving area is higher than that of the water-source area. This results in a huge number of costs along the route [
19], with a total investment of 65 billion yuan (10 billion US dollars). At present, the cost-sharing scheme of SNWDP is based on PSM [
20,
21], following the principle of “who benefits, who pays”. However, the cost-sharing scheme of the ER-SNWDP among each water user is not implemented smoothly. Two main reasons may be to the cause of this problem; one is that for the sake of convenience of calculation and management, the route is divided into several sections by the government, because the engineering investment of this project is dominated by the government rather than the market [
22,
23,
24]. The second reason is that the sharing costs of each section are directly considered as a given parameter [
25]. Under this decision-making regime, the current cost-sharing method largely simplifies the amortization factor, which leads to excessively high accumulated costs for the users downstream. These might aggravate the conflict of interest between upstream and downstream users. Therefore, what is the proper way to share the costs of water supply projects between upstream and downstream users of the ER-SNWDP more fairly? This question demands both analytical and empirical analysis.
Therefore, this paper focuses on the sharing mechanism of water supply costs of the IWDP (dominated by the government), with the aim of proposing an improved sharing method of water supply costs, in order to avoid unreasonable cost-sharing for water intake users. Water supply costs in this study represent the cost of the construction and maintenance of water transmission engineering rather than the concept of water price which requires a thorough consideration of the negotiation of upstream and downstream stakeholders and the government’s policies. This study will propose a novel cost-sharing method of water supply for a government-dominated IWDP in areas with a quasi-water market. The proposed method can provide technical and governance guidance for a government-dominated IWDP in areas with a quasi-water market, to coordinate the upstream and downstream relationship and ensure the cost-efficient operation of the project.
2. Materials and Methods
2.1. Study Area and Data
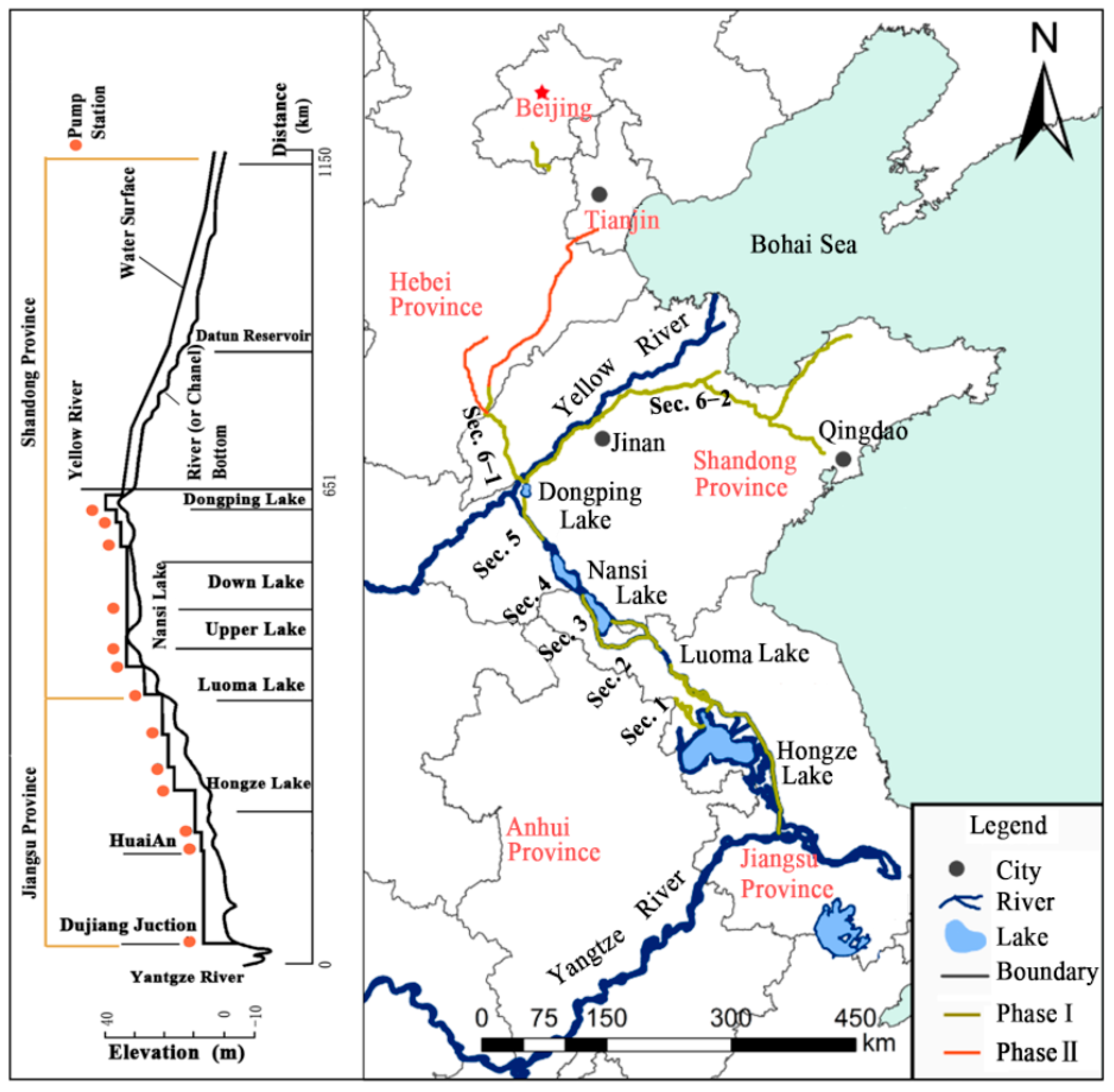
SNWDP is a government-dominated IWDP, the eastern route of which (ER-SNWDP) was officially used in 2013. The pumping station group on this route is composed of 13 large pumping stations (shown in
Figure 1), which involves a huge engineering cost. Therefore, a proper sharing strategy, to fairly determine the joint cost, is essential to ensure the efficient operation of water supplied by the ER-SNWDP.
The ER-SNWDP involves three provinces (Jiangsu, Anhui and Shandong) and a municipality directly under the central government (Tianjin) from upstream to downstream (shown in
Figure 1). In the first planning phase, Shandong is the end of the east route and the largest water-receiving province, receiving water of over 1600 MCM annually. The ER-SNWDP has 8 key junctions, dividing this route into 7 sections, with more than 120 water intakes located along the route. Each water intake represents a water user such as a county. The current cost-sharing method results in an unreasonable sharing cost for the downstream sections, especially for the 5 sections in Shandong Province, where high water price has seriously affected the willingness of the local users to purchase the water transferred along the ER-SNWDP [
26].
The costs and the net quantity of water supply for these 7 sections of the ER-SNWDP are shown in
Table 1. As shown in
Figure 1, Section #1 starts from the Hongze Lake and goes to the Luoma Lake; Section #2 reaches from the Luoma Lake to the provincial boundary between Jiangsu and Shandong; Section #3 is from the the provincial boundary between Jiangsu and Shandong to the lower part of Nansi Lake; Section #4 is from the lower part of Nansi Lake to the upper part of Nansi Lake; Section #5 is from the upper part of Nansi Lake to Dongping Lake; Section #6-1 is from Dongping Lake to Northern Shandong and Section #6-2 is from Dongping Lake to East Shandong.
2.2. Methods
2.2.1. Existing Cost-Sharing Method
In order to compare the improved cost-sharing method, the existing cost-sharing method for SNWDP is described below. The existing sharing method is called “the cost allocation formula”, hereafter entitled CAF. The principle of CAF is based on the PSM, in which the amount of sharing costs depends on the water consumption of downstream sections. According to allocation principles, the cost of the first section is shared by all of the water intakes, according to the amortized quantity of water, in proportion. The cost of the second section is shared by all intakes from the second water intake to the end, and so on until the last water intake user (the last user is at its own expense). Therefore, the cost of the
nth section is shared by all users from the
nth water intake user to the end user.
Figure 2 shows the diagram of the water supply costs along the transfer route.
The formula of CAF at the
nth water intake is as follows:
where
Sn is the sharing cost of
nth water intake;
Sin is the water supply cost of the
ith section, shared by the
nth water intake in accordance with the amortized water quantity in proportion;
Cn is the water supply cost of the
nth section;
Wn is the net quantity of water supply for the
nth section, in million cubic meters (MCM);
Kn is the water supply costs of the
nth section, in million RMB;
m is the total number of users.
The unit water supply cost (UWSC) for the
nth section is defined as:
where
Dn is UWSC of the
nth section, RMB/m
3.
2.2.2. Improved Cost-Sharing Method
It has been found that the significant discrepancy of the sharing costs between upstream and downstream water users usually leads to low willingness of the downstream water users to pay and use water provided by the water distribution system project. To attenuate such a concern, this paper proposes an improved cost-sharing method (denoted as ICSM hereafter), based on two balance equations, namely, one balance equation of water quantity g(x) and the other of the project cost between upstream and downstream users y(x).
The specific calculation steps of the ICSM are as follows:
First, we need to clarify the distribution of water users along the route of IWDP (in order to be consistent with CAF, we still use the division in
Figure 2.
Then, the connection equation between upstream and downstream users is established. Taking a water supply route divided into two sections as an example, namely the upstream section (0, n) and downstream section (n + 1, m), to illustrate the connection equation, as shown in Equation (3). The term represents the water supply costs within the upstream section, and the term represents the cost of water supply from the upstream section to the downstream section.
Finally, α in Equation (3) can be obtained using the iterative method in Matlab.
where,
Wi is the amount of water withdrawn by the
ith section.
α is the correction coefficient. When the water intake users are evenly distributed along the line, the correction coefficient
α can be easily proven to be 0.5.
Equation (3) can be further derived to be:
The unit water supply cost (UWSC) for the
nth section is thus expressed as:
2.2.3. ICSM for Branch Route
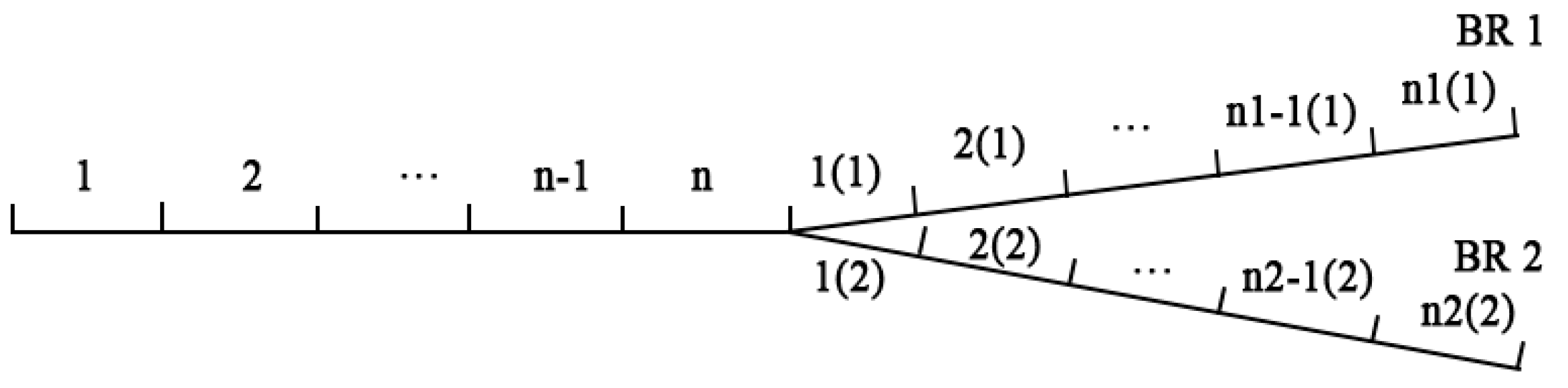
When the route has some branches, the costs sharing method before the branch point is the same as that without any branches. The cost of each branch route can be calculated separately. Given that there are
n stakeholders before the bifurcation point of an IWDP, which is followed by two branch routes, named
BR 1 and
BR 2,
Figure 3 shows the schematic diagram of the IWDP with two branches. The calculation of sharing cost before the bifurcation point is the same as Equation (5).
For the stakeholder in the
BR 1 branch, its
UWSC can be calculated as:
The equation of the
UWSC for each stakeholder in the
BR 2 branch is as follows:
where
D(
n + 1(1)) is the
UWSC of the first stakeholder in the
BR 1 branch,
D(
n + 1(2)) is the
UWSC of first stakeholder in the
BR 2 branch. The other symbols are the same as those defined before.
3. Results
3.1. Comparison of the UWSC between CAF and ICSM in the Different Scenarios
Figure 4 shows the route diagram of the ER- SNWDP in this paper. According to the divided scenario (
Figure 4), substituting the data of
Table 1 into the Equations (1), (2), (6) and (7) respectively, the
UWSC of the CAF and ICSM can be obtained. The parameter
α is calculated by using iteration method in MATLAB, which is determined to be 0.5705. The results of
UWSC are shown in
Table 2.
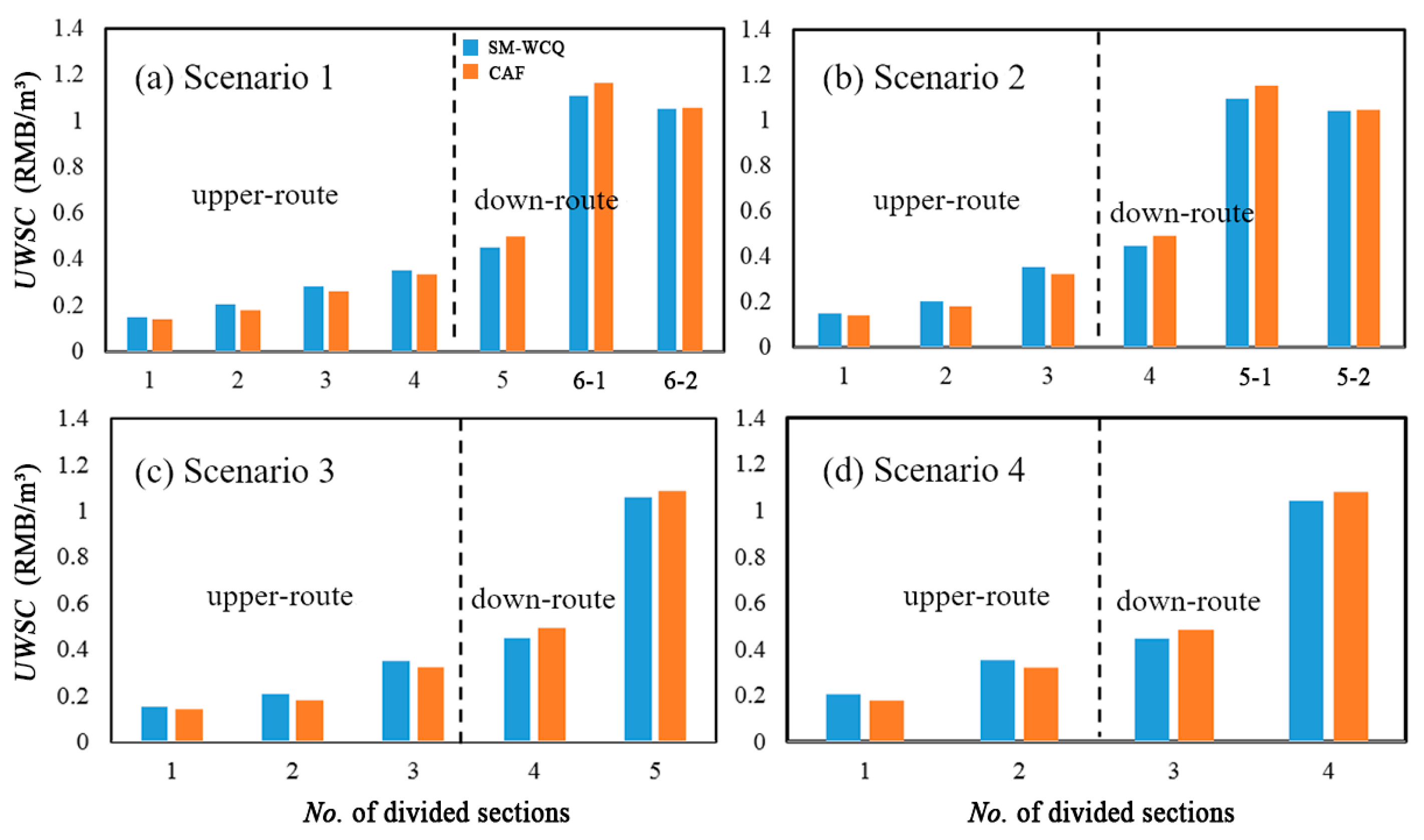
To further illustrate the differences between CAF and ICSM, the UWSC was calculated using these two sharing methods in four scenarios, with different numbers of sections. Scenario #1 is the basic scenario, representing the route divided into seven sections, which is the same as described in Section 4.1. Scenario #2 represents the route divided into six sections, where sections 4 and 5 in Scenario #1 are merged as the new section 4. Scenario #3 represents the route divided into five sections, where sections 5 and 6 in Scenario #2 are merged as the new section 5. Scenario #4 represents the route divided into four sections, where sections 1 and 2 in Scenario #3 are merged as the new section 1. The comparison results of the UWSC between the CAF and ICSM in different scenarios are shown in
Figure 5.
Figure 5 shows that the UWSC of ICSM is larger than that of CAF upstream, while opposite conclusion is observed downstream. This illustrates that the differences of the UWSC between the upper-route and down-route are declining trends for the ICSM.
The differences in annual sharing costs between the CAF and the ICSM are shown in
Table 3.
Table 3 shows that although the differences in the UWSC between the CAF and the ICSM are small, the differences in the annual sharing costs of each section will be large, due to the large volume of water transferred. Under the basic scenario (scenario #1), most downstream water intake users (in the two branches) can save 20.82 and 3.44 million RMB, respectively, and these savings will be shared by all upstream users. The results will make a more even distribution of sharing costs along the route.
3.2. Analysis of Mathematical Characteristics of CAF and ICSM
To further investigate the differences in mathematical features between CAF and ICSM formulas, the convergence characteristics of the two formulas have been analyzed by mathematical derivations.
- (1)
CAF
To simplify the analysis, we assume that the mainline of the ER- SNWDP in Shandong Province is evenly divided into
m sections and the costs of each section are the same, that is
Ci = C and
Wi = W. According to Equations (1) and (2), the general expression of the UWSC of the
nth user (
Dn) based on CAF can be derived as:
where,
Dn is the
UWSC of the
nth section,
CTm and
WTm are the cost and water supply of a single section.
Equation (8) contains a harmonic progression , which indicates that this equation is divergent. Furthermore, it illustrates that although the total costs and the total amount of water supply of the project have been given, the sharing costs of each section (Dn) still change nonlinearly with the increase in the total number of users.
- (2)
ICSM
Following the same assumptions used in the case of CAF, the general expression of
Dn based on ICSM is derived by using Equations (4) and (5), shown in Equation (9). It shows that
Dn will be a constant value when
n approaches infinity, i.e.,
Dn = 2
C/
W, under the condition that
n is no larger than
m. This illustrates that the formula of ICSM is a convergent function and the
UWSC in the last section (the
nth section) is double the average unit water supply costs of the entire water supply route:
where
Dn is the UWSC of the
nth section,
m is the number of total sections of the whole route, and
n is the number of calculated sections.
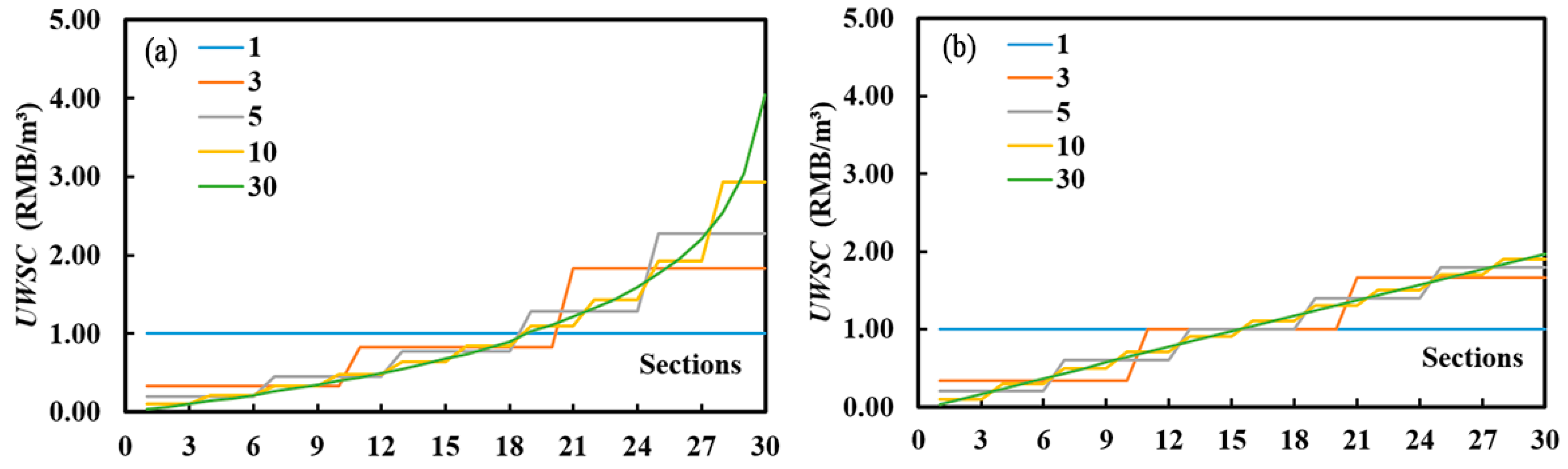
In order to intuitively compare the differences between the two calculation methods under different numbers of divided sections, taking a total number of water users as 30 users as an example, it is evenly divided into 1, 3, 5, 10 and 30 sections, respectively. The comparison of the
UWSC of each section between the CAF and the ICSM is shown in
Figure 6.
Figure 6 shows that the differences between the two adjacent sections of UWSC of ICSM are smaller than that of the CAF.
Figure 6a shows that the UWSC of CAF increases approximately exponentially, while
Figure 6b shows that UWSC of ICSM increases linearly.
4. Discussion
Due to differences in the development of economy and infrastructure among water users, it is difficult to make an absolutely fair cost-sharing strategy, to satisfy all upstream and downstream users at the same time. Therefore, the method by which to propose a reasonable strategy in order to ensure relatively fair costs sharing, so as to improve the participation enthusiasm both of upstream and downstream water users, has been a challenge for such large-scale projects.
This paper analyses the existing method (CAF) and the proposed method (ICSM) by which to share the water supply costs between the upstream and downstream users. The results provide a detailed case study of the two kinds of solutions.
For the SNWDP, the basic principle of CAF (“who benefits, who pays for it”) still shines in today’s cost-sharing method. However, the determination of the divided section number by the municipality significantly affects the sharing costs, which results in uncertainty of UWSC for the downstream users. Moreover, the sharing cost of downstream users increases sharply with the increase in the number of divided sections, which will weaken the enthusiasm of downstream users to participate.
Compared with the CAF, there is no additional data required by the ICSM. However, the results of the ICSM in sections 4.1 and 4.2 illustrate that it does not matter whether the number of divided sections is 3, 4 or 5, as the difference in the UWSC—between any two sections in which one is located upstream and the other one is downstream— shows a decreasing trend, compared to the results obtained by using CAF. More specifically, results of the ICSM show that the sharing cost of the upstream section increases slightly, whereas the sharing cost of the downstream section decreases slightly, compared with results of the CAF. This can be explained by the fact of the non-converge of the CAF formula. With the increase in the total section number, the cumulative sharing cost of the downstream section increases with exponential growth. Another reason is that the ICSM proposed in this study not only follows the principle of “who benefits, who pays”, but is also controlled by additional factors, such as the changes in the water supply cost and water intake factors along the route.
After the construction of a project, the total investment and total water supply cost are generally a fixed value, so the sharing cost of any given water-intake location should also be a relatively fixed value, especially for the downstream section. To some extent, the ICSM avoids the non-convergent and non-linear increasing trend of the cumulative sharing cost of downstream with the increase in the total section number determined by the CAF.
Above all, the sharing cost of ICSM proposed in this study may promote the willingness of the water supply users downstream to purchase the water provided by the IWDP. Since the sharing cost method is based on a convergent formula and the total section number of the route, it can ensure a relatively fair pricing mechanism. This is of great importance, especially in an area without a mature water market or a clear market mechanism.
In addition, it should be noted that cost-sharing is only a part of the water price, albeit a relatively certain part. The purchasing motivation of upstream and downstream water users is also affected by the water price determined by political factors, such as incentive policies and environmental factors [
27].
5. Conclusions
This case study contributes to debates about the selection of a proper sharing method for the ER-SNWDP. The proposed ICSM avoids the weakness of the non-convergence of CAF’s formula, by considering the balance equations of both water quantity and project costs between upstream and downstream. Two key findings can be concluded:
(1) The proposed ICSM will alleviate the conflict of interest between upstream and downstream users in the sharing cost of water supply projects, especially in areas with quasi-water markets and government-dominated IWDPs. This method treats the water supply quantity and investment cost of each section along the route as key variables, based on the continuity equation of water quantity balance between upstream and downstream and the balance equation of the project cost.
(2) The formula of the traditional CAF is divergent, in terms of mathematics, through a proof of derivation. For an IWDP in operation, the UWSC of each section along the route increases nonlinearly with the total section number increase. This non-linear relationship results in increased sharing costs for the downstream sections.
In addition, it is noted that the details of the empirical results depend on the properties and purpose of water supply engineering along the IWDP’s route, the policy control measures of the central government (or superior government), and other locally specific variables.