Response of Low Flows of Polish Rivers to Climate Change in 1987–1989
Abstract
:1. Introduction
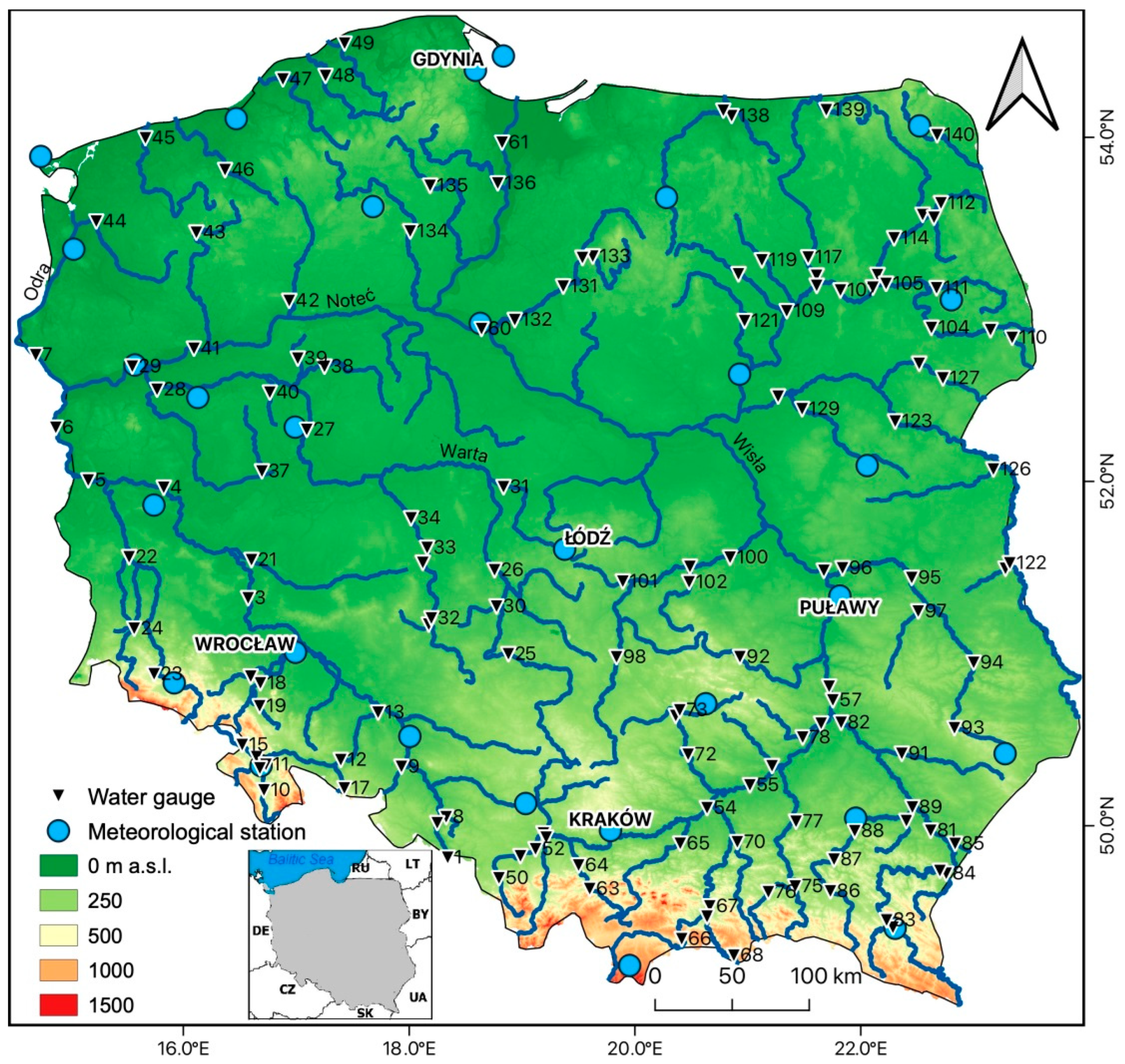
2. Materials
3. Methods
4. Changes in Climatic Conditions in 1951–2020 and Their Scope
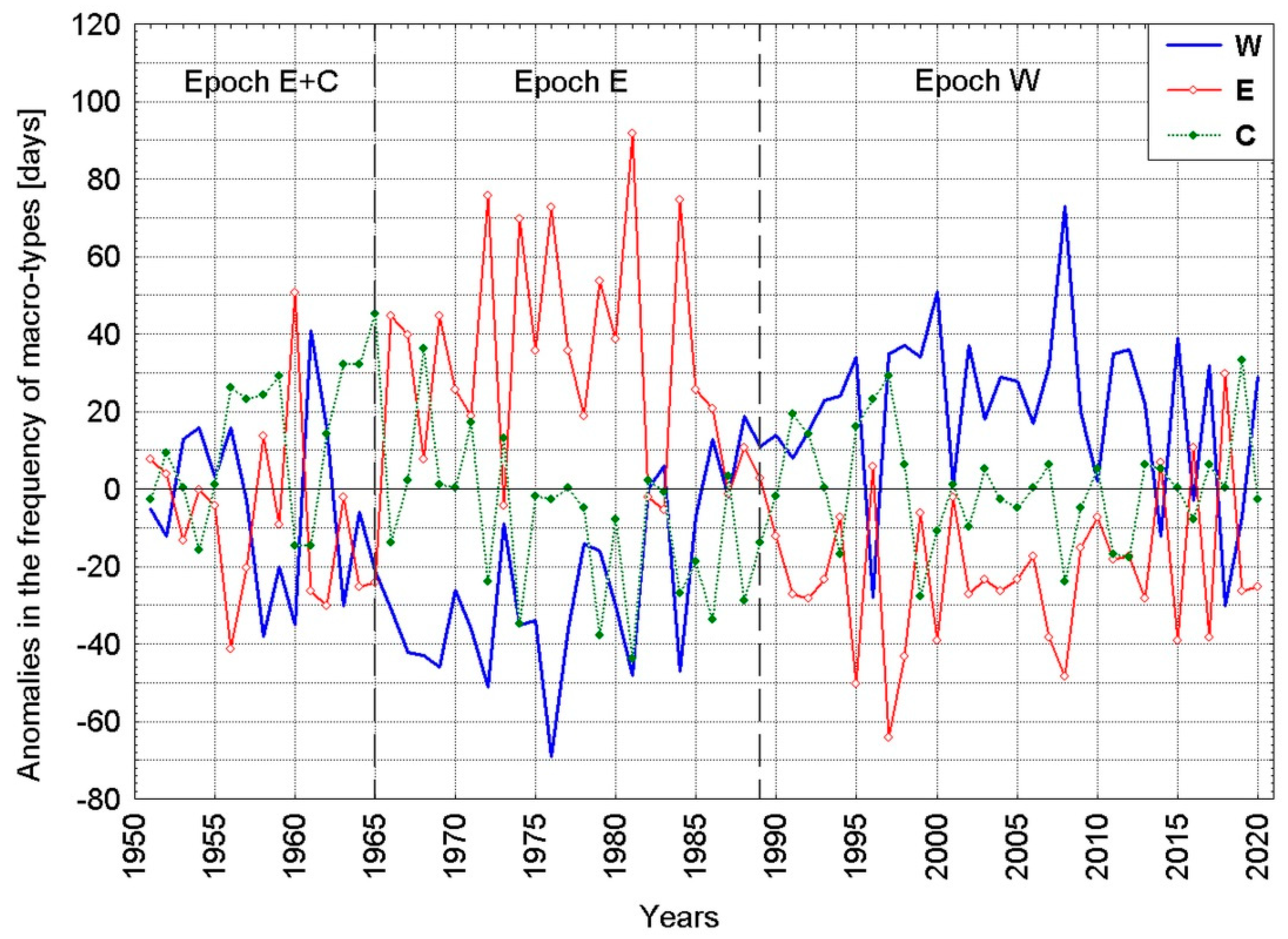
4.1. Changes in Macro-Circulation Conditions
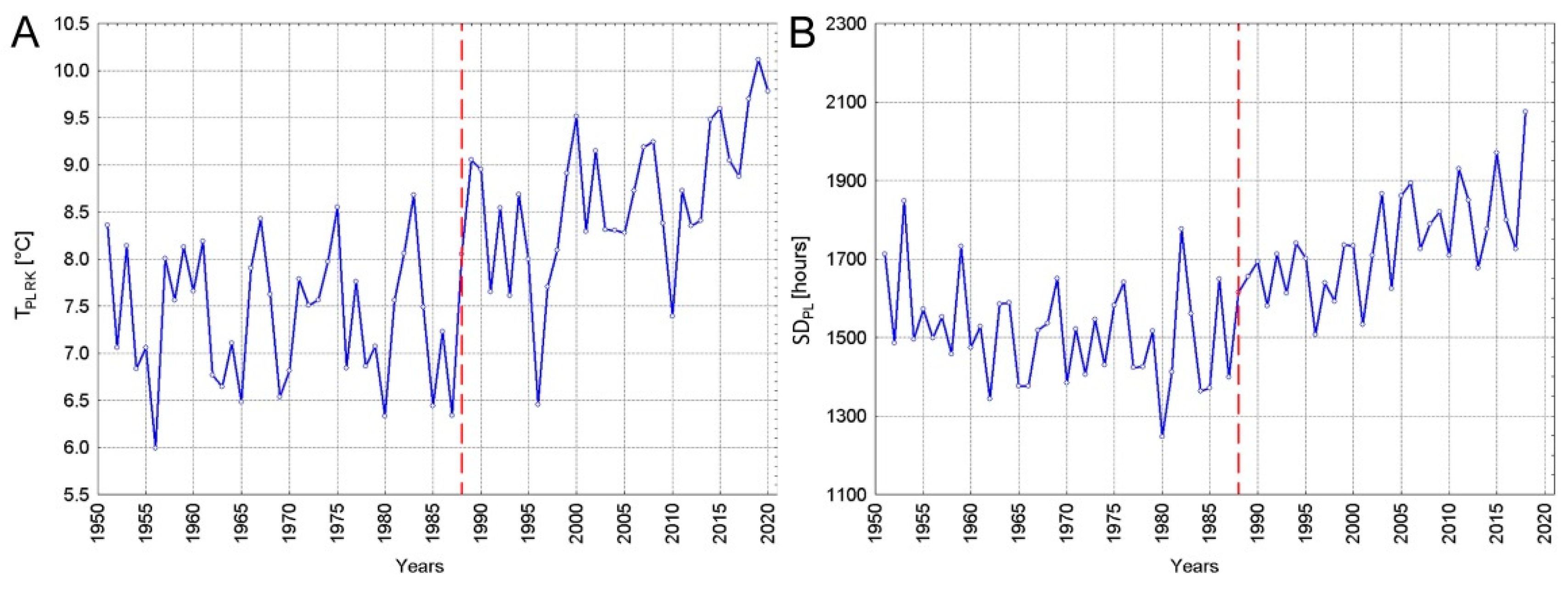
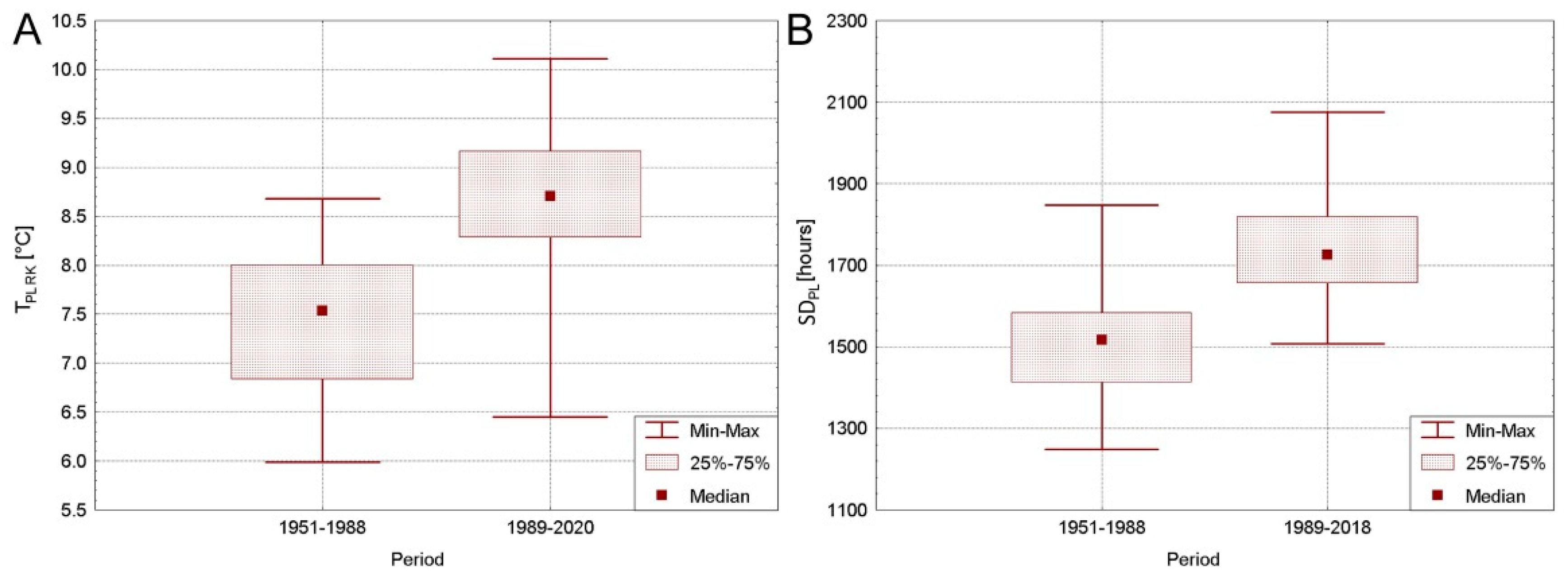
4.2. Changes in the Course of Climatic Elements in Poland in 1951–2000
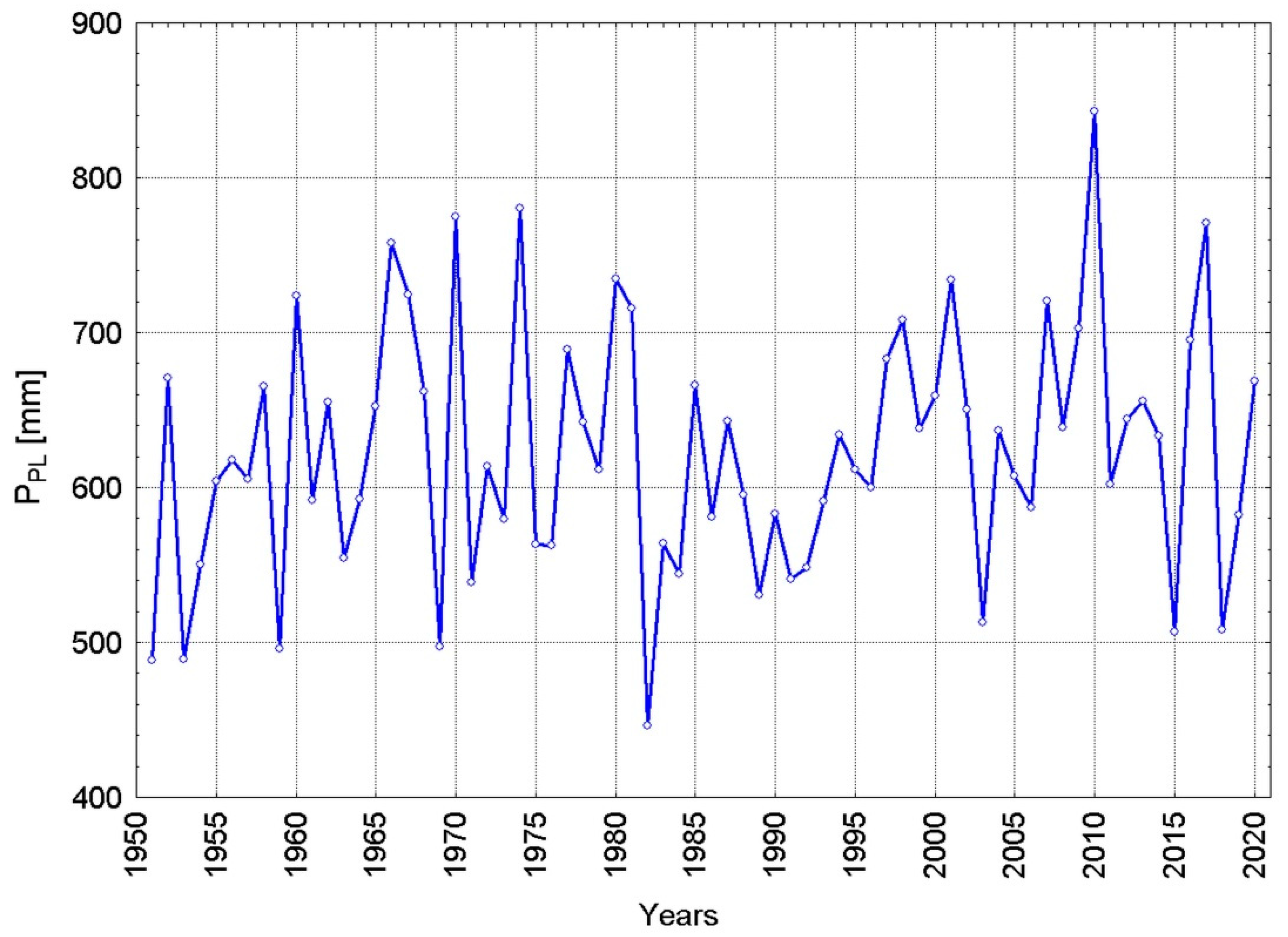
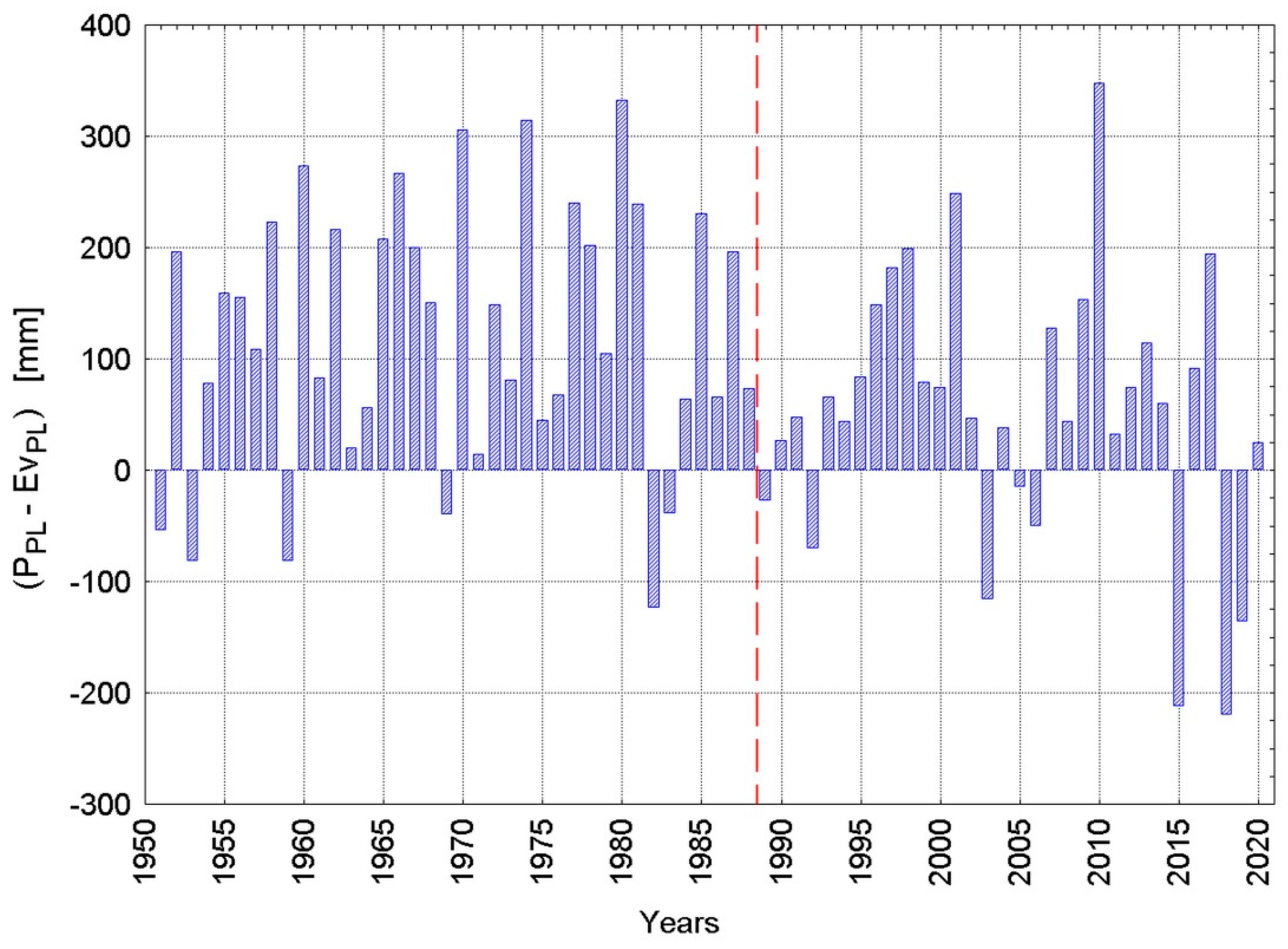
4.3. Changes in the Water Balance
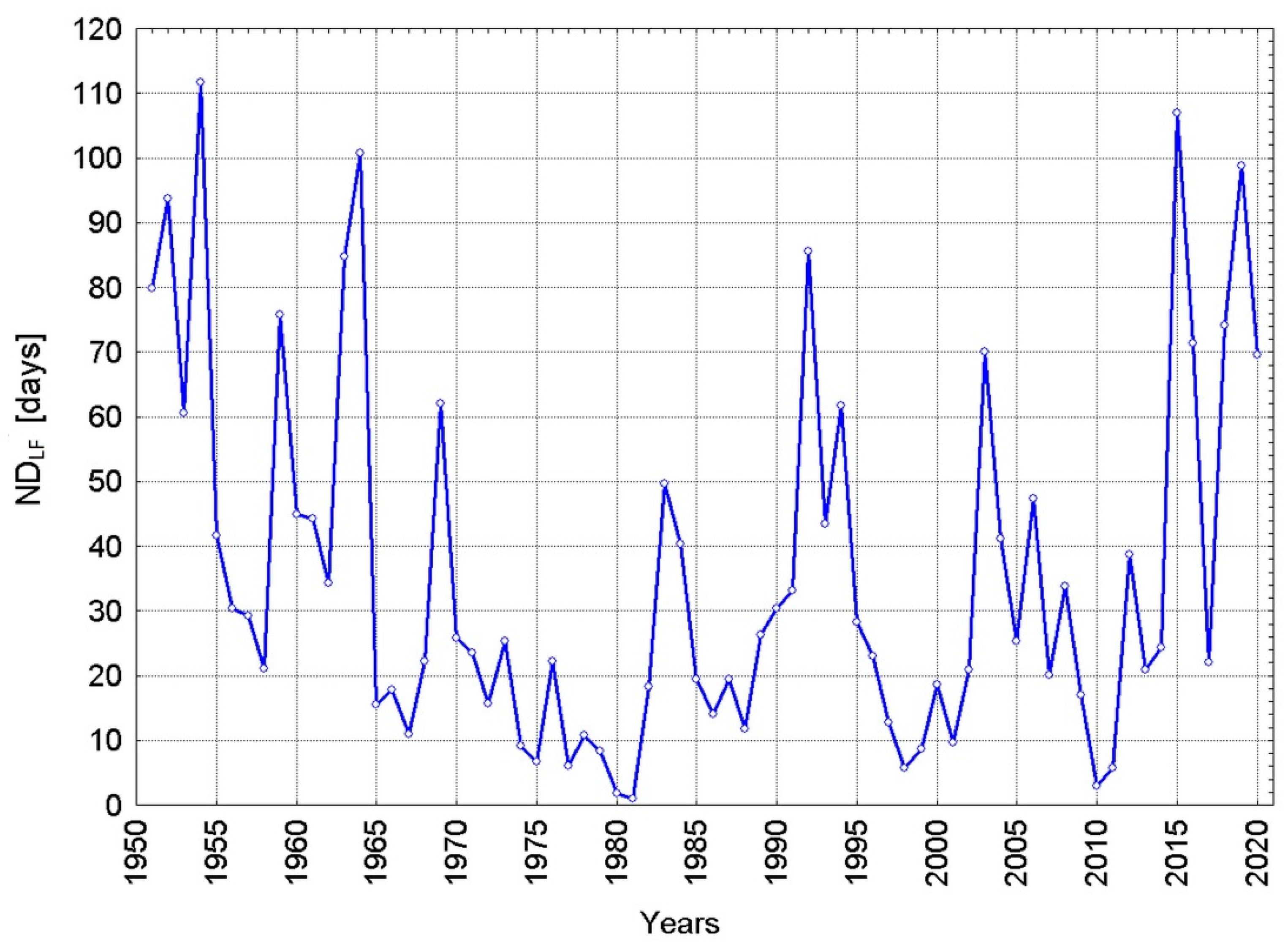
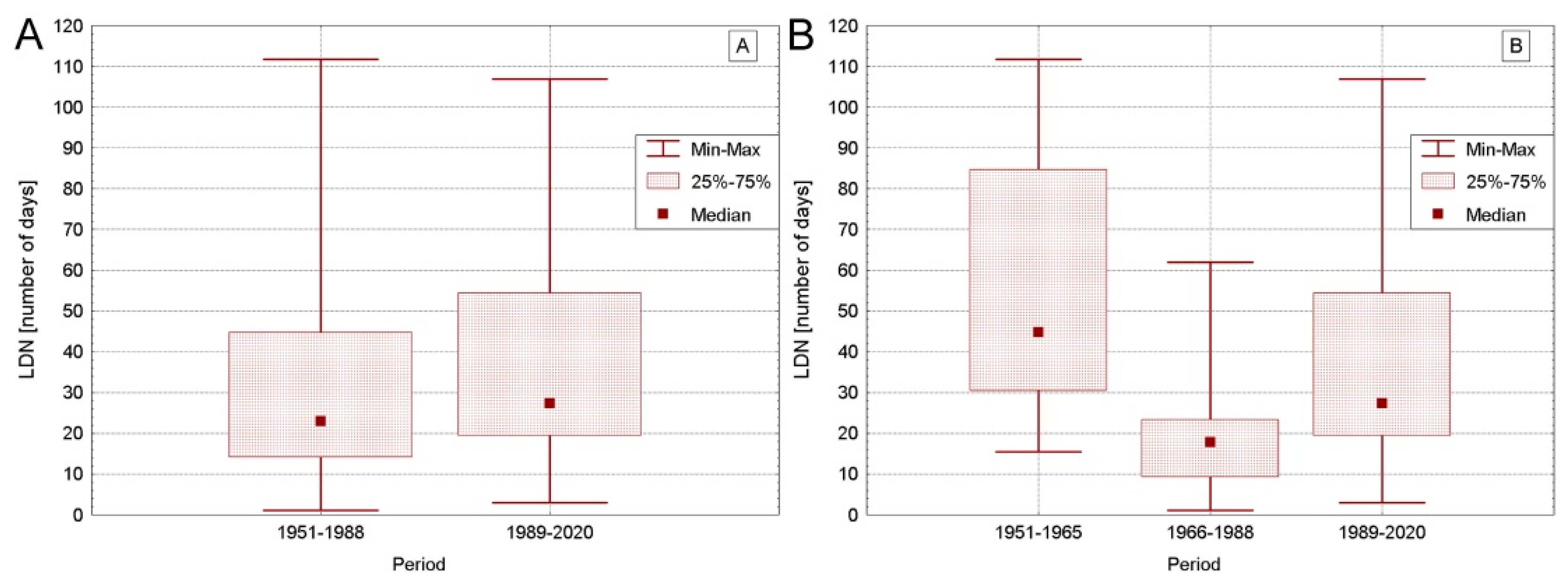
5. Number of Days with Low Flows (NDLF) on Polish Rivers
5.1. Results of the Principal Component Analysis
5.2. Spatial Analysis of the Relationship between the Number of Days with Low Flows (NDLF) and Changes in Climatic Conditions
6. Discussion
7. Conclusions
- (1)
- In 1987–1989, there was an abrupt change in climatic conditions in Poland.
- (2)
- Climate change in Poland was caused by macro-circulation conditions, controlled by changes in the intensity of thermohaline circulation in the North Atlantic (NA THC).
- (3)
- Climate change consisted of an abrupt increase in sunshine duration and air temperature, and a decrease in relative humidity after 1988. Along with the lack of changes in precipitation totals, characterized by a strong yearly variability, and an increase in field evaporation, it led to noticeable changes in the water balance.
- (4)
- In 1951–2020, the average number of NDFL days was from 30 to 70, with the dominance of upward trends on rivers in central and western Poland and negative trends on the southern and eastern tributaries of the Vistula River.
- (5)
- After climate change in 1989–2020 there was a significant increase in NDFL (even by 1 month) detected in about 2/3 of the area of Poland (in the central and western parts of the country).
- (6)
- With the change in the NA THC phase and the macro-circulation conditions, there was also a change in the spatial distribution of areas drained by rivers with increased NDFL. In 1951–1988, these included the eastern parts of Poland, while after the climate change (1989–2020)—its western and south-western parts.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | River | Water Gauge | Longitude (°E) | Latitude (°N) | Catchment Area (km2) | Runoff Depth [mm] | River Regime * |
|---|---|---|---|---|---|---|---|
| 1 | Odra | Chałupki | 18.33 | 49.92 | 4666 | 282.4 | 4 |
| 2 | Odra | Racibórz-Miedonia | 18.23 | 50.12 | 6744 | 300.8 | 4 |
| 3 | Odra | Ścinawa | 16.44 | 51.41 | 29,584 | 188.9 | 4 |
| 4 | Odra | Cigacice | 15.61 | 52.03 | 40,106 | 170.6 | 2 |
| 5 | Odra | Połęcko | 14.89 | 52.05 | 47,370 | 167.1 | 2 |
| 6 | Odra | Słubice | 14.56 | 52.35 | 53,600 | 174.2 | 2 |
| 7 | Odra | Gozdowice | 14.32 | 52.76 | 109,729 | 146.9 | 2 |
| 8 | Sumina | Nędza | 18.31 | 50.16 | 94.4 | 191.3 | 4 |
| 9 | Biała | Dobra | 17.90 | 50.45 | 353 | 99.4 | 4 |
| 10 | Nysa Kłodzka | Bystrzyca Kłodzka | 16.65 | 50.29 | 260 | 466.7 | 4 |
| 11 | Nysa Kłodzka | Kłodzko | 16.66 | 50.44 | 1084 | 364.9 | 4 |
| 12 | Nysa Kłodzka | Nysa | 17.34 | 50.48 | 3276 | 278.6 | 4 |
| 13 | Nysa Kłodzka | Skorogoszcz | 17.67 | 50.76 | 4514 | 249.8 | 4 |
| 14 | Bystrzyca Dusznicka | Szalejów Dolny | 16.60 | 50.42 | 175 | 378.1 | 2 |
| 15 | Ścinawka | Tłumaczów | 16.44 | 50.55 | 256 | 279.8 | 2 |
| 16 | Ścinawka | Gorzuchów | 16.57 | 50.49 | 511 | 274.8 | 4 |
| 17 | Biała Głuchołaska | Głuchołazy | 17.38 | 50.32 | 283 | 542.0 | 4 |
| 18 | Bystrzyca | Krasków | 16.58 | 50.92 | 683 | 205.9 | 4 |
| 19 | Piława | Mościsko | 16.58 | 50.78 | 291 | 172.6 | 4 |
| 20 | Strzegomka | Łażany | 16.49 | 50.95 | 356 | 198.0 | 4 |
| 21 | Barycz | Osetno | 16.46 | 51.63 | 4579 | 101.6 | 3 |
| 22 | Bóbr | Żagań | 15.32 | 51.62 | 4254 | 275.8 | 4 |
| 23 | Kamienica | Barcinek | 15.60 | 50.94 | 97.2 | 389.7 | 2 |
| 24 | Kwisa | Nowogrodziec | 15.40 | 51.20 | 736 | 306.9 | 4 |
| 25 | Warta | Działoszyn | 18.87 | 51.11 | 4088 | 185.8 | 2 |
| 26 | Warta | Sieradz | 18.74 | 51.60 | 8140 | 171.3 | 2 |
| 27 | Warta | Poznań | 16.95 | 52.40 | 25,126 | 124.5 | 2 |
| 28 | Warta | Skwierzyna | 15.50 | 52.60 | 31,268 | 123.4 | 2 |
| 29 | Warta | Gorzów Wielkopolski | 15.25 | 52.73 | 52,186 | 124.4 | 2 |
| 30 | Oleśnica | Niechmirów | 18.76 | 51.39 | 592 | 126.7 | 3 |
| 31 | Ner | Dąbie | 18.82 | 52.08 | 1712 | 181.6 | 2 |
| 32 | Prosna | Mirków | 18.16 | 51.32 | 1255 | 126.0 | 2 |
| 33 | Prosna | Piwonice | 18.11 | 51.73 | 2938 | 119.2 | 2 |
| 34 | Prosna | Bogusław | 17.95 | 51.90 | 4304 | 114.3 | 2 |
| 35 | Niesób | Kuźnica Skakawska | 18.13 | 51.28 | 246 | 123.8 | 3 |
| 36 | Ołobok | Ołobok | 18.07 | 51.64 | 447 | 110.7 | 3 |
| 37 | Mogilnica | Konojad | 16.53 | 52.15 | 663 | 77.3 | 3 |
| 38 | Wełna | Pruśce | 17.10 | 52.77 | 1130 | 92.5 | 3 |
| 39 | Flinta | Ryczywół | 16.84 | 52.82 | 276 | 74.1 | 3 |
| 40 | Sama | Szamotuły | 16.58 | 52.61 | 395 | 83.4 | 3 |
| 41 | Noteć | Nowe Drezdenko | 15.84 | 52.85 | 15,970 | 143.2 | 2 |
| 42 | Gwda | Piła | 16.74 | 53.15 | 4704 | 180.0 | 1 |
| 43 | Drawa | Drawsko Pomorskie | 15.81 | 53.53 | 609 | 209.2 | 2 |
| 44 | Ina | Goleniów | 14.83 | 53.56 | 2163 | 185.5 | 2 |
| 45 | Rega | Trzebiatów | 15.26 | 54.06 | 2628 | 239.4 | 2 |
| 46 | Parsęta | Tychówko | 16.07 | 53.90 | 896 | 289.1 | 2 |
| 47 | Wieprza | Stary Kraków | 16.61 | 54.44 | 1519 | 327.0 | 1 |
| 48 | Słupia | Słupsk | 17.03 | 54.47 | 1450 | 338.5 | 1 |
| 49 | Łupawa | Smołdzino | 17.21 | 54.66 | 805 | 325.7 | 1 |
| 50 | Wisła | Skoczów | 18.79 | 49.80 | 297 | 641.0 | 4 |
| 51 | Wisła | Goczałkowice | 18.99 | 49.93 | 738 | 381.0 | 5 |
| 52 | Wisła | Jawiszowice | 19.12 | 49.97 | 971 | 426.1 | 5 |
| 53 | Wisła | Bieruń Nowy | 19.19 | 50.06 | 1748 | 381.8 | 4 |
| 54 | Wisła | Jagodniki | 20.68 | 50.20 | 12,058 | 334.4 | 4 |
| 55 | Wisła | Szczucin | 21.08 | 50.33 | 23,901 | 307.4 | 4 |
| 56 | Wisła | Sandomierz | 21.75 | 50.67 | 31,846 | 284.8 | 4 |
| 57 | Wisła | Zawichost | 21.86 | 50.81 | 50,732 | 261.9 | 4 |
| 58 | Wisła | Annopol | 21.83 | 50.89 | 51,518 | 261.8 | 4 |
| 59 | Wisła | Dęblin | 21.83 | 51.56 | 68,234 | 227.9 | 4 |
| 60 | Wisła | Toruń | 18.61 | 53.01 | 181,033 | 167.5 | 2 |
| 61 | Wisła | Tczew | 18.80 | 54.10 | 194,376 | 167.3 | 2 |
| 62 | Soła | Oświęcim | 19.22 | 50.04 | 1386 | 473.1 | 4 |
| 63 | Skawa | Sucha Beskidzka | 19.61 | 49.74 | 468 | 507.9 | 4 |
| 64 | Skawa | Wadowice | 19.51 | 49.88 | 836 | 465.0 | 4 |
| 65 | Raba | Proszówki | 20.43 | 50.00 | 1470 | 356.6 | 4 |
| 66 | Dunajec | Krościenko | 20.43 | 49.44 | 1580 | 634.9 | 5 |
| 67 | Dunajec | Nowy Sącz | 20.69 | 49.63 | 4341 | 472.8 | 4 |
| 68 | Poprad | Muszyna | 20.89 | 49.34 | 1514 | 365.9 | 4 |
| 69 | Poprad | Stary Sącz | 20.66 | 49.57 | 2071 | 380.5 | 4 |
| 70 | Biała | Koszyce Wielkie | 20.95 | 50.00 | 957 | 290.5 | 4 |
| 71 | Nida | Brzegi | 20.41 | 50.74 | 2259 | 177.1 | 2 |
| 72 | Nida | Pińczów | 20.52 | 50.51 | 3352 | 168.2 | 2 |
| 73 | Czarna Nida | Tokarnia | 20.45 | 50.77 | 1216 | 171.4 | 2 |
| 74 | Czarna | Połaniec | 21.28 | 50.43 | 1354 | 149.2 | 3 |
| 75 | Wisłoka | Żółków | 21.46 | 49.73 | 581 | 384.7 | 4 |
| 76 | Ropa | Klęczany | 21.22 | 49.70 | 483 | 406.9 | 4 |
| 77 | Brzeźnica | Brzeźnica | 21.49 | 50.11 | 484 | 212.5 | 4 |
| 78 | Koprzywianka | Koprzywnica | 21.57 | 50.60 | 502 | 127.1 | 3 |
| 79 | San | Lesko | 22.32 | 49.47 | 1614 | 555.0 | 4 |
| 80 | San | Przemyśl | 22.77 | 49.78 | 3686 | 444.9 | 4 |
| 81 | San | Jarosław | 22.70 | 50.02 | 7041 | 312.7 | 4 |
| 82 | San | Radomyśl | 21.93 | 50.67 | 16,824 | 241.6 | 4 |
| 83 | Osława | Zagórz | 22.27 | 49.51 | 505 | 509.0 | 4 |
| 84 | Wiar | Krówniki | 22.82 | 49.77 | 789 | 252.7 | 4 |
| 85 | Wisznia | Nienowice | 22.92 | 49.94 | 1185 | 178.6 | 4 |
| 86 | Wisłok | Krosno | 21.77 | 49.69 | 596 | 327.8 | 4 |
| 87 | Wisłok | Żarnowa | 21.82 | 49.88 | 1427 | 287.3 | 4 |
| 88 | Wisłok | Rzeszów | 22.02 | 50.04 | 2086 | 263.1 | 4 |
| 89 | Wisłok | Tryńcza | 22.55 | 50.16 | 3516 | 227.7 | 4 |
| 90 | Mleczka | Gorliczyna | 22.49 | 50.08 | 529 | 173.2 | 4 |
| 91 | Tanew | Harasiuki | 22.47 | 50.48 | 2034 | 189.7 | 2 |
| 92 | Kamienna | Wąchock | 21.02 | 51.08 | 476 | 192.7 | 2 |
| 93 | Wieprz | Zwierzyniec | 22.97 | 50.61 | 405 | 160.1 | 1 |
| 94 | Wieprz | Krasnystaw | 23.18 | 50.99 | 3001 | 129.8 | 2 |
| 95 | Wieprz | Lubartów | 22.64 | 51.50 | 6364 | 111.7 | 2 |
| 96 | Wieprz | Kośmin | 22.00 | 51.57 | 10,231 | 113.2 | 2 |
| 97 | Bystrzyca | Sobianowice | 22.69 | 51.30 | 1265 | 125.6 | 2 |
| 98 | Pilica | Przedbórz | 19.88 | 51.09 | 2536 | 185.9 | 2 |
| 99 | Pilica | Nowe Miasto | 20.57 | 51.61 | 6717 | 166.9 | 2 |
| 100 | Pilica | Białobrzegi | 20.95 | 51.66 | 8664 | 160.4 | 2 |
| 101 | Wolbórka | Zawada | 19.94 | 51.53 | 616 | 137.5 | 2 |
| 102 | Drzewiczka | Odrzywół | 20.56 | 51.52 | 1004 | 166.9 | 2 |
| 103 | Narew | Narew | 23.52 | 52.92 | 1978 | 146.0 | 3 |
| 104 | Narew | Suraż | 22.96 | 52.95 | 3376 | 139.5 | 3 |
| 105 | Narew | Strękowa Góra | 22.54 | 53.22 | 7181 | 141.4 | 3 |
| 106 | Narew | Wizna | 22.41 | 53.20 | 14,308 | 148.4 | 3 |
| 107 | Narew | Piątnica-Łomża | 22.09 | 53.19 | 15,296 | 150.9 | 3 |
| 108 | Narew | Nowogród | 21.86 | 53.23 | 20,106 | 152.4 | 3 |
| 109 | Narew | Ostrołęka | 21.56 | 53.08 | 21,862 | 155.8 | 3 |
| 110 | Narewka | Narewka | 23.73 | 52.86 | 590 | 156.9 | 3 |
| 111 | Supraśl | Fasty | 23.03 | 53.18 | 1817 | 153.3 | 2 |
| 112 | Biebrza | Sztabin | 23.12 | 53.67 | 846 | 171.5 | 3 |
| 113 | Biebrza | Dębowo | 22.93 | 53.61 | 2322 | 167.3 | 3 |
| 114 | Biebrza | Osowiec | 22.64 | 53.48 | 4365 | 160.0 | 3 |
| 115 | Biebrza | Burzyn | 22.46 | 53.27 | 6900 | 158.0 | 3 |
| 116 | Brzozówka | Karpowicze | 23.04 | 53.59 | 650 | 154.1 | 3 |
| 117 | Pisa | Ptaki | 21.79 | 53.39 | 3562 | 181.6 | 1 |
| 118 | Pisa | Dobrylas | 21.87 | 53.28 | 4061 | 182.4 | 2 |
| 119 | Rozoga | Myszyniec | 21.34 | 53.39 | 231 | 155.2 | 2 |
| 120 | Omulew | Krukowo | 21.11 | 53.31 | 1265 | 170.0 | 2 |
| 121 | Orzyc | Krasnosielc | 21.15 | 53.04 | 1268 | 142.2 | 2 |
| 122 | Bug | Włodawa | 23.57 | 51.55 | 14,410 | 120.5 | 3 |
| 123 | Bug | Frankopol | 22.56 | 52.41 | 31,336 | 118.1 | 3 |
| 124 | Bug | Wyszków | 21.45 | 52.59 | 39,119 | 122.5 | 3 |
| 125 | Włodawka | Okuninka | 23.52 | 51.52 | 576 | 116.5 | 3 |
| 126 | Krzna | Malowa Góra | 23.47 | 52.10 | 3128 | 108.1 | 3 |
| 127 | Nurzec | Boćki | 23.04 | 52.65 | 556 | 134.0 | 3 |
| 128 | Nurzec | Brańsk | 22.82 | 52.74 | 1227 | 126.8 | 3 |
| 129 | Liwiec | Łochów | 21.68 | 52.51 | 2466 | 134.1 | 3 |
| 130 | Drwęca | Nowe Miasto Lubawskie | 19.59 | 53.42 | 2725 | 188.9 | 2 |
| 131 | Drwęca | Brodnica | 19.40 | 53.26 | 3526 | 192.5 | 2 |
| 132 | Drwęca | Elgiszewo | 18.93 | 53.06 | 4959 | 173.7 | 2 |
| 133 | Wel | Kuligi | 19.69 | 53.43 | 764 | 206.3 | 1 |
| 134 | Brda | Tuchola | 17.90 | 53.57 | 2462 | 248.6 | 1 |
| 135 | Wda | Czarna Woda | 18.09 | 53.84 | 940 | 210.7 | 1 |
| 136 | Wierzyca | Brody Pomorskie | 18.76 | 53.86 | 1544 | 175.0 | 2 |
| 137 | Łyna | Sępopol | 21.01 | 54.27 | 3647 | 211.7 | 2 |
| 138 | Guber | Prosna | 21.09 | 54.23 | 1568 | 171.6 | 2 |
| 139 | Gołdapa | Banie Mazurskie | 22.03 | 54.25 | 548 | 266.9 | 3 |
| 140 | Czarna Hańcza | Czerwony Folwark | 23.12 | 54.07 | 454 | 262.6 | 2 |
References
- Schmuck, A. Outline of Hydrometeorology; Wydawnictwo Naukowe PWN: Wrocław-Warsaw, Poland, 1960; pp. 1–108. (In Polish) [Google Scholar]
- Bac, S. Studies on evaporation of free water surface field, field evaporation and potential evapotranspiration. Zesz. Nauk. WSR We Wrocławiu 1968, 80, Melioracja 13, 7–68. (In Polish) [Google Scholar]
- Kędziora, A. Fundamentals of Agro-Meteorology; Państwowe Wydawnictwo Rolnicze i Leśne: Warsaw, Poland, 1999; pp. 1–364. (In Polish) [Google Scholar]
- Giuntoli, I.; Renard, B.; Vidal, J.-P.; Bard, A. Low flows in France and their relationship to large-scale climate indices. J. Hydrol. 2013, 482, 105–118. [Google Scholar] [CrossRef]
- Shorthouse, C.; Arnell, N. Spatial and temporal variability in European river flows and the North Atlantic Oscillation. In FRIEND 97-Regional Hydrology: Concepts and Models for Sustainable Water Resource Management; IAHS Publ: Wallingford, UK, 1997; Volume 246. [Google Scholar]
- Bouwer, L.M.; Vermaat, J.E.; Aerts, J.C.J.H. Regional sensitivities of mean and peak river discharge to climate variability in Europe. J. Geophys. Res. 2008, 113, D19103. [Google Scholar] [CrossRef]
- Wilby, R.; O’Hare, G.; Barnsley, N. The North Atlantic Oscillation and British Isles climate variability, 1865–1996. Weather 1997, 52, 266–276. [Google Scholar] [CrossRef]
- Kiely, G. Climate change in Ireland from precipitation and streamflow observations. Adv. Water Resour. 1999, 23, 141–151. [Google Scholar] [CrossRef]
- Kingston, D.G.; Hannah, D.M.; Lawler, D.M.; McGregor, G.R. Interactions between Large-Scale Climate and River Flow across the Northern North Atlantic Margin; IAHS-AISH Publ: Havana, Cuba, 2006; pp. 350–355. [Google Scholar]
- Wedgbrow, C.S.; Wilby, R.L.; Fox, H.R.; O’Hare, G. Prospects for seasonal forecasting of summer drought and low river flow anomalies in England and Wales. Int. J. Climatol. 2002, 22, 219–236. [Google Scholar] [CrossRef]
- Stefan, S.; Ghioca, M.; Rimbu, N.; Boroneant, C. Study of meteorological and hydrological drought in southern Romania from observational data. Int. J. Climatol. 2004, 24, 871–881. [Google Scholar] [CrossRef]
- Mager, P.; Kuźnicka, M.; Kępińska-Kasprzak, M.; Farat, R. Changes in the intensity and frequency of occurrence of droughts in Poland (1891–1995). Geogr. Pol. 2000, 73, 41–48. [Google Scholar]
- Łabędzki, L. Estimation of local drought frequency in central Poland using the standardized precipitation index SPI. Irrig. Drain. 2007, 56, 6777. [Google Scholar] [CrossRef]
- Tokarczyk, T. Widely applied indices for drought assessment and Polish application. In Infrastruktura i Ekologia Terenów Wiejskich; Stowarzyszenie Infrastruktura i Ekologia Terenów Wiejskich: Kraków, Poland, 2008; Volume 7, pp. 167–182. (In Polish) [Google Scholar]
- Tokarczyk, T. Low-Water Flows as an Indicator of Hydrological Drought; Instytut Meteorologii i Gospodarki Wodnej: Warsaw, Poland, 2010; pp. 1–164. (In Polish) [Google Scholar]
- Tokarczyk, T. Classification of low flow and hydrological drought for a river basin. Acta Geophys. 2013, 61, 404–421. [Google Scholar] [CrossRef]
- Szalińska, W. Combined analysis of precipitation and water deficit for drought hazard assessment. Hydrol. Sci. J. 2014, 59, 1675–1689. [Google Scholar] [CrossRef]
- Tomaszewski, E.; Kozek, M. Dynamics, Range, and Severity of Hydrological Drought in Poland. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Tomaszewski, E.; Kubiak-Wójcicka, K. 2021: Low-Flows in Polish Rivers. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Szwed, M.; Karg, G.; Pinskwar, I.; Radziejewski, M.; Graczyk, D.; Kędziora, A.; Kundzewicz, Z.W. Climate change and its effect on agriculture, water resources and human health sectors in Poland. Nat. Hazards Earth Syst. Sci. 2010, 10, 1725–1737. [Google Scholar] [CrossRef]
- Meresa, H.K.; Osuch, M.; Romanowicz, R. Hydro-Meteorological Drought Projections into the 21-st Century for Selected Polish Catchments. Water 2016, 8, 206. [Google Scholar] [CrossRef]
- Instytut Meteorologii i Gospodarki Wodnej–Państwowy Instytut Badawczy. Dane Publiczne. Available online: https://danepubliczne.imgw.pl (accessed on 20 May 2021). (In Polish).
- Bryś, K. Dynamics of Net Radiation Balance of Grass Surface and Bare Soil; Monografie CLXII, Wydawnictwo Uniwersytetu Przyrodniczego we Wrocławiu: Wrocław, Poland, 2013; pp. 1–288. (In Polish) [Google Scholar]
- Matuszko, D. Long-term variability in solar radiation in Krakow based on measurements of sunshine duration. Int. J. Climatol. 2014, 34, 228–234. [Google Scholar] [CrossRef]
- Matuszko, D.; Piotrowicz, K. Relationship between sunshine duration and air temperature on the basis of long-term climatological series in Krakow (1884–2016). Przegląd Geofiz. 2018, 63, 15–29. (In Polish) [Google Scholar]
- Podstawczyńska, A. The solar characteristics of climate of Łódź. Acta Univ. Lodz. Folia Geogr. Phys. 2007, 7, 1–220. (In Polish) [Google Scholar]
- Dimitriev, A.A.; Dubravin, V.F.; Belyazo, V.A. The Atmospheric Processes in the Northern Hemisphere (1891–2018), Their Classification and Use; SUPER Izdatielstvo: Sankt Petersburg, Russia, 2018; pp. 1–305. (In Russian) [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Okołowicz, W. General Climatology; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1976; pp. 1–422. (In Polish) [Google Scholar]
- Kędziora, A. Water balance of Konin strip mine landscape in changing climatic conditions. Rocz. Glebozn. 2008, 59, 104–118. (In Polish) [Google Scholar]
- Radzka, E. Climatic water balance for the vegetation season (according to Ivanov’s equation) in Central-Eastern Poland. Woda-Środowisko-Obsz. Wiej. 2014, 14, 67–76. (In Polish) [Google Scholar]
- Okoniewska, M.; Szumińska, D. Changes in Potential Evaporation in the Years 1952–2018 in North-Western Poland in Termsof the Impact of Climatic Changes on Hydrological an Hydrochemical Condotions. Water 2020, 12, 877. [Google Scholar] [CrossRef]
- Yevjevich, V. An Objective Approach to Definitions and Investigations of Continental Hydrologic Droughts. Hydrology Papers; Colorado State University: Fort Collins, CO, USA, 1967; pp. 1–25. [Google Scholar]
- Ozga-Zielińska, M.; Brzeziński, J. Applied Hydrology; Wydawnictwo Naukowe PWN: Warsaw, Poland, 1994; pp. 1–323. (In Polish) [Google Scholar]
- Wangengejm, G.Y. Fundamentals of macrocirculation method for long-range weather forecasting for the Arctic. In Trudy; AANII: Leningrad, USSR, 1952; Volume 34, pp. 1–314. (In Russian) [Google Scholar]
- Girs, A.A. On the creation of a single classification of the northern hemisphere. Meteorol. I Gidrol. 1964, 4, 43–47. (In Russian) [Google Scholar]
- Girs, A.A. Long-Term Atmospheric Circulation Variations, and Long-Range Hydrometeorological Forecasts; Girometeoizdat: Leningrad, USSR, 1971; pp. 1–280. (In Russian) [Google Scholar]
- Savichev, A.I.; Mironicheva, N.P.; Cepelev, V.Y. Atmospheric circulation characteristics of the northern hemisphere of the Atlantic-Eurasian sector for last decades. Uchenye Zap. Ross. Gos. Gidrometeorol. Univ. 2015, 39, 120–131. (In Russian) [Google Scholar]
- Degirmendžić, J.; Kożuchowski, K. Circulation epochs based on the Vangengeim-Girs large scale patterns (1891–2010). Acta Univ. Lodz. Folia Geogr. Phys. 2018, 17, 7–13. [Google Scholar] [CrossRef]
- Degirmnedžić, J.; Kożuchowski, K. Variation of macro-circulation forms over the Atlantic-Eurasian temperate zone according to the Vangengeim-Girs classification. Int. J. Climatol. 2019, 39, 4938–4942. [Google Scholar] [CrossRef]
- Monin, A.S. An Introduction to the Theory of Climate; Gidrometoizdat: Leningrad, USSR, 1982; pp. 1–246. (In Russian) [Google Scholar]
- Marsz, A.A.; Styszyńska, A. The Influence of the Sign of NAO Phases during the Winter Period on the Water Balance and the Possibility of Drought Occurrence in the Warm Season in Poland. Ann. Univ. Mariae Curie-Skłodowska 2021, 76, 127–143. [Google Scholar] [CrossRef]
- Hill, T.; Lewicki, P. Statistics: Methods and Applications; StatSoft: Tulsa, OK, USA, 2007. [Google Scholar]
- Bednorz, E. Snow cover in eastern Europe in relation to temperature, precipitation and circulation. Int. J. Climatol. 2004, 24, 591–601. [Google Scholar] [CrossRef]
- Czarnecka, M. Frequency of occurrence and depth of snow cover in Poland. Acta Agrophys. 2012, 19, 501–514. (In Polish) [Google Scholar]
- Tomczyk, A.M. Impact of macro-scale circulation types on the occurrence of snow cover in Europe. Acta Geogr. Sil. 2014, 15, 65–69. (In Polish) [Google Scholar]
- Pociask-Karteczka, J. River Hydrology and the North Atlantic Oscillation: A General Review. AMBIO 2006, 35, 312–314. [Google Scholar] [CrossRef] [PubMed]
- Styszyńska, A.; Tamulewicz, J. Warta river discharges in Poznań and atmospheric circulation in the North Atlantic region. Quaest. Geogr. 2004, 23, 63–81. [Google Scholar]
- Wrzesiński, D. Changes of the hydrological regime of rivers of northern and central Europe in various circulation periods of the North Atlantic Oscillation. Quaest. Geogr. 2005, 24, 97–109. [Google Scholar]
- Wrzesiński, D. Typology of spatial patterns seasonality in European rivers flow regime. Quaest. Geogr. 2008, 27, 87–98. [Google Scholar]
- Wrzesiński, D. Regional differences in the influence of the North Atlantic Oscillation on seasonal river runoff in Poland. Quaest. Geogr. 2011, 30, 127–136. [Google Scholar] [CrossRef]
- Wrzesiński, D.; Paluszkiewicz, R. Spatial differences in the impact of the North Atlantic Oscillation on the flow of rivers in Europe. Hydrol. Res. 2011, 42, 30–39. [Google Scholar] [CrossRef]
- Marsz, A.A.; Styszyńska, A. Intensity of thermohaline Circulation in the North Atlantic and Droughts in Poland. Pr. I Studia Geogr. 2021, 66, 63–88. (In Polish) [Google Scholar] [CrossRef]
- Marsz, A.A.; Styszyńska, A.; Krawczyk, W.E. Long-term fluctuations of annual discharges of the main rivers in Poland and their association with the Northern Atlantic Thermohaline Circulation. Przegląd Geogr. 2016, 88, 295–316. (In Polish) [Google Scholar] [CrossRef]
- Wrzesiński, D.; Marsz, A.A.; Styszyńska, A.; Sobkowiak, L. Effect of the North Atlantic Thermohaline Circulation on Changes in Climatic Conditions and River Flow in Poland. Water 2019, 11, 1662. [Google Scholar] [CrossRef]
- Fortak, H. Meteorology; Deutsche Buch-Gemainschaft: Berlin, Germany; Darmstadt, Germany; Wien, Austria, 1971; pp. 1–287. (In German) [Google Scholar]
- Zvieriev, A.S. Synoptic Meteorology; Gidrometeoizdat: Leningrad, USSR, 1977; pp. 1–711. (In Russian) [Google Scholar]
- Stachý, J. Long-term forecast of the runoff of Polish rivers. In PIH-M Wiadomości Służby Hydrol. i Meteorol; Państwowy Instytut Hydrologiczno-Meteorologiczny: Warsaw, Poland, 1969; Volume 3, pp. 23–34. (In Polish) [Google Scholar]
- Wrzesiński, D. Use of Entropy in the Assessment of Uncertainty of River Runoff Regime in Poland. Acta Geophys. 2016, 64, 1825–1839. [Google Scholar] [CrossRef]
- Wrzesiński, D. Flow Regime Patterns and Their Changes. In Management of Water Resources in Poland; Zeleňáková, M., Kubiak-Wójcicka, K., Negm, A.M., Eds.; Springer Nature: Cham, Switzerland, 2021; pp. 163–180. [Google Scholar] [CrossRef]

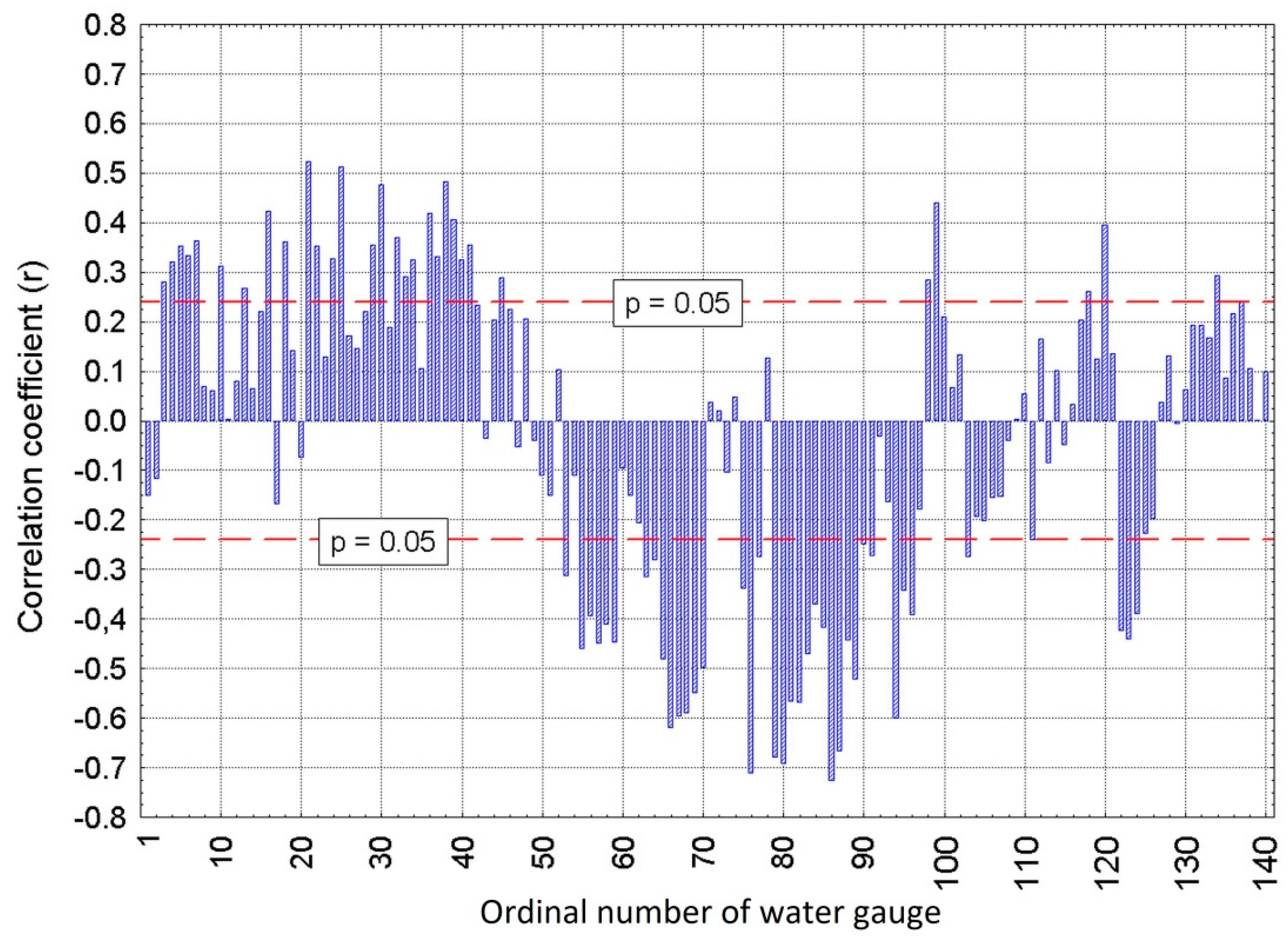
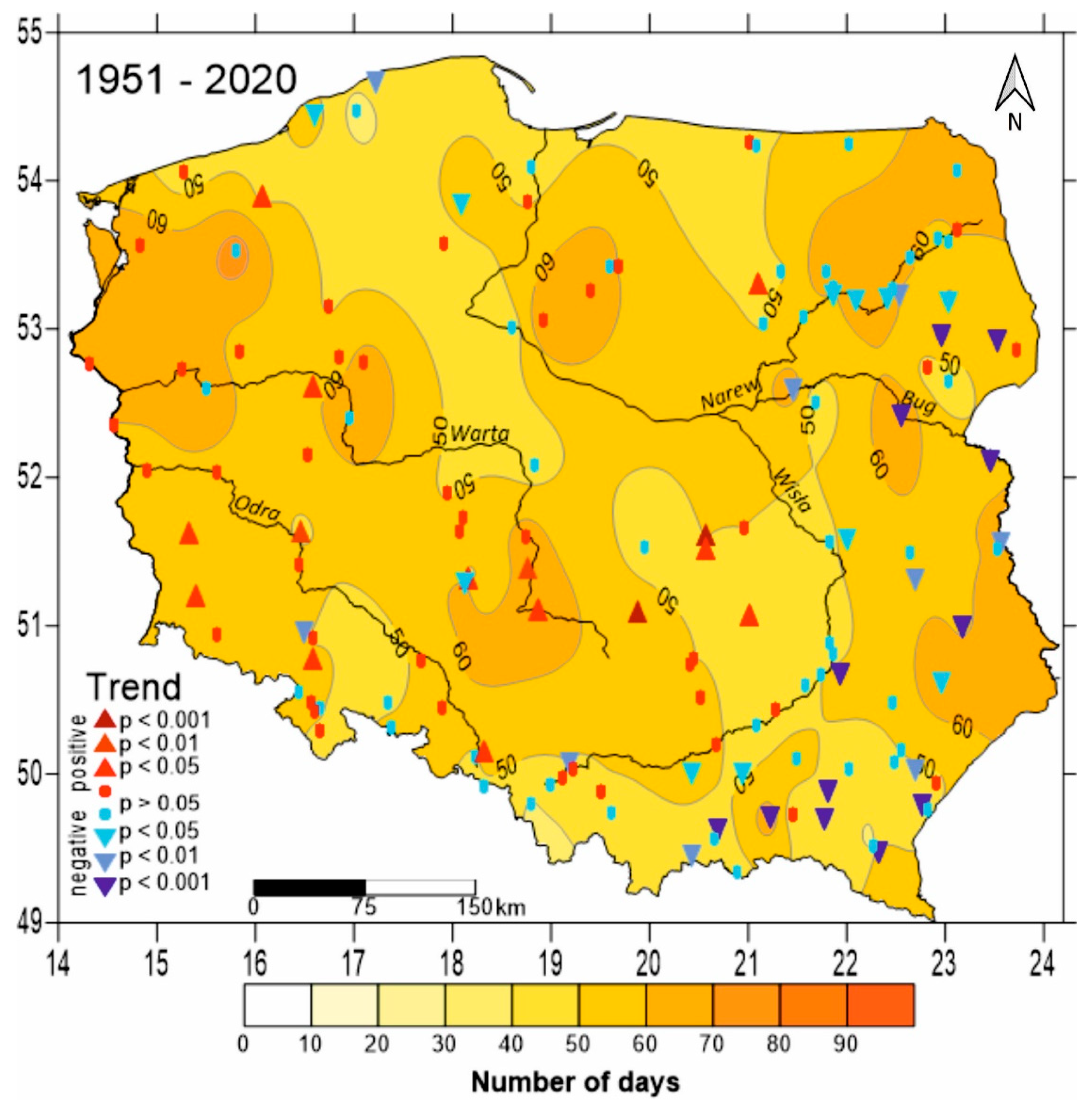
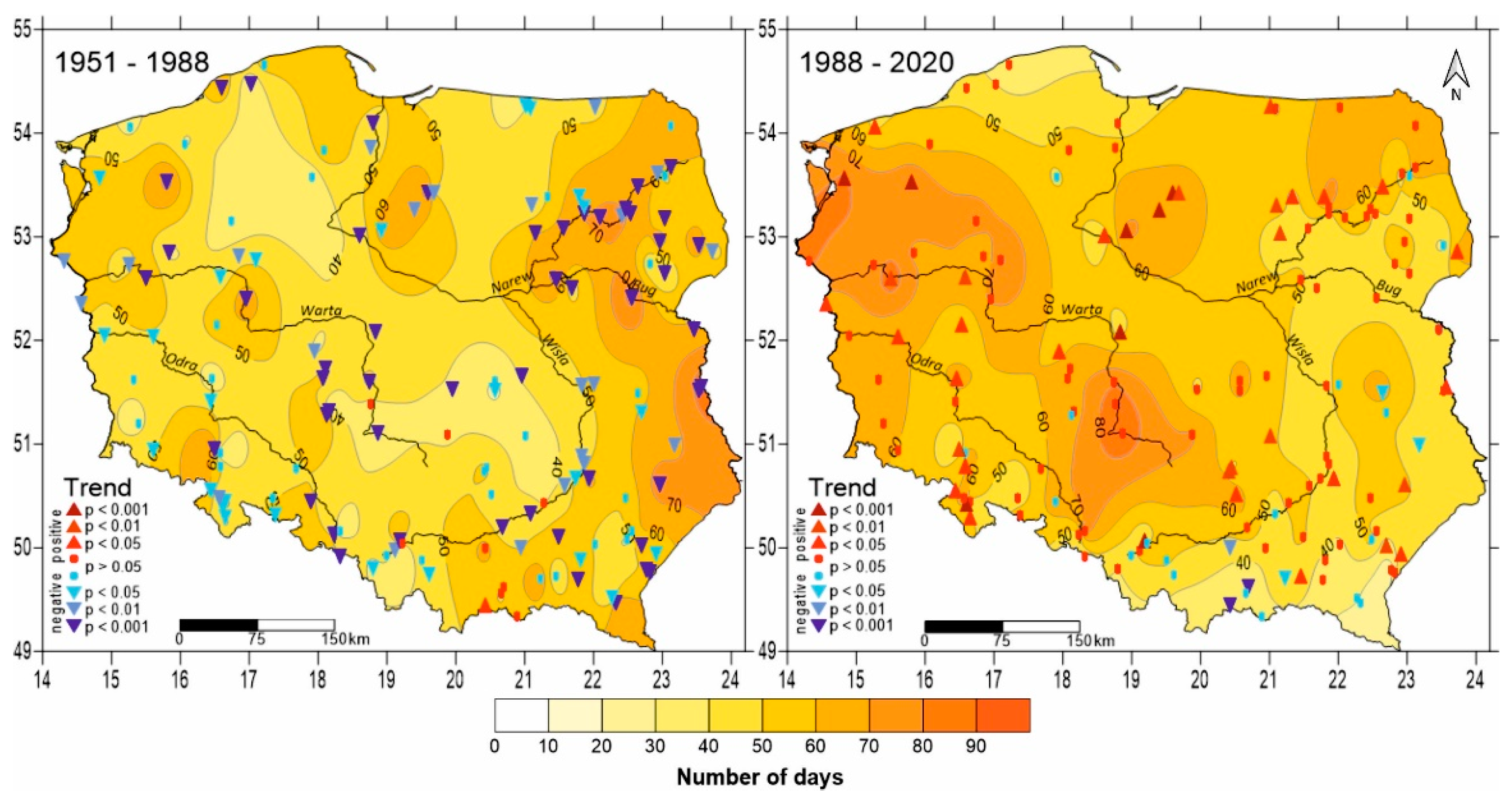
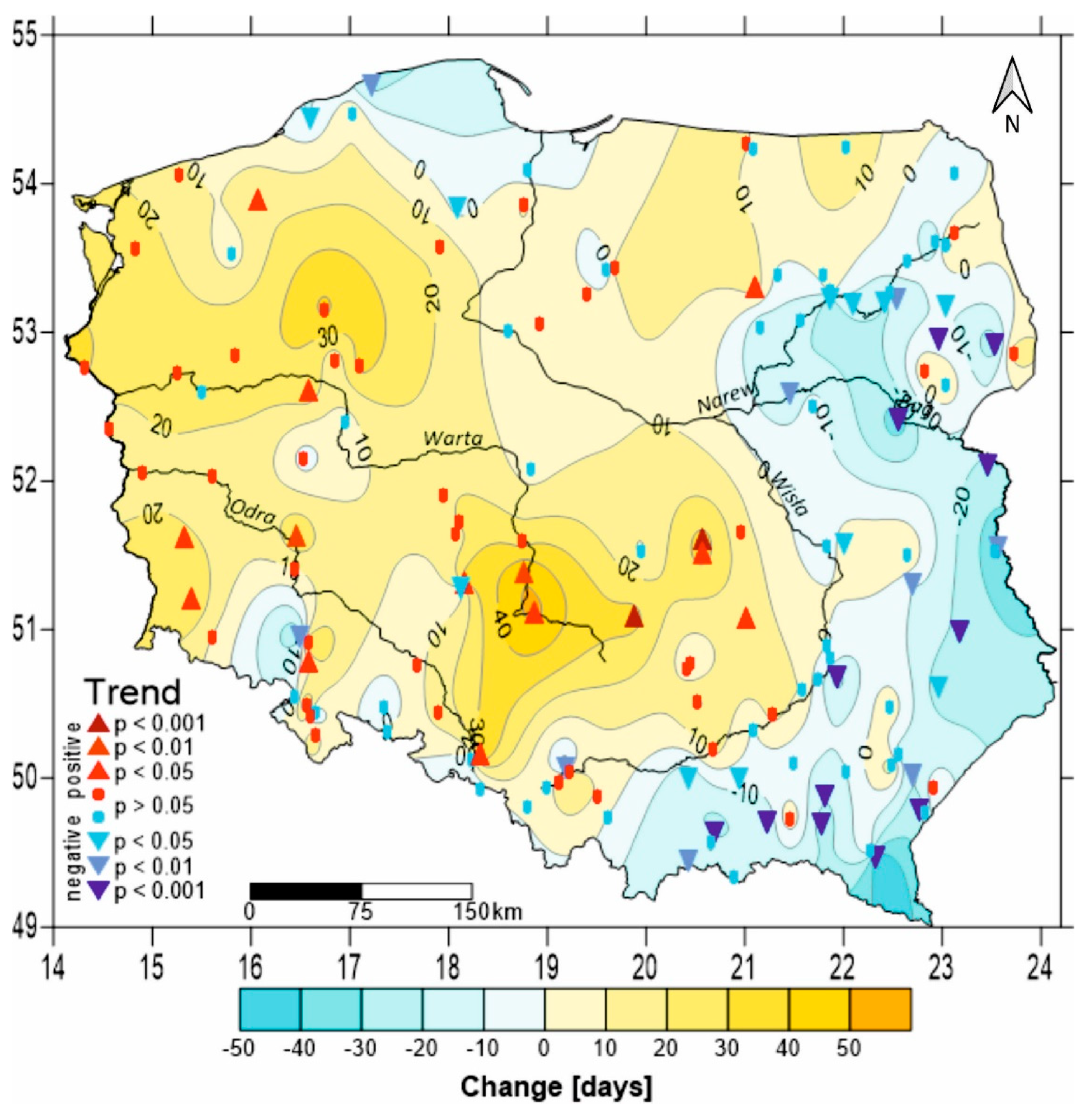
| Principal Component Number | Eigenvalue | % of Explained Variance | Cumulative Eigenvalue | Cumulative Explanation of Variance (%) |
|---|---|---|---|---|
| 1 | 58.019 | 41.442 | 58.019 | 41.442 |
| 2 | 14.277 | 10.198 | 72.296 | 51.640 |
| 3 | 10.182 | 7.273 | 82.478 | 58.913 |
| 4 | 5.428 | 3.877 | 87.907 | 62.790 |
| Eigenvector | % of Explained Variance | PPL | TPL | fPL | NPL | SDPL * | EvPL | NAOW | DG3L |
|---|---|---|---|---|---|---|---|---|---|
| 1 EV | 41.442 | −0.48 0.000 | 0.21 0.084 | −0.57 0.000 | −0.39 0.001 | 0.35 0.004 | 0.51 0.000 | 0.16 0.191 | 0.45 0.000 |
| 2 EV | 10.198 | −0.02 0.852 | 0.56 0.000 | −0.46 0.000 | 0.01 0.971 | 0.45 0.000 | 0.51 0.000 | 0.40 0.001 | 0.40 0.001 |
| 3 EV | 7.273 | 0.05 0.664 | 0.15 0.212 | −0.09 0.439 | 0.13 0.274 | 0.06 0.641 | 0.11 0.362 | 0.34 0.004 | 0.21 0.084 |
| 4 EV | 3.877 | 0.05 0.657 | 0.16 0.197 | 0.24 0.047 | 0.03 0.808 | −0.17 0.162 | −0.26 0.030 | −0.15 0.205 | −0.03 0.823 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wrzesiński, D.; Marsz, A.A.; Sobkowiak, L.; Styszyńska, A. Response of Low Flows of Polish Rivers to Climate Change in 1987–1989. Water 2022, 14, 2780. https://doi.org/10.3390/w14182780
Wrzesiński D, Marsz AA, Sobkowiak L, Styszyńska A. Response of Low Flows of Polish Rivers to Climate Change in 1987–1989. Water. 2022; 14(18):2780. https://doi.org/10.3390/w14182780
Chicago/Turabian StyleWrzesiński, Dariusz, Andrzej A. Marsz, Leszek Sobkowiak, and Anna Styszyńska. 2022. "Response of Low Flows of Polish Rivers to Climate Change in 1987–1989" Water 14, no. 18: 2780. https://doi.org/10.3390/w14182780





