Review of Groundwater Withdrawal Estimation Methods
Abstract
:1. Introduction
2. Methodology
2.1. Search Strategy
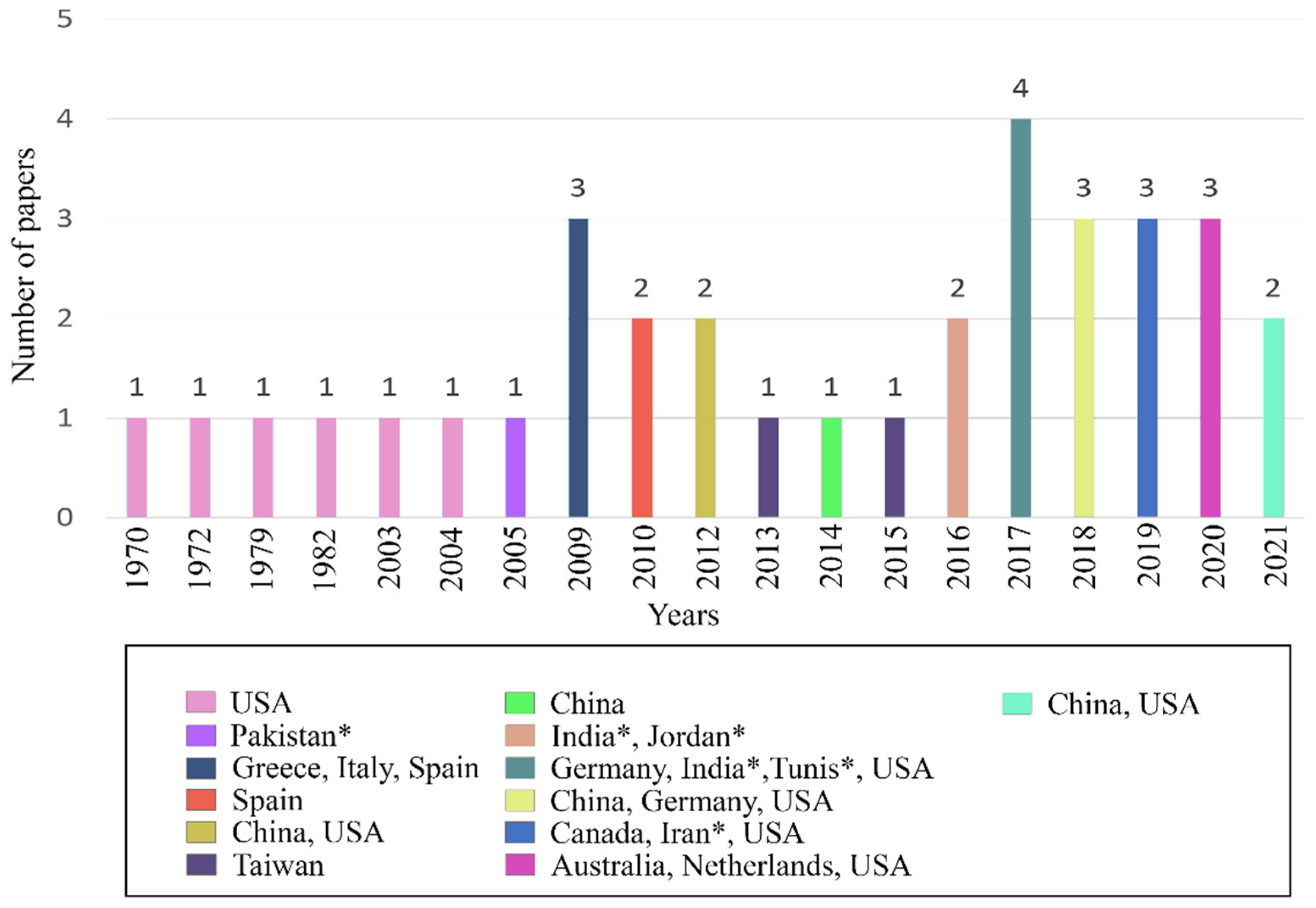
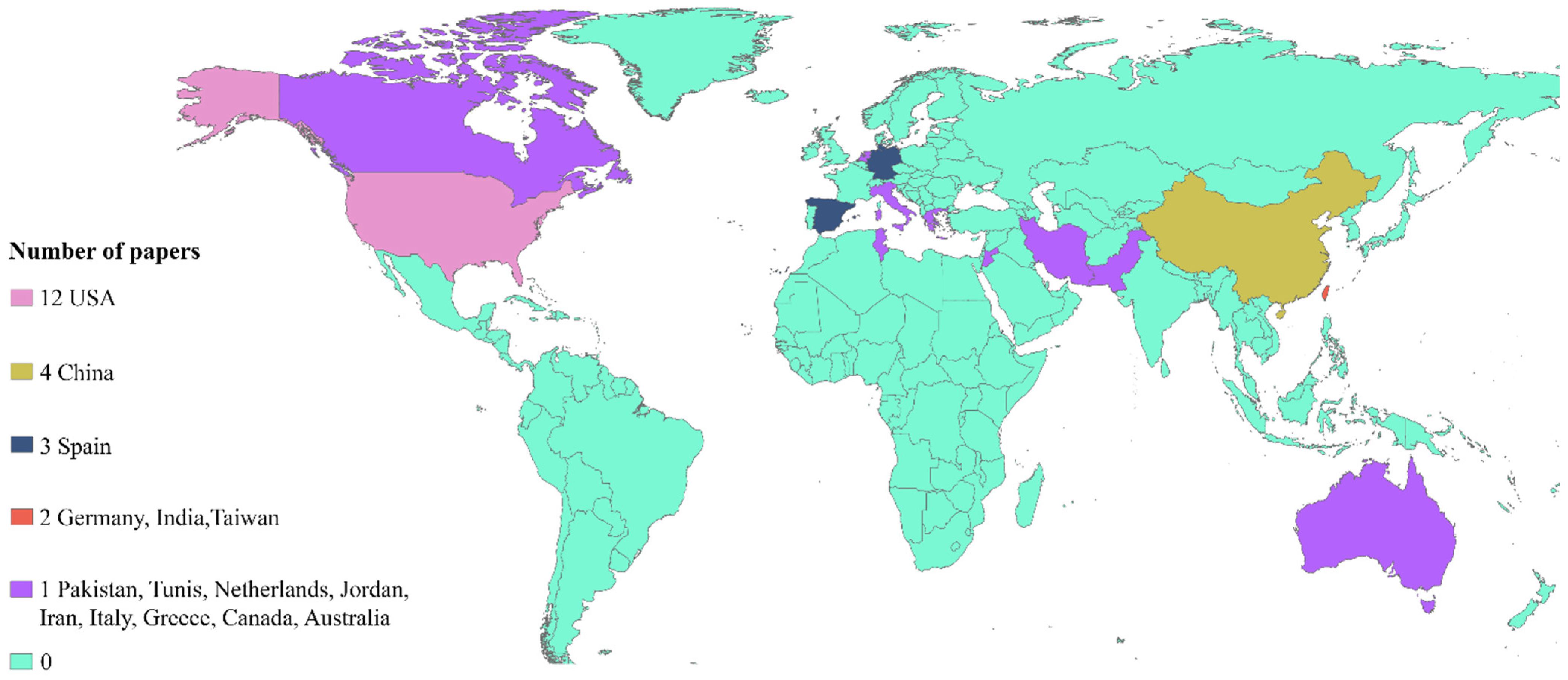
2.2. Screening and Eligibility Results
3. Results
3.1. Direct Approaches to Estimating GWW
3.2. Indirect Approaches to GWW Estimation
4. Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Petronici, F.; Pujades, E.; Jurado, A.; Marcaccio, M.; Borgatti, L. Numerical Modelling of the Mulino Delle Vene Aquifer (Northern Italy) as a Tool for Predicting the Hydrogeological System Behavior under Different Recharge Conditions. Water 2019, 11, 2505. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Döl, P. Will groundwater ease freshwater stress under climate change? Hydrol. Sci. J. 2009, 54, 665–675. [Google Scholar] [CrossRef]
- Martínez-Santos, P.; Castaño-Castaño, S.; Hernández-Espriú, A. Revisiting groundwater overdraft based on the experience of the Mancha Occidental Aquifer, Spain. Appl. Hydrogeol. 2018, 26, 1083–1097. [Google Scholar] [CrossRef]
- FAO. Escasez de Agua: Uno de Los Grandes Retos de Nuestro Tiempo; The Food and Agriculture Organization of the United Nations: Rome, Italy, 2017; Available online: www.fao.org (accessed on 25 September 2021).
- Döll, P.; Hoffmann-Dobrev, H.; Portmann, F.; Siebert, S.; Eicker, A.; Rodell, M.; Strassberg, G.; Scanlon, B. Impact of water withdrawals from groundwater and surface water on continental water storage variations. J. Geodyn. 2012, 59–60, 143–156. [Google Scholar] [CrossRef]
- Famiglietti, J.S.; Lo, M.; Ho, S.L.; Bethune, J.; Anderson, K.J.; Syed, T.H.; Rodell, M. Satellites measure recent rates of groundwater depletion in California’s Central Valley. Geophys. Res. Lett. 2011, 38, L03403. [Google Scholar] [CrossRef]
- Margat, J.; Foster, S.; Droubi, A. Concept and importance of non-renewable resources. In Non-Renewable Groundwater Resources: A Guidebook on Socially-Sustainable Management for Water-Policy Makers; UNESCO: London, UK, 2006. [Google Scholar]
- Amiri, V.; Nakhaei, M.; Lak, R.; Kholghi, M. Assessment of seasonal groundwater quality and potential saltwater intrusion: A study case in Urmia coastal aquifer (NW Iran) using the groundwater quality index (GQI) and hydrochemical facies evolution diagram (HFE-D). Stoch. Environ. Res. Risk Assess. 2016, 30, 1473–1484. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.H.; Van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Chang, F.-J.; Huang, C.-W.; Cheng, S.-T.; Chang, L.-C. Conservation of groundwater from over-exploitation—Scientific analyses for groundwater resources management. Sci. Total Environ. 2017, 598, 828–838. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Hera-Portillo, Á.D.; López-Gutiérrez, J.; Mayor, B.; López-Gunn, E.; Henriksen, H.J.; Gejl, R.N.; Martínez-Santos, P. An Initial Framework for Understanding the Resilience of Aquifers to Groundwater Pumping. Water 2021, 13, 519. [Google Scholar] [CrossRef]
- Ruud, N.; Harter, T.; Naugle, A. Estimation of groundwater pumping as closure to the water balance of a semi-arid, irrigated agricultural basin. J. Hydrol. 2004, 297, 51–73. [Google Scholar] [CrossRef]
- Massuel, S.; Amichi, F.; Ameur, F.; Calvez, R.; Jenhaoui, Z.; Bouarfa, S.; Kuper, M.; Habaieb, H.; Hartani, T.; Hammani, A. Considering groundwater use to improve the assessment of groundwater pumping for irrigation in North Africa. Appl. Hydrogeol. 2017, 25, 1565–1577. [Google Scholar] [CrossRef]
- Luckey, R.R. Analyses of selected statistical methods for estimating groundwater withdrawal. Water Resour. Res. 1972, 8, 205–210. [Google Scholar] [CrossRef]
- Page, M.J.; McKenzie, J.E.; Bossuyt, P.M.; Boutron, I.; Hoffmann, T.C.; Mulrow, C.D.; Shamseer, L.; Tetzlaff, J.M.; Akl, E.A.; Brennan, S.E.; et al. The PRISMA 2020 statement: An updated guideline for reporting systematic reviews. BMJ 2021, 372, n71. [Google Scholar] [CrossRef] [PubMed]
- Bierkens, M.F.P.; Reinhard, S.; De Bruijn, J.A.; Veninga, W.; Wada, Y. The Shadow Price of Irrigation Water in Major Groundwater-Depleting Countries. Water Resour. Res. 2019, 55, 4266–4287. [Google Scholar] [CrossRef]
- Martos-Rosillo, S.; Rodríguez-Rodríguez, M.; Moral, F.; Cruz-Sanjulián, J.J.; Rubio, J.C. Analysis of groundwater mining in two carbonate aquifers in Sierra de Estepa (SE Spain) based on hydrodynamic and hydrochemical data. Appl. Hydrogeol. J. 2009, 17, 1617–1627. [Google Scholar] [CrossRef]
- Forstner, T.; Gleeson, T. Unseen and overlooked: Methods for quantifying groundwater abstraction from different sectors in a data-scarce region, British Columbia, Canada. Can. Water Resour. J. Rev. Can. Ressour. Hydr. 2019, 44, 382–400. [Google Scholar] [CrossRef]
- Vu, H.; Shanafield, M.; Nhat, T.; Partington, D.; Batelaan, O. Mapping catchment-scale unmonitored groundwater abstractions: Approaches based on soft data. J. Hydrol. Reg. Stud. 2020, 30, 100695. [Google Scholar] [CrossRef]
- Tsanis, I.K.; Apostolaki, M.G. Estimating Groundwater Withdrawal in Poorly Gauged Agricultural Basins. Water Resour. Manag. 2009, 23, 1097–1123. [Google Scholar] [CrossRef]
- Yang, L.; Qi, Y.; Zheng, C.; Andrews, C.B.; Yue, S.; Lin, S.; Li, Y.; Wang, C.; Xu, Y.; Li, H. A Modified Water-Table Fluctuation Method to Characterize Regional Groundwater Discharge. Water 2018, 10, 503. [Google Scholar] [CrossRef] [Green Version]
- Bhadra, B.K.; Kumar, S.; Paliwal, R.; Jeyaseelan, A.T. Modeling of groundwater draft based on satellite-derived crop acreage estimation over an arid region of northwest India. Appl. Hydrogeol. 2016, 24, 1681–1698. [Google Scholar] [CrossRef]
- Casa, R.; Rossi, M.; Sappa, G.; Trotta, A. Assessing Crop Water Demand by Remote Sensing and GIS for the Pontina Plain, Central Italy. Water Resour. Manag. 2009, 23, 1685–1712. [Google Scholar] [CrossRef]
- Li, D.; Hu, L.; Zhang, M.; Liu, X. Evaluation of groundwater withdrawals in Tongzhou District, Beijing, China. Hum. Ecol. Risk Assess. Int. J. 2019, 1–17. [Google Scholar] [CrossRef]
- Dubois, C.; Stoffner, F.; Kalia, A.C.; Sandner, M.; Labiadh, M.; Mimouni, M. Copernicus sentinel-2 data for the determination of groundwater withdrawal in the maghreb region. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 37–44. [Google Scholar] [CrossRef]
- Lin, H.-T.; Ke, K.-Y.; Tan, Y.-C.; Wu, S.-C.; Hsu, G.; Chen, P.-C.; Fang, S.-T. Estimating Pumping Rates and Identifying Potential Recharge Zones for Groundwater Management in Multi-Aquifers System. Water Resour. Manag. 2013, 27, 3293–3306. [Google Scholar] [CrossRef]
- Liu, H.-J.; Hsu, N.-S.; Yeh, W.W.-G. Independent component analysis for characterization and quantification of regional groundwater pumping. J. Hydrol. 2015, 527, 505–516. [Google Scholar] [CrossRef]
- Ray, R.K.; Syed, T.H.; Saha, D.; Sarkar, B.C.; Patre, A.K. Assessment of village-wise groundwater draft for irrigation: A field-based study in hard-rock aquifers of central India. Appl. Hydrogeol. 2017, 25, 2513–2525. [Google Scholar] [CrossRef]
- Baker, C.H., Jr. Evaluation of Methods for Estimating Groundwater Withdrawals in Western Kansas; US Geological Survey: Drive Reston, VA, USA, 1979.
- Martínez-Santos, P.; Martínez-Alfaro, P. Estimating groundwater withdrawals in areas of intensive agricultural pumping in central Spain. Agric. Water Manag. 2010, 98, 172–181. [Google Scholar] [CrossRef]
- Castaño, S.; Sanz, D.; Gómez-Alday, J.J. Methodology for Quantifying Groundwater Abstractions for Agriculture via Remote Sensing and GIS. Water Resour. Manag. 2010, 24, 795–814. [Google Scholar] [CrossRef]
- Parizi, E.; Hosseini, S.M.; Ataie-Ashtiani, B.; Simmons, C.T. Representative pumping wells network to estimate groundwater withdrawal from aquifers: Lessons from a developing country, Iran. J. Hydrol. 2019, 578, 124090. [Google Scholar] [CrossRef]
- Su, C.; Cui, Y.L.; Wang, L.C.; Li, L. Estimation of the Groundwater Exploitation Based on Land Subsidence Numerical Model: A Case Study in the Plain Area of Tianjin. Adv. Mater. Res. 2012, 610–613, 2734–2739. [Google Scholar] [CrossRef]
- Al-Bakri, J.T.; Shawash, S.; Ghanim, A.; AbdelKhaleq, R. Geospatial Techniques for Improved Water Management in Jordan. Water 2016, 8, 132. [Google Scholar] [CrossRef]
- Moreo, M.T.; Halford, K.J.; La Camera, R.J.; Laczniak, R.J. Estimated ground-water withdrawals from the Death Valley regional flow system, Nevada and California, 1913–98. Water Resour. Investig. Rep. 2003, 4245. [Google Scholar]
- Shao, J.; Cui, Y.; Hao, Q.; Han, Z.; Cheng, T. Study on the estimation of groundwater withdrawals based on groundwater flow modeling and its application in the North China Plain. J. Earth Sci. 2014, 25, 1033–1042. [Google Scholar] [CrossRef]
- Tillman, F.; Callegary, J.; Nagler, P.; Glenn, E. A simple method for estimating basin-scale groundwater discharge by vegetation in the basin and range province of Arizona using remote sensing information and geographic information systems. J. Arid Environ. 2012, 82, 44–52. [Google Scholar] [CrossRef]
- Wray, J.R. Estimating irrigation water use and withdrawal of ground water on the High Plains, U.S.A. Adv. Space Res. 1982, 2, 127–129. [Google Scholar] [CrossRef]
- Ahmad, M.-U.; Bastiaanssen, W.G.M.; Feddes, R.A. A new technique to estimate net groundwater use across large irrigated areas by combining remote sensing and water balance approaches, Rechna Doab, Pakistan. Appl. Hydrogeol. 2005, 13, 653–664. [Google Scholar] [CrossRef]
- Ogilbee, W.; Mitten, H.T. A Continuing Program for Estimating Ground-Water Pumpage in California–Methods; US Geological Survey: Drive Reston, VA, USA, 1970. [CrossRef]
- Alfaro, P.; Liesch, T.; Goldscheider, N. Modelling groundwater over-extraction in the southern Jordan Valley with scarce data. Appl. Hydrogeol. 2017, 25, 1319–1340. [Google Scholar] [CrossRef]
- Harris, M.A.; Diehl, T.H. A Comparison of Three Federal Datasets for Thermoelectric Water Withdrawals in the United States for 2010. JAWRA J. Am. Water Resour. Assoc. 2017, 53, 1062–1080. [Google Scholar] [CrossRef]
- Majumdar, S.; Smith, R.; Butler, J.J.; Lakshmi, V.J., Jr. Groundwater Withdrawal Prediction Using Integrated Multitemporal Remote Sensing Data Sets and Machine Learning. Water Resour. Res. 2020, 56, e2020WR028059. [Google Scholar] [CrossRef]
- Kent, C.R.; Pandey, S.; Turner, N.; Dickinson, C.G.; Jamieson, M. Estimating current and historical groundwater abstraction from the Great Artesian Basin and other regional-scale aquifers in Queensland, Australia. Appl. Hydrogeol. 2020, 28, 393–412. [Google Scholar] [CrossRef]
- Martindill, J.R.; Good, R.T.; Loge, F.J. Estimating Agricultural Groundwater Withdrawals with Energy Data. J. Water Resour. Plan. Manag. 2021, 147, 04021018. [Google Scholar] [CrossRef]
- Hurr, R.; Litke, D. Estimating Pumping Time and Ground-Water Withdrawals Using Energy–Consumption Data; Department of the Interior, US Geological Survey: Drive Reston, VA, USA, 1989. [CrossRef]
- Austin, C. Reactions: Legislators and Organizations Respond to the Passage of Groundwater Legislation. 2014. Available online: https://mavensnotebook.com/2014/08/30/reactions-legislators-and-organizations-respond-to-the-passage-of-groundwater-legislation/ (accessed on 13 October 2021).
- Richey, A.S.; Thomas, B.F.; Lo, M.-H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef]
- Haiduk, A.; Ishemo, A.A. Energy Demand Considerations for the Supply of Domestic Water in Jamaica. Int. J. Water Resour. Dev. 2011, 27, 759–768. [Google Scholar]
- Karimi, P.; Qureshi, A.S.; Bahramloo, R.; Molden, D. Reducing carbon emissions through improved irrigation and groundwater management: A case study from Iran. Agric. Water Manag. 2012, 108, 52–60. [Google Scholar] [CrossRef]
- Maupin, M.A.; Kenny, J.F.; Hutson, S.S.; Lovelace, J.K.; Barber, N.L.; Linsey, K.S. Estimated Use of Water in the United States in 2010; US Geological Survey: Drive Reston, VA, USA, 2014.
- Diehl, T.H.; Harris, M.A. Withdrawal and Consumption of Water by Thermoelectric Power Plants in the United States, 2010. In Scientific Investigations Report; US Geological Survey: Reston, VA, USA, 2014; p. 38. [Google Scholar]
- Belmonte, A.C.; Jochum, A.M.; García, A.C.; Rodríguez, A.M.; Fuster, P.L. Irrigation management from space: Towards user-friendly products. Irrig. Drain. Syst. 2005, 19, 337–353. [Google Scholar] [CrossRef]
- Zhang, Y.; Gong, H.; Gu, Z.; Wang, R.; Li, X.; Zhao, W. Characterization of land subsidence induced by groundwater withdrawals in the plain of Beijing city, China. Appl. Hydrogeol. 2014, 22, 397–409. [Google Scholar] [CrossRef]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the human contribution to groundwater depletion in the Middle East, from GRACE data, land surface models, and well observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Jones, J.E.; Woodward, C.S. Newton–Krylov-multigrid solvers for large-scale, highly heterogeneous, variably saturated flow problems. Adv. Water Resour. 2001, 24, 763–774. [Google Scholar] [CrossRef]
- Kollet, S.J.; Maxwell, R.M. Capturing the influence of groundwater dynamics on land surface processes using an integrated, distributed watershed model. Water Resour. Res. 2008, 44, W02402. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Yang, Z.L. The common land model (CLM). Bull. Am. Meteorol. Soc. 2003, 84, 1013–1023. [Google Scholar] [CrossRef]
- Thatch, L.M.; Maxwell, R.M.; Gilbert, J.M.; Condon, L.E. Evaluating Groundwater Use and Sustainability in the California Central Valley: Using Remote Sensing Data to Dynamically Constrain Groundwater Extraction Rates in an Integrated Hydrologic Model. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2018; p. H21H-1731. [Google Scholar]
- Thatch, L.M.; Gilbert, J.M.; Maxwell, R.M. Remotely estimating groundwater pumping and irrigation: A synthesis approach using GRACE and advances in integrated hydrologic modeling. In AGU Fall Meeting Abstracts; AGU: Washington, DC, USA, 2019; p. H43M-2225. [Google Scholar]
- Di Salvo, C. Improving Results of Existing Groundwater Numerical Models Using Machine Learning Techniques: A Review. Water 2022, 14, 2307. [Google Scholar] [CrossRef]
- Ch, A.; Ch, R.; Gadamsetty, S.; Iwendi, C.; Gadekallu, T.R.; Ben Dhaou, I. ECDSA-Based Water Bodies Prediction from Satellite Images with UNet. Water 2022, 14, 2234. [Google Scholar] [CrossRef]
- Fienen, M.N.; Nolan, B.T.; Kauffman, L.J.; Feinstein, D.T. Metamodeling for Groundwater Age Forecasting in the Lake Michigan Basin. Water Resour. Res. 2018, 54, 4750–4766. [Google Scholar] [CrossRef]
- Arsene, D.; Predescu, A.; Pahonțu, B.; Chiru, C.G.; Apostol, E.-S.; Truică, C.-O. Advanced Strategies for Monitoring Water Consumption Patterns in Households Based on IoT and Machine Learning. Water 2022, 14, 2187. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Moslemi, K.; Karami, G. Prediction the Groundwater Level of Bastam Plain (Iran) by Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS). Water Resour. Manag. 2014, 28, 5433–5446. [Google Scholar] [CrossRef]
- Güldal, V.; Tongal, H. Comparison of Recurrent Neural Network, Adaptive Neuro-Fuzzy Inference System and Stochastic Models in Eğirdir Lake Level Forecasting. Water Resour. Manag. 2010, 24, 105–128. [Google Scholar] [CrossRef]

| Study | Approach | Study Aquifer/Study Area | Number of Selected Pumping Wells | Scale of the Study | Accuracy of the Method or Characteristics | Method Classifiation |
|---|---|---|---|---|---|---|
| Martos-Rosillo et al. [18] | Time series analysis and numerical groundwater modeling | Lora and Mingo aquifers in Seville, Spain | 3 observation points | Area of smaller than 5 square kilometers | In the Lora aquifer, the mean annual extraction was estimated at 0.342 × 106 m3, and that in the Mingo aquifer was estimated at 0.213 × 106 m3. | Indirect |
| Forstner and Gleeson [19] | Multi-method sectoral approach | British Columbia, Canada | - | The average size of the aquifers varies, depending on the type, between 4 and 27 km2 | Annual distribution of groundwater by sector: agriculture (38%), finfish aquaculture (21%), industry (16%), municipal water distribution systems (15%) and domestic users of private wells (11%). | Indirect |
| Vu et al. [20] | Two approaches: (1) local knowledge through a qualitative field study (of farmers), and (2) land use data combined with local knowledge on cropping and irrigation practices | La Vi River Basin, Vietnam | 77 wells | 100 km2 | For the groundwater balance approach, an absolute error of 42.65 × 106 m3 was calculated, which is equivalent to a relative error of 137% of the estimate. For the land use-based approach, the error estimate was 36.19 × 106 m3, with a resulting range of 0–99.90 × 106 m3. | Indirect |
| Tsanis et al. [21] | Combining surface-water and groundwater potentials using a conceptual rainfall–runoff model (the Sacramento hydrologic model) | Messara Valley, Crete, Greece | 11 climatological stations | 400 km2 | The average error for the entire period 1981–2002 is 20%. | Indirect |
| Yang et al. [22] | Water table fluctuation regression (WTFR) method | Dagu aquifer, coastal area in eastern China | 82 wells | 430 km2 | The RMS of water level in all wells ranged from 0.05 to 0.49 m, with a mean of 0.22 m (0.22 m). | Indirect |
| Bhadra et al. [23] | Three methods: (1) Discharge discharge factor (DF); (2) linear groundwater consumption models (LGDM), and (3) irrigation depth | 70 villages in Sikar district, Rajasthan state, northwest India | 6696 wells to determine the DF and 39 observation wells | 620 km2 | The RMSE with the LGDM model in elevation zones: shallow, intermediate, deep and combined vary between 0.43 and 0.34. | Indirect |
| Casa et al. [24] | Based on crop needs, using GIS and remote sensing techniques in combination with water balance | Pontina Plain in Central Italy | - | 700 km2 | The results of this study estimated a demand of 70 Mm3 per year, i.e., 100 Mm3 per year of irrigation needs if an average irrigation application efficiency of 70% is considered. | Indirect |
| Li et al. [25] | Two methods: (1) the water balance method, and (2) back-propagation artificial neural network (BPANN) | Tongzhou, southeast Beijing | 14 wells | 906 km2 | The water balance method R2 = 0.9914 and the BPANN method R2 = 0.9069. | Indirect |
| Dubois et al. [26] | Approach based on water requirements for crops | Nebhana Plain, northeastern Tunisia | - | 1221 km2 | Accuracy crop classification improves by 10% with multitemporal features. | Indirect |
| Ruud et al. [13] | Water balance model based on geographic information systems (GIS) | Southern San Joaquin Valley, California, USA | - | 2300 km2 | The model estimate has an error of 38%. | Indirect |
| Lin et al. [27] | Groundwater equilibrium model with coupling surface-water (SWAT) and groundwater (MODFLOW) modeling | Multi-aquifer system in an alluvial fan of the Choushui River, Taiwan | The entire aquifer | 2500 km2 | MAE = 5.1%. | Indirect |
| Liu et al. [28] | Two-part approach, Independent Component Analysis (ICA) and groundwater modeling | Aquifer in the Sijhou municipality, in the alluvial fan of the Jhuoshuei River, west-central Taiwan | 136 observation wells | 2562 km2 | The calibration of the groundwater model had an RMSE of 1.00 m. The total amount of groundwater pumped is 37,565 m/day, of which more than 58% is for agriculture and 42% is for industrial use. | Indirect |
| Ray et al. [29] | Approach based on spatio-temporal patterns of groundwater consumption for irrigation | Seonath-Kharun, India | 43 wells | 2867 km2 | Annual estimate of groundwater consumption for irrigation was 212 × 106 m3. | Indirect |
| Baker [30] | Statistical approach, agricultural water uses and electrical measurements | Kansas, USA | 78 wells equipped with flowmeters | 1800 mi2 | Statistical method: the standard deviation was 1.22; estimates of the variance for irrigated area of the total sample was 40.23 and pooled was 0.77. The estimates of the sample variance from energy consumption coefficients was 1.868. | Direct |
| Martínez-Santos and Martínez-Alfaro [31] | Coupling of the water table fluctuation (WTF) method with the groundwater balance equation | Western Mancha Aquifer, Spain | - | 5500 km2 | Average error rate of 10%. | Indirect |
| Castaño et al. [32] | GIS-based method focused on the quantification of withdrawals irrigation | Mancha Oriental, Spain | - | 7260 km2 | Accuracies greater than 95% with a cost 60-fold lower than traditional methods. | Indirect |
| Parizi et al. [33] | This approach called “representative pumping well network” (RPWN) | Three aquifers in Iran: Tehran, Arak and Qazvin | 50 pumping wells for each aquifer | Tehran aquifer with an area of 2250 km2, Arak aquifer with an area of 1945.5 km2 and Qazvin aquifer with an area of 3952.0 km2 | RPWN shows errors between 0.2% and 1.41% with respect to actual RPWN. | Indirect |
| Su et al. [34] | Numerical model coupled with ModFlow2005: groundwater flow and land subsidence | Multi-aquifer system in Tianjin Plain, China | 136, 87, 53, 42, and 4 wells, respectively for each aquifer | 10,600 km2 | The average annual exploitation based on the model was estimated of 8.35 × 108 m3 per year. The average annual exploitation derived from the quota method and statistical data were 9.73 × 108 m3 and 5.45 × 108 m3 per year, respectively. | Indirect |
| Al-Bakri et al. [35] | GIS-based method focused on the quantification of irrigation withdrawals | Three basins in Jordan: Yarmouk, Amman-Zarqa and Azraq | Yarmouk 129 wells, Amman-Zarqa 590 and Azraq 488 wells. | The area of the Yarmouk basin is approximately 1393 km2, the Amman-Zarqa basin has an area of 3600 km2, the Azraq basin has an area of 11,742 km2. | Irrigated crop maps showed good agreement between irrigation maps and soil data, with an overall accuracy of 87%. Groundwater over-extraction was estimated to be between 144% and 360% of the safe yield in the three basins. | Indirect |
| Moreo et al. [36] | Three-dimensional numerical and transient model | 34 study areas in Death Valley region (Nevada and eastern California), USA | 9300 wells | 19,000 mi2 | Error in extractions estimation was 8.3%. | Indirect |
| Shao et al. [37] | Inversion method based on a numerical model | North China Plain (NCP) | 101 observation wells | 139,000 km2 | In a synthetic case with an accuracy of 0.1 m, the average error during 10 years was 1.47% and 1.54% in two pumping subareas. Instead, with an accuracy of 0.01 the average error was 0.06% and 0.13%. The average estimate of the groundwater extraction for the NCP was of 24.92 × 109 m3 per year. | Indirect |
| Tillman et al. [38] | Approach based on crop water requirements | Alluvial basins of southwestern Arizona, USA | - | 190,000 km2 | The annual estimated volume of groundwater discharge by vegetation was between 1.4 and 1.9 million of m3 per year, with an annual mean of 1.6 million of m3. Correlation coefficients between monthly and annual groundwater discharge by vegetation and precipitation were low, (r = 0.182, p > 0.05) and (p > 0.05), respectively. | Indirect |
| Wray [39] | Approach based on water requirements for crops | High Plains, USA | - | 455,000 km2 | Groundwater pumping was sampled in 15 counties in the region. | Indirect |
| Ahmad et al. [40] | GIS-based water balance model | Rechna Doab, Pakistan | - | Area of approximately 2.97 million hectares | The specific yield method produced 65% lower net groundwater use compared to specific yield. | Indirect |
| Ogilbee & Mitten [41] | Two methods: (1) electrical energy consumption, and (2) electrical consumption coefficient | Santa Clara County and Fresno County, California, USA | 200 wells | - | Electricity consumption 4%, 10% for electricity consumption coefficient. | Direct |
| Luckey [15] | Random sampling combined with regression analysis | Arkansas River Valley in southeastern Colorado, USA | 225 wells | - | Estimation of the standard error, 14% for random sampling and 10% for regression analysis. | Direct |
| Alfaro et al. [42] | Numerical model-based approach and crop water requirements | Eastern part of the Lower Jordan Valley southern part | 6 wells | - | Pearson correlation coefficient (R), calculated versus measured values of 0.90 and 0.97, for the calibration period. | Indirect |
| Harris and Diehl [43] | The USGS model is compared to two source data, the EIA (Energy Information Administration) and the USGS compilation | Groundwater-fired power plants in USA | 470 plants for the USGS compilation; 742 plants the EIA | - | Error percentage of the estimates was 17% for EIA and 24.6% for USGS compilation. | Direct |
| Massuel et al. [14] | Direct measurement methods and adaptive methodology that sought to involve the users | Three locations in North Africa (Morocco, Tunisia and Algeria) | Saïss 430 wells; Kairouan 928 wells, and Ziban 1255 wells | - | Water pumping in Saïss has a −20% of discrepancy compared with the developed method. The average annual pumping time in Kairouan was 4300 h/year corresponding to a calculated average annual volume of 71,000 m3/year. At Ghrouss, the annual groundwater abstraction was estimated in 170 hm3/year. | Direct |
| Majumdar et al. [44] | Holistic approach combining water balance components with a machine learning model | The High Plains Aquifer (HPA), located in the central United States | - | - | In a test case, the method predicted groundwater withdrawals with R2 ≈ 0.23, MAE ≈ 16.01 mm, RMSE ≈ 31.51 mm and normalized MAE ≈ 0.84. | Indirect |
| Kent et al. [45] | Approach based on historical records and data hierarchy to establish the number of wells and their extraction characteristics | Extent of catchments associated with the Great Artesian Basin (GAB) and other regional-scale groundwater basins in Queensland, Australia | 96,174 drill holes | - | Current GAB groundwater use in Queensland was estimated at 322 GL/year. | Indirect |
| Martindill et al. [46] | Ratio-based approach between pump energy consumption and Efficiency Lift Method (ELM) | San Joaquin Valley, California, USA | 30 wells studied from 2010 to 2015 | - | For individual tests, MAE = 13.5%; per month, MAE = 5%. | Direct |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meza-Gastelum, M.A.; Campos-Gaytán, J.R.; Ramírez-Hernández, J.; Herrera-Oliva, C.S.; Villegas-León, J.J.; Figueroa-Núñez, A. Review of Groundwater Withdrawal Estimation Methods. Water 2022, 14, 2762. https://doi.org/10.3390/w14172762
Meza-Gastelum MA, Campos-Gaytán JR, Ramírez-Hernández J, Herrera-Oliva CS, Villegas-León JJ, Figueroa-Núñez A. Review of Groundwater Withdrawal Estimation Methods. Water. 2022; 14(17):2762. https://doi.org/10.3390/w14172762
Chicago/Turabian StyleMeza-Gastelum, Marco Antonio, José Rubén Campos-Gaytán, Jorge Ramírez-Hernández, Claudia Soledad Herrera-Oliva, José Juan Villegas-León, and Alejandro Figueroa-Núñez. 2022. "Review of Groundwater Withdrawal Estimation Methods" Water 14, no. 17: 2762. https://doi.org/10.3390/w14172762







