A Hybrid Spatial–Analytical Network Process Model for Groundwater Inventory in a Semi-Arid Hard Rock Aquifer System—A Case Study
Abstract
:1. Introduction
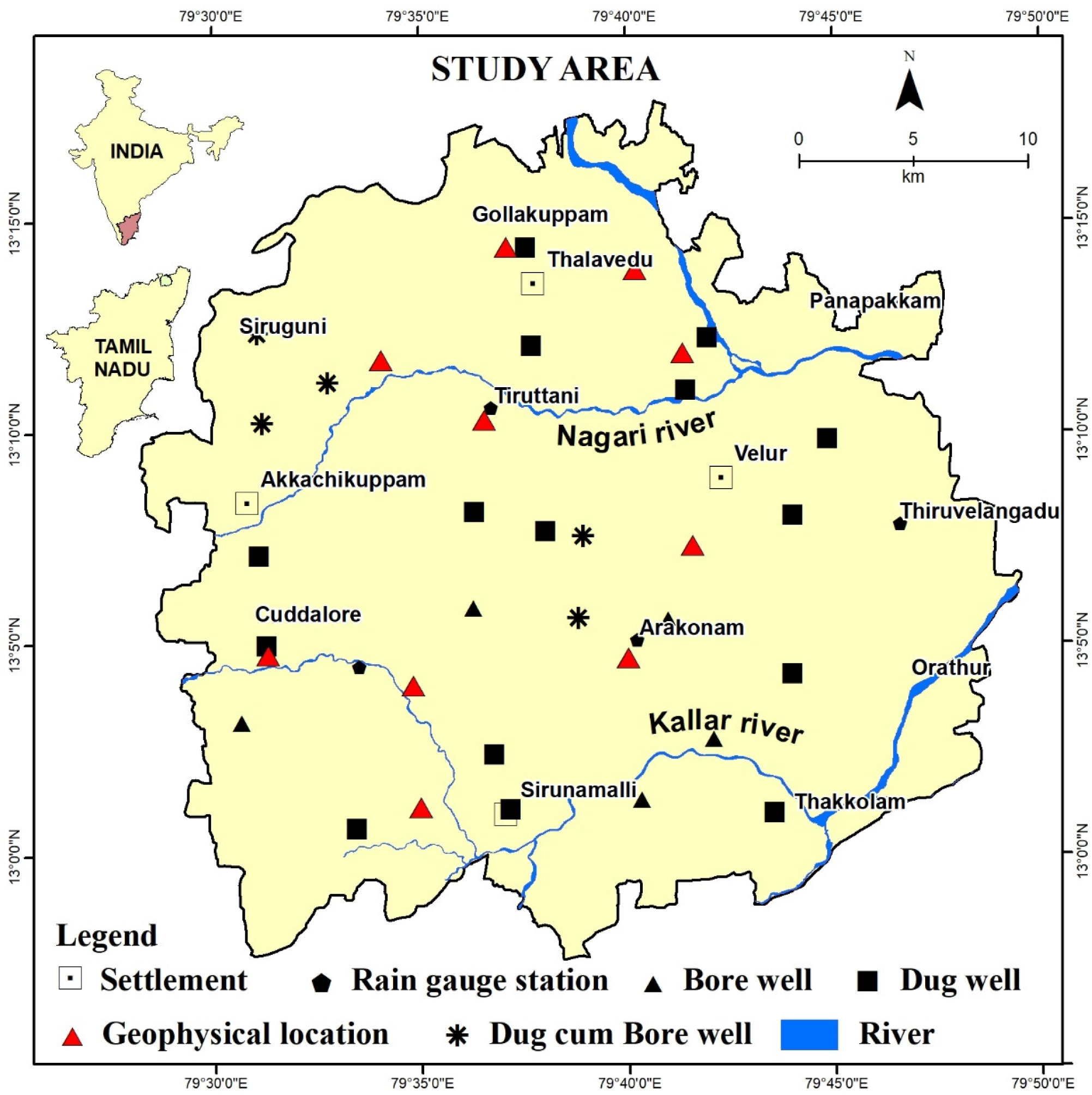
2. Description of the Study Area
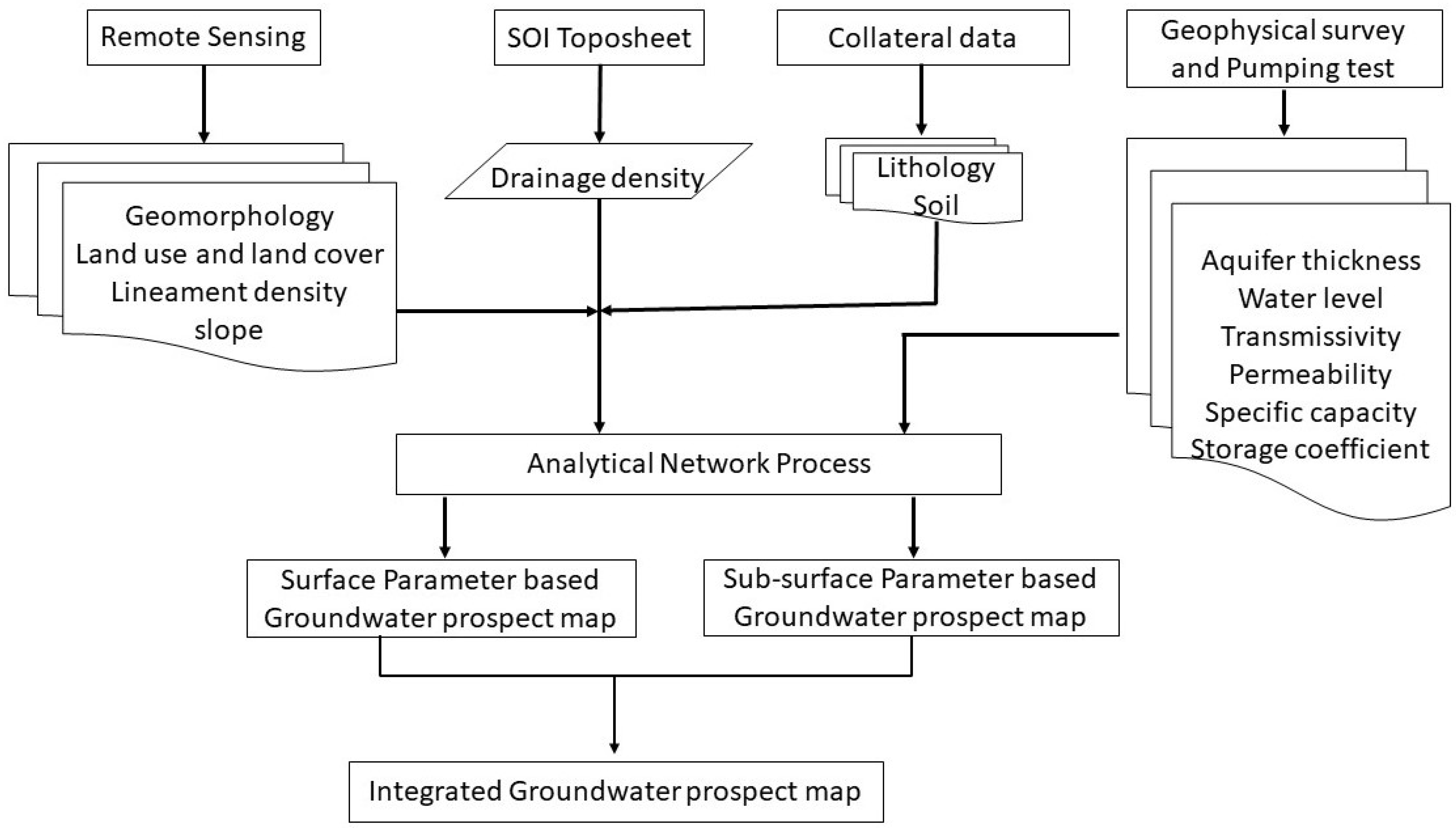
3. Material and Methods
3.1. Constructing Thematic Layers
3.2. Analytical Network Process Model
4. Database on Factors Influencing Groundwater Potential
4.1. Surface Parameters
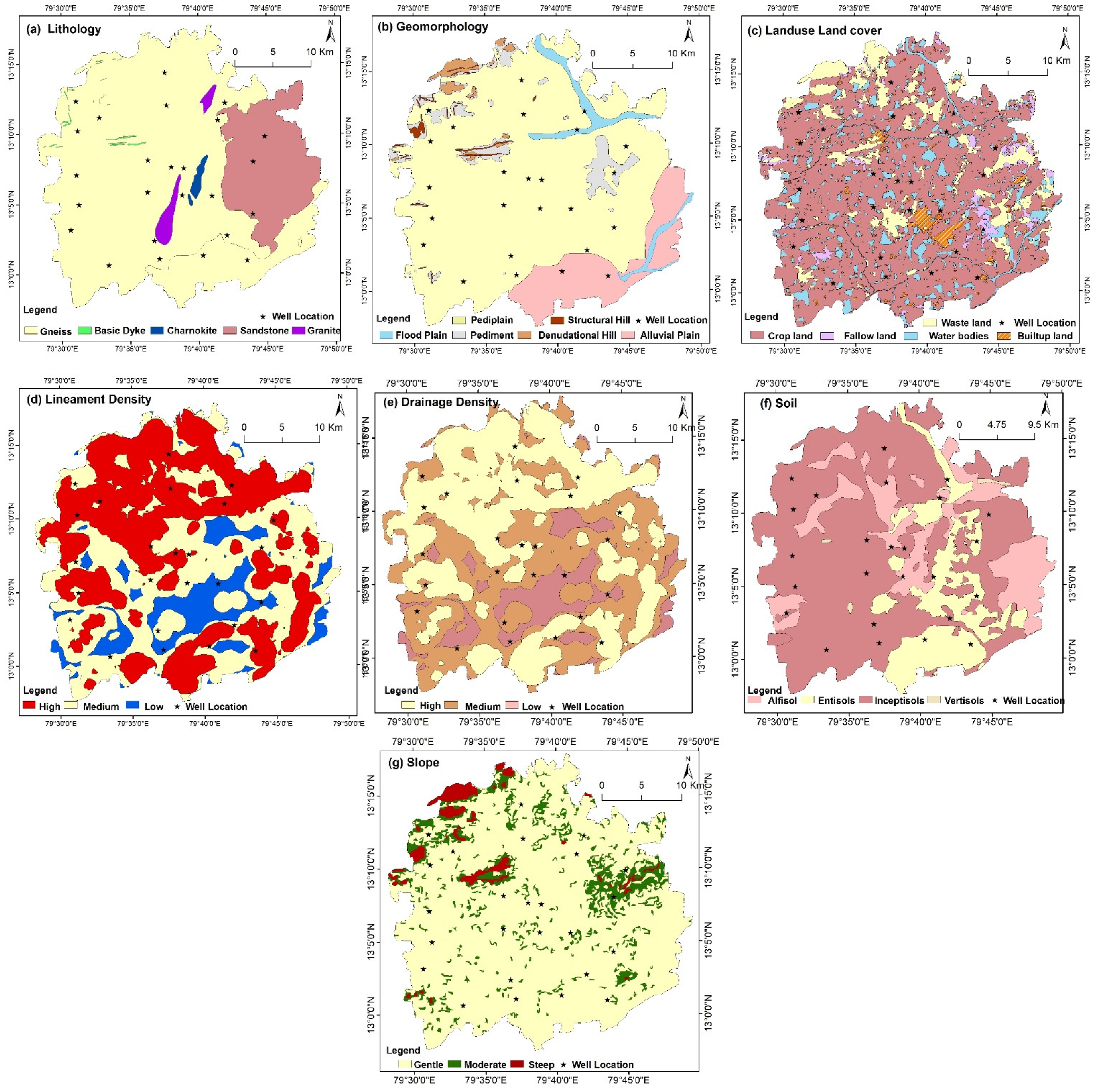
4.1.1. Lithology
4.1.2. Geomorphology
4.1.3. Land Use and Land Cover
4.1.4. Lineament Density
4.1.5. Drainage Density
4.1.6. Soil
4.1.7. Slope
4.2. Subsurface Parameters
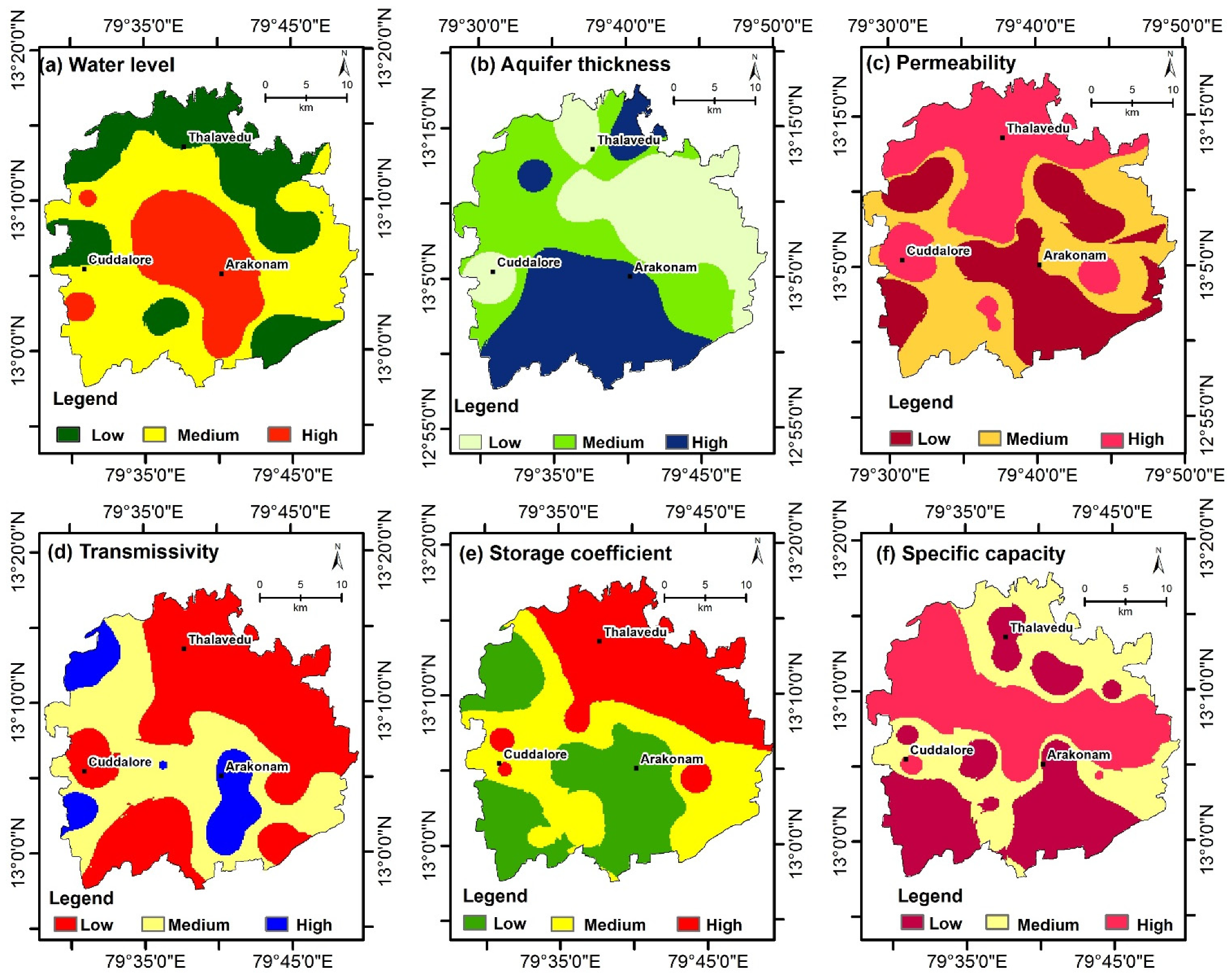
4.2.1. Water Level
4.2.2. Aquifer Thickness
4.2.3. Permeability
4.2.4. Transmissivity
4.2.5. Storage Coefficient
4.2.6. Specific Capacity
5. Results and Discussion
5.1. Mapping Potential Groundwater Zones
5.2. Validation of Results
5.2.1. Spatial Correlation between Water Level and Surface Parameters-Based Groundwater Potential Zones
5.2.2. Spatial Correlation between Water Level and Subsurface Parameters-Based Groundwater Potential Zones
5.2.3. Spatial Correlation between Water Level and Integrated Groundwater Potential Zones
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Milly, P.C.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef]
- Okello, C.; Tomasello, B.; Greggio, N.; Wambiji, N.; Antonellini, M. Impact of Population Growth and Climate Change on the Freshwater Resources of Lamu Island, Kenya. Water 2015, 7, 1264–1290. [Google Scholar] [CrossRef]
- Hoekstra, A.Y.; Chapagain, A.K. Water footprints of nations: Water use by people as a function of their consumption pattern. In Integrated Assessment of Water Resources and Global Change; Springer: Dordrecht, The Netherlands, 2006; pp. 35–48. [Google Scholar] [CrossRef]
- Wada, Y.; Bierkens, M.F.; De Roo, A.; Dirmeyer, P.A.; Famiglietti, J.S.; Hanasaki, N.; Wheater, H. Human–water interface in hydrological modelling: Current status and future directions. Hydrol. Earth Syst. Sci. 2017, 21, 4169–4193. [Google Scholar] [CrossRef]
- Boretti, A.; Rosa, L. Reassessing the projections of the World Water Development Report. NPJ Clean Water 2019, 2, 15. [Google Scholar] [CrossRef]
- Pykhtin, A.I. Problems of rational use and protection of groundwater within the Russian Federation. J. Appl. Eng. Sci. 2019, 17, 3. [Google Scholar]
- Gleeson, T.; Wada, Y.; Bierkens, M.F.; Van Beek, L.P. Water balance of global aquifers revealed by groundwater footprint. Nature 2012, 488, 197–200. [Google Scholar] [CrossRef] [PubMed]
- World Bank. India Groundwater: A Valuable but Diminishing Resource. 2012. Available online: https://www.worldbank.org/en/news/feature/2012/03/06/india-groundwater-critical-diminishing (accessed on 6 November 2020).
- MoWR. Annual Report 2020-21. 2021. Available online: https://dpiit.gov.in/sites/default/files/annualReport-English2020-21.pdf (accessed on 10 April 2021).
- Srinivasan, V.; Thompson, S.; Madhyastha, K.; Penny, G.; Jeremiah, K.; Lele, S. Why is the Arkavathy River drying? A multiple-hypothesis approach in a data-scarce region. Hydrol. Earth Syst. Sci. 2015, 19, 1905–1917. [Google Scholar] [CrossRef]
- Penny, G.; Srinivasan, V.; Dronova, I.; Lele, S.; Thompson, S. Spatial characterization of long-term hydrological change in the Arkavathy watershed adjacent to Bangalore, India. Hydrol. Earth Syst. Sci. 2018, 22, 595–610. [Google Scholar] [CrossRef]
- Grasso, V. 2020 State of Climate Services Report: Risk Information and Early Warning Systems. In Proceedings of the EGU General Assembly Conference Abstracts 2021, EGU21-74, Vienna, Austria, 19–30 April 2021. [Google Scholar]
- Wada, Y.; van Beek, L.P.; Bierkens, M.F. Nonsustainable groundwater sustaining irrigation: A global assessment. Water Resour. Res. 2012, 48, W00L06. [Google Scholar] [CrossRef]
- MacDonald, A.M.; Bonsor, H.C.; Ahmed, K.M.; Burgess, W.G.; Basharat, M.; Calow, R.C.; Dixit, A.; Foster, S.S.D.; Gopal, K.; Lapworth, D.J.; et al. Groundwater quality and depletion in the Indo-Gangetic Basin mapped from in situ observations. Nat. Geosci. 2016, 9, 762–766. [Google Scholar] [CrossRef]
- Mishra, V.; Asoka, A.; Vatta, K.; Lall, U. Groundwater depletion and associated CO2 emissions in India. Earth’s Future 2018, 6, 1672–1681. [Google Scholar] [CrossRef]
- Luo, P.; Kang, S.; Zhou, M.; Lyu, J.; Aisyah, S.; Binaya, M.; Regmi, R.K.; Nover, D. Water quality trend assessment in Jakarta: A rapidly growing Asian megacity. PLoS ONE 2019, 14, e0219009. [Google Scholar] [CrossRef]
- Russo, T.A.; Lall, U. Depletion and response of deep groundwater to climate-induced pumping variability. Nat. Geosci. 2017, 10, 105–108. [Google Scholar] [CrossRef]
- MacDonald, A.; Davies, J.; Calow, R.; Chilton, J. Developing groundwater: A guide for rural water supply. In NERC Open Research Archive; ITDG Publishing: Rugby, UK, 2005. [Google Scholar]
- Porsani, J.L.; Elis, V.R.; Hiodo, F.Y. Geophysical investigations for the characterization of fractured rock aquifers in Itu, SE Brazil. J. Appl. Geophys. 2005, 57, 119–128. [Google Scholar] [CrossRef]
- Anomohanran, O.; Ofomola, M.O.; Okocha, F.O. Investigation of groundwater in parts of Ndokwa District in Nigeria using geophysical logging and electrical resistivity methods: Implications for groundwater exploration. J. Afr. Earth Sci. 2017, 129, 108–116. [Google Scholar] [CrossRef]
- Cook, P.G.; Walker, G.R.; Jolly, I.D. Spatial variability of groundwater recharge in a semiarid region. J. Hydrol. 1989, 111, 195–212. [Google Scholar] [CrossRef]
- Selvam, S.; Sivasubramanian, P. Groundwater potential zone identification using geoelectrical survey: A case study from Medak district, Andhra Pradesh, India. Int. J. Geomat. Geosci. 2012, 3, 55. [Google Scholar]
- Solomon, S.; Quiel, F. Groundwater study using remote sensing and geographic information systems (GIS) in the central highlands of Eritrea. Hydrogeol. J. 2006, 14, 1029–1041. [Google Scholar] [CrossRef]
- Kudamnya, E.A.; Edet, A.E.; Ekwere, A.S. Advances in Sustainable and Environmental Hydrology, Hydrogeology, Hydrochemistry and Water Resources. In Proceedings of the 1st Springer Conference of the Arabian Journal of Geosciences (CAJG-1), Tunisia, North Africa, 25–28 November 2019; pp. 249–252. [Google Scholar]
- Ozdemir, A. GIS-based groundwater spring potential mapping in the Sultan Mountains (Konya, Turkey) using frequency ratio, weights of evidence and logistic regression methods and their comparison. J. Hydrol. 2011, 411, 290–308. [Google Scholar] [CrossRef]
- Pourtaghi, Z.S.; Pourghasemi, H.R. GIS-based groundwater spring potential assessment and mapping in the Birjand Township, southern Khorasan Province, Iran. Hydrogeol. J. 2014, 22, 643–662. [Google Scholar] [CrossRef]
- Chenini, I.; Ben Mammou, A. Groundwater recharge study in arid region: An approach using GIS techniques and numerical modeling. Comput. Geosci. 2010, 36, 801–817. [Google Scholar] [CrossRef]
- Corsini, A.; Cervi, F.; Ronchetti, F. Weight of evidence and artificial neural networks for potential groundwater spring mapping: An application to the Mt. Modino area (Northern Apennines, Italy). Geomorphology 2009, 111, 79–87. [Google Scholar] [CrossRef]
- Naghibi, S.A.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Rezaei, A. Groundwater qanat potential mapping using frequency ratio and Shannon’s entropy models in the Moghan watershed, Iran. Earth Sci. Inform. 2015, 8, 171–186. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.K.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Mehdinejadiani, B.; Ramezani Etedali, H.; Brouziyne, Y.; Towfiqul Islam, A.R.M.; et al. Prediction of combined terrestrial evapotranspiration index (Ctei) over large river basin based on machine learning approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Saraf, A.K.; Choudhury, P.R. Integrated remote sensing and gis for groundwater exploration and identification of artificial recharge sites. Int. J. Remote Sens. 1998, 19, 1825–1841. [Google Scholar] [CrossRef]
- Thakur, G.S.; Raghuwanshi, R.S. Perspect and assessment of groundwater resources using remote sensing techniques in and around Choral river basin, Indore and Khargone districts, M.P. J. Indian Soc. Remote Sens. 2008, 36, 217–225. [Google Scholar] [CrossRef]
- Dar, I.A.; Sankar, K.; Dar, M.A. Deciphering groundwater potential zones in hard rock terrain using geospatial technology. Environ. Monit. Assess. 2011, 173, 597–610. [Google Scholar] [CrossRef]
- Oikonomidis, D.; Dimogianni, S.; Kazakis, N.; Voudouris, K. A GIS/Remote Sensing-based methodology for groundwater potentiality assessment in Tirnavos area, Greece. J. Hydrol. 2015, 525, 197–208. [Google Scholar] [CrossRef]
- Magesh, N.S.; Chandrasekar, N.; Soundranayagam, J.P. Delineation of groundwater potential zones in Theni district, Tamil Nadu, using remote sensing, GIS and MIF techniques. Geosci. Front. 2012, 3, 189–196. [Google Scholar] [CrossRef]
- Saravanan, S.; Pitchaikani, S.; Venkatesan, G. Assessment and evaluation of groundwater vulnerability index maps of Upper Palar River Basin, Tamilnadu, India. J. Earth Syst. Sci. 2020, 129, 1–13. [Google Scholar] [CrossRef]
- Gumma, M.K.; Pavelic, P. Mapping of groundwater potential zones across Ghana using remote sensing, geographic information systems, and spatial modeling. Environ. Monit. Assess. 2013, 185, 3561–3579. [Google Scholar] [CrossRef] [PubMed]
- Senanayake, I.P.; Dissanayake, D.M.D.O.K.; Puswewala, U.G.A. Analysis of the abundance of abandoned tanks in Hambantota District, Sri Lanka using GIS techniques. Egypt. J. Remote Sens. Space Sci. 2012, 15, 143–150. [Google Scholar] [CrossRef]
- Kumar, T.; Gautam, A.K.; Kumar, T. Appraising the accuracy of GIS-based Multi-criteria decision making technique for delineation of Groundwater potential zones. Water Resour. Manag. 2014, 28, 4449–4466. [Google Scholar] [CrossRef]
- Rahmati, O.; Nazari Samani, A.; Mahdavi, M.; Pourghasemi, H.R.; Zeinivand, H. Groundwater potential mapping at Kurdistan region of Iran using analytic hierarchy process and GIS. Arab. J. Geosci. 2015, 8, 7059–7071. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Jenifer, M.A.; Jha, M.K. Comparison of Analytic Hierarchy Process, Catastrophe and Entropy techniques for evaluating groundwater prospect of hard-rock aquifer systems. J. Hydrol. 2017, 548, 605–624. [Google Scholar] [CrossRef]
- Kamaraju, M.V.V.; Bhattacharya, A.; Reddy, G.S.; Rao, G.C.; Murthy, G.S.; Rao, T.C.M. Ground–Water Potential Evaluation of West Godavari District, Andhra Pradesh State, India—A GIS Approach. Ground Water 1996, 34, 318–325. [Google Scholar] [CrossRef]
- Shaban, A.; Khawlie, M.; Abdallah, C. Use of remote sensing and GIS to determine recharge potential zones: The case of Occidental Lebanon. Hydrogeol. J. 2011, 14, 433–443. [Google Scholar] [CrossRef]
- Manap, M.A.; Sulaiman, W.N.A.; Ramli, M.F.; Pradhan, B.; Surip, N. A knowledge-driven GIS modeling technique for groundwater potential mapping at the Upper Langat Basin, Malaysia. Arab. J. Geosci. 2013, 6, 1621–1637. [Google Scholar] [CrossRef]
- Trabelsi, F.; Lee, S.; Khlifi, S.; Arfaoui, A. Frequency Ratio Model for Mapping Groundwater Potential Zones Using GIS and Remote Sensing; Medjerda Watershed Tunisia. In Advances in Sustainable and Environmental Hydrology, Hydrogeology, Hydrochemistry and Water Resources; Springer: Berlin/Heidelberg, Germany, 2019; pp. 341–345. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process. In European Journal of Operational Research; McGraw-Hill: New York, NY, USA, 1982; Volume 9, pp. 97–98. [Google Scholar]
- Rajani, R.; Palanivel, K.; Selvakumar, R. Delineation of Groundwater Potential Zones Using Subsurface Parameters: An ANP Approach in and Around Tiruttani Area, Tamilnadu, India. Int. J. Pure Appl. Math. 2018, 119, 575–587. [Google Scholar]
- Siva, G.; Nasir, N.; Selvakumar, R. Delineation of Groundwater Potential Zone in Sengipatti for Thanjavur District using Analytical Hierarchy Process. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Sanya, China, 20–22 November 2017; Volume 80. [Google Scholar]
- Sujatha, E.R. A spatial model for the assessment of debris flow susceptibility along the Kodaikkanal-Palani traffic corridor. Front. Earth Sci. 2020, 14, 326–343. [Google Scholar] [CrossRef]
- Gebru, H.; Gebreyohannes, T.; Hagos, E. Identification of Groundwater Potential Zones Using Analytical Hierarchy Process (AHP) and GIS-Remote Sensing Integration, the Case of Golina River Basin, Northern Ethiopia. Int. J. Adv. Remote Sens. GIS 2020, 9, 3289–3311. [Google Scholar] [CrossRef]
- Meade, L.; Sarkis, J. Strategic analysis of logistics and supply chain management systems using the analytical network process. Transp. Res. Part E Logist. Transp. Rev. 1998, 34E, 201–215. [Google Scholar] [CrossRef]
- Sujatha, E.R.; Sridhar, V. Mapping debris flow susceptibility using analytical network process in Kodaikkanal Hills, Tamil Nadu (India). J. Earth Syst. Sci. 2017, 126, 116. [Google Scholar] [CrossRef]
- Saraf, A.K.; Choudhury, P.R.; Roy, B.; Sarma, B.; Vijay, S.; Choudhury, S. GIS based surface hydrological modelling in identification of groundwater recharge zones. Int. J. Remote Sens. 2004, 25, 5759–5770. [Google Scholar] [CrossRef]
- NRSC, I. Manual of National Land Use/Land Cover Mapping (Second Cycle) Using Multi Temporal Satellite Data; Department of Space, Hyderabad: Hyderabad, India, 2012.
- Abdalla, F. Mapping of groundwater prospective zones using remote sensing and GIS techniques: A case study from the Central Eastern Desert, Egypt. J. Afr. Earth Sci. 2012, 70, 8–17. [Google Scholar] [CrossRef]
- Krishnamurthy, J.; Mani, A.; Jayaraman, V.; Manivel, M. Groundwater resources development in hard rock terrain—An approach using remote sensing and GIS techniques. ITC J. 2000, 2, 204–215. [Google Scholar] [CrossRef]
- Kale, V.S.; Gupta, A. Introduction to Geomorphology; Orient Longman: Hyderabad, India, 2001. [Google Scholar]
- Rajaveni, S.P.; Brindha, K.; Elango, L. Geological and geomorphological controls on groundwater occurrence in a hard rock region. Appl. Water Sci. 2017, 7, 1377–1389. [Google Scholar] [CrossRef]
- Yeh, H.F.; Cheng, Y.S.; Lin, H.I.; Lee, C.H. Mapping groundwater recharge potential zone using a GIS approach in Hualian River, Taiwan. Sustain. Environ. Res. 2016, 26, 33–43. [Google Scholar] [CrossRef]
- Duiker, S.W.; Flanagan, D.C.; Lal, R. Erodibility and infiltration characteristics of five major soils of southwest Spain. Catena 2001, 45, 103–121. [Google Scholar] [CrossRef]
- Ballukraya, P.N.; Sharma, K.K. Estimation of Storativity from Recovery Data. Groundwater 1991, 29, 495–498. [Google Scholar] [CrossRef]
- Banton, O.; Bangoy, L.M. A New Method to Determine Storage Coefficient from Pumping Test Recovery Data. Ground Water 1996, 34, 772–777. [Google Scholar] [CrossRef]
- Sanders, L.L. Field Hydrogeology; Prentice Hall: Englewood Cliffs, NJ, USA, 1998. [Google Scholar]
- Hassan, H.; Waru, S.M.; Bukar, G.A.; Abdullahi, K.M. Groundwater Potentials Estimation of a Basement Terrain Using Pumping Test Data for Parts of Sanga Local Government Area, Kaduna State, Northwestern Nigeria. Open J. Mod. Hydrol. 2016, 06, 222–229. [Google Scholar] [CrossRef]
- Suganthi, S.; Elango, L.; Subramanian, S.K. Groundwater potential zonation by remote sensing and GIS techniques and its relation to the groundwater level in the coastal part of the Arani and Koratalai river basin, Southern India. Earth Sci. Res. J. 2013, 17, 87–95. [Google Scholar]
- Da Costa, A.M.; de Salis, H.H.C.; Viana, J.H.M.; Pacheco, F.A.L. Groundwater recharge potential for sustainable water use in urban areas of the Jequitiba River Basin, Brazil. Sustainability 2019, 11, 2955. [Google Scholar] [CrossRef]
- Hasan, M.; Shang, Y.; Jin, W.; Akhter, G. Estimation of hydraulic parameters in a hard rock aquifer using integrated surface geoelectrical method and pumping test data in southeast Guangdong, China. Geosci. J. 2021, 25, 223–242. [Google Scholar] [CrossRef]
- Sridharan, K.; Mohan Kumar, M.S.; Sekhar, M. Groundwater flow and storage in hard rocks aquifers. In Proceedings of the Workshop on Artificial Recharge of Groundwater in Granite Terrain, Bangalore, India; 1995. [Google Scholar]
- Summers, W.K. Specific Capacities of Wells in Crystalline Rocks. Groundwater 1972, 10, 37–47. [Google Scholar] [CrossRef]
- Feibert, D.; Sørup, C.M.; Jacobsen, P. Using the Analytic Network Process (ANP) to assess the distribution of pharmaceuticals in hospitals—A comparative case study of a Danish and American hospital. In Proceedings of the 5th World Conference on Production and Operations Management, Havana, Cuba, 6–10 September 2016; pp. 1–10. [Google Scholar]
- Hazell, J.R.T.; Cratchley, C.R.; Jones, C.R.C. The hydrogeology of crystalline aquifers in northern Nigeria and geophysical techniques used in their exploration. Geol. Soc. Lond. Spec. Publ. 1992, 66, 155–182. [Google Scholar] [CrossRef]
- Chilton, J.; Chorus, I. Protecting groundwater for health. In Managing the Quality of Drinking Water Sources; IWA Publishers: London, UK, 2006; pp. 20–24. [Google Scholar]
- Verma, N.; Patel, R.K. Delineation of groundwater potential zones in lower Rihand River Basin, India using geospatial techniques and AHP. Egypt. J. Remote Sens. Space Sci. 2021, 24, 559–570. [Google Scholar] [CrossRef]
- Thapa, R.; Gupta, S.; Guin, S.; Kaur, H. Assessment of groundwater potential zones using multi-influencing factor (MIF) and GIS: A case study from Birbhum district, West Bengal. Appl. Water Sci. 2017, 7, 4117–4131. [Google Scholar] [CrossRef]
- Ramaiah, S.N.; Gopalakrishna, G.S.; Srinivasa Vittala, S.; Najeeb, K.M. Geomorphological mapping for identification of ground water potential zones in hard rock areas using geo-spatial information—A case study in Malur Taluk, Kolar District, Karnataka, India. Nat. Environ. Pollut. Technol. 2012, 11, 369–376. [Google Scholar]
- Varughese, A.; Suhail, A.; Chitra, M.G.; Jiji, P.S.; Deepthy, C. Identification of shallow groundwater potential zones using GIS—A case study. Int. J. Adv. Eng. Appl. 2012, 1, 65–70. [Google Scholar]
- Das, S. Delineation of groundwater potential zone in hard rock terrain in Gangajalghati block, Bankura district, India using remote sensing and GIS techniques. Modeling Earth Syst. Environ. 2017, 3, 1589–1599. [Google Scholar] [CrossRef] [Green Version]
- Jaafarzadeh, M.S.; Tahmasebipour, N.; Haghizadeh, A.; Pourghasemi, H.R.; Rouhani, H. Groundwater recharge potential zonation using an ensemble of machine learning and bivariate statistical models. Sci. Rep. 2021, 11, 5587. [Google Scholar] [CrossRef]
- Rashid, M.; Lone, M.A.; Ahmed, S. Integrating geospatial and ground geophysical information as guidelines for groundwater potential zones in hard rock terrains of south India. Environ. Monit. Assess. 2012, 184, 4829–4839. [Google Scholar] [CrossRef]
- Bagyaraj, M.; Ramkumar, T.; Venkatramanan, S.; Gurugnanam, B. Application of remote sensing and GIS analysis for identifying groundwater potential zone in parts of Kodaikanal Taluk, South India. Front. Earth Sci. 2013, 7, 65–75. [Google Scholar] [CrossRef]
- Lentswe, G.B.; Molwalefhe, L. Delineation of potential groundwater recharge zones using analytic hierarchy process-guided GIS in the semi-arid Motloutse watershed, eastern Botswana. J. Hydrol. Reg. Stud. 2020, 28, 100674. [Google Scholar] [CrossRef]
- Raji, W.O.; Abdulkadir, K.A. Evaluation of groundwater potential of bedrock aquifers in Geological Sheet 223 Ilorin, Nigeria, using geo-electric sounding. Appl. Water Sci. 2020, 10, 220. [Google Scholar] [CrossRef]
- Chatterjee, S.; Dutta, S. Assessment of groundwater potential zone for sustainable water resource management in south-western part of Birbhum District, West Bengal. Appl. Water Sci. 2022, 12, 40. [Google Scholar] [CrossRef]
- Machiwal, D.; Rangi, N.; Sharma, A. Integrated knowledge-and data-driven approaches for groundwater potential zoning using GIS and multi-criteria decision making techniques on hard-rock terrain of Ahar catchment, Rajasthan, India. Environ. Earth Sci. 2015, 73, 1871–1892. [Google Scholar] [CrossRef]
- Akhter, G.; Hasan, M. Determination of aquifer parameters using geoelectrical sounding and pumping test data in Khanewal District, Pakistan. Open Geosci. 2016, 8, 630–638. [Google Scholar] [CrossRef]
- Kumar, T.; Balasubramanian, A.; Kumar, R.S.; Dushiyanthan, C.; Thiruneelakandan, B.; Suresh, R.; Karthikeyan, K.; Davidraju, D. Assessment of groundwater potential based on aquifer properties of hard rock terrain in the Chittar–Uppodai watershed, Tamil Nadu, India. Appl. Water Sci. 2016, 6, 179–186. [Google Scholar] [CrossRef]
- Nsiah, E.; Appiah-Adjei, E.K.; Adjei, K.A. Hydrogeological delineation of groundwater potential zones in the Nabogo basin, Ghana. J. Afr. Earth Sci. 2018, 143, 1–9. [Google Scholar] [CrossRef]
- Dhakate, R. Distribution of aquifer characteristics in different geomorphologic units in a granitic terrain. Appl. Water Sci. 2020, 10, 231. [Google Scholar] [CrossRef]
- Hasan, M.; Shang, Y.; Jin, W.; Akhter, G. Joint geophysical prospecting for groundwater exploration in weathered terrains of South Guangdong, China. Environ. Monit. Assess. 2021, 193, 1–24. [Google Scholar] [CrossRef]
- Masoud, A.M.; Pham, Q.B.; Alezabawy, A.K.; El-Magd, S.A.A. Efficiency of geospatial technology and multi-criteria decision analysis for groundwater potential mapping in a Semi-Arid region. Water 2022, 14, 882. [Google Scholar] [CrossRef]
- Central Ground Water Board. Manual on Artificial Recharge of Groundwater; Ministry of Water Resource Board, Government of India: Delhi, India, 2007.
- Garewal, S.K.; Vasudeo, A.D.; Landge, V.S.; Ghare, A.D. A GIS-based Modified DRASTIC (ANP) method for assessment of groundwater vulnerability: A case study of Nagpur city, India. Water Qual. Res. J. 2015, 52, 121–135. [Google Scholar] [CrossRef]
- Owolabi, S.T.; Madi, K.; Kalumba, A.M.; Orimoloye, I.R. A groundwater potential zone mapping approach for semi-arid environments using remote sensing (RS), geographic information system (GIS), and analytical hierarchical process (AHP) techniques: A case study of Buffalo catchment, Eastern Cape, South Africa. Arab. J. Geosci. 2020, 13, 1–17. [Google Scholar] [CrossRef]
- Singha, S.S.; Pasupuleti, S.; Singha, S.; Singh, R.; Venkatesh, A.S. Analytic network process based approach for delineation of groundwater potential zones in Korba district, Central India using remote sensing and GIS. Geocarto Int. 2021, 36, 1489–1511. [Google Scholar] [CrossRef]


| Importance | Scale |
|---|---|
| Extreme importance | 9 |
| Very, very strong | 8 |
| Very strong importance | 7 |
| Strong | 6 |
| Strong importance | 5 |
| Moderate plus | 4 |
| Moderate importance | 3 |
| Weak | 2 |
| Equal importance | 1 |
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 | 1.49 | 1.51 | 1.53 | 1.56 | 1.57 | 1.59 |
| Sl.No | Alternatives | Total | Normal | Ideal | Ranking |
|---|---|---|---|---|---|
| 1 | Floodplain | 0.0573 | 0.1311 | 1 | 1 |
| 2 | Cropland | 0.0446 | 0.102 | 0.7782 | 2 |
| 3 | Pediplain | 0.0423 | 0.0967 | 0.7377 | 3 |
| 4 | DD *—low | 0.0321 | 0.0734 | 0.5599 | 4 |
| 5 | LD *—high | 0.0312 | 0.0713 | 0.5441 | 5 |
| 6 | Water bodies | 0.0238 | 0.0545 | 0.4154 | 6 |
| 7 | Gentle slope | 0.0231 | 0.053 | 0.4038 | 7 |
| 8 | Entisols | 0.0227 | 0.0519 | 0.3958 | 8 |
| 9 | Gneiss | 0.0218 | 0.05 | 0.3812 | 9 |
| 10 | Charnokite | 0.0148 | 0.0339 | 0.2586 | 10 |
| 11 | Pediment | 0.0127 | 0.029 | 0.2211 | 11 |
| 12 | Fallow land | 0.0126 | 0.0289 | 0.2205 | 12 |
| 13 | Vertisols | 0.0121 | 0.0277 | 0.2114 | 13 |
| 14 | Medium slope | 0.011 | 0.0251 | 0.1917 | 14 |
| 15 | LD medium | 0.0092 | 0.0211 | 0.161 | 15 |
| 16 | Built-up land | 0.0087 | 0.0198 | 0.1512 | 16 |
| 17 | DD medium | 0.0084 | 0.0191 | 0.1459 | 17 |
| 18 | Sandstone | 0.0076 | 0.0173 | 0.1322 | 18 |
| 19 | Alfisols | 0.006 | 0.0137 | 0.1048 | 19 |
| 20 | Dyke | 0.0053 | 0.0122 | 0.0934 | 20 |
| 21 | Wasteland | 0.0053 | 0.0121 | 0.0921 | 21 |
| 22 | Inceptisols | 0.0052 | 0.012 | 0.0916 | 22 |
| 23 | LD—low | 0.0051 | 0.0116 | 0.0882 | 23 |
| 24 | Structural hill | 0.0044 | 0.01 | 0.0766 | 24 |
| 25 | Granite | 0.0033 | 0.0076 | 0.0578 | 25 |
| 26 | DD—high | 0.0033 | 0.0075 | 0.057 | 26 |
| 27 | Steep slope | 0.0032 | 0.0072 | 0.0553 | 27 |
| Sl.No. | Alternatives | Total | Normal | Ideal | Ranking |
|---|---|---|---|---|---|
| 1 | Aquifer thickness—deep | 0.0887 | 0.2085 | 1 | 1 |
| 2 | Water level—shallow | 0.0614 | 0.1444 | 0.6929 | 2 |
| 3 | Permeability—high | 0.0486 | 0.1143 | 0.5484 | 3 |
| 4 | Specific capacity—high | 0.0363 | 0.0853 | 0.4094 | 4 |
| 5 | Storage coefficient—high | 0.032 | 0.0753 | 0.3612 | 5 |
| 6 | Transmissivity—high | 0.0287 | 0.0675 | 0.3237 | 6 |
| 7 | Transmissivity—moderate | 0.0193 | 0.0453 | 0.2175 | 7 |
| 8 | Aquifer thickness—moderate | 0.0163 | 0.0383 | 0.1838 | 8 |
| 9 | Specific capacity—moderate | 0.0156 | 0.0367 | 0.1761 | 9 |
| 10 | Water level—moderate | 0.0141 | 0.0331 | 0.1586 | 10 |
| 11 | Storage coefficient—moderate | 0.0129 | 0.0304 | 0.146 | 11 |
| 12 | Permeability—moderate | 0.0116 | 0.0273 | 0.1308 | 12 |
| 13 | Specific capacity—low | 0.0097 | 0.0228 | 0.1092 | 13 |
| 14 | Water level—deep | 0.0084 | 0.0198 | 0.0951 | 14 |
| 15 | Aquifer thickness—shallow | 0.0071 | 0.0167 | 0.0803 | 15 |
| 16 | Transmissivity—low | 0.0051 | 0.0121 | 0.058 | 16 |
| 17 | Storage coefficient—low | 0.0048 | 0.0113 | 0.0542 | 17 |
| 18 | Permeability—low | 0.0046 | 0.0109 | 0.0521 | 18 |
| Potential Zone Category | No. of Pixels | CP/TP | No. of Wells | W/TW | FR |
|---|---|---|---|---|---|
| Shallow water level | |||||
| High | 466,483 | 0.435734929 | 13 | 0.371429 | 0.852419 |
| Moderate | 374,608 | 0.349915839 | 1 | 0.028571 | 0.081652 |
| Low | 229,475 | 0.214349232 | 0 | 0 | 0 |
| Moderate water level | |||||
| High | 466,483 | 0.435734929 | 5 | 0.142857 | 0.327853 |
| Moderate | 374,608 | 0.349915839 | 7 | 0.2 | 0.571566 |
| Low | 229,475 | 0.214349232 | 1 | 0.028571 | 0.133294 |
| Deep water level | |||||
| High | 466,483 | 0.435734929 | 3 | 0.085714 | 0.196712 |
| Moderate | 374,608 | 0.349915839 | 3 | 0.085714 | 0.244957 |
| Low | 229,475 | 0.214349232 | 2 | 0.057143 | 0.266588 |
| Total | 1,070,566 | 35 | |||
| Potential Zone Category | No. of Pixels | CP/TP | No. of Wells | W/TW | FR |
|---|---|---|---|---|---|
| Shallow water level | |||||
| High | 410,225 | 0.383185 | 11 | 0.314286 | 0.820193 |
| Moderate | 466,341 | 0.435602 | 1 | 0.028571 | 0.065591 |
| Low | 194,000 | 0.181213 | 2 | 0.057143 | 0.315336 |
| Moderate water level | |||||
| High | 410,225 | 0.383185 | 5 | 0.142857 | 0.372815 |
| Moderate | 466,341 | 0.435602 | 4 | 0.114286 | 0.262363 |
| Low | 194,000 | 0.181213 | 4 | 0.114286 | 0.630672 |
| Deep water level | |||||
| High | 410,225 | 0.383185 | 2 | 0.057143 | 0.149126 |
| Moderate | 466,341 | 0.435602 | 1 | 0.028571 | 0.065591 |
| Low | 194,000 | 0.181213 | 5 | 0.142857 | 0.78834 |
| Total | 1,070,566 | 35 | |||
| Potential Zone Category | No. of Pixels | CP/TP | No. of Wells | W/TW | FR |
|---|---|---|---|---|---|
| Shallow water level | |||||
| High | 389,427 | 0.363758 | 13 | 0.371429 | 1.021087 |
| Moderate | 484,959 | 0.452993 | 1 | 0.028571 | 0.063073 |
| Low | 196,180 | 0.183249 | 0 | 0 | 0 |
| Moderate water level | |||||
| High | 389,427 | 0.363758 | 0 | 0 | 0 |
| Moderate | 484,959 | 0.452993 | 12 | 0.342857 | 0.756871 |
| Low | 196,180 | 0.183249 | 1 | 0.028571 | 0.155916 |
| Deep water level | |||||
| High | 389,427 | 0.363758 | 0 | 0 | 0 |
| Moderate | 484,959 | 0.452993 | 0 | 0 | 0 |
| Low | 196,180 | 0.183249 | 8 | 0.228571 | 1.247328 |
| Total | 1,070,566 | 35 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radhakrishnan, S.; Ramachandran, R.; Murali, G.; Vatin, N.I. A Hybrid Spatial–Analytical Network Process Model for Groundwater Inventory in a Semi-Arid Hard Rock Aquifer System—A Case Study. Water 2022, 14, 2743. https://doi.org/10.3390/w14172743
Radhakrishnan S, Ramachandran R, Murali G, Vatin NI. A Hybrid Spatial–Analytical Network Process Model for Groundwater Inventory in a Semi-Arid Hard Rock Aquifer System—A Case Study. Water. 2022; 14(17):2743. https://doi.org/10.3390/w14172743
Chicago/Turabian StyleRadhakrishnan, Selvakumar, Rajani Ramachandran, Gunasekaran Murali, and Nikolai Ivanovich Vatin. 2022. "A Hybrid Spatial–Analytical Network Process Model for Groundwater Inventory in a Semi-Arid Hard Rock Aquifer System—A Case Study" Water 14, no. 17: 2743. https://doi.org/10.3390/w14172743







