Implementing the CCME Water Quality Index for the Evaluation of the Physicochemical Quality of Greek Rivers
Abstract
:1. Introduction
2. Materials and Methods
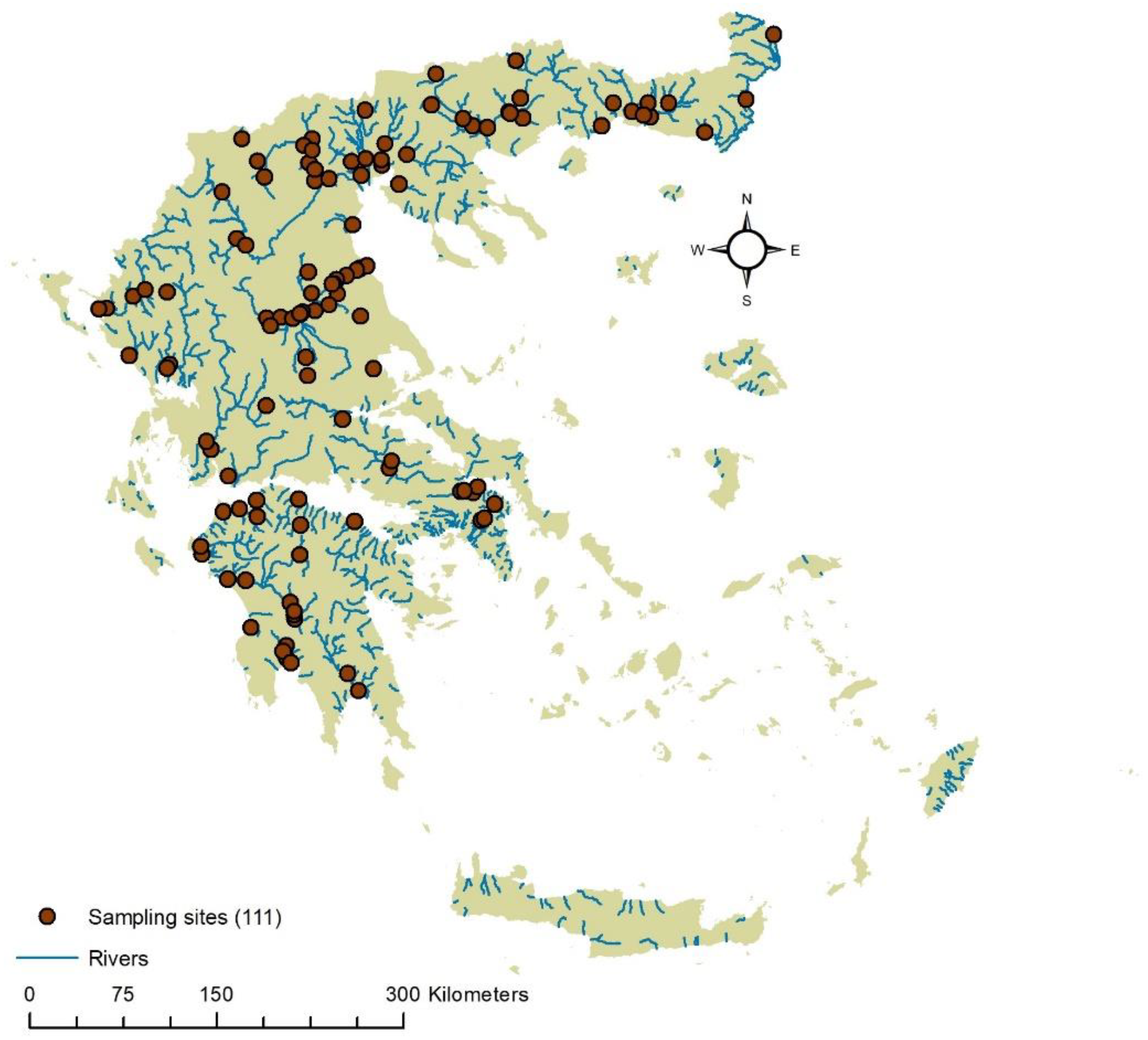
2.1. The Greek Monitoring Data for Rivers of the Period 2018–2020
2.2. The Hellenic Water Quality Index (HWQI) Based on Nutrients and DO
2.3. The CCME Water Quality Index (CCME WQI)
2.4. Building a Sound Basis for Comparing Indices
3. Results
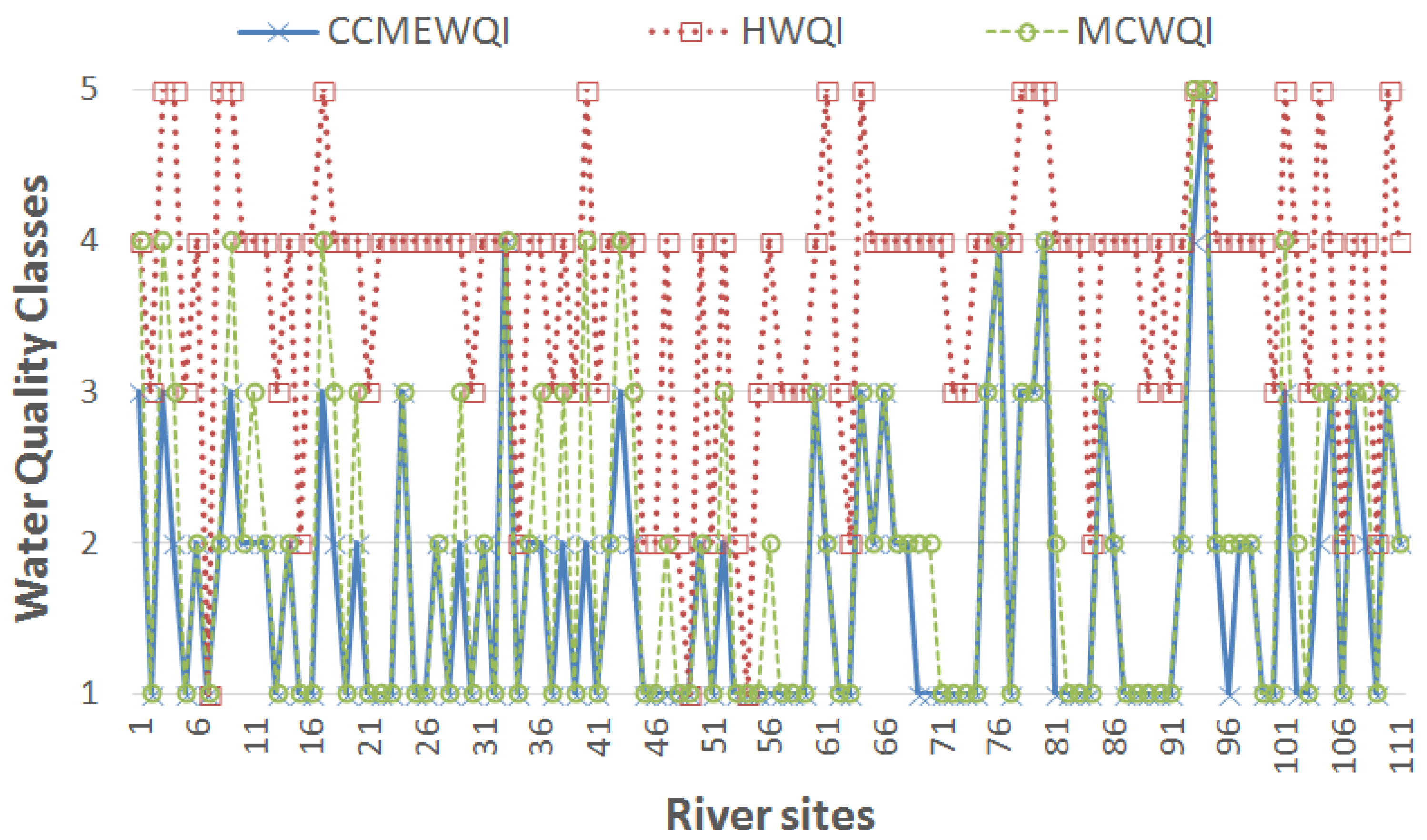
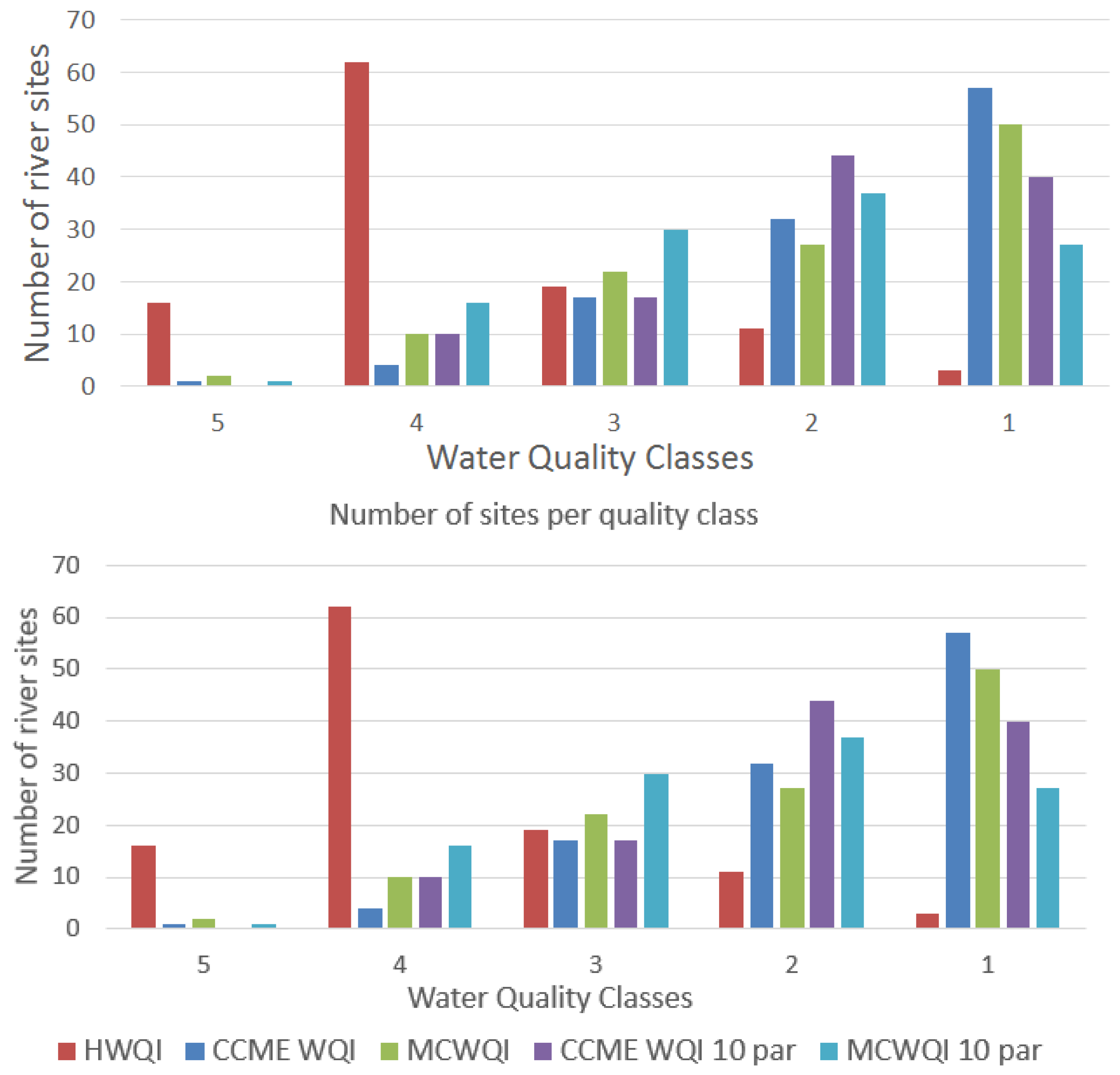
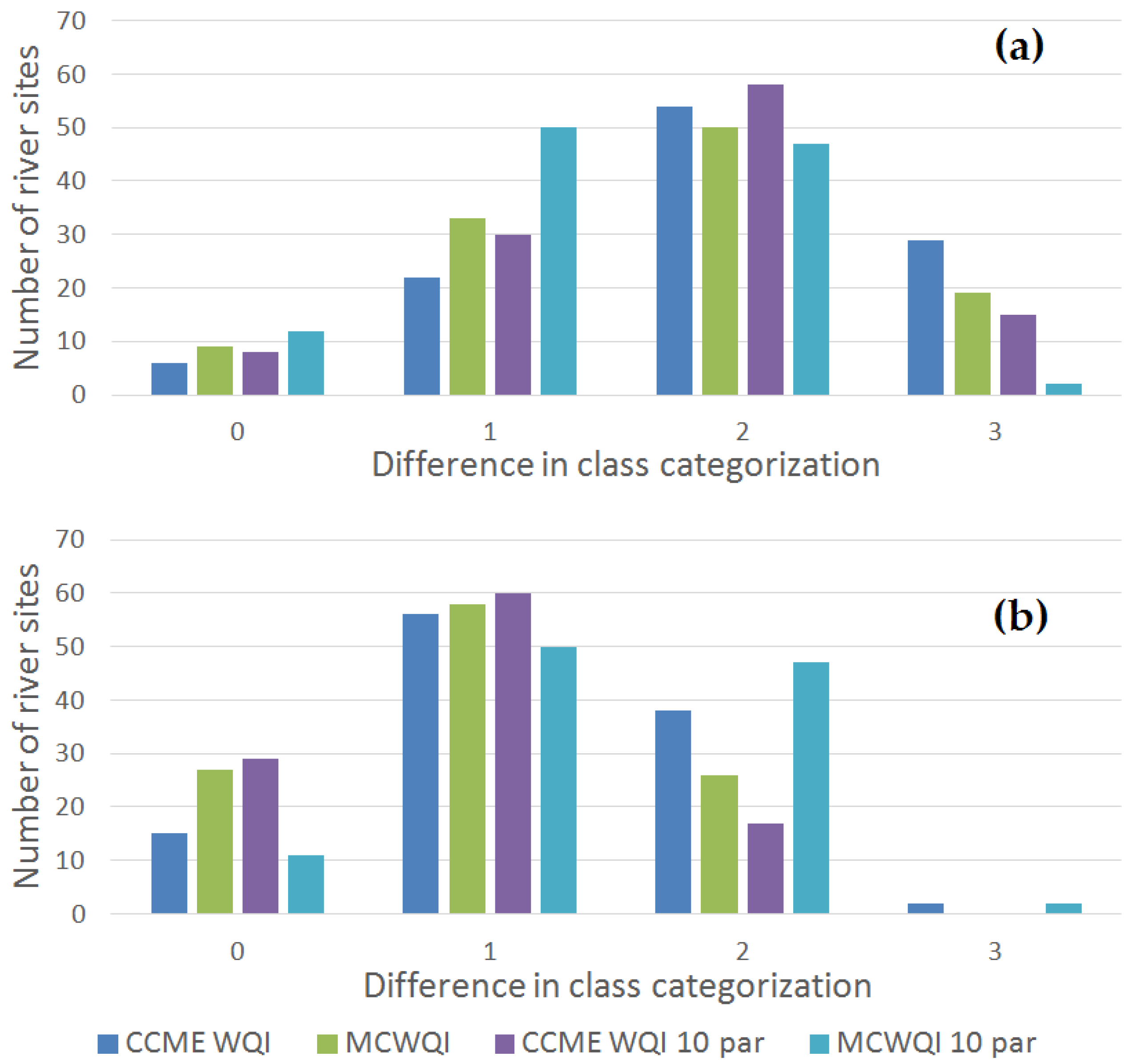
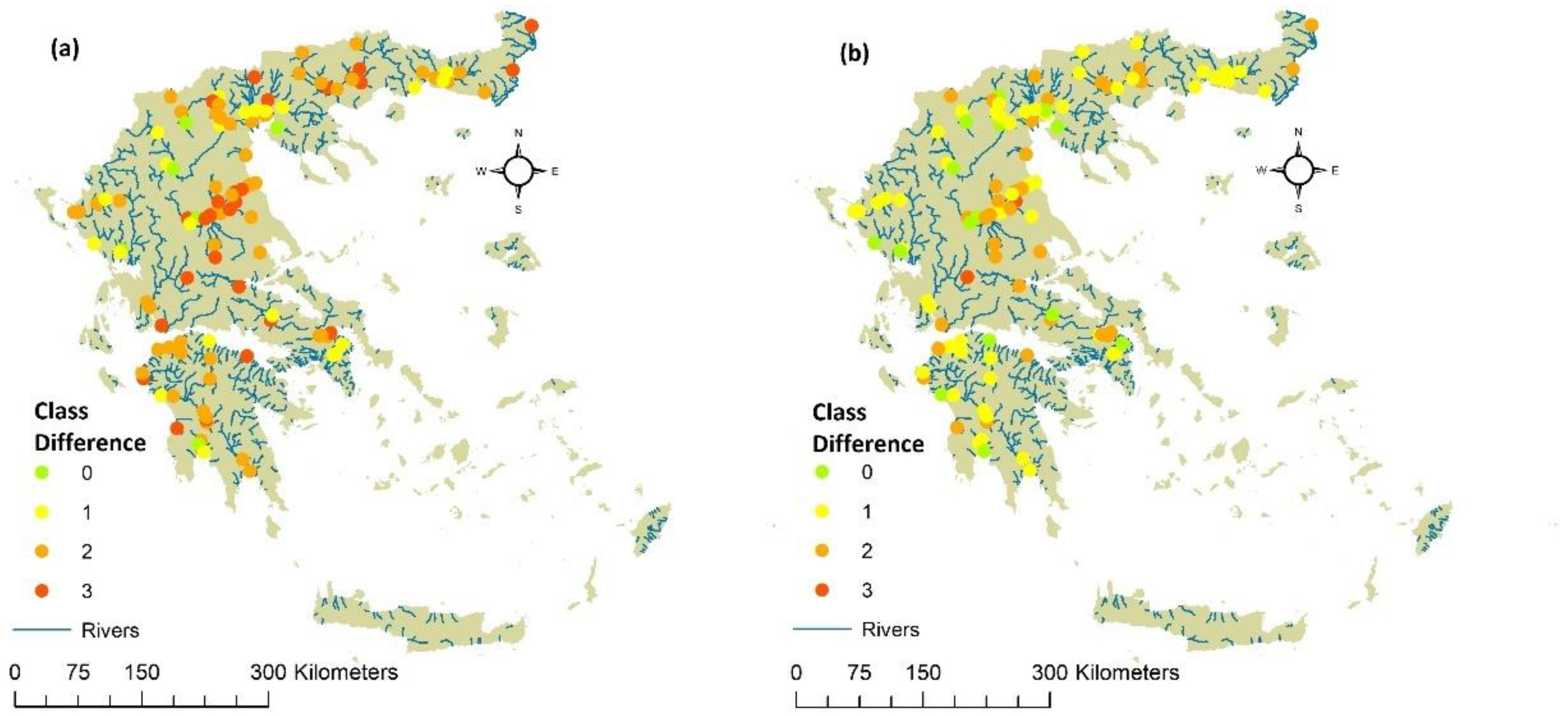
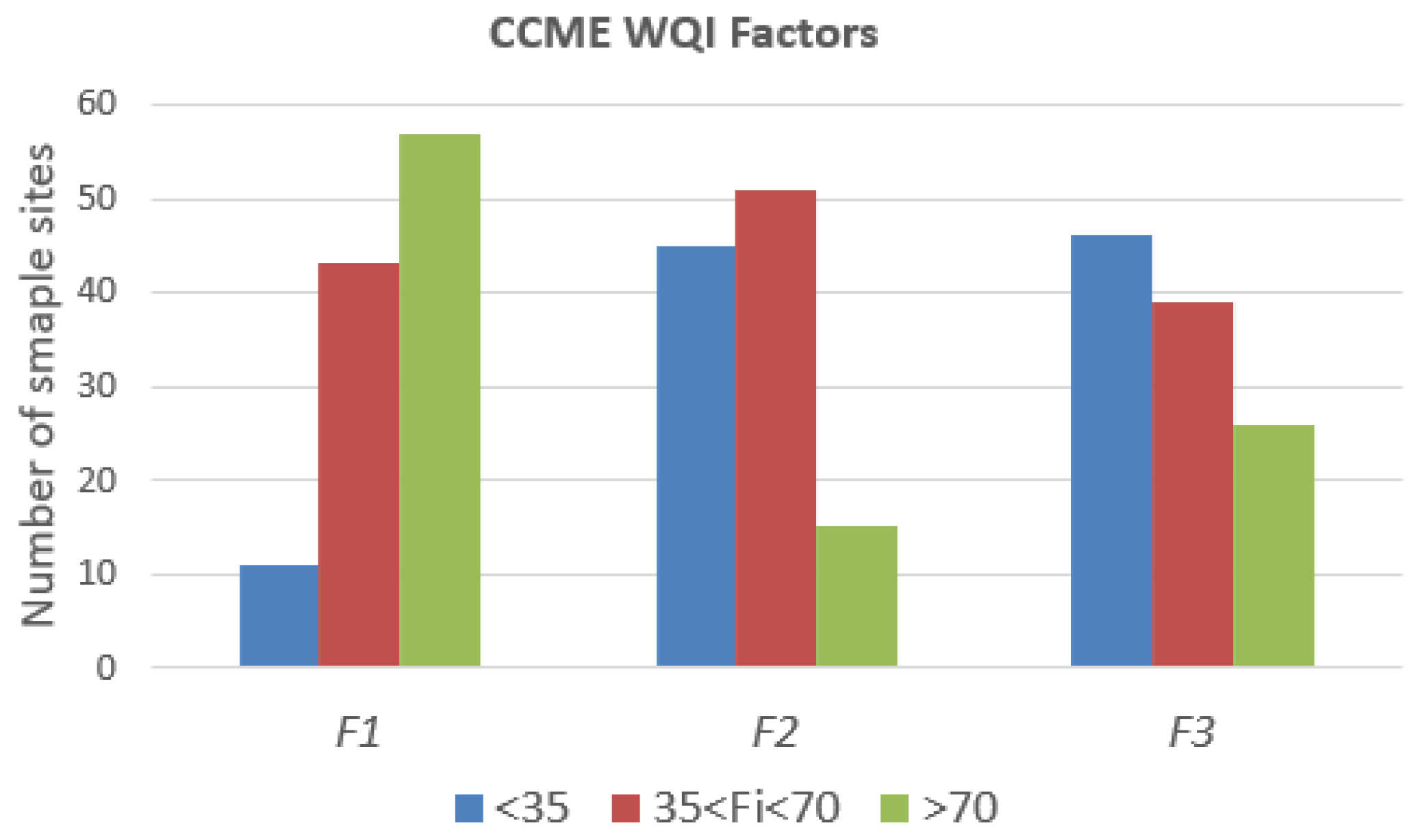
Comparison of Water Quality with the HWQI and the CCME WQI
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| No. | Site Name | Hydrologic Basin | Lat | Long | Elev m | Area Km2 | DO mg/L | N-NO2 mg/L | N-NO3 mg/L | N-NH4 mg/L | P-PO4 mg/L | TP mg/L | HWQI 6par | CCME 6par | MCWQI 6par | CCME 10par | MCWQI 10par |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | DIMHKOS | Acheloos | 38.57 | 21.29 | 17 | 711 | 8.31 | 0.007 | 0.773 | 0.024 | 0.015 | 0.024 | 3.72 | 58.17 | 73.35 | 69.19 | 81.58 |
| 2 | GURIOTISA | Acheloos | 38.63 | 21.25 | 26 | 225 | 5.42 | 0.005 | 0.206 | 0.033 | 0.054 | 0.073 | 3.88 | 49.27 | 69.36 | 63.75 | 79.03 |
| 3 | PARK_KYKL | Acheloos | 41.10 | 25.56 | 33 | 65 | 8.7 | 0.009 | 1.093 | 0.358 | 0.097 | 0.098 | 3.05 | 21.78 | 26.80 | 40.28 | 43.82 |
| 4 | PENTALOFOS_ ACHEL | Acheloos | 40.94 | 23.69 | 4 | 5560 | 8.21 | 0.003 | 0.246 | 0.013 | 0.005 | 0.009 | 4.05 | 80.29 | 92.30 | 82.33 | 93.09 |
| 5 | MAVROPOTAMO | Acherontas | 39.23 | 20.50 | 5 | 791 | 9.27 | 0.004 | 0.738 | 0.031 | 0.013 | 0.019 | 3.88 | 67.08 | 78.01 | 68.41 | 78.66 |
| 6 | AG_THOMAS | Agrilias | 38.38 | 21.46 | 5 | 27 | 10 | 0.004 | 0.212 | 0.063 | 0.02 | 0.024 | 4.05 | 58.75 | 72.73 | 57.62 | 75.04 |
| 7 | 3POTAMO | Alfeios | 37.36 | 22.09 | 375 | 8 | 8.53 | 0.079 | 1.685 | 0.635 | 0.048 | 0.053 | 2.53 | 15.99 | 20.21 | 29.33 | 35.00 |
| 8 | APIDITSA | Alfeios | 37.39 | 22.09 | 356 | 280 | 9.48 | 0.03 | 0.414 | 0.022 | 0.005 | 0.014 | 4.05 | 50.19 | 57.22 | 57.85 | 65.39 |
| 9 | EPITALION | Alfeios | 37.64 | 21.48 | 1 | 3404 | 10.9 | 0.01 | 0.72 | 0.018 | 0.003 | 0.006 | 3.88 | 65.97 | 73.82 | 74.13 | 81.94 |
| 10 | KARYTAINA | Alfeios | 37.48 | 22.05 | 324 | 884 | 8.56 | 0.083 | 2.287 | 0.108 | 0.005 | 0.007 | 2.70 | 39.79 | 44.25 | 46.89 | 53.20 |
| 11 | OLYMPIA | Alfeios | 37.63 | 21.64 | 22 | 3141 | 10.5 | 0.008 | 0.722 | 0.015 | 0.002 | 0.004 | 4.05 | 66.62 | 74.58 | 74.11 | 81.81 |
| 12 | THOKNA | Alfeios | 37.83 | 22.12 | 449 | 234 | 9.32 | 0.177 | 1.286 | 0.514 | 0.002 | 0.006 | 2.87 | 27.96 | 33.15 | 34.46 | 43.69 |
| 13 | TIMIOS | Alfeios | 39.79 | 22.38 | 58 | 291 | 7.89 | 0.001 | 0.909 | 0.012 | 0.006 | 0.009 | 4.05 | 77.32 | 82.58 | 75.25 | 85.14 |
| 14 | 3POTAM | Aliakmonas | 40.53 | 22.20 | 101 | 198 | 11.37 | 0.004 | 1.007 | 0.028 | 0.015 | 0.027 | 3.88 | 76.37 | 80.58 | 80.05 | 85.22 |
| 15 | AMYNTAS | Aliakmonas | 40.66 | 21.65 | 593 | 220 | 7.06 | 0.03 | 0.798 | 0.084 | 0.023 | 0.036 | 3.38 | 45.88 | 48.51 | 55.35 | 60.01 |
| 16 | ARAP_DW | Aliakmonas | 40.66 | 22.13 | 55 | 165 | 11.38 | 0.022 | 1.308 | 0.068 | 0.067 | 0.077 | 3.38 | 55.16 | 55.51 | 61.99 | 64.29 |
| 17 | GREVENIOT_ VIOLOGIKOS | Aliakmonas | 40.10 | 21.47 | 484 | 171 | 10.1 | 0.025 | 0.973 | 1.12 | 0.372 | 0.417 | 1.86 | 13.78 | 15.69 | 28.05 | 30.80 |
| 18 | KOSTARAZI | Aliakmonas | 40.44 | 21.32 | 614 | 309 | 8.26 | 0.07 | 2.746 | 0.723 | 0.307 | 0.328 | 1.53 | 16.74 | 16.91 | 29.44 | 30.68 |
| 19 | PROFITIS_ILIAS | Aliakmonas | 41.31 | 23.34 | 60 | 984 | 10.56 | 0.01 | 0.902 | 0.029 | 0.02 | 0.028 | 3.72 | 65.87 | 73.31 | 68.16 | 78.67 |
| 20 | RIZARI | Aliakmonas | 40.99 | 23.60 | 9 | 2424 | 10.04 | 0.057 | 1.126 | 0.154 | 0.051 | 0.061 | 3.38 | 31.91 | 33.81 | 46.41 | 49.50 |
| 21 | SIMB_BEN | Aliakmonas | 36.85 | 22.68 | 12 | 4197 | 9.31 | 0.001 | 0.034 | 0.017 | 0.001 | 0.004 | 4.55 | 100.00 | 100.00 | 82.36 | 94.50 |
| 22 | T1 | Aliakmonas | 40.55 | 22.33 | 16 | 3724 | 11.2 | 0.016 | 1.006 | 0.183 | 0.034 | 0.055 | 3.55 | 46.02 | 47.91 | 54.59 | 57.39 |
| 23 | T2 | Aliakmonas | 39.63 | 22.35 | 79 | 10767 | 10.31 | 0.021 | 1.116 | 0.154 | 0.041 | 0.041 | 3.55 | 55.40 | 55.77 | 61.49 | 63.48 |
| 24 | ANTHEM_DW | Anthemountas | 40.52 | 22.99 | 5 | 299 | 3.72 | 0.638 | 1.514 | 32.5 | 5.92 | 6.096 | 0.85 | 1.80 | 1.85 | 11.30 | 12.35 |
| 25 | ASSOPOS_DW | Asopos Viotia | 38.29 | 23.71 | 38 | 653 | 13.58 | 0.038 | 3.852 | 0.045 | 0.135 | 0.159 | 2.71 | 16.90 | 19.92 | 31.89 | 35.84 |
| 26 | ASSOPOS_UP | Asopos Viotia | 38.30 | 23.59 | 89 | 385 | 9.82 | 0.012 | 2.761 | 0.028 | 0.007 | 0.024 | 3.38 | 49.47 | 53.89 | 62.74 | 67.12 |
| 27 | CHALKOUTSI | Asopos Viotia | 38.33 | 23.75 | 2 | 690 | 11.77 | 0.037 | 3.391 | 0.032 | 0.046 | 0.07 | 3.21 | 30.49 | 33.93 | 37.67 | 43.02 |
| 28 | INDUSTRY | Asopos Viotia | 38.31 | 23.62 | 74 | 436 | 8.93 | 0.025 | 4.279 | 0.051 | 0.11 | 0.121 | 2.88 | 22.79 | 26.81 | 39.97 | 44.95 |
| 29 | FLORINA | Axios | 40.82 | 21.50 | 600 | 255 | 7.58 | 0.031 | 0.823 | 0.105 | 0.146 | 0.153 | 2.72 | 21.59 | 25.02 | 35.03 | 41.20 |
| 30 | LOUDIAS_DW | Axios | 40.58 | 22.63 | 1 | 1136 | 8 | 0.05 | 0.778 | 0.384 | 0.209 | 0.214 | 2.22 | 17.44 | 19.63 | 25.17 | 30.21 |
| 31 | PSAR_DW | Axios | 40.78 | 22.09 | 73 | 621 | 10.54 | 0.034 | 4.886 | 0.062 | 0.013 | 0.025 | 3.04 | 36.40 | 38.40 | 49.87 | 53.07 |
| 32 | VARDAROV | Axios | 38.21 | 23.90 | 302 | 306 | 5.12 | 0.077 | 1.211 | 0.254 | 0.524 | 0.566 | 1.36 | 10.11 | 10.72 | 27.44 | 28.31 |
| 33 | VOZVOZ | Bospos | 36.97 | 22.58 | 109 | 315 | 8.33 | 0.404 | 2.178 | 4.52 | 0.699 | 0.726 | 1.01 | 7.86 | 8.84 | 22.05 | 25.75 |
| 34 | APOKRIMNO_DW | Evros | 40.88 | 25.90 | 23 | 228 | 9.44 | 0.006 | 0.797 | 0.02 | 0.01 | 0.01 | 4.05 | 77.04 | 81.24 | 80.76 | 86.24 |
| 35 | EVROS_MD | Evros | 41.57 | 26.59 | 28 | 35260 | 7.7 | 0.007 | 1.006 | 0.036 | 0.162 | 0.163 | 3.22 | 32.14 | 44.47 | 47.43 | 58.63 |
| 36 | LYKOFOS | Evros | 41.11 | 26.30 | 14 | 39264 | 8.69 | 0.009 | 1.482 | 0.019 | 0.129 | 0.154 | 3.05 | 40.36 | 47.37 | 47.23 | 57.93 |
| 37 | DS_SKOURA | Evrotas | 36.99 | 22.52 | 127 | 1202 | 8.39 | 0.007 | 0.765 | 0.027 | 0.024 | 0.028 | 3.72 | 56.47 | 66.03 | 61.11 | 69.95 |
| 38 | SKALA | Evrotas | 39.12 | 22.16 | 467 | 1680 | 9.07 | 0.009 | 0.45 | 0.024 | 0.015 | 0.026 | 3.88 | 55.96 | 64.44 | 60.92 | 69.34 |
| 39 | VRODAMAS | Evrotas | 41.09 | 23.29 | 25 | 1362 | 8.16 | 0.007 | 0.2 | 0.011 | 0.01 | 0.017 | 4.22 | 68.33 | 76.69 | 66.71 | 72.98 |
| 40 | GALLIKOS_DW | Gallikos | 40.65 | 22.83 | 6 | 935 | 8.92 | 0.012 | 0.937 | 0.034 | 0.008 | 0.013 | 3.55 | 55.75 | 63.77 | 61.58 | 70.89 |
| 41 | GALLIKOS_MD | Gallikos | 40.81 | 22.86 | 55 | 851 | 9.25 | 0.027 | 4.043 | 0.041 | 0.037 | 0.043 | 3.38 | 33.02 | 36.83 | 50.27 | 54.54 |
| 42 | GRIBOVO | Kalamas | 39.66 | 20.52 | 100 | 1569 | 10.29 | 0.043 | 0.982 | 0.129 | 0.071 | 0.075 | 3.22 | 51.59 | 51.91 | 59.18 | 60.86 |
| 43 | KASTRI_(Kalamas) | Kalamas | 39.56 | 20.28 | 47 | 1538 | 8.23 | 0.019 | 0.74 | 0.035 | 0.041 | 0.045 | 3.55 | 53.67 | 60.04 | 71.81 | 75.10 |
| 44 | KESTRINI | Kalamas | 39.56 | 20.21 | 3 | 2302 | 6.99 | 0.003 | 0.708 | 0.057 | 0.021 | 0.031 | 3.72 | 58.55 | 79.63 | 69.43 | 86.23 |
| 45 | KLIMATIA | Kalamas | 39.71 | 20.63 | 186 | 513 | 8.29 | 0.04 | 1.243 | 1.821 | 0.373 | 0.421 | 1.53 | 11.04 | 12.77 | 28.53 | 32.67 |
| 46 | LAPSISTA | Kalamas | 39.69 | 20.84 | 466 | 404 | 6.89 | 0.006 | 0.215 | 0.069 | 0.022 | 0.033 | 3.88 | 62.95 | 65.68 | 66.22 | 71.53 |
| 47 | KIFISOS_MD | Kifisos Attiki | 38.09 | 23.78 | 185 | 73 | 11.33 | 0.14 | 4.024 | 0.027 | 0.472 | 0.515 | 1.68 | 22.45 | 23.20 | 40.15 | 42.78 |
| 48 | ERKYNA | Kifisos Viotia | 38.46 | 22.93 | 107 | 88 | 8.52 | 0.03 | 0.962 | 0.16 | 0.058 | 0.074 | 3.38 | 34.93 | 38.34 | 47.68 | 52.28 |
| 49 | ORXO | Kifisos Viotia | 38.51 | 22.96 | 102 | 326 | 9.15 | 0.003 | 2.625 | 0.027 | 0.01 | 0.014 | 3.54 | 69.73 | 71.70 | 76.25 | 78.71 |
| 50 | KIFISOS_UP | Lekanopedio Attikis | 38.11 | 23.81 | 235 | 38 | 9.96 | 0.2342 | 4.456 | 0.375 | 0.955 | 0.987 | 1.35 | 15.99 | 16.24 | 33.73 | 36.81 |
| 51 | PLATY | Loudias | 40.83 | 22.16 | 36 | 590 | 4.95 | 0.059 | 0.746 | 0.462 | 0.302 | 0.322 | 1.88 | 12.35 | 13.80 | 27.11 | 29.35 |
| 52 | GEF. KALOGIROU | Louros | 39.18 | 20.89 | 8 | 471 | 8.48 | 0.003 | 0.837 | 0.032 | 0.017 | 0.027 | 3.72 | 85.79 | 87.46 | 80.97 | 87.91 |
| 53 | KERASOUNTA | Louros | 39.15 | 20.86 | 5 | 485 | 8.98 | 0.004 | 0.786 | 0.045 | 0.023 | 0.029 | 3.72 | 77.50 | 83.80 | 81.00 | 88.32 |
| 54 | VARNAVAS | Marathonas (Lake) | 37.87 | 21.22 | 6 | 17 | 9.47 | 0.002 | 3.048 | 0.009 | 0.001 | 0.004 | 3.88 | 71.73 | 77.16 | 80.28 | 85.40 |
| 55 | MAVRONER | Mavroneri | 40.22 | 22.56 | 7 | 636 | 9 | 0.052 | 0.54 | 2.087 | 0.295 | 0.32 | 2.04 | 18.61 | 21.05 | 23.82 | 28.77 |
| 56 | DESPATI | Nestos | 41.41 | 24.11 | 385 | 778 | 10.45 | 0.006 | 0.528 | 0.013 | 0.044 | 0.051 | 4.22 | 70.59 | 90.43 | 70.17 | 83.94 |
| 57 | LASPO_DW | Nestos | 40.94 | 24.92 | 2 | 203 | 6.76 | 0.162 | 1.732 | 2.246 | 0.663 | 0.692 | 1.18 | 5.04 | 5.21 | 24.93 | 26.93 |
| 58 | AG_FLOROS | Pamisou- Nedontos-Neda | 37.17 | 22.02 | 15 | 9 | 9.5 | 0 | 0.819 | 0.013 | 0.003 | 0.007 | 4.22 | 68.38 | 81.13 | 81.02 | 88.58 |
| 59 | ARIS | Pamisou- Nedontos-Neda | 37.08 | 22.03 | 7 | 129 | 6.85 | 0.003 | 0.988 | 0.024 | 0.018 | 0.02 | 3.72 | 57.10 | 67.46 | 62.85 | 75.01 |
| 60 | PAMISSOS | Pamisou- Nedontos-Neda | 39.26 | 21.41 | 365 | 564 | 8.76 | 0.003 | 0.627 | 0.035 | 0.012 | 0.022 | 3.72 | 88.14 | 93.18 | 87.42 | 94.38 |
| 61 | TZIROREMA | Pamisou- Nedontos-Neda | 40.70 | 22.68 | 6 | 155 | 8.45 | 0.005 | 0.765 | 0.038 | 0.017 | 0.023 | 3.72 | 67.51 | 74.50 | 63.19 | 75.93 |
| 62 | FARAI | Peirou-Verga- Pineiou | 38.10 | 21.73 | 122 | 138 | 9.53 | 0.008 | 0.583 | 0.023 | 0.152 | 0.197 | 3.55 | 46.09 | 58.48 | 55.74 | 68.27 |
| 63 | K_AXAIA | Peirou-Verga- Pineiou | 38.15 | 21.57 | 1 | 535 | 8.78 | 0.009 | 1.271 | 0.049 | 0.027 | 0.036 | 3.55 | 63.02 | 66.70 | 72.46 | 76.73 |
| 64 | MANNA | Peirou-Verga- Pineiou | 38.13 | 21.42 | 3 | 32 | 9.67 | 0.032 | 2.14 | 0.113 | 0.155 | 0.155 | 2.54 | 21.86 | 25.95 | 33.20 | 39.38 |
| 65 | VARTHOLOMIO_US | Peirou-Verga- Pineiou | 41.01 | 25.32 | 13 | 12 | 6.61 | 0.006 | 1.104 | 0.038 | 0.029 | 0.033 | 3.72 | 56.34 | 66.79 | 61.67 | 72.19 |
| 66 | KALONERO | Peristera | 37.29 | 21.70 | 8 | 186 | 10.8 | 0.002 | 0.588 | 0.012 | 0.004 | 0.007 | 4.38 | 60.16 | 80.93 | 64.07 | 79.97 |
| 67 | PINIOS | Pinios Peloponnisos | 40.67 | 22.54 | 5 | 844 | 6.03 | 0.024 | 1.207 | 0.125 | 0.057 | 0.071 | 3.22 | 26.03 | 31.67 | 43.52 | 49.80 |
| 68 | ELASSON_MD | Pinios Thessalia | 39.87 | 22.15 | 245 | 247 | 4.92 | 0.015 | 0.083 | 0.094 | 1.342 | 1.427 | 2.20 | 9.46 | 10.97 | 17.35 | 20.30 |
| 69 | ENIPEA | Pinios Thessalia | 39.56 | 22.09 | 87 | 2640 | 8.01 | 0.038 | 1.436 | 0.126 | 0.064 | 0.083 | 3.05 | 25.75 | 31.11 | 41.84 | 46.94 |
| 70 | KIT_TRIK | Pinios Thessalia | 39.53 | 21.77 | 104 | 5 | 8.26 | 0.016 | 5.271 | 0.035 | 0.027 | 0.034 | 3.21 | 44.35 | 47.11 | 53.88 | 58.58 |
| 71 | LITHEO_DW | Pinios Thessalia | 39.54 | 21.90 | 96 | 148 | 3.91 | 0.203 | 2.368 | 0.928 | 0.633 | 0.652 | 0.68 | 4.83 | 5.01 | 18.88 | 20.08 |
| 72 | MAKRY | Pinios Thessalia | 39.26 | 22.15 | 119 | 41 | 7.6 | 0.013 | 2.604 | 0.037 | 0.171 | 0.181 | 2.38 | 23.27 | 27.45 | 41.00 | 45.60 |
| 73 | MEGA | Pinios Thessalia | 39.53 | 22.01 | 87 | 348 | 10.48 | 0.002 | 0.018 | 0.028 | 0.053 | 0.053 | 4.38 | 48.20 | 64.54 | 50.83 | 68.39 |
| 74 | MELISSA | Pinios Thessalia | 39.56 | 22.65 | 54 | 587 | 6.79 | 0.008 | 2.326 | 0.019 | 0.257 | 0.289 | 2.54 | 25.50 | 30.99 | 48.28 | 52.19 |
| 75 | OMOLIO_DS | Pinios Thessalia | 39.90 | 22.64 | 6 | 9731 | 9.62 | 0.016 | 1.327 | 0.036 | 0.076 | 0.091 | 3.38 | 53.30 | 59.89 | 60.98 | 70.01 |
| 76 | P004 | Pinios Thessalia | 39.92 | 22.70 | 3 | 10721 | 9.85 | 0.014 | 1.166 | 0.03 | 0.082 | 0.089 | 3.55 | 53.14 | 60.71 | 49.10 | 63.33 |
| 77 | P028 | Pinios Thessalia | 39.89 | 22.61 | 15 | 10610 | 9.96 | 0.015 | 1.243 | 0.022 | 0.073 | 0.085 | 3.72 | 53.45 | 60.31 | 61.06 | 70.31 |
| 78 | P061 | Pinios Thessalia | 39.85 | 22.51 | 15 | 10389 | 9.82 | 0.02 | 1.63 | 0.025 | 0.083 | 0.1 | 3.38 | 41.59 | 48.56 | 48.08 | 59.32 |
| 79 | P073 | Pinios Thessalia | 39.81 | 22.40 | 60 | 10332 | 10.15 | 0.018 | 1.612 | 0.037 | 0.089 | 0.098 | 3.38 | 41.21 | 48.09 | 47.05 | 57.36 |
| 80 | P088 | Pinios Thessalia | 39.79 | 22.39 | 56 | 8425 | 9.81 | 0.019 | 1.541 | 0.097 | 0.092 | 0.099 | 3.22 | 37.31 | 41.35 | 44.68 | 51.91 |
| 81 | P223 | Pinios Thessalia | 39.59 | 22.22 | 85 | 6333 | 8.92 | 0.02 | 1.256 | 0.088 | 0.122 | 0.14 | 2.88 | 25.71 | 31.86 | 38.27 | 47.15 |
| 82 | P263 | Pinios Thessalia | 39.58 | 22.11 | 86 | 6012 | 8.72 | 0.024 | 1.266 | 0.091 | 0.113 | 0.14 | 2.88 | 27.32 | 34.14 | 38.82 | 48.07 |
| 83 | P266 | Pinios Thessalia | 39.57 | 22.08 | 86 | 3370 | 9.26 | 0.023 | 1.587 | 0.07 | 0.109 | 0.115 | 3.05 | 26.90 | 33.29 | 38.47 | 47.42 |
| 84 | PAMISOS | Pinios Thessalia | 39.48 | 21.81 | 101 | 222 | 9.84 | 0.005 | 1.174 | 0.051 | 0.018 | 0.029 | 3.88 | 67.58 | 74.68 | 63.26 | 76.61 |
| 85 | PIN_IND | Pinios Thessalia | 37.81 | 21.23 | 1 | 8275 | 9.94 | 0.021 | 1.649 | 0.133 | 0.105 | 0.113 | 3.22 | 24.41 | 29.79 | 37.60 | 45.68 |
| 86 | T_XINIADA | Pinios Thessalia | 40.75 | 22.17 | 27 | 23 | 9.3 | 0.014 | 2.274 | 0.023 | 0.052 | 0.06 | 3.54 | 40.53 | 48.03 | 46.20 | 55.61 |
| 87 | TERPSITHEA | Pinios Thessalia | 37.42 | 22.09 | 361 | 6517 | 8.9 | 0.02 | 1.443 | 0.048 | 0.08 | 0.101 | 3.22 | 28.22 | 36.16 | 39.82 | 50.59 |
| 88 | TITAR_DW | Pinios Thessalia | 39.72 | 22.19 | 117 | 1884 | 10.67 | 0.017 | 0.313 | 0.047 | 0.1 | 0.131 | 3.55 | 34.89 | 48.97 | 43.84 | 60.83 |
| 89 | TITAR_MD | Pinios Thessalia | 38.08 | 22.62 | 5 | 1566 | 10.31 | 0.025 | 1.975 | 0.066 | 0.162 | 0.189 | 2.54 | 29.21 | 30.52 | 44.40 | 46.60 |
| 90 | FILIUR_DW | Rema Komotinis- Loutrou Evrou | 41.00 | 25.39 | 8 | 1381 | 9.13 | 0.006 | 1.801 | 0.037 | 0.028 | 0.032 | 3.54 | 64.35 | 68.49 | 72.59 | 76.68 |
| 91 | MESOHOR | Rema Komotinis- Loutrou Evrou | 41.10 | 25.37 | 22 | 125 | 4.27 | 0.093 | 1.627 | 5.4 | 0.693 | 0.762 | 1.02 | 5.71 | 6.12 | 23.42 | 25.95 |
| 92 | PASSOS | Rema Komotinis- Loutrou Evrou | 38.21 | 21.72 | 2 | 311 | 12.17 | 0.002 | 1.468 | 0.009 | 0.004 | 0.007 | 4.05 | 66.51 | 72.26 | 68.55 | 77.33 |
| 93 | ASPROPO | Rema Xanthis- Xirorema | 41.04 | 25.21 | 3 | 114 | 8.74 | 0.004 | 1.22 | 0.039 | 0.051 | 0.063 | 3.72 | 45.97 | 58.09 | 50.55 | 66.93 |
| 94 | KOSSYNTHOS_DW | Rema Xanthis- Xirorema | 41.10 | 25.03 | 18 | 397 | 9.08 | 0.019 | 1.46 | 0.037 | 0.017 | 0.024 | 3.55 | 60.21 | 61.83 | 70.36 | 72.78 |
| 95 | KALAVRITA | Remata Paralias Vor Peloponnisou | 38.04 | 22.13 | 693 | 138 | 5.87 | 0.021 | 0.848 | 0.04 | 0.121 | 0.143 | 2.88 | 28.82 | 36.90 | 50.85 | 56.59 |
| 96 | PATRA | Remata Paralias Vor Peloponnisou | 38.49 | 21.24 | 6 | 100 | 10.02 | 0.002 | 0.627 | 0.024 | 0.008 | 0.012 | 4.05 | 67.07 | 73.63 | 74.65 | 81.50 |
| 97 | TRIKALITIKOS | Remata Paralias Vor Peloponnisou | 37.05 | 22.06 | 1 | 161 | 11.58 | 0.002 | 0.315 | 0.009 | 0.001 | 0.004 | 4.38 | 59.48 | 74.87 | 63.79 | 78.47 |
| 98 | SELINOUS | Selinous | 40.05 | 21.56 | 431 | 356 | 11.2 | 0.001 | 0.411 | 0.012 | 0.001 | 0.004 | 4.38 | 90.28 | 98.56 | 82.50 | 97.49 |
| 99 | ELKE | Spercheios | 38.81 | 22.49 | 13 | 1393 | 7.55 | 0.015 | 0.642 | 0.101 | 0.074 | 0.076 | 3.22 | 28.04 | 34.94 | 48.12 | 52.48 |
| 100 | DRAMA | Strymonas | 41.14 | 24.14 | 90 | 117 | 9.85 | 0.014 | 1.796 | 0.123 | 0.029 | 0.039 | 3.38 | 36.44 | 40.07 | 54.62 | 57.45 |
| 101 | FILIPP | Strymonas | 41.00 | 24.17 | 46 | 248 | 7.52 | 0.04 | 1.221 | 0.082 | 0.063 | 0.069 | 3.22 | 34.44 | 37.46 | 52.29 | 54.96 |
| 102 | PETHELINO | Strymonas | 39.71 | 22.43 | 64 | 14016 | 10.38 | 0.013 | 0.32 | 0.102 | 0.0963 | 0.116 | 3.55 | 44.06 | 53.32 | 54.63 | 64.55 |
| 103 | PROMAXON | Strymonas | 41.05 | 22.66 | 26 | 11090 | 9.57 | 0.015 | 0.755 | 0.035 | 0.053 | 0.057 | 3.72 | 55.12 | 63.39 | 61.95 | 72.71 |
| 104 | S10 | Strymonas | 41.04 | 24.04 | 48 | 12570 | 7.47 | 0.026 | 0.834 | 0.159 | 0.1706 | 0.194 | 2.55 | 19.52 | 24.27 | 39.43 | 43.54 |
| 105 | S12 | Strymonas | 41.03 | 24.05 | 50 | 495 | 9.1 | 0.0415 | 2.948 | 0.046 | 0.0962 | 0.11 | 3.04 | 27.24 | 33.75 | 43.25 | 49.97 |
| 106 | S16 | Strymonas | 40.93 | 23.83 | 8 | 1349 | 8.81 | 0.08 | 1.816 | 0.147 | 0.086 | 0.1 | 2.53 | 29.61 | 31.59 | 42.75 | 45.89 |
| 107 | S18 | Strymonas | 38.23 | 22.11 | 35 | 2148 | 10.04 | 0.036 | 2.114 | 0.052 | 0.066 | 0.069 | 3.21 | 45.05 | 46.80 | 59.82 | 62.11 |
| 108 | ZEVGO | Strymonas | 40.11 | 20.72 | 447 | 11949 | 9.85 | 0.0094 | 0.308 | 0.111 | 0.016 | 0.029 | 3.72 | 61.64 | 64.19 | 60.22 | 67.51 |
| 109 | KOILADA | Vegoritida (Lake) | 40.55 | 21.71 | 578 | 1005 | 5.46 | 0.264 | 2.856 | 2.19 | 0.402 | 0.421 | 0.84 | 3.75 | 3.84 | 16.22 | 17.31 |
| 110 | BOGDANO | Volvi (Lake) | 40.73 | 23.06 | 91 | 201 | 2.7 | 0.076 | 0.053 | 38 | 3.78 | 3.953 | 1.35 | 7.65 | 9.01 | 20.12 | 24.08 |
| 111 | ALMYR_DW | Xirias (Almyros) | 39.18 | 22.78 | 37 | 154 | 10.2 | 0.008 | 5.237 | 0.065 | 0.369 | 0.384 | 2.20 | 18.78 | 21.83 | 34.52 | 38.05 |
References
- Uddin, G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Sutadian, A.D.; Muttil, N.; Yilmaz, A.; Perera, C. Development of River Water Quality Indices—A Review. Environ. Monit. Assess. 2016, 188, 58. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, T.; Abbasi, S.A. Water Quality Indices; Elsevier: Amsterdam, The Netherlands, 2012; p. 363. [Google Scholar]
- Kachroud, M.; Troland, F.; Kefi, M.; Jebari, S.; Bourrie, G. Water quality indices: Challenges and application limits in the literature. Water 2019, 11, 361. [Google Scholar] [CrossRef]
- Aljanabi, Z.Z.; Al-Obaidy, A.H.M.J.; Hassan, F.M. A brief review of water quality indices and their applications. IOP Conf. Ser. Earth Environ. Sci. 2021, 779, 012088. [Google Scholar] [CrossRef]
- Banda, T.D.; Kumarasamy, M.V. Development of Water Quality Indices (WQIs): A Review. Pol. J. Environ. Stud. 2020, 29, 2011–2021. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, K.; Hao, Q.; Xiao, D.; Zhu, Y.; Yin, S.; Zhang, Y. Hydrogeochemical insights into the signatures, genesis and sustainable perspective of nitrate enriched groundwater in the piedmont of Hutuo watershed, China. CATENA 2022, 212, 106020. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, K.; Yan, H.; Zhou, B.; Huand, X.; Hao, Q.; Zhang, Y.; Zhang, Y.; Liao, X.; Yin, S. Hydrogeochemical constraints on groundwater resource sustainable development in the arid Golmud alluvial fan plain on Tibetan plateau. Environ. Earth Sci. 2021, 80, 750. [Google Scholar] [CrossRef]
- Canadian Council of Ministers of the Environment (CCME). Canadian Water Quality Guidelines for the Protection of Aquatic Life: CCME Water Quality Index 1.0, Technical Report. In Canadian Environmental Quality Guidelines, 1999; Canadian Council of Ministers of the Environment: Winnipeg, MB, Canada, 2001. [Google Scholar]
- Canadian Council of Ministers of the Environment (CCME). Canadian Water Quality Guidelines for the Protection of Aquatic Life: CCME Water Quality Index, User’s Manual—2017 Update. In Canadian Environmental Quality Guidelines, 1999; Canadian Council of Ministers of the Environment: Winnipeg, MB, Canada, 2017. Available online: https://ccme.ca/en/res/wqimanualen.pdf (accessed on 10 January 2022).
- Hurley, T.; Sadiq, R.; Mazumder, A. Adaptation and evaluation of the Canadian Council of Ministers of the Environment Water Quality Index (CCME WQI) for use as an effective tool to characterize drinking sourcewater quality. Water Res. 2012, 46, 3544–3552. [Google Scholar] [CrossRef]
- Khan, A.A.; Paterson, R.; Khan, H. Modification and application of the Canadian Council of Ministers of the Environment Water Quality Index (CCME WQI) for the communication of drinking water quality in Newfoundland and Labrador. Water Qual. Res. J. Can. 2004, 39, 285–293. [Google Scholar] [CrossRef]
- Davies, J.M. Application and tests of the Canadian Water Quality Index for assessing changes in water quality in lakes and rivers of central North America. Lake Reserv. Manag. 2006, 22, 308–320. [Google Scholar] [CrossRef] [Green Version]
- Khan, F.; Husain, T.; Lumb, A. Water quality evaluation and trend analysis in selected watersheds of the Atlantic region of Canada. Environ. Monit. Assess. 2003, 88, 221–248. [Google Scholar] [CrossRef]
- Lumb, A.; Halliwell, D.; Sharma, T. Application of CCME water quality index to monitor water quality: A case of the Mackenzie River basin, Canada. Environ. Monit. Assess. 2006, 113, 411–429. [Google Scholar] [CrossRef]
- Boyacioglu, H. Utilization of the water quality index method as a classification tool. Environ. Monit. Assess. 2010, 167, 115–124. [Google Scholar] [CrossRef]
- Sharma, D.; Kansal, A. Water quality analysis of River Yamuna using water quality index in the national capital territory, India (2000–2009). Appl. Water Sci. 2011, 1, 147–157. [Google Scholar] [CrossRef]
- Espejo, L.; Kretschmer, N.; Oyarzún, J.; Meza, F.; Núñez, J.; Maturana, H. Application of water quality indices and analysis of the surface water quality monitoring network in semiarid North-Central Chile. Environ. Monit. Assess. 2012, 184, 5571–5588. [Google Scholar] [CrossRef]
- Mostafaei, A. Application of multivariate statistical methods and water quality index to evaluation of water quality in the Kashkan River. Environ. Manag. 2014, 53, 865–881. [Google Scholar] [CrossRef] [PubMed]
- Tanjung, R.H.R.; Yonas, M.N.; Suwito, S.; Maury, H.K.; Sarungu, Y.; Hamuna, B. Analysis of Surface Water Quality of Four Rivers in Jayapura Regency, Indonesia: CCME-WQI Approach. J. Ecol. Eng. 2022, 23, 73–82. [Google Scholar] [CrossRef]
- Ismail, A.H.; Robescu, D.; Hameed, M.A. Application of CCME WQI in the Assessment of the Water Quality of Danube River, Romania. Eng. Technol. J. 2018, 36, 142–146. [Google Scholar]
- Alexakis, D.; Tsihrintzis, V.A.; Tsakiris, G.; Gikas, G.D. Suitability of water quality indices for application in lakes in the Mediterranean. Water Resour. Manag. 2016, 30, 1621–1633. [Google Scholar] [CrossRef]
- Alexakis, D.E. Meta-Evaluation of Water Quality Indices. Application into Groundwater Resources. Water 2020, 12, 1890. [Google Scholar] [CrossRef]
- Alexakis, D.E. Linking DPSIR Model and Water Quality Indices to Achieve Sustainable Development Goals in Groundwater Resources. Hydrology 2021, 8, 90. [Google Scholar] [CrossRef]
- Gikas, G.D. Water quantity and hydrochemical quality monitoring of Laspias River, North Greece. J. Environ. Sci. Health Part A 2017, 52, 1312–1321. [Google Scholar] [CrossRef]
- Gikas, G.D.; Sylaios, G.K.; Tsihrintzis, V.A.; Konstantinou, I.K.; Albanis, T.; Boskidis, I. Comparative evaluation of river chemical status based on WFD methodology and CCME water quality index. Sci. Total Environ. 2020, 745, 140849. [Google Scholar] [CrossRef]
- Zotou, I.; Tsihrintzis, V.A.; Gikas, G.D. Performance of seven water quality indices (WQIs) in a Mediterranean river. Environ. Monit. Assess. 2019, 191, 505. [Google Scholar] [CrossRef] [PubMed]
- European Parliament and Council. WFD 2000/60/EC—Directive 2000/60/EC of the European Parliament and of the council of 23 October 2000 establishing a framework for community action in the field of water policy. Off. J. Eur. Communities 2000, 327, 1–73. [Google Scholar]
- Stefanidis, K.; Papaioannou, G.; Markogianni, V.; Dimitriou, E. Water Quality and Hydromorphological Variability in Greek Rivers: A Nationwide Assessment with Implications for Management. Water 2019, 11, 1680. [Google Scholar] [CrossRef]
- Stefanidis, K.; Christopoulou, A.; Poulos, S.; Dassenakis, E.; Dimitriou, E. Nitrogen and Phosphorus Loads in Greek Rivers: Implications for Management in Compliance with the Water Framework Directive. Water 2020, 12, 1531. [Google Scholar] [CrossRef]
- Skoulikidis, N.; Karaouzas, I.; Amaxidis, Y.; Lazaridou, M. Impact of EU Environmental Policy Implementation on the Quality and Status of Greek Rivers. Water 2021, 13, 1858. [Google Scholar] [CrossRef]
- Skoulikidis, N.; Amaxidis, Y.; Bertahas, I.; Laschou, S.; Gritzalis, K. Analysis of factors driving stream water composition and synthesis of management tools—A case study on small/medium Greek catchments. Sci. Total Environ. 2006, 362, 205–241. [Google Scholar] [CrossRef]
- Skoulikidis, N. Defining chemical status of a temporal Mediterranean River. J. Environ. Monit. 2008, 10, 842–852. [Google Scholar] [CrossRef]
- Skoulikidis, N.; Sabater, S.; Datry, T.; Morais, M.; Buffagni, A.; Dörflinger, G.; Zogaris, S.; Sánchez-Montoya, M.M.; Bonada, N.; Kalogianni, E.; et al. Non-perennial Mediterranean rivers in Europe: Status, pressures, and challenges for research and management. Sci. Total Environ. 2017, 577, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Skoulikidis, N.; Dimitriou, E.; Karaouzas, I. The Rivers of Greece Evolution, Current Status and Perspectives. In The Handbook of Environmental Chemistry 59; Springer: Berlin/Heidelberg, Germany, 2018; Available online: https://link.springer.com/book/10.1007/978-3-662-55369-5 (accessed on 10 January 2022).
- Kerouel, R.; Aminot, A. Fluorometric determination of ammonia in sea and estuarine waters by direct segmented flow analysis. Mar. Chem. 1997, 57, 265–275. [Google Scholar] [CrossRef]
- Boltz, D.F.; Mellon, M.G. Spectrophotometric determination of phosphate as molydiphosphoric acid. Anal. Chem. 1948, 20, 749–751. [Google Scholar] [CrossRef]
- Navone, R. Proposed method for nitrate in potable waters. Am. Water Works Assoc. 1964, 56, 781. [Google Scholar] [CrossRef]
- Raimbault, P.; Pouvesle, W.; Diaz, F.; Garcia, N.; Sempere, R. Wet oxidation and automated colorimetry for simultaneous determination of organic carbon, nitrogen and phosphorus dissolved in seawater. Mar. Chem. 1999, 66, 161–169. [Google Scholar] [CrossRef]
- Greek Government Gazette II 1635 of 9 June 2016. Modification of Article 19 of Annex 19 to Presidential Decree 51/2007 (A’54), as Modified by Article 5 of Law 4117/2013 (A29), in Compliance with Directive 2014/101/EU of the European Council of 30 October 2014. Available online: www.et.gr (accessed on 27 June 2019).
- European Commission. Commission Staff Working Document European Overview (1/2) Accompanying the Document Report from the Commission to the European Parliament and the Council on the Implementation of the Water Framework Directive (2000/60/EC) River Basin Management Plans. Available online: https://publications.europa.eu/en/publication-detail/-/publication/85d9694d-d1d7-48bb-9402-d6da989eb9df/language-en (accessed on 27 June 2019).
- Skoulikidis, N.T.; Gritzalis, K.; Kouvarda, T.; Buffagni, A. The development of an ecological quality assessment and classification system for Greek running waters based on benthic macroinvertebrates. Hydrobiologia 2004, 516, 149–160. [Google Scholar] [CrossRef]
- Cardoso, A.C.; Duchemin, J.; Magoarou, P.; Premazzi, G. Criteria for the Identification of Freshwater Subject to Eutrophication. Their Use for the Implementation of the “Nitrates” and Urban Waste Water Directives. EUR 19810 EN, EU—JRC. 2001, Volume 87. Available online: https://op.europa.eu/en/publication-detail/-/publication/26a9c3bb-a4c2-11e7-837e-01aa75ed71a1 (accessed on 24 February 2022).
- European Commission (EC). Guidance Document 13, Overall Approach to the Classification of Ecological Status and Ecological Potential, Common Implementation Strategy for The Water Framework Directive (2000/60/EC). 2005. Available online: https://circabc.europa.eu/sd/a/06480e87-27a6-41e6-b165-0581c2b046ad/Guidance%20No%2013%20-%20Classification%20of%20Ecological%20Status%20(WG%20A).pdf (accessed on 24 February 2022).
- Dao, V.; Urban, W.; Hazra, B. Introducing the Canadian Water Quality Index modification. Groundw. Sustain Dev. 2020, 11, 100457. [Google Scholar] [CrossRef]
- Vigiak, O.; Grizzetti, B.; Udias-Moinelo, A.; Zanni, M.; Dorati, C.; Bouraoui, F.; Pistocchi, A. Predicting biochemical oxygen demand in European freshwater bodies. Sci. Total Environ. 2019, 666, 1089–1105. [Google Scholar] [CrossRef]
- Naddeo, N.; Zarra, T.; Belgiorno, V. Optimization of sampling frequency for river water quality assessment according to Italian implementation of the EU Water Framework Directive. Environ. Sci. Policy 2007, 10, 243–249. [Google Scholar] [CrossRef]
- Wagner, R.J.; Boulger, R.W., Jr.; Oblinger, C.J.; Smith, B.A. Guidelines and standard procedures for continuous water-quality monitors-Station operation, record computation and data reporting: U.S. Geological Survey. Tech. Methods 2006, 1-D3, 51. [Google Scholar]
- WHO. World Health Organization Guidelines for Drinking—Water Quality, Incorporating the First Addendum, 4th ed.; WHO: Geneva, Switzerland, 2017. [Google Scholar]
- del Mar Sanchez-Montoya, M.; Arce, M.-I.; Vidal-Abarca, M.-R.; Suarez, M.-L.; Prat, N.; Gomez, R. Establishing physico-chemical reference conditions in Mediterranean streams according to the European Water Framework Directive. Water Res. 2012, 46, 2257–2269. [Google Scholar] [CrossRef] [PubMed]
- Skoulikidis, N.; Mentzafou, A. Freshwater and Matter Inputs in the Aegean Coastal System. In The Aegean Sea Environment: The Natural System. The Handbook of Environmental Chemistry (698); Anagnostou, C., Kostianoy, A., Mariolakos, I., Panayotidis, P., Soilemezidou, M., Tsaltas, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; Volume I. [Google Scholar] [CrossRef]

| High | Good | Moderate | Poor | Bad | ||
|---|---|---|---|---|---|---|
| N-NO3 | mg/L | <0.22 | 0.22–0.60 | 0.60–1.30 | 1.30–1.80 | >1.80 |
| N-NH4 | mg/L | <0.024 | 0.024–0.06 | 0.06–0.20 | 0.20–0.50 | >0.50 |
| N-NO2 | μg/L | <3 | 3–8 | 8–30 | 30–70 | >70 |
| P-PO4 | μg/L | <70 | 70–105 | 105–165 | 165–340 | >340 |
| TP | μg/L | <125 | 125–165 | 165–220 | 220–405 | >405 |
| DO | mg/L | >9 | 6.4–9 | 4–6.4 | 2–4 | <2 |
| Classes | Boundaries | Score |
|---|---|---|
| 5 or H (High) | >4 and ≤5 | (4.1 + 5)/2 = 4.55 |
| 4 or G (Good) | >3 and ≤4 | (3.1 + 4)/2 = 3.55 |
| 3 or M (Moderate) | >2 and ≤3 | (2.1 + 3)/2 = 2.55 |
| 2 or P (Poor) | >1 and ≤2 | (1.1 + 2)/2 = 1.55 |
| 1 or B (Bad) | ≤1 | 1/2 = 0.5 |
| Classes | Boundaries | Water Quality Description |
|---|---|---|
| Excellent | 95–100 | water quality is protected with a virtual absence of threat or impairment, conditions very close to natural or pristine levels. |
| Good | 80–94 | water quality is protected with only a minor degree of threat or impairment; conditions rarely depart from natural or desirable levels. |
| Fair | 65–79 | water quality is usually protected but occasionally threatened or impaired; conditions sometimes depart from natural or desirable levels. |
| Marginal | 45–64 | water quality is frequently threatened or impaired; conditions often depart from natural or desirable levels. |
| Poor | 0–44 | water quality is almost always threatened or impaired; conditions usually depart from natural or desirable levels. |
| Classes Numbers | Classes HCMR WQI/ CCME WQI * | Class Boundaries HCMR WQI * | Class Boundaries CCME WQI * | Modified Boundaries CCME WQI ** |
|---|---|---|---|---|
| 5 | High/Excellent | 4–5 | 95–100 | 80–100 |
| 4 | Good/Good | 3–4 | 80–94 | 65–79 |
| 3 | Moderate/Fair | 2–3 | 65–79 | 45–64 |
| 2 | Poor/Marginal | 1–2 | 45–64 | 20–44 |
| 1 | Bad/Poor | ≤1 | 0–44 | 0–19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panagopoulos, Y.; Alexakis, D.E.; Skoulikidis, N.T.; Laschou, S.; Papadopoulos, A.; Dimitriou, E. Implementing the CCME Water Quality Index for the Evaluation of the Physicochemical Quality of Greek Rivers. Water 2022, 14, 2738. https://doi.org/10.3390/w14172738
Panagopoulos Y, Alexakis DE, Skoulikidis NT, Laschou S, Papadopoulos A, Dimitriou E. Implementing the CCME Water Quality Index for the Evaluation of the Physicochemical Quality of Greek Rivers. Water. 2022; 14(17):2738. https://doi.org/10.3390/w14172738
Chicago/Turabian StylePanagopoulos, Yiannis, Dimitrios E. Alexakis, Nikolaos Theodor Skoulikidis, Sofia Laschou, Anastasios Papadopoulos, and Elias Dimitriou. 2022. "Implementing the CCME Water Quality Index for the Evaluation of the Physicochemical Quality of Greek Rivers" Water 14, no. 17: 2738. https://doi.org/10.3390/w14172738
APA StylePanagopoulos, Y., Alexakis, D. E., Skoulikidis, N. T., Laschou, S., Papadopoulos, A., & Dimitriou, E. (2022). Implementing the CCME Water Quality Index for the Evaluation of the Physicochemical Quality of Greek Rivers. Water, 14(17), 2738. https://doi.org/10.3390/w14172738











