Application of Head Loss Coefficient for Surcharge Straight Path Manhole to Improve the Accuracy of Urban Inundation Analysis
Abstract
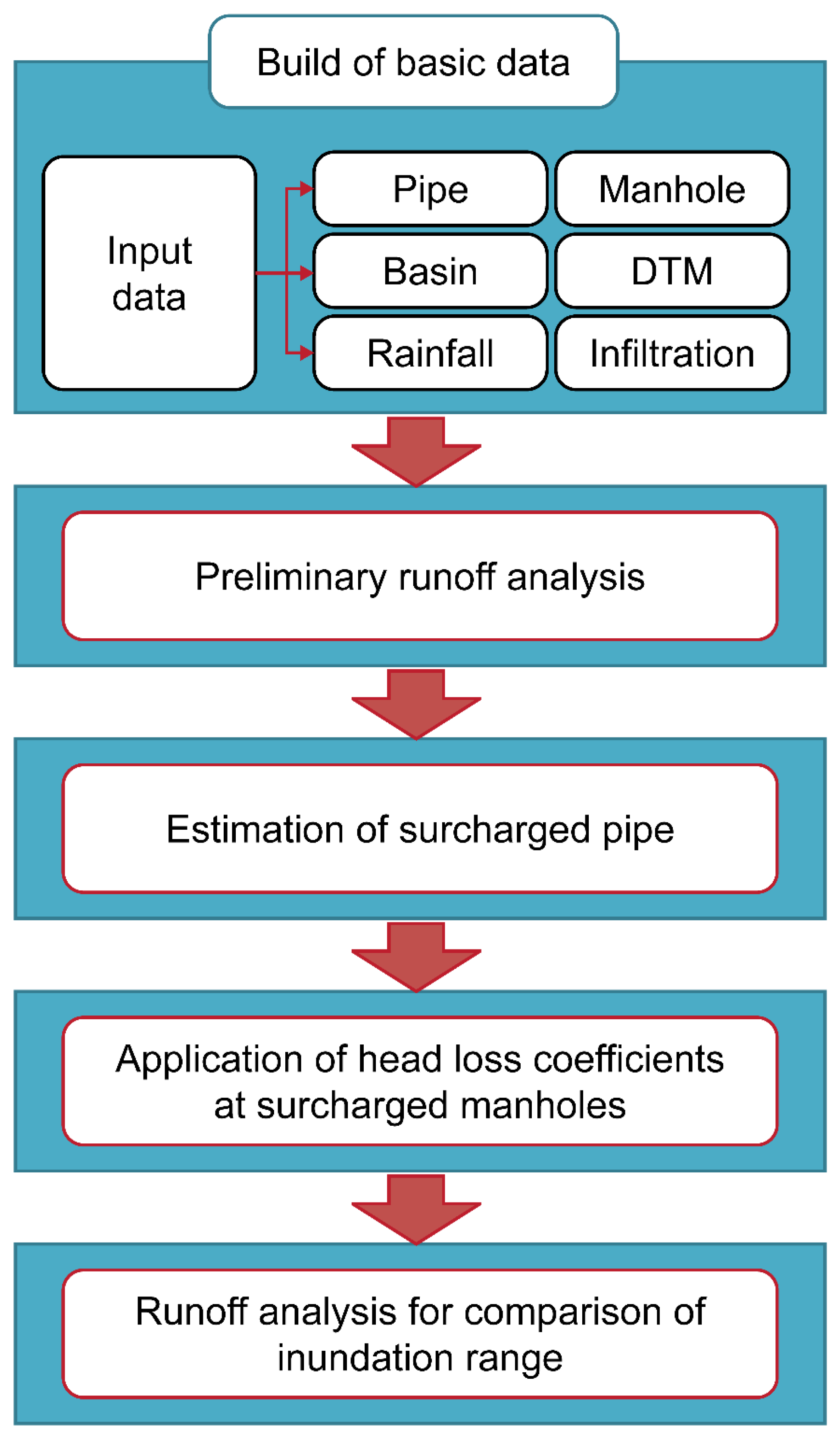
:1. Introduction
2. Calculation of Head Loss Coefficient at Manhole in Surcharge Straight Path
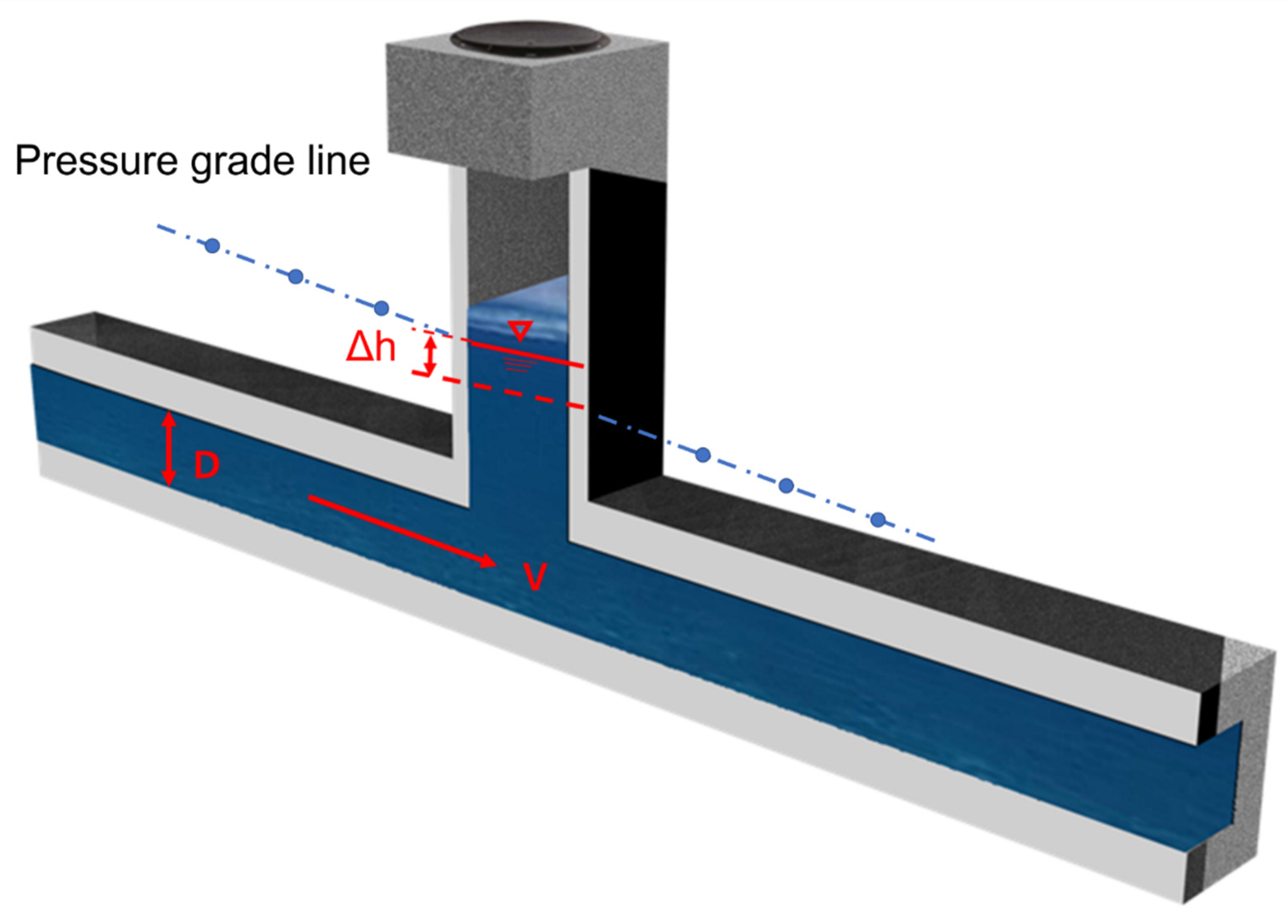
2.1. Loss of Surcharge Manhole
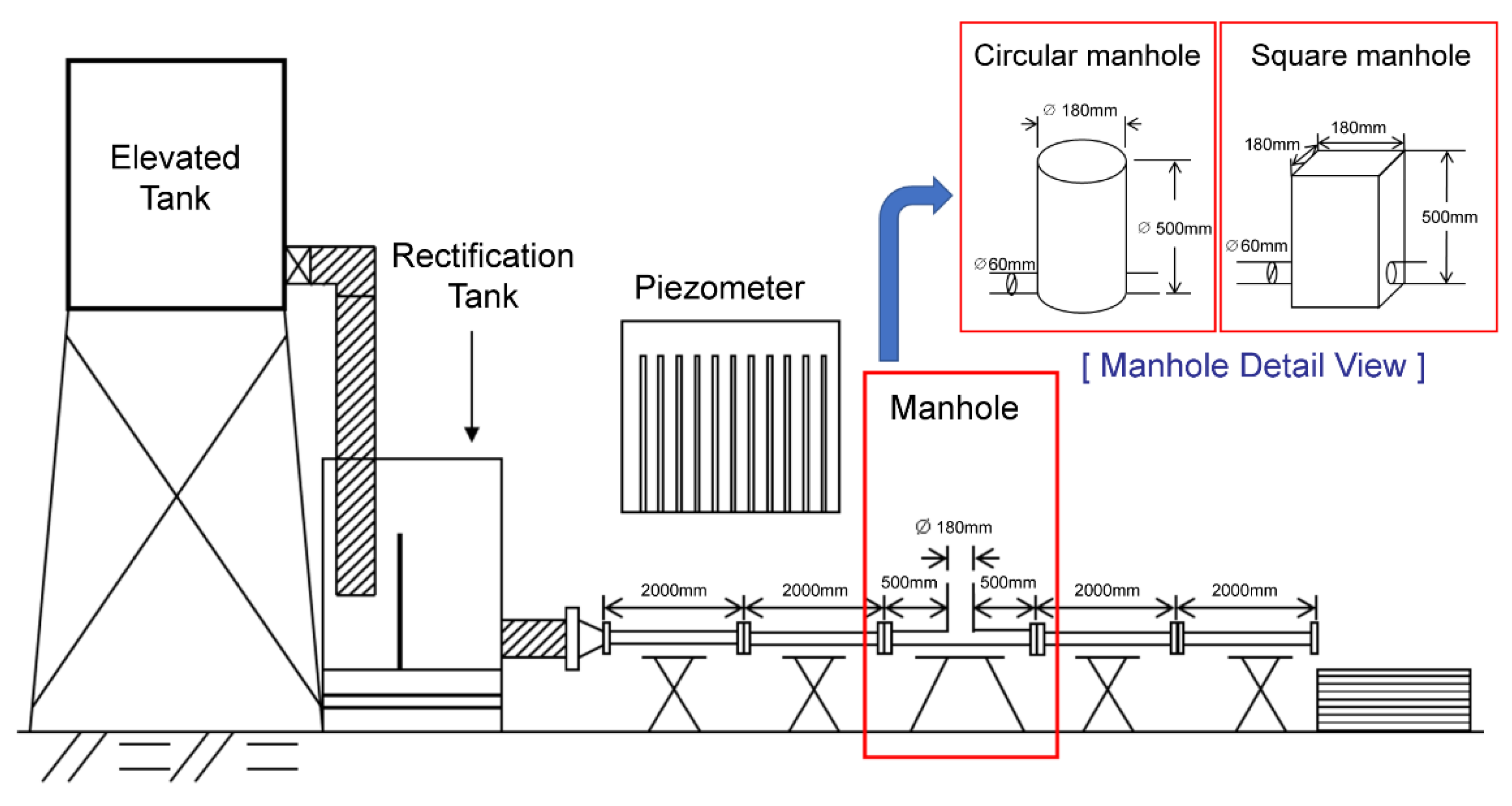
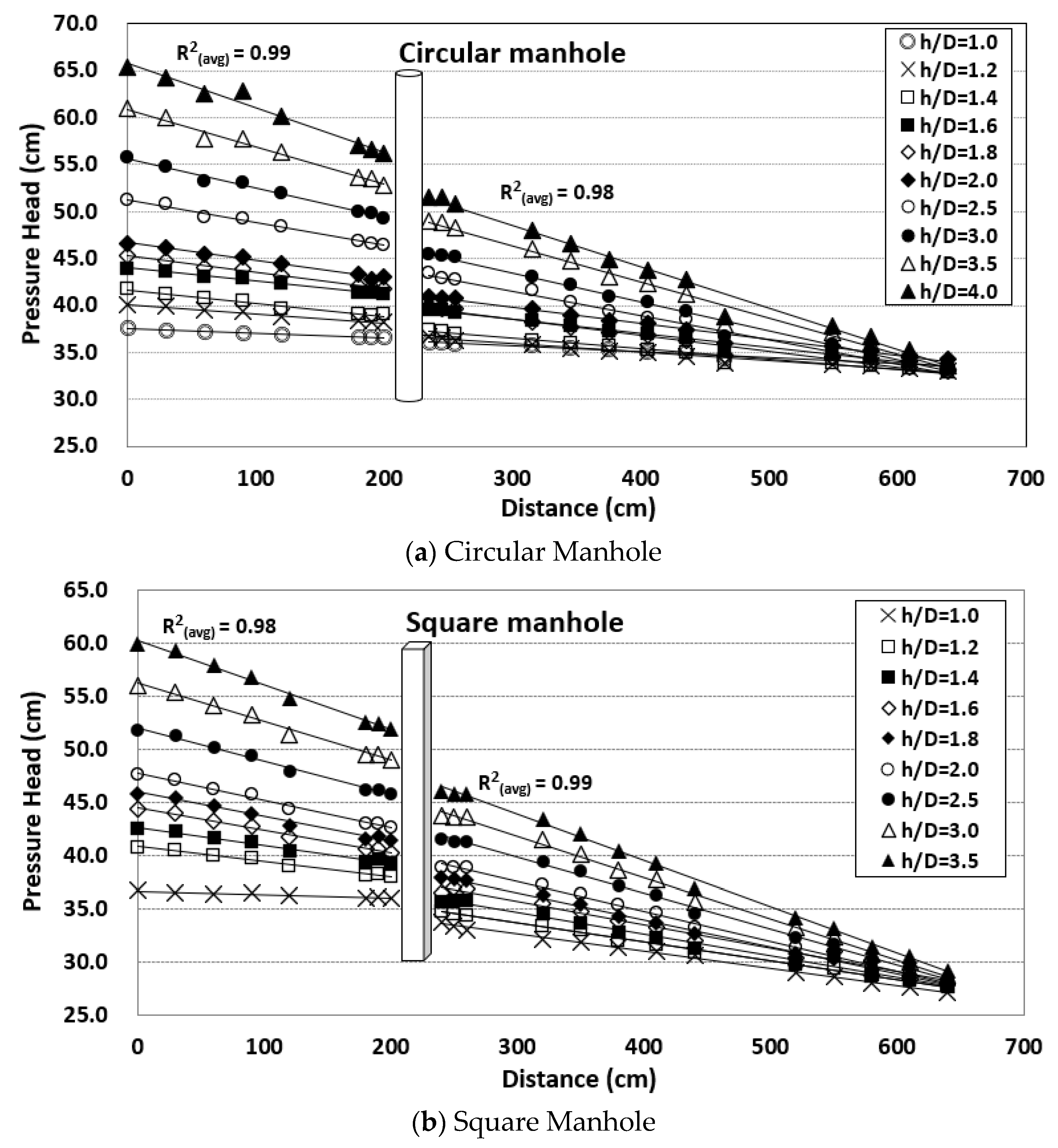
2.2. Hydraulic Experiments
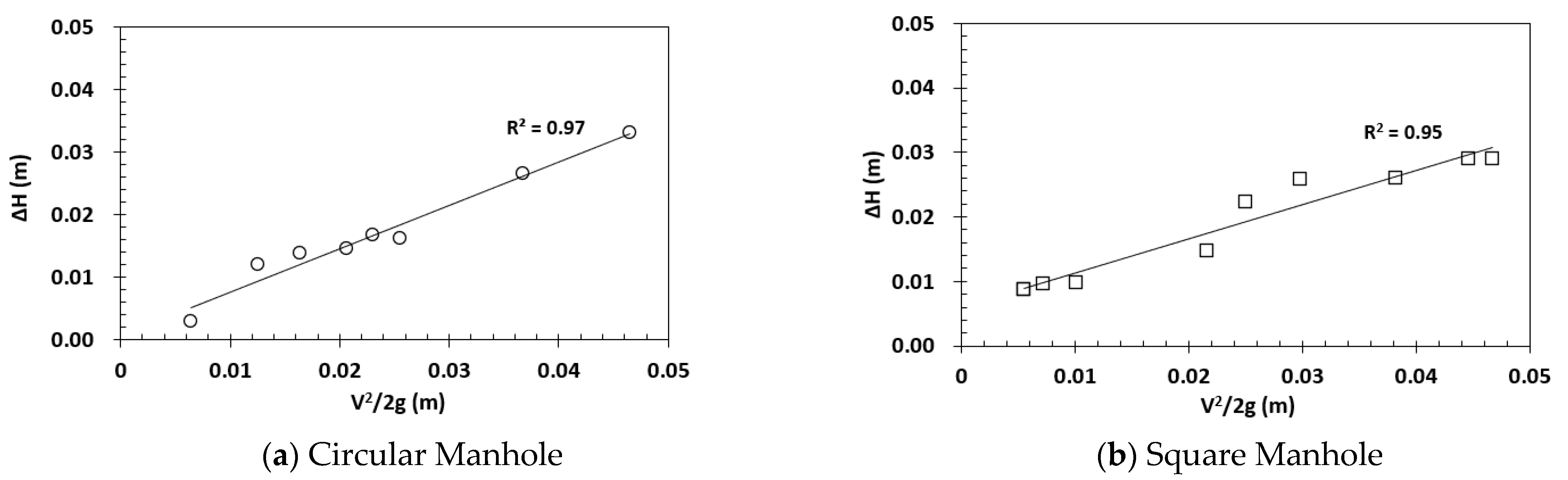
2.3. Calculation of the Head Loss Coefficient
2.4. Application of Head Loss Coefficient in Inland Flood Inundation Analysis
3. Result and Discussions
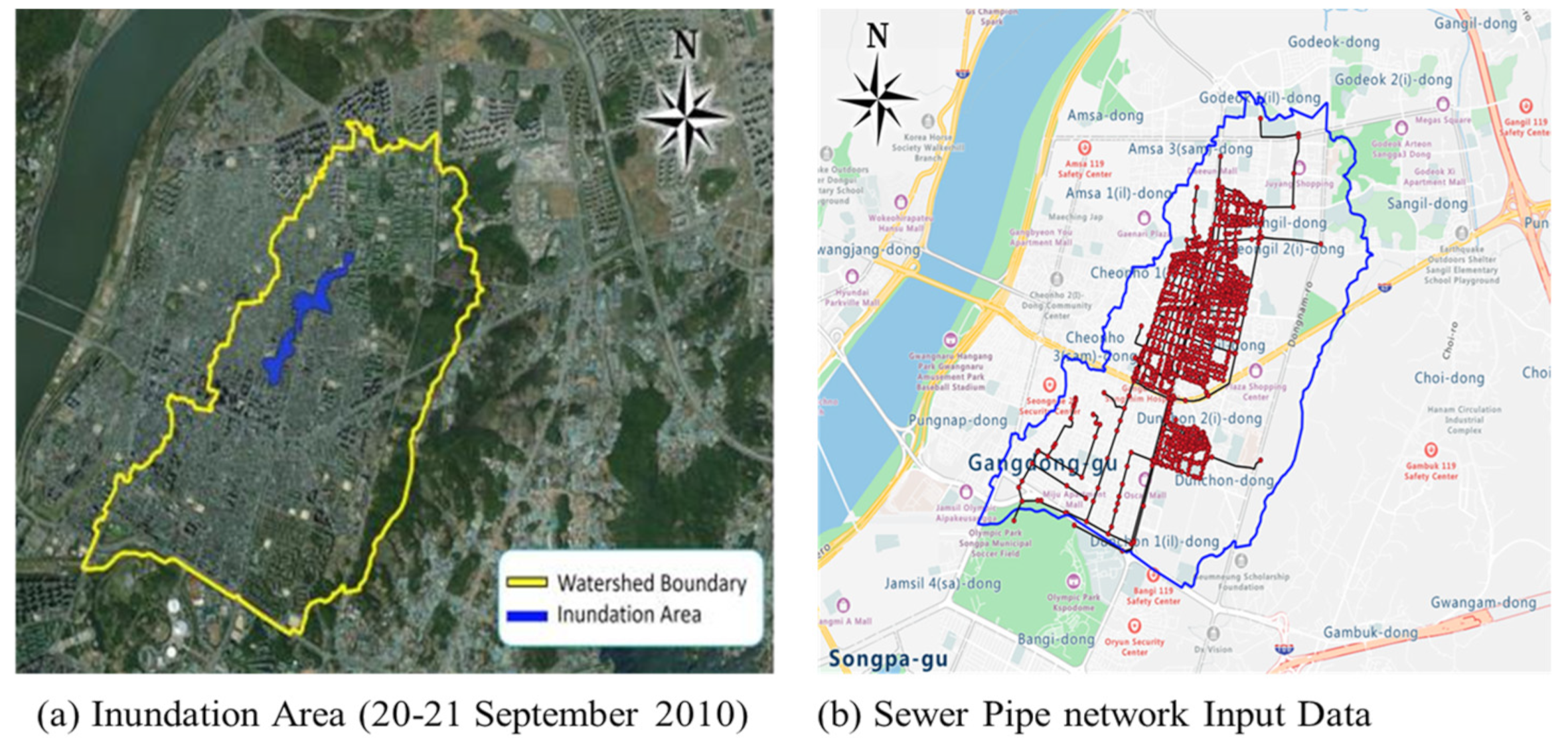
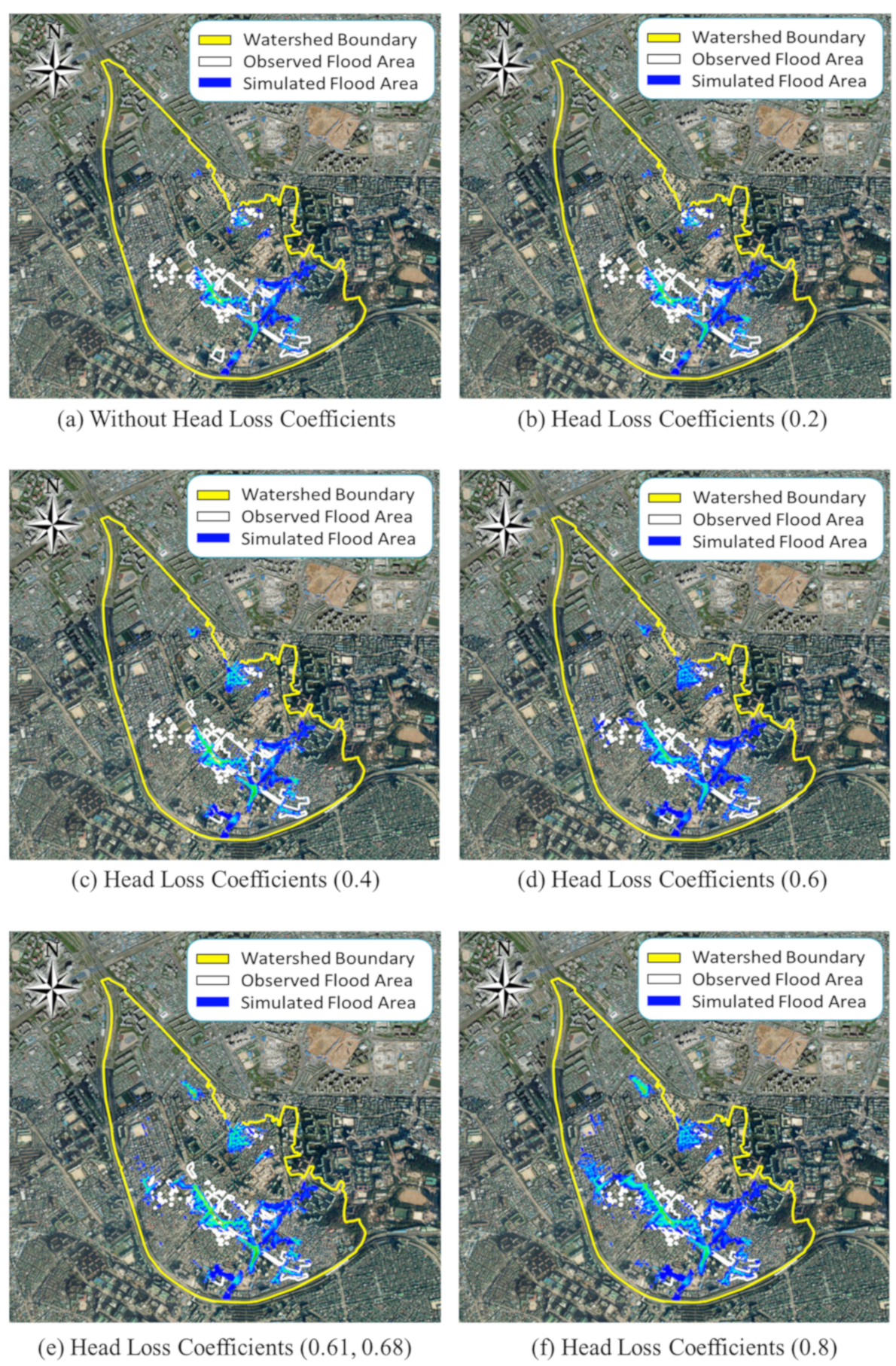
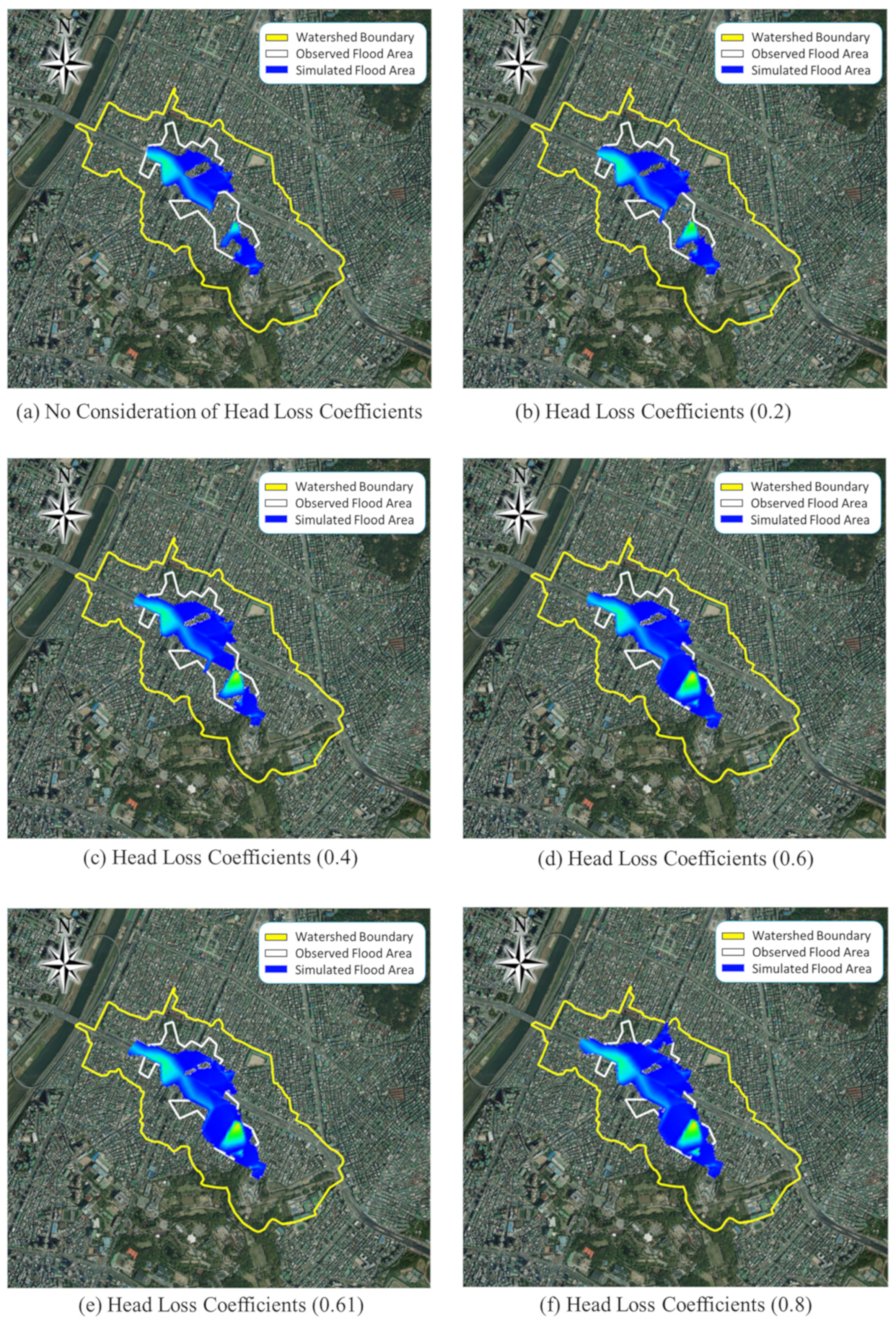
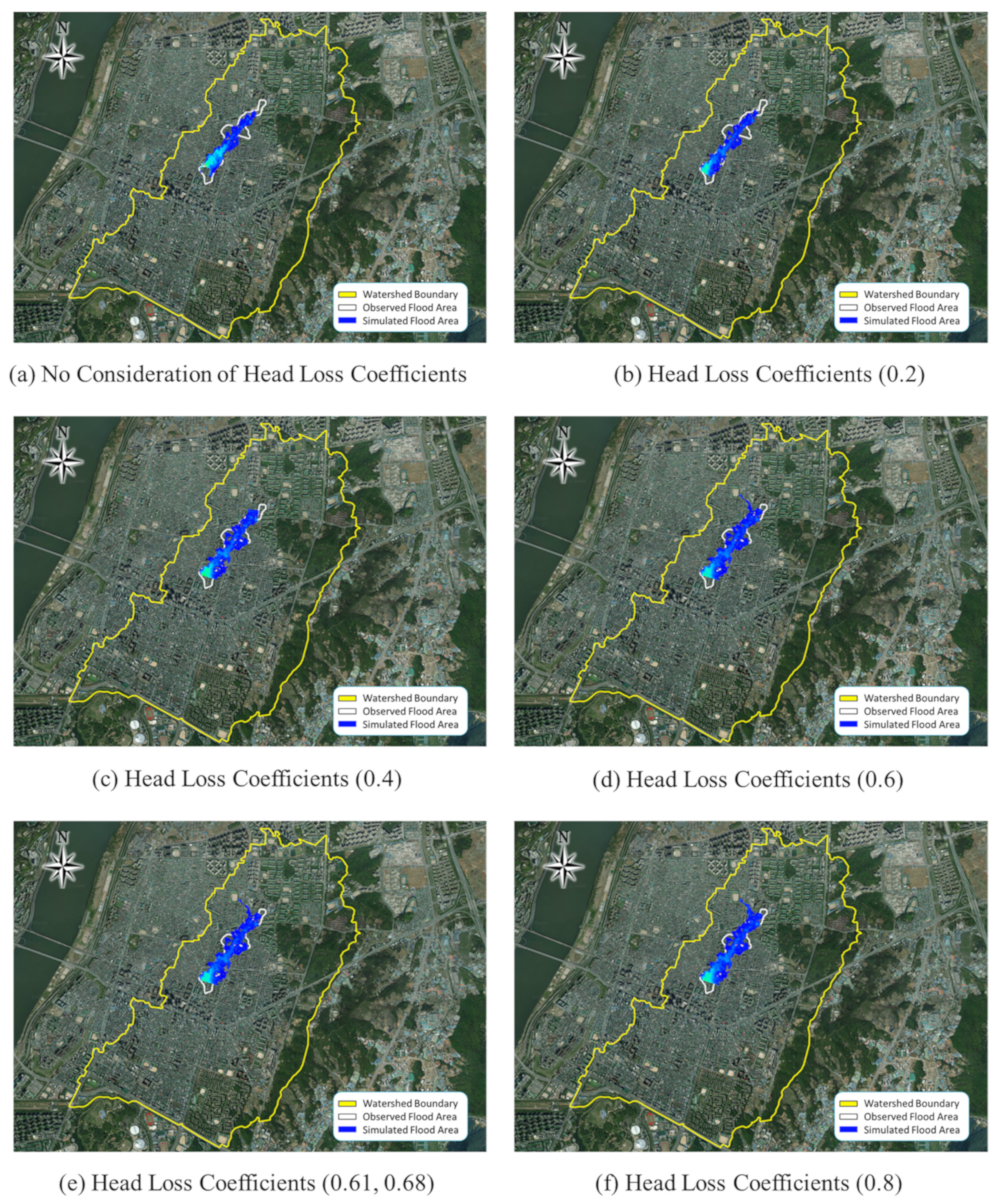
3.1. Analysis of the Effect of the Head Loss Coefficient in Flood Area Analysis
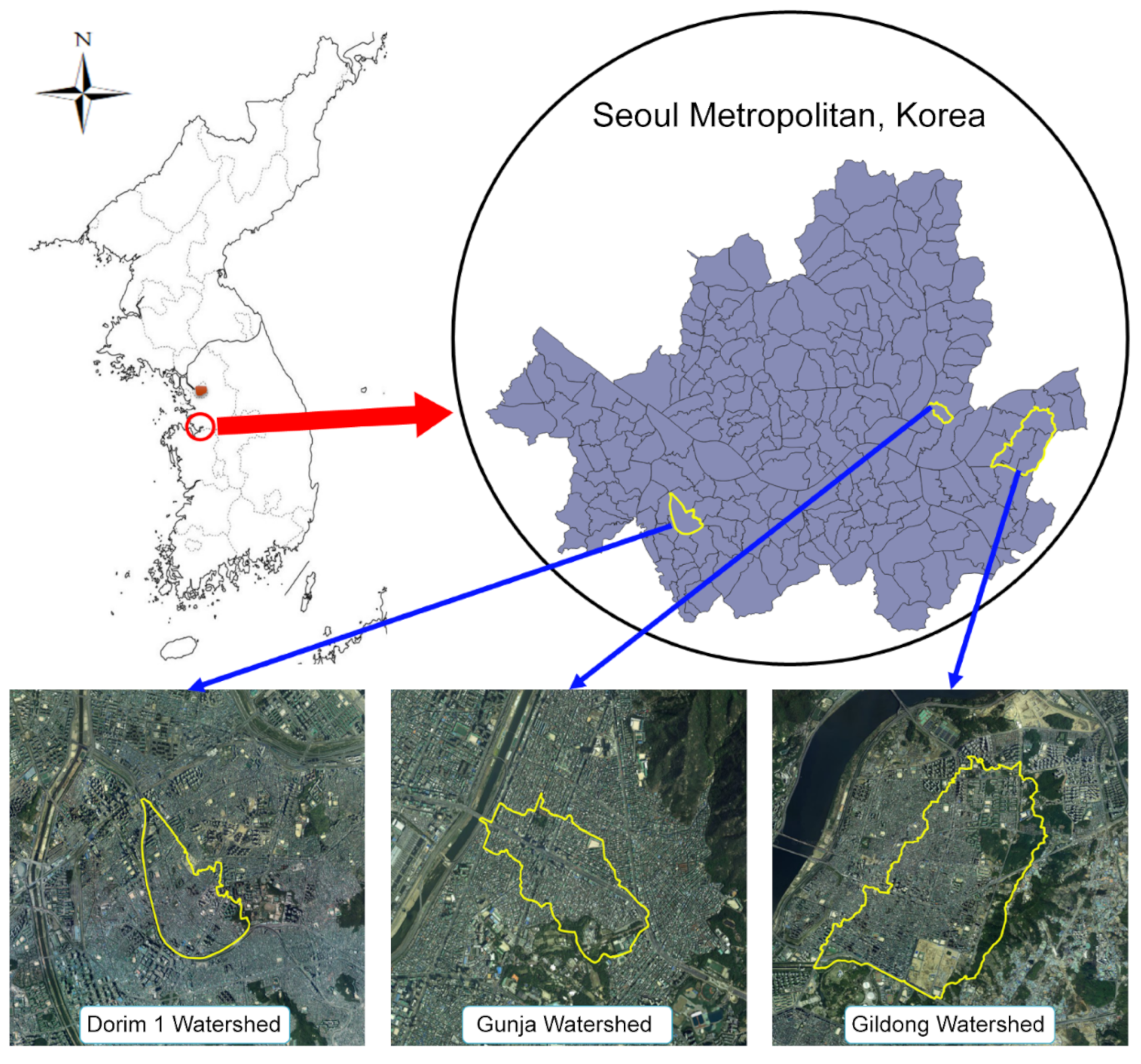
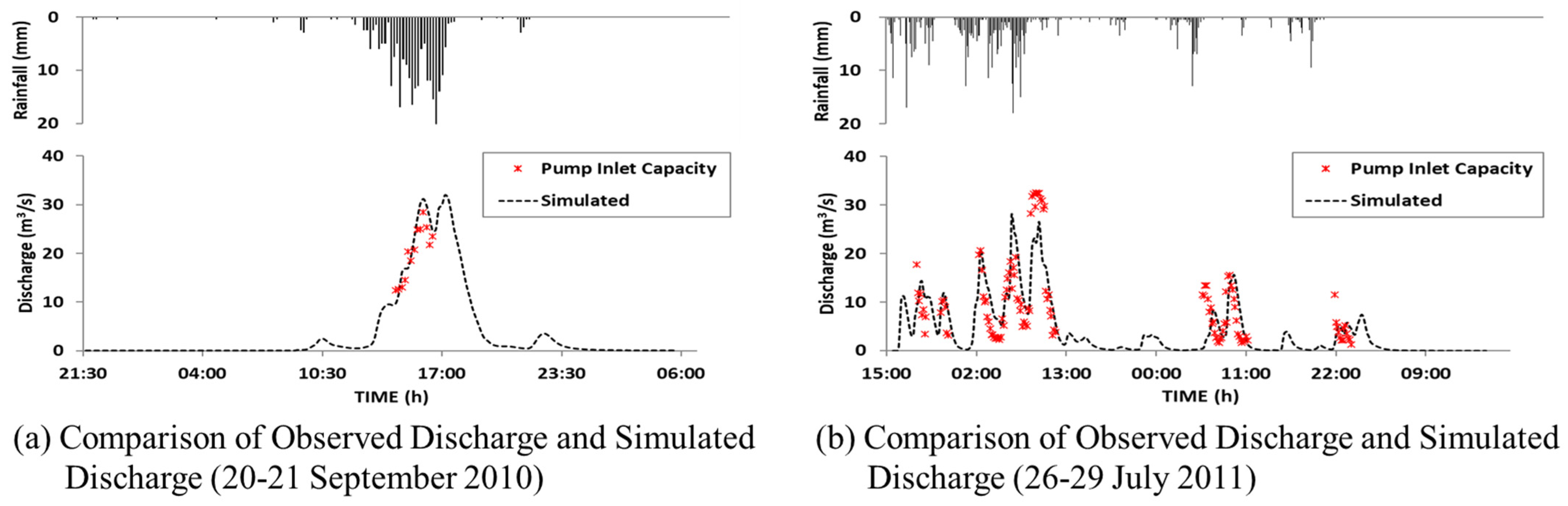
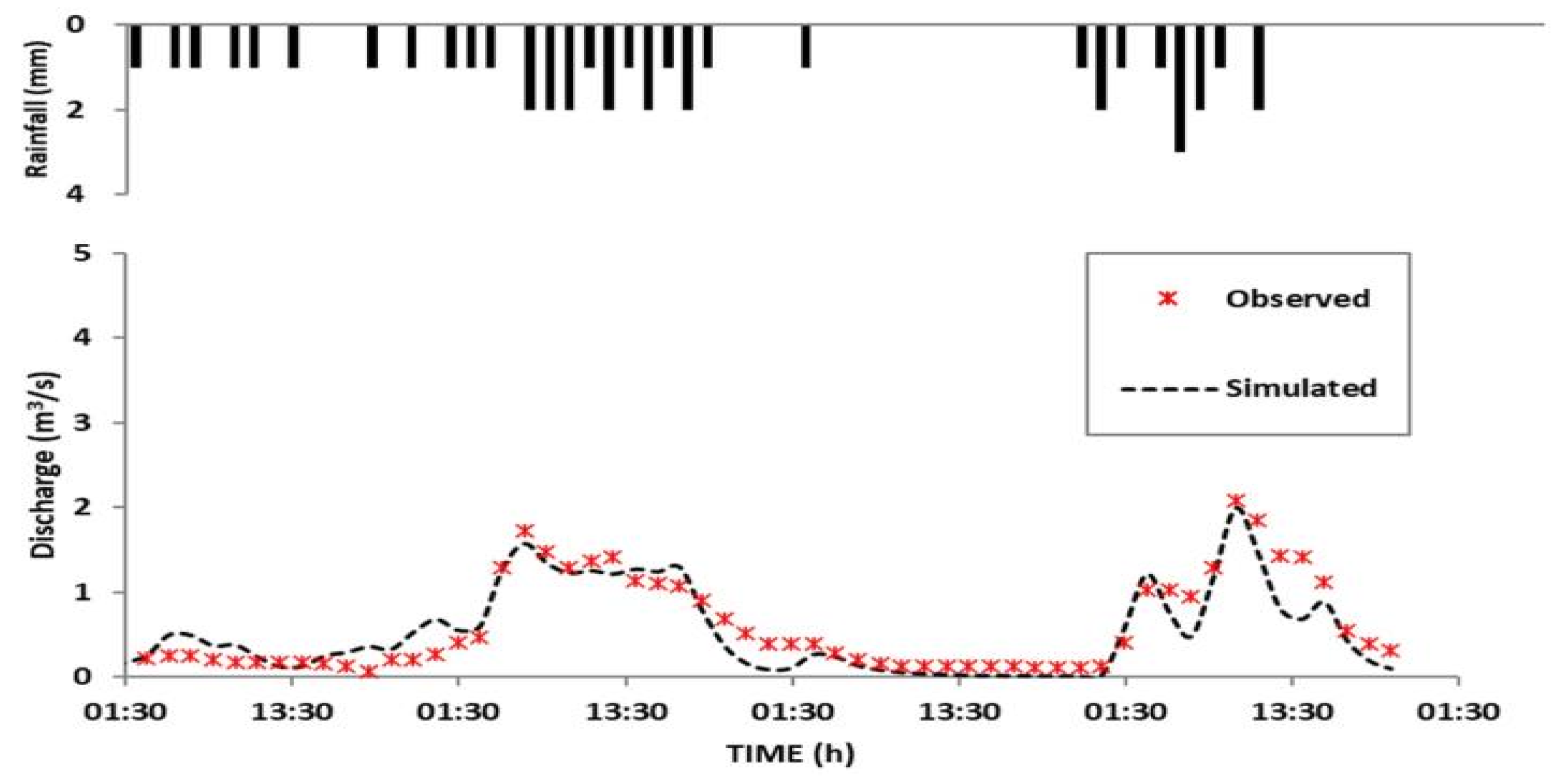
3.2. Current Status of Target Watersheds and Correction of Parameters
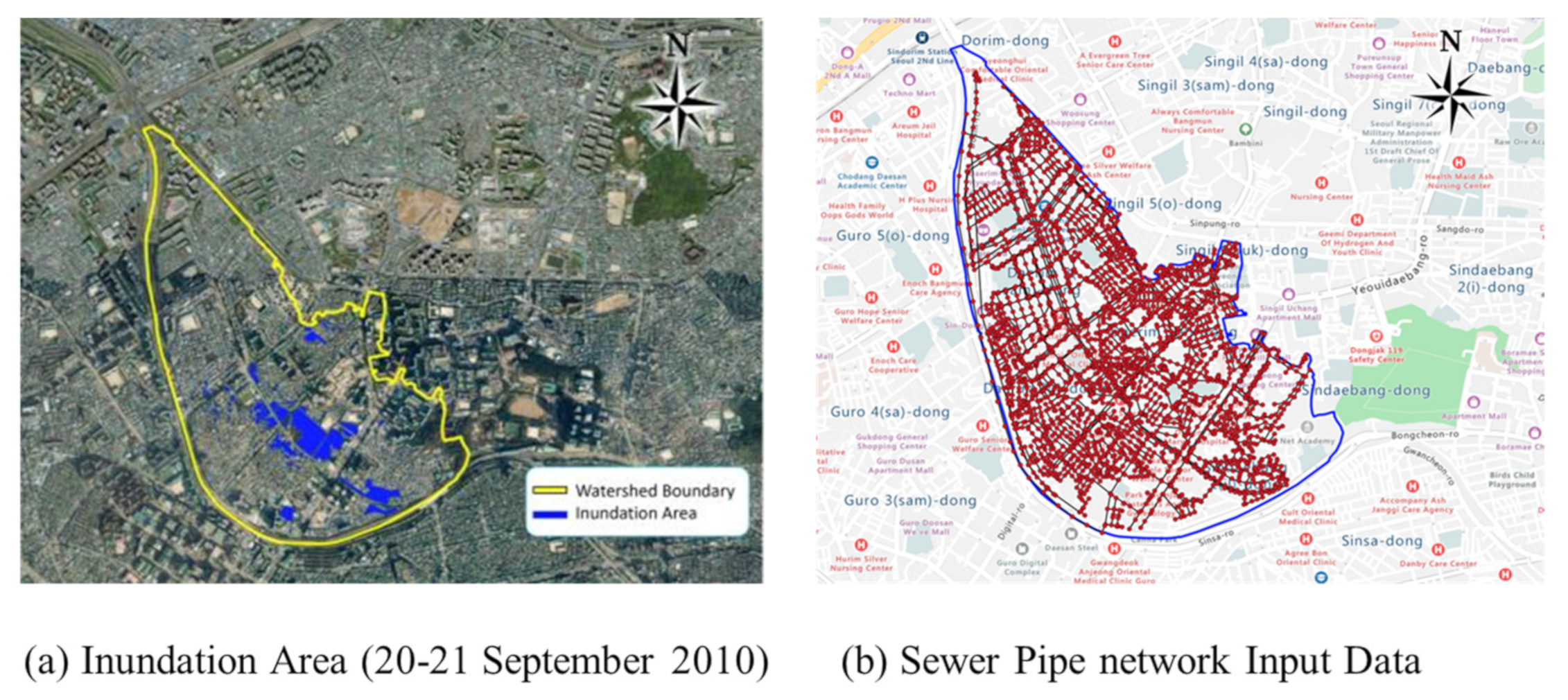
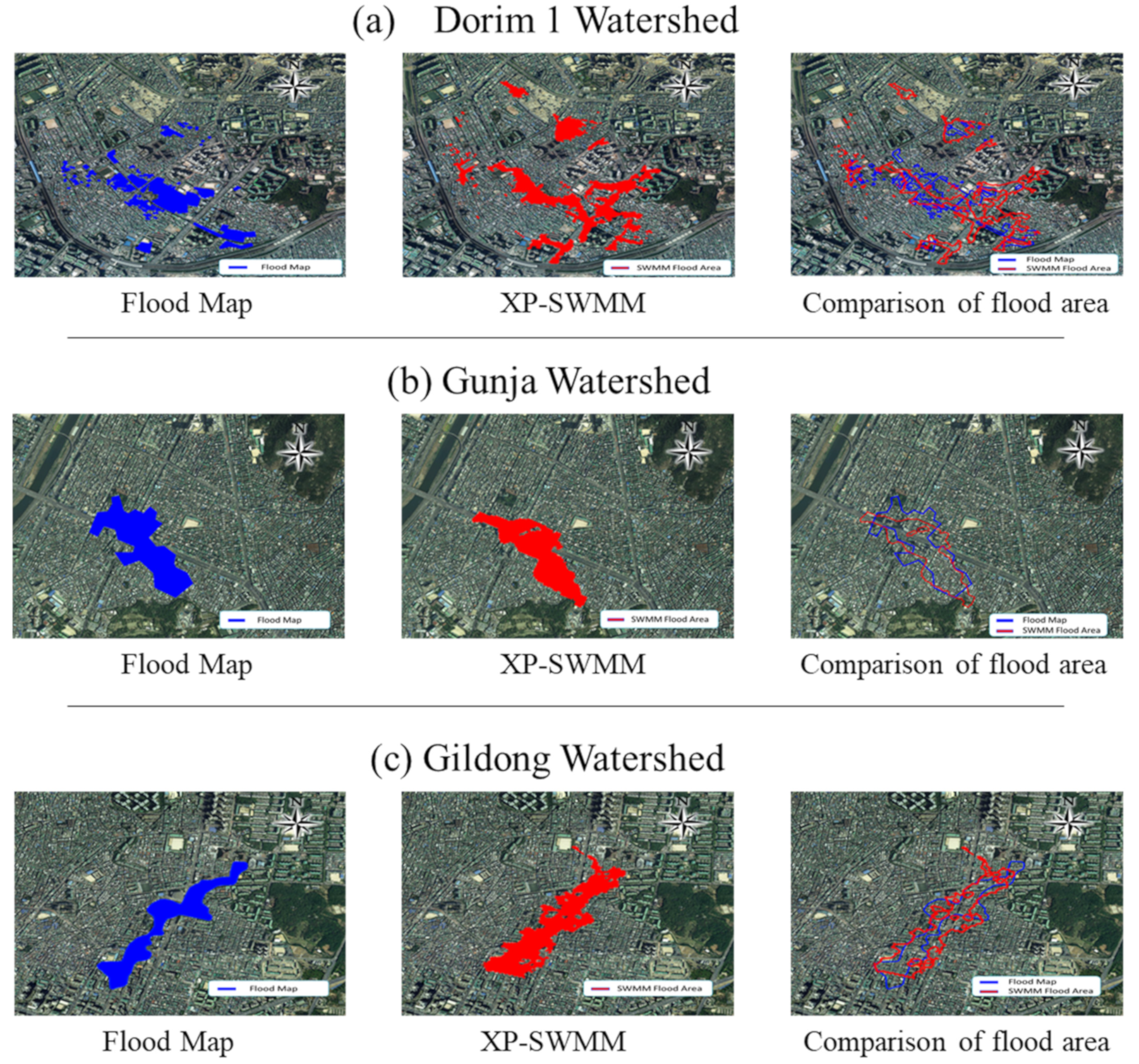
3.2.1. Dorim 1 Watershed
3.2.2. Gunja Watershed
3.2.3. Gildong Watershed
3.3. Analysis of Flood Area According to Whether or Not the Head Loss Coefficient Is Applied
3.3.1. Dorim 1 Watershed
3.3.2. Gunja Watershed
3.3.3. Gildong Watershed
4. Accuracy of Inundation Result Using LSSI
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, S.; Shi, P.; Van Rompaey, A.; Wen, J. Quantifying the impact of im-pervious surface location on flood peak discharge in urban areas. Nat. Hazards 2015, 76, 1457–1471. [Google Scholar] [CrossRef]
- Sobieraj, J.; Bryx, M.; Metelski, D. Stormwater Management in the City of Warsaw: A Review and Evaluation of Technical Solutions and Strategies to Improve the Capacity of the Combined Sewer System. Water 2022, 14, 2109. [Google Scholar] [CrossRef]
- Muroi, H.; Mine, K.; Eguchi, Y. Scenario Analysis of Sluice Gate Operations for Evaluating Inland Flood Damage. J. Disaster Res. 2021, 16, 429–436. [Google Scholar] [CrossRef]
- Koyama, N.; Yamada, T. A Proposed Simultaneous Calculation Method for Flood by River Water, Inland Flood, and Storm Surge at Tidal Rivers of Metropolitan Cities: A Case Study of Katabira River in Japan. Water 2020, 12, 1769. [Google Scholar] [CrossRef]
- Russo, B.; Valentín, M.G.; Tellez-Álvarez, J. The relevance of grated inlets within surface drainage systems in the field of urban flood resilience. A review of several experimental and numerical simulation approaches. Sustainability 2021, 13, 7189. [Google Scholar] [CrossRef]
- Martínez, C.; Vojinovic, Z.; Price, R.; Sanchez, A. Modelling Infiltration Process, Overland Flow and Sewer System Interactions for Urban Flood Mitigation. Water 2021, 13, 2028. [Google Scholar] [CrossRef]
- XP Solutions. XP SWMM 2013 User Manual; XP Solutions: Portland, OR, USA, 2013. [Google Scholar]
- O’Loughlin, G.; Stack, B. Algorithms for Pit Pressure Changes and Head Losses in Stormwater Drainage Systems. In Proceedings of the 9th International Conference on Urban Drainage, Portland, OR, USA, 8–13 September 2002. [Google Scholar] [CrossRef]
- Hsu, M.; Chen, S.; Chang, T. Inundation simulation for urban drainage basin with storm sewer system. J. Hydrol. 2000, 234, 21–37. [Google Scholar] [CrossRef]
- Choi, G.W.; Lee, H.S.; Han, M.S.; Lee, B.J. Study on Reduction of Flooding Area Using XP-SWMM at In-undation Region in the Reclaimed Land near the Incheon Bridge. In Proceedings of the KWRA Conference 2004; KWRA: Seoul, Korea, 2004; pp. 500–505. (In Korean). [Google Scholar]
- Beak, H.S.; Gang, Y.B.; Choi, S.K.; Choi, H.K. A Comparative Study of XP-SWMM and Hydraulic Model Experiment. In Proceedings of the KSCE Conference 2005; KSCE: Seoul, Korea, 2005; pp. 2760–2763. (In Korean). [Google Scholar]
- Phillips, B.C.; Yu, S.; Thompson, G.R.; De Silva, N. 1D and 2D modelling of urban drainage systems using XP-SWMM and TUFLOW. In Proceedings of the 10th International Conference on Urban Drainage, Copenhagen, Denmark, 21–26 August 2005. [Google Scholar] [CrossRef]
- Lee, C.H.; Han, K.Y.; Choi, K.H. DEM Based Urban Inundation Analysis Model Linked with SWMM. J. Korea Water Resour. Assoc. 2006, 39, 441–452. (In Korean) [Google Scholar]
- Smith, J.; Phillips, B.C.; Yu, S. Modelling Overland Flows and Drainage Augmentations in Dubbo. In Proceedings of the 46th Floodplain Management Authorities Conference, Lismore, Australia, 28 February–2 March 2006; pp. 1–14. [Google Scholar]
- Lee, J.H.; Yeon, K.S. Flood Inundation Analysis using XP-SWMM Model in Urban Area. J. Korean Soc. Hazard Mitig. 2008, 8, 155–161. (In Korean) [Google Scholar]
- Rangarajan, S.; Takamatsu, M.; Grey, G. An Integrated Modelling approach to Storm-water Management. In Proceedings of the World Environmental and Water Resources Congress, Ahupua’a, Honolulu, HI, USA, 12–16 May 2008; pp. 1–7. [Google Scholar]
- Kim, Y.J.; Han, G.Y.; Cho, W.H. Analysis on the Effects of Flood Damage Mitigation according to Installation of Underground Storage Facility. J. Korean Soc. Civ. Eng. 2010, 30, 41–51. (In Korean) [Google Scholar]
- Ahn, J.; Cho, W.; Jung, J. Flood Simulation for Basin-Shaped Urban Watershed Considering Surface Flow. J. Korean Soc. Civ. Eng. 2014, 34, 841–847. [Google Scholar] [CrossRef]
- Rosa, D.J.; Clausen, J.C.; Dietz, M.E. Calibration and Verification of SWMM for Low Impact Development. JAWRA J. Am. Water Resour. Assoc. 2015, 51, 746–757. [Google Scholar] [CrossRef]
- Del Giudice, G.; Padulano, R. Sensitivity Analysis and Calibration of a Rainfall-Runoff Model with the Combined Use of EPA-SWMM and Genetic Algorithm. Acta Geophys. 2016, 64, 1755–1778. [Google Scholar] [CrossRef]
- Kim, Y.D.; Tak, Y.H.; Park, M.H.; Kang, B. Improvement of urban flood damage estimation using a high-resolution digital terrain. J. Flood Risk Manag. 2019, 13, e12575. [Google Scholar] [CrossRef]
- Hasan, H.H.; Razali, S.F.M.; Zaki, A.Z.I.A.; Hamzah, F.M. Integrated Hydrological-Hydraulic Model for Flood Simulation in Tropical Urban Catchment. Sustainability 2019, 11, 6700. [Google Scholar] [CrossRef]
- Shen, J.; Tan, F. Effects of DEM resolution and resampling technique on building treatment for urban inun-dation modeling: A case study for the 2016 flooding of the HUST campus in Wuhan. Nat. Hazards 2020, 104, 927–957. [Google Scholar] [CrossRef]
- Choo, Y.M.; Sim, S.B.; Choe, Y.W. A Study on Urban Inundation Using SWMM in Busan, Korea, Using Existing Dams and Artificial Underground Waterways. Water 2021, 13, 1708. [Google Scholar] [CrossRef]
- Parnas, F.E.; Abdalla, E.M.H.; Muthanna, T.M. Evaluating three commonly used infiltration methods for permeable surfaces in urban areas using the SWMM and STORM. Water Policy 2021, 52, 160–175. [Google Scholar] [CrossRef]
- Kim, J.S. An Experimental Study for Flow Improvement at Surcharged Manholes. Ph.D. Thesis, Kyonggi University, Suwon, Korea, 2010. (In Korean). [Google Scholar]
- Sangster, W.M.; Wood, H.W.; Smerden, E.T.; Bossy, H.G. Pressure Changes at Storm Drain Junctions; Bulletin. No. 41; Engineering Experiment Station, University of Missouri: Columbia, MI, USA, 1958. [Google Scholar]
- Marsalek, J. Head Losses at Sewer Junction Manholes. J. Hydraul. Eng. 1984, 110, 1150–1154. [Google Scholar] [CrossRef]
- Pedersen, F.B.; Mark, O. Head Losses in Storm Sewer Manholes: Submerged Jet Theory. J. Hydraul. Eng. 1990, 116, 1317–1328. [Google Scholar] [CrossRef]
- Shinji, A.; Tetsuya, K. Manhole profiles for energy loss reduction. Proc. HydraStorm 1998, 98, 235–240. [Google Scholar]
- Ministry of Environment. Design Criteria of Sewerage. Korean Design Standard. Available online: https://eng.me.go.kr/eng/web/main.do (accessed on 11 November 2019). (In Korean).
- Frost, W.H.; Technologies, I.K. Minor Loss Coefficients for Storm Drain Modeling with SWMM. J. Water Manag. Model. 2006, 14, 517–545. [Google Scholar] [CrossRef] [Green Version]
- Lee, D.; Sallee, G. A Method of measuring shape. Geogr. Rev. 1970, 60, 555–563. [Google Scholar] [CrossRef]
- Clarke, K.C.; Hoppen, S.; Gaydos, L.J. Method and techniques for rigorous calibration of a cellular automaton model of urban growth. In Proceedings of the Third International Conference/Workshop on Integrating GIS and Environmental Modeling, Sante Fe, NM, USA, 21–25 January 1996. [Google Scholar]
- Wentz, E.A. Shape analysis in GIS. Proc. Auto-Cart. 1997, 13, 204–213. [Google Scholar]


| Manhole Type | K |
|---|---|
| Circular-Mean values 95% confidence limits | 0.61 (0.529~0.697) |
| Square-Mean values 95% confidence limits | 0.68 (0.587~0.773) |
| Main Input Parameters of XP-SWMM | Initial Parameters Value | Correction Parameters Value | |
|---|---|---|---|
| Catchment parameters | Width (m) | 2.24~114.02 | 2.24~114.02 |
| Impervious area (%) | 1.6~100 | 1.6~100 | |
| Slope (m/m) | 0.000~36.980 | 0.000~36.980 | |
| Channel parameters | Circular Size (D mm) | D200~D1100 | D200~D1100 |
| Rectangular Size (m × m) | 1.0 × 1.0~3.0 × 2.5 | 1.0 × 1.0~3.0 × 2.5 | |
| Manning roughness of channel | 0.014~0.020 | 0.020 | |
| Infiltration parameters | Decay rate (Horton’s) (1/s) | 0.001 | 2.0 |
| Ultimate infiltration rate (Horton’s) (mm/h) | 10.0 | 2.5~25.4 | |
| Manning roughness of impervious area | 0.014 | 0.014~0.015 | |
| Depression storage of impervious area (mm) | 0.0 | 2.0 | |
| Main Input Parameters of XP-SWMM | Initial Parameters Value | Estimation Parameters Value | |
|---|---|---|---|
| Catchment parameters | Width (m) | 25.0~1207.24 | 25.0~1207.24 |
| Impervious area (%) | 22.4~100.0 | 22.4~100.0 | |
| Slope (m/m) | 0.002~0.108 | 0.002~0.108 | |
| Channel parameters | Circular Size (D mm) | D450~D1000 | D200~D1000 |
| Rectangular Size (m × m) | 1.3 × 1.3~2.5 × 2.5 | 1.3 × 1.3~2.5 × 2.5 | |
| Manning roughness of channel | 0.014~0.020 | 0.020 | |
| Infiltration parameters | Decay rate (Horton’s) (1/s) | 0.001 | 0.00056 |
| Ultimate infiltration rate (Horton’s) (mm/h) | 10.0 | 12.7 | |
| Manning roughness of impervious area | 0.014 | 0.020 | |
| Depression storage of impervious area (mm) | 0.0 | 1.3 | |
| Drainage System | Watershed Area (km2) | Benefiter Area (km2) | Pump (HP × EA) | Discharge (m3/min) | Storage Capacity (m3) | Reservoir Water Level (m) | ||
|---|---|---|---|---|---|---|---|---|
| H.W.L | L.W.L | Depth | ||||||
| Seongnaecheon | 6.34 | 1.13 | 950 × 10 1110 × 3 | 4500 | 237,000 | 13.0 | 9.5 | 3.5 |
| Main Input Parameters of XP-SWMM | Initial Parameters Value | Estimation Parameters Value | |
|---|---|---|---|
| Catchment parameters | Width (m) | 4.0~126.0 | 4.0~126.0 |
| Impervious area (%) | 37.8~98.0 | 37.8~98.0 | |
| Slope (m/m) | 0.005~0.200 | 0.005~0.200 | |
| Channel parameters | Circular Size (D mm) | D300~D1600 | D300~D1600 |
| Rectangular Size (m × m) | 0.8 × 1.3~3.5 × 2.5 | 0.8 × 1.3~3.5 × 2.5 | |
| Manning Roughness of channel | 0.015~0.020 | 0.020 | |
| Infiltration parameters | Decay rate (Horton’s) (1/s) | 0.001 | 0.015 |
| Ultimate infiltration rate (Horton’s) (mm/h) | 10.0 | 4.5 | |
| Manning roughness of impervious area | 0.014 | 0.014 | |
| Depression storage of impervious area (mm) | 0.0 | 3.3 | |
| Head Loss Coefficients | None | 0.20 | 0.40 | 0.60 | 0.61, 0.68 | 0.80 | |
|---|---|---|---|---|---|---|---|
| Result | |||||||
| Number of Flooded Cells | 1213 | 1526 | 1819 | 2005 | 2039 | 2172 | |
| Simulated Area (km2) | 0.2086 | 0.2625 | 0.3128 | 0.3448 | 0.3506 | 0.3735 | |
| Observed Area(km2) | 0.3565 | ||||||
| Rate of Concordance (%) | 58.51 | 73.63 | 87.74 | 96.72 | 98.35 | 104.79 | |
| Head Loss Coefficients | None | 0.20 | 0.40 | 0.60 | 0.61, 0.68 | 0.80 | |
|---|---|---|---|---|---|---|---|
| Result | |||||||
| Number of Flooded Cells | 1270 | 1348 | 1440 | 1599 | 1636 | 1809 | |
| Simulated Area (km2) | 0.1438 | 0.1527 | 0.1629 | 0.1811 | 0.1852 | 0.2048 | |
| Observed Area (km2) | 0.1917 | ||||||
| Rate of Concordance (%) | 75.01 | 79.66 | 85.01 | 94.48 | 96.61 | 106.83 | |
| Head Loss Coefficients | None | 0.20 | 0.40 | 0.60 | 0.61, 0.68 | 0.80 | |
|---|---|---|---|---|---|---|---|
| Result | |||||||
| Number of Flooded Cells | 513 | 630 | 759 | 828 | 835 | 892 | |
| Simulated Area (km2) | 0.1154 | 0.1417 | 0.1708 | 0.1863 | 0.1879 | 0.2005 | |
| Observed Area (km2) | 0.1893 | ||||||
| Rate of Concordance (%) | 60.96 | 74.85 | 90.23 | 98.43 | 99.27 | 105.92 | |
| Range of LSSI | Degrees of Accuracy |
|---|---|
| 40.0 over | Excellent |
| 30.0 over | Good |
| 20.0 over | Fair |
| 10.0 over | Poor |
| 5.0 over | Fail |
| Watershed | Flood Area (km2) | LSSI (%) | Degree | |||
|---|---|---|---|---|---|---|
| Flood Map (A) | XP-SWMM (B) | A ∩ B | A ∪ B | |||
| (a) Dorim 1 | 0.3565 | 0.3506 | 0.1951 | 0.5865 | 32.27 | Good |
| (b) Gunja | 0.1917 | 0.1852 | 0.1277 | 0.2398 | 53.25 | Excellent |
| (c) Gildong | 0.1893 | 0.1879 | 0.1348 | 0.2919 | 46.19 | Excellent |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, C.; Kim, J.; Lee, S.; Yoo, I. Application of Head Loss Coefficient for Surcharge Straight Path Manhole to Improve the Accuracy of Urban Inundation Analysis. Water 2022, 14, 2725. https://doi.org/10.3390/w14172725
Kwak C, Kim J, Lee S, Yoo I. Application of Head Loss Coefficient for Surcharge Straight Path Manhole to Improve the Accuracy of Urban Inundation Analysis. Water. 2022; 14(17):2725. https://doi.org/10.3390/w14172725
Chicago/Turabian StyleKwak, Changjae, Jungsoo Kim, Sungho Lee, and Ingi Yoo. 2022. "Application of Head Loss Coefficient for Surcharge Straight Path Manhole to Improve the Accuracy of Urban Inundation Analysis" Water 14, no. 17: 2725. https://doi.org/10.3390/w14172725






