Hydraulic Characteristics of Lateral Deflectors with Different Geometries in Gentle-Slope Free-Surface Tunnels
Abstract
:1. Introduction
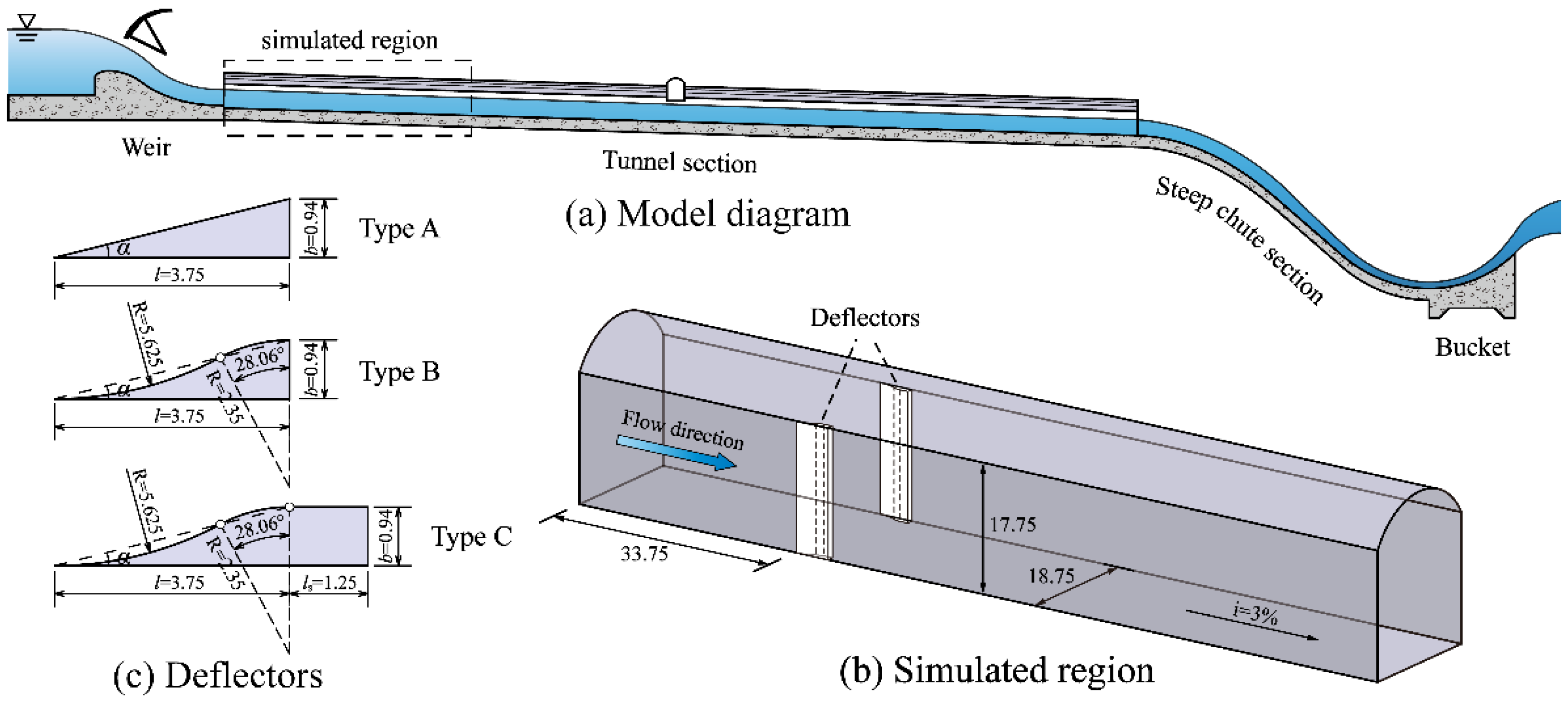
2. Experiment Setup
3. Numerical Models and Simulation Setup
3.1. Governing Equations
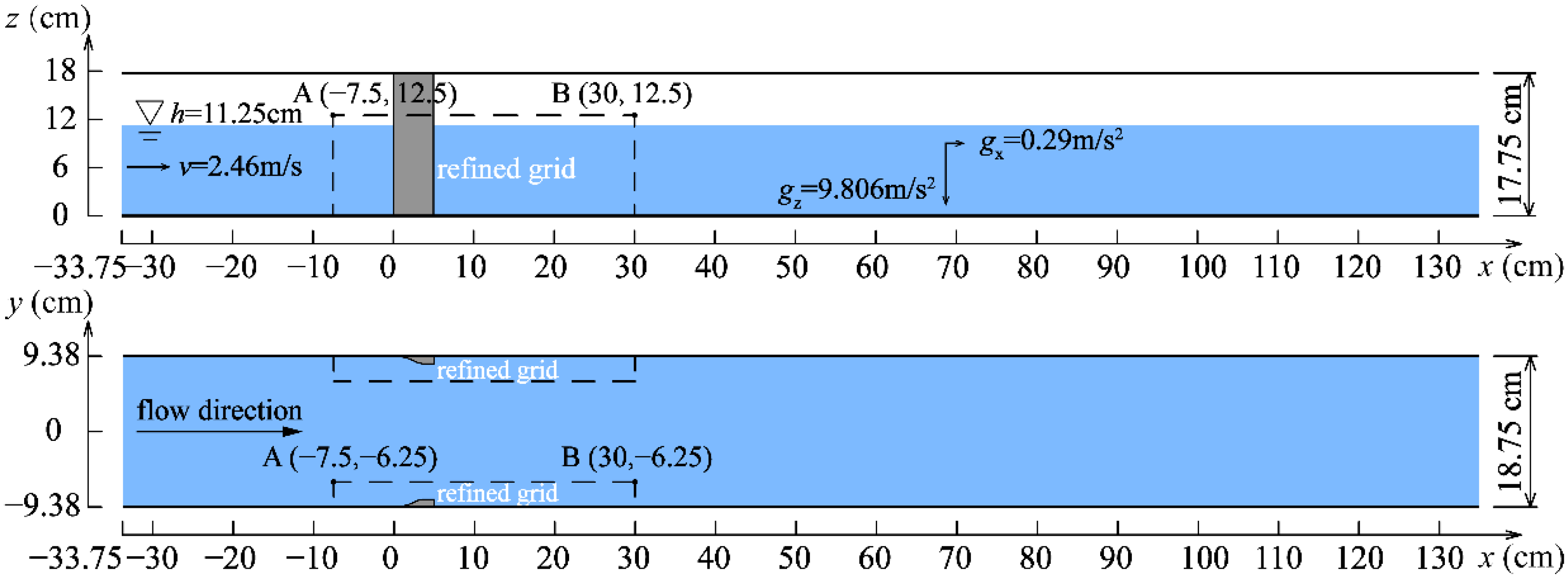
3.2. Simulation Setup
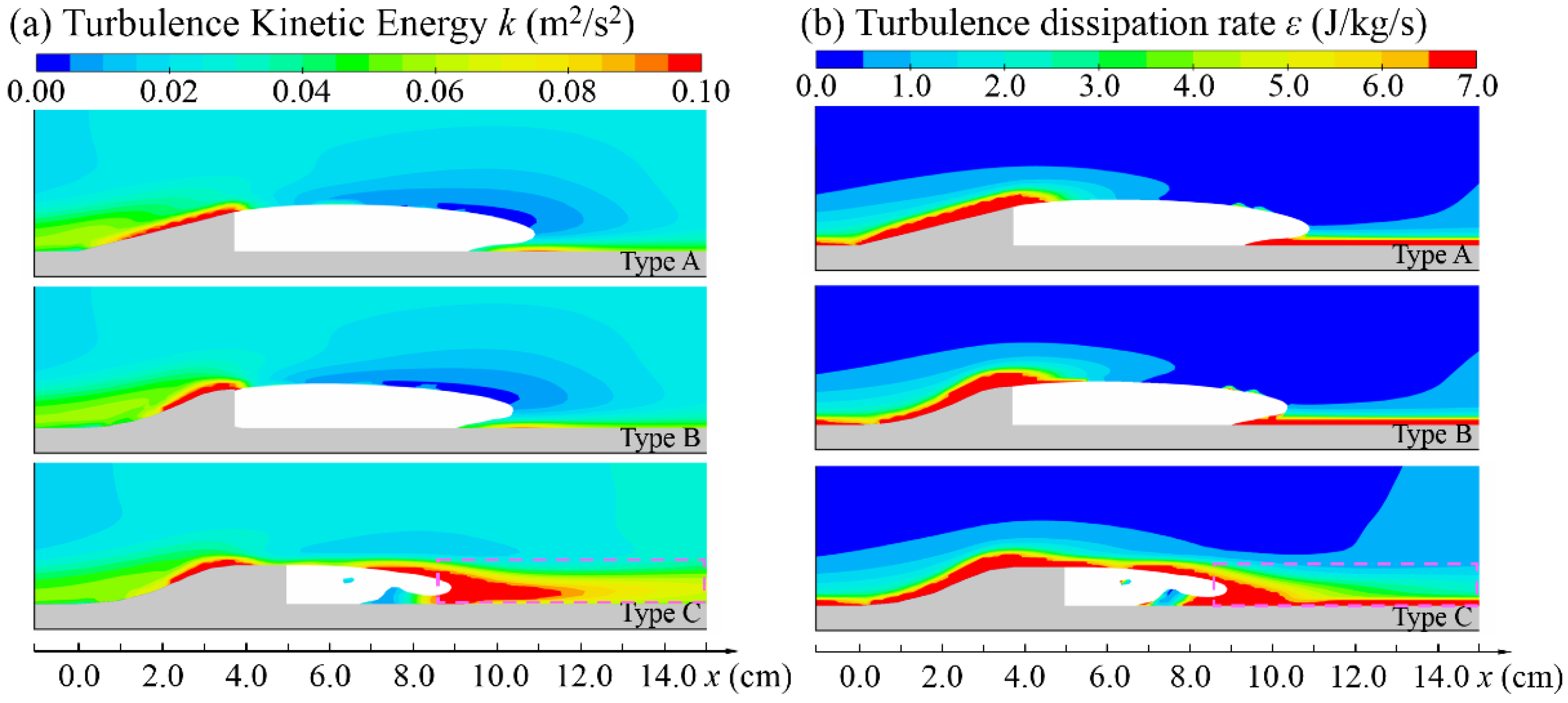
4. Results and Discussion
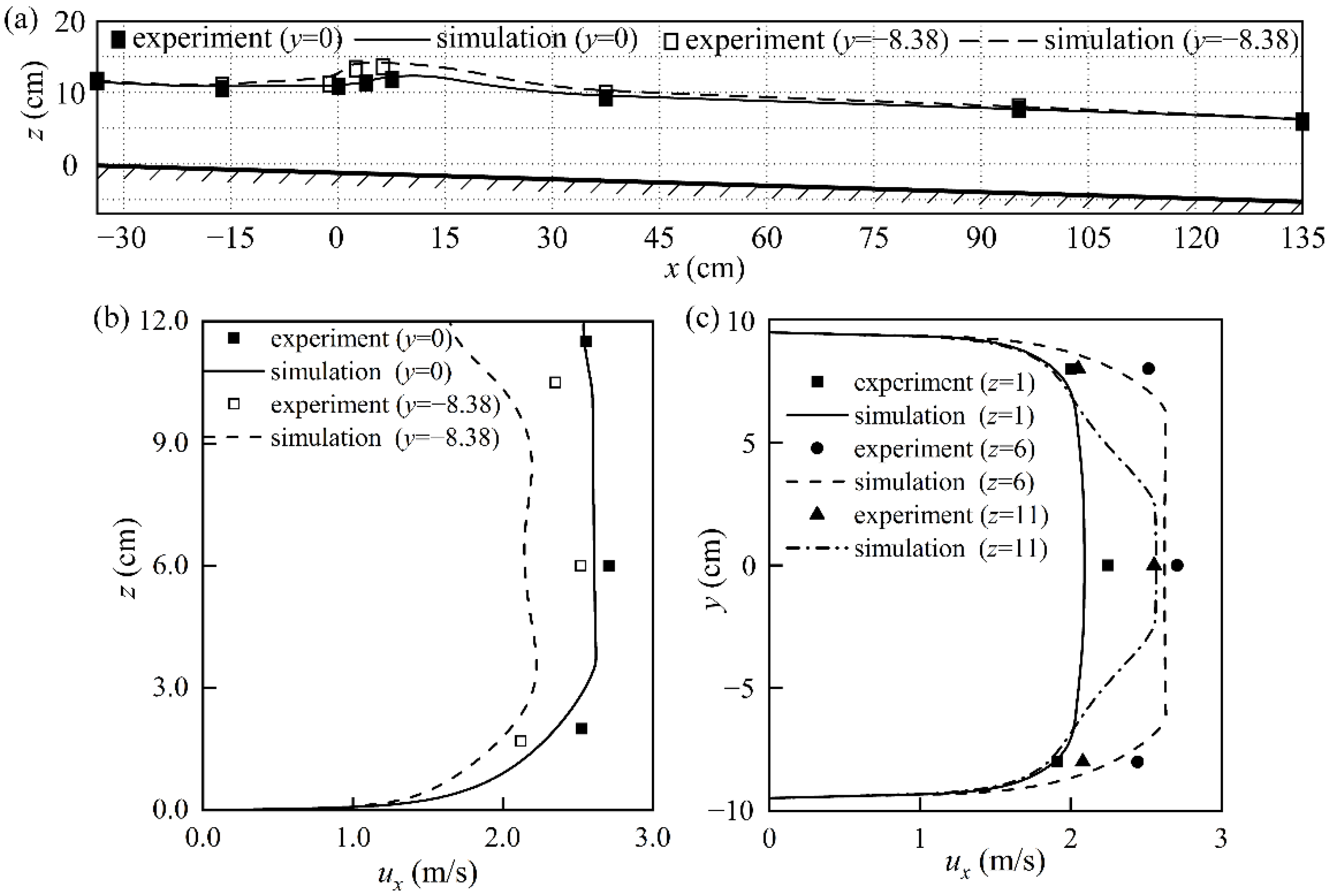
4.1. Model Validation
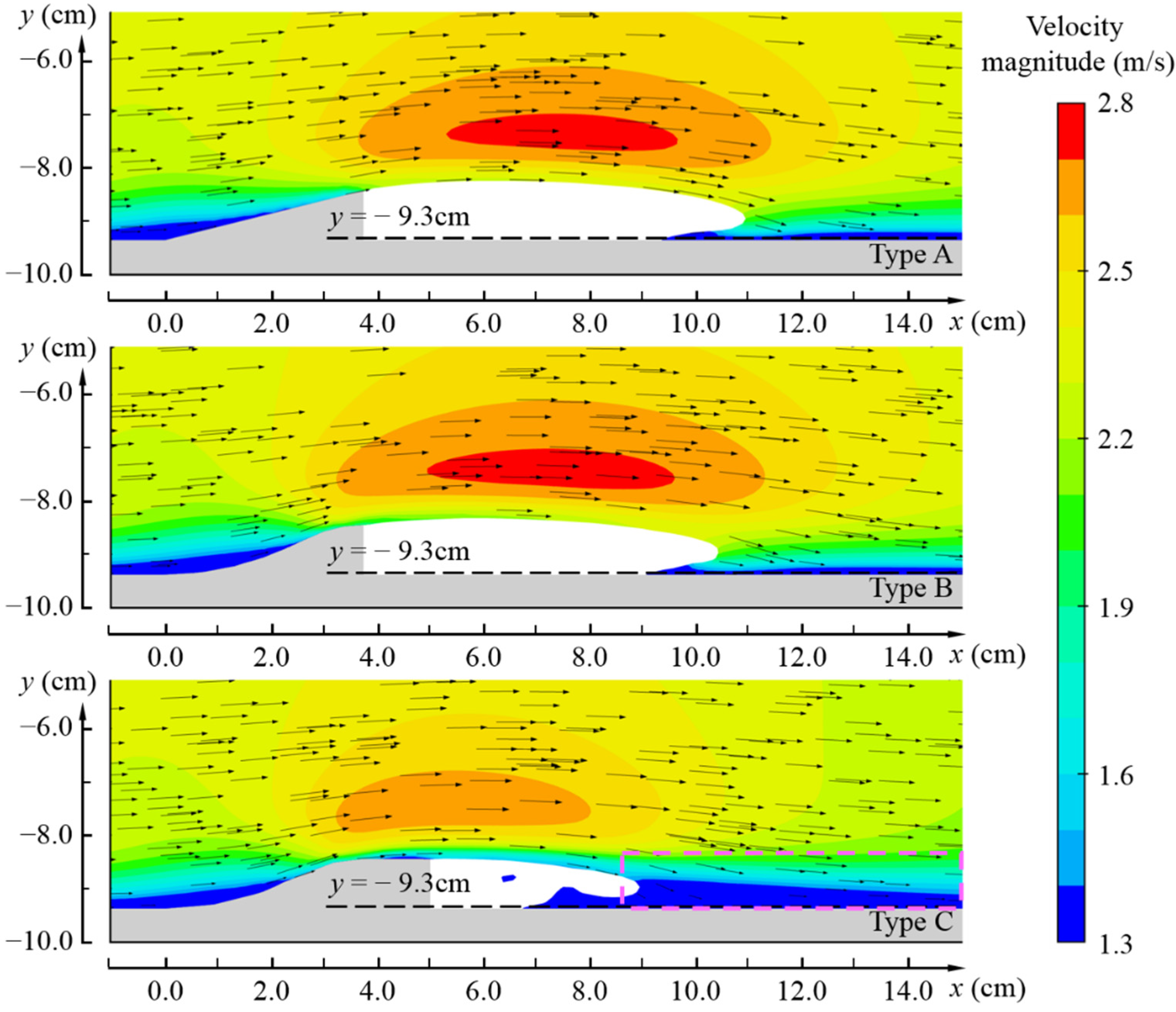
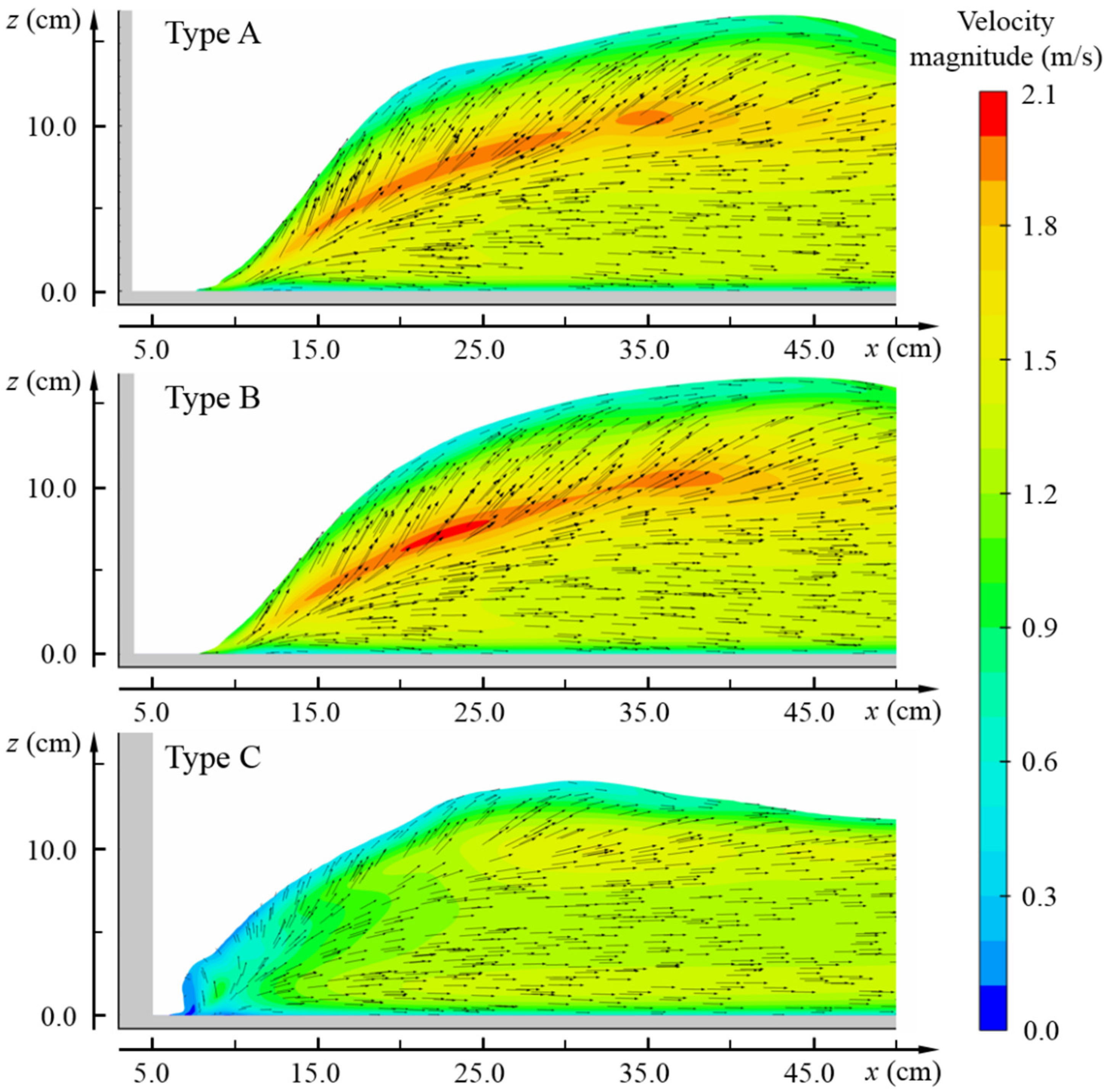
4.2. Flow Pattern
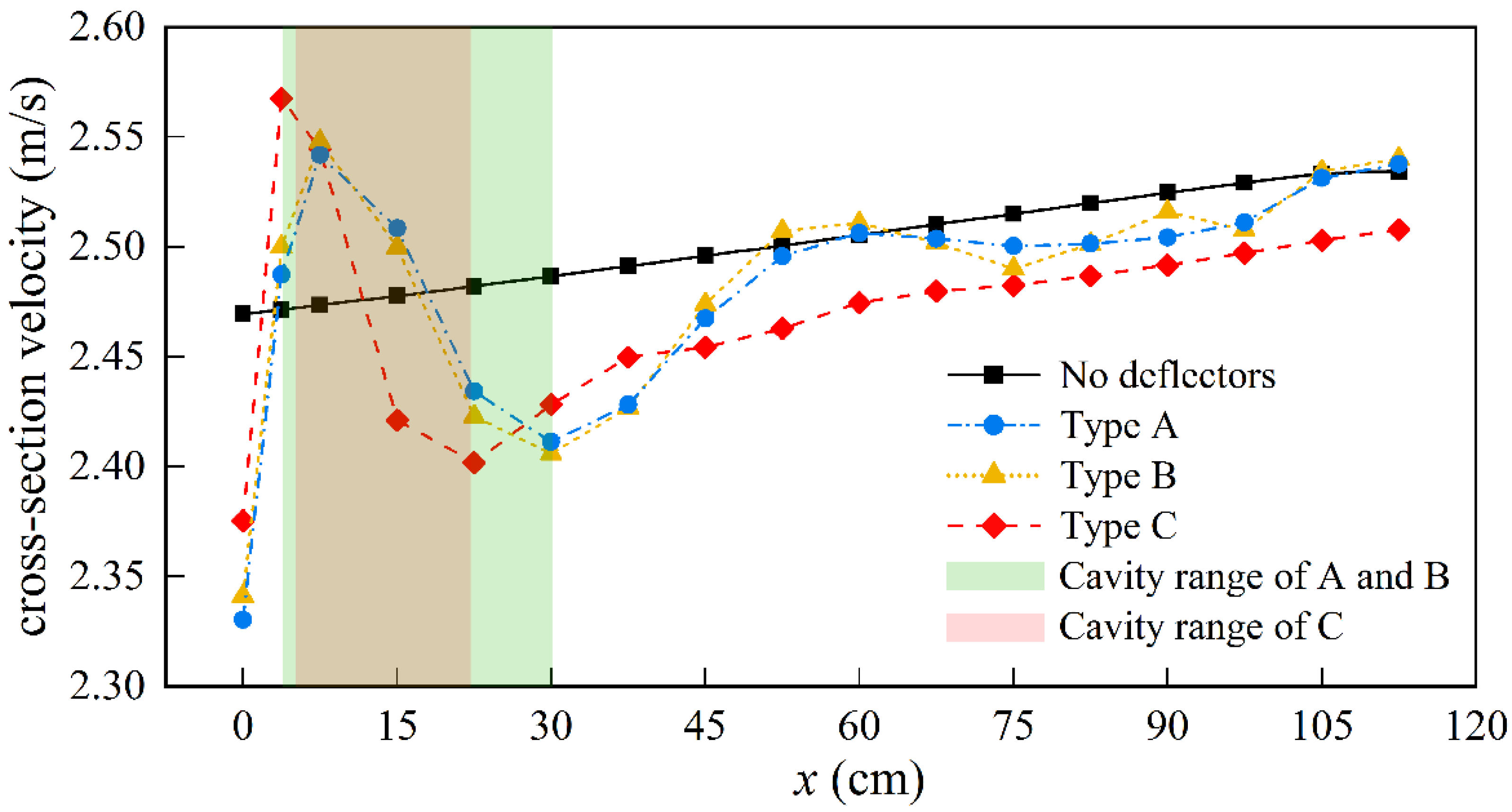
4.3. Velocity Distribution
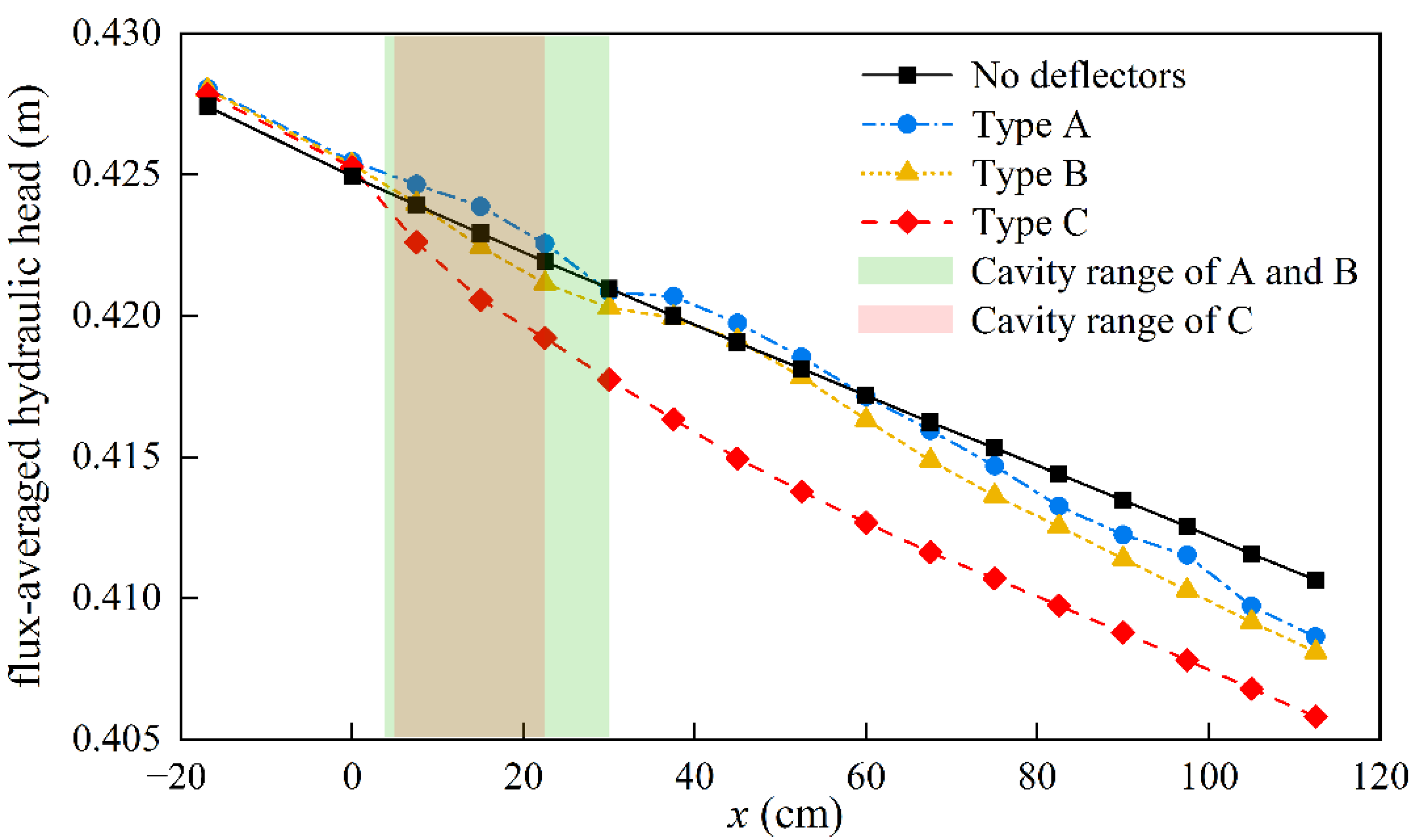
4.4. Energy Dissipation Characteristics
5. Conclusions
- The cavity formed behind lateral deflectors usually features a right-angled trapezoid shape with a larger streamwise length at higher elevations because of non-uniform velocity distributions. This makes the deflected flow rise up along the impacting region inside the cavity and potentially induced shock waves depending on the interaction of the rising up water-wings and the jet surfaces.
- The traditional triangular deflector forms an adequately wide cavity that allows for the free rising up of the water-wings inside the cavity, which further contributes to the development of the buddle-type shock wave, whereas the two-arc deflector yields a jet with fluctuating surface, resulting from the non-uniform planar velocity distribution caused by the continuously varying curvature of the arcs. Water-wings also develop inside the cavity and eventually produce a diamond-type shock wave downstream. In contrast, the jet behind the two-arc deflector with a straight guiding line at the tail is stabler and travels a shorter distance before impacting the side wall. The jet could thus restrict the development of the rising flow, and thereby eliminate the formation of water-wings and shock waves. Based on these observations, it is concluded that a continuous variation of the lateral deflector surface at the tail with an additional flow guiding extension is the key to the elimination of the water-wings and shock waves.
- Compared to the triangular deflector and the two-arc deflector, the two-arc deflector with a straight line exhibits more effective energy dissipation, as reflected in the local energy loss coefficient. The underlying reason for its effective energy dissipation is the more intensive turbulence introduced by the stronger interaction between the deflected flow and the jet surface, which also leads to more intensive aeration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
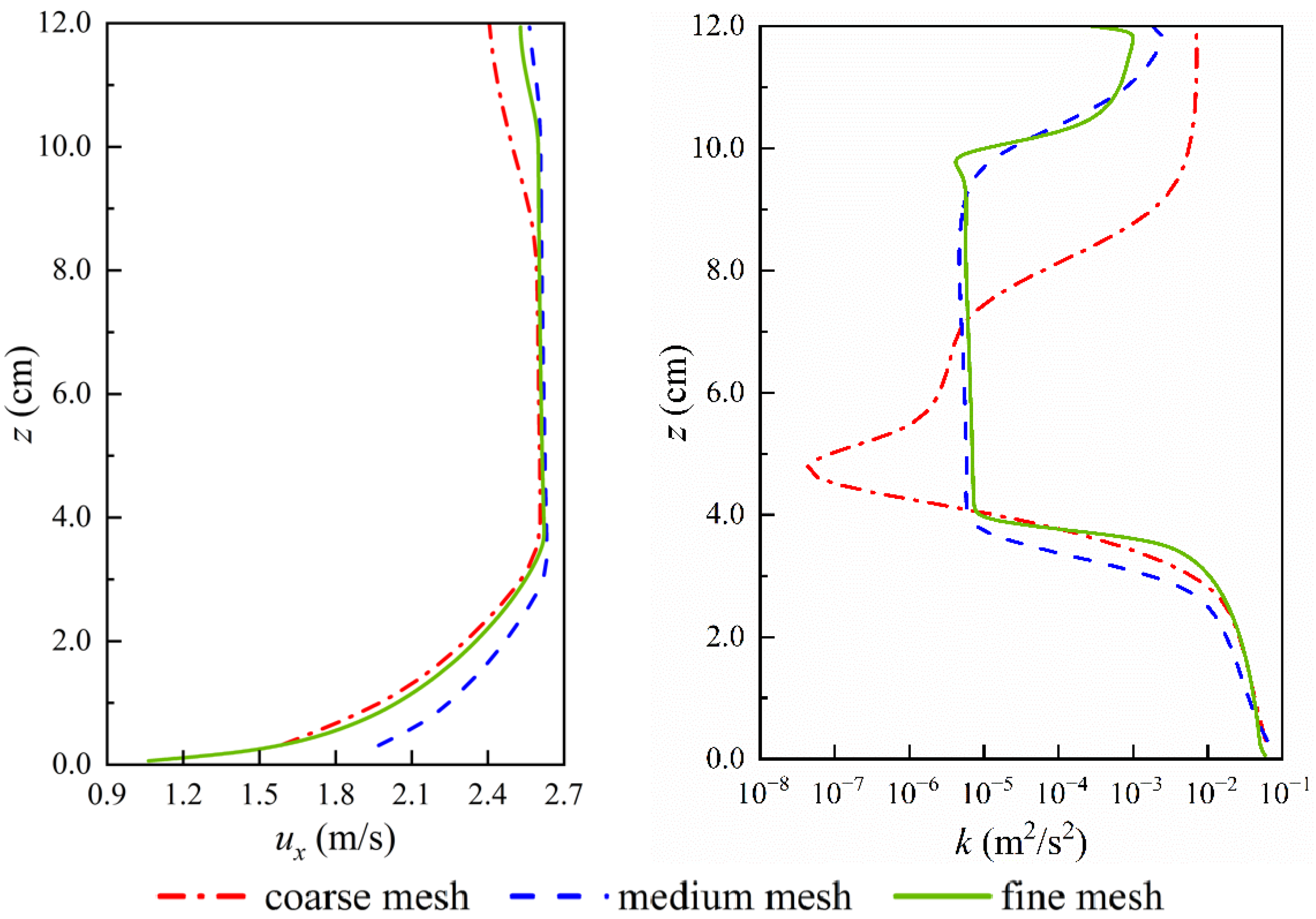
| Mesh | /cm | r | p(umax) | f(umax)/(m·s−1) | ε(umax)/% | GCI(umax)/% |
|---|---|---|---|---|---|---|
| coarse | 0.496 | - | 1.84 | 2.607 | - | - |
| medium | 0.297 | 1.67 | 2.633 | 0.997 | 2.040 | |
| fine | 0.149 | 1.99 | 2.621 | 0.456 | 0.224 |
References
- Xie, Z.S.; Wu, Y.H.; Chen, W.X. New technology and innovation on flood discharge and energy dissipation of high dams in China. J. Hydraul. Eng. 2016, 47, 324–336. (In Chinese) [Google Scholar] [CrossRef]
- Ma, H.; Chi, F. Major technologies for safe construction of high earth-rockfill dams. Engineering 2016, 2, 498–509. [Google Scholar] [CrossRef]
- Ma, H.; Chi, F. Technical progress on researches for the safety of high concrete-faced rockfill dams. Engineering 2016, 2, 332–339. [Google Scholar] [CrossRef]
- Fan, L.; Zhang, H.W.; Liu, Z.P.; Zhang, D. Numerical study on hydraulic characteristic of free surface flow in spillway tunnel with different configuration. J. Hydroelectr. Eng. 2009, 28, 126–131. (In Chinese) [Google Scholar]
- Guo, J.; Zhang, D.; Liu, Z.P.; Fan, L. Achievements on hydraulic problems in large spillway tunnel with a high head and large discharge flow and its risk analysis. J. Hydraul. Eng. 2006, 37, 1193–1198. (In Chinese) [Google Scholar] [CrossRef]
- Pang, C.J.; Yuan, Y.Z. Research on type of aerator in large gentle-slope free-surface ‘dragon-head-up’ spillway tunnel. J. Hydraul. Eng. 1993, 6, 61–66. (In Chinese) [Google Scholar] [CrossRef]
- Bai, R.; Liu, S.; Wang, W.; Zhang, F. Experimental investigation of the dissipation rate in a chute aerator flow. Exp. Therm. Fluid Sci. 2019, 101, 201–208. [Google Scholar] [CrossRef]
- Suo, L.S.; Liu, N. Handbook of Hydraulic Structure Design, 2nd ed.; China Waterpower Press: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Chanson, H. Study of air entrainment and aeration devices. J. Hydraul. Res. 1989, 27, 301–319. [Google Scholar] [CrossRef]
- Du, L.Q.; Tang, Y.Q.; Wang, J.S. Construction technology of slip form for bottom plate of turning point section of spillway tunnel of Wudongde Hydropower Station. Yangtze River 2020, 51, 193–196. (In Chinese) [Google Scholar] [CrossRef]
- Suo, H.M.; Zhou, Z.J.; He, L.; Zhang, J.M. Study on type of tunnel spillway in Shuangjiangkou Hydropower Station. Des. Hydroelectr. Power Stn. 2021, 37, 9–12. (In Chinese) [Google Scholar] [CrossRef]
- Wang, H.Y.; Dai, G.Q.; Yang, Q.; Liu, C. Experimental study on V-type aerator for spillway tunnel with inlet raised. J. Hydraul. Eng. 2005, 36, 102–105. (In Chinese) [Google Scholar] [CrossRef]
- Yang, J.; Teng, P.; Zhang, H. Experiments and cfd modeling of high-velocity two-phase flows in a large chute aerator facility. Eng. Appl. Comp. Fluid Mech. 2019, 13, 48–66. [Google Scholar] [CrossRef]
- Hager, W.H.; Boes, R.M. Hydraulic structures: A positive outlook into the future. J. Hydraul. Res. 2014, 52, 299–310. [Google Scholar] [CrossRef]
- Li, S.; Zhang, J.; Xu, W.; Chen, J.; Peng, Y.; Li, J.; He, X. Simulation and experiments of aerated flow in curve-connective tunnel with high head and large discharge. Int. J. Civ. Eng. 2016, 14, 23–33. [Google Scholar] [CrossRef]
- Juon, R.; Hager, W.H. Flip bucket without and with deflectors. J. Hydraul. Eng. 2000, 126, 837–845. [Google Scholar] [CrossRef]
- Wang, H.Y.; Yang, Q.; Dai, G.Q.; Liu, C. Study on hydraulic characteristic of aerator with side-walls sudden enlargement in free-flow spillway tunnel. Adv. Mater. Res. 2012, 614, 613–616. [Google Scholar] [CrossRef]
- Ma, X.; Dai, G.; Yang, Q.; Li, G.; Zhao, L. Analysis of influence factors of cavity length in the spillway tunnel downstream of middle gate chamber outlet with sudden lateral enlargement and vertical drop aerator. J. Hydrodyn. 2010, 22, 657–663. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Chute aerators. II: Hydraulic design. J. Hydraul. Eng. 2010, 136, 360–367. [Google Scholar] [CrossRef]
- Nie, M.; Wang, X.; Wu, G. Effect of lateral deflector on outlet cavity lengths. J. Hydraul. Eng. 2003, 129, 536–540. [Google Scholar] [CrossRef]
- Xu, J.; Wu, J.; Peng, Y.; Ma, F. Fin performance of 3-d aerator devices with backward lateral deflectors. J. Hydrodyn. 2020, 32, 410–413. [Google Scholar] [CrossRef]
- Siying, W.; Jinbo, Y.; Caihuan, W. Study on the aerator of spillway tunnel in one large-scale project. In Proceedings of the 35th World Congress of the International-Association-for-Hydro-Environment-Engineering-and-Research (IAHR), Chengdu, China, 8–13 September 2013. [Google Scholar]
- Ye, F.; Xu, W.; Wei, W. Experimental study of the air concentration diffusion in aerated chute flows downstream of lateral and bottom aerators. AIP Adv. 2022, 12, 25221. [Google Scholar] [CrossRef]
- Nie, M.X.; Wu, G.G. Effect of the lateral deflector on cavity design. J. Tsinghua Univ. 2002, 42, 546–550. (In Chinese) [Google Scholar] [CrossRef]
- Nie, M. Comparison of energy dissipation with and without aerators. Tsinghua Sci. Technol. 2000, 5, 222–225. [Google Scholar]
- Lucas, J.; Hager, W.H.; Boes, R.M. Deflector effect on chute flow. J. Hydraul. Eng. 2013, 139, 444–449. [Google Scholar] [CrossRef]
- Nie, M.X.; Duan, B.; Li, L.L. Hydraulic characteristics along the sidewall of a sluice downstream of a sudden lateral enlargement and vertical drop. J. Tsinghua Univ. 2006, 46, 1969–1972. (In Chinese) [Google Scholar] [CrossRef]
- Liu, C.; Zhang, G.K.; Li, N.W.; Zhang, G.B.; Wang, H.Y. The effect of base aerator on the length of lateral cavity. Adv. Eng. Sci. 2008, 40, 1–4. (In Chinese) [Google Scholar]
- Wu, G.L.; Ma, F.; Wu, J.H.; Xu, J.R.; Peng, Y.; Wang, Z. Experimental investigation of flow regime control for dragon-drop-tail section of the spillway tunnel. Chin. J. Hydrodyn. 2015, 30, 140–145. (In Chinese) [Google Scholar] [CrossRef]
- Wu, J.; Li, D.; Ma, F.; Qian, S. Fin characteristics of aerator devices with lateral deflectors. J. Hydrodyn. 2013, 25, 258–263. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, Z.P.; Zhang, D.; Wu, Y.H. Study on hydraulic characteristics of sidewall aerators in high-head large-discharge spillway tunnel. J. Hydroelectr. Eng. 2015, 34, 111–116. (In Chinese) [Google Scholar] [CrossRef]
- Li, F.T.; Liu, P.Q.; Xu, W.L.; Tian, Z. Experimental study on effect of flaring piers on weir discharge capacity in high arch dam. J. Hydraul. Eng. 2003, 11, 43–47. (In Chinese) [Google Scholar] [CrossRef]
- Zheng, X.; Zhang, L.; Wu, S.; Song, K. Study on the shape of the aerator of high-head discharge tunnel with mild bottom slope. Water-Sui. 2021, 13, 2128. [Google Scholar] [CrossRef]
- Li, S.; Zhang, J.; Xu, W.; Chen, J.; Peng, Y. Evolution of pressure and cavitation on side walls affected by lateral divergence angle and opening of radial gate. J. Hydraul. Eng. 2016, 142, 05016003. [Google Scholar] [CrossRef]
- Yang, B.; Wang, Z.; Wu, M. Numerical simulation of naval ship’s roll damping based on cfd. Procedia Eng. 2012, 37, 287–293. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhang, L.; Wu, S.; Wang, F.; Zhan, Z.; Zheng, X.; Zhang, H.; Bao, W. Research on flood discharge and energy dissipation of a tunnel group layout for a super-high rockfill dam in a high-altitude region. Water 2021, 13, 3408. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Zhou, C.; Dong, Z.; Zhou, Z. Numerical simulation of hydraulic characteristics in a vortex drop shaft. Water 2018, 10, 1393. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Chute aerators. I: Air transport characteristics. J. Hydraul. Eng. 2010, 136, 352–359. [Google Scholar] [CrossRef]
- Feurich, R.; Rutschmann, P. Efficient design optimization and investigation by combining numerical and physical models. In Proceedings of the Korea Water Resources Association Conference, Korea Water Resources Association, Seoul, Korea, 11–16 September 2005. [Google Scholar]
- Johnson, M.C.; Savage, B.M. Physical and numerical comparison of flow over ogee spillway in the presence of tailwater. J. Hydraul. Eng. 2006, 132, 1353–1357. [Google Scholar] [CrossRef]
- Stamou, A.I.; Chapsas, D.G.; Christodoulou, G.C. 3-d numerical modeling of supercritical flow in gradual expansions. J. Hydraul. Res. 2008, 46, 402–409. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (vof) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A.; Thangam, S.; Gatski, T.B.; Spezialea, C.G. Development of turbulence models for shear flows by a double expansion technique. Phys. Fluids A Fluid Dyn. 1992, 4, 1510–1520. [Google Scholar] [CrossRef]
- Dong, Z.; Bürgler, M.; Hohermuth, B.; Vetsch, D.F. Density-based turbulence damping at large-scale interface for reynolds-averaged two-fluid models. Chem. Eng. Sci. 2022, 247, 116975. [Google Scholar] [CrossRef]
- Hirt, C.W. Modeling Turbulent Entrainment of Air at a Free Surface; Technical Note FSI-01-12; Flow Science, Inc.: Santa Fe, NM, USA, 2003. [Google Scholar]
- Dong, Z.; Wang, J.; Vetsch, D.F.; Boes, R.M.; Tan, G. Numerical simulation of air–water two-phase flow on stepped spillways behind x-shaped flaring gate piers under very high unit discharge. Water 2019, 11, 1956. [Google Scholar] [CrossRef]
- Pfister, M.; Hager, W.H. Deflector-jets affected by pre-aerated approach flow. J. Hydraul. Res. 2012, 50, 181–191. [Google Scholar] [CrossRef] [Green Version]
- Pfister, M.; Lucas, J.; Hager, W.H. Chute aerators: Preaerated approach flow. J. Hydraul. Eng. 2011, 137, 1452–1461. [Google Scholar] [CrossRef]
- Pfister, M.; Chanson, H. Scale effects in physical hydraulic engineering models. J. Hydraul. Res. 2011, 49, 293–306. [Google Scholar] [CrossRef]
- Hohermuth, B.; Schmocker, L.; Boes, R.M.; Vetsch, D.F. Numerical simulation of air entrainment in uniform chute flow. J. Hydraul. Res. 2021, 59, 378–391. [Google Scholar] [CrossRef]
- Hohermuth, B.F. Aeration and Two-Phase Flow Characteristics of Low-Level Outlets. Ph.D. Thesis, ETH Zurich, Zürich, Switzerland, 2019. [Google Scholar]
- Roache, P.J. Quantification of uncertainty in computational fluid dynamics. Annu. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef] [Green Version]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Da, J.; Wang, J.; Dong, Z.; Du, S. Hydraulic Characteristics of Lateral Deflectors with Different Geometries in Gentle-Slope Free-Surface Tunnels. Water 2022, 14, 2689. https://doi.org/10.3390/w14172689
Da J, Wang J, Dong Z, Du S. Hydraulic Characteristics of Lateral Deflectors with Different Geometries in Gentle-Slope Free-Surface Tunnels. Water. 2022; 14(17):2689. https://doi.org/10.3390/w14172689
Chicago/Turabian StyleDa, Jinrong, Junxing Wang, Zongshi Dong, and Shuaiqun Du. 2022. "Hydraulic Characteristics of Lateral Deflectors with Different Geometries in Gentle-Slope Free-Surface Tunnels" Water 14, no. 17: 2689. https://doi.org/10.3390/w14172689






