Experimental Investigation on Bragg Resonant Reflection of Waves by Porous Submerged Breakwaters on a Horizontal Seabed
Abstract
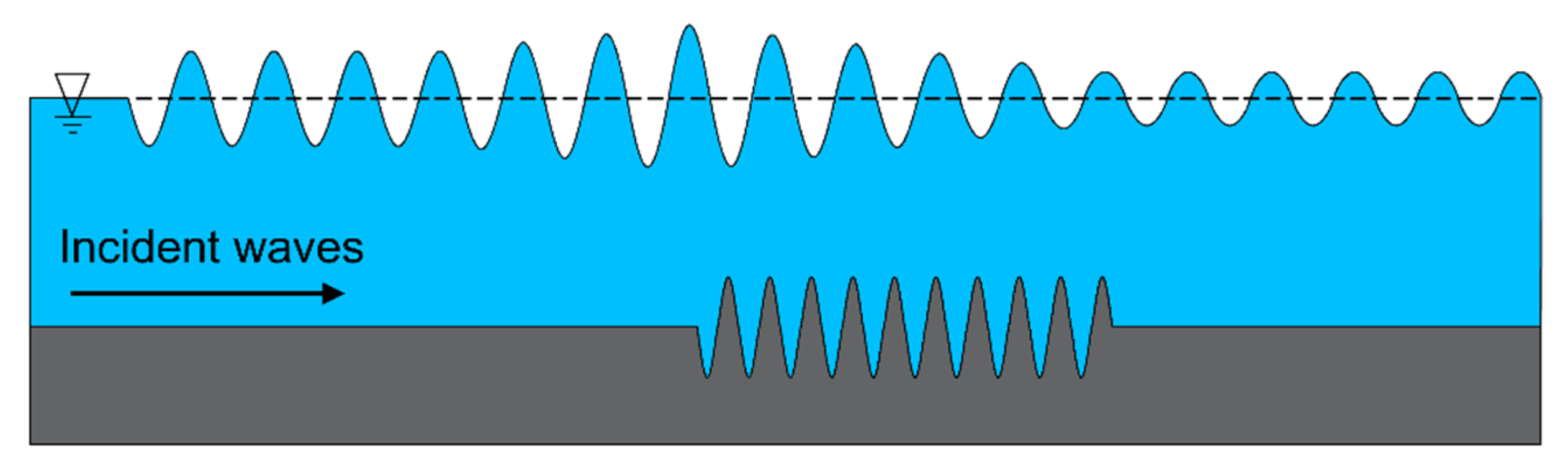
:1. Introduction
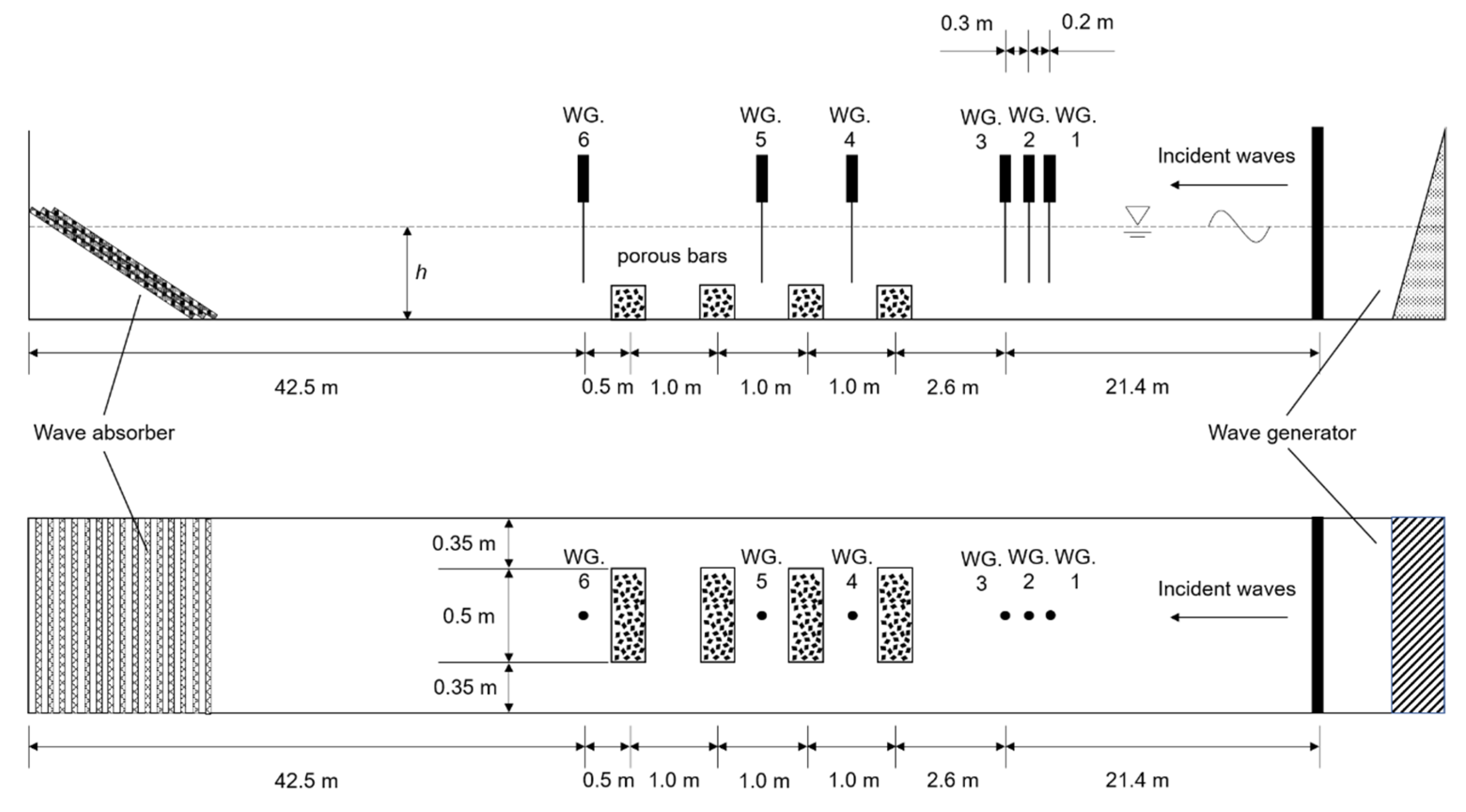
2. Experimental Setup and Conditions
2.1. Wave Flume and Porous Submerged Breakwaters
2.2. Wave Parameters and Experimental Conditions
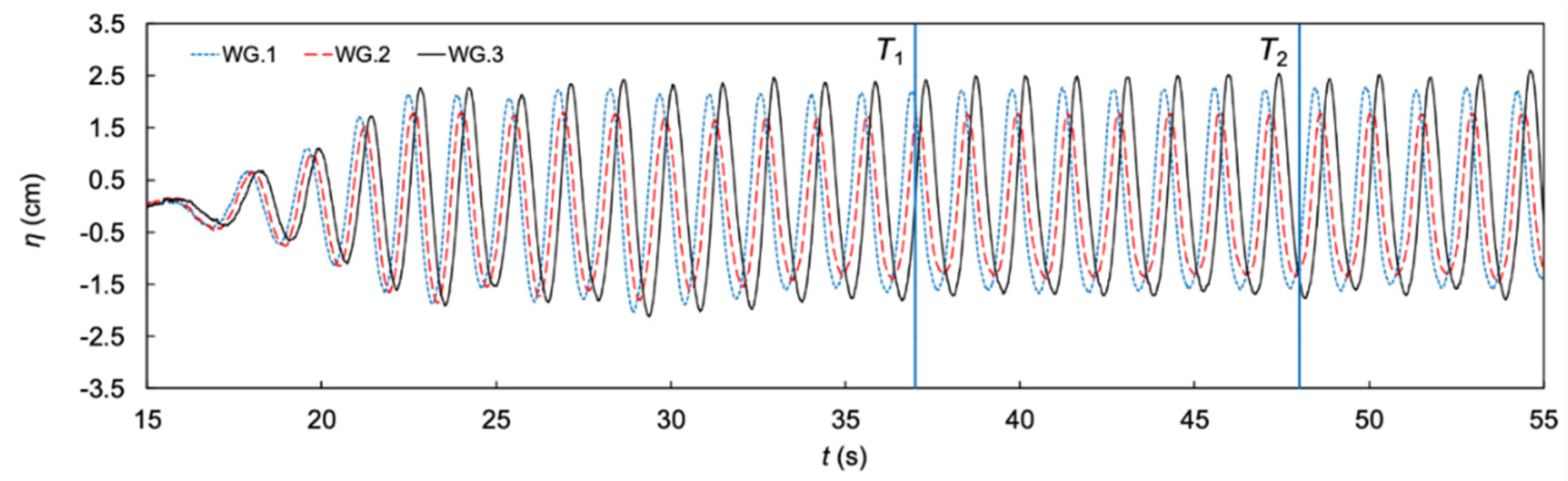
3. Experimental Results
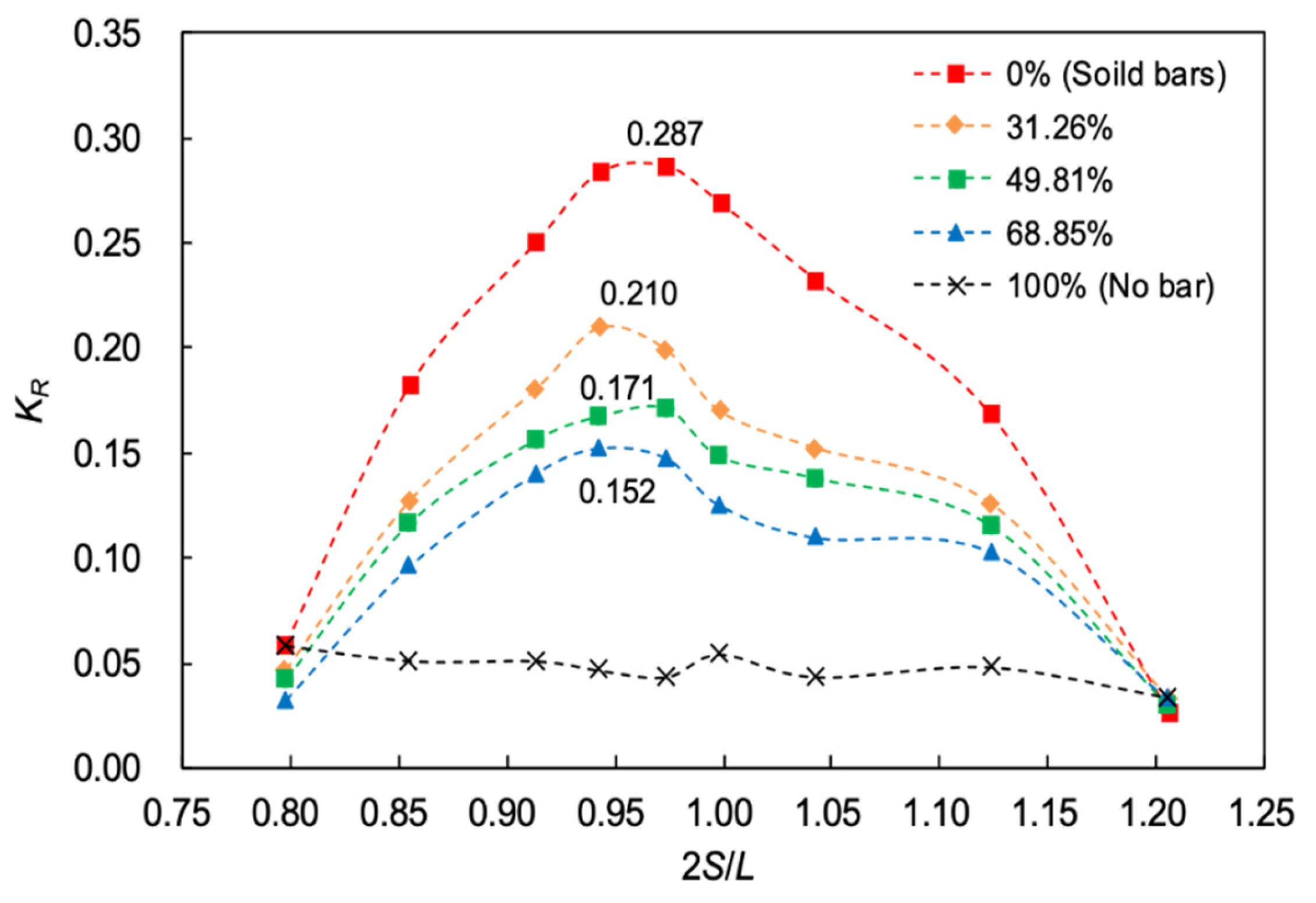
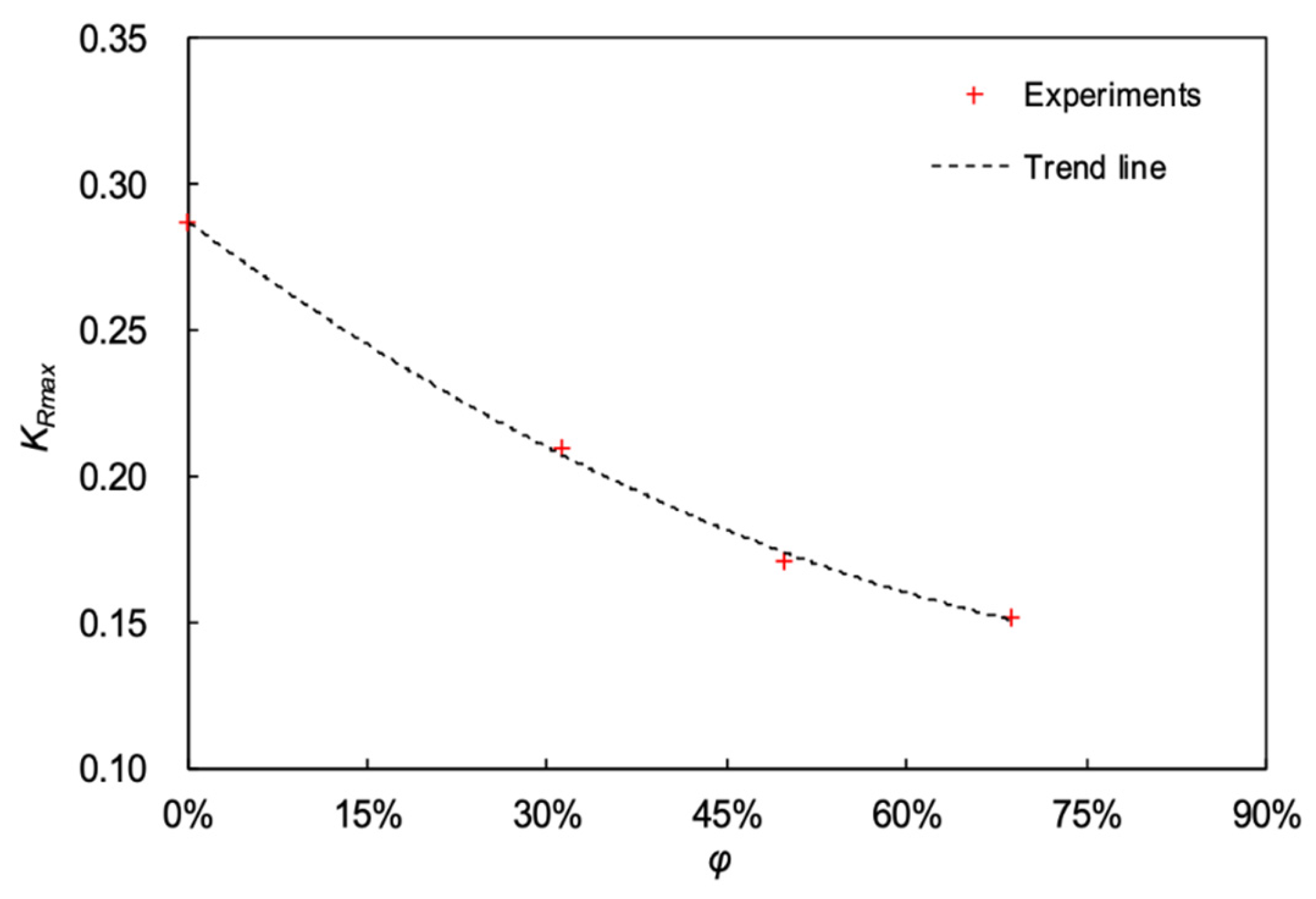
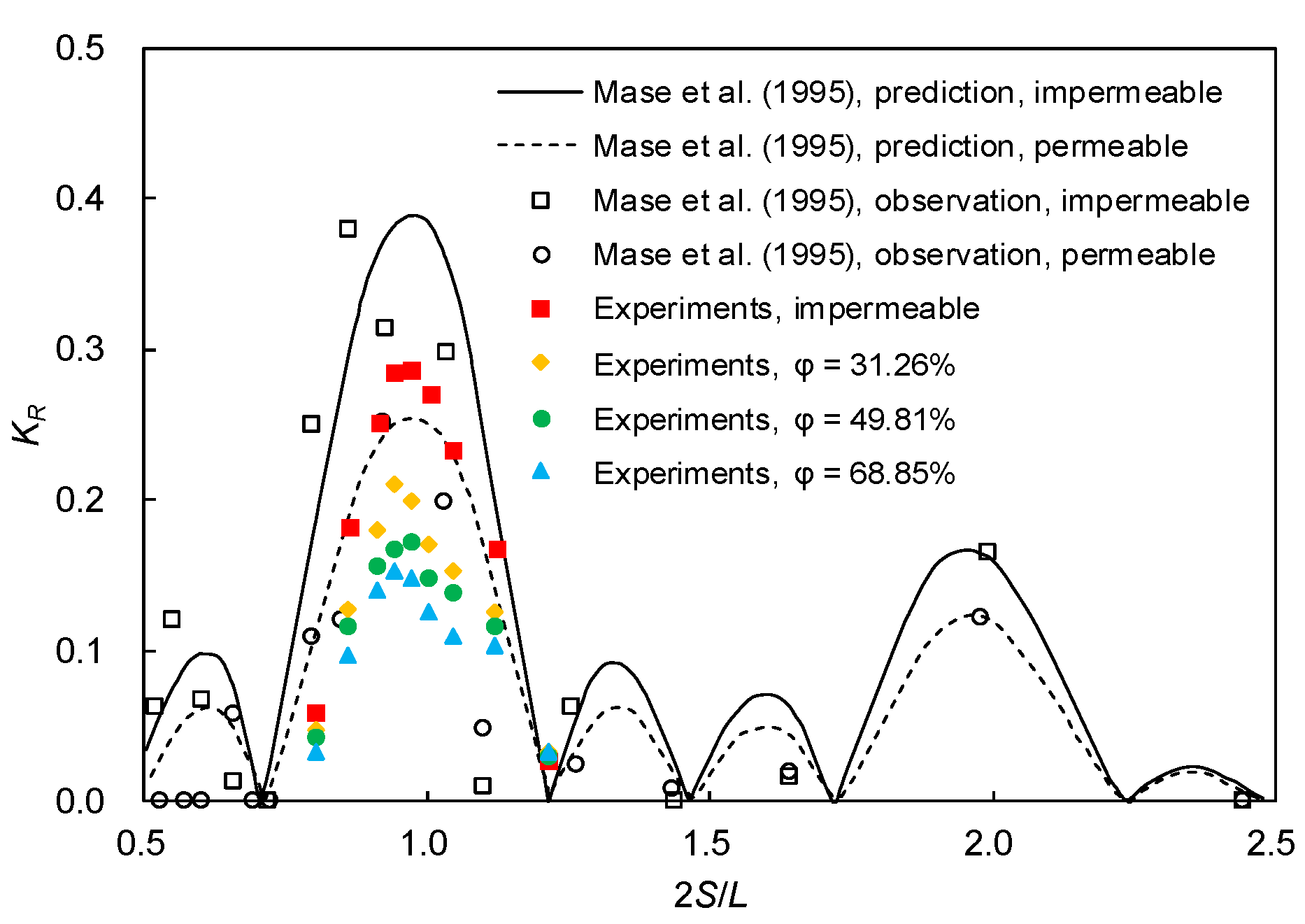
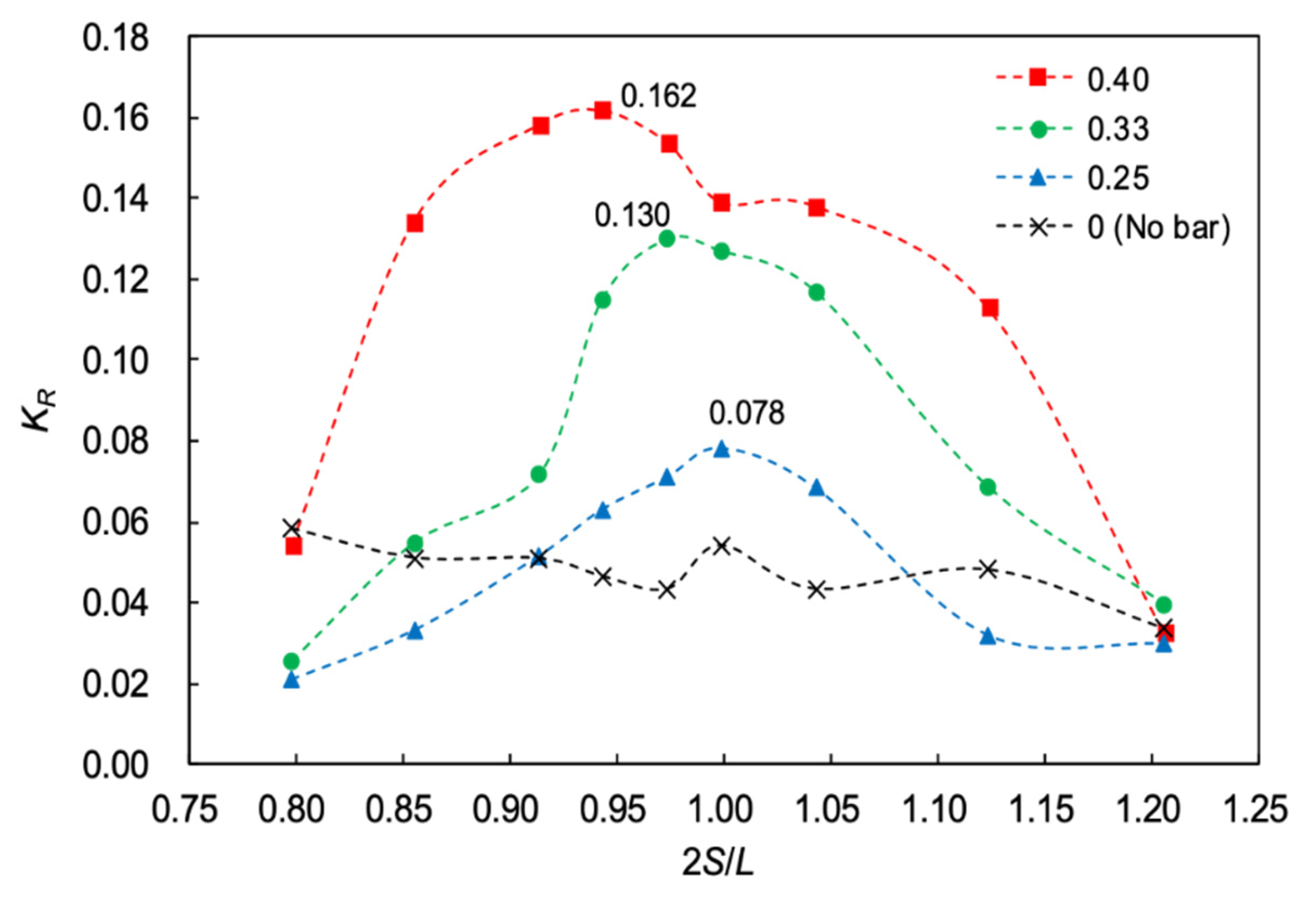
3.1. Influence of Bar Permeability on Bragg Resonant Reflection
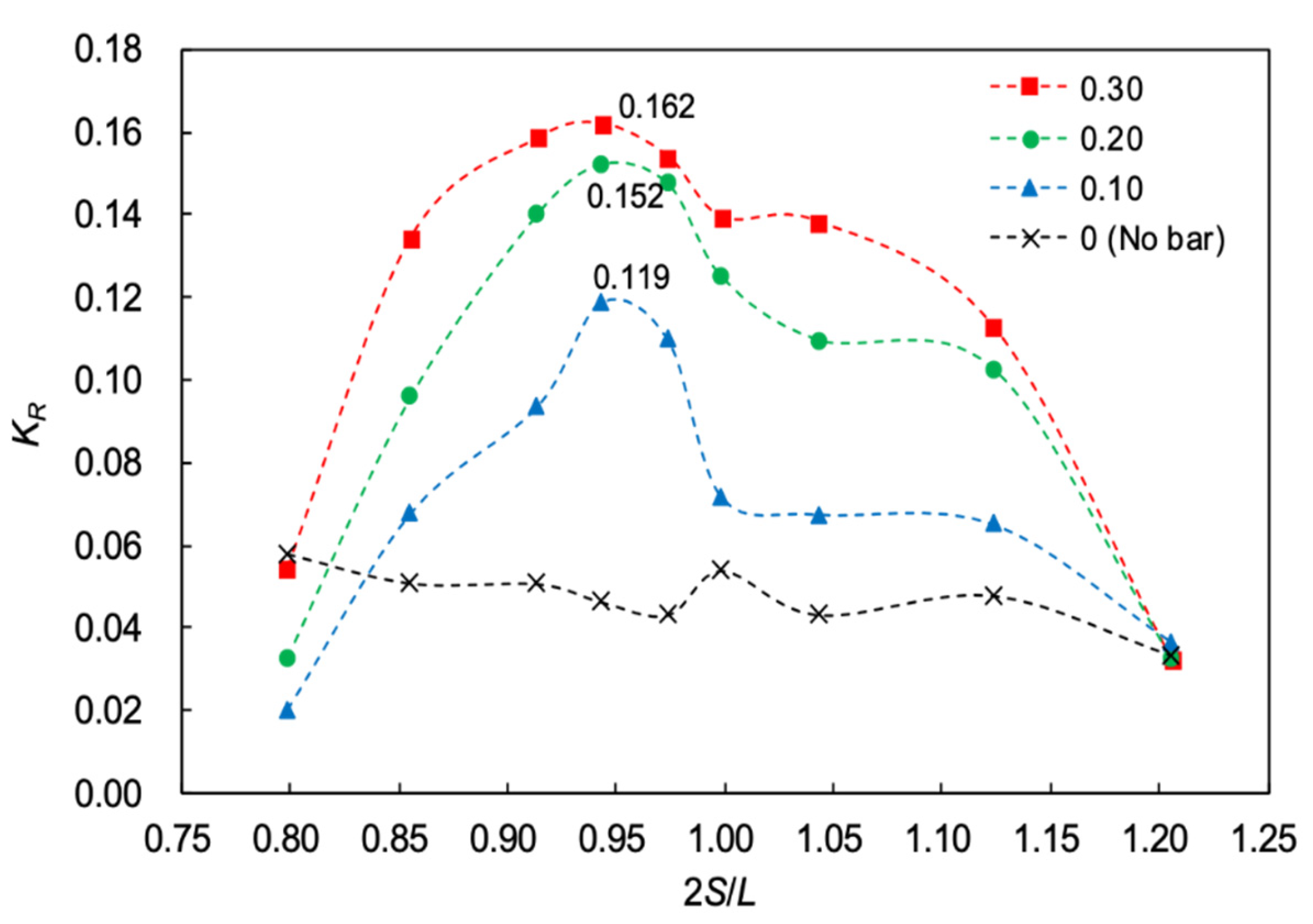
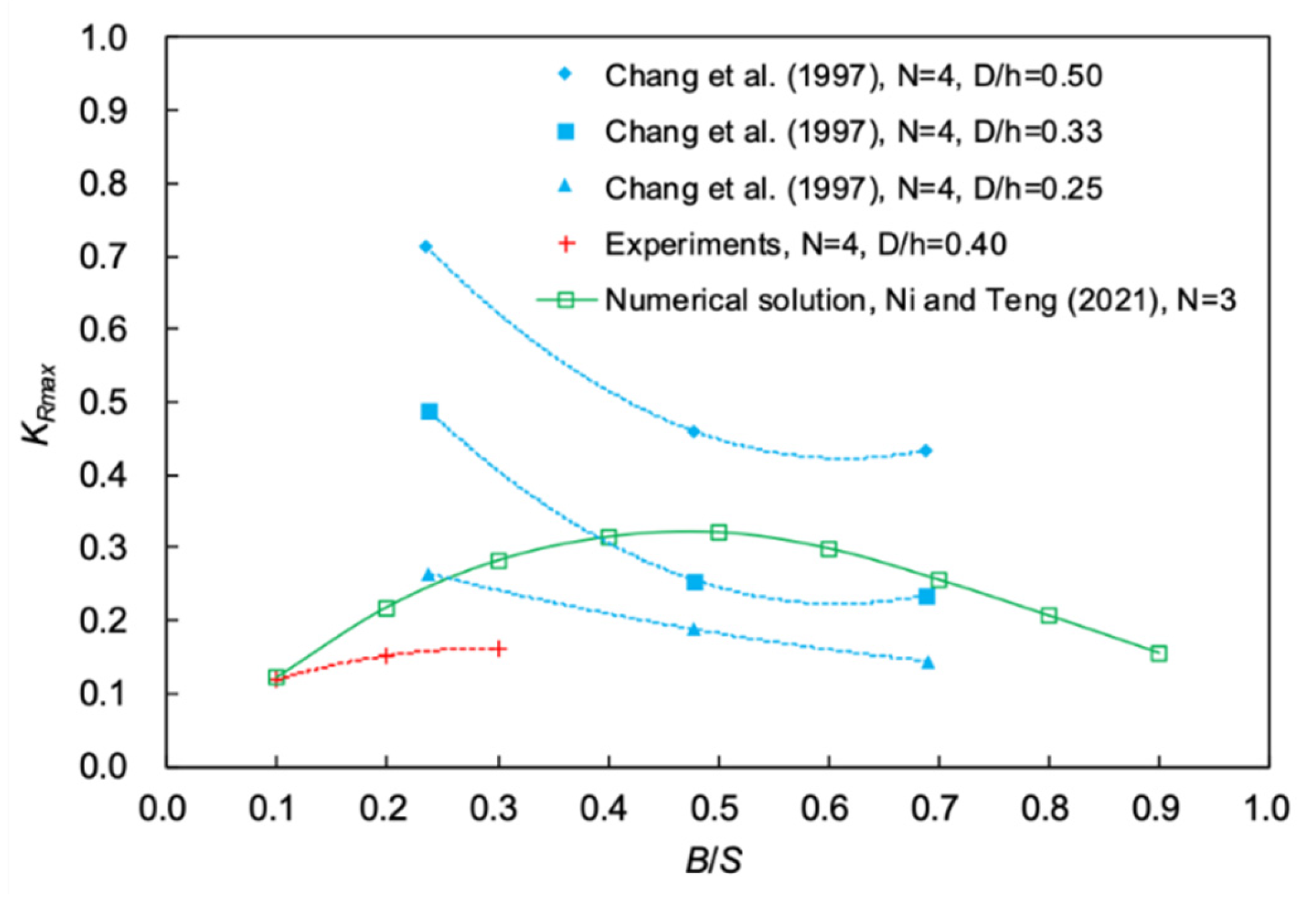
3.2. Influence of the Relative Width on Bragg Resonant Reflection
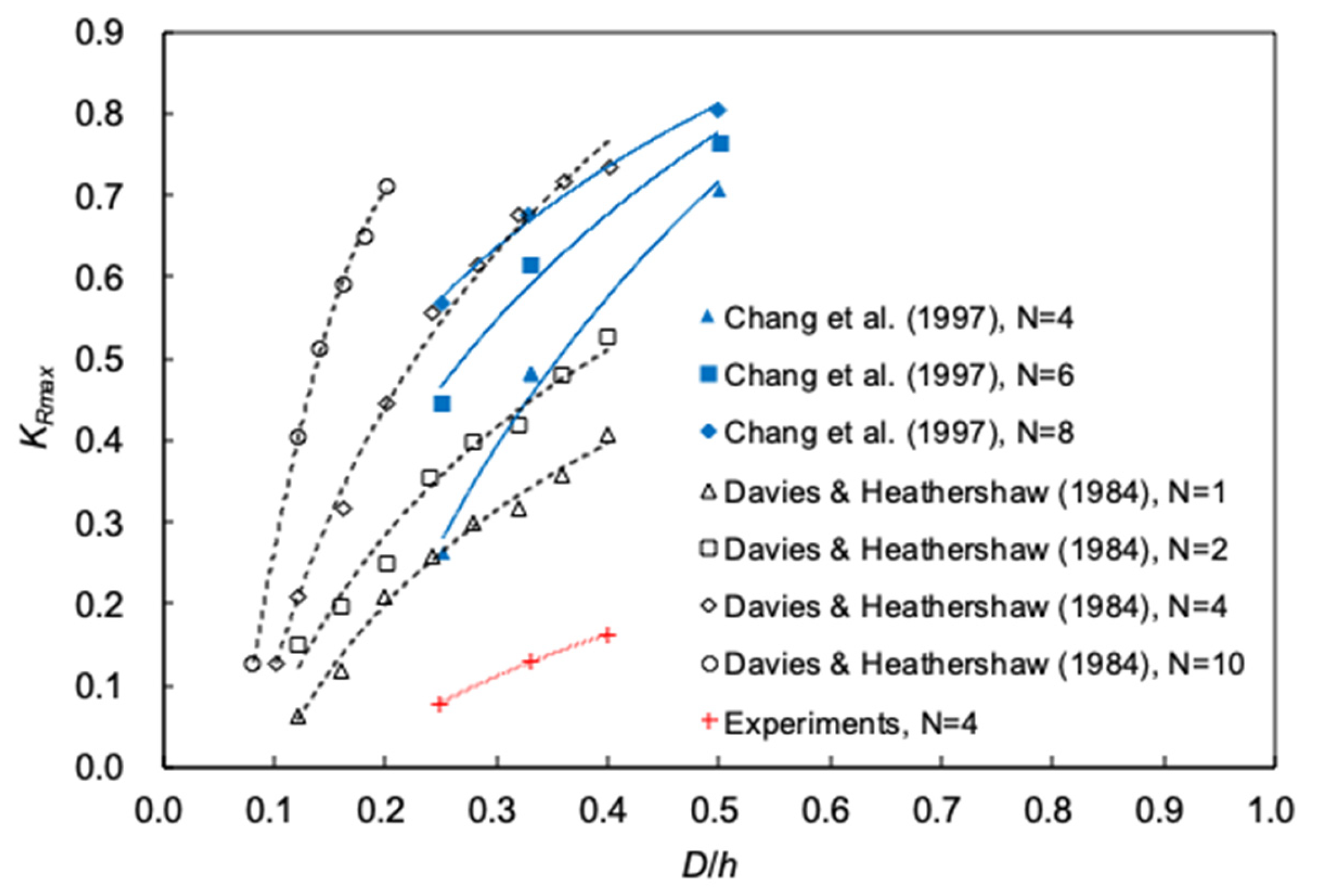
3.3. Influence of the Relative Height on Bragg Resonant Reflection
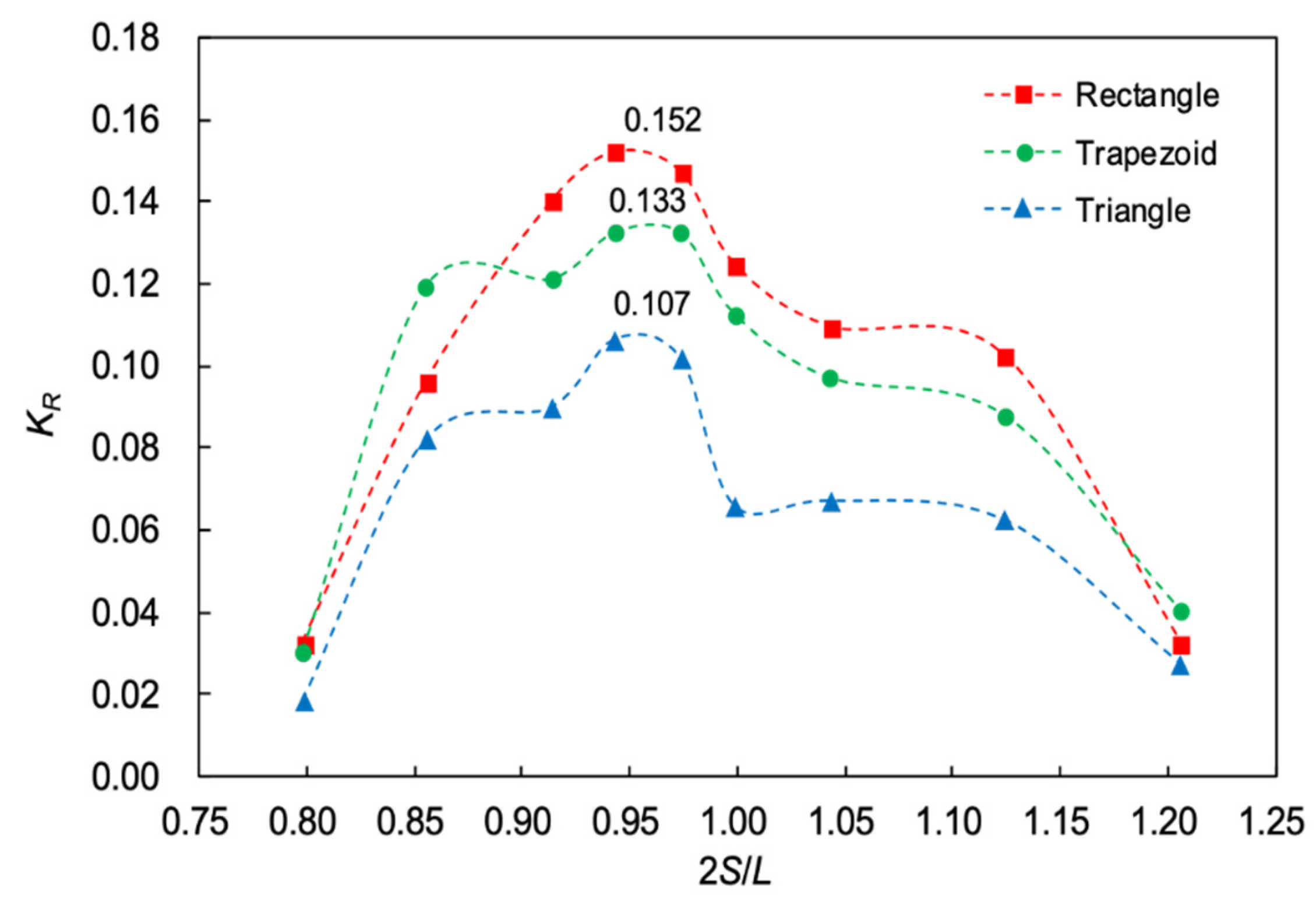
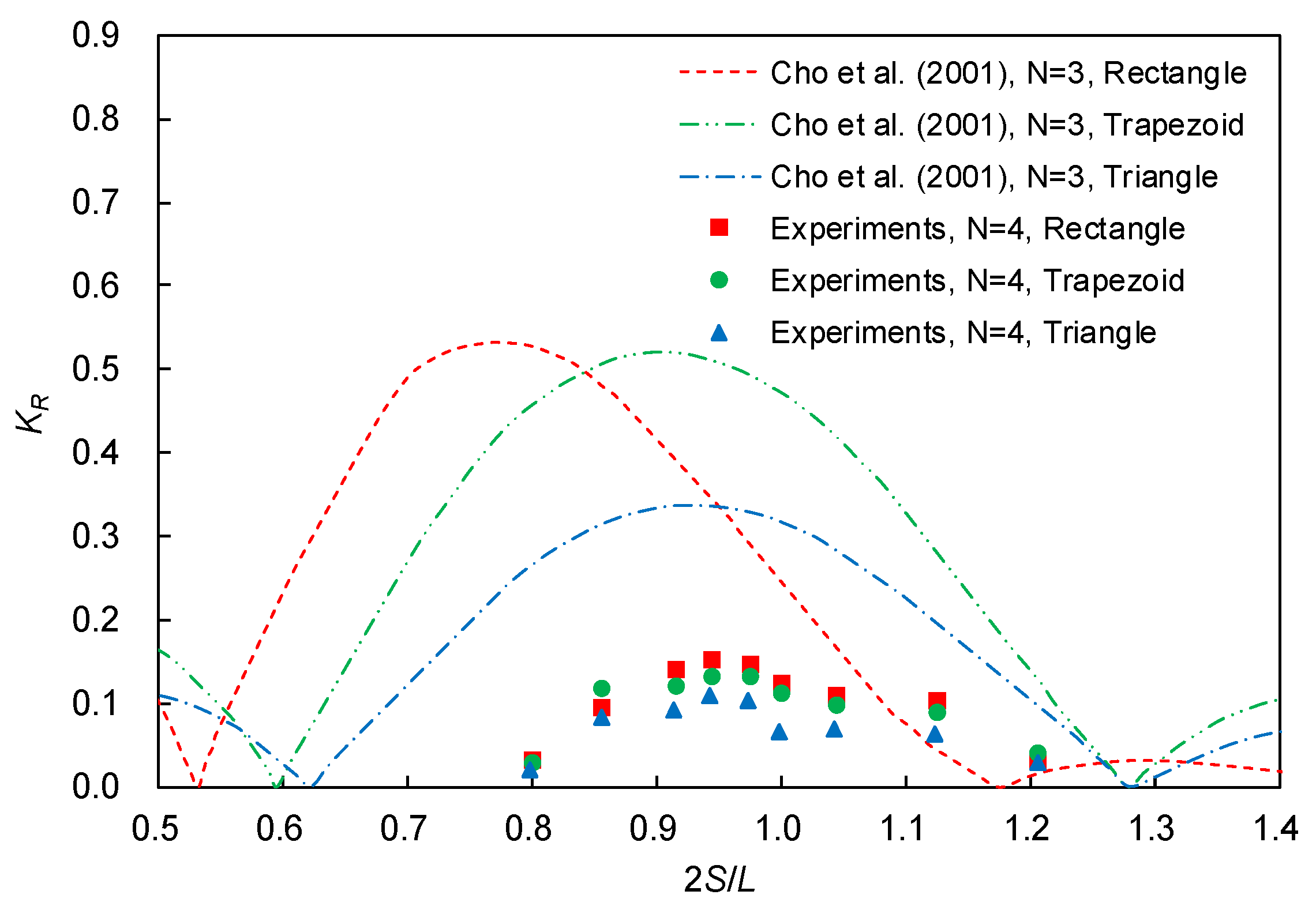
3.4. Influence of Section Shapes of Bars on Bragg Resonant Reflection
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bragg, W.H.; Bragg, W.L. The Reflection of X-rays by Crystals. Proc. R. Soc. London Ser. A Math. Phys. Eng. Sci. 1913, 88, 428–438. [Google Scholar] [CrossRef]
- Davies, A.G. The Reflection of Wave Energy by Undulations on the Seabed. Dyn. Atmos. Oceans 1982, 6, 207–232. [Google Scholar] [CrossRef]
- Mei, C.C.; Hara, T.; Naciri, M. Note on Bragg Scattering of Water Waves by Parallel Bars on the Seabed. J. Fluid Mech. 1988, 186, 147–162. [Google Scholar] [CrossRef]
- Kirby, J.T.; Anton, J.P. Bragg Reflection of Waves by Artificial Bars. In Proceedings of the 22nd International Conference on Coastal Engineering, Delft, The Netherlands, 2–6 July 1990; pp. 757–768. [Google Scholar]
- Cho, Y.S.; Yoon, S.B.; Lee, J.I.; Yoon, T.H. A Concept of Beach Protection with Submerged Breakwaters. J. Coast. Res. 2001, 34, 671–678. [Google Scholar]
- Hsu, T.W.; Chang, H.K.; Tsai, L.H.; Li, Y.X. Experiments on the Bragg Reflection of Waves by Different Types of Artificial Bars. In Proceedings of the 11th International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; pp. 601–606. [Google Scholar]
- Hsu, T.W.; Chang, H.K.; Tsai, L.H. Bragg Reflection of Waves by Different Shapes of Artificial Bars. China Ocean Eng. 2002, 16, 343–358. [Google Scholar]
- Hsu, T.W.; Tsai, L.H.; Huang, Y.T. Bragg Scattering of Water Waves by Multiply Composite Artificial Bars. Coast Eng. J. 2003, 45, 235–253. [Google Scholar] [CrossRef]
- Hsu, T.W.; Hsiao, S.C.; Ou, S.H.; Wang, S.K.; Yang, B.D.; Chou, S.E. An Application of Boussinesq Equations to Bragg Reflection of Irregular Waves. Ocean Eng. 2007, 34, 870–883. [Google Scholar] [CrossRef]
- Jeon, C.H.; Cho, Y.S. Bragg Reflection of Sinusoidal Waves Due to Trapezoidal Submerged Breakwaters. Ocean Eng. 2006, 33, 2067–2082. [Google Scholar] [CrossRef]
- Wang, S.K.; Hsu, T.W.; Tsai, L.H.; Chen, S.H. An Application of Miles’ Theory to Bragg Scattering of Water Waves by Doubly Composite Artificial Bars. Ocean Eng. 2006, 33, 331–349. [Google Scholar] [CrossRef]
- Tsai, L.H.; Kuo, Y.S.; Lan, Y.J.; Hsu, T.W.; Chen, W.J. Investigation of Multiply Composite Artificial Bars for Bragg Scattering of Water Waves. Coast Eng. J. 2011, 53, 521–548. [Google Scholar]
- Gao, J.L.; Ma, X.Z.; Dong, G.H.; Chen, H.Z.; Liu, Q.; Zang, J. Investigation on the Effects of Bragg Reflection on Harbor Oscillations. Coast. Eng. 2021, 170, 103977. [Google Scholar] [CrossRef]
- Davies, A.G.; Heathershaw, A.D. Surface-wave Propagation over Sinusoidally Varying Topography. J. Fluid Mech. 1984, 144, 419–443. [Google Scholar] [CrossRef]
- Mei, C.C. Resonant Reflection of Surface Water Waves by Periodic Sandbars. J. Fluid Mech. 1985, 152, 315–335. [Google Scholar] [CrossRef]
- Guazzelli, E.; Rey, V.; Belzons, M. Higher-order Bragg Reflection of Gravity Surface Waves by Periodic Beds. J. Fluid Mech. 1992, 245, 301–317. [Google Scholar] [CrossRef]
- Rey, V.; Guazzelli, E.; Mei, C.C. Resonant Reflection of Surface Gravity Waves by One-dimensional Doubly Sinusoidal Beds. Phys. Fluids. 1996, 8, 1525–1530. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, D.K. On Generalized Bragg Scattering of Surface Waves by Bottom Ripples. J. Fluid Mech. 1998, 356, 297–326. [Google Scholar] [CrossRef]
- Peng, J. Influence Mechanism of Higher Order Nonlinearity on Gravity Wave Bragg Resonance; Hohai University: Nanjing, China, 2020. (In Chinese) [Google Scholar]
- Fan, J.; Zheng, J.H.; Tao, A.F.; Liu, Y.M. Upstream-propagating Waves Induced by Steady Current over A Rippled Bottom: Theory and Experimental Observation. J. Fluid Mech. 2021, 910, A49. [Google Scholar] [CrossRef]
- Yu, H.F. The Downshift Characteristics of Critical Frequency Research during Wave Bragg Resonance Processes; Hohai University: Nanjing, China, 2016. (In Chinese) [Google Scholar]
- Peng, J.; Tao, A.F.; Fan, J.; Zheng, J.H.; Liu, Y.M. On the Downshift of Wave Frequency for Bragg Resonance. China Ocean Eng. 2022, 36, 76–85. [Google Scholar] [CrossRef]
- Bailard, J.A.; DeVries, J.; Kirby, J.T.; Guza, R.T. Bragg Reflection Breakwater: A New Shore Protection Method. Coast. Eng. 1990, 1, 1702–1715. [Google Scholar]
- Chang, H.K.; Liou, J.C. Long Wave Reflection from Submerged Trapezoidal Breakwaters. Ocean Eng. 2007, 34, 185–191. [Google Scholar] [CrossRef]
- Zhang, J.S.; Jeng, D.S.; Liu, P.F.; Zhang, C.; Zhang, Y. Response of a Porous Seabed to Water Waves over Permeable Submerged Breakwaters with Bragg Reflection. Ocean Eng. 2012, 43, 1–12. [Google Scholar] [CrossRef]
- Ouyang, H.T.; Chen, K.H.; Tsai, C.M. Wave Characteristics of Bragg Reflections from a Train of Submerged Bottom Breakwaters. J. Hydro-Environ. Res. 2016, 11, 91–100. [Google Scholar] [CrossRef]
- Zeng, H.; Qin, B.; Zhang, J. Optimal Collocation of Bragg Breakwaters with Rectangular Bars on Sloping Seabed for Bragg Resonant Reflection by Long Waves. Ocean Eng. 2017, 130, 156–165. [Google Scholar] [CrossRef]
- Liu, H.W.; Zeng, H.D.; Huang, H.D. Bragg Resonant Reflection of Surface Waves from Deep Water to Shallow Water by a Finite Array of Trapezoidal Bars. Appl. Ocean Res. 2020, 94, 101976. [Google Scholar] [CrossRef]
- Ni, Y.L.; Teng, B. Bragg Resonant Reflection of Water Waves by a Bragg Breakwater with Porous Rectangular Bars on a Sloping Permeable Seabed. Ocean Eng. 2021, 235, 109333. [Google Scholar] [CrossRef]
- Ni, Y.L.; Teng, B. Bragg Resonant Reflection of Water Waves by a Bragg Breakwater with Porous Trapezoidal Bars on a Sloping Permeable Seabed. Appl. Ocean Res. 2021, 114, 102770. [Google Scholar] [CrossRef]
- Tang, H.J.; Huang, C.C. Bragg Reflection in a Fully Nonlinear Numerical Wave Tank Based on Boundary Integral Equation Method. Ocean Eng. 2008, 35, 1800–1810. [Google Scholar] [CrossRef]
- Hsu, T.W.; Lin, J.F.; Hsiao, S.C.; Ou, S.H.; Babanin, A.V.; Wu, Y.T. Wave Reflection and Vortex Evolution in Bragg Scattering in Real Fluids. Ocean Eng. 2014, 88, 508–519. [Google Scholar] [CrossRef]
- Ouyang, H.T.; Chen, K.H.; Tsai, C.M. Investigation on Bragg Reflection of Surface Water Waves Induced by a Train of Fixed Floating Pontoon Breakwaters. Int. J. Nav. Archit. Ocean Eng. 2015, 7, 951–963. [Google Scholar] [CrossRef]
- Liu, Y.; Li, H.J.; Zhu, L. Bragg Reflection of Water Waves by Multiple Submerged Semi-circular Breakwaters. Appl. Ocean Res. 2016, 56, 67–78. [Google Scholar] [CrossRef]
- Yueh, C.Y.; Chuang, S.H.; Wen, C.C. Bragg Reflection of Water Waves Due to Submerged Wavy Plate Breakwater. J. Hydro-Environ. Res. 2018, 21, 52–59. [Google Scholar] [CrossRef]
- Mase, H.; Oki, S.I.; Takeba, K. Wave Equation over Permeable Rippled Bed and Analysis of Bragg Scattering of Surface Gravity Waves. J. Hydraul. Res. 1995, 33, 789–812. [Google Scholar] [CrossRef]
- Mase, H.; Kimura, A.; Sakakibara, H. Resonant Reflection and Refraction-diffraction of Surface Waves Due to Porous Submerged Breakwaters. Coast. Eng. Proc. 1996, 15, 2366–2376. [Google Scholar]
- Mohapatra, A.K.; Vijay, K.G.; Sahoo, T. Bragg Scattering of Surface Gravity Waves by a Submerged Wavy Porous Plate. Ocean Eng. 2021, 219, 108273. [Google Scholar] [CrossRef]
- Goda, Y.; Suzuki, T. Estimation of Incident and Reflected Waves in Random Wave Experiments. Coast. Eng. Proc. 1976, 15, 47. [Google Scholar] [CrossRef] [Green Version]
- Harwalkar, V.R.; Kalab, M. Comparison of Centrifugation and Drainage Methods. Milchwissenschaft 1983, 38, 517–522. [Google Scholar]
- Heathershaw, A.D. Seabed-wave Resonance and Sand Bar Growth. Nature 1982, 296, 343–345. [Google Scholar] [CrossRef]
- Chang, H.K.; Hsu, T.W.; Lee, Y.H. Experimental Study of Waves Passing through Artificial Sandbars. In Proceedings of the 19th Ocean Engineering, Taichung, China, 17–18 November 1997; pp. 242–249. (In Chinese). [Google Scholar]
- Tsai, L.H. Bragg Reflection of Water Waves by a Series of Submerged Breakwaters; National Cheng Kung University: Taichung, China, 2003. (In Chinese) [Google Scholar]



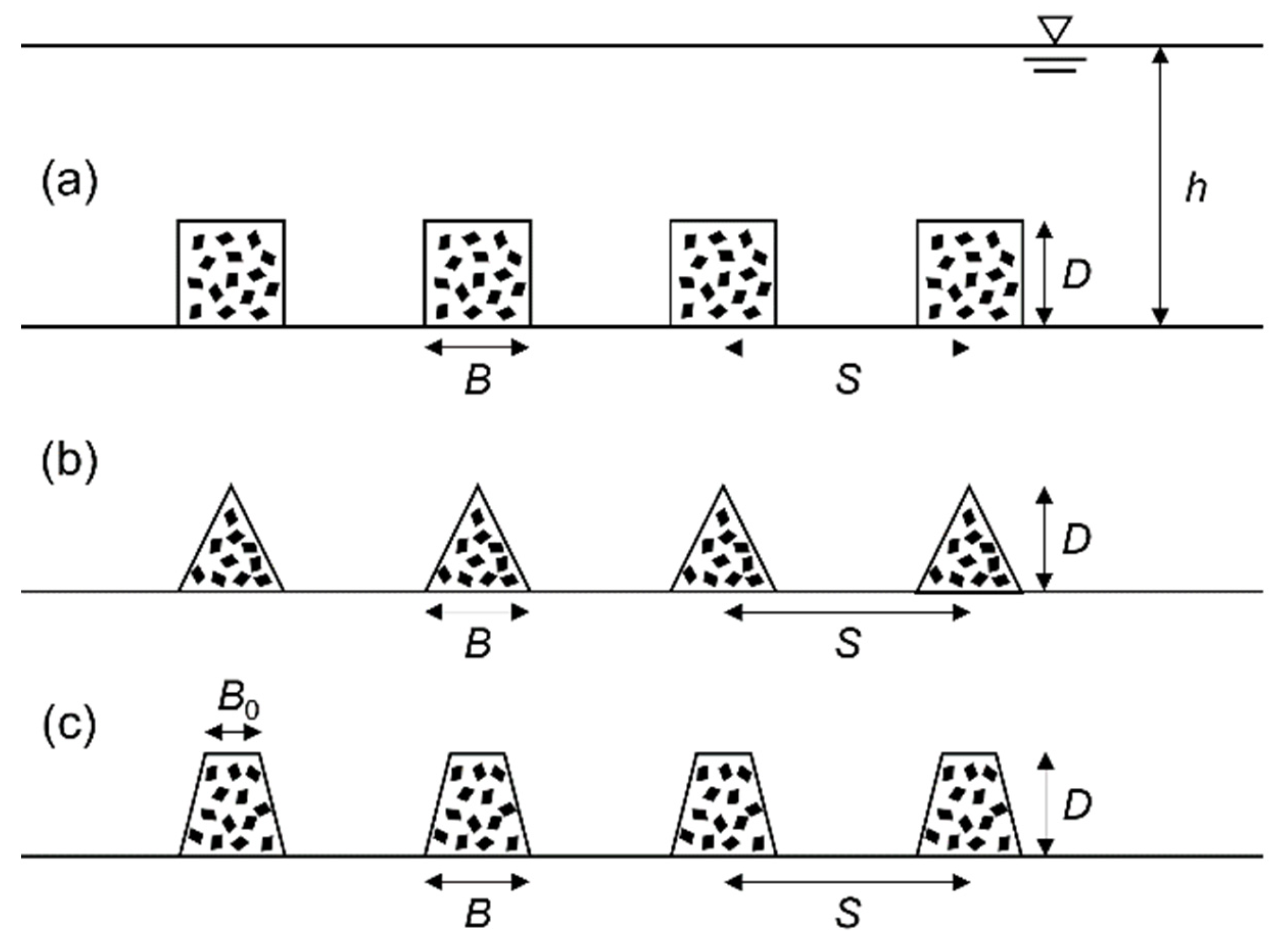
| Section Shapes | Long (m) | B (m) | D (m) | B0 (m) | S (m) |
|---|---|---|---|---|---|
| Rectangle | 0.5 | 0.1 | 0.1 | - | 1.0 |
| Triangle | 0.5 | 0.1 | 0.1 | - | 1.0 |
| Trapezoid | 0.5 | 0.1 | 0.1 | 0.06 | 1.0 |
| Fillers | V1 (cm3) | V2 (cm3) | φ (%) |
|---|---|---|---|
| A | 30,937.48 | 44,934.61 | 68.85 |
| B | 29,186.32 | 58,595.26 | 49.81 |
| C | 32,370.26 | 103,551.70 | 31.26 |
| Case | h (m) | T (s) | H (m) | φ (%) | Section Shapes | B (m) | D (m) | N |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.25 | 1.20–1.70 | 0.04 | 0, 31.26, 49.81, 68.85, 100 | Rectangle | 0.2 | 0.1 | 4 |
| 2 | 0.25 | 1.20–1.70 | 0.04 | 68.85 | Rectangle | 0.1, 0.2, 0.3 | 0.1 | 4 |
| 3 | 0.25, 0.30, 0.40 | 1.05–1.70 | 0.04 | 68.85 | Rectangle | 0.3 | 0.1 | 4 |
| 4 | 0.25 | 1.20–1.70 | 0.04 | 68.85 | Rectangle, triangle, trapezoid | 0.2 | 0.1 | 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, W.; Chen, C.; Htet, M.H.; Sarkar, M.S.I.; Tao, A.; Wang, Z.; Fan, J.; Jiang, D. Experimental Investigation on Bragg Resonant Reflection of Waves by Porous Submerged Breakwaters on a Horizontal Seabed. Water 2022, 14, 2682. https://doi.org/10.3390/w14172682
Xu W, Chen C, Htet MH, Sarkar MSI, Tao A, Wang Z, Fan J, Jiang D. Experimental Investigation on Bragg Resonant Reflection of Waves by Porous Submerged Breakwaters on a Horizontal Seabed. Water. 2022; 14(17):2682. https://doi.org/10.3390/w14172682
Chicago/Turabian StyleXu, Wei, Chun Chen, Min Han Htet, Mohammad Saydul Islam Sarkar, Aifeng Tao, Zhen Wang, Jun Fan, and Degang Jiang. 2022. "Experimental Investigation on Bragg Resonant Reflection of Waves by Porous Submerged Breakwaters on a Horizontal Seabed" Water 14, no. 17: 2682. https://doi.org/10.3390/w14172682







