Research on Parameter Spatialization and Adaptive Correction Models in Fluid Numerical Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.1.1. Data Introduction
DEM (Digital Elevation Model)
Initial data
Verification Data
2.2. Model and Methods
- The spatial design of the Manning coefficient of the numerical simulation model in the calculation area;
- The logic of the adaptive adjustment of the Manning coefficient.
2.2.1. Numerical Simulation Model
2.2.2. Spatialized Design of the Manning Coefficient
2.2.3. Cost Function
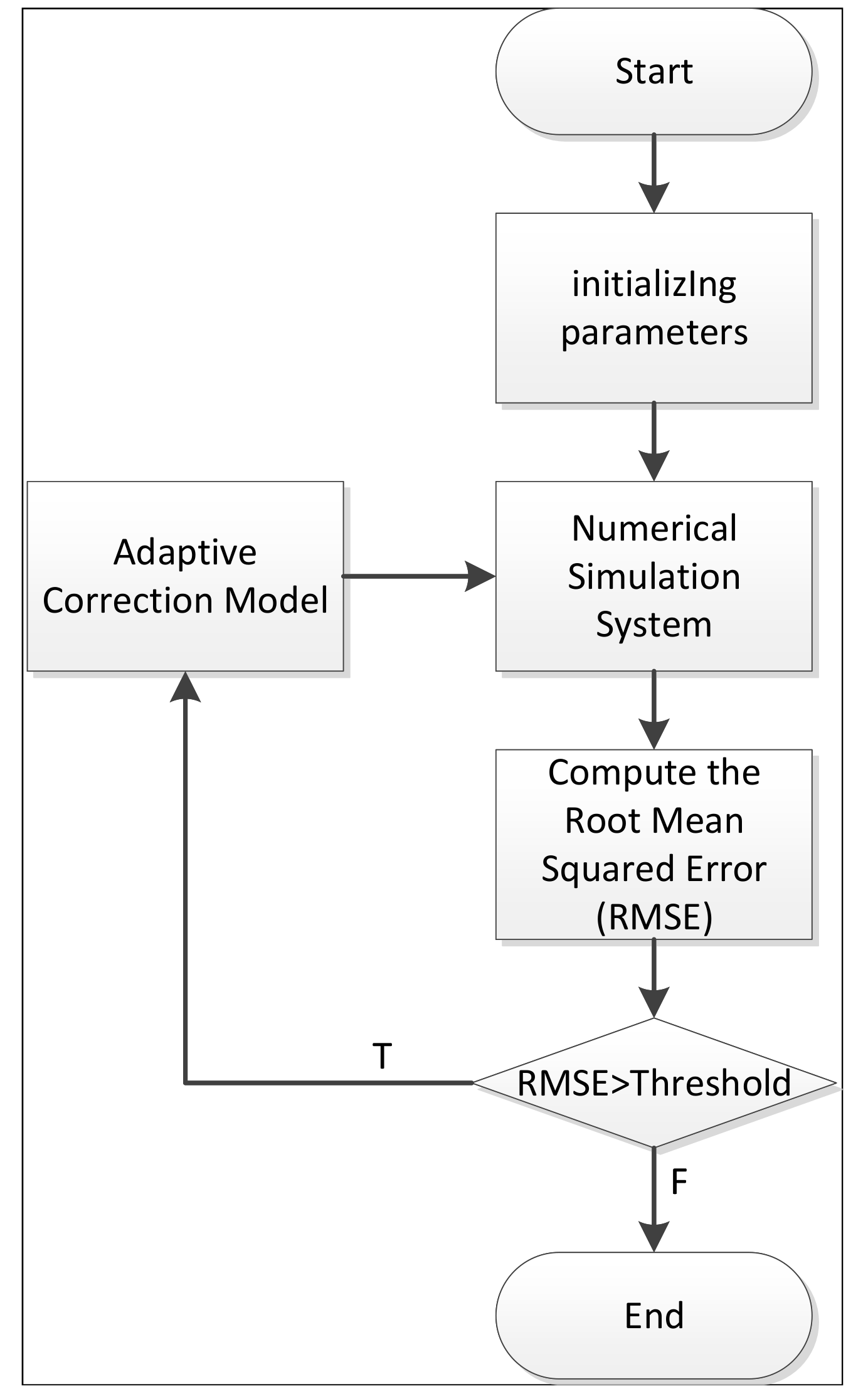
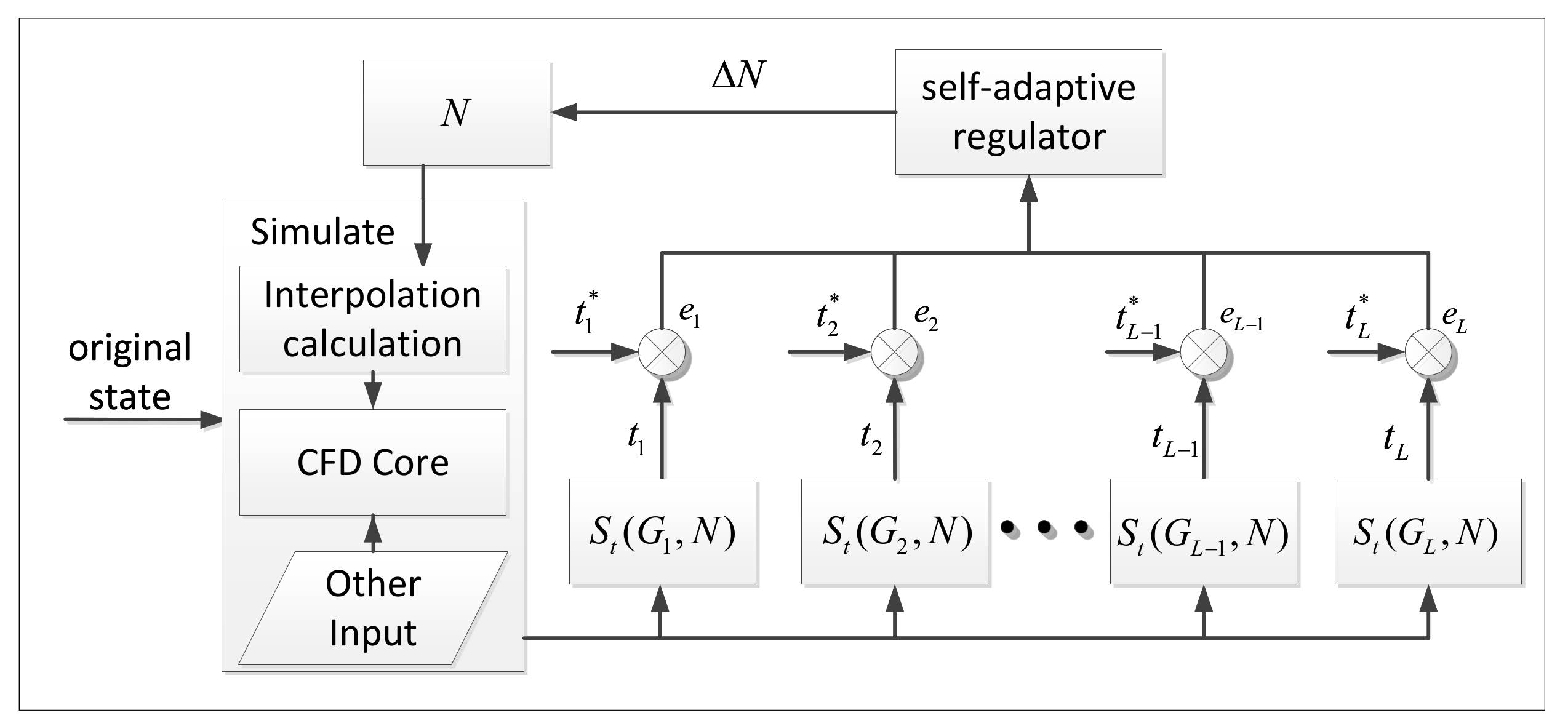
2.2.4. Adaptive Correction Model
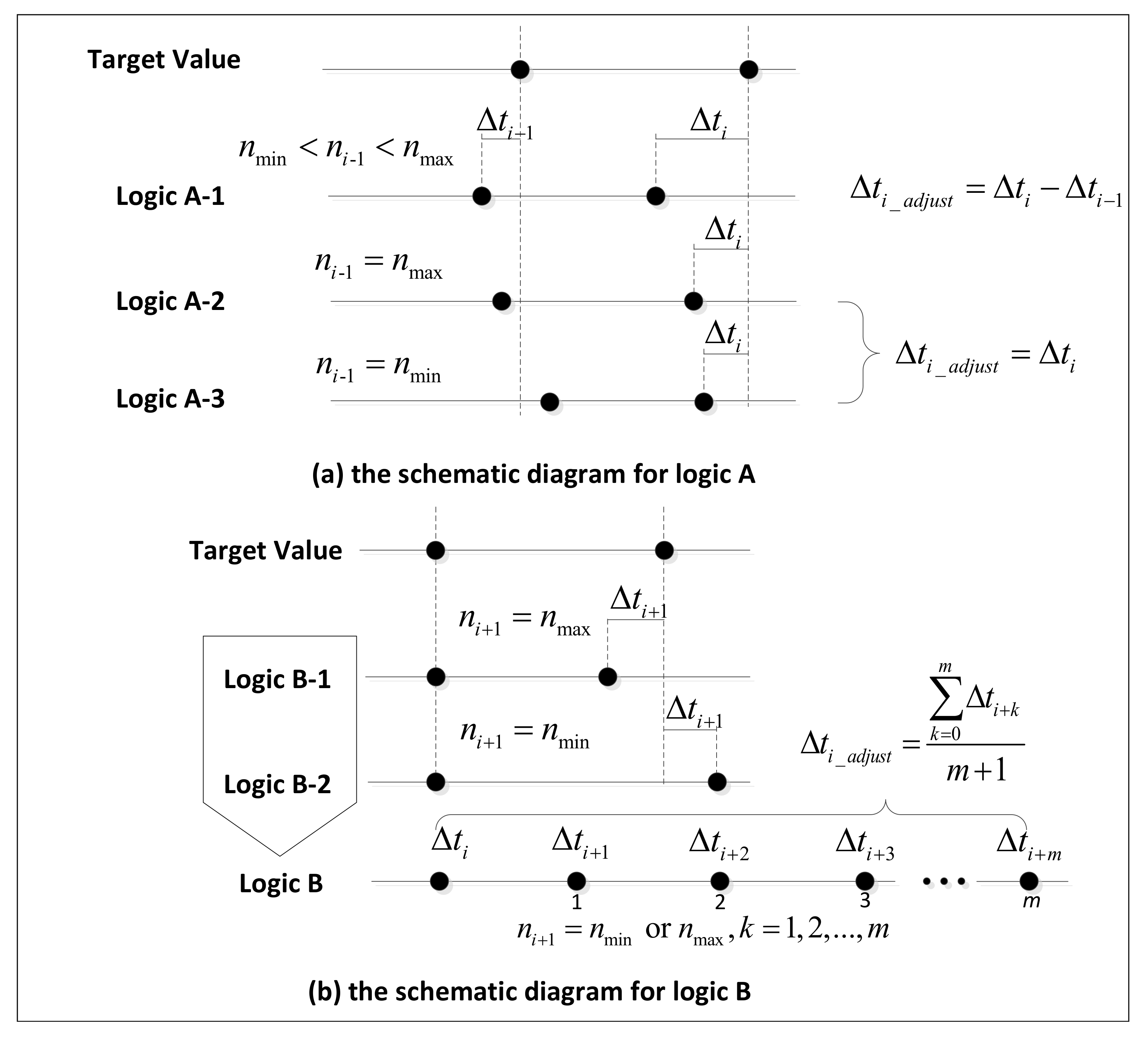
Logic-A
Logic-B
2.2.5. Adaptive Correction Function
| Algorithm 1: for adjustment of each gauge. |
 |
2.3. Model Running Conditions
2.3.1. Boundary Conditions
2.3.2. Stable Conditions
2.4. Experimental Design
2.4.1. Control Point Selection
2.4.2. Parameter Settings
3. Results and Discussion
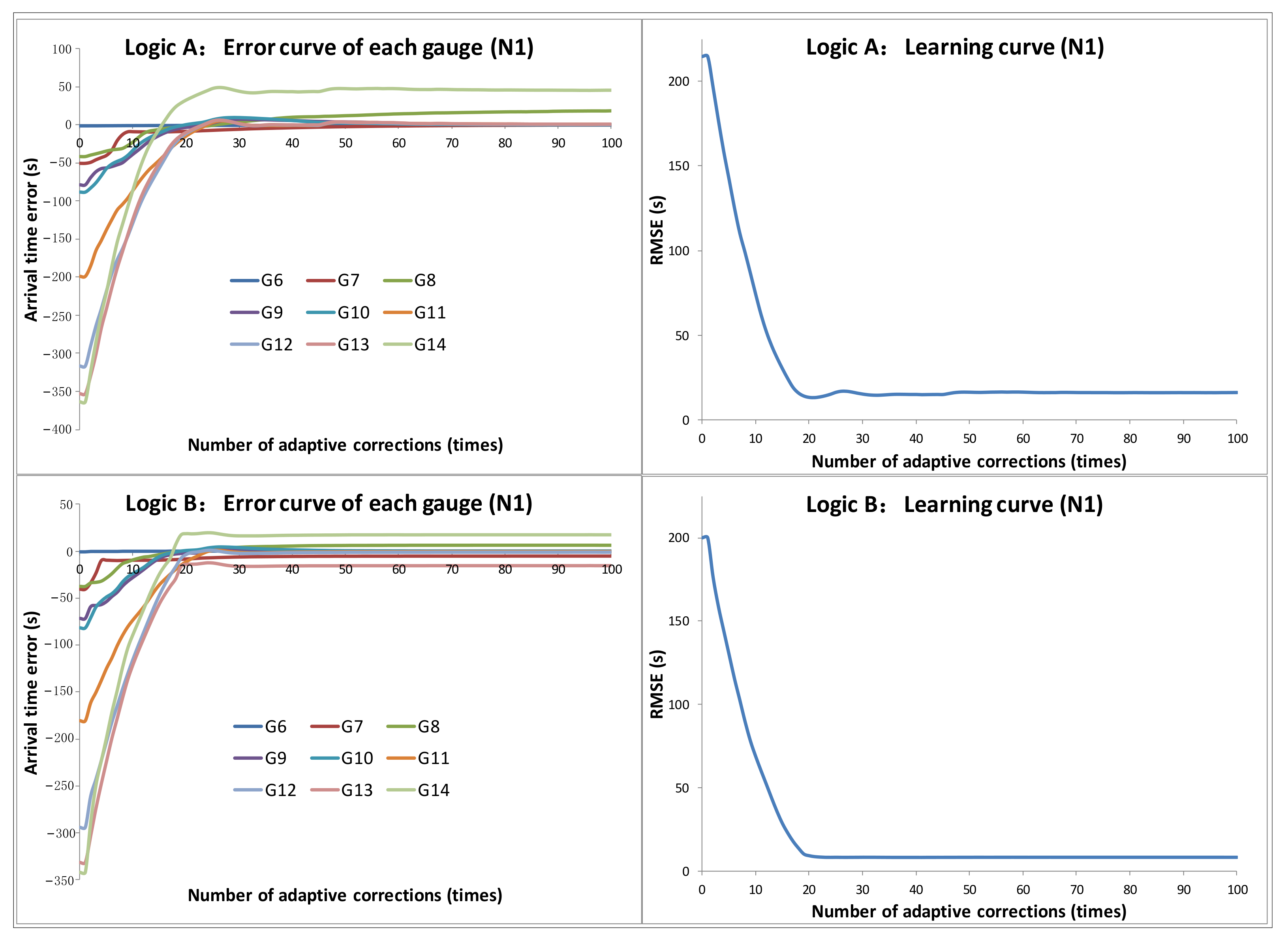
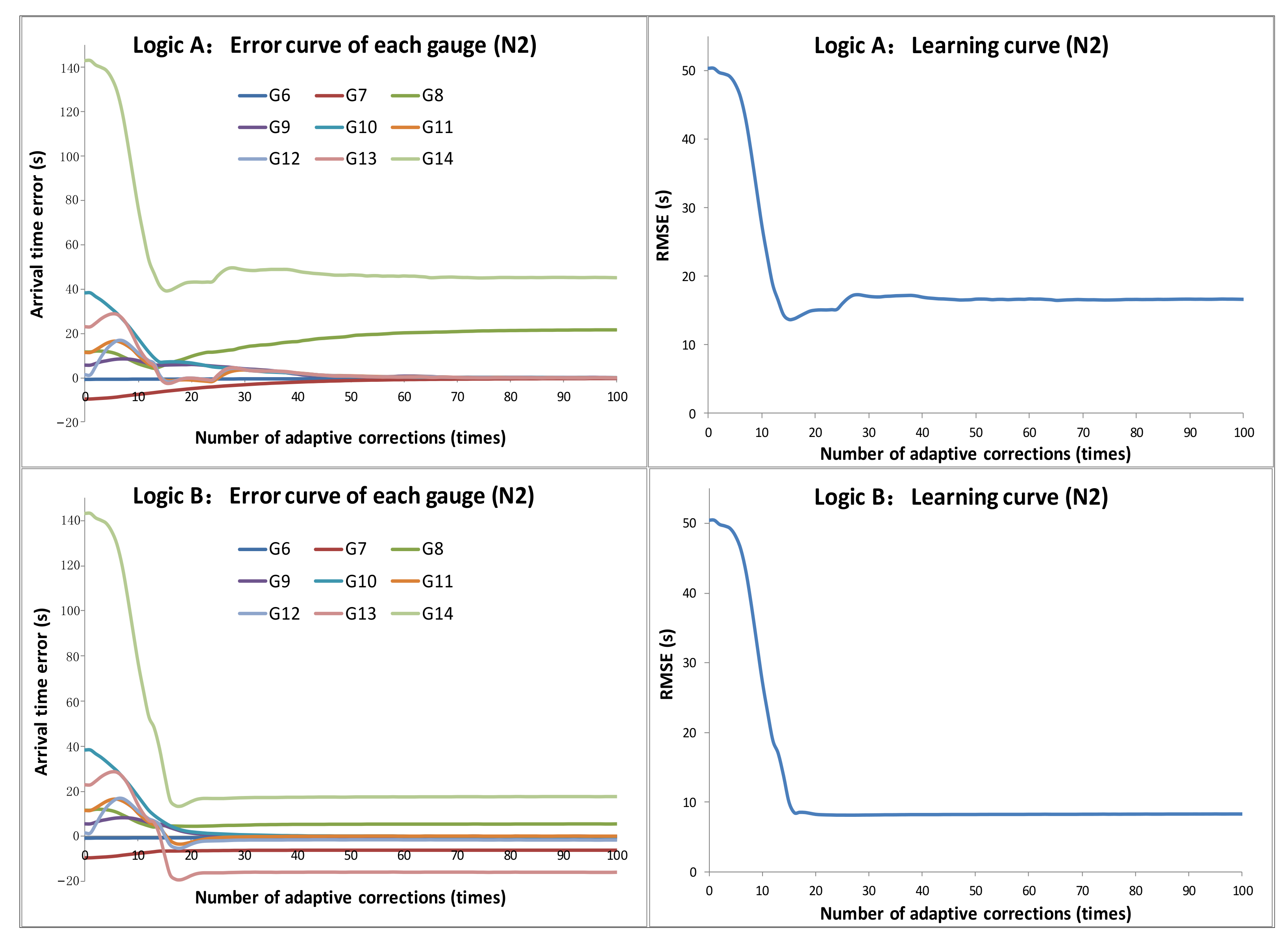
3.1. Verification of the Logic and Stability of Adaptive Correction
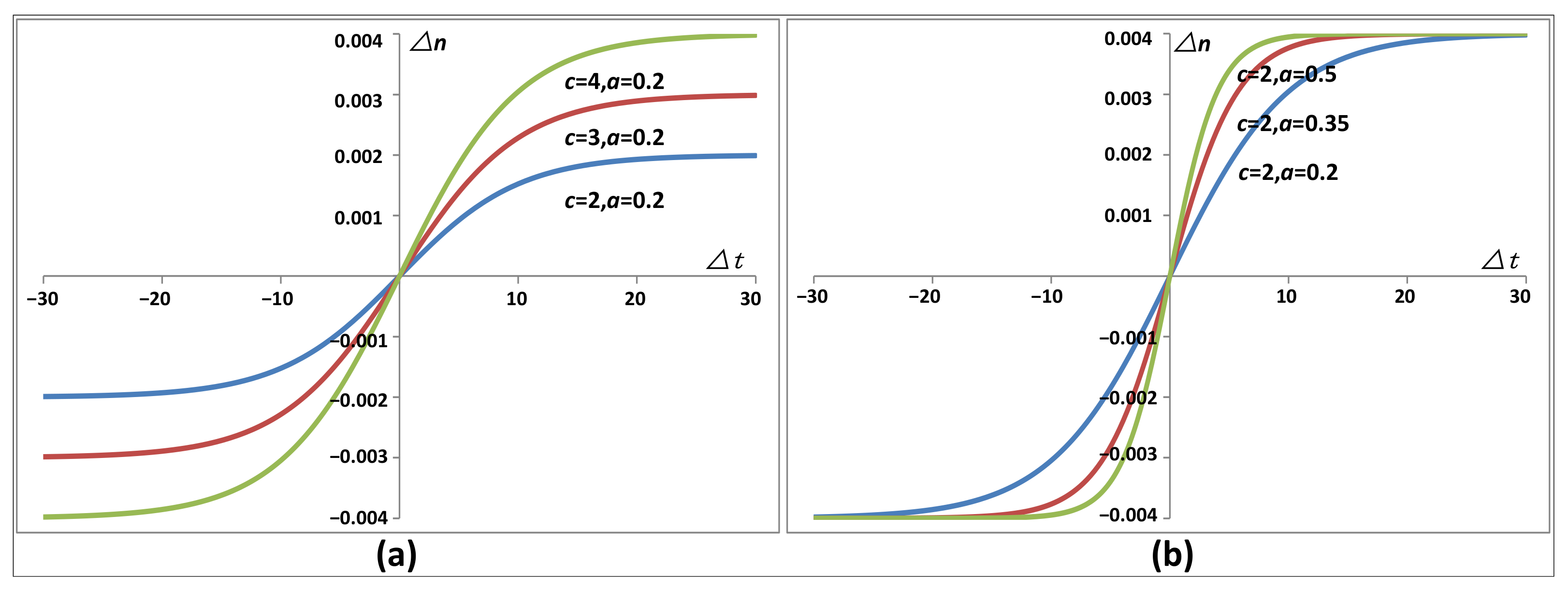
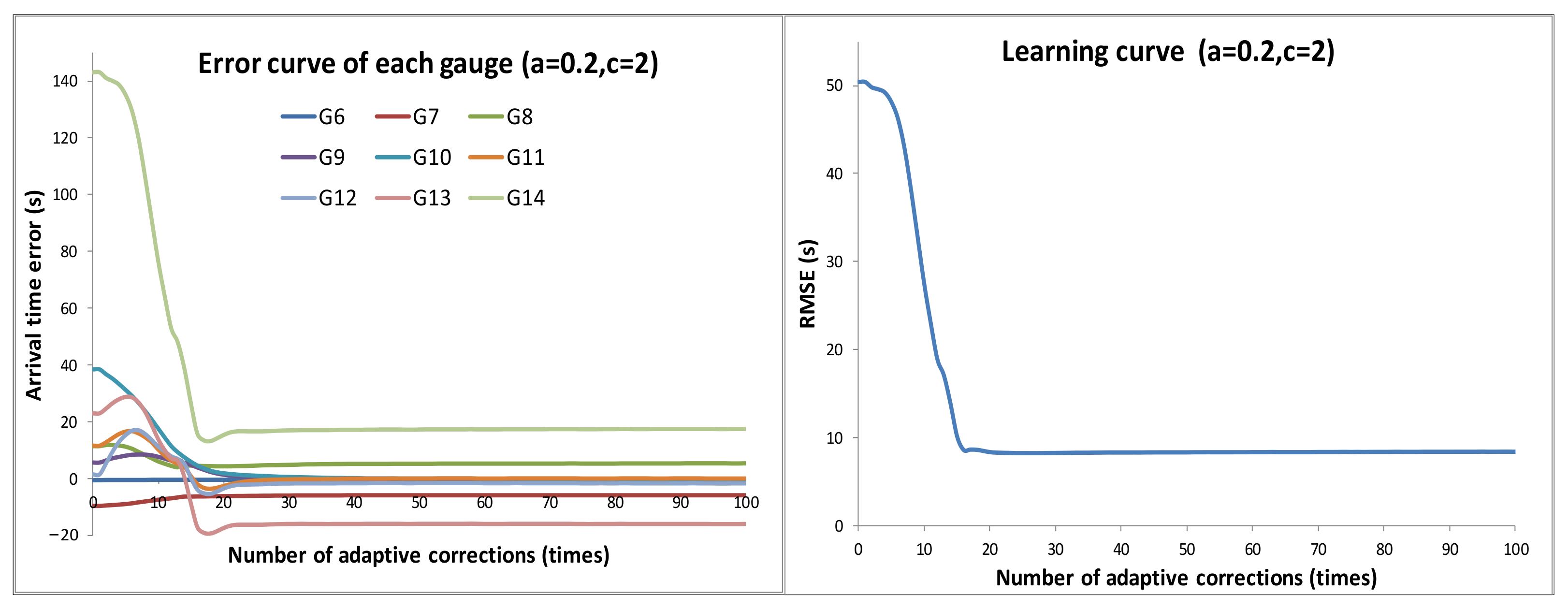
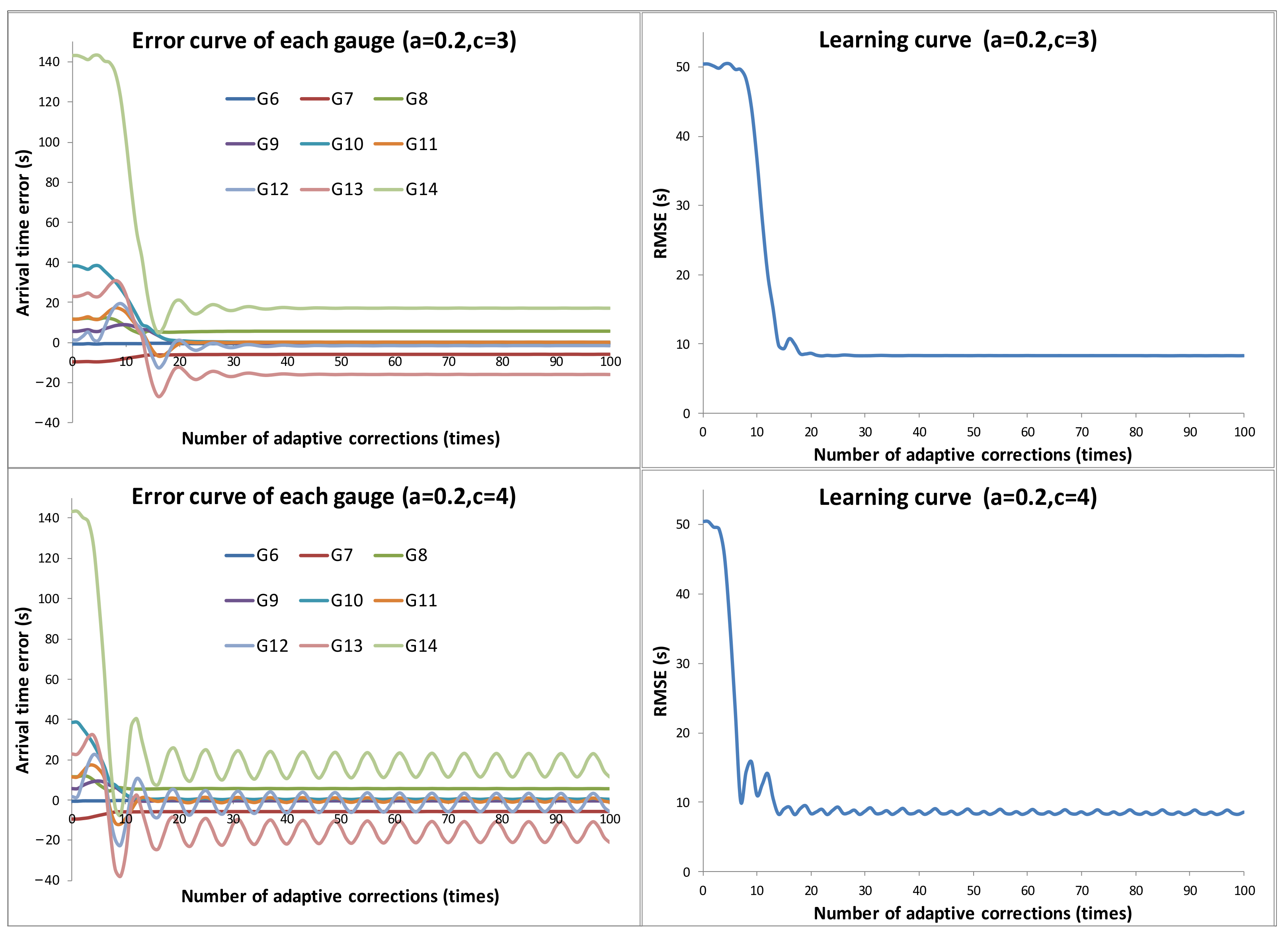
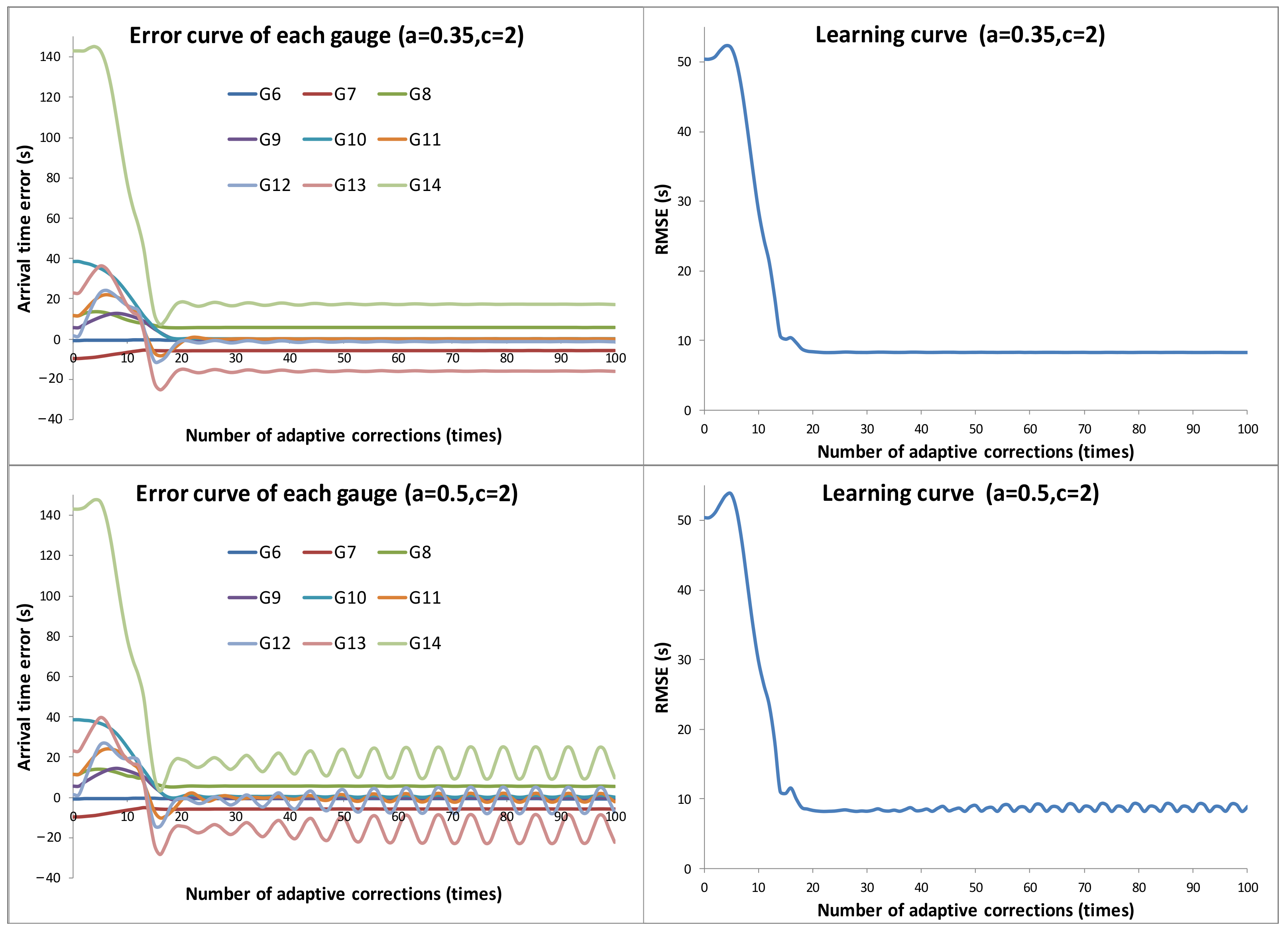
3.2. Verification of the Convergence of Adaptive Correction
- To analyze the effect of relaxation factor c, and , 3, and 4 were set for three sets of data for the experiments.
- To analyze the effect of parameter a, and , 0.35, and 0.5 were set for three sets of data for the experiments.
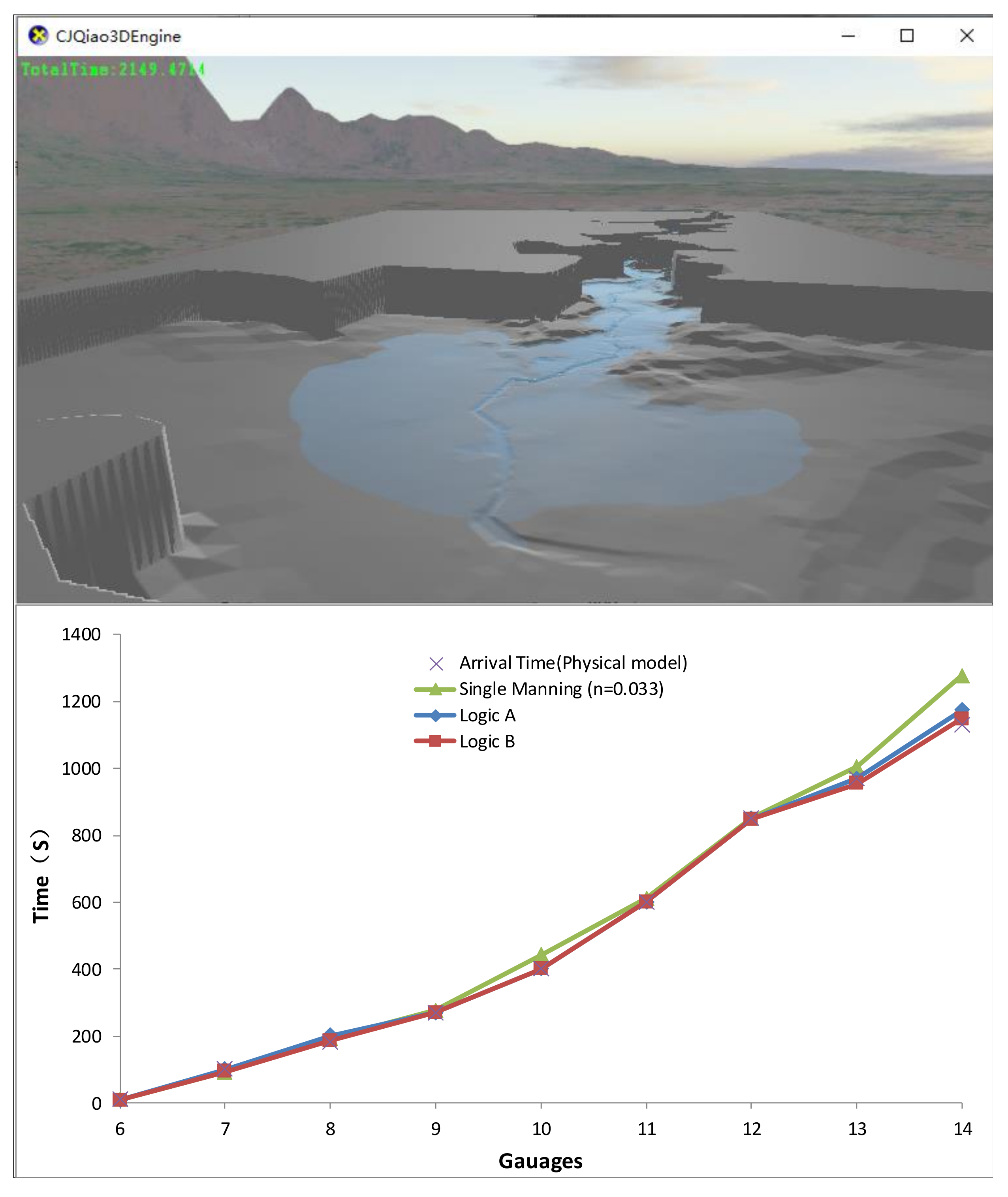
3.3. Evaluation of the Accuracy of Adaptive Correction
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. 2D numerical simulation of unsteady flows for large scale floods prediction in real time. Adv. Water Resour. 2019, 134, 103444. [Google Scholar] [CrossRef]
- Shi, H.B.; Si, P.F.; Dong, P.; Yu, X.P. A two-phase SPH model for massive sediment motion in free surface flows. Adv. Water Resour. 2019, 129, 80–98. [Google Scholar] [CrossRef]
- Haridas, A.; Vadlamani, N.R.; Minamoto, Y. Deep Neural Networks to Correct Sub-Precision Errors in CFD. arXiv 2022, arXiv:2202.04233. [Google Scholar]
- Qiao, C.; Li, J.; Tian, Z. A new approach for fluid dynamics simulation: The Short-lived Water Cuboid Particle model. J. Hydrol. 2016, 540, 437–456. [Google Scholar] [CrossRef]
- Kurganov, A.; Petrova, G. A second-order well-balanced positivity preserving central-upwind scheme for the Saint-Venant system. Commun. Math. Sci. 2007, 5, 133–160. [Google Scholar] [CrossRef]
- Chertock, A.; Cui, S.; Kurganov, A.; Wu, T. Well-balanced positivity preserving central-upwind scheme for the shallow water system with friction terms. Int. J. Numer. Methods Fluids 2015, 78, 355–383. [Google Scholar] [CrossRef]
- Garg, N.K.; Gowda, G. Godunov-type schemes for the pressureless gas dynamics and related models. Appl. Math. Comput. 2022, 418, 126790. [Google Scholar] [CrossRef]
- Maia, A.; Cavalca, D.F.; Tomita, J.T.; Costa, F.P.; Bringhenti, C. Evaluation of an effective and robust implicit time-integration numerical scheme for Navier-Stokes equations in a CFD solver for compressible flows. Appl. Math. Comput. 2022, 413, 126612. [Google Scholar] [CrossRef]
- Chiapolino, A.; Saurel, R. Models and methods for two-layer shallow water flows. J. Comput. Phys. 2018, 371, 1043–1066. [Google Scholar] [CrossRef]
- Roe, P.L. Approximate Riemann solvers, parameter vectors, and difference schemes. J. Comput. Phys. 1981, 43, 357–372. [Google Scholar] [CrossRef]
- Glaister, P. Approximate Riemann solutions of the shallow water equations. J. Hydraul. Res. 1988, 26, 293–306. [Google Scholar] [CrossRef]
- Zhao, D.; Shen, H.; Lai, J.; Tabios, G.Q., III. Approximate Riemann Solvers in FVM for 2D Hydraulic Shock Wave Modeling. J. Hydraul. Eng. 1996, 122, 692–702. [Google Scholar] [CrossRef]
- Aizinger, V.; Dawson, C. A discontinuous Galerkin method for two-dimensional flow and transport in shallow water. Adv. Water Resour. 2002, 25, 67–84. [Google Scholar] [CrossRef]
- Lai, W.; Khan, A.A. A discontinuous Galerkin method for two-dimensional shock wave modeling. Model. Simul. Eng. 2011, 2011, 782832. [Google Scholar] [CrossRef]
- Lai, W.; Khan, A.A. Modeling dam-break flood over natural rivers using Discontinuous Galerkin method. J. Hydrodyn. 2012, 24, 467–478. [Google Scholar] [CrossRef]
- Hu, R.; Fang, F.; Salinas, P.; Pain, C.C.; Domingo, N.D.S.; Mark, O. Numerical simulation of floods from multiple sources using an adaptive anisotropic unstructured mesh method. Adv. Water Resour. 2019, 123, 173–188. [Google Scholar] [CrossRef]
- Ziliani, M.G.; Ghostine, R.; Ait-El-Fquih, B.; McCabe, M.F.; Hoteit, I. Enhanced flood forecasting through ensemble data assimilation and joint state-parameter estimation. J. Hydrol. 2019, 577, 123924. [Google Scholar] [CrossRef]
- Patankar, S.V.; Spalding, D.B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Issa, R.; Ahmadi-Befrui, B.; Beshay, K.; Gosman, A. Solution of the implicitly discretised reacting flow equations by operator-splitting. J. Comput. Phys. 1991, 93, 388–410. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Blocken, B.; Gualtieri, C. Ten iterative steps for model development and evaluation applied to Computational Fluid Dynamics for Environmental Fluid Mechanics. Environ. Model. Softw. 2012, 33, 1–22. [Google Scholar] [CrossRef]
- Fu, B.; Horsburgh, J.S.; Jakeman, A.J.; Gualtieri, C.; Arnold, T.; Marshall, L.; Green, T.R.; Quinn, N.W.T.; Volk, M.; Hunt, R.J.; et al. Modeling Water Quality in Watersheds: From Here to the Next Generation. Water Resour. Res. 2020, 56, e2020WR027721. [Google Scholar] [CrossRef]
- Jiang, C.; Soh, Y.C.; Li, H.; Masood, M.K.; Wei, Z.; Zhou, X.; Zhai, D. CFD results calibration from sparse sensor observations with a case study for indoor thermal map. Build. Environ. 2017, 117, 166–177. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar]
- Nguyen, V.T.; Georges, D.; Besancon, G. Adjoint-method-based estimation of Manning roughness coefficient in an overland flow model. In Proceedings of the American Control Conference, Chicago, IL, USA, 1–3 July 2015; Volume 2015, pp. 1977–1982. [Google Scholar]
- Kajero, O.T.; Thorpe, R.B.; Chen, T.; Wang, B.; Yao, Y. Kriging meta-model assisted calibration of computational fluid dynamics models. AIChE J. 2016, 62, 4308–4320. [Google Scholar] [CrossRef]
- Guillas, S.; Glover, N.; Malki-Epshtein, L. Bayesian calibration of the constants of the k-ϵ turbulence model for a CFD model of street canyon flow. Comput. Methods Appl. Mech. Eng. 2014, 279, 536–553. [Google Scholar] [CrossRef]
- Azamathulla, H.M. Use of Gene-Expression Programming to Estimate Manning’s Roughness Coefficient for High Gradient Streams. Water Resour. Manag. 2013, 27, 715–729. [Google Scholar] [CrossRef]
- Becker, R.; Koppa, A.; Schulz, S.; Usman, M.; aus der Beek, T.; Schüth, C. Spatially distributed model calibration of a highly managed hydrological system using remote sensing-derived ET data. J. Hydrol. 2019, 577, 123944. [Google Scholar] [CrossRef]
- Sætra, M.L.; Brodtkorb, A.R.; Lie, K.A. Efficient GPU-Implementation of Adaptive Mesh Refinement for the Shallow-Water Equations. J. Sci. Comput. 2015, 63, 23–48. [Google Scholar] [CrossRef]
- Hervouet, J.M. A high resolution 2-D dam-break model using parallelization. Hydrol. Process. 2000, 14, 2211–2230. [Google Scholar] [CrossRef]
- Singh, J.; Altinakar, M.S.; Ding, Y. Two-dimensional numerical modeling of dam-break flows over natural terrain using a central explicit scheme. Adv. Water Resour. 2011, 34, 1366–1375. [Google Scholar] [CrossRef]
- Valiani, A.; Caleffi, V.; Zanni, A. Case Study: Malpasset Dam-Break Simulation using a Two-Dimensional Finite Volume Method. J. Hydraul. Eng. 2002, 128, 460–472. [Google Scholar] [CrossRef]
- Hervouet, J.M.; Petitjean, A. Malpasset dam-break revisited with two-dimensional computations. J. Hydraul. Res. 1999, 37, 777–788. [Google Scholar] [CrossRef]
- Savant, G.; Trahan, C.J.; Pettey, L.; Mcalpin, T.O.; Bell, G.L.; Mcknight, C.J. Urban and overland flow modeling with dynamic adaptive mesh and implicit diffusive wave equation solver. J. Hydrol. 2019, 573, 13–30. [Google Scholar] [CrossRef]
- Soares-Frazão, S.; Alcrudo, F.; Goutal, N. Dam-break Test Cases Summary. In Proceedings of the 4th CADAM Meeting, Zaragoza, Spain, 18–19 November 1999; European Commission: Bruxelles, Belgium, 1999. [Google Scholar]
- An, H.; Yu, S.; Lee, G.; Kim, Y. Analysis of an open source quadtree grid shallow water flow solver for flood simulation. Quat. Int. 2015, 384, 118–128. [Google Scholar] [CrossRef]
- Chen, T.Y.K.; Capart, H. Kinematic wave solutions for dam-break floods in non-uniform valleys. J. Hydrol. 2020, 582, 124381. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, W. A two dimensional hydrodynamic and sediment transport model for dam break based on finite volume method with quadtree grid. Appl. Ocean Res. 2011, 33, 297–308. [Google Scholar] [CrossRef]
- Bennett, N.D.; Croke, B.F.; Guariso, G.; Guillaume, J.H.; Hamilton, S.H.; Jakeman, A.J.; Marsili-Libelli, S.; Newham, L.T.; Norton, J.P.; Perrin, C.; et al. Characterising Performance of Environmental Models. Environ. Model. Softw. 2013, 40, 1–20. [Google Scholar] [CrossRef]
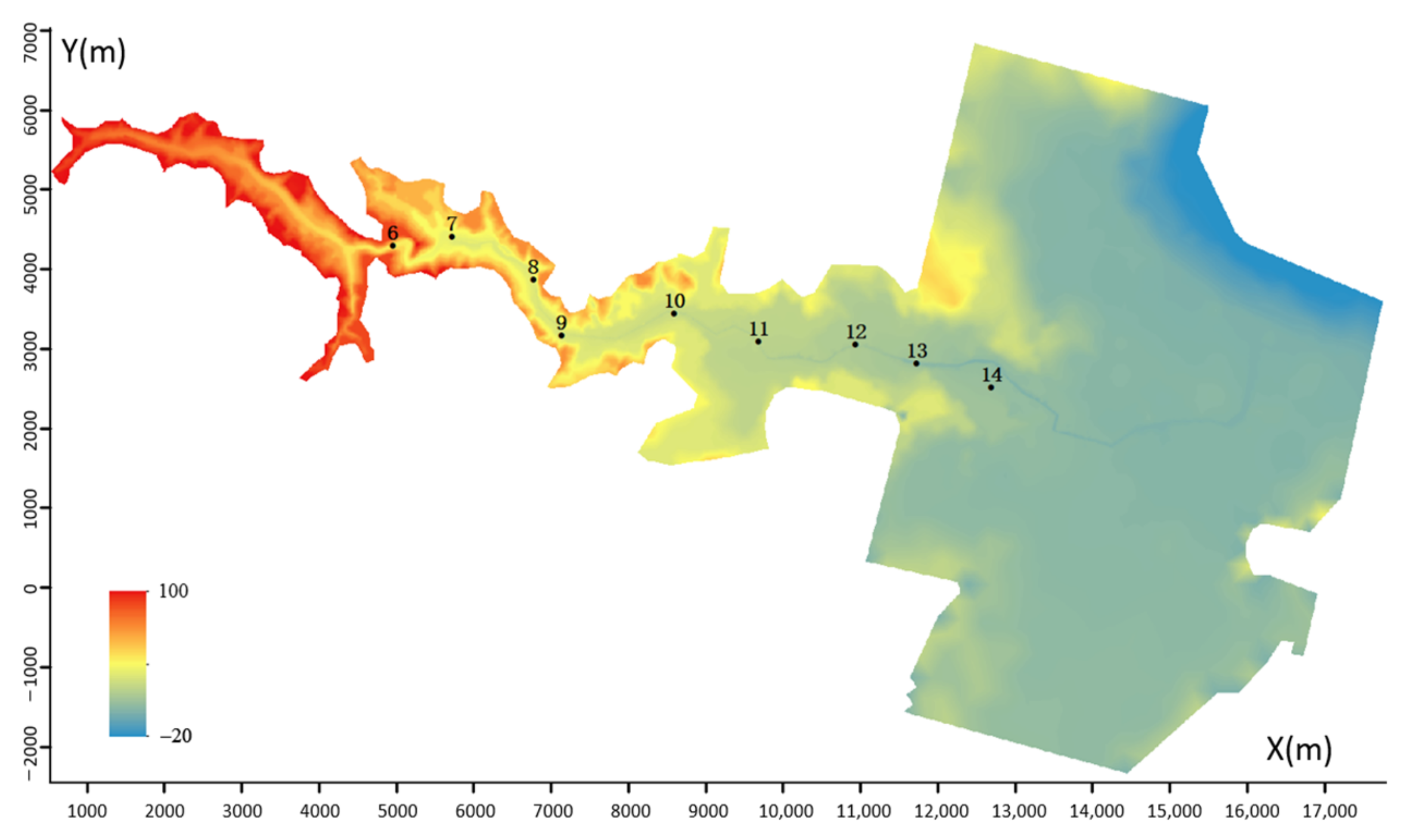


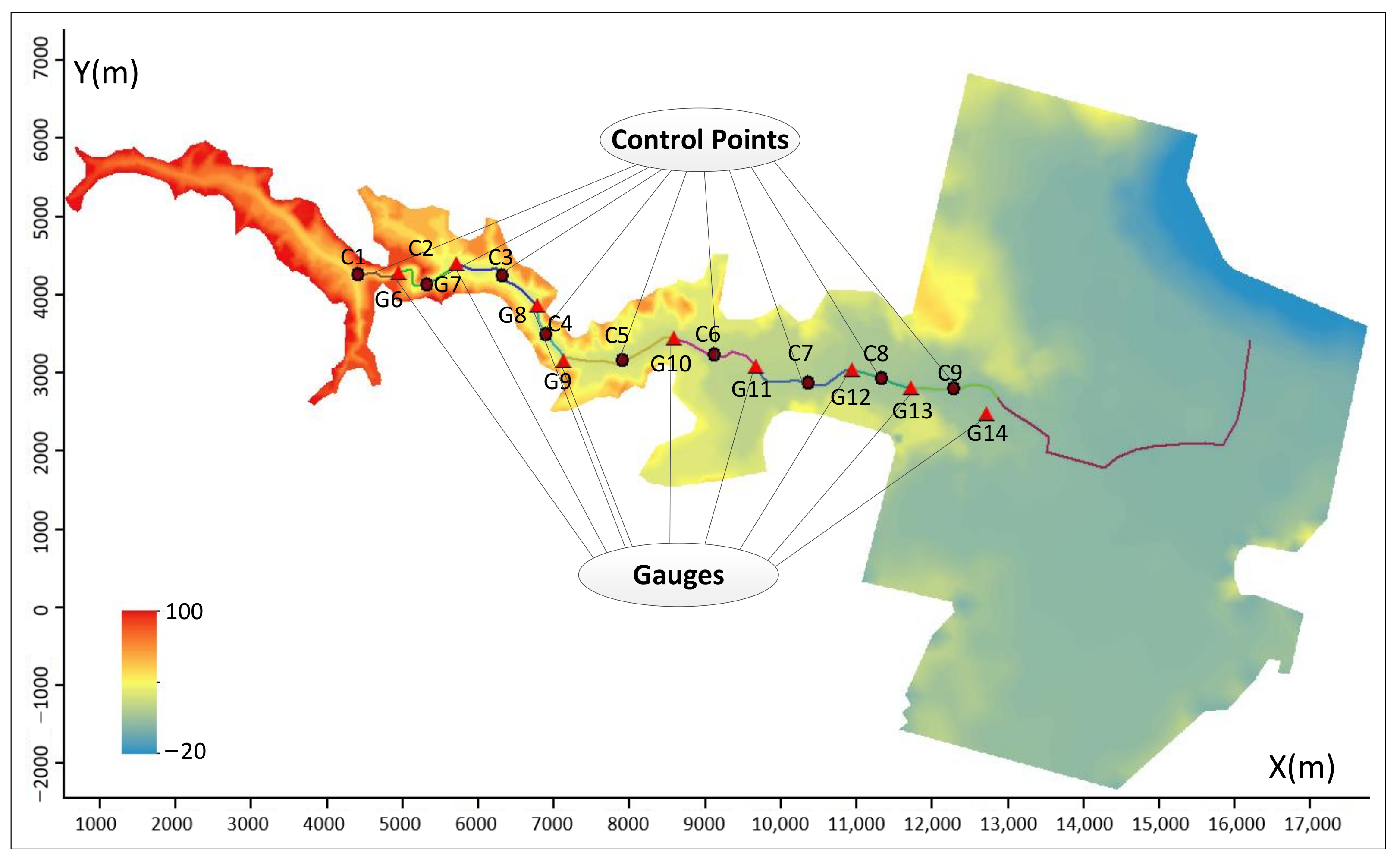

| Gauge ID | X (m) | Y (m) | Water Arrival Time (s) | The Max Water Level (m) |
|---|---|---|---|---|
| 6 | 4947.46 | 4289.71 | 9 | 84.2 |
| 7 | 5717.30 | 4407.61 | 100 | 49.1 |
| 8 | 6775.14 | 3869.23 | 180 | 54 |
| 9 | 7128.20 | 3162.00 | 270 | 40.2 |
| 10 | 8585.30 | 3443.08 | 400 | 34.9 |
| 11 | 9674.97 | 3085.89 | 600 | 27.4 |
| 12 | 10,939.15 | 3044.78 | 850 | 21.5 |
| 13 | 11,724.3 | 2810.41 | 970 | 16.1 |
| 14 | 12,723.70 | 2485.08 | 1130 | 12.9 |
| G6 | G7 | G8 | G9 | G10 | G11 | G12 | G13 | G14 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Physical model | Water arrival time (s) | 9.00 | 100.00 | 180.00 | 270.00 | 400.00 | 600.00 | 850.00 | 970.00 | 1130.00 |
| Max. water level (m) | 84.20 | 49.10 | 54.00 | 40.20 | 34.90 | 27.40 | 21.50 | 16.10 | 12.90 | |
| Telemac-2D | Max. water level (m) | 87.97 | 54.43 | 53.25 | 47.91 | 36.51 | 25.37 | 19.13 | 17.65 | 12.76 |
| RE (%) | 4.48 | 10.86 | 1.39 | 19.18 | 4.61 | 7.41 | 11.02 | 9.63 | 1.09 | |
| MRE (%) | 7.74 | |||||||||
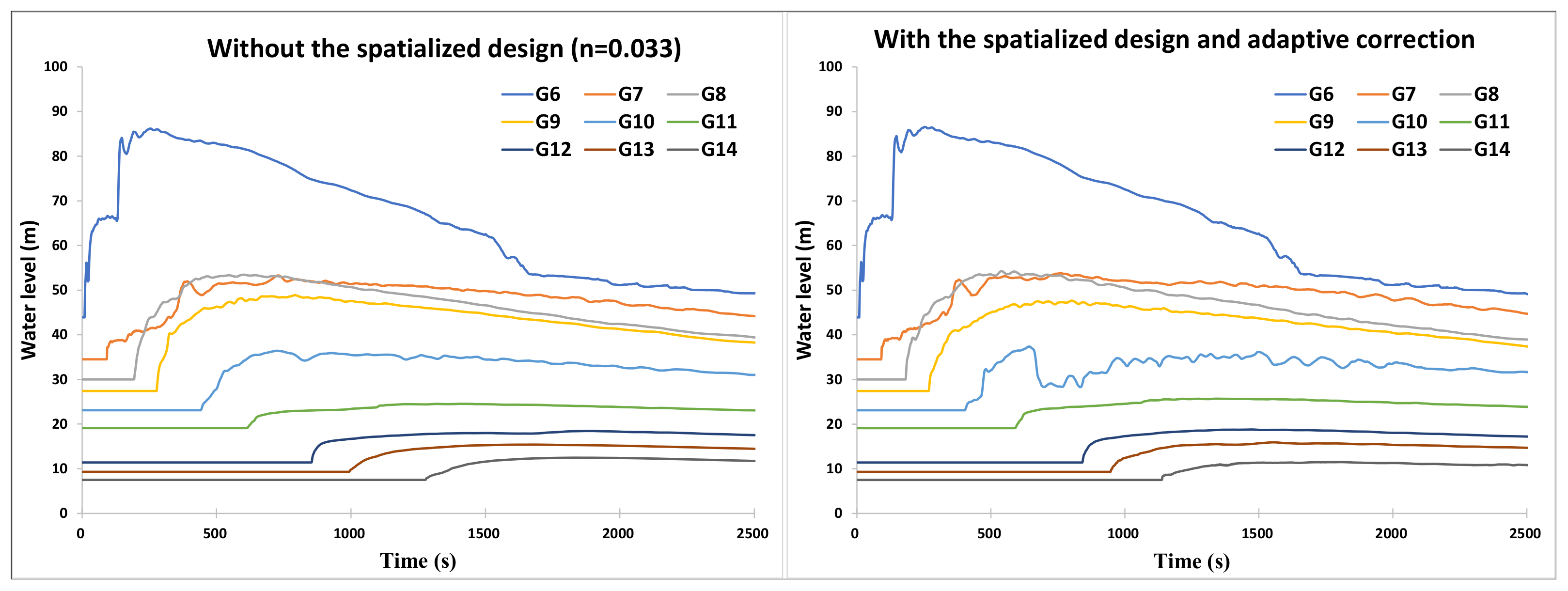
| Without the spatialized design (n = 0.033) | Water arrival time (s) | 8.50 | 90.35 | 191.61 | 275.61 | 438.42 | 611.52 | 851.47 | 992.98 | 1273.12 |
| RE (%) | 5.56 | 9.65 | 6.45 | 2.08 | 9.60 | 1.92 | 0.17 | 2.37 | 12.67 | |
| MRE (%) | 5.61 | |||||||||
| Max. water level (m) | 86.18 | 53.29 | 53.45 | 48.87 | 36.41 | 24.53 | 18.45 | 15.40 | 12.47 | |
| RE (%) | 2.35 | 8.53 | 1.01 | 21.56 | 4.33 | 10.49 | 14.17 | 4.37 | 3.36 | |
| MRE (%) | 7.80 | |||||||||
| With the Spatialized design and adaptive correction | Water arrival time (s) | 8.50 | 94.30 | 185.61 | 269.31 | 399.98 | 598.03 | 842.87 | 947.79 | 1139.99 |
| RE (%) | 5.56 | 5.70 | 3.11 | 0.26 | 0.01 | 0.33 | 0.84 | 2.29 | 0.88 | |
| MRE (%) | 2.11 | |||||||||
| Max. water level (m) | 86.55 | 53.77 | 54.29 | 47.65 | 37.38 | 25.69 | 18.79 | 15.92 | 11.50 | |
| RE (%) | 2.79 | 9.52 | 0.53 | 18.53 | 7.11 | 6.25 | 12.61 | 1.14 | 10.87 | |
| MRE (%) | 7.70 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiao, C. Research on Parameter Spatialization and Adaptive Correction Models in Fluid Numerical Simulations. Water 2022, 14, 2671. https://doi.org/10.3390/w14172671
Qiao C. Research on Parameter Spatialization and Adaptive Correction Models in Fluid Numerical Simulations. Water. 2022; 14(17):2671. https://doi.org/10.3390/w14172671
Chicago/Turabian StyleQiao, Changjian. 2022. "Research on Parameter Spatialization and Adaptive Correction Models in Fluid Numerical Simulations" Water 14, no. 17: 2671. https://doi.org/10.3390/w14172671




