A Comparison between Variable Deficit Irrigation and Farmers’ Irrigation Practices under Three Fertilization Levels in Cotton Yield (Gossypium hirsutum L.) Using Precision Agriculture, Remote Sensing, Soil Analyses, and Crop Growth Modeling
Abstract
:1. Introduction
2. Materials and Methods
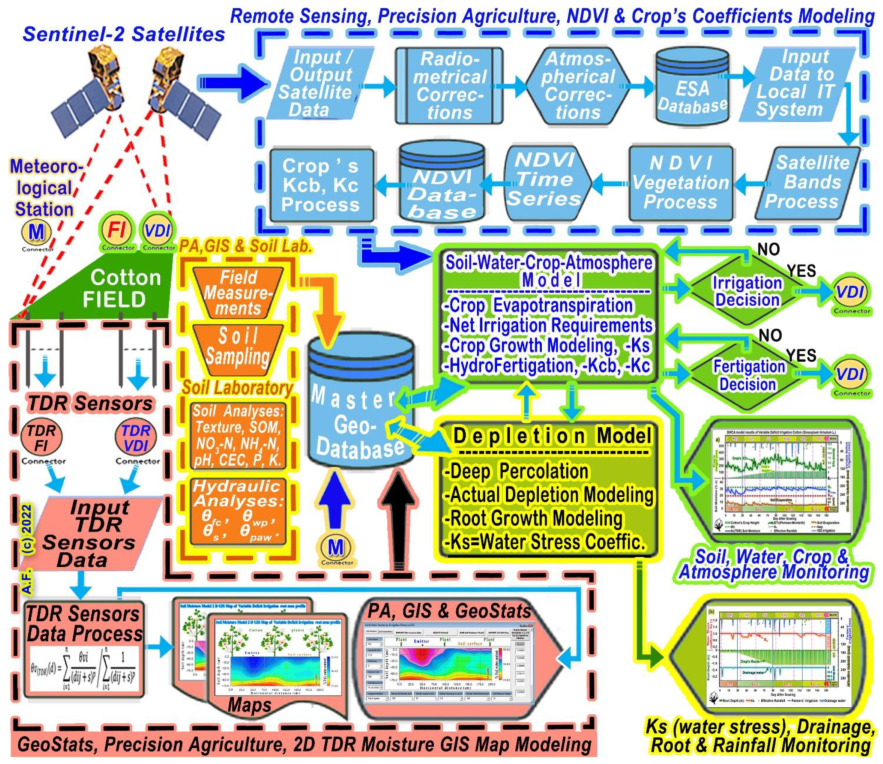
2.1. Experimental Plot Design, Irrigation and Fertilization Treatments, Soil Sampling, and Laboratory Soil and Hydraulic Analysis
- (a)
- Blue dash line input section, named “Remote sensing, Precision Agriculture, NDVI & Crop’s coefficients Modeling”;
- (b)
- Brown dash line input section, named “PA, GIS & Soil Lab.”;
- (c)
- Black dash line input section, named “Geostats, Precision Agriculture, 2D-TDR Soil Moisture GIS Map Modeling”;
- (d)
- The “M” input section, named “Meteorological Station”, with various sensors providing the local climatic data.
- (a)
- The soil–water–crop–atmosphere model;
- (b)
- The depletion model.
2.2. Farm machines, Irrigation Network, Soil, Fertilization, and Crop Management
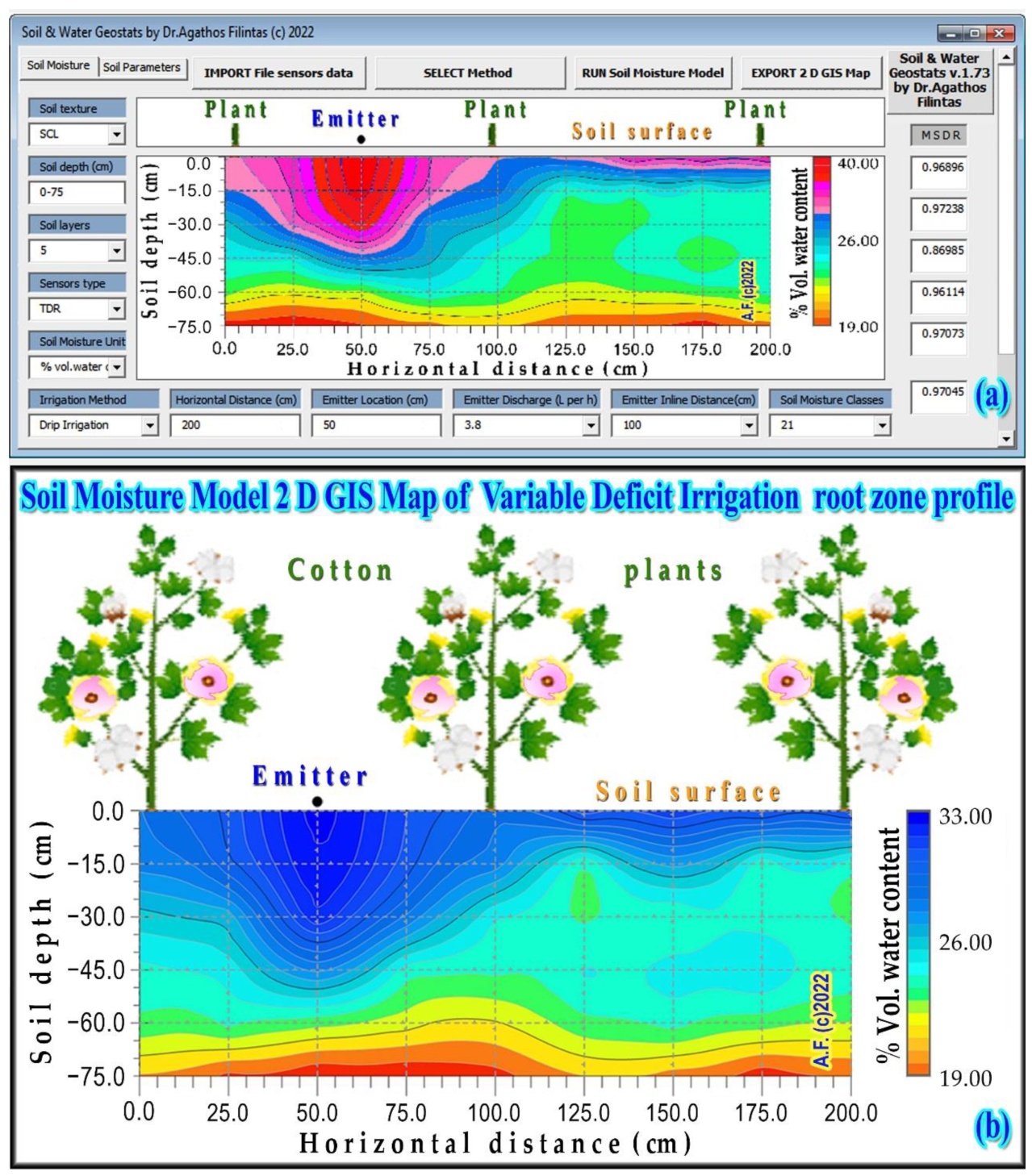
2.3. Soil Moisture Measurements, Digital 2D GIS Moisture Maps Utilizing GIS, Precision Agriculture, Geostatistics, and Average Soil Water Content of Soil Layers
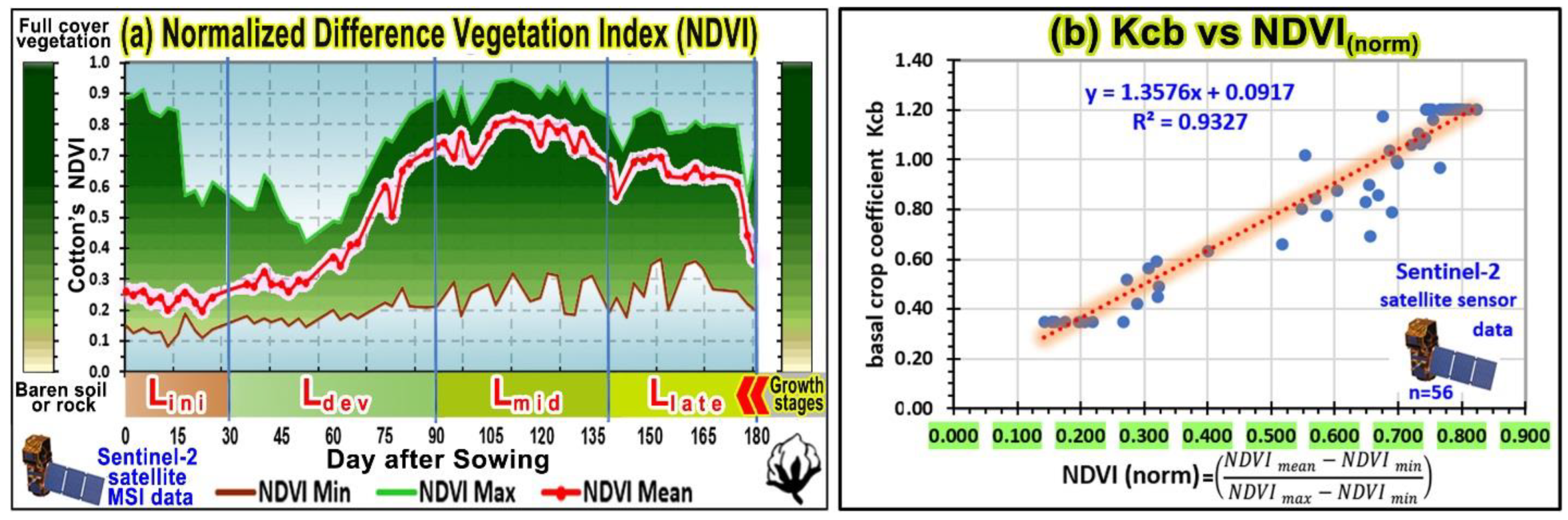
2.4. Remote-Sensing (Satellite) Data and Crop’s NDVI
- (a)
- 4 × 10 m bands: three classical RGB bands (blue (~493 nm), green (560 nm), and red (~665 nm)) and a near-infrared (~833 nm) band;
- (b)
- 6 × 20 m bands: 4 narrow bands in the VNIR vegetation red edge spectral domain (~704 nm, ~740 nm, ~783 nm, and ~865 nm) and 2 wider SWIR bands (~1610 nm and ~2190 nm);
- (c)
- 3 × 60 m bands mainly focused towards cloud screening and atmospheric correction (~443 nm for aerosols and ~945 nm for water vapor) and cirrus detection (~1374 nm).
2.5. Climatic Data Sensors’ Measurements; Net Irrigation Requirements; Reference, Crop, and Actual Evapotranspiration; the Soil–Water–Crop–Atmosphere (SWCA) Model; the Soil Moisture Depletion Model; and the Water Stress Coefficient Ks-Weighted Average
2.6. Nitrogen Partial Factor Productivity, Nitrogen–Phosphorus–Potassium Fertilizer Partial Factor Productivity, and Water Use Efficiency (WUE)
2.7. Field Measurements of Cotton Plant Height, Plant Stem, Boll Weight, and Above-Ground Biomass Dry Matter
2.8. Statistical Data Analysis
2.9. Geostatistical Analysis and Modeling, Spatial Interpolation Methodology, and Model Validation Process
3. Results and Discussion
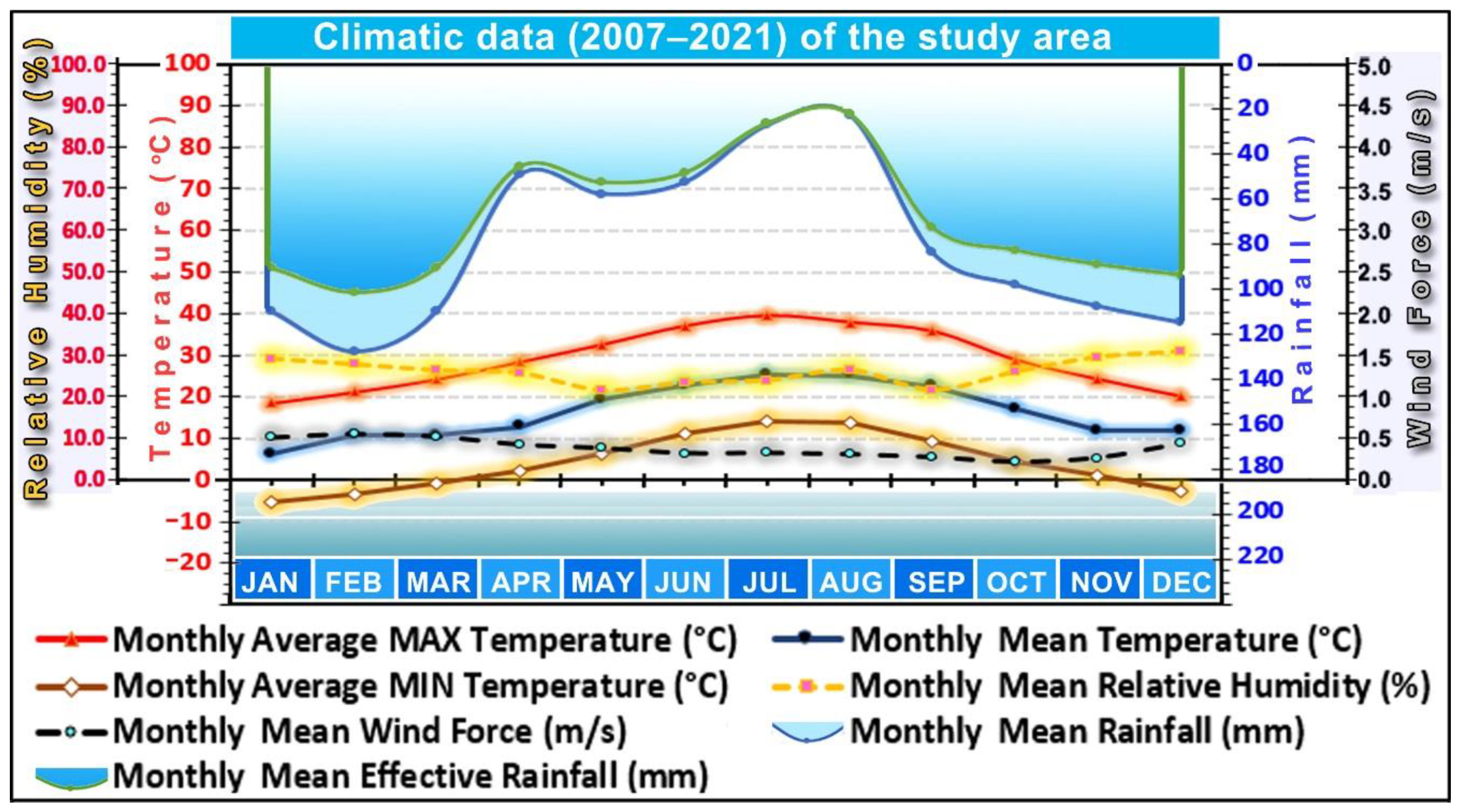
3.1. Study Area of the Farm Field, Climatic Data Analysis for The Recent 15 Years (2007–2021), and Results and Discussion of Soil and Hydraulic Analysis of the Field’s Soil
3.2. Results and Discussion of the 2D Moisture Model and GIS Maps of Cotton’s Root-Zone Soil Profile Utilizing GIS, Precision Agriculture, and Geostatistics
3.3. Results of Sentinel-2 Satellite MSI Sensor Data Analysis and NDVI Vegetation Index of the Cotton’s Farm Field
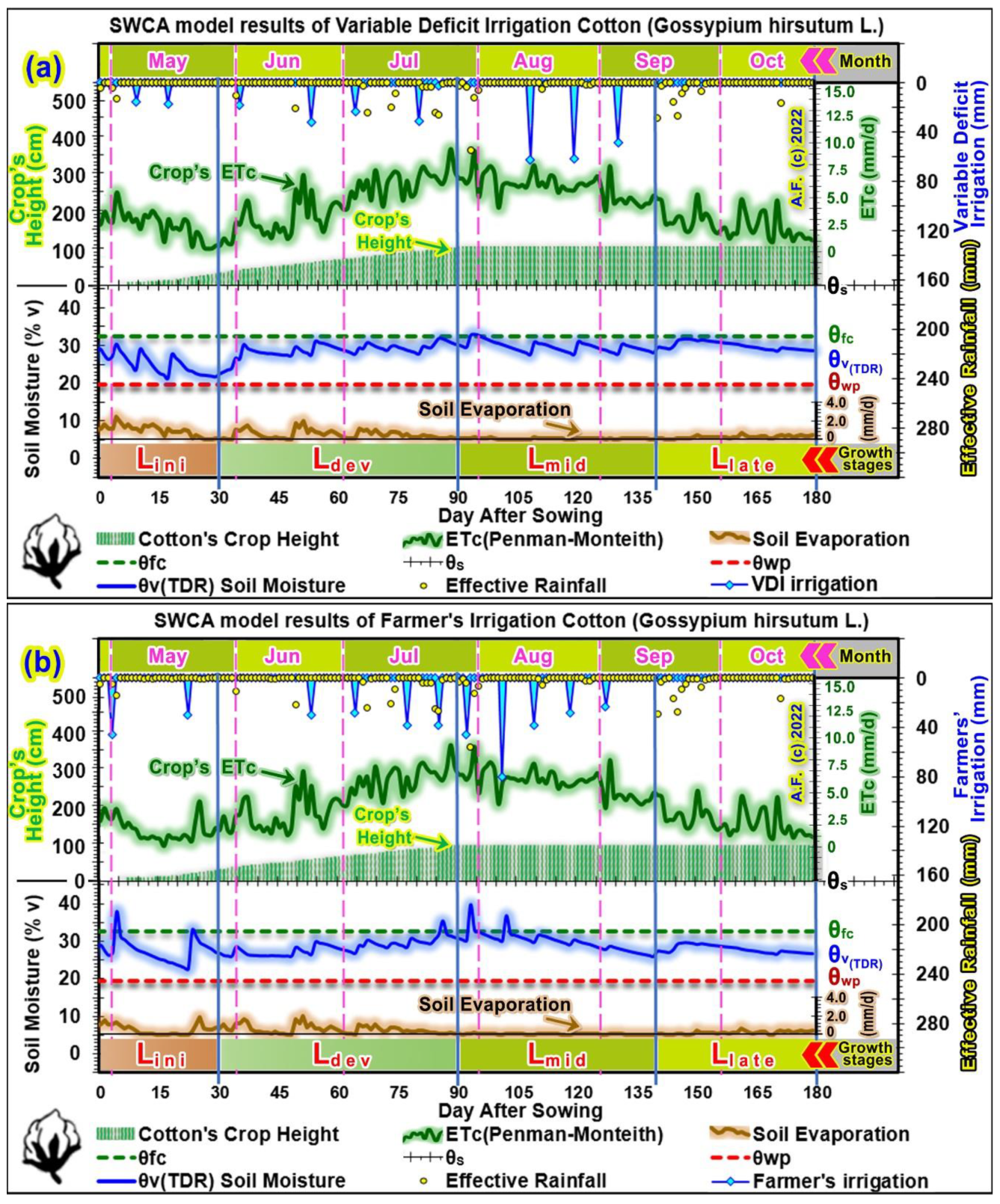
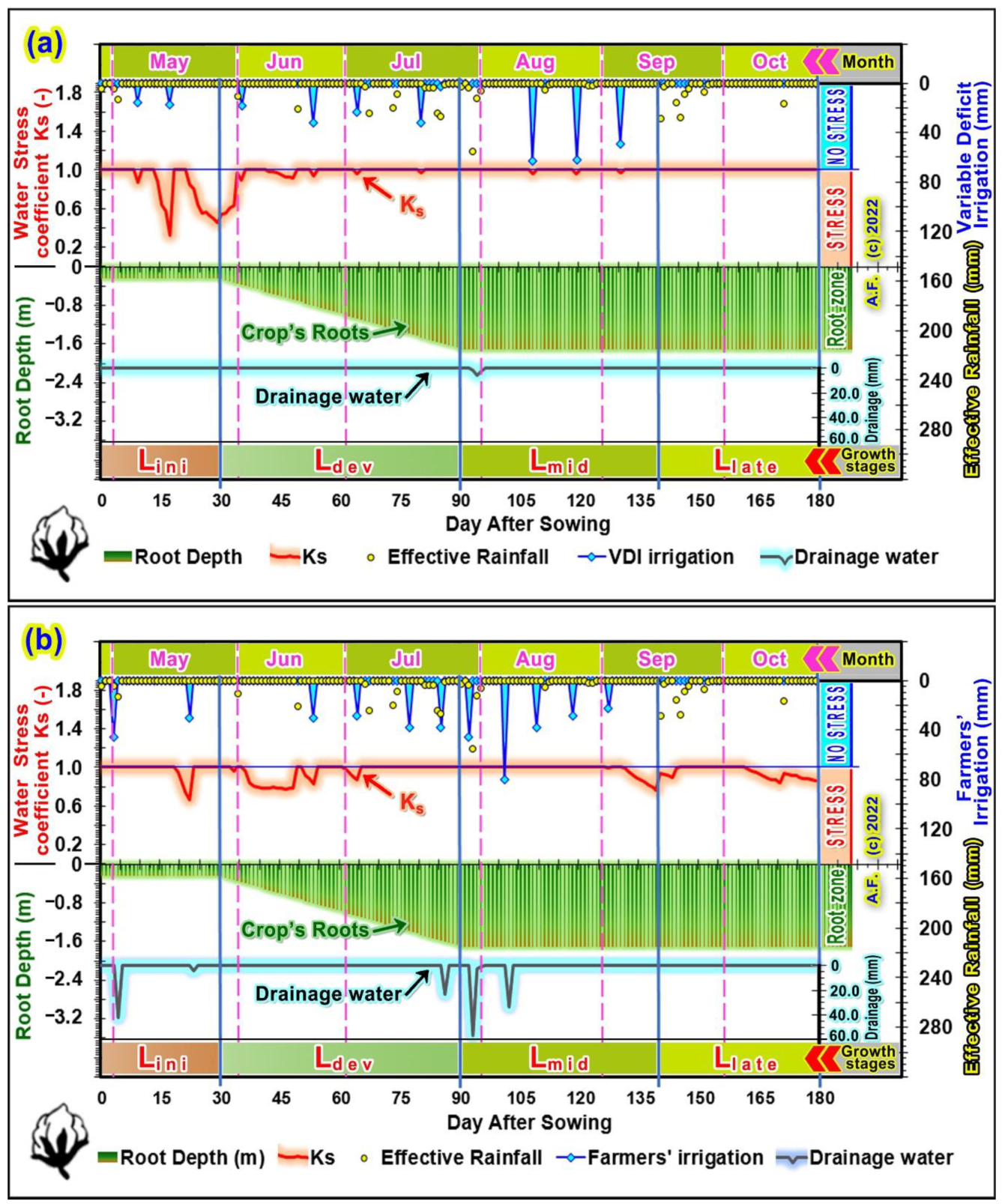
3.4. Results and Discussion of The Variable Deficit Irrigation, Farmers’ Irrigation, Daily Soil–Water–Crop–Atmosphere (SWCA) Model, Water Stress Coefficient Ks, and the Availiable Soil Moisture Depletion Model
3.4.1. Results and Discussion of the Lini: Initial Crop Growth Stage or Seedling
3.4.2. Results and Discussion of the Ldev: Crop Development Stage or Flowering
3.4.3. Results and Discussion of the Lmid: Mid-Season Growth Stage or Bolling
3.4.4. Results and Discussion of the Llate: Late-Season Growth Stage or Maturity
3.4.5. Results and Discussion of Plants Growth Characteristics Statistical Analysis of the Entire Growth Season
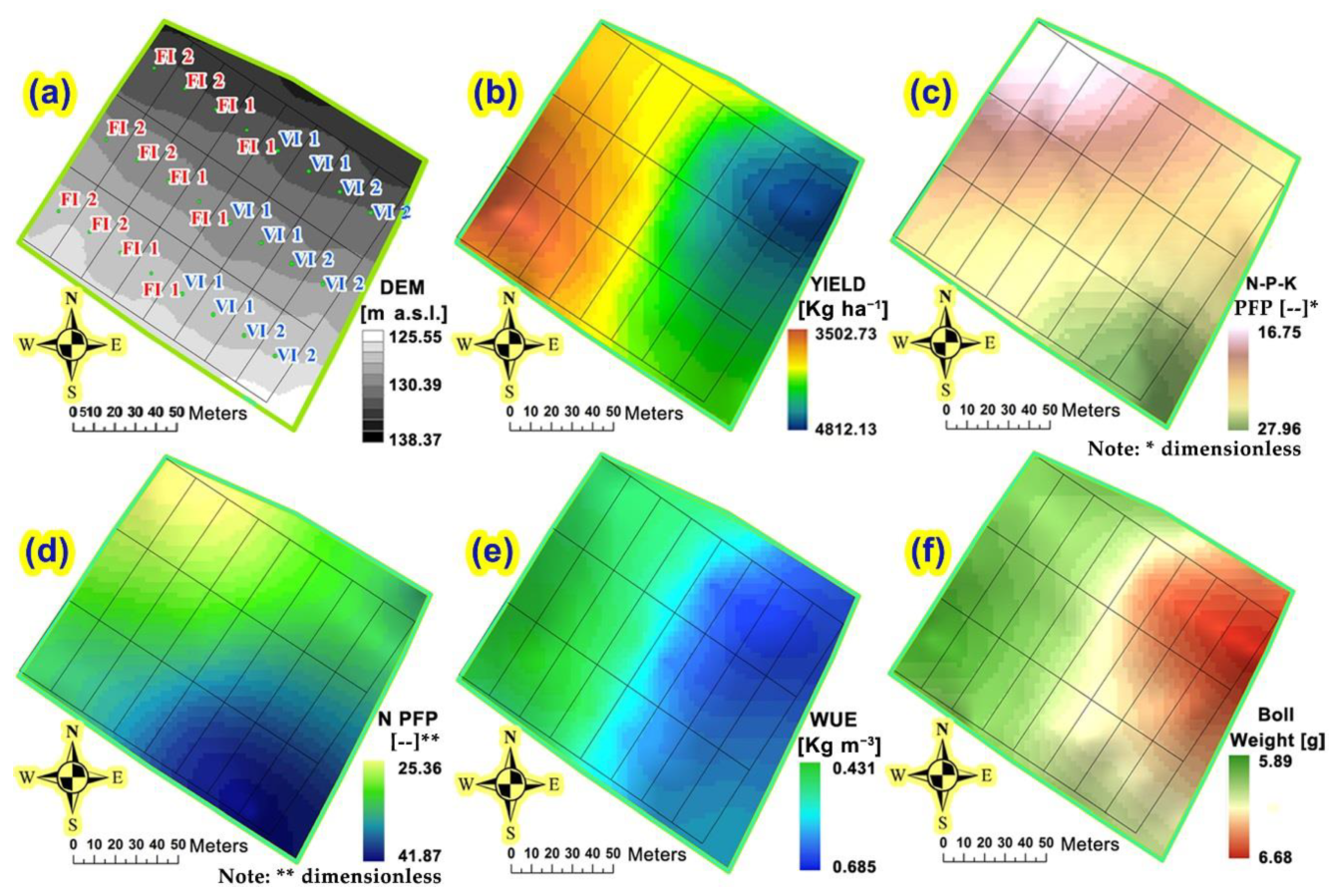
3.4.6. Results and Discussion of Statistical Analysis; Geostatistical Analysis and Modeling Using Precision Agriculture; and Model Validation of the Cotton Yield, Nitrogen Fertilizer PFP, N-P-K Fertilizer PFP, and Water Use Efficiency of the Entire Growth Season
- (a)
- the exponential model for the field’s digital elevation model (DEM);
- (b)
- the exponential model for the cotton yield [Kg ha−1];
- (c)
- the Gaussian model for N-P-K fertilizer PF productivity (dimensionless) [–];
- (d)
- the Gaussian model for nitrogen PF productivity (dimensionless) [–];
- (e)
- the Gaussian model for WUE [Kg m−3];
- (f)
- the Gaussian model for the cotton boll weight [g].
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Küppers, M.; O’Rourke, L.; Bockelée-Morvan, D.; Zakharov, V.; Lee, S.; Von Allmen, P.; Carry, B.; Teyssier, D.; Marston, A.; Müller, T.; et al. Localized sources of water vapour on the dwarf planet (1). Ceres Nat. 2014, 505, 525–527. [Google Scholar] [CrossRef] [PubMed]
- Siddique, K.H.M.; Bramley, H. Water Deficits: Development; CRC Press: Boca Raton, FL, USA, 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Filintas, A. Land Use Evaluation and Environmental Management of Biowastes, for Irrigation with Processed Wastewaters and Application of Bio-Sludge with Agricultural Machinery, for Improvement-Fertilization of Soils and Crops, with the Use of GIS-Remote Sensing, Precision Agriculture and Multicriteria Analysis. Ph.D. Thesis, University of the Aegean, Mitilini, Greece, 2011. [Google Scholar]
- Gleick, P.H.; Palaniappan, M. Peak water limits to freshwater withdrawal and use. Proc. Natl. Acad. Sci. USA 2010, 107, 11155–11162. [Google Scholar] [CrossRef] [PubMed]
- Shiklomanov, I.A. Appraisal and assessment of world water resources. Water Int. 2000, 25, 11–32. [Google Scholar] [CrossRef]
- Schiermeier, Q. The parched planet: Water on tap. Nature 2014, 510, 326–328. [Google Scholar] [CrossRef]
- Gan, Y.; Siddique, K.H.M.; Turner, N.C.; Li, X.-G.; Niu, J.-Y.; Yang, C.; Liu, L.; Chai, Q. Ridge-furrow mulching systems—An innovative technique for boosting crop productivity in semiarid rain-fed environments. Adv. Agron. 2013, 118, 429–476. [Google Scholar] [CrossRef]
- FAO. Coping with Water Scarcity: An Action Framework for Agriculture and Food Security; FAO: Rome, Italy, 2012; p. 100. [Google Scholar]
- Stamatis, G.; Parpodis, K.; Filintas, A.; Zagana, E. Groundwater quality, nitrate pollution and irrigation environmental management in the Neogene sediments of an agricultural region in central Thessaly (Greece). Environ. Earth Sci. 2011, 64, 1081–1105. [Google Scholar] [CrossRef]
- ΕΕA. Use of Freshwater Resources in Europe, CSI 018; European Environment Agency (EEA): Copenhagen, Denmark, 2019. [Google Scholar]
- Koutseris, Ε.; Filintas, A.; Dioudis, P. Antiflooding prevention, protection, strategic environmental planning of aquatic resources and water purification: The case of Thessalian basin, in Greece. Desalination 2010, 250, 318–322. [Google Scholar] [CrossRef]
- Κoutseris, Ε.; Filintas, A.; Dioudis, P. Environmental control of torrents environment: One valorisation for prevention of water flood disasters. WIT Trans. Ecol. Environ. 2007, 104, 249–259. [Google Scholar] [CrossRef]
- Islam, S.M.F.; Karim, Z. World’s Demand for Food and Water: The Consequences of Climate Change. In Desalination-Challenges and Opportunities; Farahani, M.H.D.A., Vatanpour, V., Taheri, A.H., Eds.; IntechOpen: London, UK, 2019; Chapter 4; pp. 1–27. [Google Scholar] [CrossRef] [Green Version]
- Filintas, A.; Wogiatzi, E.; Gougoulias, N. Rainfed cultivation with supplemental irrigation modelling on seed yield and oil of Coriandrum sativum L. using Precision Agriculture and GIS moisture mapping. Water Supply 2021, 21, 2569–2582. [Google Scholar] [CrossRef]
- Siebert, S.; Kummu, M.; Porkka, M.; Döll, P.; Ramankutty, N.; Scanlon, B.R. A global data set of the extent of irrigated land from 1900 to 2005. Hydrol. Earth Syst. Sci. 2015, 19, 1521–1545. [Google Scholar] [CrossRef]
- Garrote, L.; Iglesias, A.; Granados, A.; Mediero, L.; Martin-Carrasco, F. Quantitative assessment of climate change vulnerability of irrigation demands in Mediterranean Europe. Water Resour. Manag. 2015, 29, 325–338. [Google Scholar] [CrossRef]
- Kreins, P.; Henseler, M.; Anter, J.; Herrmann, F.; Wendland, F. Quantification of climate change impact on regional agricultural irrigation and groundwater demand. Water Resour. Manag. 2015, 29, 3585–3600. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration; Drainage & Irrigation paper Nº56; FAO: Rome, Italy, 1998. [Google Scholar]
- Kang, S.; Zhang, J.; Liang, Z.; Hu, X.; Cai, H. The controlled alternative irrigation-A new approach for water saving regulation in farm land. Agric. Res. Arid Areas 1997, 15, 1–6. (In Chinese) [Google Scholar] [CrossRef]
- Dioudis, P.; Filintas, A.; Koutseris, E. GPS and GIS based N-mapping of agricultural fields’ spatial variability as a tool for non-polluting fertilization by drip irrigation. Int. J. Sus. Dev. Plann. 2009, 4, 210–225. [Google Scholar] [CrossRef]
- Dioudis, P.; Filintas, A.; Papadopoulos, A. Corn yield response to irrigation interval and the resultant savings in water and other overheads. Irrig. Drain. 2009, 58, 96–104. [Google Scholar] [CrossRef]
- Filintas, A.; Dioudis, P.; Prochaska, C. GIS modeling of the impact of drip irrigation, of water quality and of soil’s available water capacity on Zea mays L, biomass yield and its biofuel potential. Desalin. Water Treat. 2010, 13, 303–319. [Google Scholar] [CrossRef]
- Bakhsh, A.; Hussein, F.; Ahmad, N.; Hassan, A.; Farid, H.U. Modeling deficit irrigation effects in maize to improve water use efficiency. Pak. J. Agric. Sci. 2012, 49, 365–374. [Google Scholar]
- Jinxia, Z.; Ziyong, C.; Rui, Z. Regulated deficit drip irrigation influences on seed maize growth and yield under film. Proc. Engin. 2012, 28, 464–468. [Google Scholar] [CrossRef]
- Igbadun, H.E.; Ramalan, A.A.; Oiganji, E. Effects of regulated deficit irrigation and mulch on yield, water use and crop water productivity of onion in Samaru, Nigeria. Agric. Water Manage. 2012, 109, 162–169. [Google Scholar] [CrossRef]
- Qiu, Y.F.; Meng, G. The effect of water saving and production increment by drip irrigation schedules. In Proceedings of the Third International Conference on Intelligent System Design and Engineering Applications (ISDEA), Hong Kong, China, 16–18 January 2013. [Google Scholar]
- Tsakmakis, I.; Kokkos, N.; Pisinaras, V.; Papaevangelou, V.; Hatzigiannakis, E.; Arampatzis, G.; Gikas, G.D.; Linker, R.; Zoras, S.; Evagelopoulos, V.; et al. Operational precise irrigation for cotton cultivation through the coupling of meteorological and crop growth models. Water Resour. Manag. 2017, 31, 563–580. [Google Scholar] [CrossRef]
- Filintas, A. Soil Moisture Depletion Modelling Using a TDR Multi-Sensor System, GIS, Soil Analyzes, Precision Agriculture and Remote Sensing on Maize for Improved Irrigation-Fertilization Decisions. Eng. Proc. 2021, 9, 36. [Google Scholar] [CrossRef]
- Cheng, M.; Wang, H.; Fan, J.; Zhang, F.; Wang, X. Effects of Soil Water Deficit at Different Growth Stages on Maize Growth, Yield, and Water Use Efficiency under Alternate Partial Root-Zone Irrigation. Water 2021, 13, 148. [Google Scholar] [CrossRef]
- Ahmad, H.S.; Imran, M.; Ahmad, F.; Rukh, S.; Ikram, R.M.; Rafique, H.M.; Iqbal, Z.; Alsahli, A.A.; Alyemeni, M.N.; Ali, S.; et al. Improving Water Use Efficiency through Reduced Irrigation for Sustainable Cotton Production. Sustainability 2021, 13, 4044. [Google Scholar] [CrossRef]
- Geerts, S.; Raes, D. Deficit irrigation as an on-farm strategy to maximize crop water productivity in dry areas. Agric. Water Manag. 2009, 96, 1275–1284. [Google Scholar] [CrossRef]
- Howell, T.A.; Evett, S.R.; Tolk, J.A.; Schneider, A.D. Evapotranspiration of Full-, defiit-Irrigated, and dryland cotton on the northern texas high plains. J. Irrig. Drain. Eng. 2004, 130, 277–285. [Google Scholar] [CrossRef]
- Onder, D.; Akiscan, Y.; Onder, S.; Mert, M. Effect of different irrigation water level on cotton yield and yield components. Afr. J. Biotechnol. 2009, 8, 1536–1544. [Google Scholar]
- Abdel-Fattah, I.M.; Abd-Elmotaal, A.A.; Hassan, H.E. A technical and economic study for the effect of irrigation water scheduling on cotton yield productivity. Nat. Sci. 2019, 17, 14–23. [Google Scholar]
- USDA. Cotton: World Markets and Trade; United States Department of Agriculture: New York, NY, USA, 2022; p. 29.
- Filintas, A.; Nteskou, A.; Katsoulidi, P.; Paraskebioti, A.; Parasidou, M. Rainfed and Supplemental Irrigation Modelling 2D GIS Moisture Rootzone Mapping on Yield and Seed Oil of Cotton (Gossypium hirsutum) Using Precision Agriculture and Remote Sensing. Eng. Proc. 2021, 9, 37. [Google Scholar] [CrossRef]
- Bordovsky, J.P.; Mustian, J.T.; Ritchie, G.L.; Lewis, K.L. Cotton irrigation timing with variable seasonal irrigation capacities in the Texas South Plains. Appl. Eng. Agric. 2015, 31, 883–897. [Google Scholar] [CrossRef]
- Page, A.L.; Miller, R.H.; Keeney, D.R. Methods of Soil Analysis Part 2: Chemical and Microbiological Properties; Agronomy, ASA and SSSA: Madison, WI, USA, 1982; p. 1159. [Google Scholar]
- ISO S9261; Agricultural Irrigation Equipment Emitting Pipe Systems-Specifications and Test Methods. International Organization for Standardization (ISO): Geneva, Switzerland, 1991.
- Dioudis, P.; Filintas, A.; Papadopoulos, A.; Sakellariou-Makrantonaki, M. The influence of different drip irrigation layout designs on sugar beet yield and their contribution to environmental sustainability. Fresenious Environ. Bull. 2010, 19, 818–831. [Google Scholar]
- Topp, G.C.; Davis, J.L. Measurement of soil water content using time-domain reflectometry: A field evaluation. Soil Sci. Soc. Am. J. 1985, 49, 19–24. [Google Scholar] [CrossRef]
- Zegelin, S.J.; White, I.; Russel, G.F. A critique of the time domain reflectometry technique for determining field soil-water content. In Advances in Measurement of Soil Physical Properties: Bringing Theory into Practice; SSSA Special Publication: Madison, WI, USA, 1992; Volume 30, pp. 187–208. [Google Scholar]
- Environmental Sensors, Inc. MP-917 Soil Moisture Instrument Operational Manual; E.S.I.: Sidney, BC, Canada, 1997. [Google Scholar]
- Kalavrouziotis, I.K.; Filintas, A.Τ.; Koukoulakis, P.H.; Hatzopoulos, J.N. Application of multicriteria analysis in the Management and Planning of Treated Municipal Wastewater and Sludge reuse in Agriculture and Land Development: The case of Sparti’s Wastewater Treatment Plant, Greece. Fresenious Environ. Bull. 2011, 20, 287–295. [Google Scholar]
- Copernicus Open Access Hub. European Space Agency. Available online: https://scihub.copernicus.eu/ (accessed on 1 April 2020).
- European Space Agency. STEP—Science Toolbox Exploitation Platform. Available online: http://step.esa.int (accessed on 1 April 2020).
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with ERTS. In Proceedings of the Third ERTS Symposium, Washington, DC, USA, 10–14 December 1973; Volume 1, pp. 309–317. [Google Scholar]
- Davis Instruments. Wireless Vantage Pro2™ & Vantage Pro2™ Plus Stations, Technical Specifications, Rev. Z 12/7/18; Davis Instruments: Hayward, CA, USA, 2018; pp. 1–10. [Google Scholar]
- USDA-SCS. Irrigation Water Requirements; Technical, R. No. 21; USDA Soil Conservation Service: Washington, DC, USA, 1970.
- Cassman, K.G.; Gines, G.C.; Dizon, M.A.; Samson, M.I.; Alcantara, J.M. Nitrogen use efficiency in tropical low land rice systems: Contributions from indigenous and applied nitrogen. Field Crops Res. 1996, 47, 1–12. [Google Scholar] [CrossRef]
- Ierna, A.; Pandino, G.; Lombardo, S.; Mauromicale, G. Tuber yield, water and fertilizer productivity in early potato as affected by a combination of irrigation and fertilization. Agric. Water Manag. 2011, 101, 35–41. [Google Scholar] [CrossRef]
- Munger, P.; Bleiholder, H.; Hack, H. Phenological growth stages of the cotton plant (Gossypium hirsutum L.): Codification and description according to the BBCH scale. J. Agron. Crop Sci. 1998, 180, 143–149. [Google Scholar] [CrossRef]
- Norusis, M.J. IBM SPSS Statistics 19 Advanced Statistical Procedures Companion; Pearson: London, UK, 2011. [Google Scholar]
- Steel, R.G.D.; Torrie, J.H. Principles and Procedures of Statistics. In A Biometrical Approach, 2nd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1982; p. 633. [Google Scholar]
- Hatzigiannakis, E.; Filintas, A.; Ilias, A.; Panagopoulos, A.; Arampatzis, G.; Hatzispiroglou, I. Hydrological and rating curve modelling of Pinios River water flows in Central Greece, for environmental and agricultural water resources management. Desalin. Water Treat. 2016, 57, 11639–11659. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Filintas, A.; Gougoulias, N.; Salonikioti, A.; Prapa, E. Study of soil erodibility by water on tillage and no tillage treatments of a Helianthus Tuberosus crop using field measurements, soil laboratory analyses, GIS and deterministic models. Ann. Univ. Craiova Ser. Biol. Hortic. Food Prod. Process. Technol. Environ. Eng. 2019, XXIV, 529–536. [Google Scholar]
- Filintas, A.; Gougoulias, N.; Papachatzis, A. Soil organic matter modeling and digital mapping of a Triticum turgidum cropfield using as auxiliary variables the plant available water, texture, field measurements, soil laboratory analyses, GIS and geostatistical models. Ann. Univ. Craiova Ser. Biol. Hortic. Food Prod. Process. Technol. Environ. Eng. 2019, XXIV, 537–544. [Google Scholar]
- Filintas, A.; Gougoulias, N.; Papachatzis, A. Soil’s plant available water and nitrogen inorganic modeling and digital GIS mapping of winter wheat, utilizing precision agriculture, geostatistical models, soil’s pH, water holding capacity, sand, clay and silt. Ann. Univ. Craiova Ser. Biol. Hortic. Food Prod. Process. Technol. Environ. Eng. 2020, XXV, 368–375. [Google Scholar]
- Filintas, A.; Hatzopoulos, J.; Parlantzas, V. Agriculture Spray Machinery Pattern Testing and Validation by the use of GIS and the use of a Dilution of Active Ingredient in Wastewater. In Proceedings of the 5th International Conference on ENERGY, ENVIRONMENT, ECOSYSTEMS and SUSTAINABLE DEVELOPMENT (EEESD ‘09)-WSEAS, Athens, Greece, 28–30 September 2009; pp. 334–339. [Google Scholar]
- Loague, K.; Green, R.E. Statistical and graphical methods for evaluating solute transport models: Overview and application. J. Contam. Hydrol. 1991, 7, 51–73. [Google Scholar] [CrossRef]
- Hatzopoulos, N.J. Topographic Mapping, Covering the Wider Field of Geospatial Information Science & Technology (GIS&T); Universal Publishers: Irvine, CA, USA, 2008. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Bausch, W.C.; Neale, C.M.U. Spectral inputs improve corn crop coefficients and irrigation scheduling. Trans. ASAE 1989, 32, 1901–1908. [Google Scholar] [CrossRef]
- Gene, S. Cotton Fertility Management. Missuri University Extension; Missuri University: Columbia, MO, USA, 2019; Available online: https://extension.missouri.edu/publications/g4256 (accessed on 9 August 2022).
- Pace, P.F.; Harry, T.C.; Sherif, H.M.; El-Halawany, J.; Tom, C.; Scott, A.S. Drought-induced changes in shoot and root growth of young cotton plants. J. Cotton Sci. 1999, 3, 183–187. [Google Scholar]
- Xiao, J.F.; Liu, Z.G.; Yu, X.G.; Zhang, J.Y.; Duan, A.W. Effects of different water application on lint yield and fiber quality of cotton under drip irrigation. Acta Gossypii Sin. 2000, 12, 194–197. [Google Scholar]
- Du, T.; Kang, S.; Zhang, J.; Li, F. Water use and yield responses of cotton to alternate partial root-zone drip irrigation in the arid area of north-west China. Irrig Sci. 2008, 26, 147–159. [Google Scholar] [CrossRef]
- Unlu, M.; Kanber, R.; Senyigit, U.; Onaran, H.; Diker, K. Trickle and sprinkler irrigation of potato (Solanum tuberosum L.) in the middle Anatolian region in Turkey. Agr. Water Manag. 2006, 79, 43–71. [Google Scholar] [CrossRef]
| Parameter | Sensor Type | Range | Resolution | Accuracy |
|---|---|---|---|---|
| Temperature | Electronic PN junction silicon diode | −40 to + 65 °C | 0.1 °C, −23.3 to +37.8 °C 0.2 °C otherwise | 0.3 °C, +15.6 to +37.8 °C 1.7 °C, −40 to +15.6 °C 1.1 °C, +37.8 to +65 °C |
| Relative humidity | Electronic film capacitor element | 0–100% | 1% | 3%, 0–90% 4%, 90–100% |
| Atmospheric pressure | Electronic | 540–1100 hPa | 0.1 hPa | ±1.0 hPa |
| Wind speed | Wind cups with magnetic switch | 1–67 m/s, 3–241 km/h (large wind cups) 1.5–79 m/s, 5–282 km/h (small wind cups) | 0.5 m/s, 1 km/h | Max (5%, 3 km/h, 1 m/s) (large wind cups) max (5%, 5 km/h, 1.5 m/s) (small wind cups) |
| Wind Direction | Wind vane with potentiometer | 0–360° | 1° | 3° |
| Rainfall | Tipping bucket | (0–100 mm/h) | 0.2 mm | Max (3%, 0.2 mm), for rain rates up to 50 mm/h max (3%, 0.25 mm), otherwise |
| Solar radiation | Silicon photodiode with diffuser (400–1100 nm) | 0–1800 W/m2 | 1 W/m2 | 5% |
| Sn | Water Deficit Level | Abbreviation | Soil Water Level | Description |
|---|---|---|---|---|
| 1 | Severe water deficit | SevWD | ||
| 2 | Moderate water deficit | ModWD | ||
| 3 | Mild water deficit | MildWD | ||
| 4 | Light water deficit | LightWD | ||
| 5 | No deficit or full irrigation | NoWD | during the key plant growth period | |
| 6 | Over-irrigation | OverIRR | irrigation water amount may be greater than plant’s water requirements for optimal growth |
| Crop Growth Stage of Cotton (Gossypium hirsutum L.) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Parameter | L Ini | L Dev | L Mid | L Late | Total | |||||
| Stage duration in days | 30 | 60 | 50 | 40 | 180 | |||||
| Irrigation treatment | IR1:VDI | IR2:FI | IR1:VDI | IR2:FI | IR1:VDI | IR2:FI | IR1:VDI | IR2:FI | IR1:VDI | IR2:FI |
| Water deficit [%] | 60–70% | 95–110% | 45–77% | 95–110% | 55–75% | 95–110% | --* | --* | 45–77% | 95–110% |
| ASMD average [%] | 56.43 | 37.69 | 29.47 | 31.29 | 21.92 | 18.91 | 19.73 | 34.76 | 29.85 | 29.74 |
| ASMD max [%] | 86.10 | 75.62 | 77.09 | 49.21 | 37.65 | 49.78 | 30.95 | 45.34 | 86.10 | 75.62 |
| Ks average [–] | 0.845 | 0.975 | 0.963 | 0.946 | 0.998 | 0.977 | 1.000 | 0.949 | 0.960 | 0.960 |
| Ks max [–] | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| Ks min [–] | 0.319 | 0.662 | 0.540 | 0.772 | 0.957 | 0.764 | 1.000 | 0.836 | 0.319 | 0.662 |
| Ks-weighted average [–] | 0.830 | 0.969 | 0.941 | 0.918 | 0.994 | 0.964 | 1.000 | 0.919 | 0.918 | 0.883 |
| Number of days with Ks < 1 (indicates water stress to plants) | 13 | 4 | 16 | 21 | 3 | 10 | 0 | 23 | 32 | 58 |
| Percentage of days with Ks < 1 (indicates water stress to plants) | 43.33 | 13.33 | 26.67 | 35.00 | 6.00 | 20.00 | 0.00 | 57.50 | 17.78 | 32.22 |
| Irrigation NIR [mm] | 33.11 | 76.08 | 109.71 | 134.50 | 176.55 | 214.90 | 0.00 | 0.00 | 319.37 | 425.48 |
| Effective rainfall Pe = P-RO [mm] | 27.05 | 27.05 | 154.25 | 154.25 | 91.84 | 91.84 | 115.82 | 115.82 | 388.96 | 388.96 |
| TWI = (NIR + Pe) [mm] | 60.16 | 103.13 | 263.96 | 288.75 | 268.39 | 306.74 | 115.82 | 115.82 | 708.33 | 814.44 |
| Etc [mm/stage] | 81.10 | 60.81 | 276.52 | 282.84 | 302.01 | 302.97 | 107.28 | 107.15 | 766.90 | 753.77 |
| Etα [mm/stage] | 77.15 | 59.90 | 273.60 | 275.77 | 301.34 | 297.84 | 107.28 | 103.13 | 759.36 | 736.64 |
| Deep percolation DP [mm] | 0.00 | 46.81 | 0.00 | 23.30 | 5.32 | 95.01 | 0.00 | 0.00 | 5.32 | 165.12 |
| DP (% losses of NIR) | 0.00 | 61.53 | 0.00 | 17.32 | 3.01 | 44.21 | 0.00 | 0.00 | 1.67 | 38.81 |
| DP (% losses of TWI) | 0.00 | 45.39 | 0.00 | 8.07 | 1.98 | 30.97 | 0.00 | 0.00 | 0.75 | 20.27 |
| TWI-DP [mm] | 60.16 | 56.32 | 263.96 | 265.45 | 263.07 | 211.73 | 115.821 | 115.821 | 703.01 | 649.32 |
| Kcb average | 0.35 | 0.35 | 0.78 | 0.78 | 1.20 | 1.20 | 0.91 | 0.91 | -- | -- |
| Kcb deviation | 0.35 | 0.35 | 0.42–1.20 | 0.42–1.20 | 1.20 | 1.20 | 1.18–0.35 | 1.18–0.35 | -- | -- |
| Kc average | 0.90 | 0.72 | 1.01 | 1.04 | 1.24 | 1.24 | 1.14 | 1.13 | -- | -- |
| Growth Characteristics of Cotton Plants (Gossypium hirsutum L.) | ||||||
|---|---|---|---|---|---|---|
| Treatment | Irrigation Level Water Deficit [%] | Fertilization Treatment | Plant Height (cm) | Plant Stem (mm) | Boll Weight (g) | Dry Matter (g) |
| Irrigation IR1:VDI-1 | 55.0–77.0% | Ft1: N-P-K | 90.2a | 14.9a | 6.33a | 89.96a |
| 55.0–77.0% | Ft2: N-P-K | 92.3b | 15.7b | 6.65b | 94.47b | |
| 55.0–77.0% | Ft3: N-P-K | 89.7c | 14.8c | 6.31c | 84.51c | |
| IR1:VDI-1 mean | Total | 90.7d | 15.1 | 6.43 | 89.64d | |
| Irrigation IR1:VDI-2 | 45.0–77.0% | Ft1: N-P-K | 93.3a | 15.5a | 6.45a | 91.52a |
| 45.0–77.0% | Ft2: N-P-K | 97.4b | 16.7b | 6.67b | 97.34b | |
| 45.0–77.0% | Ft3: N-P-K | 87.3c | 13.8c | 6.28c | 86.88c | |
| IR1:VDI-2 mean | Total | 92.7d | 15.3 | 6.46 | 91.91d | |
| IR1:VDI mean | Total | 91.7i | 15.2i | 6.45i | 90.78i | |
| Irrigation IR2:FI-2 | 95.0–110.0% | Ft1: N-P-K | 79.5e | 12.0e | 5.99e | 78.92e |
| 95.0–110.0% | Ft2: N-P-K | 87.8f | 13.9f | 6.07f | 86.55f | |
| 95.0–110.0% | Ft3: N-P-K | 77.6g | 10.3g | 5.89g | 75.09g | |
| IR2:FI-2 mean | Total | 81.6 | 12.1 | 5.99 | 80.19 | |
| Irrigation IR2:FI-1 | 90.0–95.0% | Ft1: N-P-K | 81.3e | 12.2e | 6.02e | 80.27e |
| 90.0–95.0% | Ft2: N-P-K | 85.8f | 13.6f | 6.08f | 84.58f | |
| 90.0–95.0% | Ft3: N-P-K | 80.1g | 11.2g | 6.02g | 77.19g | |
| IR2:FI-1 mean | Total | 82.4 | 12.3 | 6.04 | 80.68 | |
| IR2:FI mean | Total | 82.0i | 12.2i | 6.01i | 80.43i | |
| Statistical Analysis Results of The Experimental Cotton Field Data | ||||||||
| Dependent Variable | Cotton Yield | Nitrogen PFP | N-P-K PFP | WUE | ||||
| Source | F | Sig. | F | Sig. | F | Sig. | F | Sig. |
| Corrected model | 509.14 | 0.00000 | 1194.22 | 0.00000 | 1232.41 | 0.00000 | 389.27 | 0.00000 |
| Intercept | 534,823.42 | 0.00000 | 595,990.61 | 0.00000 | 594,225.73 | 0.00000 | 148,322.836 | 0.00000 |
| Irrigation treatments (Level 4) | 1532.77 | 0.00000 | 1697.84 | 0.00000 | 1693.12 | 0.00000 | 1332.77 | 0.00000 |
| Fertilization treatments (Level 3) | 490.87 | 0.00000 | 3996.22 | 0.00000 | 4210.84 | 0.00000 | 136.35 | 0.00000 |
| [Irrigation * fertilization] | 3.42 | 0.03323 | 8.42 | 0.00098 | 9.24 | 0.00064 | 1.84 | 0.17445 |
| Geostatistical analysis and precision agriculture validation results of the experimental cotton field data | ||||||||
| Dependent variable | Cotton Yield | Nitrogen PFP | N-P-K PFP | WUE | ||||
| Modeling method | Ord. Kriging | Ord. Kriging | Ord. Kriging | Ord. Kriging | ||||
| Model | Exponential | Gaussian | Gaussian | Gaussian | ||||
| Mean error (MPE) | 4.07874 | 0.01392 | −0.00250 | −0.00052 | ||||
| Root-mean-square error (RMSE) | 26.75137 | 2.49285 | 1.73536 | 0.06163 | ||||
| Mean standardized error (MSPE) | 0.01188 | 0.00073 | 0.00013 | −0.00686 | ||||
| Root-mean-square standardized error (RMSSE) | 0.82655 | 0.98004 | 1.05435 | 0.98469 | ||||
| Results (Final) on the Experimental Cotton Field | ||||
|---|---|---|---|---|
| Irrigation Treatment | Fertilization Treatment | Mean Cotton Yield | Nitrogen PFP | WUE |
| [Kg·ha−1] | [--] * | [kg·m−3] | ||
| IR1-VDI-1 | Ft1: N-P-K | 4516.0 ** | 36.30 ** | 0.628 ** |
| Ft2: N-P-K | 4782.4 | 31.70 | 0.665 | |
| Ft3: N-P-K | 4270.3 | 41.74 | 0.594 | |
| Total | 4522.9 | 36.58 | 0.629 | |
| IR1-VDI-2 | Ft1: N-P-K | 4486.8 | 36.07 | 0.649 |
| Ft2: N-P-K | 4721.5 | 31.29 | 0.683 | |
| Ft3: N-P-K | 4260.4 | 41.65 | 0.616 | |
| Total | 4489.6 | 36.34 | 0.649 | |
| IR2-FI-1 | Ft1: N-P-K | 3798.0 | 30.53 | 0.458 |
| Ft2: N-P-K | 4036.0 | 26.75 | 0.487 | |
| Ft3: N-P-K | 3623.5 | 35.42 | 0.437 | |
| Total | 3819.2 | 30.90 | 0.461 | |
| IR2-FI-2 | Ft1: N-P-K | 3666.9 | 29.48 | 0.457 |
| Ft2: N-P-K | 3854.2 | 25.54 | 0.480 | |
| Ft3: N-P-K | 3508.7 | 34.30 | 0.437 | |
| Total | 3676.6 | 29.77 | 0.458 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filintas, A.; Nteskou, A.; Kourgialas, N.; Gougoulias, N.; Hatzichristou, E. A Comparison between Variable Deficit Irrigation and Farmers’ Irrigation Practices under Three Fertilization Levels in Cotton Yield (Gossypium hirsutum L.) Using Precision Agriculture, Remote Sensing, Soil Analyses, and Crop Growth Modeling. Water 2022, 14, 2654. https://doi.org/10.3390/w14172654
Filintas A, Nteskou A, Kourgialas N, Gougoulias N, Hatzichristou E. A Comparison between Variable Deficit Irrigation and Farmers’ Irrigation Practices under Three Fertilization Levels in Cotton Yield (Gossypium hirsutum L.) Using Precision Agriculture, Remote Sensing, Soil Analyses, and Crop Growth Modeling. Water. 2022; 14(17):2654. https://doi.org/10.3390/w14172654
Chicago/Turabian StyleFilintas, Agathos, Aikaterini Nteskou, Nektarios Kourgialas, Nikolaos Gougoulias, and Eleni Hatzichristou. 2022. "A Comparison between Variable Deficit Irrigation and Farmers’ Irrigation Practices under Three Fertilization Levels in Cotton Yield (Gossypium hirsutum L.) Using Precision Agriculture, Remote Sensing, Soil Analyses, and Crop Growth Modeling" Water 14, no. 17: 2654. https://doi.org/10.3390/w14172654






