Modelling Infiltration Systems’ Performance for Efficient, Sustainable or Circular Urban Water Drainage
Abstract
:1. Introduction
2. Material and Methods
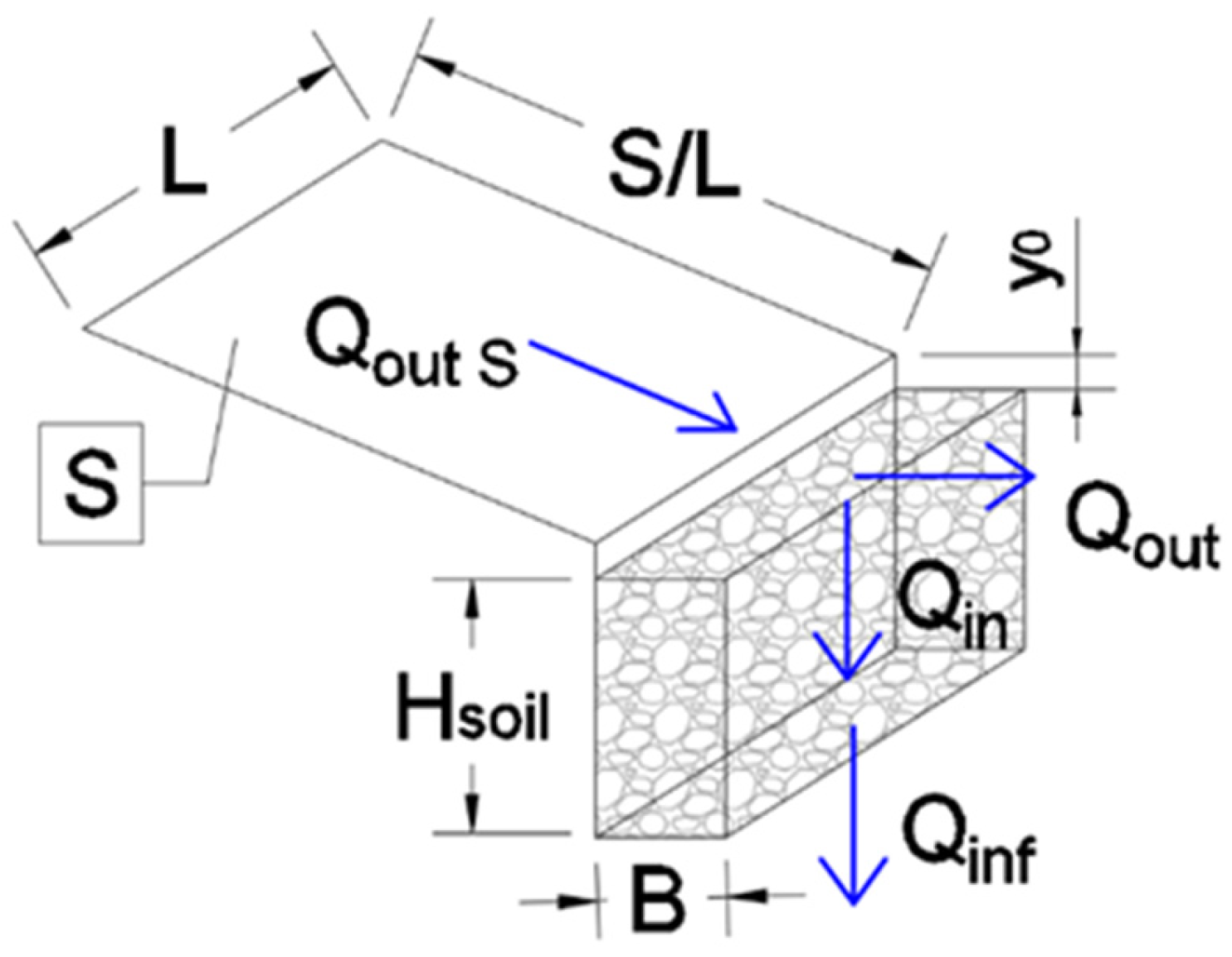
2.1. Static Design
2.2. Hydrodynamic Model
2.3. Efficiency
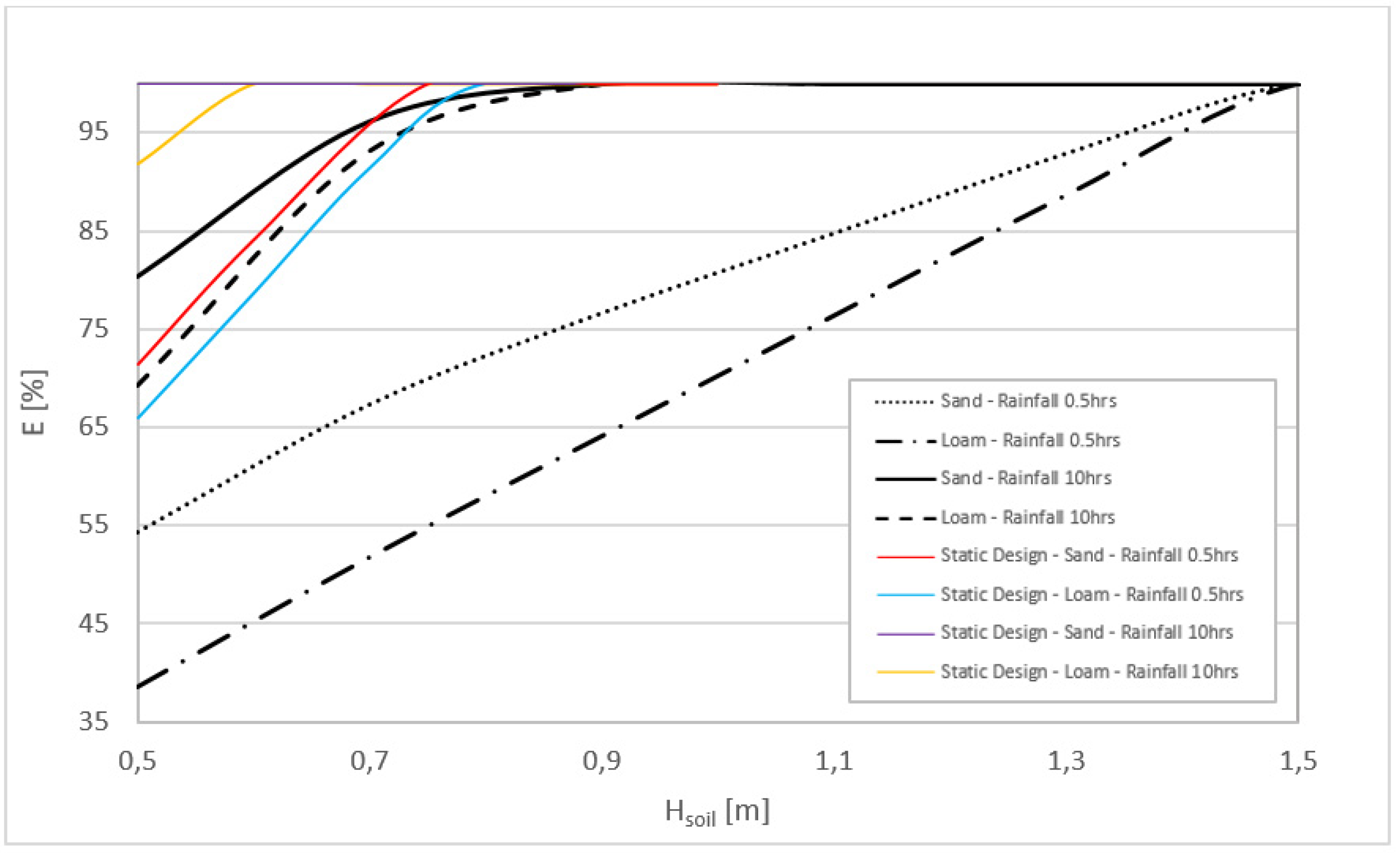
3. Results
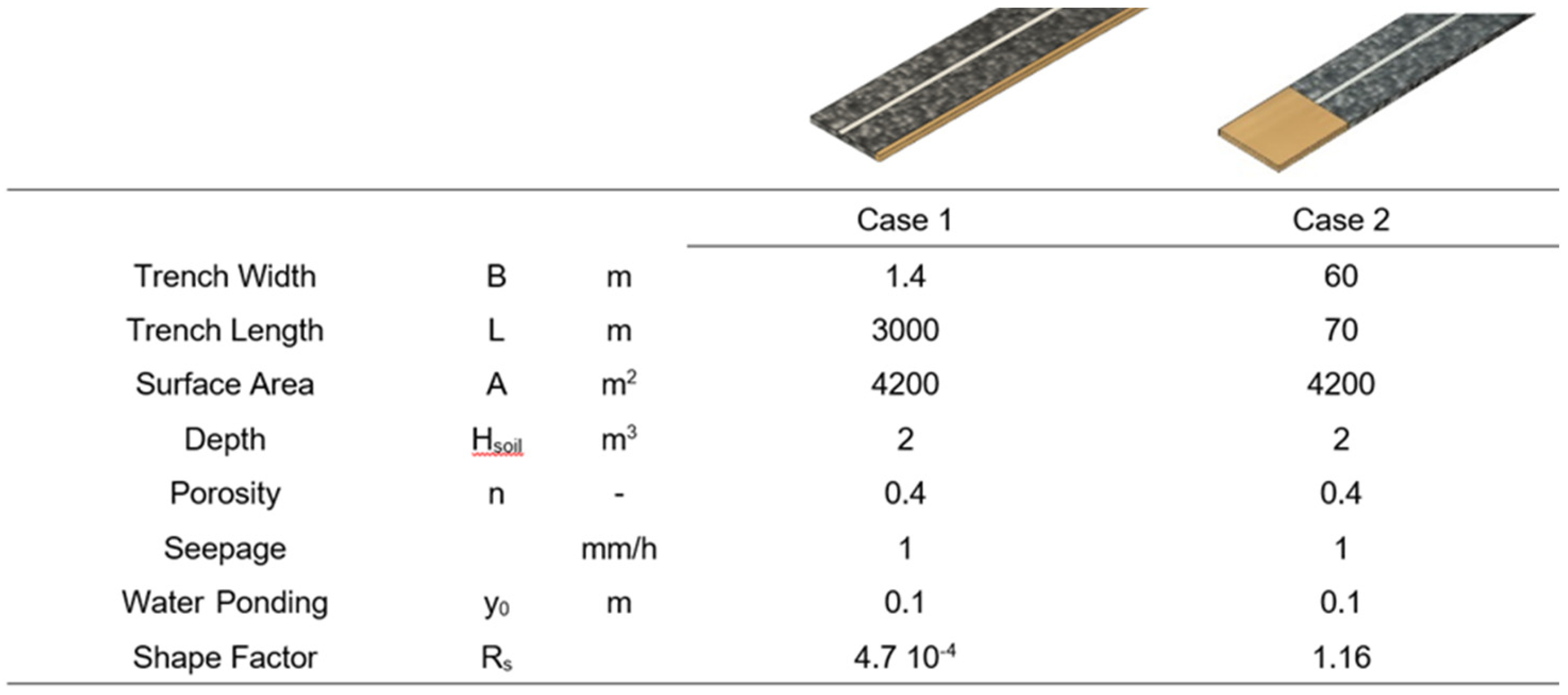
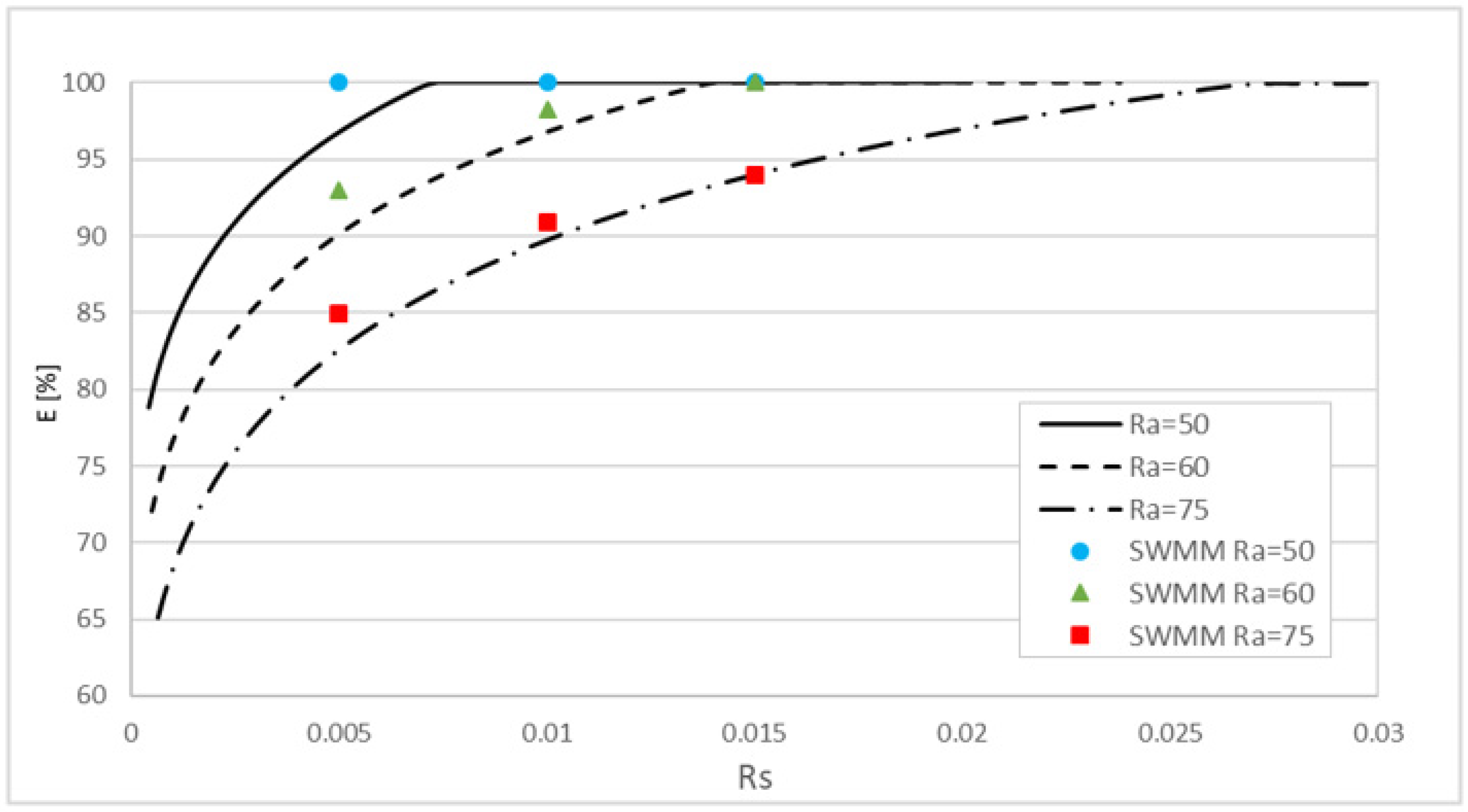
3.1. Case Study 1
3.2. Case Study 2
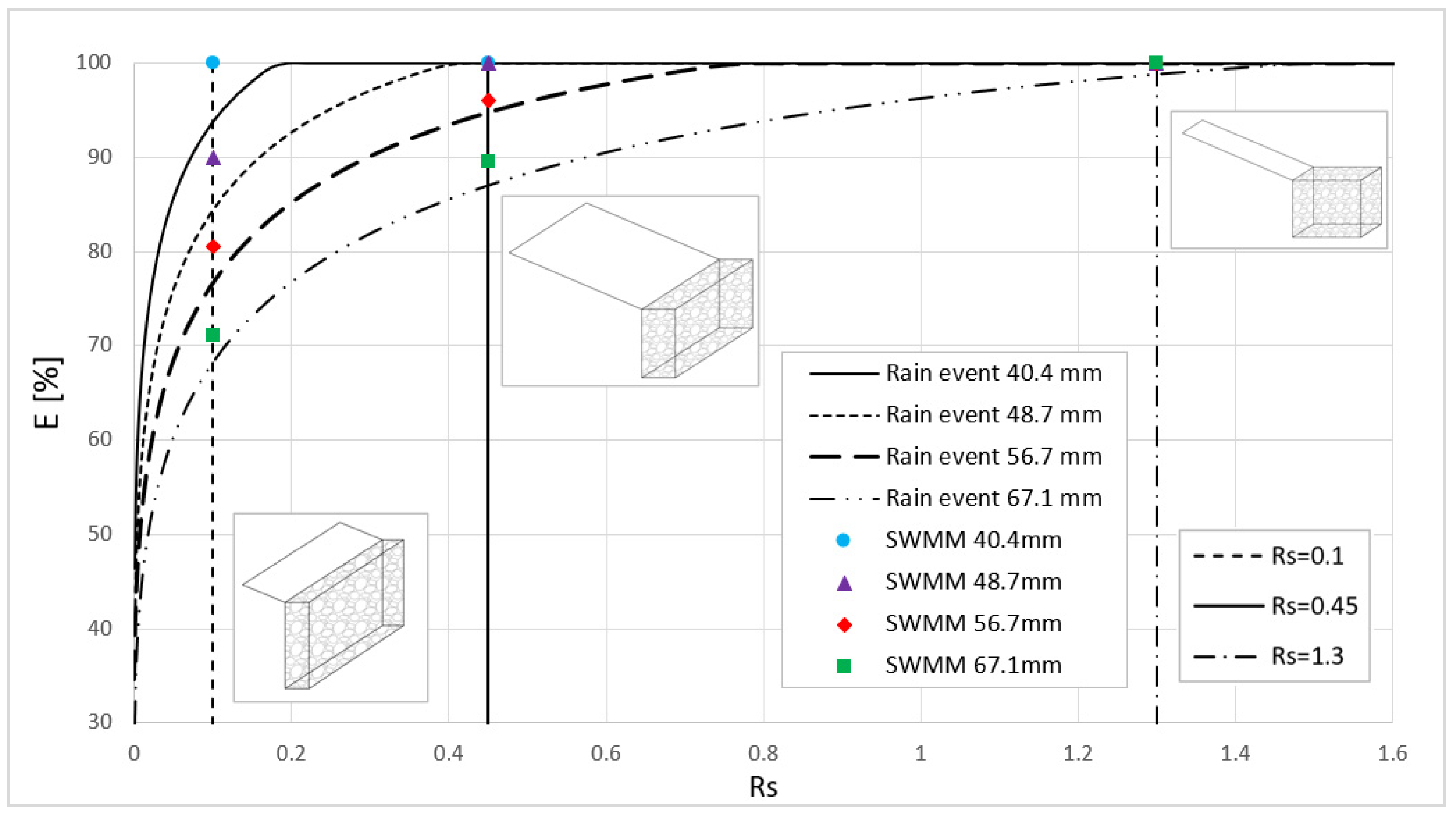
3.3. Case Study 3
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Acuto, M.; Parnell, S.; Seto, K.S.; Contestable, M. Science and the Future of Cities, Report of the International Expert Panel on Science and the Future of Cities; The University of Melbourne: Melbourne, Australia, 2018. [Google Scholar]
- Bakker, K. Water security: Research challenges and opportunities. Science 2012, 337, 914–915. [Google Scholar] [CrossRef] [PubMed]
- Marsalek, J. Urban Water Cycle Processes and Interactions; CRC Press: London, UK, 2008. [Google Scholar] [CrossRef]
- ISTAT. Forme, Livelli e Dinamiche Dell’urbanizzazione in Italia; ISTAT: Rome, Italy, 2017. [Google Scholar]
- Allen, J.; Barlow, J.; Leal, J.; Maloutas, T.; Padovani, L. Housing and Welfare in Southern Europe; Wiley: London, UK, 2004. [Google Scholar]
- Decreto Legislativo del 3 Aprile 2006, n. 152—Norme in Materia Ambientale. Available online: https://www.gazzettaufficiale.it/dettaglio/codici/materiaAmbientale (accessed on 1 August 2022).
- Pendergrass, A.G.; Hartmann, D.L. Changes in the distribution of rain frequency and intensity in response to global warming. J. Clim. 2014, 27, 8372–8383. [Google Scholar] [CrossRef]
- De Moel, H.; Aerts, J.C.J.H. Effect of uncertainty in land use, damage models and inundation depth on flood damage estimates. Nat. Hazards 2011, 58, 407–425. [Google Scholar] [CrossRef]
- Merz, B.; Kreibich, H.; Schwarze, R.; Thieken, A. Review article “Assessment of economic flood damage”. Nat. Hazards Earth Syst. Sci. 2010, 10, 1697–1724. [Google Scholar] [CrossRef]
- Bertilsson, L.; Wiklund, K.; Tebaldi, I.D.M.; Rezende, O.M.; Veról, A.P.; Miguez, M.G. Urban flood resilience—A multi-criteria index to integrate flood resilience into urban planning. J. Hydrol. 2019, 573, 970–982. [Google Scholar] [CrossRef]
- Jalilov, S.-M.; Kefi, M.; Kumar, P.; Masago, Y.; Mishra, B.K. Sustainable Urban Water Management: Application for Integrated Assessment in Southeast Asia. Sustainability 2018, 10, 122. [Google Scholar] [CrossRef]
- Williams, J. Circular Cities: What Are the Benefits of Circular Development? Sustainability 2021, 13, 5725. [Google Scholar] [CrossRef]
- UN-WWAP (United Nations World Water Assessment Programme)/UN-Water The United Nations World Water Development Report 2018: Nature-based Solutions for Water UNESCO, Paris (2018). Available online: https://www.unwater.org/publications/world-water-development-report-2018/ (accessed on 1 August 2022).
- European Commission (EC). Towards an EU Research and Innovation Policy Agenda for Nature-Based Solutions & Re-Naturing Cities; Final Report of the Horizon 2020 Expert Group on ‘Nature-Based Solutions and Re-Naturing Cities’; Directorate-General for Research and Innovation European Union: Luxembourg, 2015. [Google Scholar]
- Hasan, S.S.; Zhen, L.; Miah, M.G.; Ahamed, T.; Samie, A. Impact of land use change on ecosystem services: A review. Environ. Dev. 2020, 34, 100527. [Google Scholar] [CrossRef]
- EEA. Urban Adaptation to Climate Change in Europe: Challenges and Opportunities for Cities Together with Supportive National and European Policies; EEA Report No. 2/2012: Agency European Environment; Office for Official Publications of the European Union: Luxembourg, 2012. [Google Scholar] [CrossRef]
- Raymond, C.M.; Frantzeskaki, N.; Kabisch, N.; Berry, P.; Breil, M.; Nita, M.R.; Geneletti, D.; Calfapietra, C. A framework for assessing and implementing the co-benefits of nature-based solutions in urban areas. Environ. Sci. Policy 2017, 77, 15–24. [Google Scholar] [CrossRef]
- Zeng, S.; Guo, H.; Dong, X. Understanding the synergistic effect between LID facility and drainage network: With a comprehensive perspective. J. Environ. Manag. 2019, 246, 849–859. [Google Scholar] [CrossRef]
- AECOM. Georgia Stormwater Management Manual—Volume 2: Technical Handbook; Atlanta Regional Commission: Atlanta, GA, USA, 2016.
- Blecken, G.-T.; Hunt, W.F.; Al-Rubaei, A.M.; Viklander, M.; Lord, W.G. Stormwater control measure (SCM) maintenance considerations to ensure designed functionality. Urban Water J. 2017, 14, 278–290. [Google Scholar] [CrossRef]
- Bonneau, J.; Fletcher, T.D.; Costelloe, J.F.; Burns, M.J. Stormwater infiltration and the ‘urban karst’—A review. J. Hydrol. 2017, 552, 141–150. [Google Scholar] [CrossRef]
- Rossman, L. Storm Water Management Model Reference Manual Volume I—Hydrology (Revised); EPA/600/R-15/162A; United States Environmental Protection Agency: Cincinnati, OH, USA, 2010.
- VDOT. B BMP Design Manual of Practice; Virginia Department of Transportation: Richmond, VA, USA, 2013. [Google Scholar]
- Adams, B.; Papa, F. Urban Stormwater Management Planning with Analytical Probabilistic Models; Willy: New York, NY, USA, 2000; Available online: https://scholar.google.com/scholar_lookup?title=Urban%20stormwater%20management%20planning%20with%20analytical%20probabilistic%20models&author=B.J.%20Adams&publication_year=2000 (accessed on 1 August 2022).
- Wang, J.; Guo, Y. Dynamic water balance of infiltration-based stormwater best management practices. J. Hydrol. 2020, 589, 125174. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Wasko, C.; Sharma, A. Steeper temporal distribution of rain intensity at higher temperatures within Australian storms. Nat. Geosci. 2015, 8, 527–529. [Google Scholar] [CrossRef]
- Endreny, T.A. 126: Land Use and Land Cover Effects on Runoff Processes: Urban and Suburban Development. 2005. Available online: https://www.researchgate.net/profile/Theodore-Endreny/publication/229749876_Land_Use_and_Land_Cover_Effects_on_Runoff_Processes_Urban_and_Suburban_Development/links/59e7eb520f7e9bc89b509578/Land-Use-and-Land-Cover-Effects-on-Runoff-Processes-Urban-and-Suburban-Development.pdf (accessed on 1 August 2022).
- Wang, M.; Zhang, D.Q.; Su, J.; Dong, J.W.; Tan, S.K. Assessing hydrological effects and performance of low impact development practices based on future scenarios modeling. J. Clean. Prod. 2018, 179, 12–23. [Google Scholar] [CrossRef]
- Nika, C.-E.; Expósito, A.; Kisser, J.; Bertino, G.; Oral, H.V.; Dehghanian, K.; Vasilaki, V.; Iacovidou, E.; Fatone, F.; Atanasova, N.; et al. Validating Circular Performance Indicators: The Interface between Circular Economy and Stakeholders. Water 2021, 13, 2198. [Google Scholar] [CrossRef]
- Krauze, K.; Wagner, I. From classical water-ecosystem theories to nature-based solutions—Contextualizing nature-based solutions for sustainable city. Sci. Total Environ. 2018, 655, 697–706. [Google Scholar] [CrossRef]
- Ebrahimian, A.; Sokolovskaya, N.; Wadzuk, B. Modeling dynamic performance of urban infiltration trench systems: Methodology and a case study in Philadelphia. J. Hydrol. 2020, 594, 125938. [Google Scholar] [CrossRef]
- Duchene, M.; McBean, E.A.; Thomson, N.R. Modeling of Infiltration from Trenches for Storm-Water Control. J. Water Resour. Plan. Manag. 1994, 120, 276–293. [Google Scholar] [CrossRef]
- MATLAB, version 7.10.0 (R2010a); The MathWorks Inc.: Natick, MA, USA, 2010.
- Huber, W.C. Storm Water Management Model (SWMM) Bibliography; U.S. Environmental Protection Agency: Athens, GA, USA, 1985. Available online: https://www.epa.gov/water-research/storm-water-management-model-swmm (accessed on 1 August 2022).
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGrawl-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Kumar, P.; Debele, S.E.; Sahani, J.; Rawat, N.; Marti-Cardona, B.; Alfieri, S.M.; Basu, B.; Basu, A.S.; Bowyer, P.; Charizopoulos, N.; et al. Nature-based solutions efficiency evaluation against natural hazards: Modelling methods, advantages and limitations. Sci. Total Environ. 2021, 784, 147058. [Google Scholar] [CrossRef]
- Oral, H.V.; Radinja, M.; Rizzo, A.; Kearney, K.; Andersen, T.R.; Krzeminski, P.; Buttiglieri, G.; Ayral-Cinar, D.; Comas, J.; Gajewska, M.; et al. Management of Urban Waters with Nature-Based Solutions in Circular Cities—Exemplified through Seven Urban Circularity Challenges. Water 2021, 13, 3334. [Google Scholar] [CrossRef]
- Peng, Y.-H.; Li, Z.; Ding, Y.-S. Research on the schemes formulation and optimization method of sponge reconstruction in a highway service area. Water Sci. Technol. 2020, 82, 2889–2901. [Google Scholar] [CrossRef]
- Pacetti, T.; Cioli, S.; Castelli, G.; Bresci, E.; Pampaloni, M.; Pileggi, T.; Caporali, E. Planning Nature Based Solutions against urban pluvial flooding in heritage cities: A spatial multi criteria approach for the city of Florence (Italy). J. Hydrol. Reg. Stud. 2022, 41, 101081. [Google Scholar] [CrossRef]

[min] | Case 1 | Case 2 | [mm/h] | [mm] |
|---|---|---|---|---|
| 10 | 100 | 100 | 150 | 25.3 |
| 30 | 75.96 | 100 | 93 | 46.5 |
| 60 | 81.31 | 100 | 55.9 | 55.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piazza, P.; Ursino, N. Modelling Infiltration Systems’ Performance for Efficient, Sustainable or Circular Urban Water Drainage. Water 2022, 14, 2620. https://doi.org/10.3390/w14172620
Piazza P, Ursino N. Modelling Infiltration Systems’ Performance for Efficient, Sustainable or Circular Urban Water Drainage. Water. 2022; 14(17):2620. https://doi.org/10.3390/w14172620
Chicago/Turabian StylePiazza, Paola, and Nadia Ursino. 2022. "Modelling Infiltration Systems’ Performance for Efficient, Sustainable or Circular Urban Water Drainage" Water 14, no. 17: 2620. https://doi.org/10.3390/w14172620
APA StylePiazza, P., & Ursino, N. (2022). Modelling Infiltration Systems’ Performance for Efficient, Sustainable or Circular Urban Water Drainage. Water, 14(17), 2620. https://doi.org/10.3390/w14172620





