1. Introduction
The Climate-Water-Energy-Food nexus is the hot topic of current scientific research directly linked to water resources [
1]. The global fixed available water resource is becoming scarce due to human consumption, increasing population, industrialization, global warming, and climate change around the globe, especially in Asian countries [
2,
3]. Economic growth and environmental developments are being realized to develop new water storage projects (Dams and Canal systems) that yield sustainable water resource management [
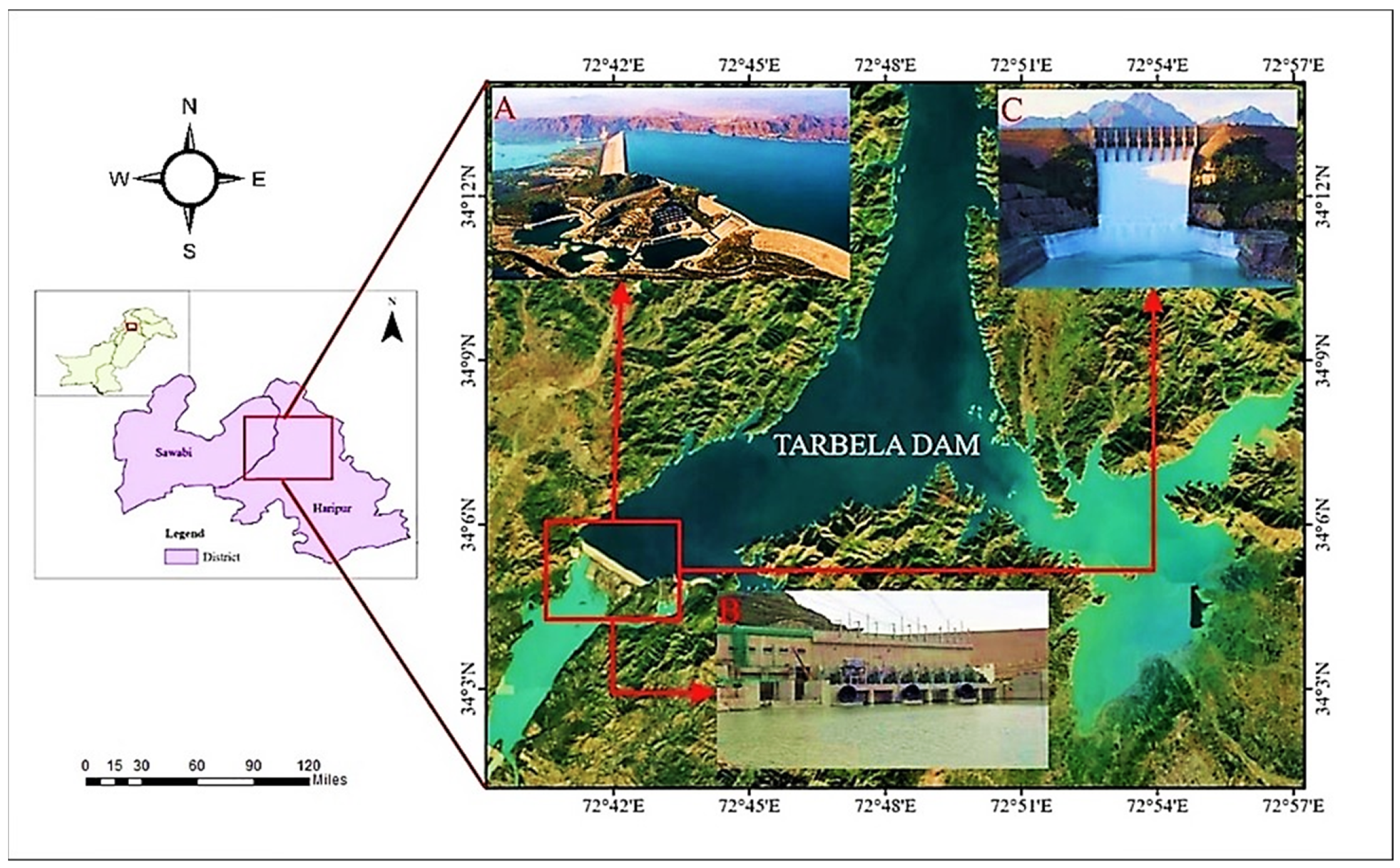
4]. Conservation of water resources is of utmost importance in recent times. Dams are the important infrastructure for power generation, agriculture and water resource management which has been under the influence of climatic deformation over the last decade. Earth fill dams such as the Tarbela Dam in Pakistan is the most important reservoir, which provides 52% of irrigation and 30% of hydropower generation needed for the country [
5,
6]. This reservoir plays an important role in melted glacier freshwater conservation flowing through the Indus river into the Tarbela Dam [
7]. The seepage of water in dams is the a critical problem for any dam foundation. Seepage is defined as the slow movement of water from an upstream side to the downstream side from the body or foundation of dam. Controlling the seepage problem in a dam ensures the health stability of the dam. On the contrary, uncontrollable seepage is critical for dam stability and may cause water losses with dam structural failure. Seepage in dams is a consequence of the following reasons: The increase in water level from the desired limit [
8,
9], poor quality construction material used in Dams rehabilitation works [
10], Earthquake and Artificial seismicity generated in Dams [
11], Unconsolidated soil property [
12], Joint and fracture in Dams structures [
13].
The seepage inspection has been carried out using the geophysical base investigation to diagnose the seepage flow through the dam [
14,
15,
16]. Several real-world concerns are connected to dam management, safety, and stability that can only be addressed by accurately calculating the seepage flow and its variability [
17]. The statistics from previous literature show that dam failure due to seepage accounts for 30–40% of total dam failure [
18]. The laboratory-based physical model experiment proves that the increase in seepage appreciably affects the health of dam [
19]. This reason has led the dam management authority to continuously monitor the dam seepage throughout its life [
20]. Dam safety can be evaluated by measuring the seepage flow in real-time daily monitoring. Such analysis is important during the construction phase of the dam structure. According to Adamo and Al-Ansari the precise detection of seepage flow can help to improve the anti-seepage with advanced scientific techniques, especially in peak sessions of water inflow in dam reservoirs [
21,
22]. In an earth-fill dam, seepage is important as it has been one of the major causes of dam failure in the past [
23]. To avoid the dam failure problem, it is recommended to detect seepage flow for fast and accurate warning. Globally all countries agree that these dams must undergo a regular assessment and diagnostic for improvement of the life of dam.
The seepage can be greatly influenced by climatic parameters, water inflow, reservoir level, sedimentation load, and soil properties [
24,
25]. Water pressure is the main parameter used for seepage measurement with the help of a piezometer tube that has been largely adopted for tracking the seepage flow [
26]. These parameters require extensive instrumental installation for the measurement of seepage flow [
27]. Many earth-fill dams have proven the importance and applicability of geophysical methods in dam site investigations and safety monitoring. Dam seepage problems can be diagnosed using geophysical instruments on both the surface and the subsurface. For example, the Abu Baara earth dam in northeastern Syria was studied [
28], where electrical resistivity tomography (ERT) survey was conducted, and the presence of cracked and karstified limestone rocks was discovered in ERT sections. Within the fragmented bedrock, several underlying structural anomalies were also discovered. [
29] used Electrical resistivity tomography to identify subsidence anomalies in the body of an embankment dam in Iran, and the efficiency of this technique for the observed subsidence was confirmed. There are several geophysical techniques used for the dam seepage problem which are Electromagnetic profiling [
30], Electrical resistivity Tomography [
28], Self-potential methods [
31], Ground penetrating radar [
32], and Seismic methods [
33]. These precise and reliable tools are used to check the health and monitor the dam stability and safety caused by a structural internal problem. Adamo et al. [
21] discussed in detail the application of geophysical methods and their applicability in dam stability and safety monitoring.
Earth-fill dams are more prone to internal erosion and leaking due to seepage problems. Deterministic approaches for precisely estimating seepage flow through these dams have been studied in the literature [
34]. Seepage analysis shows that if there is enough silty sand soil, the best design is a homogeneous earth-fill dam with a medium drain length and a thickness of 0.5 m. This seepage analysis depends on an equation describing water flow through a porous medium that follows Darcy law. Seepage volume, flow path, and velocity are all important considerations when assessing the structural behavior of a dam, all of which represent serious threats to the structure’s stability and security [
35]. The finite element method has been used to measure as well as control seepage through embankment dams, among other techniques. [
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46,
47,
48,
49], Finite difference method [
50], weak form quadrature element method [
51,
52], and element free Method [
53], etc. Recently [
54] proposed a new approach to adjusting seepage issues through the earth-fill dam known as the multi-quadric method. Technological advancement has put seepage research in a new direction over the last decade, such as the integration of numerical modeling with machine learning, which can improve the seepage problem in the earth-fill dam and minimize the failure risk in water resources management system.
Many researchers have employed Machine Learning, and Artificial Intelligence (AI) based modeling to solve earth-fill dam seepage concerns in the last decade [
55,
56,
57,
58,
59,
60,
61]. Previous research proves that AI methods are effective for dam seepage interpretation. For example, X. Zhang et al. [
62] employed a genetic algorithm (GA) to optimize the weights and thresholds of a backpropagation neural network (BPNN), resulting in the development of the backpropagation neural network-Genetic Algorithm (BPNN-GA) seepage prediction model, which was used to increase dam seepage prediction accuracy and efficiency. Similarly, several different models are used in the literature for modeling water resources management problems, such as AI-based neural network [
56,
57,
63,
64,
65], Genetic programming (GP) [
66,
67], Gaussian processes regression (GPR) [
68], Support Vector Machine (SVM) [
56,
69], fuzzy logic and adaptive neuro-fuzzy inference system (ANFIS) [
56]. Rehamnia, I. et. al. [
57] investigated the estimation of dam seepage flow across concrete and embankment dams in Algeria using different algorithms (Support Vector Machine (SVM), M5Tree, and Multivariate Adaptive Regression Splines (MARS)) and discovered that SVM is more practical for doing so. The adaptive kernel extreme learning machine (KELM) approach developed by [
69] was used to assess dam seepage. The researchers correlated the findings obtained using Multiple Linear Regression (MLR), Extreme Learning Machine (ELM), and Random Forest (RF). They discovered that the adaptive kernel extreme learning machine (EKLM) model performed well as compared to other models. Predicting seepage from observation data is an accurate strategy to assure dam stability. The rough set-Long short-term memory (RS-LSTM) model and Rough Set Theory have been used to predict the dam seepage pressure. As a result, it can do computations quickly and accurately [
70].
Global warming and climatic changes trigger extreme metrological events such as rapid glacier melting, drought and heat waves worldwide and in Pakistan. These extreme events affect the normal trend of the hydrological cycle in terms of temperature, precipitation, sediment transportation and water inflow in river Indus which effect the Tarbela Dam structural stability and safety. Tarbela Dam was constructed in 1974, which wasn’t constructed according to the latest standards, that ensures resilience against such extreme global climatic events. Geoscientists say hydro-climatological parameters play an important role in seepage control and measurement in earth-fill dams. Numerous studies have been undertaken to model the relationship between various input factors, such as hydraulic parameters [
71], piezometric data [
72], etc., and dam seepage. However, the effect of hydro-climatological parameters on dam seepage has not been investigated. Furthermore, the Artificial Intelligence (AI) techniques used to model dam seepage based on different input parameters focus more on the accuracy of predictions made by the models; however, the explainability of the model predictions is not studied, which is necessary to explain the individual effect of each input on the output parameter and understand the dam seepage problem in detail.
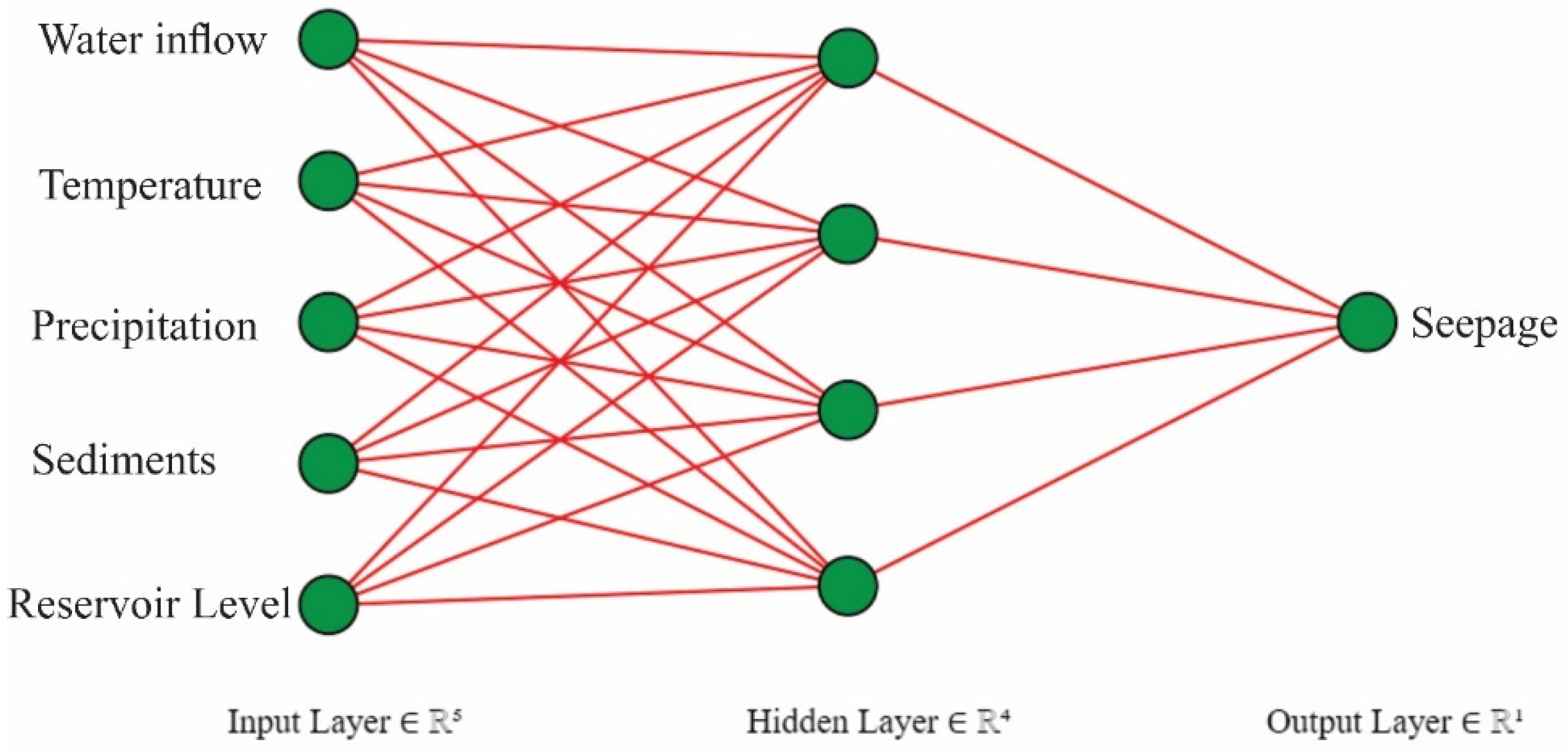
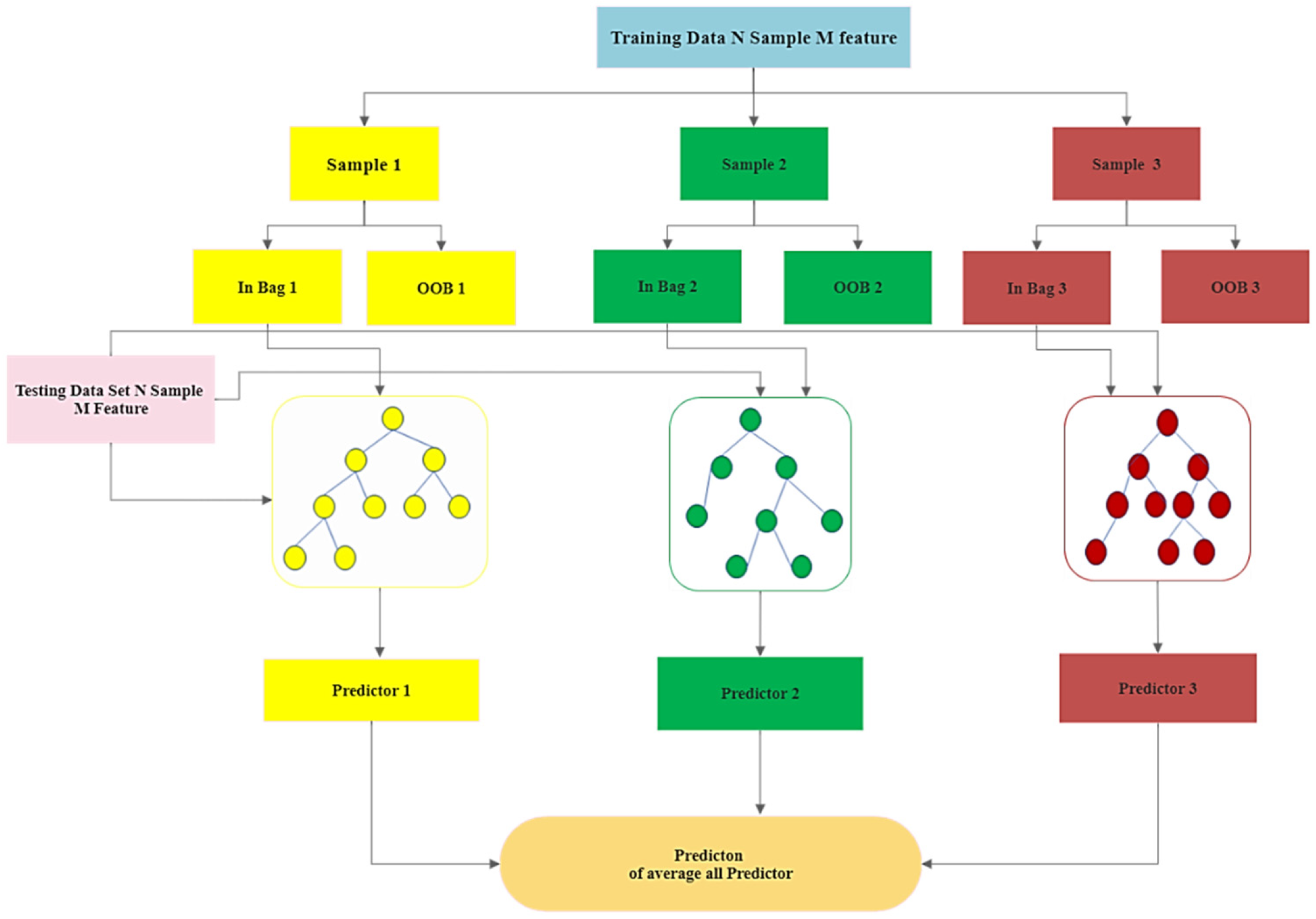
This study focuses on the use of different machine learning techniques to understand the effect of hydro-climatological parameters, i.e., temperature, precipitation, water inflow in the dam, sediment load, and reservoir level on the target, i.e., the average seepage in Tarbela Dam. Secondly, Shapley Additive Explanations (SHAP), a model explanation algorithm, was used to understand these Machine Learning (ML) algorithms’ model predictions, breaking down the predictions into individual feature impacts. Shapley Additive Explanations (SHAP) gives useful insight into the seepage problem in the Tarbela Dam and provides guidelines to control the seepage problem and avoid dam failure. The data collection was a difficult task because of the limited access to data on the dam site for research purposes. The data was gathered from Tarbela Dam project office and compiled for the experimental purposes. This study is organized into following (1) Modelling seepage based on hydro-climatological parameters using AI techniques, (2) Random forest (RF), CatBoost (CB), Artificial Neural Network (ANN) and Support Vector Machine (SVM) are used to predict Dam seepage, (3) Compare the Artificial Intelligence (AI) models accuracy in predicting dam seepage, (4) Use Explainable Artificial Intelligence (XAI) method, i.e., SHAP, to understand the model’s prediction and feature importance and (5) Emphasize the importance of Machine learning algorithms in resolving the dam seepage problem.
4. Conclusions
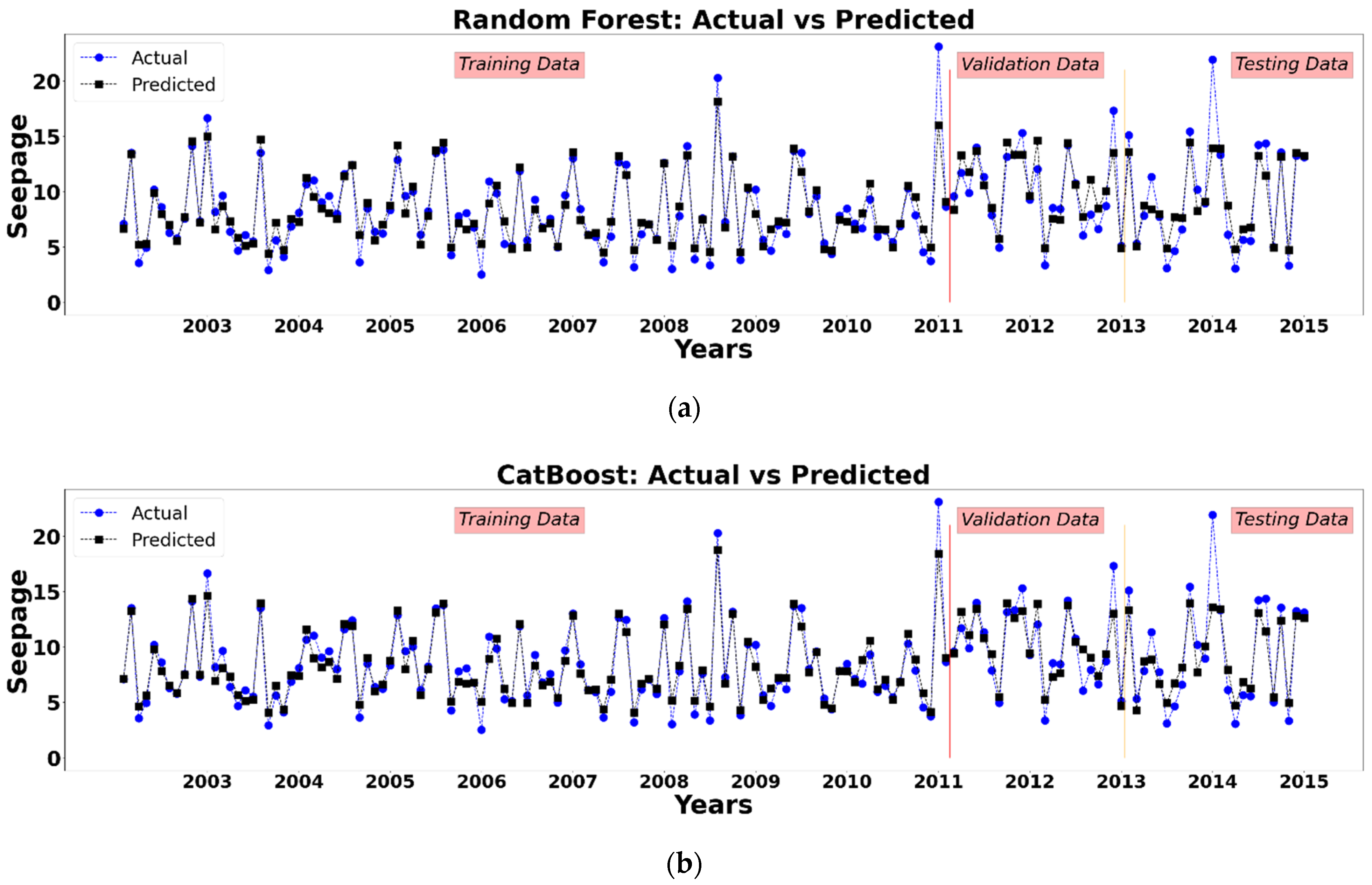
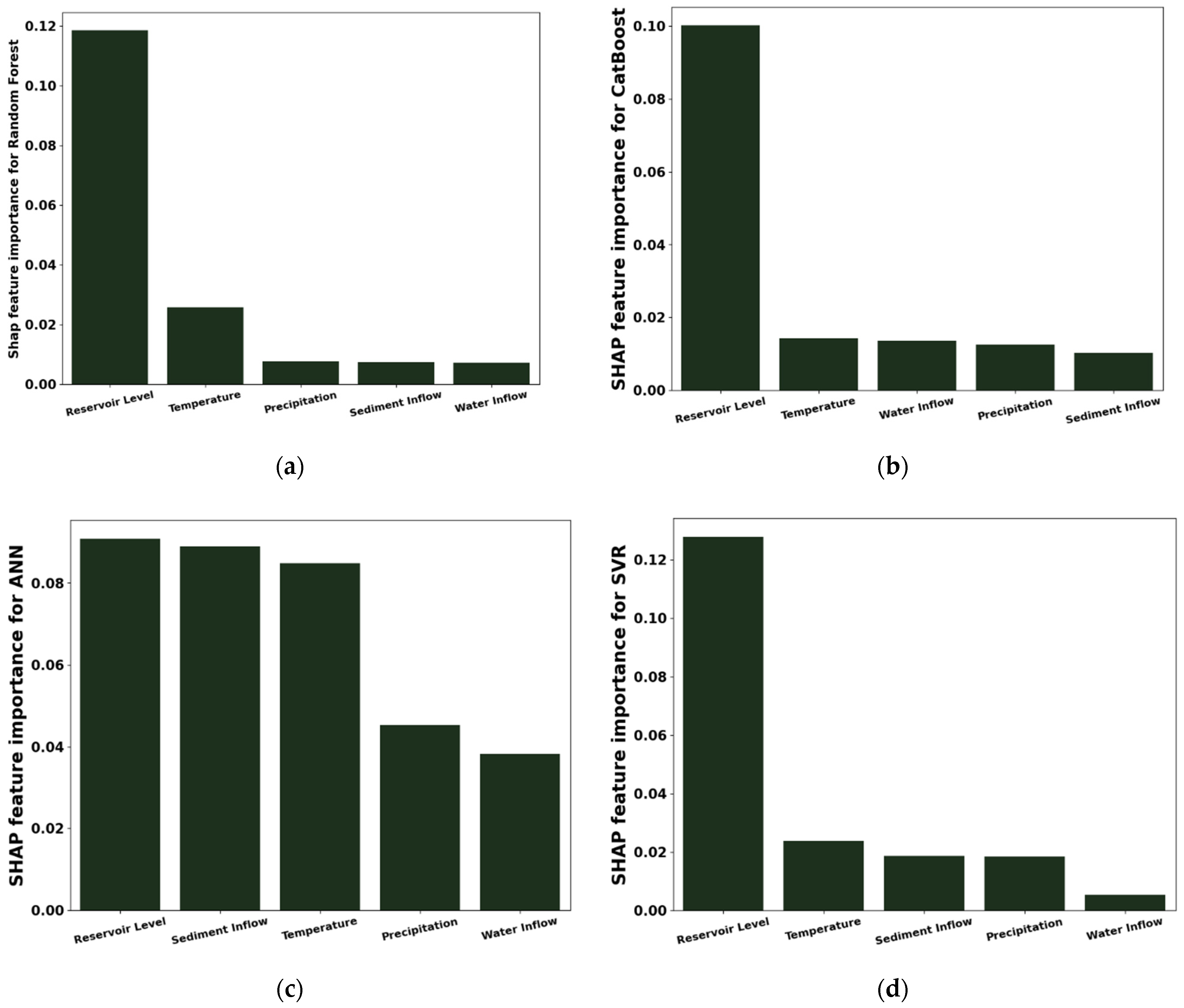
In this research, hydro-climatological parameters (Reservoir Level, Temperature, Sediment Inflow, Precipitation and Water Inflow and Water Outflow) were observed from 2003 to 2015 to understand their effect on the seepage in the Tarbela Dam, built on the Indus River of Pakistan. Firstly, four different machine learning algorithms, i.e., Random Forest, CatBoost, Support Vector Machine, and Artificial Neural Network, were used to model the relationship between the input variables and output to compare their performance in predicting the average seepage in the Tarbela Dam. Secondly, to explain the predictions of the machine learning models on the output, Shapley’s Additive ExPlanations (SHAP) algorithm (XAI: Model Explanation Algorithm) was used for each model to explain the sensitivity and effect of each parameter on the output variable (Average Seepage).
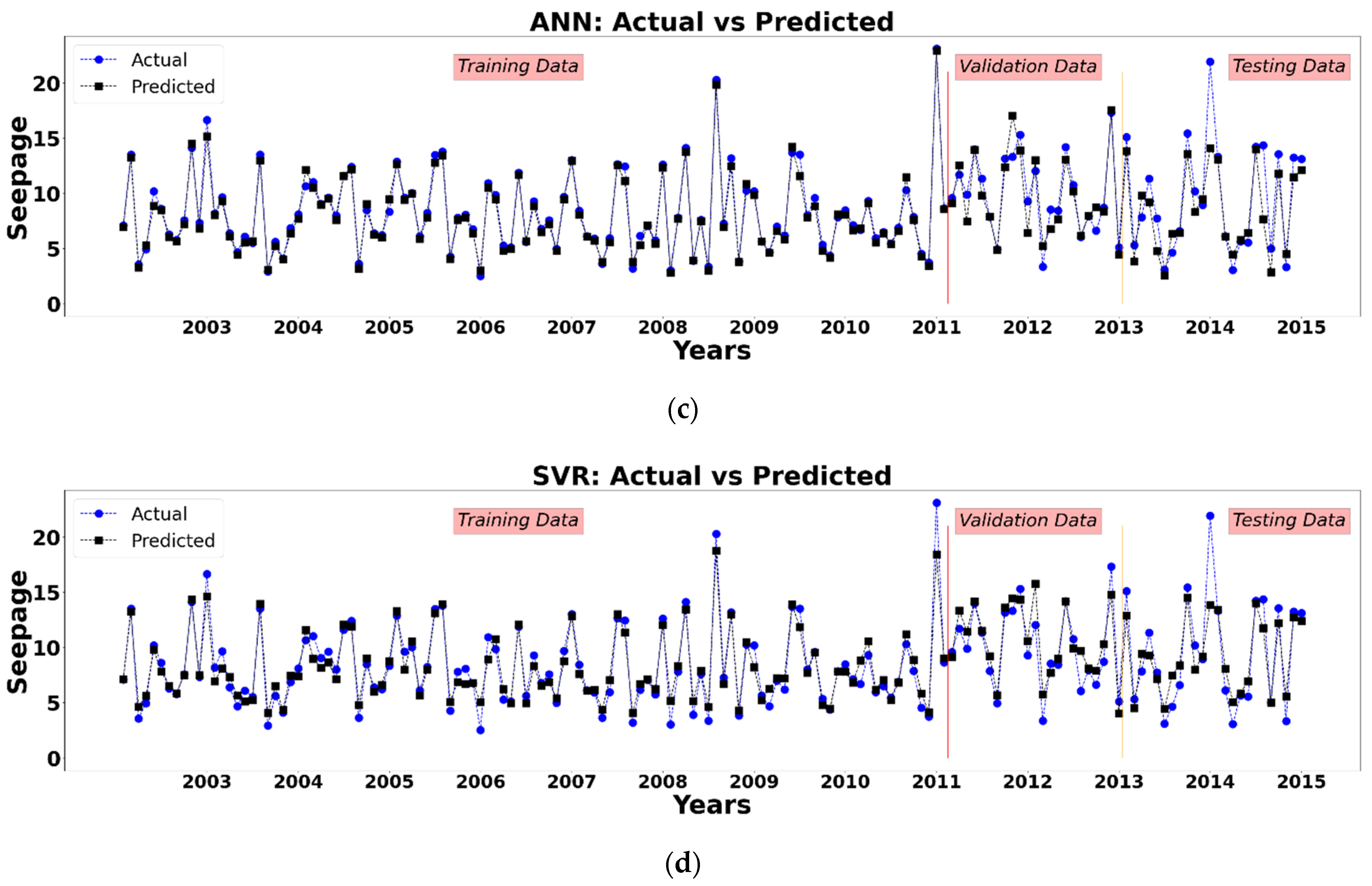
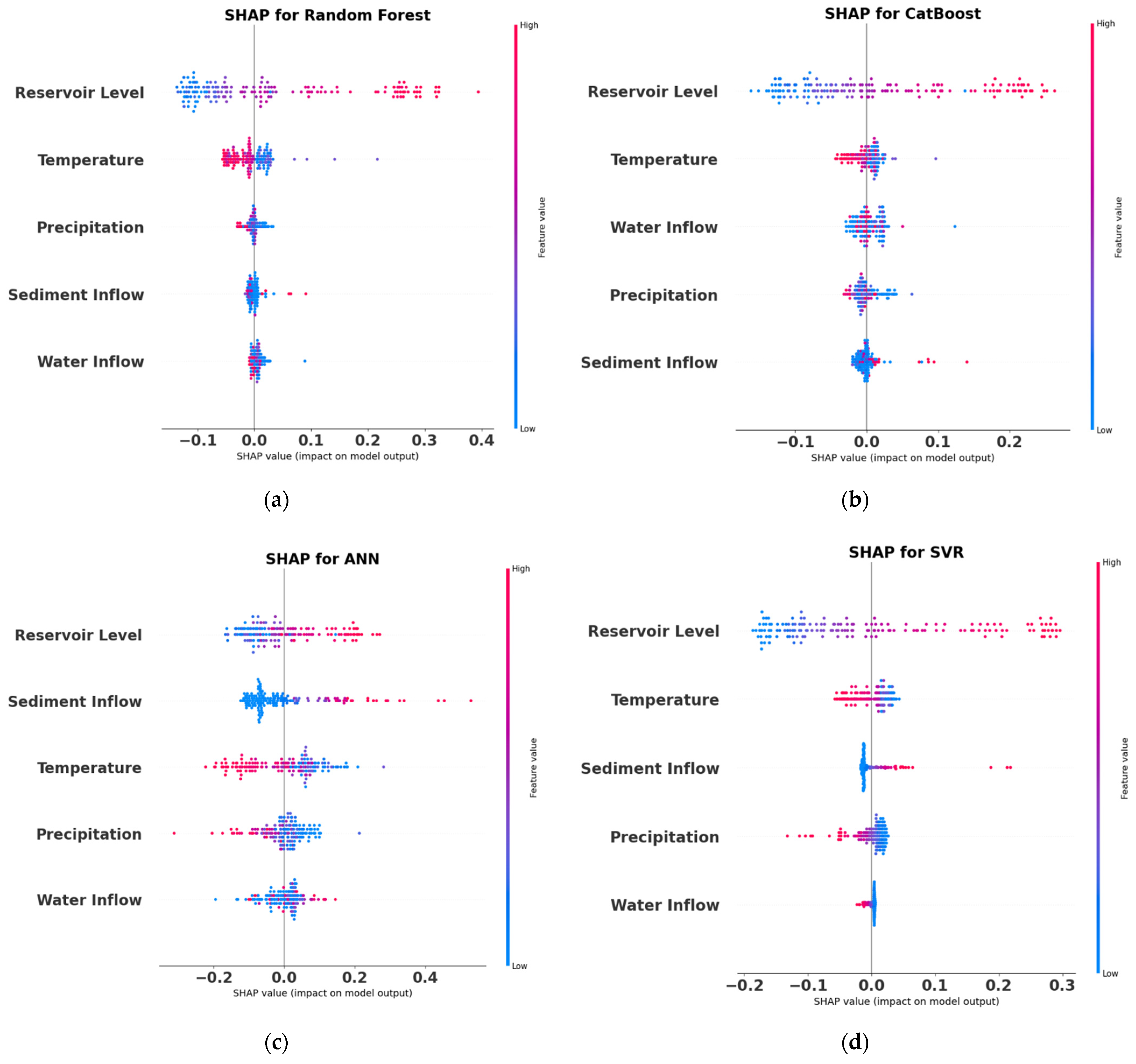
According to the findings of this study, the Random Forest, CatBoost, Support Vector Machine and Artificial Neural Network approach may be used to predict dam seepage based on hydro-climatological parameters in the Tarbela Dam. However, the CatBoost algorithm outperforms all the algorithms used for modeling by reporting the least RMSE and highest R2 score during the training, testing and validation stage. The recommended algorithm is CatBoost for water resources management decision-making and policymaking and improved monitoring of seepage losses at Tarbela Dam using Artificial Intelligence-based modeling approaches. Furthermore, the SHAP algorithm for all the models, reports the Reservoir Level as the most important parameter affecting the average dam seepage. Increasing the Reservoir Level increases, the average dam seepage and vice versa.
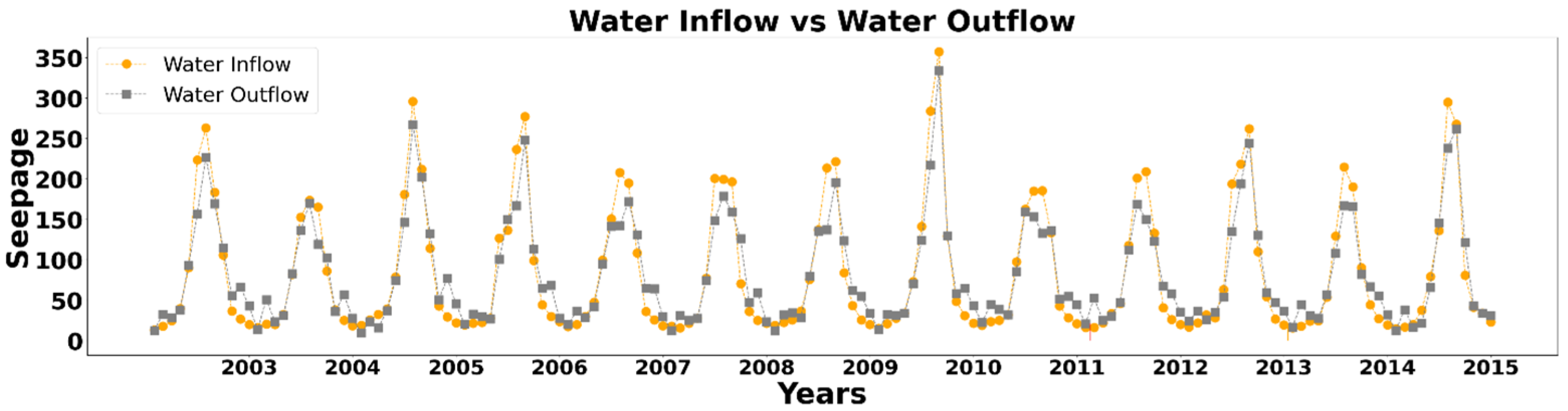
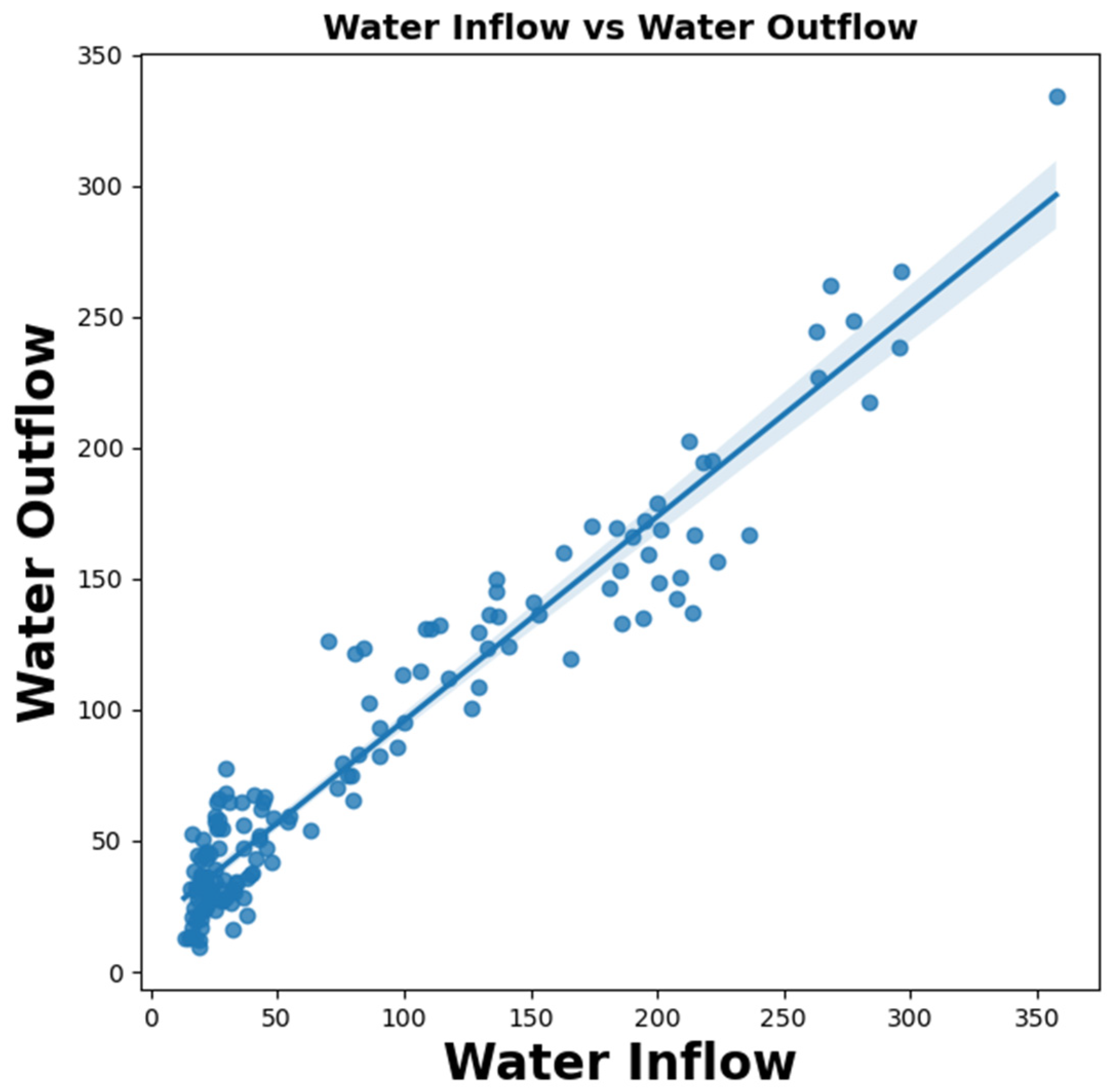
The SHAP summary plots concluded that reservoir level directly impacts dam seepage compared to other parameters (water inflow, temperature, precipitation, sediment inflow). Sediment has a moderate positive effect on dam seepage compared to reservoir level. The SHAP values for water inflow shows a minimal effect compared to reservoir level and sediment inflow. It is also concluded that temperature and precipitation have a negative effect on dam seepage. Still, they play an important role in glacier melting and increasing water inflow from the source to the Tarbela Dam. The AI based modelling and SHAP feature importance highlights the role of the hydro-climatological variable on Tarbela Dam seepage which is an interesting analysis identifying the importance of reservoir level for dam seepage prediction.
A proper plan should be established in the coming decade to properly manage the droughts, floods and water inflow at downstream side of the dam. In addition, the model’s applicability will be superior in locations where data collecting is limited, in contrast with existing physical methods. Therefore, it is possible to increase sustainable water resource management through AI based analysis for seepage modelling in the dam. Water resources management, dam’s stability and safety should be a research priority in light of climate change. It is recommended to create a database of all relevant variables from the entire hydrological cycle and metrological data on dam sites for data collection, which will enable application of various AI based techniques to understand and improve dam seepage problems. Furthermore, this work could be extended by including more parameters, e.g., climatological parameters from region, induced seismicity data from dam, seismic events data such as earthquakes, soil parameters, and structural deformation such as crack and joints data in the dam for better AI based modelling, that will lead to better decision making, devising better policies to improve the dam stability and prevent against structural failures in the dam.