High-Precision Calculation of the Proportions of Water with δ2H and δ18O, the Cumulative Effect of Evaporation in the Vertical Direction and Depleted δ2H and δ18O of the Shallow Soil Water Caused by Evaporation
Abstract
:1. Introduction
2. Materials and Methods
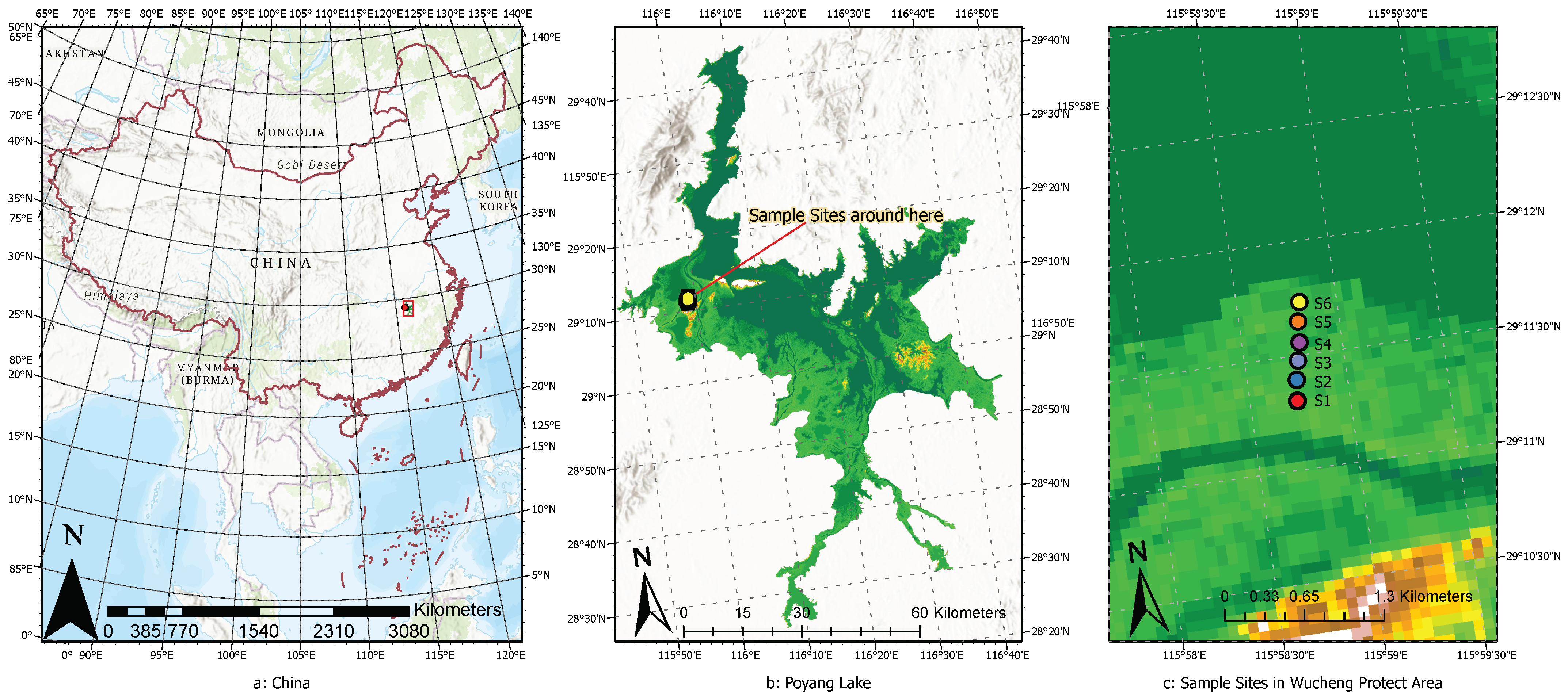
2.1. Sampling Sties
2.2. Sample Collection and Processing
2.3. Methods
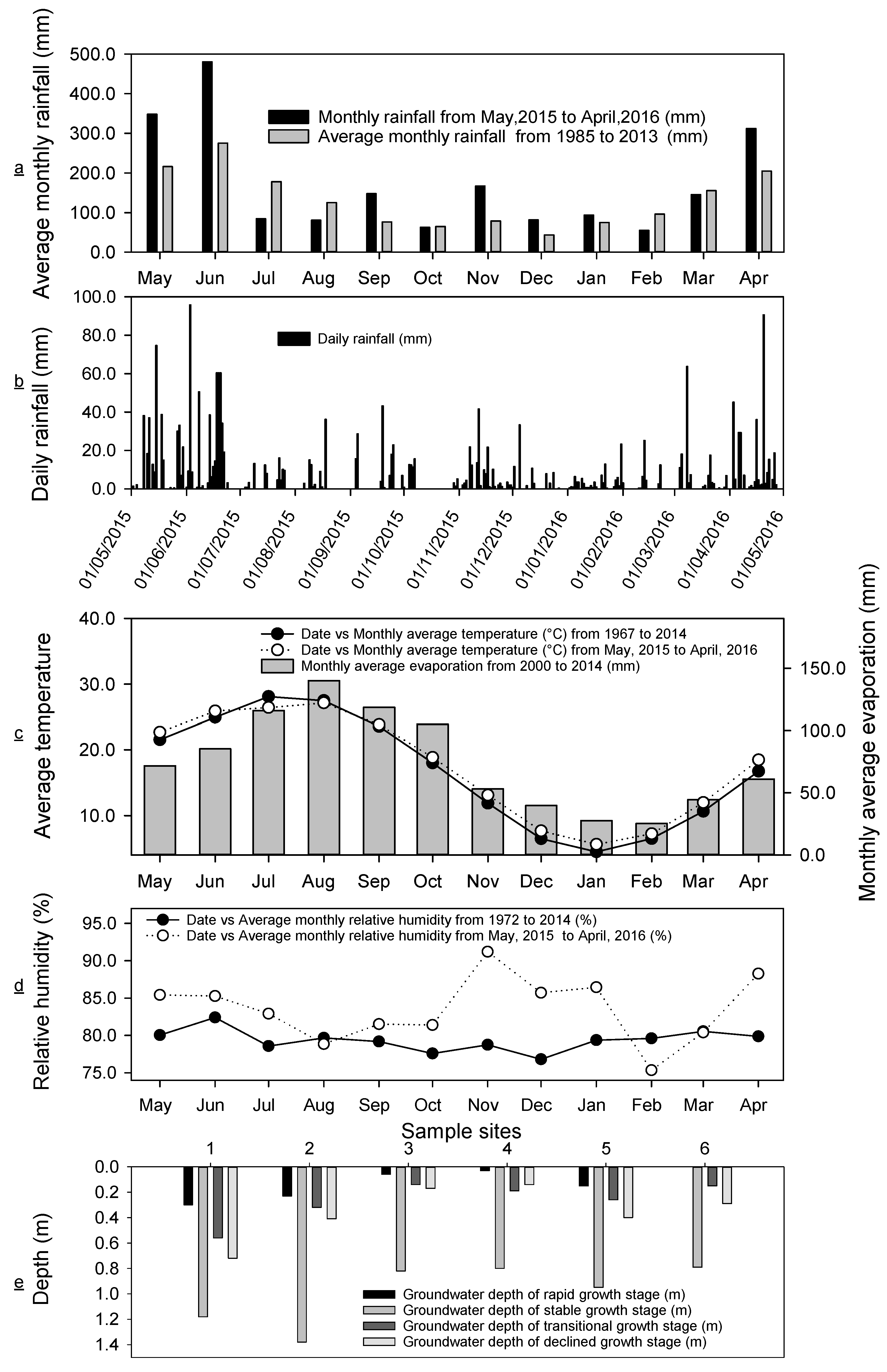
2.4. Climatic and Hydrological Characteristics
3. Results and Discussion
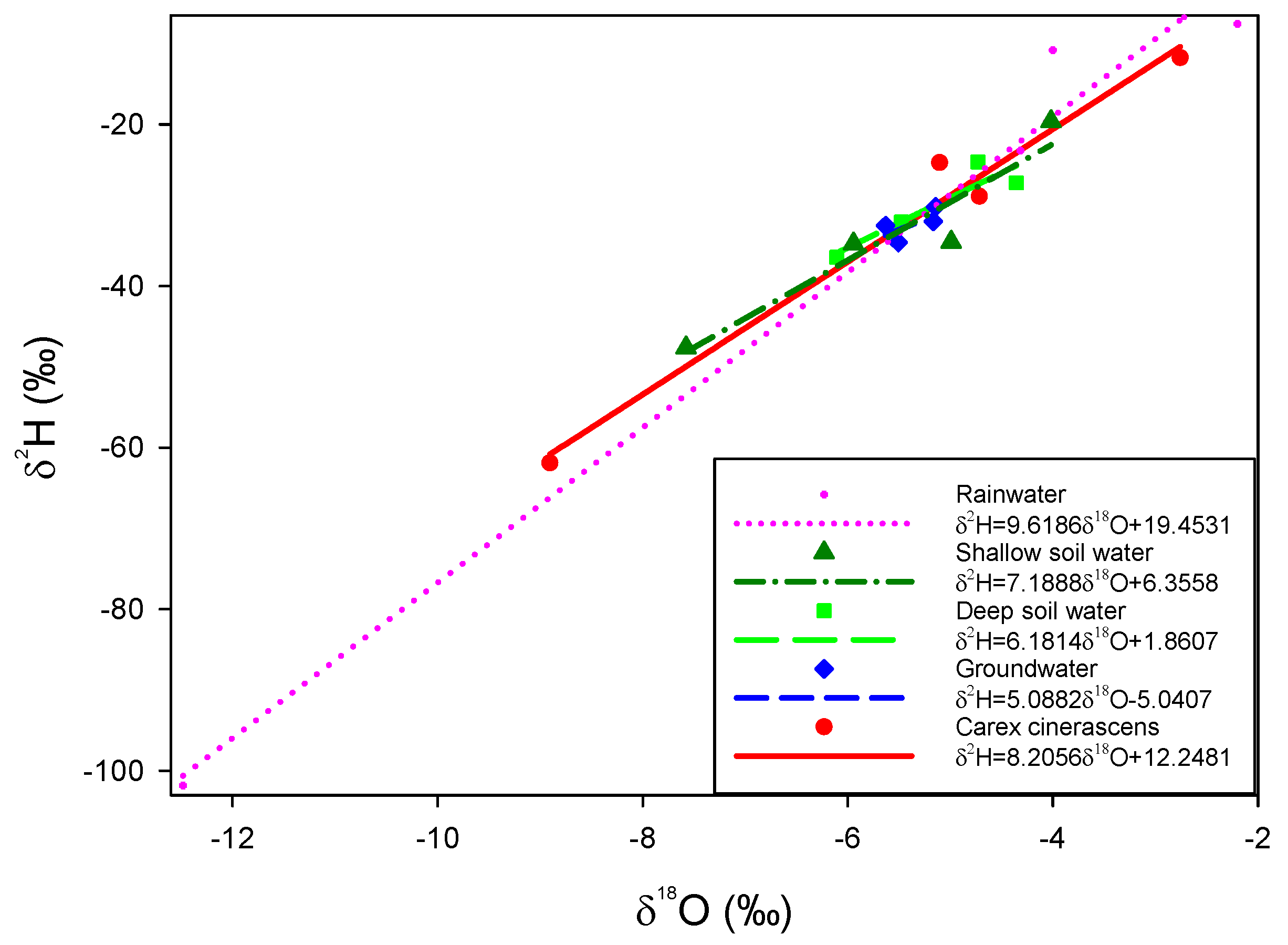
3.1. Secondary Sources Characteristics
- Using the isotope compositions of various substances together, such as rainwater, shallow soil water, deep soil water, Carex cinerascens and groundwater, to plot the H–O relationship lines can also reflect the secondary sources characteristic, which is the embodiment of the H–O relationship of rainfall in the aquatic ecosystem;
- There are also secondary sources effects similar to lakes in plants, shallow soil water, deep soil water, and groundwater, which should be studied in the future. No matter where, no matter how small, as long as there is evaporation and condensation, there is secondary sources. How big the impact is a further question;
- The first explanation and the second explanation work together.
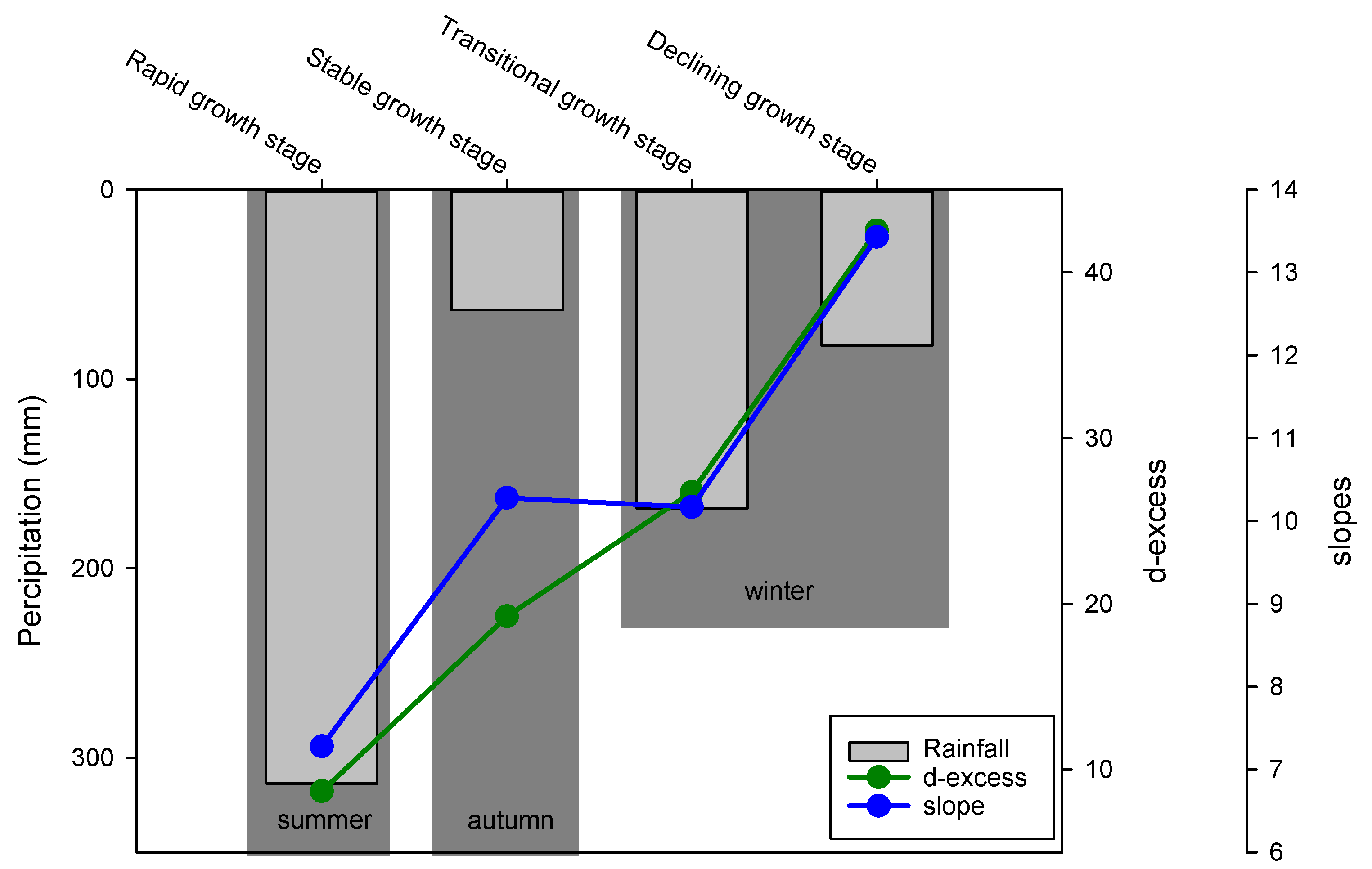
3.2. The Vertical Cumulative Effect of Evaporation Is Reflected in the Monotonically Decreasing Slope and Intercept of H–O
- Rainwater on the ground is affected by evaporation, which will cause the H and O of water to increase [73] and lower the slope and the intercept of H–O relationship line;
- When rainwater flows from shallow soil to deep soil and to groundwater, it is still affected by evaporation. The rainwater flows into the soil and then reaches the groundwater. The deeper the flow, the stronger the total evaporation. For example, when rainwater becomes groundwater, it needs to experience surface evaporation, shallow soil evaporation, lower soil evaporation, and groundwater evaporation, but shallow soil water only needs to experience surface evaporation and the shallow soil water evaporation.;
- In every month or every season, there are changes in isotopes compositions of rainwater and so is the water seeping into the soil. But in the soil and groundwater, the previous water which bears more evaporation than the newer water seeping in already exists. So, further down, the average evaporation of the water body subjected is still increasing as depths increases. That’s the reason that when we fitted the line about H–O values through the points from different stages of those materials respectively, there is a decreasing trend in slopes and intercept of those lines from the ground to underground.
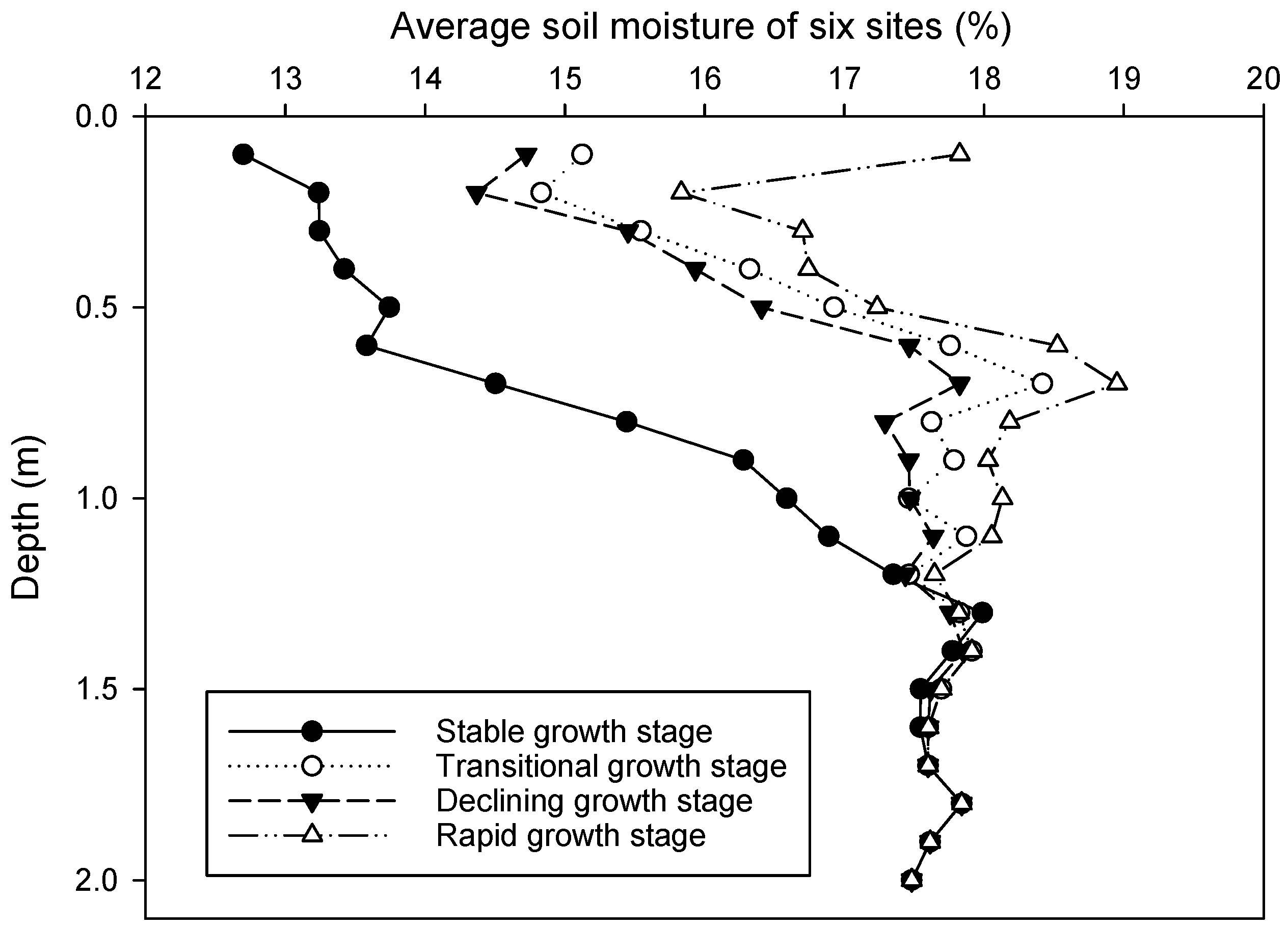
- D-excess is not only lowered by accumulation of evaporation, but also by the increasing of soil moisture.
3.3. Exact Solutions for Proportion of Potential Water Sources in Carex Cinerascens Stem Water
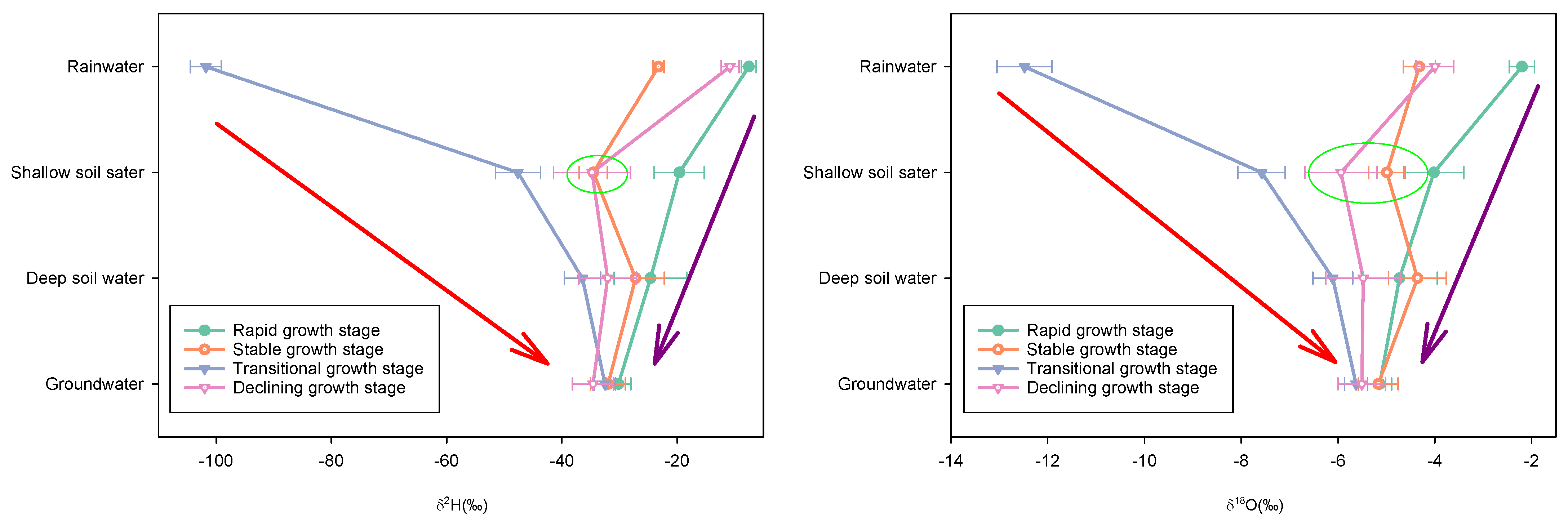
3.4. H and O of the Shallow Soil Water Is More Depleted Due to Evaporation
- Partial evaporation of the shallow soil water, which caused the isotopic composition of the shallow soil water to enrich;
- After the process 1, the shallow soil water was insufficient due to evaporation, and then the deep soil water moved from bottom to top to replenish the shallow soil water. At this time, since lighter water molecules were easier to move upwards, the isotope composition of the recharging water was depleted;
- If the effect of the process 2 was greater than that of the process 1, then the isotope composition of shallow soil water becomes depleted.
4. Conclusions
- The intercept of the LMWL of Poyang Lake was close to that of the LMWL of Dongting Lake which is about 300 kilometres away from Poyang Lake, and different from those surrounding areas, indicating that the large lakes indeed have the ability to regulate d-excess through secondary sources. Wouldn’t the GMWL rebuilted when large waters were excluded be different from GMWL of Craig [13]?
- Although the LMWL of Poyang Lake was not established by seasons, it is impossible to know the d-excess change of the LMWL of Poyang Lake from summer to winter, but in the H–O relationship lines established by rainwater, plant water, shallow soil water, deep soil water, and groundwater the d-excess showed a clear and gradually increasing trend from summer to winter. Can the multi-substance H–O relationship lines also reflect the secondary moisture sources of large lakes or are there also micro-secondary sources in soil and groundwater?
- By plotting the H–O relationship lines for rainwater, shallow soil water, deep soil water, and groundwater respectively, there is a clear trend of decreasing slope and intercept from top to bottom, which is likely to be the vertical cumulative effect of evaporation on the isotope compositions. The vertical effect of evaporation on the isotope composition has not received the attention it deserves.
- It is common to calculate the respective water source ratios by IsoSource model, but the importance of giving an exact solution is not emphasized. Whether there is a solution (non-approximate solution) and the full range of the solution contains errors, need to be decided by the exact solution.
- Regardless of the changes in the H and O values of rainwater and changes of seasons, the H and O values of groundwater varied very little. If we want to study the mechanism of isotope composition changes and isotope changes in the global water cycle, the stable H and O value of groundwater is a good intervention point.
- Evaporation did enrich H and O values in the remaining shallow soil water, but the isotope fractionation accompanying the recharge of shallow soil water by deep soil water eventually resulted in depleted H and O values of shallow soil water. This isotope fractionation effect needs to be theoretically studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Exact Solutions of the Equation (3) and the Table 3
Appendix A.1. Rapid Growth Stage
Appendix A.2. Stable Growth Stage
Appendix A.3. Transitional Growth Stage
Appendix A.3.1. Solution 1
Appendix A.3.2. Solution 2
Appendix A.4. Declining Growth Stage
References
- Takahashi, K. Oxygen isotope ratios between soil water and stem water of trees in pot experiments. Ecol. Res. 1998, 13, 1–5. [Google Scholar] [CrossRef]
- Parnell, A.C.; Inger, R.; Bearhop, S.; Jackson, A.L. Source Partitioning Using Stable Isotopes: Coping with Too Much Variation. PLoS ONE 2010, 5, e9672. [Google Scholar] [CrossRef] [PubMed]
- Guerrero, A.I.; Rogers, T.L. Evaluating the performance of the Bayesian mixing tool MixSIAR with fatty acid data for quantitative estimation of diet. Sci. Rep. 2020, 10, 20780. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Gao, Y.; Wang, X.; Wang, G. Seasonal Variation in Water Uptake Depth of Jujube Estimated with Stable Isotopes: Comparative Study of Drip and Basin Irrigation. J. Soil Sci. Plant Nutr. 2022, 22, 443–454. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, Y.; Niu, Y.; Song, X.; Yu, H.; Lan, W.; Kang, X. Warming changed seasonal water uptake patterns of summer maize. Agric. Water Manag. 2021, 258, 107210. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, Y. Using isotopic labeling to investigate root water uptake in an alley cropping system within Taklimakan Desert Oasis, China. Agrofor. Syst. 2021, 95, 907–918. [Google Scholar] [CrossRef]
- Wang, S.; An, J.; Zhao, X.; Gao, X.; Wu, P.; Huo, G.; Robinson, B.H. Age- and climate- related water use patterns of apple trees on China’s Loess Plateau. J. Hydrol. 2020, 582, 124462. [Google Scholar] [CrossRef]
- Rao, W.; Chen, X.; Meredith, K.T.; Tan, H.; Gao, M.; Liu, J. Water uptake of riparian plants in the lower Lhasa River Basin, South Tibetan Plateau using stable water isotopes. Hydrol. Process. 2020, 34, 3492–3505. [Google Scholar] [CrossRef]
- Pan, Y.X.; Wang, X.P.; Ya, R.H.; Zhang, F.; Zhao, Y. Variation in water source of sand-binding vegetation across a chronosequence of artificial desert revegetation in Northwest China. Sci. Cold Arid. Reg. 2020, 12, 306–316. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, F.y.; Hu, T.x.; Zhao, K.g.; Gao, T.p.; Zhao, H.x.; Ning, T.y. Using stable isotopes to quantify water uptake from different soil layers and water use efficiency of wheat under long-term tillage and straw return practices. Agric. Water Manag. 2020, 229, 105933. [Google Scholar] [CrossRef]
- Li, P.; Cao, X.; Tan, H.; Wang, J.; Ren, S.; Yang, P. Studies on water uptake and heat status of cherry root under water-saving measures. Agric. Water Manag. 2020, 242, 106359. [Google Scholar] [CrossRef]
- Zheng, L.; Ma, J.; Sun, X.; Guo, X.; Li, Y.; Ren, R.; Cheng, Q. Effective root growth zone of apple tree under water storage pit irrigation using stable isotope methodology. Arch. Agron. Soil Sci. 2019, 65, 1521–1535. [Google Scholar] [CrossRef]
- Craig, H. Isotopic variations in meteoric waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef]
- Wang, H.; Jin, J.; Cui, B.; Si, B.; Ma, X.; Wen, M. Technical note: Evaporating water is different from bulk soil water in δ2H and δ18O and has implications for evaporation calculation. Hydrol. Earth Syst. Sci. 2021, 25, 5399–5413. [Google Scholar] [CrossRef]
- Vargas, A.I.; Schaffer, B.; Yuhong, L.; Sternberg, L.D.S.L. Testing plant use of mobile vs immobile soil water sources using stable isotope experiments. New Phytol. 2017, 215, 582–594. [Google Scholar] [CrossRef]
- Goldsmith, G.R.; Allen, S.T.; Braun, S.; Engbersen, N.; González-Quijano, C.R.; Kirchner, J.W.; Siegwolf, R.T.W. Spatial variation in throughfall, soil, and plant water isotopes in a temperate forest. Ecohydrology 2018, 12, e2059. [Google Scholar] [CrossRef]
- Yan, Y.; Zhou, X.; Liao, L.; Tian, J.; Li, Y.; Shi, Z.; Liu, F.; Ouyang, S. Hydrogeochemical Characteristic of Geothermal Water and Precursory Anomalies along the Xianshuihe Fault Zone, Southwestern China. Water 2022, 14, 550. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, Y.; Song, X. How Elevated CO2 Shifts Root Water Uptake Pattern of Crop? Lessons from Climate Chamber Experiments and Isotopic Tracing Technique. Water 2020, 12, 3194. [Google Scholar] [CrossRef]
- Xia, Z.; Winnick, M.J. The competing effects of terrestrial evapotranspiration and raindrop re-evaporation on the deuterium excess of continental precipitation. Earth Planet. Sci. Lett. 2021, 572, 117120. [Google Scholar] [CrossRef]
- Malik, F.; Butt, S.; Mujahid, N. Variation in isotopic composition of precipitation with identification of vapor source using deuterium excess as tool. J. Radioanal. Nucl. Chem. 2022, 331, 683–690. [Google Scholar] [CrossRef]
- Kopec, B.G.; Feng, X.; Posmentier, E.S.; Sonder, L.J. Seasonal Deuterium Excess Variations of Precipitation at Summit, Greenland, and their Climatological Significance. J. Geophys. Res. Atmos. 2019, 124, 72–91. [Google Scholar] [CrossRef]
- Nakamura, T.; Nishida, K.; Kazama, F. Influence of a dual monsoon system and two sources of groundwater recharge on Kofu basin alluvial fans, Japan. Hydrol. Res. 2017, 48, 1071–1087. [Google Scholar] [CrossRef]
- Machavaram, M.V.; Krishnamurthy, R.V. Earth surface evaporative process: A case study from the Great Lakes region of the United States based on deuterium excess in precipitation. Geochim. Cosmochim. Acta 1995, 59, 4279–4283. [Google Scholar] [CrossRef]
- Hu, Y.; Xiao, W.; Wang, J.; Welp, L.R.; Xie, C.; Chu, H.; Lee, X. Quantifying the contribution of evaporation from Lake Taihu to precipitation with an isotope-based method. Isot. Environ. Health Stud. 2022, 58, 258–276. [Google Scholar] [CrossRef]
- Liao, F.; Wang, G.; Yi, L.; Shi, Z.; Cheng, G.; Kong, Q.; Mu, W.; Guo, L.; Cheng, K.; Dong, N.; et al. Applying radium isotopes to estimate groundwater discharge into Poyang Lake, the largest freshwater lake in China. J. Hydrol. 2020, 585, 124782. [Google Scholar] [CrossRef]
- Shao, M.; Gong, H.; Dai, N.; Zhi, Y.; Xu, N.; Lu, P. Study on time budgets and behavioral rhythm of wintering Siberian Cranes in a lotus pond reclamation area in Poyang Lake. Acta Ecol. Sin. 2018, 38, 5206–5212. [Google Scholar] [CrossRef]
- Wang, X.; Xu, L.; Xu, J.; Wu, Z. Effects of Prescribed Fire on Plant Traits and Community Characteristics of Triarrhena Lutarioriparia in Poyang Lake, China. Wetlands 2019, 39, 161–172. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y.; Zhang, L.; Liu, X.; Wang, Y.; Ji, Y. Assessing environmental and plant community changes by phytolith characteristics in sediments from Nanjishan Nature Reserve, Lake Poyang. Ecol. Inform. 2022, 69, 101586. [Google Scholar] [CrossRef]
- Wang, X.; Xu, J.; Wu, Z.; Shen, Y.; Cai, Y. Effect of annual prescribed burning of wetlands on soil organic carbon fractions: A 5-year study in Poyang, China. Ecol. Eng. 2019, 138, 219–226. [Google Scholar] [CrossRef]
- Chen, S.; Su, X.; Fang, L.; Chen, L. CarexDynamics as an Environmental Indicator in the Poyang Lake Wetland Area: Remote Sensing Mapping and GIS Analysis. Ann. GIS 2007, 13, 44–50. [Google Scholar] [CrossRef]
- Liu, C.Y.; Gong, X.F.; Tang, Y.P.; Chen, C.L. Lead sequestration in iron plaques developed on Phalaris arundinacea Linn. and Carex cinerascens Kukenth. from Poyang Lake (China). Aquat. Bot. 2015, 122, 54–59. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, J.; Jiang, Y.; Wang, H. Relationship between the hydrological conditions and the distribution of vegetation communities within the Poyang Lake National Nature Reserve, China. Ecol. Inform. 2012, 11, 65–75. [Google Scholar] [CrossRef]
- Lei, S.; Zhang, X.-P.; Li, R.-F.; Xu, X.-H.; Fu, Q. Analysis the changes of annual for Poyang Lake wetland vegetation based on MODIS monitoring. Procedia Environ. Sci. 2011, 10, 1841–1846. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R. Relating seasonal patterns of the AVHRR vegetation index to simulated photosynthesis and transpiration of forests in different climates. Remote Sens. Environ. 1988, 24, 347–367. [Google Scholar] [CrossRef]
- Ministry of Ecology and Environment of the People’s Republic of China. Soil–Determination of Dry Matter and Water Content–Gravimetric Method; Ministry of Ecology and Environment of the People’s Republic of China: Beijing, China, 2011.
- Zhang, X.; Xiao, Y.; Wan, H.; Deng, Z.; Pan, G.; Xia, J. Using stable hydrogen and oxygen isotopes to study water movement in soil-plant-atmosphere continuum at Poyang Lake wetland, China. Wetl. Ecol. Manag. 2017, 25, 221–234. [Google Scholar] [CrossRef]
- Wang, J.; Fu, B.; Lu, N.; Zhang, L. Seasonal variation in water uptake patterns of three plant species based on stable isotopes in the semi-arid Loess Plateau. Sci. Total Environ. 2017, 609, 27–37. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency. Stable Isotope Mixing Models for Estimating Source Proportions; United States Environmental Protection Agency: Washington, DC, USA, 2022. [Google Scholar]
- White, J.W.C.; Cook, E.R.; Lawrence, J.R.; Wallace, S.B. The DH ratios of sap in trees: Implications for water sources and tree ring DH ratios. Geochim. Cosmochim. Acta 1985, 49, 237–246. [Google Scholar] [CrossRef]
- Zimmermann, U.; Ehhalt, D.; Muennich, K.O. Soil–Water Movement and Evapotranspiration: Changes in the Isotopic Composition of the Water; International Atomic Energy Agency: Viennam, Austria, 1967; pp. 567–585. [Google Scholar]
- Ronghui, H.; Yifang, W. The influence of ENSO on the summer climate change in China and its mechanism. Adv. Atmos. Sci. 1989, 6, 21–32. [Google Scholar] [CrossRef]
- Renhe, Z.; Sumi, A.; Kimoto, M. A Diagnostic Study of the Impact of El Nino on the Precipitation in China. Adv. Atmos. Sci. 1999, 16, 229–241. [Google Scholar]
- Zhang, X.; Yao, T. Relations Between δ D and δ18O in Precipitation at Present in the Northeast Tibetan Plateau. J. Glaciolgy Geocryol. 1996, 18, 360–365. [Google Scholar]
- Yang, Y.; Xiao, H.; Qin, Z.; Zou, S. Hydrogen and oxygen isotopic records in monthly scales variations of hydrological characteristics in the different landscape zones of alpine cold regions. J. Hydrol. 2013, 499, 124–131. [Google Scholar] [CrossRef]
- Silverman, S.R. The isotope geology of oxygen. Geochim. Cosmochim. Acta 1951, 2, 26–42. [Google Scholar] [CrossRef]
- Hu, Y.B.; Xiao, W.; Qian, Y.F.; Liu, Q.; Xie, C.Y.; Zhang, X.F.; Zhang, W.Q.; Wen, X.F.; Liu, S.D.; Lee, X.H. Effects of Water Vapor Source and Local Evaporation on the Stable Hydrogen and Oxygen Isotopic Compositions of Precipitation. Huan Jing Ke Xue= Huanjing Kexue 2019, 40, 573–581. [Google Scholar] [CrossRef]
- Wu, H.; Huang, Q.; Fu, C.; Song, F.; Liu, J.; Li, J. Stable isotope signatures of river and lake water from Poyang Lake, China: Implications for river–lake interactions. J. Hydrol. 2021, 592, 125619. [Google Scholar] [CrossRef]
- Zhan, L.; Chen, J.; Zhang, S.; Li, L.; Huang, D.; Wang, T. Isotopic signatures of precipitation, surface water, and groundwater interactions, Poyang Lake Basin, China. Environ. Earth Sci. 2016, 75, 1307. [Google Scholar] [CrossRef]
- Xu, B.; Wang, G. Surface water and groundwater contaminations and the resultant hydrochemical evolution in the Yongxiu area, west of Poyang Lake, China. Environ. Earth Sci. 2016, 75, 184. [Google Scholar] [CrossRef]
- Li, J.; Wu, H.W.; Zhou, Y.Q.; Zhao, Z.H.; Wang, X.L.; Cai, Y.J.; He, B.; Chen, W.; Sun, W. Variations of Stable Oxygen and Deuterium Isotopes in River and Lake Waters During Flooding Season Along the Middle and Lower Reaches of the Yangtze River Regions. Huan Jing Ke Xue= Huanjing Kexue 2020, 41, 1176–1183. [Google Scholar] [CrossRef] [PubMed]
- Liao, F.; Wang, G.; Shi, Z.; Cheng, G.; Kong, Q.; Mu, W.; Guo, L. Estimation of groundwater discharge and associated chemical fluxes into Poyang Lake, China: Approaches using stable isotopes (δ D and δ18O) and radon. Hydrogeol. J. 2018, 26, 1625–1638. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M.J.; Qu, D.Y.; Duan, W.G.; Wang, J.X.; Su, P.Y.; Guo, R. Water Use Strategies of Dominant Species (Caragana korshinskiiandReaumuria soongorica) in Natural Shrubs Based on Stable Isotopes in the Loess Hill, China. Water 2020, 12, 1923. [Google Scholar] [CrossRef]
- Jiang, C.; Yin, L.; Wen, X.; Du, C.; Wu, L.; Long, Y.; Liu, Y.; Ma, Y.; Yin, Q.; Zhou, Z.; et al. Microplastics in Sediment and Surface Water of West Dongting Lake and South Dongting Lake: Abundance, Source and Composition. Int. J. Environ. Res. Public Health 2018, 15, 2164. [Google Scholar] [CrossRef]
- Zhan, L.; Chen, J.; Zhang, S. Spatial and temporal characteristics of δ2H and δ18O in the basin of Dongting Lake: Impact of monsoon precipitation. J. Radioanal. Nucl. Chem. 2016, 307, 479–490. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, L.; Jiang, J.; Fan, H. Spatiotemporal Variations of Summer Precipitation and Their Correlations with the East Asian Summer Monsoon in the Poyang Lake Basin, China. Water 2019, 11, 1705. [Google Scholar] [CrossRef]
- Fu, X.; Li, F.; Zhu, L.; Xie, Y.; Hu, C.; Chen, X.; Deng, Z. Change in ecological stoichiometry of Carex brevicuspis in response to seasonal dynamics and elevation in Dongting Lake, China. Nord. J. Bot. 2018, 36, e01821. [Google Scholar] [CrossRef]
- Zheng, L.; Wang, X.; Li, D.; Xu, G.; Guo, Y. Spatial heterogeneity of vegetation extent and the response to water level fluctuations and micro-topography in Poyang Lake, China. Ecol. Indic. 2021, 124, 107420. [Google Scholar] [CrossRef]
- Yu, D.; Yu, S.; He, Q.; Li, C.; Wei, C. Monitoring of Dongting Lake atrophy in the past 100 years by combining historical map and remote sensing technology. Remote Sens. Land Resour. 2016, 28, 116–122. [Google Scholar] [CrossRef]
- Ji, M.; Tang, J.; Gao, X.; Yang, Y.; Wu, Z. Analysis of Spatiotemporal Changes and Driving Factors of Poyang Lake Area Based on Google Earth Engine. J. China Hydrol. 2021, 41, 40–47. [Google Scholar] [CrossRef]
- Gat, J.R.; Bowser, C.J.; Kendall, C. The contribution of evaporation from the Great Lakes to the continental atmosphere: Estimate based on stable isotope data. Geophys. Res. Lett. 1994, 21, 557–560. [Google Scholar] [CrossRef]
- Guan, H.; Zhang, X.; Skrzypek, G.; Sun, Z.; Xu, X. Deuterium excess variations of rainfall events in a coastal area of South Australia and its relationship with synoptic weather systems and atmospheric moisture sources. J. Geophys. Res. Atmos. 2013, 118, 1123–1138. [Google Scholar] [CrossRef]
- Hu, C.; Froehlich, K.; Zhou, P.; Lou, Q.; Zeng, S.; Zhou, W. Seasonal variation of oxygen-18 in precipitation and surface water of the Poyang Lake Basin, China. Isot. Environ. Health Stud. 2013, 49, 188–196. [Google Scholar] [CrossRef]
- Vimeux, F.; Masson, V.; Delaygue, G.; Jouzel, J.; Petit, J.R.; Stievenard, M. A 420,000 year deuterium excess record from East Antarctica: Information on past changes in the origin of precipitation at Vostok. J. Geophys. Res. Atmos. 2001, 106, 31863–31873. [Google Scholar] [CrossRef]
- Ren, W.; Tian, L.; Shao, L. Regional moisture sources and Indian summer monsoon (ISM) moisture transport from simultaneous monitoring of precipitation isotopes on the southeastern and northeastern Tibetan Plateau. J. Hydrol. 2021, 601, 126836. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, M.; Argiriou, A.A.; Wang, S.; Ma, Q.; Zhou, X.; Wu, X.; Chen, J. Modeling Insights into Precipitation Deuterium Excess as an Indicator of Raindrop Evaporation in Lanzhou, China. Water 2021, 13, 193. [Google Scholar] [CrossRef]
- Kavanaugh, J.L.; Cuffey, K.M. Generalized view of source-region effects on δD and deuterium excess of ice-sheet precipitation. Ann. Glaciol. 2002, 35, 111–117. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, L.; Liu, X.; Xiao, H.; Ruan, Y.; Zhou, M. The patterns and implications of diurnal variations in the d-excess of plant water, shallow soil water and air moisture. Hydrol. Earth Syst. Sci. 2014, 18, 4129–4151. [Google Scholar] [CrossRef]
- Dogramaci, S.; Skrzypek, G.; Dodson, W.; Grierson, P.F. Stable isotope and hydrochemical evolution of groundwater in the semi-arid Hamersley Basin of subtropical northwest Australia. J. Hydrol. 2012, 475, 281–293. [Google Scholar] [CrossRef]
- Gammons, C.H.; Poulson, S.R.; Pellicori, D.A.; Reed, P.J.; Roesler, A.J.; Petrescu, E.M. The hydrogen and oxygen isotopic composition of precipitation, evaporated mine water, and river water in Montana, USA. J. Hydrol. 2006, 328, 319–330. [Google Scholar] [CrossRef]
- Benettin, P.; Volkmann, T.H.M.; Von Freyberg, J.; Frentress, J.; Penna, D.; Dawson, T.E.; Kirchner, J.W. Effects of climatic seasonality on the isotopic composition of evaporating soil waters. Hydrol. Earth Syst. Sci. 2018, 22, 2881–2890. [Google Scholar] [CrossRef]
- Bershaw, J. Controls on Deuterium Excess across Asia. Geosciences 2018, 8, 257. [Google Scholar] [CrossRef]
- Benetti, M.; Reverdin, G.; Pierre, C.; Merlivat, L.; Risi, C.; Steen-Larsen, H.C.; Vimeux, F. Deuterium excess in marine water vapor: Dependency on relative humidity and surface wind speed during evaporation. J. Geophys. Res. Atmos. 2014, 119, 584–593. [Google Scholar] [CrossRef]
- Dansgaard, W. Stable isotopes in precipitation. Tellus 1964, 16, 436–468. [Google Scholar] [CrossRef]
- Phillips, D.L.; Gregg, J.W. Source partitioning using stable isotopes: Coping with too many sources. Oecologia 2003, 136, 261–269. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhang, J.; Zhao, B.; Zhu, A.; Zhang, H.; Huang, P.; Li, X. Coupling a two-tip linear mixing model with a δD–δ18O plot to determine water sources consumed by maize during different growth stages. Field Crop. Res. 2011, 123, 196–205. [Google Scholar] [CrossRef]
- Dawson, T.E.; Pate, J.S. Seasonal water uptake and movement in root systems of Australian phraeatophytic plants of dimorphic root morphology: A stable isotope investigation. Oecologia 1996, 107, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Zencich, S.J.; Froend, R.H.; Turner, J.V.; Gailitis, V. Influence of groundwater depth on the seasonal sources of water accessed by Banksia tree species on a shallow, sandy coastal aquifer. Oecologia 2002, 131, 8–19. [Google Scholar] [CrossRef]
- Bchir, A.; Escalona, J.M.; Gallé, A.; Hernández-Montes, E.; Tortosa, I.; Braham, M.; Medrano, H. Carbon isotope discrimination (δ13C) as an indicator of vine water status and water use efficiency (WUE): Looking for the most representative sample and sampling time. Agric. Water Manag. 2016, 167, 11–20. [Google Scholar] [CrossRef]
- Phillips, D.L.; Newsome, S.D.; Gregg, J.W. Combining sources in stable isotope mixing models: Alternative methods. Oecologia 2005, 144, 520–527. [Google Scholar] [CrossRef]
- Cramer, V.A.; Thorburn, P.J.; Fraser, G.W. Transpiration and groundwater uptake from farm forest plots of Casuarina glauca and Eucalyptus camaldulensis in saline areas of southeast Queensland, Australia. Agric. Water Manag. 1999, 39, 187–204. [Google Scholar] [CrossRef]
- Sprenger, M.; Stumpp, C.; Weiler, M.; Aeschbach, W.; Allen, S.T.; Benettin, P.; Dubbert, M.; Hartmann, A.; Hrachowitz, M.; Kirchner, J.W.; et al. The Demographics of Water: A Review of Water Ages in the Critical Zone. Rev. Geophys. 2019, 57, 800–834. [Google Scholar] [CrossRef]
- Renée Brooks, J.; Barnard, H.R.; Coulombe, R.; McDonnell, J.J. Ecohydrologic separation of water between trees and streams in a Mediterranean climate. Nat. Geosci. 2010, 3, 100–104. [Google Scholar] [CrossRef]
- Horton, J.H.; Hawkins, R.H. Flow path of rain from the soil surface to the water table. Soil Sci. 1965, 100, 377–383. [Google Scholar] [CrossRef]


| Sites | Groudwater Level | Land Surface Elevation | |||
|---|---|---|---|---|---|
| Rapid Growth Stage | Stable Growth Stage | Transitional Growth Stage | Declining Growth Stage | ||
| the Lake | 14.22 | 11.86 | 13.70 | 12.45 | |
| the Xiu River | 11.68 | 12.07 | 10.37 | 8.99 | |
| 1 | 15.55 | 14.67 | 15.29 | 15.13 | 15.85 |
| 2 | 15.47 | 14.32 | 15.38 | 15.29 | 15.70 |
| 3 | 15.35 | 14.59 | 15.27 | 15.24 | 15.41 |
| 4 | 14.83 | 14.06 | 14.67 | 14.72 | 14.86 |
| 5 | 14.20 | 13.40 | 14.09 | 13.95 | 14.35 |
| 6 | 13.89 | 13.10 | 13.74 | 13.60 | 13.89 |
| Isotope Compositions (‰) | Water | Rapid Growth Stage | Stable Growth Stage | Transitional Growth Stage | Declining Growth Stage |
|---|---|---|---|---|---|
| H | Rainwater | −7.56 | −23.23 | −101.81 | −10.80 |
| Shallow soil water | −19.61 | −34.55 | −47.62 | −34.76 | |
| Deep soil water | −24.62 | −27.20 | −36.42 | −32.06 | |
| Groundwater | −30.19 | −31.98 | −32.51 | −34.60 | |
| Carex cinerascens | −11.73 | −28.91 | −61.91 | −24.73 | |
| O | Rainwater | −2.20 | −4.32 | −12.48 | −4.00 |
| Shallow soil water | −4.02 | −4.99 | −7.58 | −5.94 | |
| Deep soil water | −4.73 | −4.36 | −6.11 | −5.48 | |
| Groundwater | −5.14 | −5.17 | −5.63 | −5.51 | |
| Carex cinerascens | −2.76 | −4.72 | −8.91 | −5.10 |
| Stages | Sources | Average H (‰) | Average O (‰) | Proportions | Precipitations (mm) | Average Groundwater Depths of Sample Sites (m) |
|---|---|---|---|---|---|---|
| Rapid growth stage | Rainwater | −7.56 | −2.20 | 78.22∼80.14% | 312.0 | 0.13 |
| Shallow soil water | −19.61 | −4.02 | 0.00∼7.17% | |||
| Deep soil water | −24.62 | −4.73 | 0.00∼5.82% | |||
| Groundwater | −30.19 | −5.14 | 14.04∼14.61% | |||
| Carex cinerascens | −11.73 | −2.76 | ||||
| Stable growth stage | Rainwater | −23.23 | −4.32 | 11.1∼45.46% | 62.8 | 0.99 |
| Shallow soil water | −34.55 | −4.99 | 0.00∼35.32% | |||
| Deep soil water | −27.20 | −4.36 | 0.00∼43.91% | |||
| Groundwater | −31.98 | −5.17 | 19.22∼44.99% | |||
| Carex cinerascens | −28.91 | −4.72 | ||||
| Rapid growth stage | Rainwater | −101.81 | −12.48 | 26.38% | 167.2 | 0.27 |
| Shallow soil water | −47.62 | −7.58 | 73.62% | |||
| Deep soil water | −36.42 | −6.11 | 0.00% | |||
| Groundwater | −32.51 | −5.63 | 0.00% | |||
| Carex cinerascens | −61.91 | −8.91 | ||||
| Rapid growth stage | Rainwater | −10.80 | −4.00 | 40.56∼41.82% | 81.4 | 0.36 |
| Shallow soil water | −34.76 | −5.94 | 47.89∼51.50% | |||
| Deep soil water | −32.06 | −5.48 | 0.00∼11.55% | |||
| Groundwater | −34.60 | −5.51 | 0.00∼6.69% | |||
| Carex cinerascens | −24.73 | −5.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Z.; Zhang, X.; Pan, G.; Xiao, Y. High-Precision Calculation of the Proportions of Water with δ2H and δ18O, the Cumulative Effect of Evaporation in the Vertical Direction and Depleted δ2H and δ18O of the Shallow Soil Water Caused by Evaporation. Water 2022, 14, 2594. https://doi.org/10.3390/w14172594
Zeng Z, Zhang X, Pan G, Xiao Y. High-Precision Calculation of the Proportions of Water with δ2H and δ18O, the Cumulative Effect of Evaporation in the Vertical Direction and Depleted δ2H and δ18O of the Shallow Soil Water Caused by Evaporation. Water. 2022; 14(17):2594. https://doi.org/10.3390/w14172594
Chicago/Turabian StyleZeng, Zhenyu, Xiang Zhang, Guoyan Pan, and Yang Xiao. 2022. "High-Precision Calculation of the Proportions of Water with δ2H and δ18O, the Cumulative Effect of Evaporation in the Vertical Direction and Depleted δ2H and δ18O of the Shallow Soil Water Caused by Evaporation" Water 14, no. 17: 2594. https://doi.org/10.3390/w14172594






