Abstract
The drag and lift coefficients are important parameters that affect the particle motion in a viscous fluid. In the present study, the drag and lift coefficients of a spinning sphere in a water tank were studied experimentally using a high-speed camera. To this end, 22 cases were studied to cover a wide range of dimensionless angular speeds (0.149 < Rr < 3.471) and Reynolds numbers (610 < Re < 3472). Based on the present experimental data and the results obtained from the literature, expressions were developed to calculate the lift and drag coefficients. The performed analyses on lift coefficient show that there is a critical Reynolds number (Rec) at each dimensionless angular speed. When 0 < Re < Rec, the lift coefficient decreases with increasing the Reynolds number, while it is constant when Rec < Re < 3500. The constant lift coefficient corresponding to different spin speeds was defined as the limit value of the lift coefficient. It is found that when 1 < Rr < 12, the limit value of the lift coefficient is 0.37, while the limit value of the lift coefficient increases with increasing dimensionless angular speed at 0 < Rr < 1. It is found that the spin increases the drag coefficient of a spinning sphere only when 0 < Rr < 10. Moreover, the performed analyses show that the drag coefficient of a spinning sphere is less than that of a non-spinning sphere when 10 < Rr < 25. Furthermore, the lift-to-drag ratio of a spinning sphere is discussed in this article.
1. Introduction
Drag and lift forces are loads that affect particle motion. The lift force can often be significant and can even approach the magnitude of the drag force in some circumstances for surface spin velocities on the order of the translational particle velocity. Saffman [1] and Magnus [2] pointed out that the lift force is especially important for lateral migration in tubes and particle deposition in boundary layers. Yang and Leeming [3] and Barkla and Auchterlonie [4] called the lift force originating from rotating of particles the Magnus lift force. The drag and lift coefficients have been studied by researchers using theoretical analysis, experimental tests, and numerical simulations.
Theoretical studies provide exact results but are limited to special geometries and low Reynolds numbers. In this regard, Rubinow and Keller [5] derived an analytical solution for the spin-lift force in the Stokes regime through matched asymptotic expansions. It was found that the lift coefficient depends on the dimensionless angular speed at Rr << 1 and Re << 1. Dimensionless angular speed is defined as Rr = DΩ/ur, where D is the sphere diameter, Ω is the angular speed, and ur is the relative velocity between the particle and fluid. Moreover, the Reynolds number is defined as Re = urD/ν, where ν is the kinematic viscosity.
However, the results of theoretical studies are not reliable beyond the Stokes regime, and the lift coefficient should be obtained experimentally or numerically. In terms of experimental studies, Tusji et al. [6] analyzed the trajectories of an impinging and bouncing sphere on an inclined plate and obtained the Magnus lift force on a rotating sphere at 550 < Re < 1600 and 0 < Rr < 1.4. Oesterle and Dinh [7] used stroboscopic photography technology to study the lift force of a rotating sphere moving at a constant linear and angular velocity in a viscous fluid. A mathematical expression was proposed to estimate the lift coefficient in the range 10 < Re < 140 and 2 < Rr < 12. Macoll [8] performed experiments at 46,000 < Re < 110,000 and reported that the lift coefficient was negative for 0 < Rr < 0.4. Davis [9] performed experiments at a Reynolds number Re = 90,000. Tri et al. [10] and Taneda [11] carried out experiments and studied problems with very large Reynolds numbers.
Numerical simulations do not have most of the experimental challenges, such as measuring uncertainties. Ben Salem and Oesterle [12] performed a numerical investigation, applied different expressions for the lift and drag forces, and calculated the torque in a flow at 0 < Re < 20. Kurose and Komori [13] performed numerical simulations and studied the drag and lift forces acting on a spinning rigid sphere in a homogeneous linear shear flow at 1 ≤ Re ≤ 500. Niazmand and Renksizbulut [14] studied transient wake flow patterns and dynamic forces acting on a spinning spherical particle with non-uniform surface blowing for different Reynolds numbers Re up to 300 and different dimensionless angular speeds Rr up to 1. Kim [15] numerically investigated laminar flow passing a sphere rotating in the transverse direction at Re = 100, 250, and 300 and dimensionless angular speeds of 0 ≤ Rr ≤ 2.4. Poon and Ooi [16] simulated the flow passing a transversely rotating sphere at different Reynolds numbers in the range 500 ≤ Re ≤ 1000 using an unstructured finite volume collocated code. Citro et al. [17] performed direct numerical simulations and three-dimensional global stability analyses in the ranges 150 ≤ Re ≤ 300 and 0 ≤ Rr ≤ 2.4. Leal [18], Drew [19], Magnaudet and Eames [20], Tomiyama and Tamai [21], Loth [22], and Shi and Rzehak [23] analyzed experimental and numerical results under different conditions and drew meaningful conclusions.
The drag coefficient is another important parameter that affects the motion of particles. Based on theoretical analyses, Stokes [24] derived an expression to calculate the drag force. Swamee and Chandra [25] derived an empirical expression to calculate the drag coefficient. Song et al. [26] considered the effect of particle shape and settling orientation and developed a correlation between the drag coefficient and the Reynolds number for spherical and non-spherical particles. Amin and Umut [27] proposed a drag coefficient as a function of nominal particle diameter, gravitational acceleration, ambient fluid kinematic viscosity, and particle shape. Flemmer and Banks [28] and Kelessidis [29] proposed expressions to estimate the drag coefficient of non-spinning particles in a uniform fluid. Cheng [30] performed a review study and compared different expressions for the drag coefficient of spherical particles. Malhotra and Sharma [31] performed an experimental study on the drag coefficient of spherical particles in unbounded and confined surfactant-based shear-thinning viscoelastic fluids. Wang et al. [32] studied the drag coefficient of natural particles with highly irregular shapes. It is worth noting that the drag coefficient of spinning particles differs from that of non-spinning ones. For a particle that spins at a small Reynolds number with linearized inertia terms, Rubinow and Keller [5] showed that the spin does not affect the drag coefficient of a spinning sphere. Kurose and Komori [13], Niazmand and Renksizbulut [14], Kim and Choi [15], Dobson and Poon [33], and Giacobello and Balachandar [34] studied the drag coefficient of spinning particles at high Reynolds numbers.
Reviewing the literature indicates that there have been few experiments on the lift and drag coefficients, and only a few expressions have been proposed to calculate the lift-to-drag ratio of a spinning sphere in the range of 500 < Re < 3000. Therefore, further experiments are required to study the lift and drag coefficients in this range of Reynolds numbers. The main purpose of the present study was to evaluate the drag and lift coefficients of a spinning sphere with an angular speed in the range of 0.149 < Rr < 0.471 and a Reynolds number in the range of 610 < Re < 3472 in a water tank using a high-speed camera. It was intended to develop expressions to calculate the lift and drag coefficients. Furthermore, the lift-to-drag ratio of a spinning sphere was calculated.
2. Materials and Methods
2.1. Experimental Setup
The experiments were conducted in a 0.2 m long, 0.2 m wide, and 0.5 m high plexiglass water tank. The velocities and spin speeds of settled spheres were obtained by adjusting the release height of spheres on the orbit. The vertical distance between the top of the tank and the end of the orbit was 50 mm. A high-speed camera system was used to analyze the motion of spinning spheres. The camera system mainly consists of a high-speed camera (EoSens®3CXP, Mikrotron, Unterschleißheim, Germany), a memorizer (AQ8-CXP6D, Mikrotron, Unterschleißheim, Germany), and image processing software (Stream Pix, Norpix, Montréal, Canada). The image resolution was set to 1690 × 1710 pixels. The recording rate of the camera was set to 400 frames per second (FPS) to ensure clear images. The images were analyzed in the image processing software. Figure 1 shows the schematic view of the experimental setup.
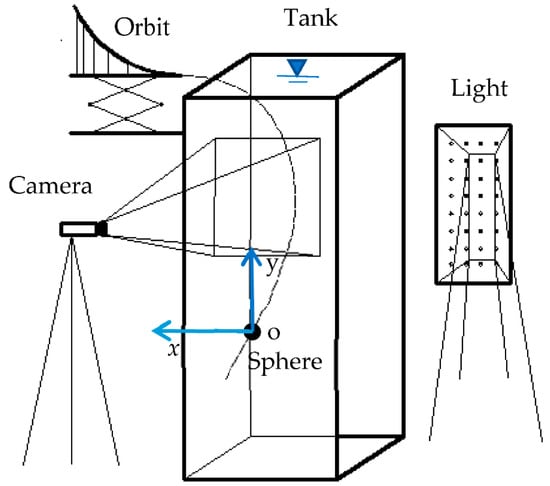
Figure 1.
Schematic view of experimental setup.
2.2. Experimental Methods
2.2.1. Measuring Procedure
The motion of spinning spheres was recorded from the tank side. The camera focused on the vertical plane that was located at the tank centerline. Then, a sufficient number of images were selected using image processing software, and the selected images were further processed by CAD software to calculate the velocity and spinning speed of spheres. To better observe the angular speed of spheres, the surfaces of the spheres were marked. Then, the connection line between the marked dots and the center of gravity of particles was obtained. The angular speed of spheres was calculated by measuring the angle change between the connection line and the gravity over time.
The diameter of spheres D varied from 2.5 mm to 8.0 mm. The densities of the spheres and the fluid were 2390 kg/m3 and 1000 kg/m3, respectively. The velocity of spinning spheres us was in the range of 0.244 m/s to 0.434 m/s. The velocity of the fluid u = 0. The relative velocity between the particle and fluid was in the range of 0.244 m/s to 0.434 m/s. The range of angular speed Ω was from 13.956 rad/s to 223.29 rad/s. The range of dimensionless angular speed Rr was from 0.149 to 3.471. The range of the Reynolds number Re was from 610 to 3472. Table 1 presents the experimental conditions.

Table 1.
Experimental conditions.
2.2.2. Data Processing Procedure
In order to describe the motion of the spinning sphere, the coordinate system was defined, as shown in Figure 1. The position of the onset of the sphere moving at a constant velocity was taken as the origin of the coordinate system. The positive direction of the x-axis is the same as the direction of the particle velocity component on the horizontal plane. Moreover, the positive direction of the y-axis is along the opposite direction of gravity. Figure 2 presents the trajectory of a 6 mm sphere as an example.
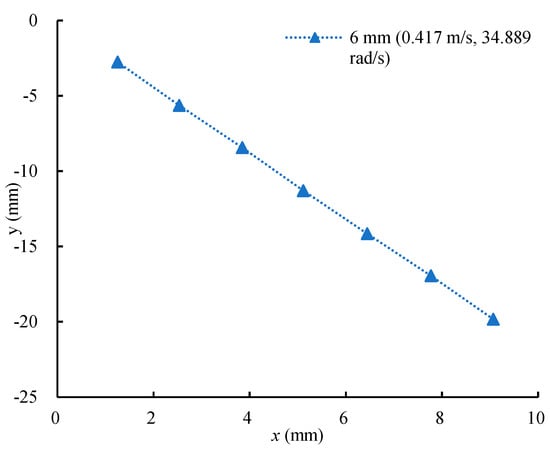
Figure 2.
The trajectory of a 6 mm sphere.
The trajectory of the sphere can be approximated to 18.77 mm. The angle between the velocity vector of the sphere and the gravity vector can be obtained by fitting the data of the trajectory of spheres corresponding to a constant velocity. For the sphere presented in Figure 2, this angle and the corresponding angular speed are β = 24.552° and Ω = 34.889 rad/s, respectively. Since the fluctuation of sphere velocity is less than 1%, it can be considered uniform. Figure 3 shows that the velocity of a spinning sphere us is 0.417 m/s.
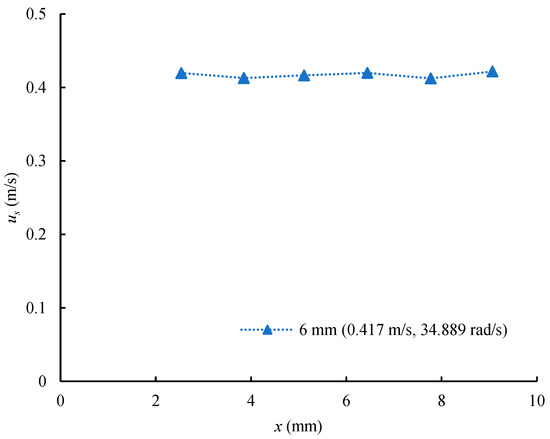
Figure 3.
The velocity of a 6 mm sphere.
The motion of spinning spheres is mainly affected by submerged weight, drag force, and lift force, as shown in Figure 4. Since the fluid is stationary, the velocity of the fluid u= 0. Therefore, the relative velocity between the particle and fluid ur is equal to the velocity of the spinning sphere us. The drag force is in the opposite direction of the sphere’s motion.
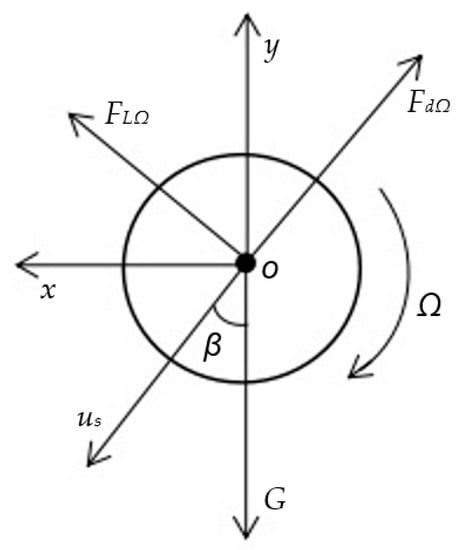
Figure 4.
Schematic diagram of the coordinate system and forces acting on a spinning sphere.
The submerged weight can be calculated using the following expression:
where G is submerged weight, g is gravitational acceleration, and ρs is the density of particles, ρ is the density of fluid. Moreover, the lift force of a spinning sphere can be obtained from the following expression:
where FLΩ is the lift force of a spinning sphere, and CLΩ is the lift coefficient of a spinning sphere. The drag force of a spinning sphere can be mathematically expressed in the form below:
where FdΩ is the drag force of a spinning sphere, and CdΩ is the drag coefficient of a spinning sphere.
According to Newton’s second law of motion-force and acceleration, when a particle moves at a constant velocity along a straight line, the acceleration of the particle is zero. Accordingly, the equation of motion of a spinning sphere that moves perpendicular to the velocity of the spinning sphere can be expressed as follows:
Meanwhile, the equation of motion of the spinning sphere can be expressed as follows:
By rearranging Equation (4), the lift coefficient can be expressed in the form below:
By rearranging Equation (5), the drag coefficient is expressed as follows:
Substituting the measured values of u, D, us, and β into Equations (6) and (7), the lift and drag coefficients of a spinning sphere can be calculated. It is note that u = 0.
3. Results and Discussion
3.1. Lift Coefficient
The experimental results are presented in Table 2, indicating that the lift coefficients of a spinning sphere vary from 0.098 to 0.449.

Table 2.
Experimental results.
The lift coefficients of the spinning sphere have been studied by other researchers. In this regard, Oesterle and Dinh [7] used stroboscopic photography technology to study the lift force of a spinning sphere moving in a viscous fluid. Kurose and Komori [13] performed three-dimensional numerical simulations and studied the lift force acting on a spinning rigid sphere in a homogeneous linear shear flow. Niazmand and Remksizbulut [14], Dobson and Poon [33], and Giacobello and Balachandar [34] investigated the lift coefficient through numerical simulation. The experimental and simulated results of the previous studies are summarized in Figure 5. They are represented by different symbols in Figure 5.
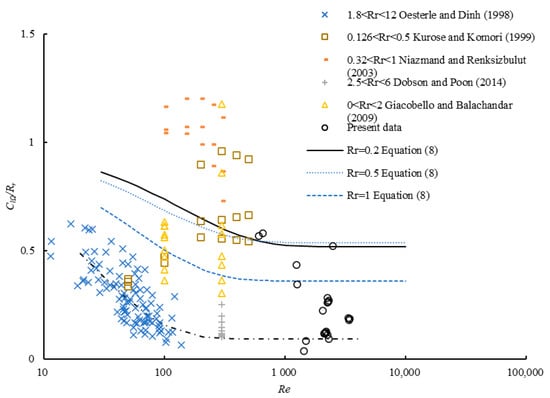
Figure 5.
The correlation between the rate of the lift coefficient to dimensionless angular speed and the Reynolds number [7,13,14,33,34].
The correlation between the ratio of the lift coefficient to the dimensionless angular speed and the Reynolds number indicates that the ratio is a variable quantity that depends on the Reynolds number.
By fitting the experimental data in Figure 5, the following expression can be established for the lift coefficient of particles in a flow with a Reynolds number and dimensionless angular speed in the ranges 0 < Re < 3500 and 0 < Rr < 12:
The calculated results corresponding to different angular speeds are presented in Figure 5. Moreover, the correlation between the present experimental data and the calculated results using Equation (8) is shown in Figure 6. It is observed that the calculated values are consistent with the present measured ones.
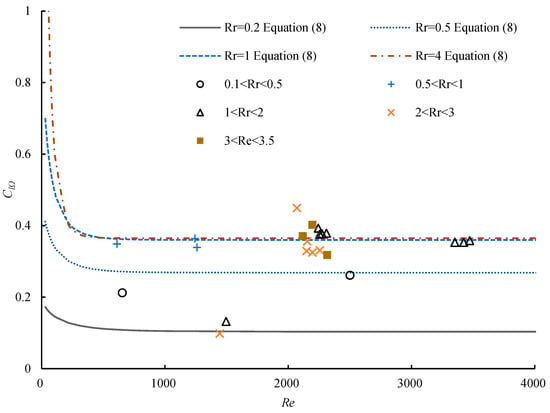
Figure 6.
Correlation between the lift coefficient and the Reynolds number.
Figure 6 shows that there is a critical Reynolds number (Rec) at each dimensionless angular speed. Until the Reynolds number is less than the critical value (i.e., 0 < Re < Rec), the lift coefficient decreases with the increase in the Reynolds number, while it is approximately constant when Rec < Re < 3500. The constant lift coefficient corresponding to different spin speeds is defined as the limit value of the lift coefficient, which is 0.37 when 1 < Rr < 12. When 0 < Rr < 1, the limit value increases with the increase in the dimensionless angular speed. Figure 7 shows the correlation among the calculated values using Equation (8), the previously measured data, and previous simulation results. It is observed that the calculated values are consistent with the previous measured data and simulation results.
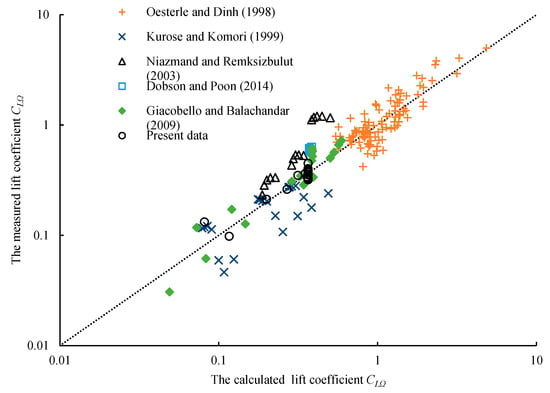
Figure 7.
Distribution of the measured lift coefficient against the calculated values [7,13,14,33,34].
Loth [22], Shi and Rzehak [23] proposed expressions to calculate the lift coefficient in flows with a Reynolds number 0 < Re < 1000. It should be noted that the proposed expression in the present study (i.e., Equation (8)) can be applied to calculate the lift coefficient in flows with a Reynolds number up to 3500. In this section, the root mean square relative error (RMSRE) is applied as an appropriate index to evaluate the accuracy of different expressions. The RMSRE index can be mathematically expressed in the form below:
where CLΩc and CLΩm are the calculated and measured lift coefficients, respectively.
The RMSRE indices reported by present paper, Loth [22] and Shi and Rzehak [23] are 0.069, 0.073, and 0.121, respectively. When the Reynolds number is in the range of 500 < Re < 3500, the RMSRE indices reported by present paper, Loth [22] and Shi and Rzehak [23] are 0.014, 0.122, and 0.116, respectively. Meanwhile, when the Reynolds number 0 < Re < 500, these indices are 0.081, 0.063, and 0.122, respectively. It is concluded that the proposed expression is reliable and can be applied to estimate the lift coefficient in high-Reynolds flows.
3.2. Drag Coefficient
3.2.1. Drag Coefficient of a Non-Spinning Sphere
The total drag force of a non-spinning sphere settling in the fluid can be decomposed into pressure and viscosity components. The correlation among the total drag force, viscosity-related drag force, and pressure-related drag force can be expressed as follows:
where Fd is the total drag force of a non-spinning sphere, Fdν is the viscosity-related drag force of a non-spinning sphere, Fdp is the pressure-related drag force of a non-spinning sphere, Cd is the total drag coefficient of a non-spinning sphere.
The pressure-related drag force can be calculated through the following expression:
where Cdp is the pressure-related drag coefficient of a non-spinning sphere. Similar to the pressure-related drag force, the viscosity-related drag force can be expressed in the form below:
where Cdv is the viscosity-related drag coefficient of a non-spinning sphere,
Substituting Equations (12) and (11) into Equation (10) yields the following expression:
The measured total drag coefficient was summarized by Kelessidis [29] and Cheng [30]. Substituting the calculated Cdv and measured Cd into Equation (14), the coefficient Cdp can be obtained. The correlation between the pressure-related drag coefficient and the Reynolds number can be expressed as follows:
Substituting Equations (13) and (15) into Equation (14), the total drag coefficient in the ranges 0 < Re < 100,000 can be expressed in the form below:
Figure 8 shows the variation in the total drag coefficient against the Reynolds number, indicating that the calculated results are consistent with the experimental data. It is observed that as the Reynolds number increases, the total drag coefficient, viscosity-related drag coefficient, and pressure-related drag coefficient decrease. The total drag coefficient is approximately equal to the viscosity-related drag coefficient at Re < 1. The viscosity-related drag coefficient can be negligible, and the total drag coefficient is approximately equal to the pressure-related drag coefficient for Re > 500.
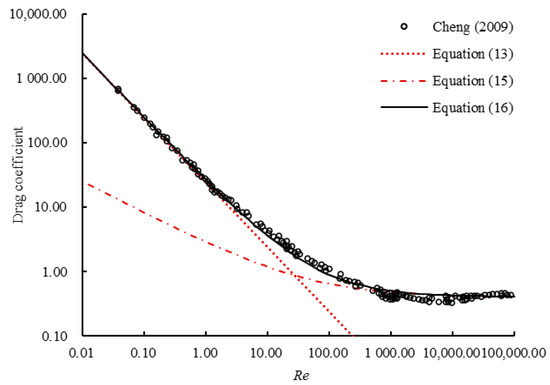
Figure 8.
Variation in the drag coefficient against the Reynolds number [30].
3.2.2. Drag Coefficient of A Spinning Sphere
The drag coefficient of the spinning sphere has been studied by other researchers. Barkla and Auchterlonie [4] measured the drag coefficient of the spinning sphere by suspending it as a pendulum. Niazmand and Reksizbulut [14], Kim [15], Dobson and Poon [33], and Giacobello and Balachandar [34] performed numerical investigations and studied the effect of spin on the drag coefficient. The ratio of the drag coefficient of a spinning sphere to the total drag coefficient of a non-spinning sphere CdΩ/Cd is equal to the ratio of the measured or simulated drag coefficient of a spinning sphere to the calculated total drag coefficient of a non-spinning sphere using Equation (16). The previous results are shown in Figure 9.
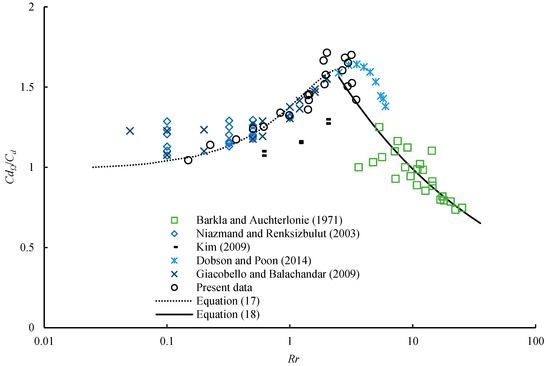
Figure 9.
Distribution of the drag coefficient against the dimensionless angular velocity [4,14,15,33,34].
Compared with the total drag coefficient of a non-spinning sphere, a spinning sphere has higher drag coefficient at 1 < Rr < 10. In this region, the ratio CdΩ/Cd varies from 1 to 1.6. However, the drag coefficient of a spinning sphere is less than the total drag coefficient of a non-spinning sphere for 10 < Rr < 25. When 0 < Rr < 2.5, the ratio CdΩ/Cd increases as Rr increases. Beyond this range, the ratio CdΩ/Cd decreases as Rr increases. To interpret this phenomenon, two empirical correlations were developed to simulate the effect of particle’s spin on the drag coefficient based on the present experimental data and the results of Barkla and Auchterlonie [4]. When 0 < Rr < 2.5 and 0 < Re < 3500, the correlation can be expressed as follows:
When 2.5 < Rr < 25 and 0 < Re < 3500, the correlation is given by
Figure 9 compares the calculated results with the previous results. It is observed that the present results are consistent with the previous ones for 0.5 < Rr < 25. The previous results show that the spin significantly affects the drag coefficient of a spinning sphere when 0 < Rr < 0.5. It is concluded that the developed equations can be successfully applied to accurately predict the small effects of spin on the drag coefficient of a spinning sphere at low Reynolds numbers.
3.3. Lift-to-Drag Ratio
The lift-to-drag ratio of a spinning sphere (kld) can be expressed in the form below:
Substituting Equations (8), (17) and (18) into Equation (19) yields the calculated lift-to-drag ratio of a spinning sphere. The previous lift-to-drag ratio of a spinning sphere can be obtained by substituting the simulated lift and drag coefficients from the previous literature into Equation (19). The previous results are compared with the calculated results in Figure 10.
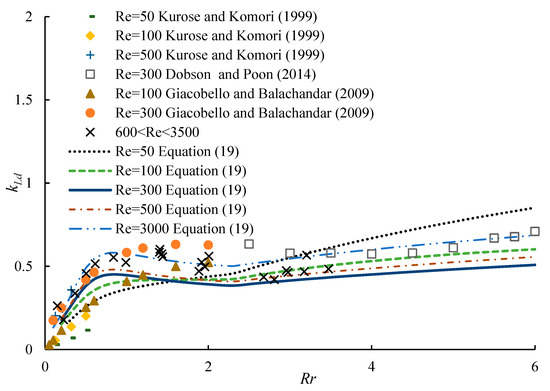
Figure 10.
The distribution of the lift-to-drag ratio against the Reynolds number [13,33,34].
It is observed that when 0 < Re < 100, kld increases with increasing dimensionless angular speed at a certain Reynolds number. At 100 < Re < 3500 and 0 < Rr < 0.85, kLd increases with increasing dimensionless angular speed at a certain Reynolds number and increases with increasing Reynolds number at a certain angular speed. At 100 < Re < 3500 and 0.85 < Rr < 6, kld increases with increasing Reynolds number at a certain angular speed and can be approximated as a constant value with increasing dimensionless angular speed at a certain Reynolds number. The present equations were preliminarily verified by the previous results.
4. Conclusions
In the present study, the motion of a spinning sphere in a viscous fluid was measured using a high-speed camera. The drag and lift coefficients of a spinning sphere were evaluated through experiments in a water tank using a high-speed camera. Measurements were performed in the ranges of dimensionless angular speed 0.149 < Rr < 3.471 and Reynolds number 610 < Re < 3472. The lift and drag coefficients were obtained by analyzing the motions of the spinning sphere.
- (1)
- The obtained experimental data reveal that the lift coefficient is related to the Reynolds number and dimensional angular speed. There is a critical Reynolds number (Rec) at each dimensionless angular speed. When 0 < Re < Rec, the lift coefficient decreases as the Reynolds number increases, while it is constant when Rec< Re < 3500. The constant lift coefficient corresponding to different spin speeds was defined as the limit value of the lift coefficient. This coefficient is 0.37 when 1 < Rr < 12, while the limit value of the lift coefficient increases with the increase in dimensionless angular speed for 0 < Rr < 1.
- (2)
- Compared with the total drag coefficient of a non-spinning sphere at a certain dimensionless angular speed, the drag coefficient of a spinning sphere is higher when 1 < Rr < 10. When 1 < Rr < 10, the ratio of the drag coefficient of a spinning sphere to the total drag coefficient of a non-spinning sphere CdΩ/Cd is between 1 and 1.6. However, the drag coefficient of a spinning sphere is less than the total drag coefficient of a non-spinning sphere when 10 < Rr < 25. The ratio CdΩ/Cd increases with increasing dimensionless angular speed in the range of 0 < Rr < 2.5, while the ratio CdΩ/Cd decreases with an increase in Rr beyond this range. To interpret this phenomenon, two empirical correlations were developed to describe the effect of particle spin on the drag coefficient based on the experimental data and the results from the literature.
- (3)
- When 0 < Re < 100, the lift-to-drag ratio of a spinning sphere kld increases with increasing dimensionless angular speed at a certain Reynolds number. At 100 < Re < 3500 and 0 < Rr < 0.85, kLd increases with increasing dimensionless angular speed at a certain Reynolds number and increases with increasing Reynolds number at a certain angular speed. At 100 < Re < 3500 and 0.85 < Rr < 6, kld increases with increasing Reynolds number at a certain angular speed and can be approximated as a constant value with increasing dimensionless angular speed at a certain Reynolds number.
Author Contributions
Writing—Original Draft Preparation, S.Z.; Writing—Review and Editing, X.X.; Validation, G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National Natural Science Foundation of China, grant numbers 51879227 and 51279170.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data are provided as tables and figures.
Conflicts of Interest
There is no conflict of interest in this study.
References
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Magnus, G. liber die Abweichung der Geschlosse, und eine auffallende Erscheinung bei rotierenden Korpern. Poggendorfs Ann. Phys. Und Chem. 1853, 88, 1. [Google Scholar]
- Young, J.; Leeming, A. A theory of particle deposition in turbulent pipe flow. J. Fluid Mech. 1997, 340, 129–159. [Google Scholar] [CrossRef]
- Barkla, H.M.; Auchterlonie, L.J. The Magnus or Robins effect on rotating spheres. J. Fluid Mech. 1971, 47, 437–447. [Google Scholar] [CrossRef]
- Rubinow, S.I.; Keller, J.B. The transverse force on a spinning sphere moving in a viscous fluid. J. Fluid Mech. 1961, 11, 447–459. [Google Scholar] [CrossRef]
- Tsuji, Y.; Morikawa, Y.; Mizuno, O. Experimental Measurement of the Magnus Force on a Rotating Sphere at Low Reynolds Numbers. J. Fluids Eng. 1985, 107, 484–488. [Google Scholar] [CrossRef]
- Oesterlé, B.; Dinh, T.B. Experiments on the lift of a spinning sphere in a range of intermediate Reynolds numbers. Exp. Fluids 1998, 25, 16–22. [Google Scholar] [CrossRef]
- Macoll, J.H. Aerodynamics of a Spinning Sphere. J. R. Aeronaut. Soc. 1928, 32, 777–798. [Google Scholar] [CrossRef]
- Davies, J.M. The Aerodynamic of Golf Balls. J. Appl. Phys. 1949, 20, 821–828. [Google Scholar] [CrossRef]
- Tri, B.D.; Oestrele, B.; Deneu, F. Premiers résultats sur la portance d’une sphère en rotation aux nombres de Reynolds intermèdiaires. Comptes Rendus L’académie Des Sciences. Série 2. Mécanique Phys. Chim. Sci. L’univers Sci. Terre 1990, 311, 27–31. [Google Scholar]
- Taneda, S. Negative Magnus Effect. Rep. Res. Inst. Appl. Phys. Kyushu Univ. 1957, 20, 123–128. [Google Scholar]
- Ben Salem, M.; Oesterle, B. A Shear Flow Around a Spinning Sphere: Numerical Study at Moderate Reynolds Numbers. Int. J. Multiph. Flow 1998, 24, 563–585. [Google Scholar] [CrossRef]
- Kurose, R.; Komori, S. Drag and lift forces on a rotating sphere in a linear shear flow. J. Fluid Mech. 1999, 384, 183–206. [Google Scholar] [CrossRef]
- Niazmand, H.; Renksizbulut, M. Surface effects on transient three-dimensional flows around rotating spheres at moderate Reynolds numbers. Comput. Fluids 2003, 32, 1405–1433. [Google Scholar] [CrossRef]
- Kim, D. Laminar flow past a sphere rotating in the transverse direction. J. Mech. Sci. Technol. 2009, 23, 578–589. [Google Scholar] [CrossRef]
- Poon, E.K.W.; Ooi, A.S.H.; Giacobello, M.; Iaccarino, G.; Chung, D. Flow past a transversely rotating sphere at Reynolds numbers above the laminar regime. J. Fluid Mech. 2014, 759, 751–781. [Google Scholar] [CrossRef]
- Citro, V.; Tchoufag, J.; Fabre, D.; Giannetti, F.; Luchini, P. Linear stability and weakly nonlinear analysis of the flow past rotating spheres. J. Fluid Mech. 2016, 807, 62–86. [Google Scholar] [CrossRef]
- Leal, L.G. Particle Motions in a Viscous Fluid. Annu. Rev. Fluid Mech. 1980, 12, 435–476. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical Modeling of Two-Phase Flow. Annu. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Magnaudet, J.; Eames, I. The Motion of High-Reynolds-Number Bubbles in Inhomogeneous Flows. Annu. Rev. Fluid Mech. 2000, 32, 659–708. [Google Scholar] [CrossRef]
- Tomiyama, A.; Tamai, H.; Zun, I.; Hosokawa, S. Transverse Migration of Single Bubbles in Simple Shear Layers. Chem. Eng. Sci. 2002, 57, 1849–1858. [Google Scholar] [CrossRef]
- Loth, E. Lift of a Spherical Particle Subject to Vorticity and/or Spin. AIAA J. 2008, 46, 801–809. [Google Scholar] [CrossRef]
- Shi, P.; Rzehak, R. Lift forces on solid spherical particles in unbounded flows. Chem. Eng. Sci. 2019, 208, 115145. [Google Scholar] [CrossRef]
- Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Philo. Soc. 1851, 9, 8–106. [Google Scholar]
- Swamee, P.K.; Chandra, S.P. Drag Coefficient and Fall Velocity of nonspherical particles. J. Hydraul. Eng. 1991, 117, 660–667. [Google Scholar] [CrossRef]
- Song, X.; Xu, Z.; Li, G.; Pang, Z.; Zhu, Z. A new model for predicting drag coefficient and settling velocity of spherical and non-spherical particle in Newtonian fluid. Powder Technol. 2017, 321, 242–250. [Google Scholar] [CrossRef]
- Amin, R.; Umut, T. The drag coefficient and settling velocity of natural sediment particles. Comput. Part. Mech. 2019, 6, 427–437. [Google Scholar]
- Flemmer, R.L.C. Banks CL. On the drag coefficient of a sphere. Powder Technol. 1986, 48, 217–221. [Google Scholar] [CrossRef]
- Kelessidis, V.C. An explicit equation for the terminal velocity of solid spheres falling in pseudoplastic liquids. Chem. Eng. Sci. 2004, 59, 4437–4447. [Google Scholar] [CrossRef]
- Cheng, N.S. Comparison of formulas for drag coefficient and settling velocity of spherical particles. Powder Technol. 2009, 189, 395–398. [Google Scholar] [CrossRef]
- Malhotra, S.; Sharma, M.M. Settling of spherical particles in unbounded and confined surfactant-based shear thinning viscoelastic fluids: An experimental study. Chem. Eng. Sci. 2012, 84, 646–655. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, L.; Wu, Y.; Yang, Q. New simple correlation formula for the drag coefficient of calcareous sand particles of highly irregular shape. Powder Technol. 2017, 326, 379–392. [Google Scholar] [CrossRef]
- Dobson, J.; Ooi, A.; Poon, E. The flow structures of a transversely rotating sphere at high rotation rates. Comput. Fluids 2014, 102, 170–181. [Google Scholar] [CrossRef]
- Giacobello, M.; Ooi, A.; Balachandar, S. Wake structure of a transversely rotating sphere at moderate Reynolds numbers. J. Fluid Mech. 2009, 621, 103–130. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).