1. Introduction
Uncontrolled air in pipelines, whether entrapped or in motion, can be a source of inefficiency, undesired vibrations, noisy flow, accelerated metal corrosion, measurement errors, or even magnified transient pressures [
1,
2]. Yet air can also, in certain cases, dampen the magnitude of transient oscillations [
3], while the release of air from solution due to a decrease in pressure levels can drastically reduce the celerity of pressure waves [
4]. Importantly, the presence of unmanaged entrapped air can hinder water conveyance, degrade economic performance, and increase the line’s overall vulnerability to misbehaviours [
5]. A well-known and widely-used strategy for coping with air–related issues in pressurized pipelines is the use of air exchange valves [
6].
The main types of air exchange valves are air-release valves (ARVs), which have relatively small discharge orifices and expel air that accumulates during normal operation; air/vacuum valves (AVVs), which have relatively large discharge orifices and thus can rapidly expel or admit air during filling, draining or water hammer events; combination air valves (CAVs), which perform in a single device the roles of ARVs and AVVs; and vacuum breakers (VBs), which admit air in relatively large quantities in an effort to avoid severe and prolonged internal sub-atmospheric pressures or macro-cavitation [
7]. Air exchange valves are typically installed at pipeline summits or at locations where air exchanges are either expected or deemed important for reasons of system safety or hydraulic performance [
8].
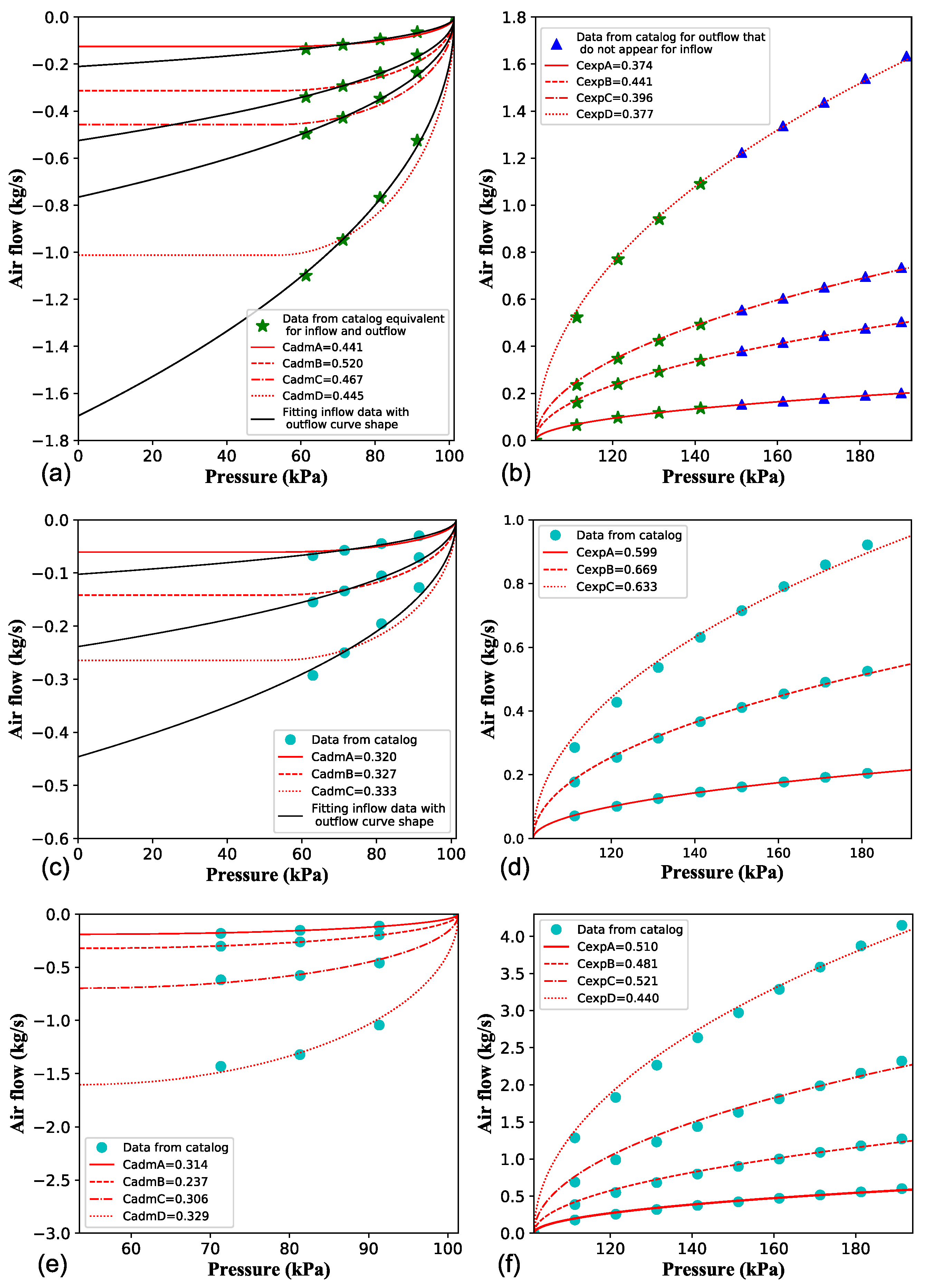
Despite the importance of air valves for the operational health of pipelines, the characteristic curves (CCs) of air valves found in a variety of manufacturers’ product catalogs (usually differential pressure versus air flow rate curves) often poorly represent expected air valve behaviour [
9,
10,
11]. Because of this, efforts have been made to facilitate the acquisition of CCs of air valves [
12,
13,
14,
15]. Although ideally air valve behaviour should be determined through experimental tests, conducting such tests in the field is often precluded due to time constraints or absence of appropriate testing infrastructure. The experimental characterization of large air valves can be especially challenging given the possibly prohibitively robust requirements for the large-capacity testing benches [
10,
14]. Nevertheless, using inaccurate CCs of air valves while undertaking system design or retrofitting could lead to significant errors in air valve selection and/or significant system misbehaviour. The current paper analyzes the overall consistency of CCs of air valves found in various product catalogs and considers about the possibility of deleterious consequences of using erroneous CCs as input data in numerical simulations of typical unsteady flow scenarios in water pipelines.
3. Challenges Associated with Air Valve Characterization
The discharge coefficients of an air valve,
and
, are determined by fitting an air flow model to air valve characterization data. The experimental characterization of an air valve should be done in two steps, namely, separately for admission and expulsion tests. The inflow discharge coefficient might significantly differ from the outflow coefficient [
10]. This is due to the asymmetric dependence between discharge coefficient and air flow direction inside the air valve [
15]. Preferably, characterization tests should collect paired values of internal absolute pressure
versus air mass flow rate
for a sufficiently extended range of internal absolute pressures. Ideally, for each
and
pair, the internal temperature should be also collected. Temperature is commonly assumed to be constant but, in operational use, temperature might vary significantly as a consequence of abrupt pressure changes inducing heating and cooling or compressing and expanding air volumes. Being aware of the magnitude of
in the characterization tests can permit a more informed interpretation of experimental results [
18].
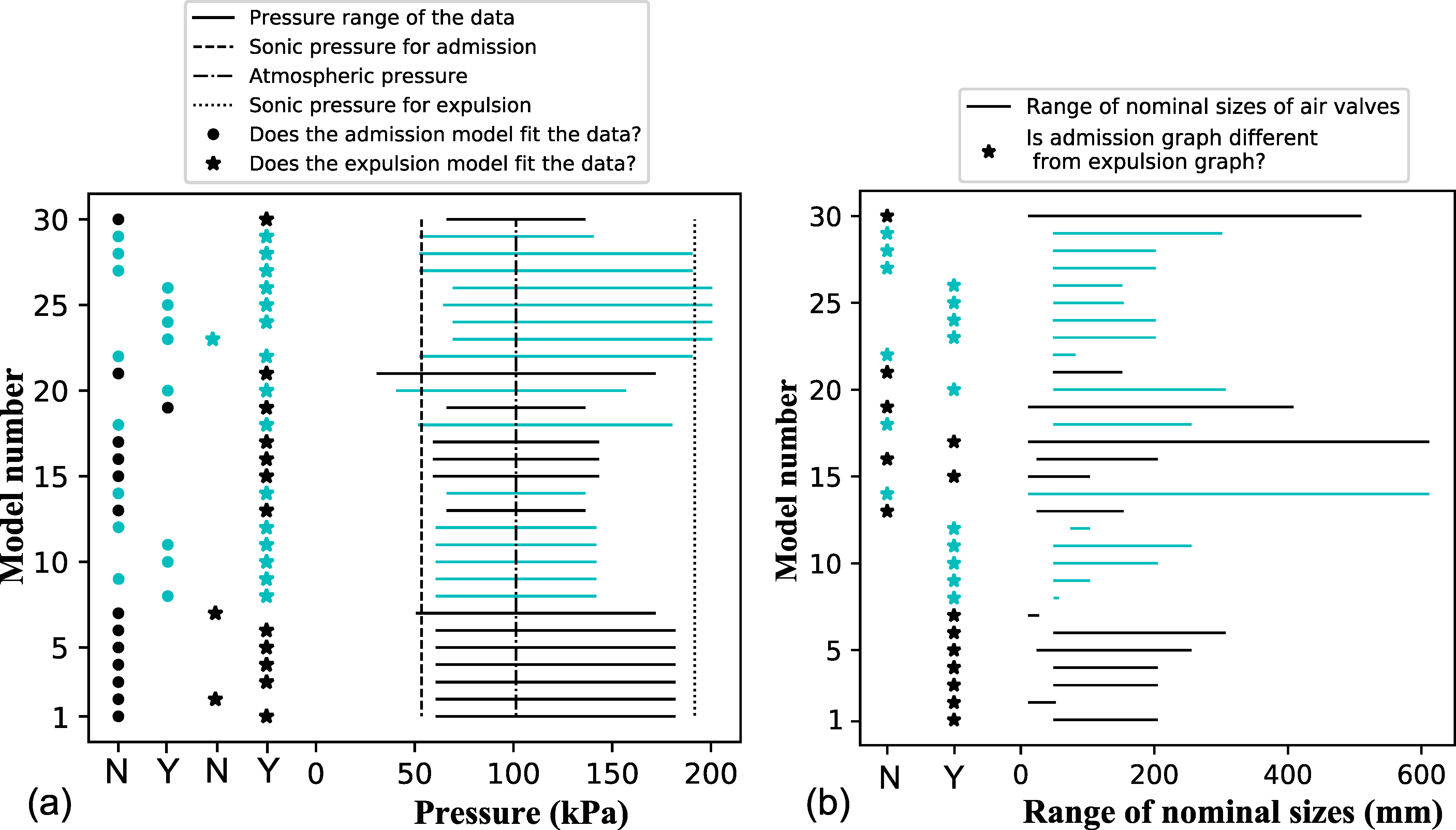
A question that may arise when planning characterization tests of air valves is how broad or encompassing the
range should be. In commercial catalogs, it is usual the presentation of data for only restricted pressure ranges [
11]. However, catalogs often claim that modern devices with anti-slam designs perform well in relation to resisting premature valve closure. Also, narrow ranges of
in characterization tests should be avoided since this hinders the viability of data extrapolation and good curve fitting. Ideally, air valves should be characterized for the whole subsonic pressure range. Actually, for expulsion, air valves should be characterized until their premature closure (“dynamic closure”) [
14]. Indeed, most AVVs close prematurely but manufacturers do not indicate this issue in catalog information. Dynamic closure is a danger during air expulsion that is caused by high exhaust velocities that can generate a sufficient drag force to slam closed the air valve float before all air is expelled [
14]. Indeed, some air valves have been found to close prematurely for relatively low differential pressures [
14].
For expulsion tests, the internal fluid pressure needs to rise above the local atmospheric pressure in order for the air valve to expel air. For admission, the differential pressure across the device should be imposed via internal depressurization. Thus, not only the differential pressure across the device matters in characterization tests but also how such differential pressure is established. Thus, to slightly belabor this point, a given differential pressure established for air valve characterization should always occur due to a variation in pressure inside the air valve. Unfortunately, the EN 1074-4 standard, however, suggests the possibility of characterizing the inflow capacity of an air valve through the provision of positive pressure values at the air valve’s outlet during tests—“positive pressure around or into the valve” [
19]. To generate over- or under-atmospheric pressure values inside air valves, experimenters typically use air compressors or fans (blowers) [
10]. Pressurized air vessels are also a possible source of air flow [
20]. Ideally, the pressure differential should be maintained long enough to establish steady flow through the air valve [
21]. The use of a pressurized air vessel in a characterization can create the complication of a non-linear (or unsteady) air pressure provision. Such air source option also has the limitation of only providing air for expulsion. The necessary robustness of air blowers or pressurized air vessels, however, might become impractical in the characterization of large air valves for near sonic flows. Since such test systems are expensive, only a few laboratories worldwide are sufficiently equipped to test and characterize relatively large air valves.
To measure air flow rates through an air valve, a suitable strategy is to use an orifice plate at the main pipe right before the air valve [
22]. Such disposition is viable for a testing bench, but not so much for a real system since the orifice plate would restrict the water flow. This is one reason why monitoring air valves
in loco is challenging. Installing an orifice plate downstream of the air valve for air flow measurement, for example, might be a possibility [
23]. However, the installation of a throttling device at an air valve’s outlet will decrease its effective outlet orifice area, compromising air valve capacity [
15]. Thermal air flow meters can also be used to measure air flow rates through air valves [
10,
24].
In order to avoid measurement errors, the air flow through the measuring device should be reasonably well behaved—this usually implies minimum lengths of straight pipe segments upstream and downstream of the measuring device. The measuring device should be placed upstream of the air valve for expulsion tests, and, especially in the case of deprimogenic flow meters, in a pipe segment with diameter larger than the diameter of the air valve. This requirement arises because the equations for deprimogenic measuring devices usually assume flows close to the incompressible regimen, which is ensured for only relatively low differential pressure values across the orifice plate—the air mass flow equation indicated by the ISO 5167-2 standard includes an expansion factor parameter, which, in its part, is obtained through a formulation restricted by
(where
is the pressure upstream of the orifice and
is the pressure downstream of it) [
25]. If this restriction is followed, however, the outflow of air can be considered incompressible while passing through the measuring device while it might possibly be compressible at the location of the air valve [
22]. For admission, the air valve should be tested with the same general testing bench configuration as described for expulsion. However, the air compressor should induce air flow in the opposite direction. Air pressure inside the measuring pipe apparatus should decrease bellow atmospheric for inflow tests. Such tests should be done ideally at least until there is sonic air flow velocity. The research conducted by Iglesias et al. (2014) [
10] and García et al. (2018) [
14] successfully measured the inflow regimen with the clear occurrence of the sonic limit.
For numerical simulations performed in the design phase of pipeline systems, the CCs provided in catalogs need to be transformed into raw data. Thus, for the sake of more accurate and practical data presentation, the following is recommended to be included in commercial catalogs for each air valve type and size: and according to the isentropic air mass flow model (obtained considering the actual value of atmospheric pressure in the location where tests were conducted); for inflow and outflow, the air mass flow values for which the regimens go from subsonic to sonic, given in units; in the case of circular outlet orifices, precise sizes of their diameters for admission and expulsion; in the case of other outlet shapes, precise areas of the outlet orifices for admission and expulsion; internal absolute pressure for which kinetic closure is expected for expulsion.
A common issue when describing flows of compressible fluids like air is the often confusing or conflicting definitions of standard or normal conditions. The definitions of such terms can vary between fields of application or locations. The main issue usually comes from the value of standard temperature to be used, while the value of standard atmospheric pressure is generally set as 101.325 kPa—i.e., the standard sea level pressure. Because of this, it is recommended that flows be defined either in terms of mass flow or in terms of volumetric flow for explicitly stated pressure and temperature values. Nevertheless, describing flow volumetrically might be more intuitive for designers. Loosely defined values for standard or normal conditions can cause disagreements, for example, between the reported values at the upstream (producer) and downstream (consumer) ends of gas pipelines. For air valve applications, unspecified conditions for characterization tests or unclear definitions regarding the units of data presented in graphs can unnecessarily bring interpretation errors regarding the expected behaviour of air valves.
The practitioner should pay attention to the reliability of the source of CCs of air valves. For one thing, the CCs for a given air valve model may be found from multiple sources online, from the manufacturer itself, or from a distribution company, for example. CCs from different information sources might sometimes be in conflict. Also, manufacturers may change or adapt CCs over time due to a change in valve design or improvements in the characterization tests. And, in the background, there is the inevitable complications that no matter how the valves were tested, the field application may create conditions different from those tests, or the valve may age or evolve as a function of either prolonged use or long-term neglect.
4. Relevance of Air Valve Capacity to Transient System Behaviour
4.1. Wave Processes Following a Pump Trip
If a pump trips, so that power to its motor is lost, inflow to the pipeline is rapidly curtailed and a sequence of sometimes-dramatic transient events can ensue. This section considers this scenario in a water rising pipeline with distinct high point with air valve, but in a line without protective upstream system such as a hydropneumatic tank. The transient phenomenon proceeds in four successive phases: (i) depressurization, which leads to (ii) air admission, (iii) re-pressurization with associated air expulsion, which leads to (iv) the creation of a secondary pressure wave.
Depressurization occurs progressively starting immediately after the pump trip and is characterized by a reduced-pressure wave that moves from the upstream pump towards (in this case) a downstream terminal reservoir. When such a sufficiently large reduced pressure wave reaches the air valve, sub-atmospheric pressure is established at the high point, and the air valve starts to admit air, thus initiating the admission phase. After the air valve opens, the discharge in the downstream branch of the pipeline is progressively arrested every pressure wave round trip between the air valve and the downstream reservoir. The discharge in the upstream branch of the line oscillates; for the results presented here, it is assumed that the upstream check valve remains closed from the moment reverse flow first occurs. When the discharge is fully arrested in the downstream branch, the maximum volume of the entrapped air pocket is achieved. Following this, the magnitude of the reverse discharge in the downstream branch gradually increases, initiating the air expulsion phase. In this stage, the previously admitted air is expelled through the air valve.
Once the entrapped air has been completely discharged, the previously air-separated water columns rejoin upon air valve closure, generating a secondary pressure spike at the air valve location. Since the upstream and downstream water columns behave nearly independently, the approaching velocities of the water columns right before air valve slam are direct but almost random determinants of the intensity of the pressure spike at the valve location upon final air valve closure. As a result of the secondary pressure wave phase, a substantial increase in head occurs at the upstream end of the pipeline, which is typically the maximum head experienced by the system during the transient event. After this first water hammer cycle, subsequent cycles, with the four described phases, usually occur with the progressive attenuation of the transient oscillations [
15,
26].
4.2. Test Pipeline and Assumptions Used in the Numerical Simulations
Based on the described scenario, numerical simulations were conducted to explore the relevance of air valve capacity and its representation in the context of the transient oscillations associated with a pump trip. The test pipeline was assumed to be composed of ductile iron pipes (with adopted celerity of propagation of pressure waves of 1000 m/s), an elevation difference between downstream and upstream reservoirs of 55 m, total length of 3000 m, and nominal diameter of 800 mm. The nominal diameter of the pipes at the pump station is 550 mm. The air valve is installed at a distinct high point of the pipeline profile, midway between the two reservoirs. To consider the sensitivity of the response to the vertical dimension, two possible vertical positions for the air valve are considered: 35 and 50 m. The pumping system comprises four pumps of the same type—two pumps in series are in parallel with two other pumps in series. The pumps are of model KSB ETA 300-35. The steady-state discharge velocity is about 1.57 m/s.
The adopted air valve orifice diameter for inflow is 150 mm with
. The adopted air valve orifice diameter for outflow is 80 mm with three possibilities for
, namely, 0.2, 0.5, or 0.8. Fuertes et al. [
21], for example, presented two example CCs related to a particular air valve: one curve from the air valve’s product catalog and another from laboratory characterization tests. In such case, the catalog’s air valve capacity was almost 4 times beyond the corresponding actual measured capacity. Such a difference would be analogous to the difference in capacity between devices having
of 0.2 and 0.8 in the current study. In the numerical simulations, the cross section of the air valve orifice is assumed constant for both admission and expulsion. Variation of outlet orifice size might be a factor for valves with anti-slam mechanisms or for a very short period during valve closure or opening. The constant area approach is a reasonable assumption for well-functioning devices not prone to dynamic closure and active during common water hammer situations. The numerical simulations presented here were produced using the software HAMMER version 10.1.1.4 by Bentley Systems. The elastic model is solved with the use of the method of characteristics. The time step was set as 0.02 s. The duration of each simulation was 300 s. The numerical model accounts for vaporous cavitation. The air pocket is treated through the polytropic gas transformation equation. The air pocket is assumed to be localized at the high point. As the check valves associated with the pumps close after the pump trip scenario, they remain closed throughout the whole transient event. The numerical simulations neglect the possibility of occurrence of the dynamic closure of the air valve for expulsion.
4.3. Results of the Numerical Study
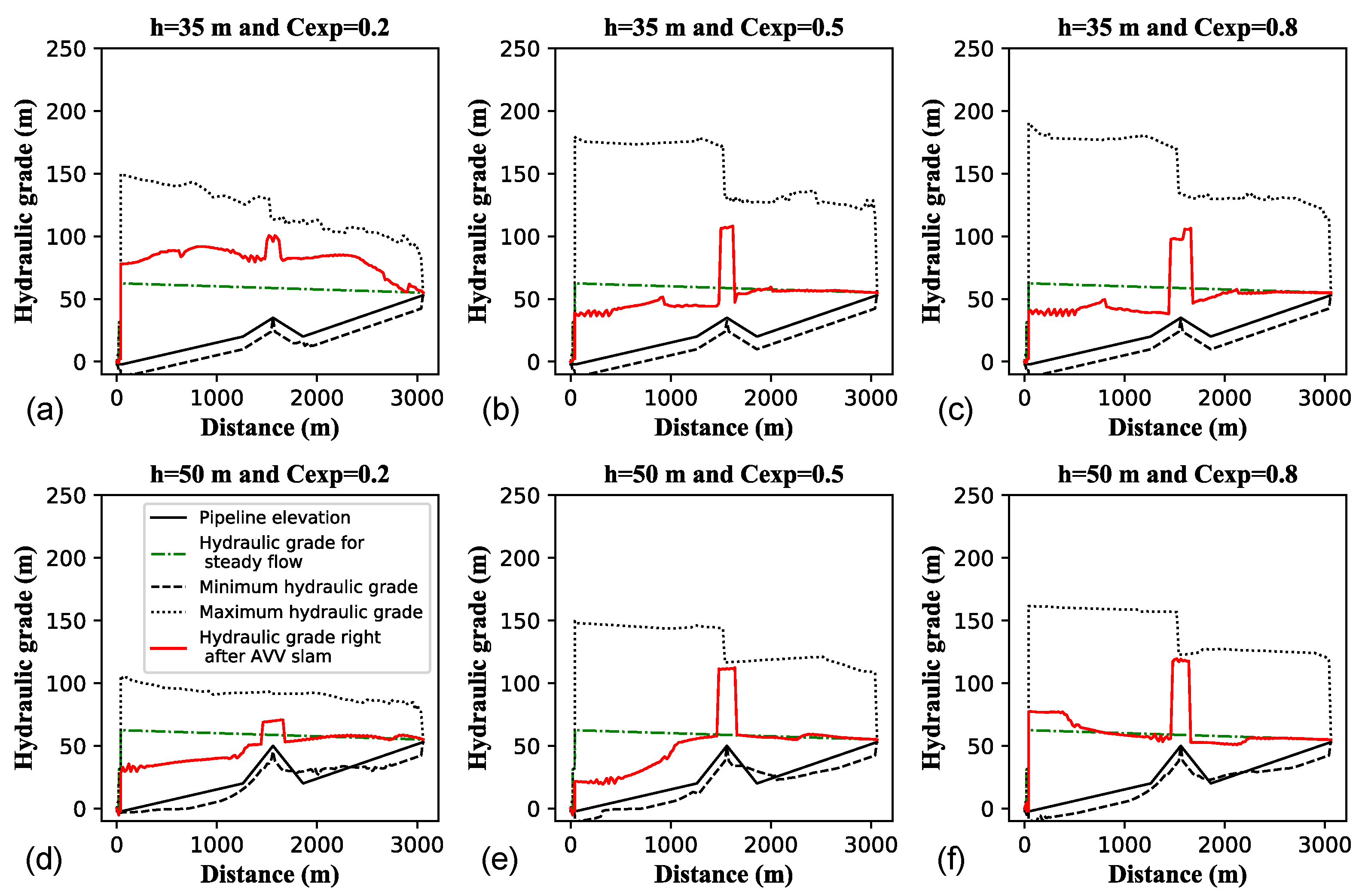
Figure 3 shows the secondary pressure waves that are formed due to air valve slam upon the completion of the air expulsion phase. Clearly, the magnitude of the secondary pressure waves (
), one that moves upstream and another that moves downstream, is sensitive to air valve vertical position
h (whether 35 or 50 m in this case study). Even more important, sensitivity is shown to air valve capacity (represented by the discharge coefficient
—0.2, 0.5, or 0.8 in this study). For both values of
h,
decreases as air valve outflow capacity decreases. While the secondary pressure waves are pronounced for the case with
, they are much reduced for the case with
. Of course, the actual magnitude of the secondary pressure waves will depend on other system characteristics including pipe diameter and water velocity during steady-state flow. It is also noticeable in
Figure 3 that the maximum transient pressure in the system
, which occurs at the upstream end of the line, decreases as
decreases. Also, the cases with air valves at the higher elevation of 50 m tend to have milder values of
than the cases with
m.
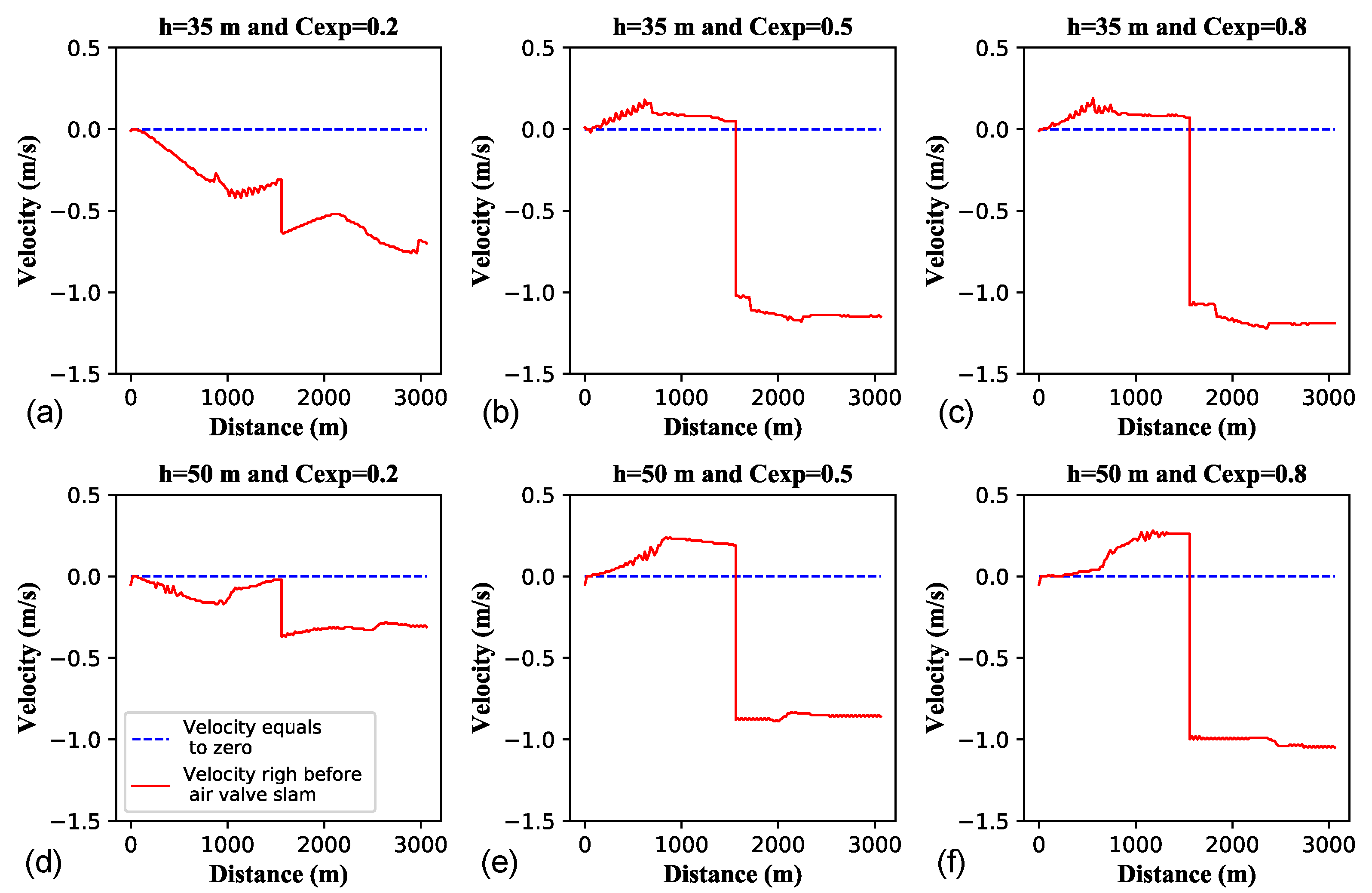
Figure 4 shows the intensities of the approaching velocities right before air valve slam. There is a clear correspondence between the magnitudes of the secondary pressure waves and the magnitudes of the approaching water velocities. More interestingly, the approaching velocity in the downstream branch
is consistently more intense than the approaching velocity in the upstream branch
.
From the numerical results, it was found that transient flow is appreciably sensitive to
(where
d is the outlet orifice of the air valve and
D is the pipeline diameter), which is indeed suggested in the literature. For the filling procedure in horizontal pipes, Martin and Lee (2000) [
27] found that, for the critical
value of 0.19, the peak pressure could reach 5 times the inlet pressure; Zhou et al. (2002) [
28] found that, for the critical
value of 0.2, the peak pressure could reach up to 15 times the inlet pressure; Zhou et al. (2020) [
29] found that, for the critical
value in the range from 0.175 to 0.225, the peak pressure could reach 9 times the inlet pressure. For vertical pipes, Zhou et al. (2019) [
30] found that, for the critical
value in the range from 0.08 to 0.15, the peak pressure could reach 11 times the inlet pressure. For transient attenuation, however, of greater importance than the critical
value per se is the limit for Type 1 behaviour during line filling (mitigated water hammer effect). According to Zhou et al. (2002) [
28], for horizontal pipes, mitigated water hammer occurs for
values less than 0.086. For horizontal pipes, Type 1 behaviour in the experiments conducted by Zhou et al. (2020) [
29] was observed in most cases for
(such limit, however, depends on air pocket length and inlet pressure and can reach 0.0875). According to Zhou et al. (2019) [
30], Type 1 behaviour, for a vertical pipe, occurs for
values less than 0.025 (such limit, however, depending on the circumstances might go up to 0.05). It should be noted, however, that the analogy between orifices and air valves is imperfect. The key difference between orifices and air valves is that, when the water column reaches the downstream aperture during a filling event, water starts to be expelled through the orifice, while the air valve readily closes upon contact with water.
In the isentropic air flow equations, air flow rate is proportional to the product of the discharge coefficient , both for admission and expulsion, times the area of the orifice A. The virtual orifice diameters that would result in a product (product between the usually adopted discharge coefficient of 0.6 and the area that corresponds to a given virtual diameter) equals to the real (for discharge coefficients of 0.2, 0.5 and 0.8 and orifice diameter of 80 mm) would respectively be 46.2, 73.0 and 92.4 mm. The adopted outflow orifice diameter of 80 mm gives a relationship between air valve orifice diameter (d) and pipeline diameter (D) of . However, considering the virtual diameters aforementioned, the relations are actually 0.058, 0.091 and 0.12 for the discharge coefficients of 0.2, 0.5 and 0.8, respectively. The reduced ratio found for the discharge coefficient of 0.2 (0.058) is within the limit of 0.086 associated with mitigated water hammer.
Another numerical study was conducted for a pipeline diameter of 500 mm and a water velocity of 1.65 m/s during steady-state flow, also considering an 80 mm outflow orifice for the air valve and three possibilities for the discharge coefficient (0.2, 0.5 and 0.8). For such case, the differences in behaviour between the discharge coefficient assumptions for expulsion were less marked than for the cases in
Figure 3 and
Figure 4. Indeed, for the pipeline with smaller diameter (500 mm), the ratios between the virtual diameters and the pipeline diameter are essentially outside the limit for mitigated water hammer.
In summary, the case study explored in this section shows that inaccuracies in CCs, typical of those often found in product catalogs, represented herein as differences in discharge coefficients, are likely to lead to (possibly serious) errors in the results of transient simulations. Of course, inaccurate CCs can also result in air valve selection errors when applying common sizing criteria for line filling or draining, like the ones suggested in the M51 manual by the American Water Works Association (AWWA) [
7].
5. Conclusions
This study provides a preliminary assessment of consistency and fundamental validity of the typical performance data published by manufacturers in air valve catalogs, data that is often used and assumed accurate by pipeline system modellers, designers, owners and operators. Overall, it is found that much of the inflow performance data that are displayed is often inconsistent with the isentropic inflow model. In fact, inflow curves are actually often shown as being consistent with the shape of the isentropic outflow model. In addition, manufacturers sometimes present the same performance data for inflow and outflow, either in separate but equivalent graphs or in graphs that supposedly pertain to both regimens. However, such equivalence is unreasonable given the intrinsic differences between the inflow and outflow phenomena. The current research would seem to indicate that manufacturers often put too little importance in the acquisition and presentation of reliable air valve performance data in their catalogs. Thus, if engineers wish to better design and operate reliable pipeline systems, undertakings which inevitably involve effective management of air flows, it would seem essential that manufacturers as a whole better characterize their air valves using reliable methodologies and laboratories and that designers and operators understand the importance of air valve performance data. The paper makes no pretense of singling out specific manufacturers as being greater or lesser contributors to this state of affairs but only wishes to raise the general issue that engineers, designers, owners and manufacturers need to be progressively more aware that certain identifiable details of components are likely to play decisive roles in the overall performance of the larger systems in which they are found.
Several specific recommendations can be advanced. It is recommended that there be a routine inclusion of the following information in air valve catalogs: atmospheric and temperature conditions present during the characterization tests; admission and expulsion discharge coefficients, according to the isentropic air mass flow model; for inflow and outflow, the air mass flow values for which the regimens go from subsonic to sonic; precise areas of the outlet orifices for admission and expulsion; internal absolute pressure for which dynamic closure is expected for expulsion; influence of auxiliary appurtenances connected to an air valve on its air flow behaviour (slow closing devices, throttling devices, pipes connected to the air valve’s outlet, protective screens installed at such pipes).
To help consolidate the importance of accurate air valve models, a numerical case study explores the transient events associated with a pump trip scenario in a rising line with an air valve at the midpoint between two reservoirs. In this way, the paper explores the question of how much of a difference incorrect air valve information can make in the results of numerical simulations of unsteady pipeline flows. It was found that meaningful errors in simulation results may arise from the use of inaccurate characteristic curves of air valves. Also, it was confirmed that, as expected, the true relevance of air valve capacity to system behaviour during transient events depends on system profile configuration and air valve location.