1. Introduction
Off-stream reservoirs are essential structures for the regulation and supply of water. In contrast to dams, they are not usually affected by surface runoff, which results in higher hydrological safety. Nonetheless, many of these structures are located in high elevations, near to urban areas and important infrastructure that can be affected in case of failure.
With the modification of the Spanish Regulation of the Hydraulic Public Domain derived from the Royal Decree 9/2008 [
1], the potential hazard of off-stream reservoirs higher than 5 m or with volume storage above 100,000 m
3 must be evaluated with the same procedure as for large dams (higher than 15 m or with more than 100,000 m
3 of capacity). This means that around 70,000 off-stream reservoirs currently in operation in Spain [
2] need to be assessed on the potential hazard due to failure.
The Spanish Technical Guide for dam classification based on potential hazard [
3], hereinafter the “Technical Guide”, lists the recommended methods to analyse the dam breach formation and flood propagation. Three categories are described in the Technical Guide, namely A, B and C, from higher to lower potential hazard. The classification process involves two main steps: (a) identification of the relevant elements potentially affected (e.g., households, roads) and (b) generation of the flood maps. This is generally performed through the application of two-dimensional (2D) hydraulic models that consider the hydraulic characteristics of the flow propagation downstream of the dam breach and provide results in terms of maximum depths and velocities, allowing for the identification of the flooded area [
4].
The complete method, which involves hydraulic 2D models, is recommended to reproduce the breach formation, the failure hydrograph and the flood propagation. Currently, different software tools meet the requirements of this method, such as the National Weather Service Dam-break Flood Forecasting Model (NWS DAMBRK) [
5], the Simplified Dam-Break model (SMPDBK) [
6], and Iber [
7], among others [
4]. The results of the hydraulic model are the basis for evaluating the affections to the zones of interest. Simplified methods are also accepted if the classification of the structure is obvious.
The necessary work to make a complete and accurate classification assessment of the potential hazard requires engineering knowledge and resources often unavailable for many owners. In addition, the administration responsible for the review and approval of the classification assessments and emergency plans requires relevant time and human resources.
Despite the increasing growth in the exploitation of off-stream reservoirs and the need for safety analyses, few studies have been published on their potential hazard. Soler et al. [
8] analysed the effect of using 1D or 2D models for flood propagation in case of failure. Two-dimensional models were more accurate for the simulation of free surface flows, allowing for a better classification of the structure. Espejo [
9] characterized the hydraulics of off-stream reservoir failures by defining the storage factor to facilitate the selection of the empirical formulas for computing breach parameters (width and formation time). Hence, the hydraulic operation regarding the breaching of the off-stream reservoir is projected based on the height and volume of the reservoir, in terms of the probability of occurrence of a specific flow discharge. Additionally, a cartographic representation of the areas most likely to be affected was created using 5000 simulations of synthetic scenarios and stochastic analysis (Monte Carlo approach). Hori et al. [
10] developed a disaster prevention support system for irrigation ponds in Japan after the failure of many off-stream reservoirs due to an earthquake in 2011. The system allows for determining the risk in heavy rain scenarios and calculating inundation areas in case of failure. Sánchez-Romero et al. [
11] explained in detail the process of generating flood maps due to the failure of off-stream reservoirs using FLDWAV and Iber for two piping and overtopping. The results showed smaller peak flows in overtopping failure, although the discharge volumes are larger than those produced by piping.
The development of simplified tools for analysing the consequences of dam breach has been a topic of increasing interest in the last years. Different methodologies have been proposed, most of which are based on Geographic Information System (GIS) tools. Cannata and Marzocchi [
12] developed a GIS-embedded approach to derive maximum flooding maps based on elevation raster maps. The tool solves the 2D shallow-water equations using a finite volume method and achieved 75% accuracy as compared to the official flooding map of an existing dam. In addition, Albano et al. [
13] implemented a GIS-based method to delineate flood-prone areas in case of dam break. A set of cross-sections are created over a digital elevation model (DEM) along the downstream river reach, and the maximum discharge, elevation and time are computed with a 1D unsteady flow solver. The tool achieved an accuracy of 86% with respect to maps generated with a 2D model.
In parallel, some authors applied machine learning (ML) techniques for simplifying dam breaching and dam safety analysis. Hooshyaripor et al. [
14] proposed an artificial neural network model (ANN) to predict the peak discharge due to breaching of embankment dams using a dataset with 93 failures. The results showed that the method is not applicable for peak outflows lower than 100 m
3/s due to the small size of the dataset. In another study, Hooshyaripor et al. [
15] reported higher accuracy on a synthetic dataset generated by means of copulas based on the independent relationship between height and volume of water in the reservoirs. ML algorithms have also been applied to other dam safety problems, such as the prediction of dam behaviour [
16,
17], the detection of anomalies [
18,
19,
20] based on monitoring data, or the prediction of flood maps [
21,
22].
The aim of this work is to present a methodology based on ML to estimate the potential affection in case of failure of an off-stream reservoir on any location in the surrounding area without the need of running a detailed 2D hydraulic model. The information required includes 10 parameters related to the geometry of the reservoir, the roughness and slope of the terrain and the relative location of the potentially affected elements. The required—large—dataset to fit the model is created with the results of synthetic cases generated using a tool based on Iber [
7,
23] and Latin Hypercube Sampling (LHS) [
24].
The paper is organised as follows: first, the methods used are explained in
Section 2, including the automated generation and parametrization of synthetic cases for construction of the database, the ML algorithms, and their calibration and validation; results are presented in
Section 3; application to a real case is shown in
Section 4.
Section 5 includes the discussion, while conclusions are summarized in
Section 6.
2. Methods
The ML models were fitted using synthetic data generated by means of complete 2D hydraulic models developed in Iber. The steps included in the overall workflow are:
Parametrization of the physical variables of the structure and the surrounding terrain.
Design and generation of synthetic cases.
Automation of Iber for computing breach formation and flood propagation and for extracting the results of each synthetic case.
Generation of the dataset and classification of the results based on the criteria established in the Spanish Regulation [
1].
Training, calibration and performance assessment of a ML classification model.
Validation of the ML model and analysis of the results.
2.1. Data Generation
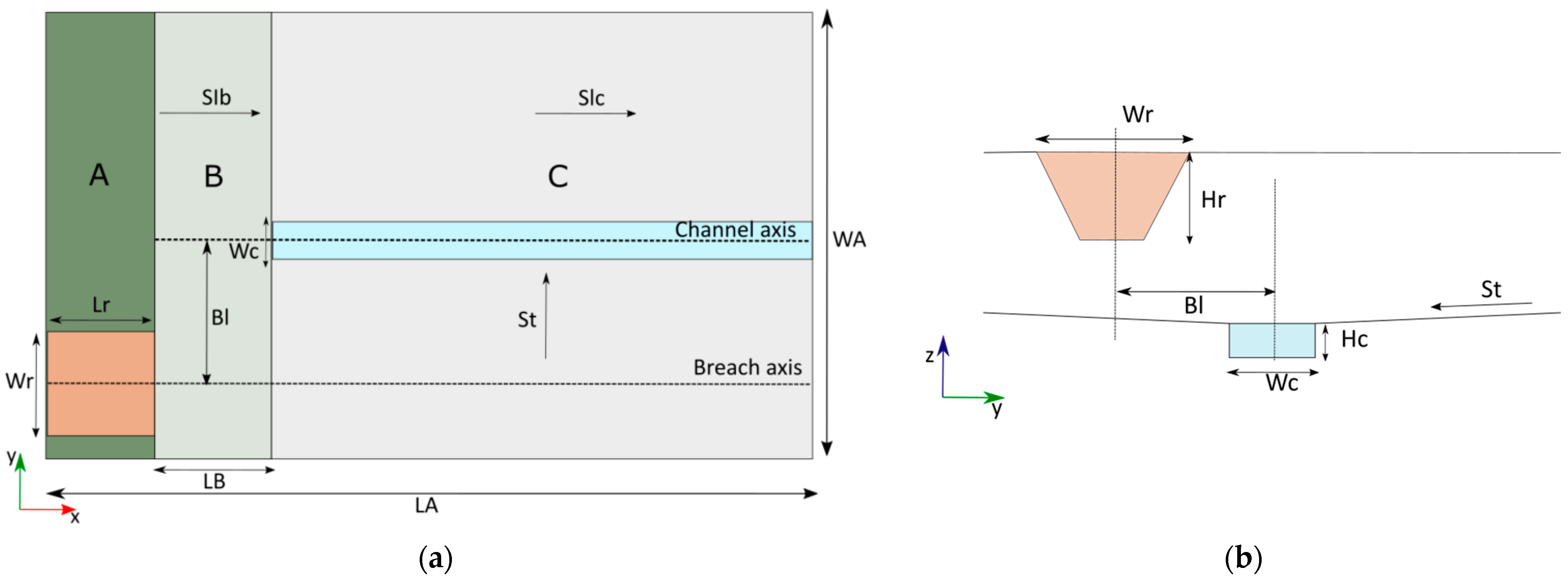
The synthetic cases were defined based on ten parameters shown in
Figure 1. The length of the domain is 4000 m (L
A), and the width is 1500 m (W
A), with three sections: A, B and C (
Figure 1a). The default maximum top elevation (E
t) is 505 m for all cases. The off-stream reservoir is located in Section A (brown area) and has the highest elevation. The location of the off-stream reservoir can vary along the y-axis. Section B represents a transition zone between the off-stream reservoir and section C with a longitudinal slope (S
lB) between 0% and 1% and no transversal slope. In section C, a main channel is assumed to exist at the origin of the y-axis (y = 0) with a rectangular shape (cyan area). The area outside the channel has a given constant transversal slope (S
t) leading the flow into the channel.
Table 1 shows the parameters with their symbols and ranges of variation. For cases without a defined channel (W
c = 0), the geometry was designed to convey the water flow towards the centre of the terrain based on the transversal slope in section C.
A design of experiment (DoE) technique based on Latin hypercube sampling (LHS) was applied for generating the combination of parameters for each synthetic case. LHS is a statistical method for sampling that ensures that the distribution of each input parameter is fully represented using all areas of the sample space. LHS allows fewer simulations to be performed while obtaining similar precision and lower variance than other methods such as random sampling, which does not take into account the previously generated sample points [
24,
25].
Two sets of samples were generated with LHS. In the first 50 samples, no main channel was defined, i.e., Hc = 0 and Wc = 0. This dataset accounts for cases in which no clear flow path exists in the vicinity of the off-stream reservoir. In the other 150 samples, all parameters were equally sampled along their range of variation, always using uniform distributions.
For each combination of parameters, the geometry was generated by means of a list of points with xyz coordinates. In section A, the separation between points is from 5 to 40 m in the x-axis, depending on the length of the off-stream reservoir, and 5 m in the y-axis. For sections B and C, the separation is 20 m for both axes, except on the main channel, where the separation is 0.5 m in the y-axis. For section A, the off-stream reservoir needed more detail for the estimation of the breach.
The breach is placed at half the width of the reservoir and starts at the crest. The storage volume in the reservoir is approximated using the volume equation of a trapezoidal prism with Hr, Wr and Lr dimensions.
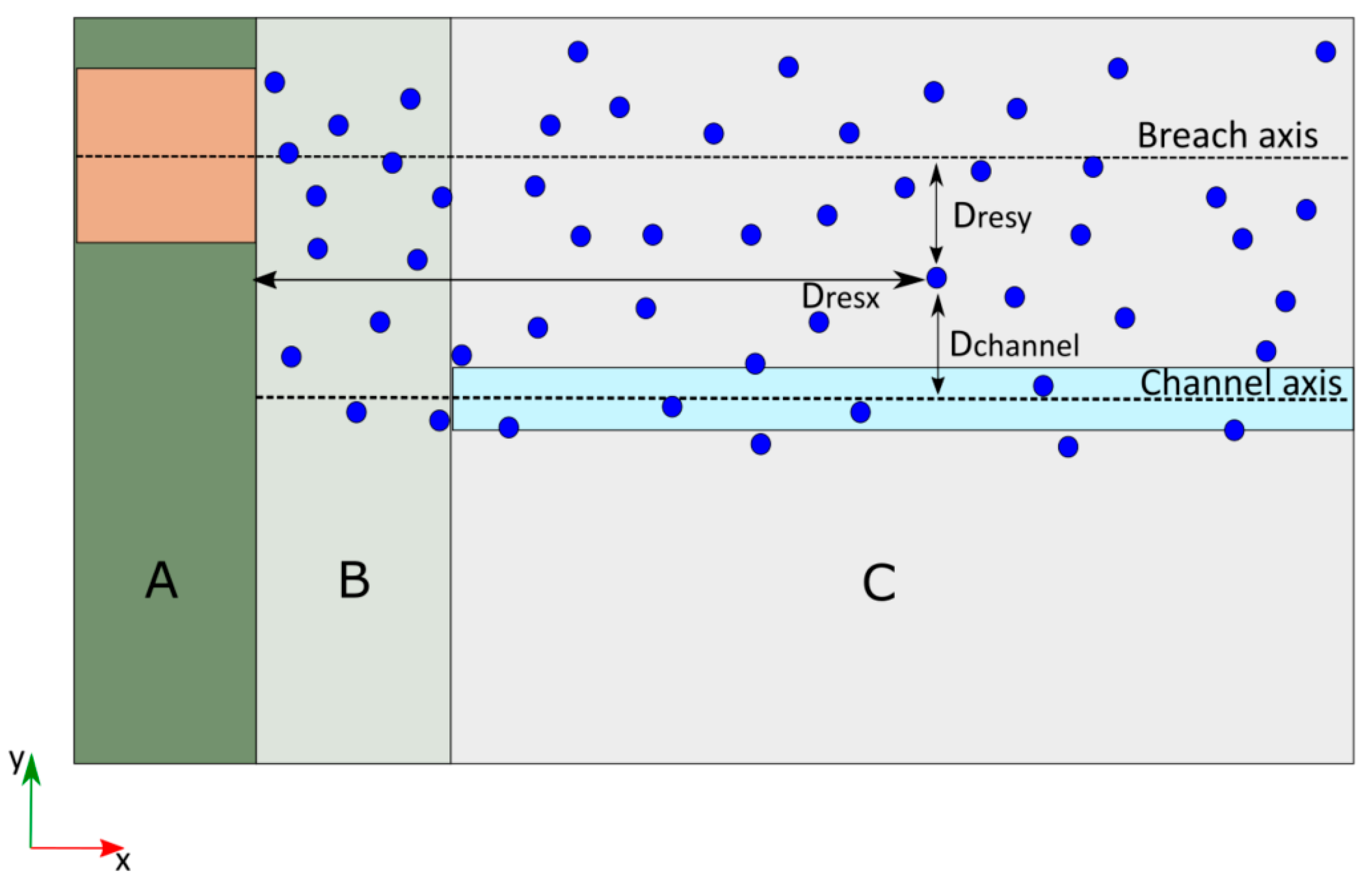
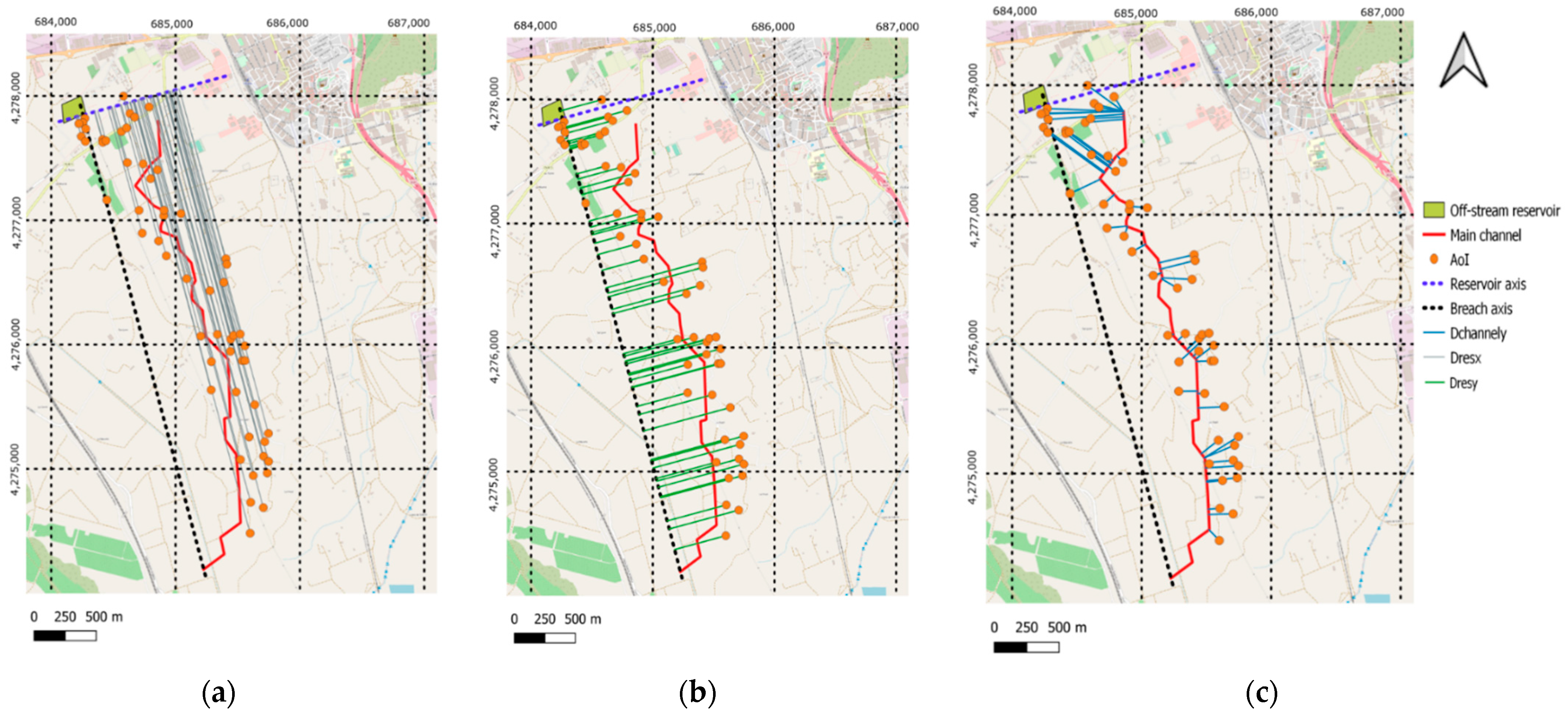
For the extraction of results, 200 points (or gauges) were considered for each case as vulnerable locations. They are situated at random in the area where the flood is expected to affect, i.e., close to the reservoir, the breach axis and the channel axis. More precisely, the location of the gauges was parametrized on the basis of three variables (
Figure 2). D
resx is the distance to the off-stream reservoir embankment (location of the breach) along the x-axis, D
resy is the distance to the breach axis, and D
channely is the distance to the main channel axis. The values for D
resy and D
channely vary from −750 to 750 and for D
resx from 60 to 3950.
2.2. Automation in Iber
Iber is a 2D numerical tool for modelling hydrodynamic and sediment transport [
7,
23], which currently includes additional calculation modules for simulating hydrological processes [
26,
27], pollutant propagation [
28], large-wood transport [
29], physical habitat suitability assessment [
30] and dam and off-stream reservoir breach formation [
31,
32,
33]. Iber uses the finite volume method to solve the 2D depth average shallow water equations and is integrated in the pre- and post-processing interface of GiD, a software for definition, meshing and results visualization of numerical models [
31,
34]. Additionally, Iber calculations can be accelerated using graphical processing units (GPUs) [
35].
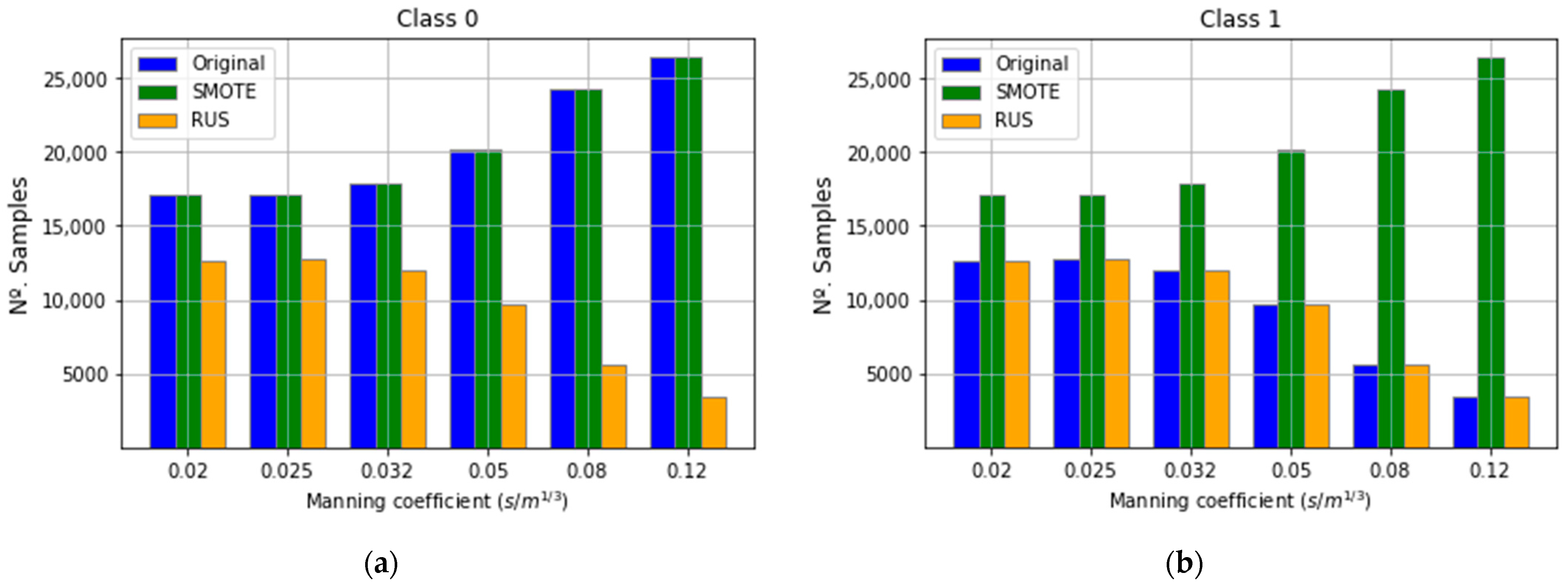
A tool in Iber was developed to automate the process of model generation and results extraction. With this tool, the information regarding the geometry, breach parameters and gauges for each synthetic case is read, and the roughness of the model is assigned. Six land use types were considered: 0.020, 0.025, 0.032, 0.050, 0.080 and 0.120 s/m1/3. Each synthetic case is computed with six different Manning coefficients, resulting in 1200 models (200 × 6). Then, the mesh is generated, the models are run and the results exported in CSV format: depth (h), specific discharge in x (qx) and specific discharge in y (qy) every 300 s for each gauge.
The total calculation time was set at 16,000 s. It was obtained from an estimated average velocity of 0.25 m/s to ensure that the flood wave propagation over the entire area is computed.
2.3. Definition of Hazard
The Spanish Regulation 9/2008 in its article 9 (2) states that a hazard to human life is considered to exist when the depth of water is 1 m or more, the velocity is 1 m/s or more, or the product of depth and velocity is 0.5 m
2/s or more [
1]. Therefore, two classes were defined: class 0 when none of the three criteria are met and class 1 when one or more criteria are true.
2.4. Machine Learning
The main goal of ML models is to reproduce the response of a system for unseen scenarios based on patterns previously identified from a typically large database (training set). The accuracy of an ML model is typically evaluated on a dataset not used for model fitting (test set).
There are two types of ML supervised models according to the type of output. Numerical responses are predicted with regression, while categorical outcomes are estimated with classification models.
In this work, supervised classification models were used, because the output is categorical (class 0 or class 1 as described in
Section 2.3). Among the available ML classification algorithms, random forests (RF) was chosen for this work because: (a) it showed to be useful and easy to implement in previous works [
19,
36]; (b) it outperformed other classification algorithms in a comprehensive comparative analysis [
37,
38]; (c) the application of RF models has increased in water engineering due to their high accuracy, flexibility and possibilities for interpretation [
37,
38,
39].
2.4.1. Random Forest
An RF model is a combination of a large number of decision trees, each of which is bootstrapped to a random sample taken from the training set. The bootstrapping involves resampling the data with replacements, eliminating some of the samples and duplicating others. Then, each decision tree is fitted with a different sample. The RF method introduces additional randomness by taking a random subset of the input variables when computing each split for each tree in the model. The final prediction of the algorithm is calculated based on the average of the results of each of the trees used. A detailed description of the algorithm can be found in the seminal work of Breiman [
40]. For more practical descriptions of the method, the reader can consult [
41,
42].
In this work, the scikit-learn package developed for Python was used, which includes the random forests classifier option [
43]. The main parameters to build an RF model are the number of trees to be ensembled (
n_estimators), the minimum number of samples required to split an internal node (
min_sample_split) and the maximum number of features considered for each tree (
max_features).
2.4.2. Balanced Dataset
Imbalance datasets are reported as a major problem to the development of accurate ML classifiers algorithms [
44]. Our training set is imbalanced because one class (class 0) heavily outnumbers the samples from the other class (class 1). Among the available methods for alleviating this problem, we tried under- and oversampling methods: synthetic minority oversampling technique (SMOTE) [
45] and random undersampling (RUS) [
46].
SMOTE is a combination of oversampling of the minority class and undersampling of the majority class. New synthetic examples based on the characteristics of the existing data are created using interpolation with the k-nearest neighbour technique. With RUS, samples corresponding to the predominant class are eliminated, and no new information is introduced. Thus, the majority class is reduced to the same amount of samples corresponding to the minority class [
44].
2.4.3. Calibration Procedure
The observations excluded from a bootstrap sample are called out-of-bag data (OOB). The OOB predictions are calculated only using the trees for which the observations are OOB [
47]. The OOB error is calculated as the average of the OOB error rate for each observation. This procedure can be considered as implicit cross-validation, which can obtain a good estimate of the prediction error without the need to explicitly separate a subset of the available data [
48].
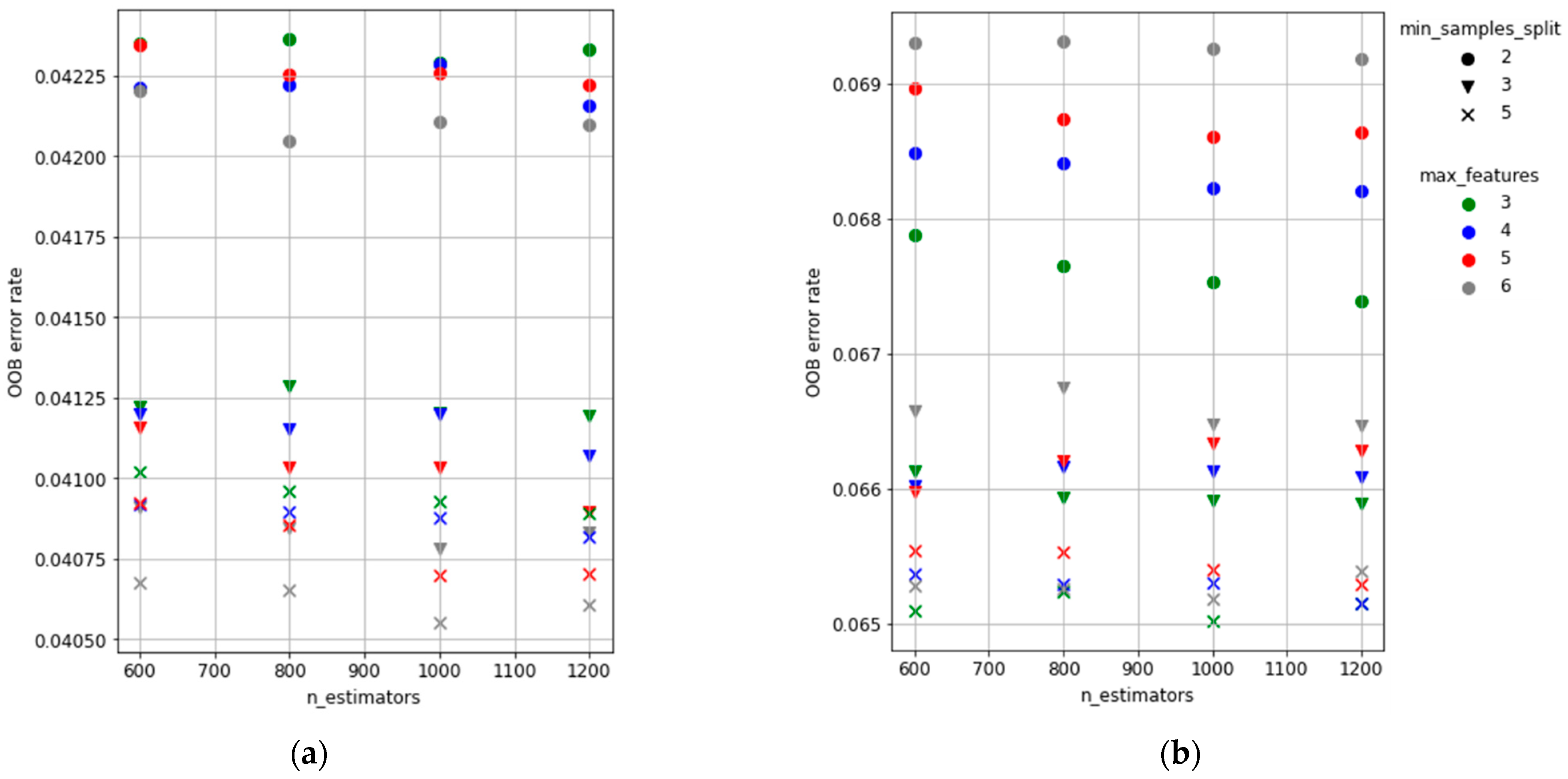
A calibration process was performed based on the OOB error rate to find the best combination of parameters for the RF model. The OOB error rate was estimated for different possible combinations of the model parameters, and the best combination (lowest OOB error) was selected to fit the final RF model. All possible combinations of n_estimators (600, 800, 1000 and 1200), min_sample_split (2, 3 and 5) and max_features (3, 4, 5 and 6) were considered to fit the RF models.
2.4.4. Measures of Accuracy
Henceforth, the correct estimation of class 1 is considered as positive experiments (true positives,
), while the correct prediction of class 0 corresponds to negative experiments (true negatives,
). False positives (
) are cases where the model predicts a risk to human life in an unaffected area, and false negatives (
) are those for which the model predicts no risk in areas with true damage [
49]. The measures of accuracy considered are:
The adjusted F-score can place higher importance on the precision or recall according to the nature of the study. Since false negatives are more relevant in our problem, recall is considered more important, and the F2 score is estimated with the generalized
-score formula with
= 2 [
50].
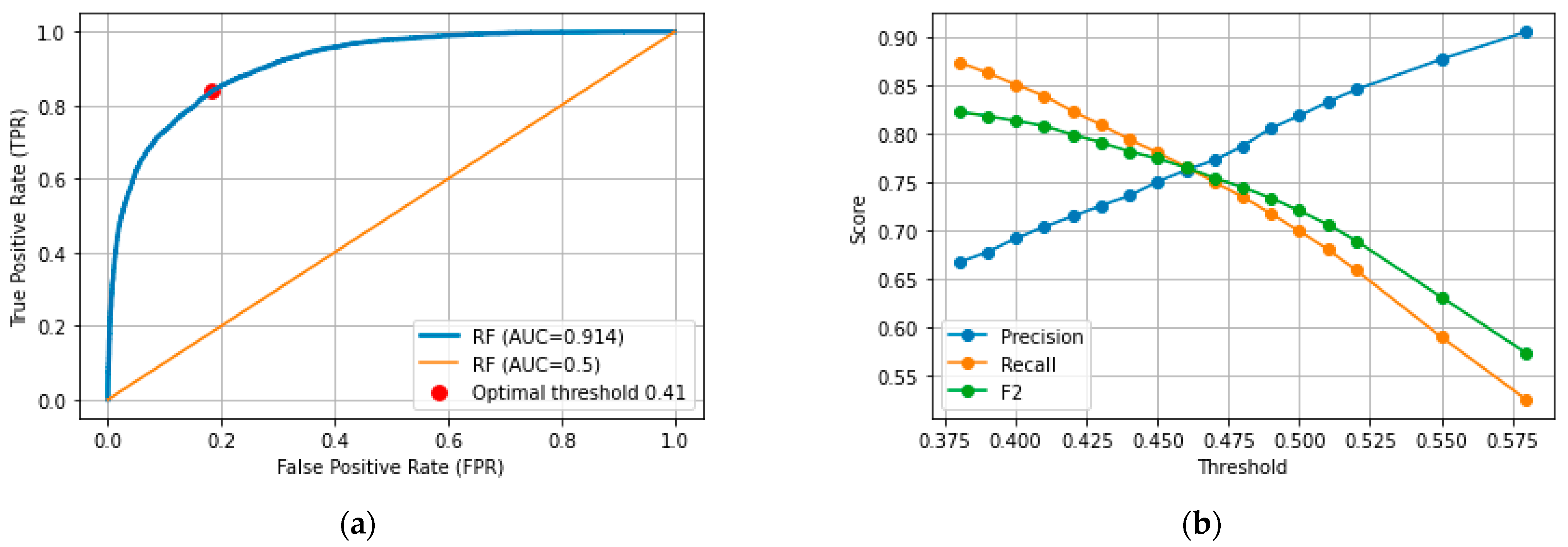
The receiver operating characteristic (ROC) curve is a useful tool to visualize the performance of binary classifier algorithms. Plotting the
against the false positive rate (
FPR) generates the ROC curve [
46]. The area under the ROC curve (AUC) is an additional measure for evaluating the predictive ability of classifiers [
51]. Values of AUC close to one represent a good classifier, while the model is not able to distinguish between classes when AUC is equal to 0.5.
5. Discussion
Automating the generation of geometries and the execution of calculations in Iber obtained a useful database for training ML models. The developed process offers possibilities for the application of Iber in other types of analyses in which cases need to be systematically executed, such as probabilistic studies or sensitivity analyses [
58,
59,
60,
61]. Similar processes are already in application to generate training sets for ML surrogate models in hydrological studies [
62,
63,
64], as well as to analyse the effect of breach properties on the floodplain [
65,
66].
The calibration of the RF models was performed by means of grid search over the parameters to choose, and the best combination was selected based on the OOB error. The results showed small variation in the OOB error among combinations, which confirms previous findings regarding the robustness of the algorithm [
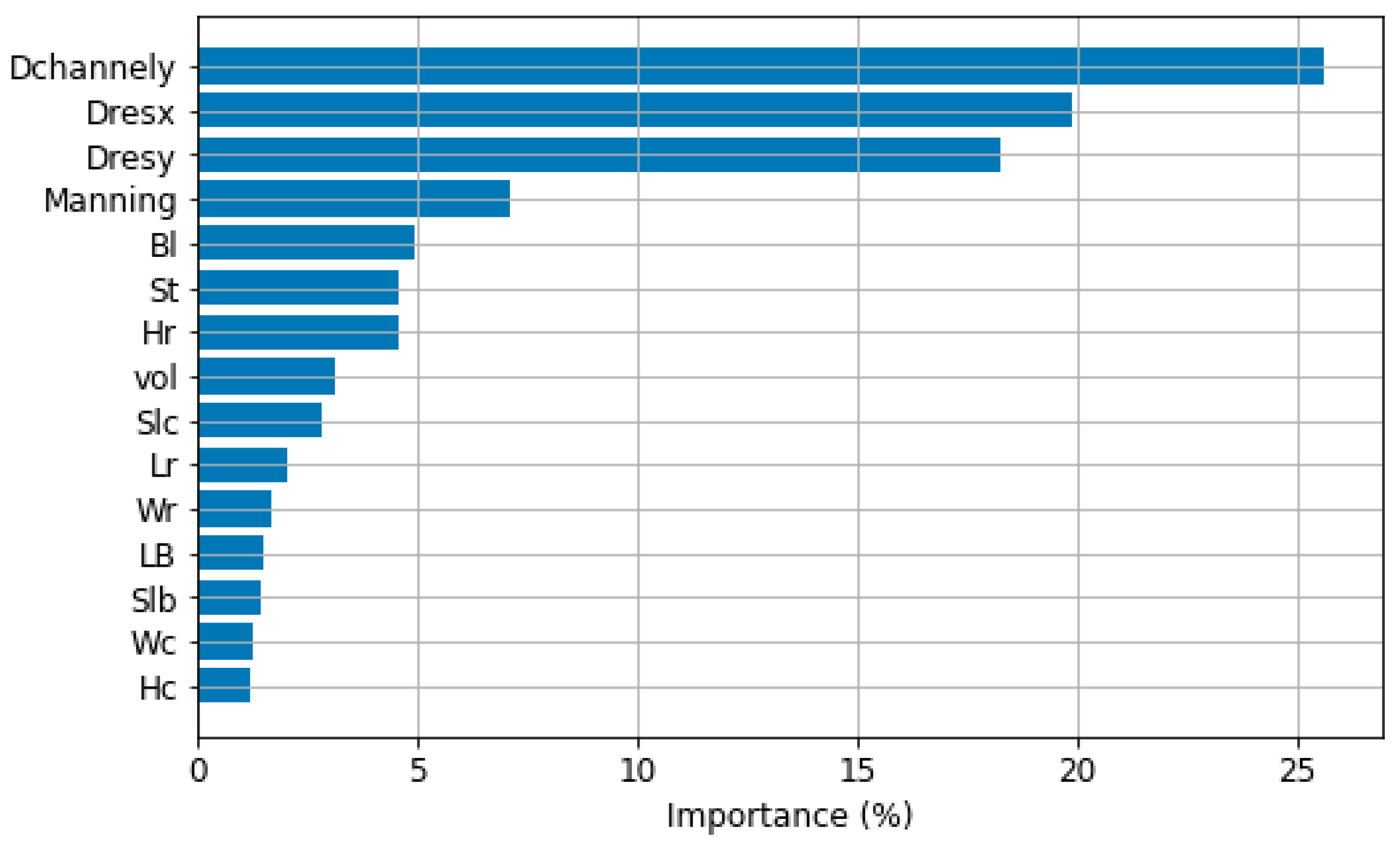
52]. The interpretation of the model in terms of the variable importance agrees with engineering intuition since the location of the AoI relative to the reservoir and the main channel were identified as the most relevant.
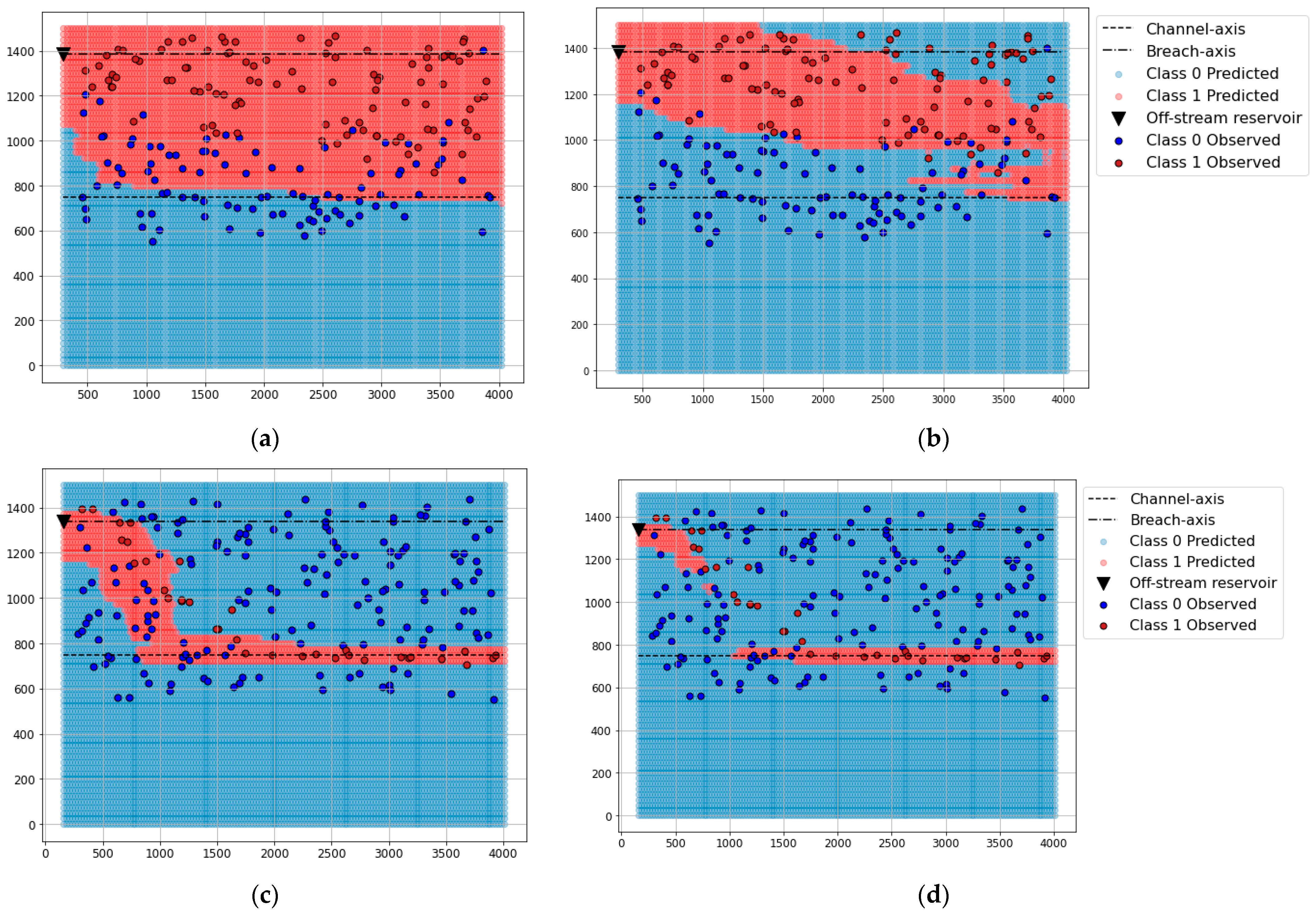
By contrast, the class distribution in the training set showed a clear effect on the performance of the models. RF-OS was trained with approximately 120,000 Class 1 samples, while the RF-US dataset had around 50,000 samples. The large training set for RF-OS produced an overestimation of Class 1, which led to lower accuracy and precision scores. Both methods can be further tuned to obtain more accurate models in general and in particular, to improve some of the accuracy indexes. For example, our results already showed that SMOTE is better for recall and worst for precision. However, the overall performance for practical applications is more dependent on other aspects, as described later.
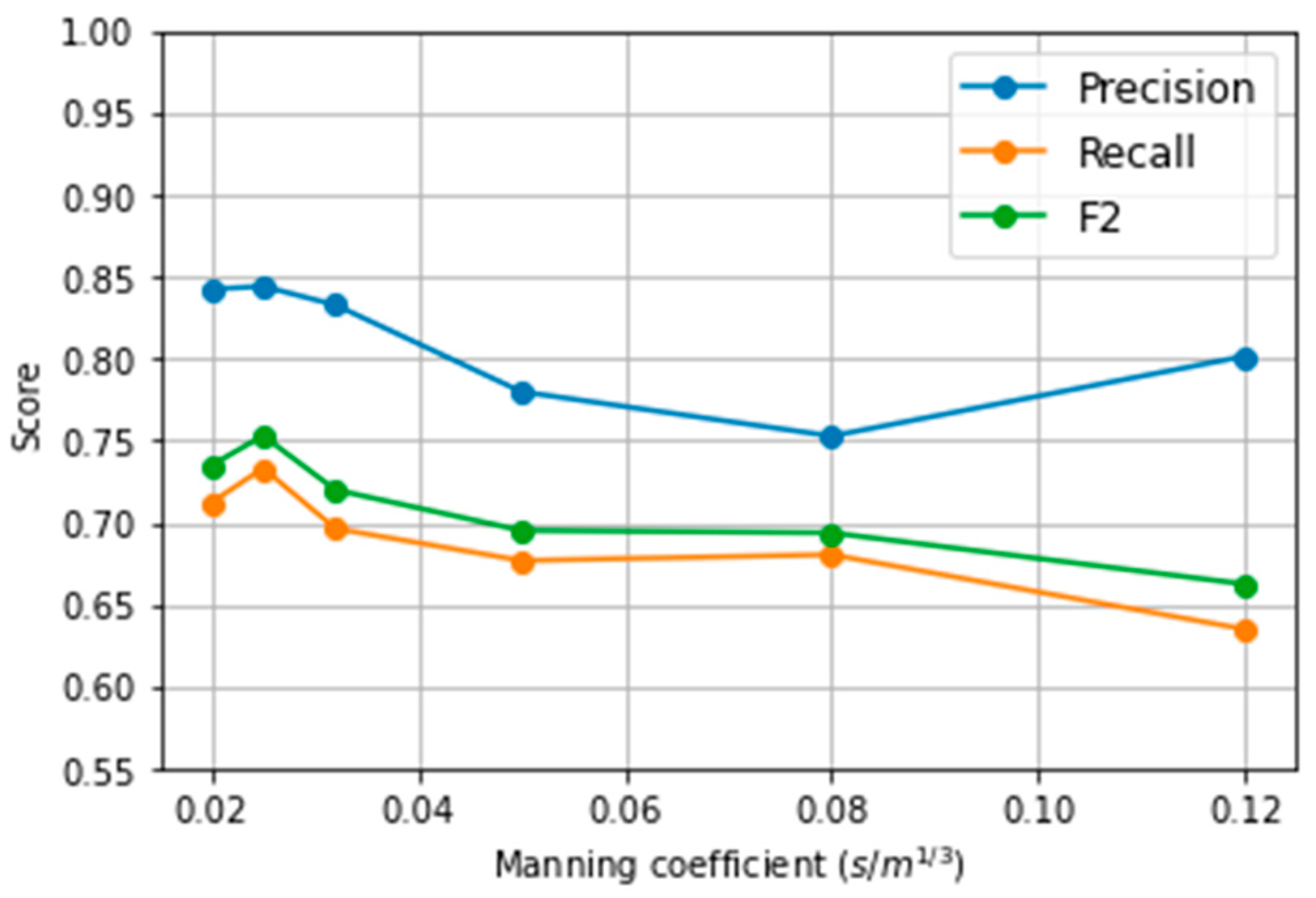
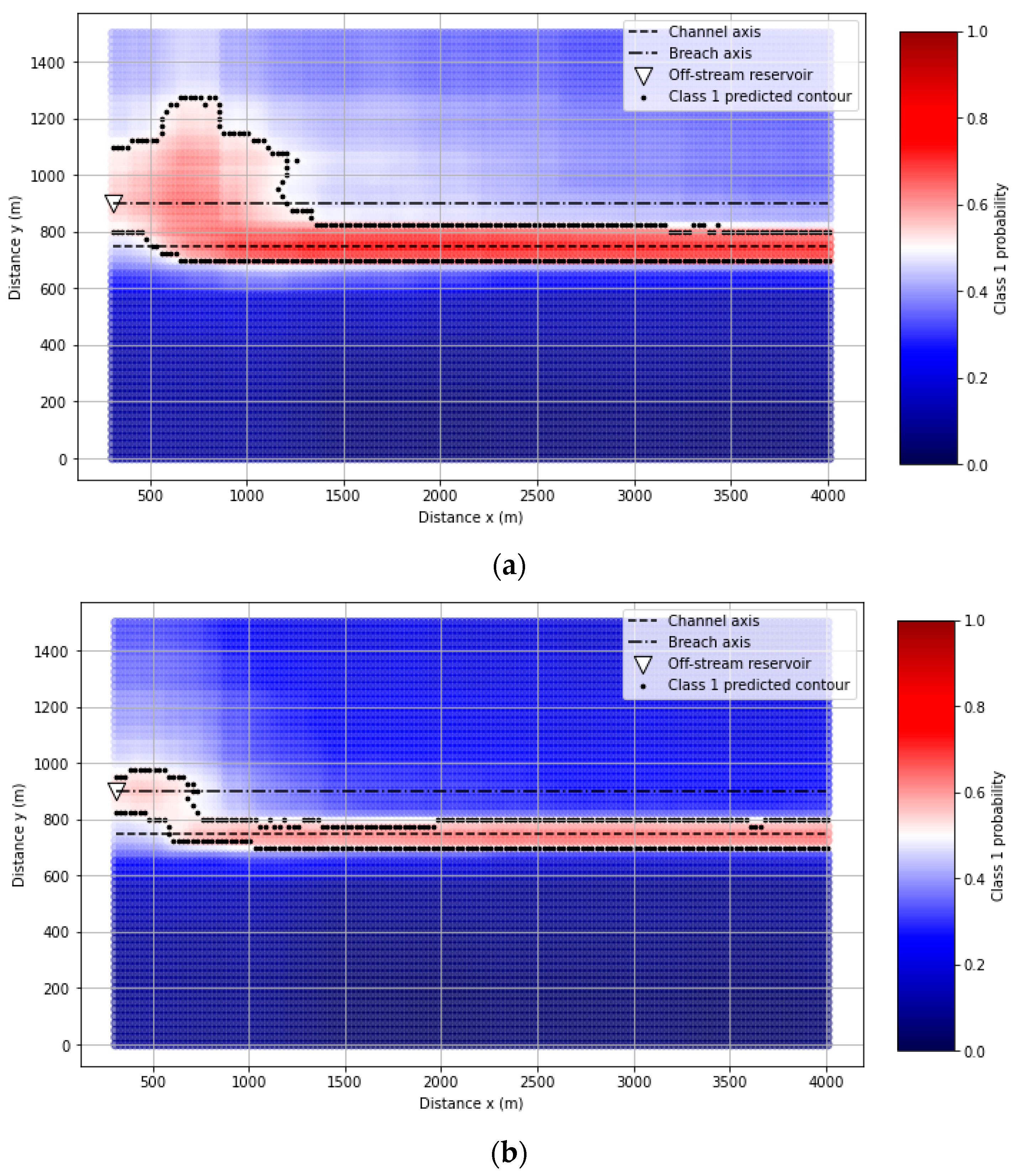
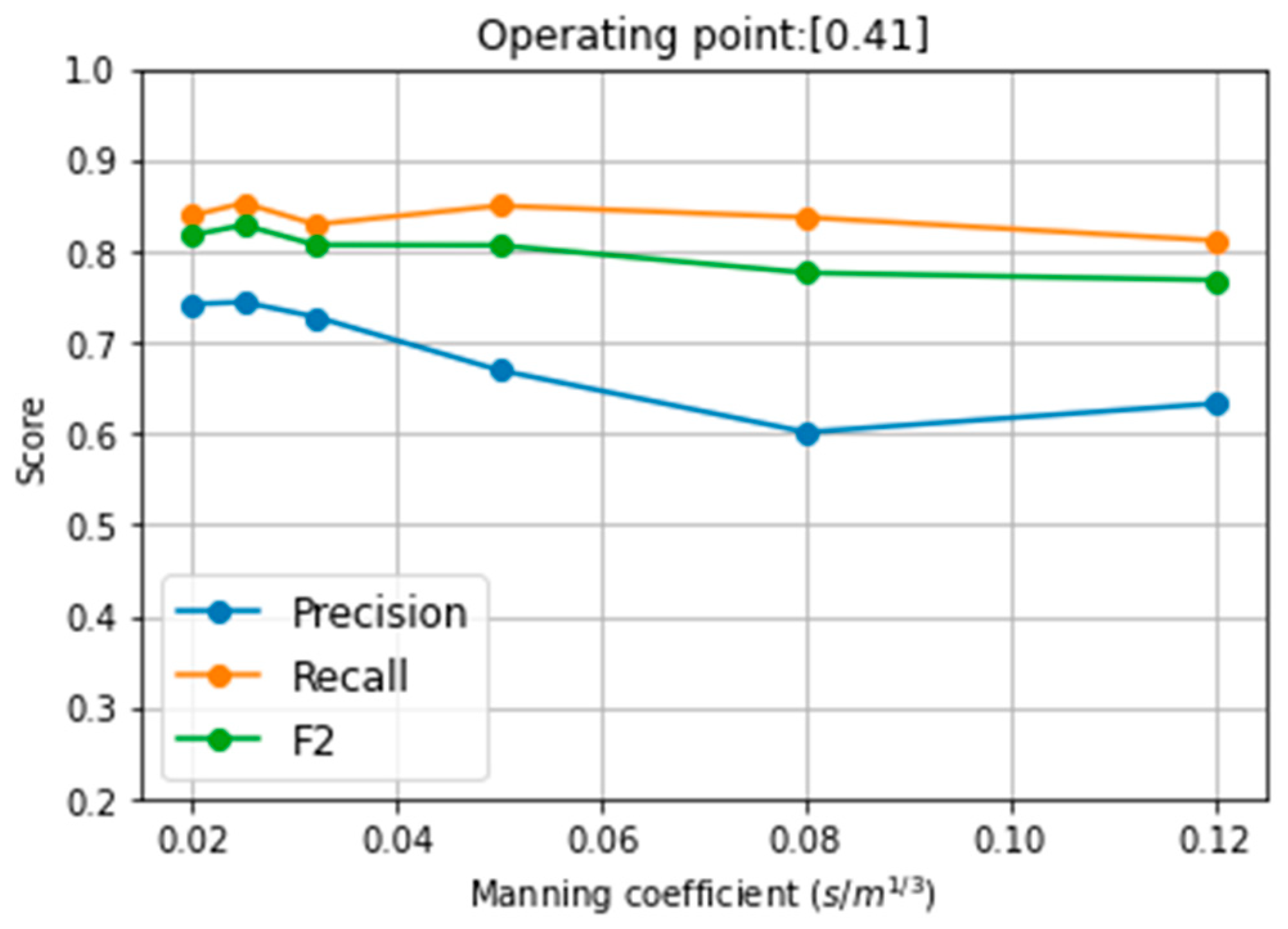
In addition, the effect of the class distribution was associated with the Manning coefficient. For a given reservoir and domain, higher values of Manning result in low velocity and risk and thus in more points belonging to Class 0 (
Figure 3). This also implies that the majority of samples in RF-OS are artificial, i.e., generated by k-nearest neighbours. Consequently, high amount of FP is reported for RF-OS. Additionally, the probability class analysis showed lower confidence of predictions (probabilities close to 0.5) in cases with larger Manning coefficients (
Figure 8). The results in terms of class probability provide additional information that can be considered for decision making. In this regard, other algorithms more specifically developed for considering uncertainty may also be useful, such as deep Gaussian processes [
67,
68].
The use of regression ML models could be considered as an alternative to the proposed procedure, i.e., models to predict the numerical value of water depth and velocity. The drawback of this approach is that it would be necessary to use two models in parallel for both variables involved in the risk estimation. In addition, the problem of imbalanced training set remains, as there would be a much higher number of points with low (Class 0) versus high (Class 1) velocity and depth. Although there are procedures to balance training sets for regression, the process should be performed twice for both variables.
The results of Iber models have been considered as the reference solution (“ground truth” in machine learning terminology) throughout this work. This allowed for analysing the prediction capacity of the algorithm itself and the effect of aspects such as the training parameters and the balance of the sample or the threshold. The models used for the validation set follow the same scheme as those in the training set, defined in
Figure 1. This is reflected in the similarity between the results obtained for the test set (
Table 4) and the validation set (
Table 5) for all the indices considered.
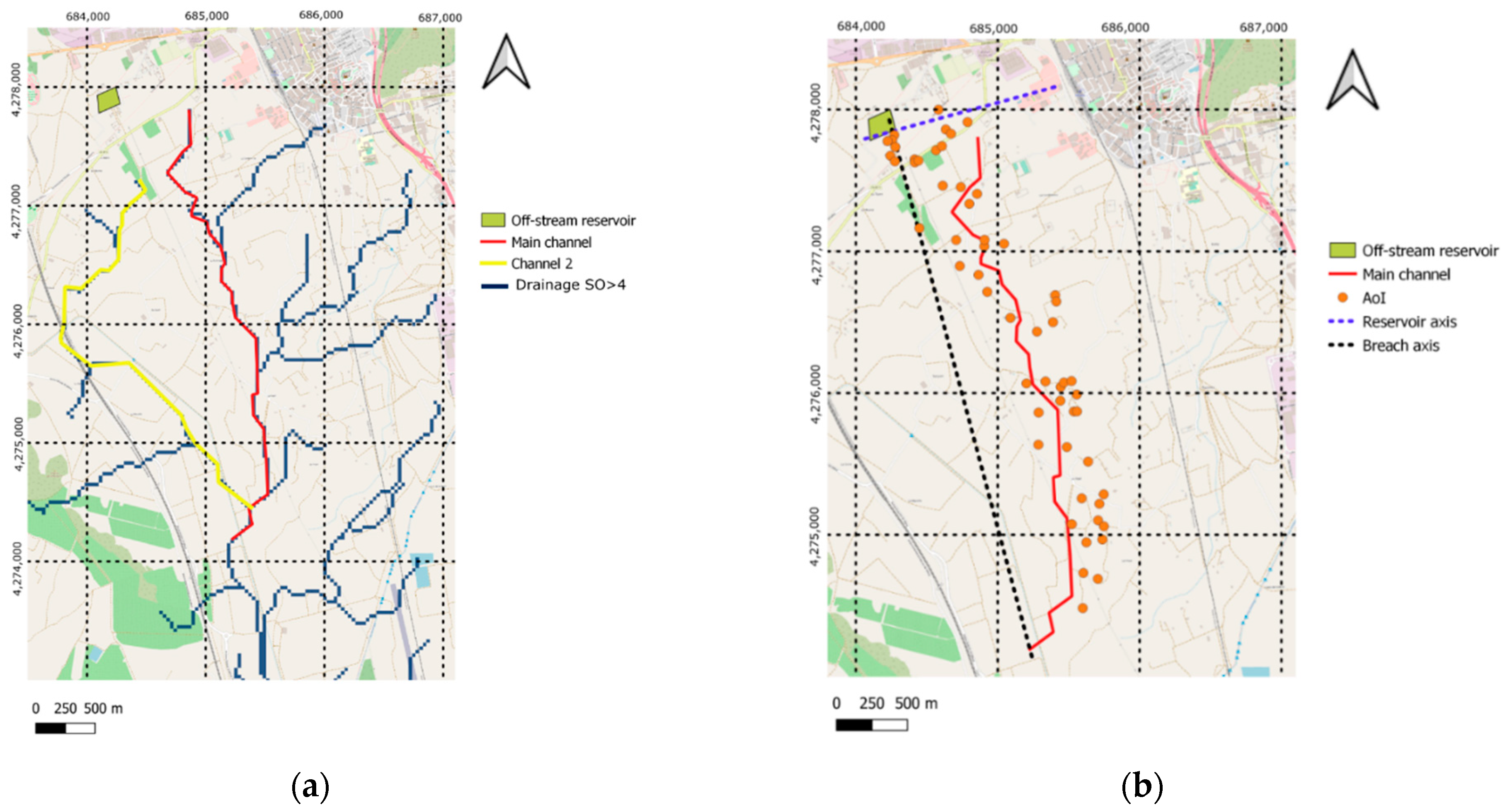
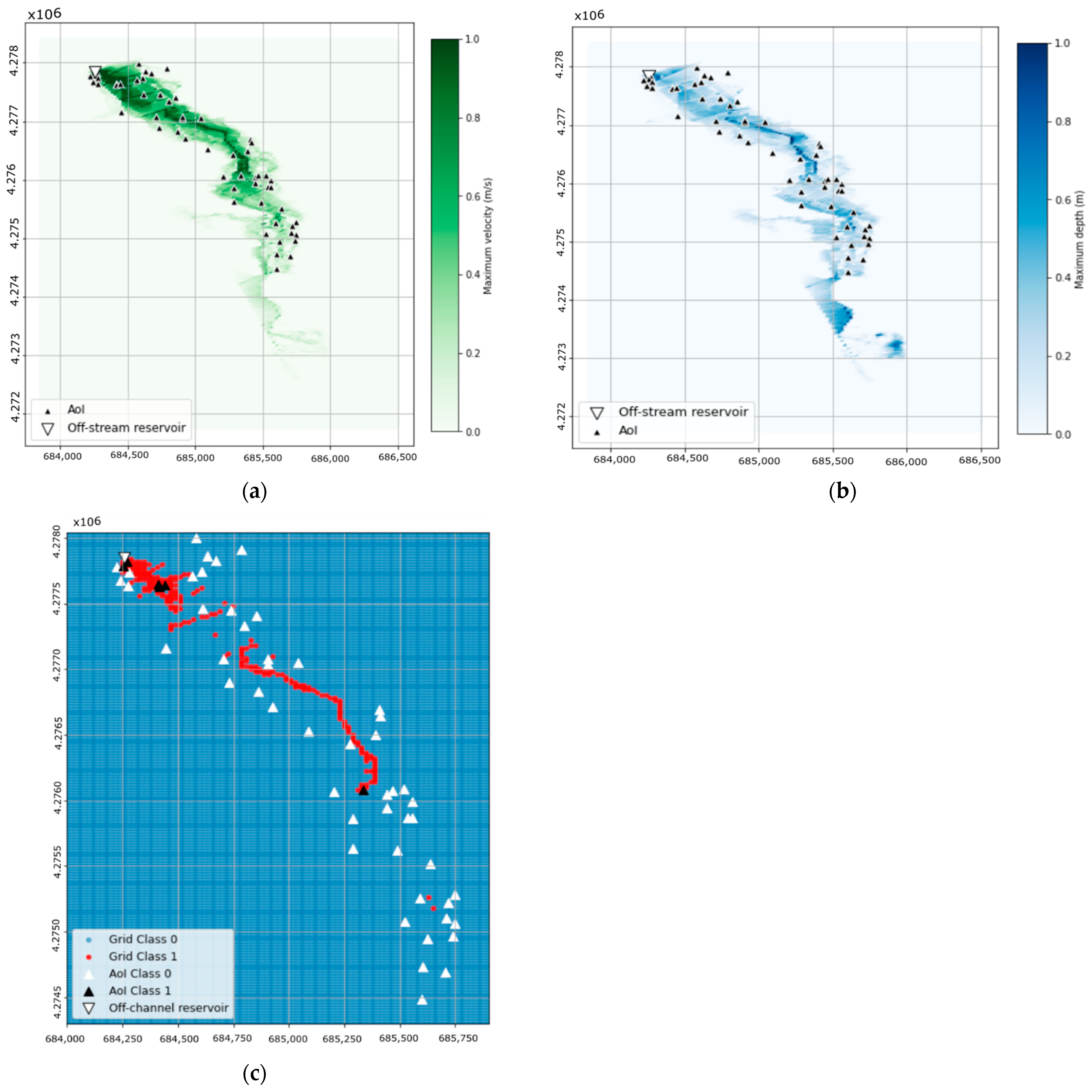
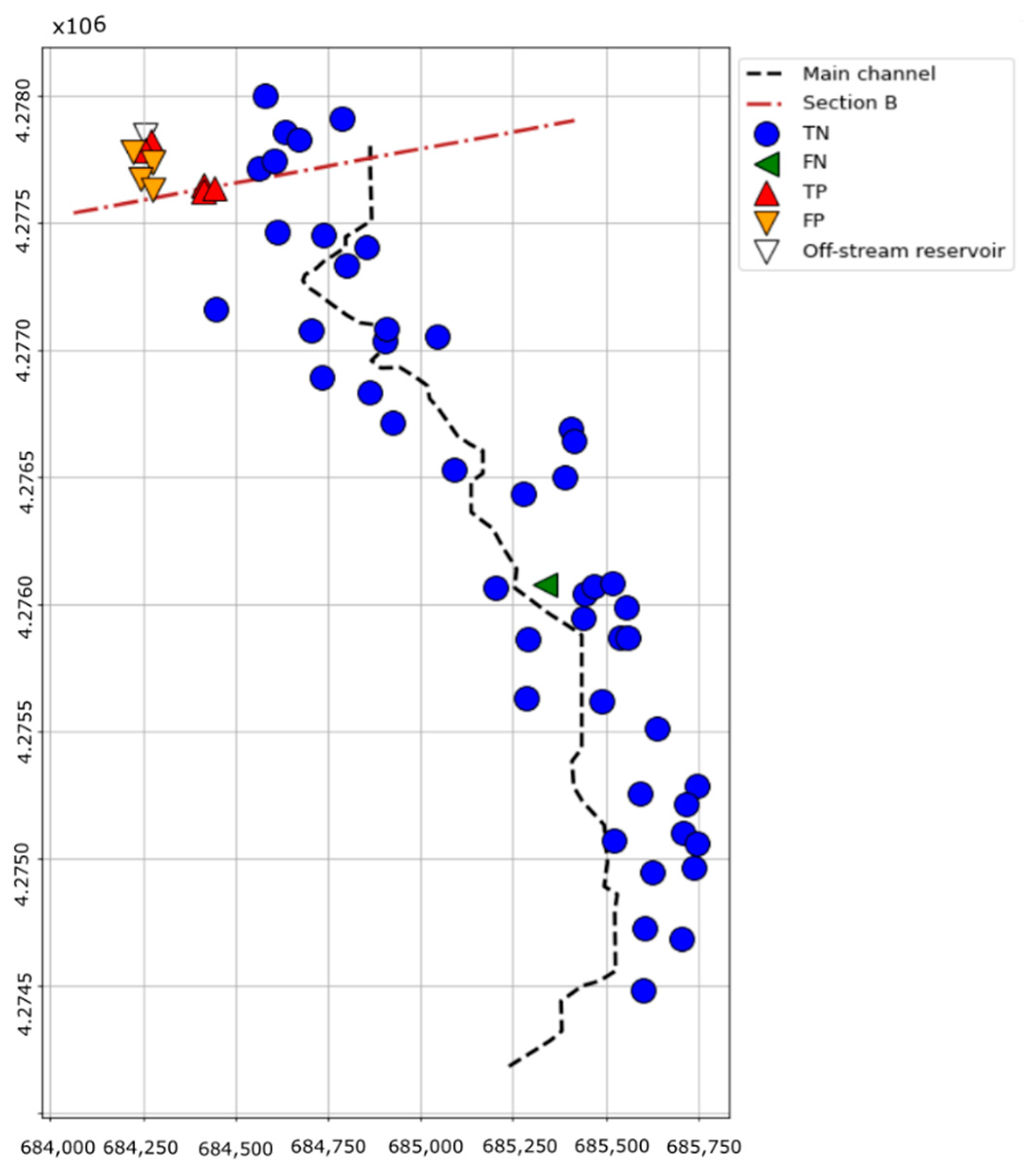
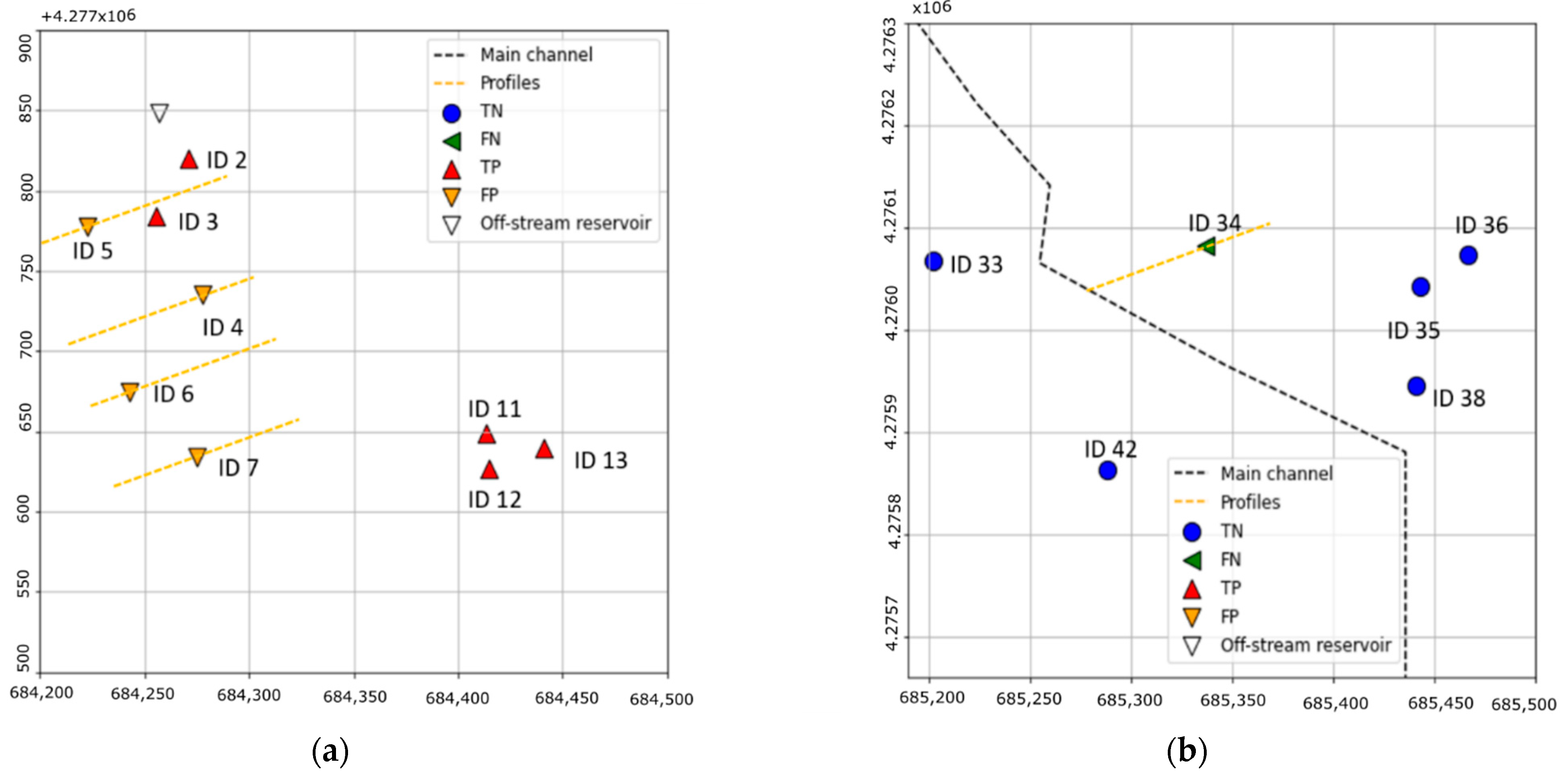
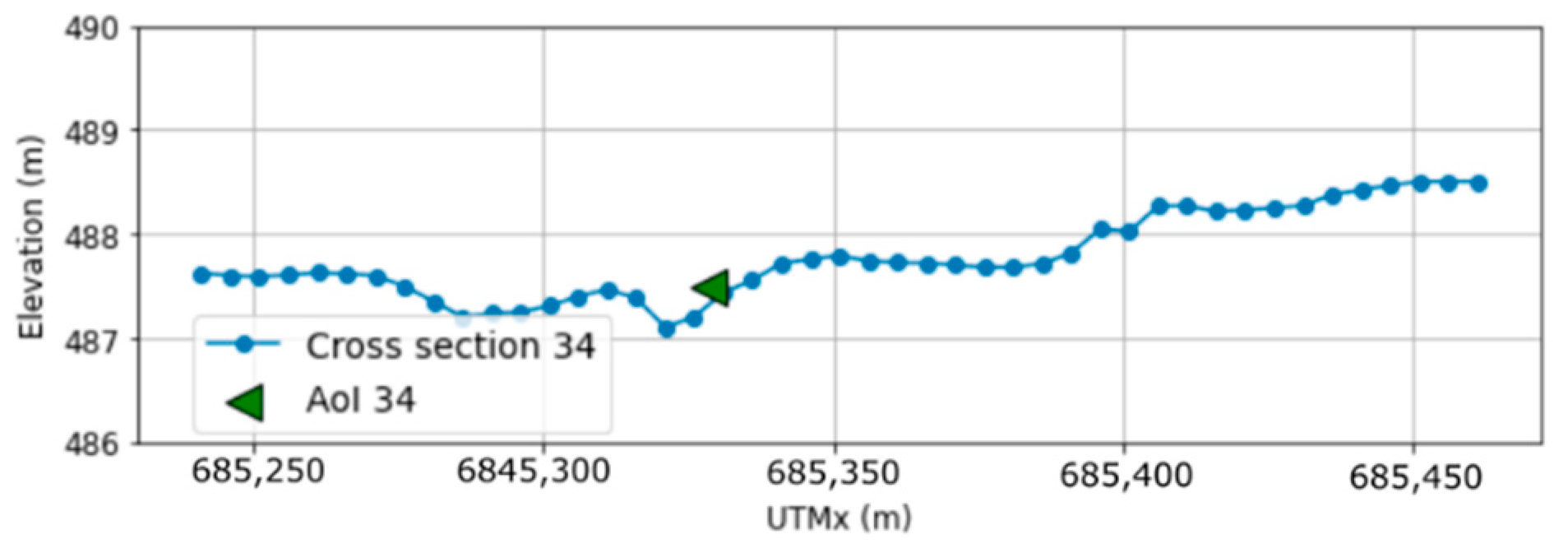
On the contrary, the case of the El Rubial reservoir presents relevant differences with respect to the artificial geometries. First, the parameterization of the geometry implies a relevant simplification of the real terrain: a constant cross-section of the main channel is used, the roughness is unique for the entire model, and average values are taken for longitudinal and transverse slopes of sections B and C. This implies a loss of accuracy. However, the results regarding the classification suggest that the main cause of the discrepancy is the resolution of the DEM used, which is higher in the complete (5 m) than in the simplified model (30 m). This is clearly the origin of the observed FN (
Figure 19) and is related to the FN recorded in the vicinity of the reservoir.
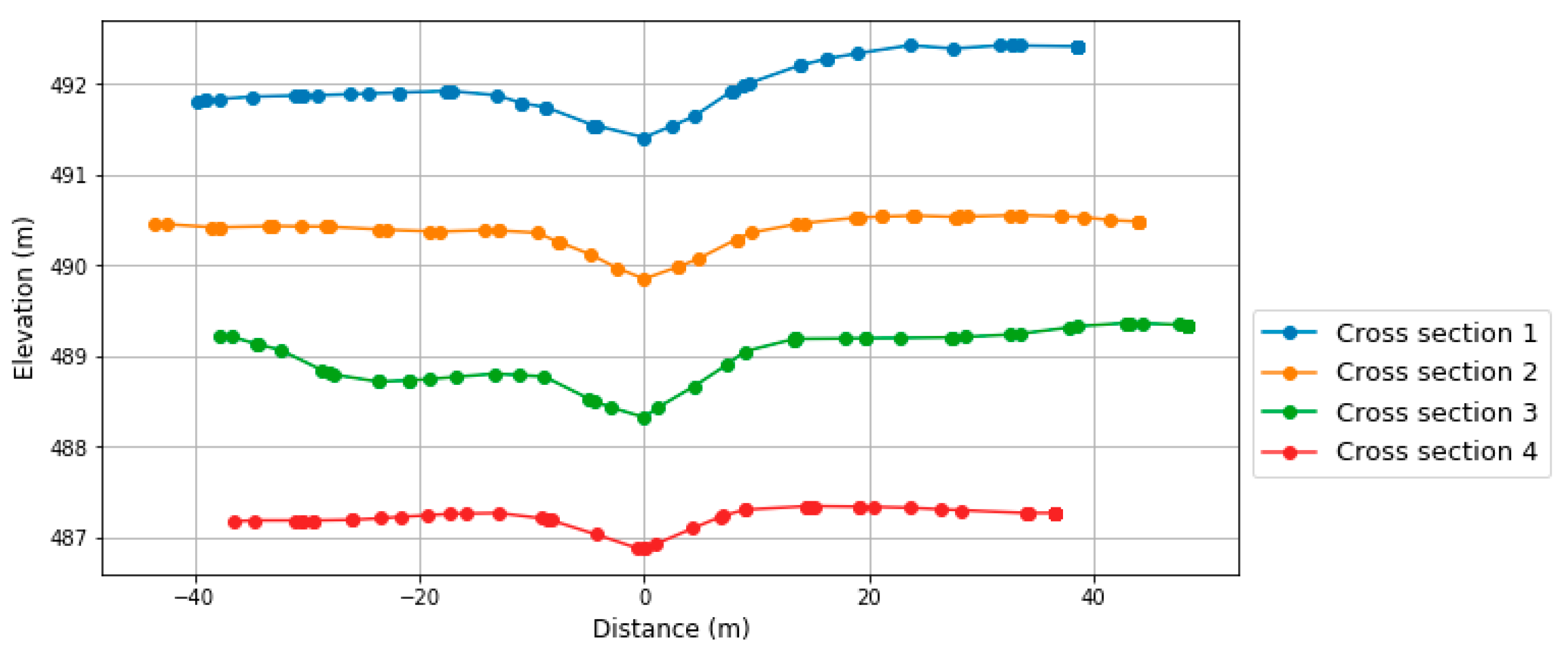
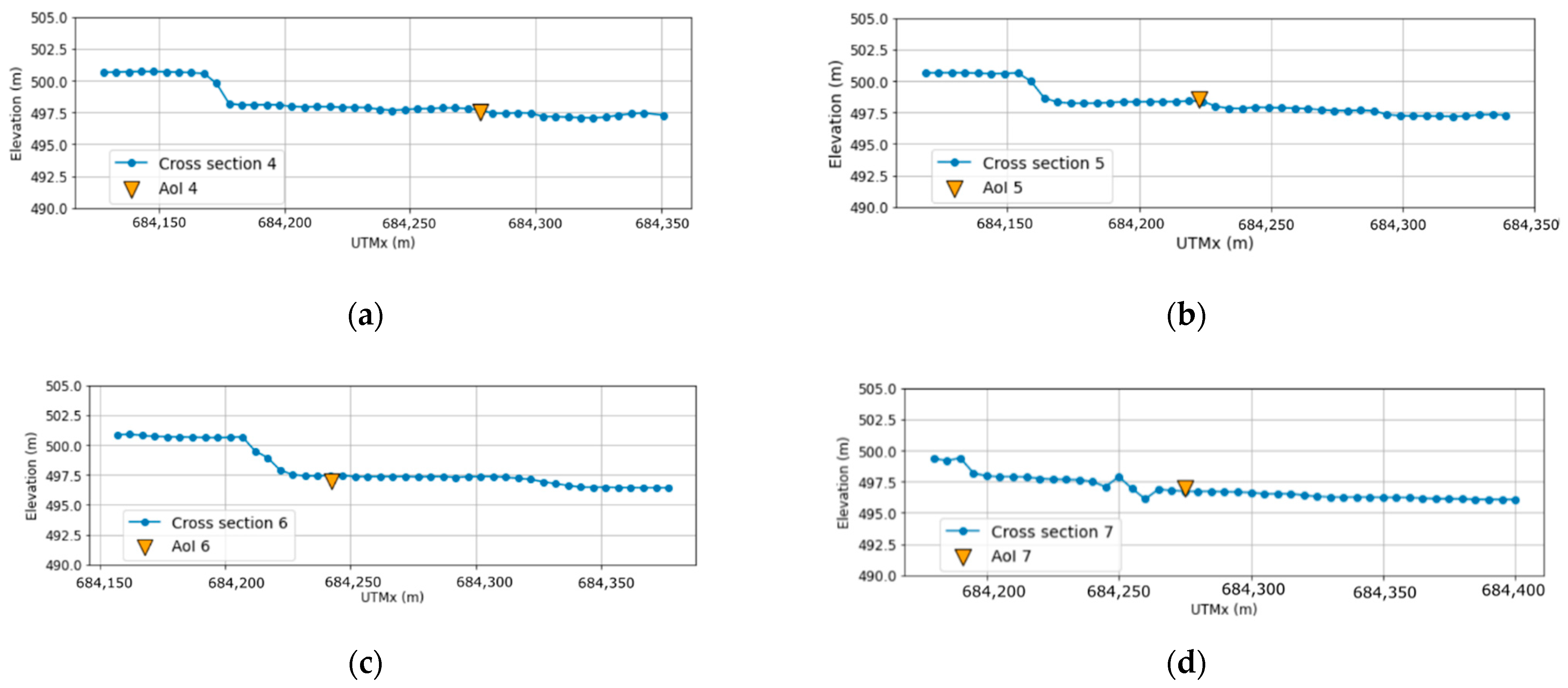
The definition of section B, where all FP are located, is also influential in prediction accuracy. While no transversal slope is considered in this section in the parameterized geometry, the profiles from the high-resolution DEM (
Figure 18) show a slope towards the northeast that conveys the main flow towards that area in the complete model, away from the AoI, which remains unaffected. This is not considered in the simplified model, which results in a large area classified as Class 1 in the vicinity of the reservoir (
Figure 20).
Although the developed model is based on the risk criteria defined by Spanish regulations, the methodology can be directly applied to other criteria, such as those proposed by Smith et al. [
69]. The models from the training database could be used with the only change of adapting the class of each point to the criteria used based on the water velocity and depth. It would suffice to train a new model with the adjusted classification, which has a low computational cost.
A limitation of the methodology and the simplified model is due to the dimensions of the domain considered and, in general, to the ranges of variation used to define the parameters of the models in the training set (
Table 1). Although they have been selected to represent the most common geometry of this type of reservoirs and its surrounding terrain, there may be cases with dimensions outside these ranges, either for the reservoir or the terrain (dimensions of the main channel or slopes). It is well known that ML-based models are unreliable when applied to cases outside the range of variation of the training data. This can be solved by expanding the training database with more cases with wider ranges of variation. As mentioned before, the cases already calculated can be used to train new, more accurate ML models.
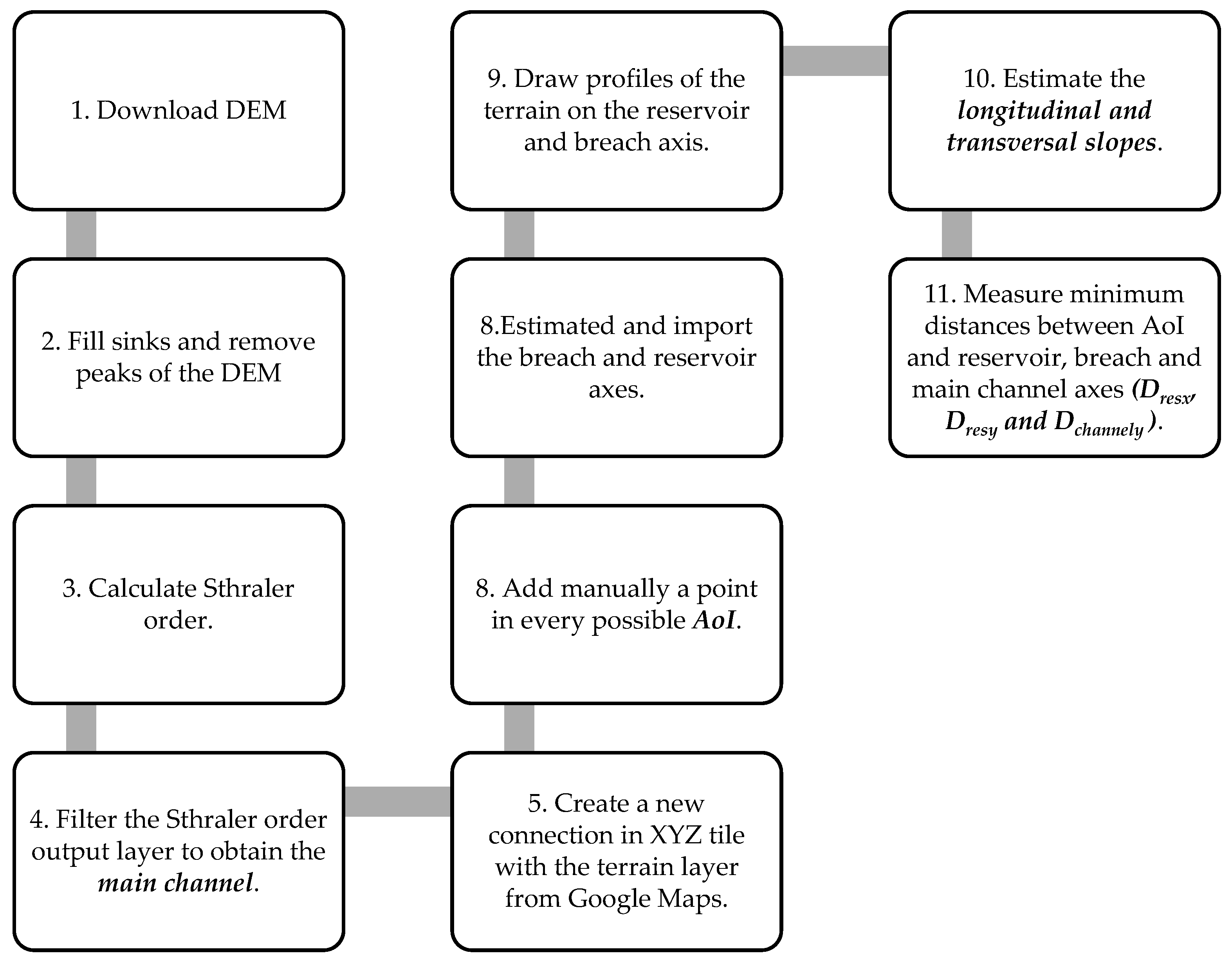
The application of the ML model to a real case led to the development of a step-by-step procedure based on the open-source software QGIS (
Figure 11). Although the definition of the parameters of the simplified geometry and the location of the AoI involve several steps involving GIS tools, the process is simpler and faster to implement than the complete method. In addition, the necessary information can also be obtained from free online tools, with lower requirements in terms of time and software.
Despite the described limitations of the model and the differences with the actual El Rubial reservoir, the ML model correctly predicted 91% of the AoI. This accuracy is higher than that obtained in related studies [
12,
13], although they cannot be directly compared due to the existing differences. Correct identification of parameters and selection of DEM is critical for the performance of the model: DEM with a small resolution can result in a more detailed drainage network and a better selection of the main channel.
6. Summary and Conclusions
A simplified methodology is presented to estimate the zones with risk to human life in case of a failure of an off-stream reservoir, based on the Spanish regulations (Class 0: no risk, Class 1: risk). The methodology makes use of a surrogate ML model based on RF and trained with a set of artificial cases automatically generated and run with Iber. Given the results for maximum flow velocity and depth, points are classified as a function of the risk to human life. The inputs to the ML model include geometrical parameters of the reservoir and surrounding area and the location of the AoI concerning the reservoir and the main channel.
The imbalanced distribution of classes in the training had a great effect in the performance of the surrogate models. Two approaches were assessed to alleviate this issue: SMOTE and random undersampling. Although the accuracy and OOB error rate of both RF models were similar, the use of different balanced datasets affects the model’s capacity to predict the risk zones. The RF-US model presented measures of accuracy higher than 0.8 and a superior capacity to estimate Class 1 areas. The model was assessed with a validation dataset, analysing the influences of the Manning coefficient, class probability and operating point of the RF model.
The analysis of the ROC curve and variation of the operating point to estimate risk areas showed that lowering the decision threshold could enhance the F2 score, especially in cases with larger roughness. However, this leads to an overestimation of risk areas. The selection of the operating point depends on the nature of the case and the preferences of the modeller.
The application of the ML model to a real case showed the needed efforts to extract the input data. The identification of the main flow path and location of AoI are essential for accurate predictions. The results are highly dependent on the quality of the geometrical information provided: the resolution of the DEM and the similarities between the simplified and the actual geometry. The best choice should be a trade-off between desired accuracy and available resources. Nonetheless, the simplified methodology can be applied in any setting and requires less time and computational resources. Therefore, the simplified RF model can be useful for owners and administrations of off-stream reservoirs to prioritize the allocation of resources to carry out detailed classification studies or to make investments to increase safety.