A Study on the Mechanism and Pricing of Drainage Rights Trading Based on the Bilateral Call Auction Model and Wealth Utility Function
Abstract
:1. Introduction
2. Study on the Transaction Mechanism of Bilateral Call Auction of Drainage Rights
2.1. Basic Assumptions
2.2. Model Construction
2.2.1. Rational Price Constraints
2.2.2. Macroscopic Control Total Quantity Constraints
2.3. Clearance Rules
2.4. Matching Rules
3. Transaction Pricing Study of Bilateral Call Auction for Drainage Rights
3.1. Wealth Utility Function Construction
3.2. Social Welfare Function Construction
3.3. Solving for the Transaction Price
4. Simulation of Calculations for Drainage Rights Trading in Jiangsu Section of Huaihe River Basin
4.1. Study Area
4.2. Simulation of Drainage Rights Trading Mechanism
4.2.1. Clearance Rule
4.2.2. Matching Transaction Sets
4.3. Simulation of the Pricing of Drainage Rights Transactions
4.3.1. Wealth Utility Function
4.3.2. Social Welfare Function
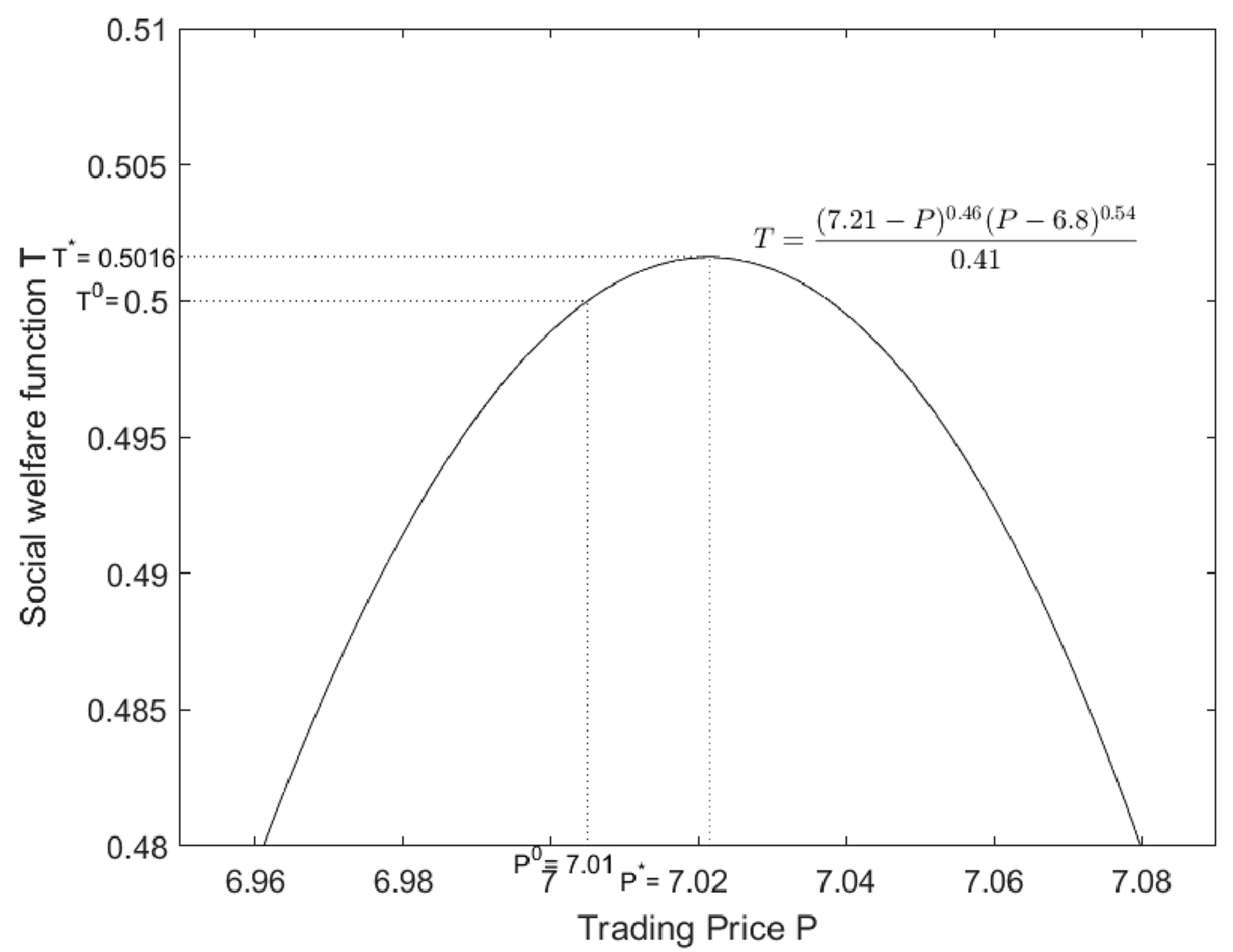
4.3.3. Optimal Transaction Price
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, P.; He, B.; Takara, K.; Xiong, Y.E.; Nover, D.; Duan, W.; Fukushi, K. Historical assessment of Chinese and Japanese flood management policies and implications for managing future floods. Environ. Sci. Policy 2015, 48, 265–277. [Google Scholar]
- Scrase, J.I.; Sheate, W.R. Integration and integrated approaches to assessment: What do they mean for the environment? J. Environ. Policy Plan. 2010, 4, 275–294. [Google Scholar]
- Krieger, K. Putting Varieties of Risk-Based Governance into Institutional Context: The Case of Flood Management Regimes in Germany and England in the 1990s and 2000s. Ph.D. Thesis, King’s College London (University of London), Strand, London, UK, 2012. [Google Scholar]
- Zhang, M.; Wang, J. Global Flood Disaster Research Graph Analysis Based on Literature Mining. Appl. Sci. 2022, 12, 3066. (In Chinese) [Google Scholar]
- Yu, F.; Wang, Y.; Yuan, X.; Jiang, S. A preliminary investigation of the concept of drainage rights and its basic characteristics. J. Irrig. Drain. 2014, 33, 134–137. (In Chinese) [Google Scholar]
- Zhang, D.; Shen, J.; Sun, F.; Liu, B.; Wang, Z.; Zhang, K.; Li, L. Research on the Allocation of Flood Drainage Rights of the Sunan Canal Based on a Bi-level Multi-Objective Programming Model. Water 2019, 11, 1769. [Google Scholar]
- Zhang, D.; Shen, J.; Liu, P.; Sun, F. Allocation of Flood Drainage Rights Based on the PSR Model and Pythagoras Fuzzy TOPSIS Method. Int. J. Environ. Res. Public Health 2020, 17, 5821. [Google Scholar]
- Zhang, K.; Shen, J.; Han, H.; Zhang, J. Study of the Allocation of Regional Flood Drainage Rights in Watershed Based on Entropy Weight TOPSIS Model: A Case Study of the Jiangsu Section of the Huaihe River, China. Int. J. Environ. Res. Public Health 2020, 17, 5020. [Google Scholar]
- Zhang, D.; Shen, J.; Liu, P.; Zhang, Q.; Sun, F. Use of Fuzzy Analytic Hierarchy Process and Environmental Gini Coefficient for Allocation of Regional Flood Drainage Rights. Int. J. Environ. Res. Public Health 2020, 17, 2063. [Google Scholar]
- Sun, F.; Lai, X.; Shen, J.; Nie, L.; Gao, X. Initial allocation of flood drainage rights based on a PSR model and entropy-based matter-element theory in the Sunan Canal, China. PLoS ONE 2020, 15, e0233570. [Google Scholar]
- Zhang, J.; Zhang, C.; Liu, L.; Shen, J.; Zhang, D.; Sun, F. The necessity and feasibility of drainage rights allocation and trading in Jiangsu Province. Water Resour. Prot. 2019, 35, 5. (In Chinese) [Google Scholar]
- Lai, X.-P.; Sun, F.-H.; Shen, J.-Q.; Gao, X.; Zhang, D. Study on the influencing factors of regional drainage rights allocation based on WSR. Water Econ. 2020, 38, 8. (In Chinese) [Google Scholar]
- Jin, G.; Wang, P.; Zhao, T.; Bai, Y.; Zhao, C.; Chen, D. Reviews on land use change induced effects on regional hydrological ecosystem services for integrated water resources management. Phys. Chem. Earth 2015, 89–90, 33–39. [Google Scholar]
- Zhang, K.; Shen, J. Research on the management of drainage rights trading in China under quasi-markets—Based on the perspective of evolutionary game. J. Henan Univ. Soc. Sci. Ed. 2019, 4, 9. (In Chinese) [Google Scholar]
- Dong, C.; Huang, Y.-Y.; Zhao, Y.; Lu, H. Analysis of the development status of urban rainwater utilization at home and abroad. China Resour. Compr. Util. 2017, 35, 30–32. (In Chinese) [Google Scholar]
- Werritty, A. Sustainable flood management: Oxymoron or new paradigm? Area 2006, 38, 16–23. [Google Scholar]
- Porter, J.; Demeritt, D. Flood-risk management, mapping, and planning: Theinstitutional politics of decision support in England. Environ. Plan. A 2012, 44, 2359–2378. [Google Scholar]
- Buuren, A.V.; Ellen, G.J.; Warner, J.F. Path-dependency and policy learning in the Dutch delta: Toward more resilient flood risk management in the Netherlands? Ecol. Soc. 2016, 21, 43. [Google Scholar]
- Shen, J.; Zhan, Q.; Cao, Q.; Sun, F.; Zhang, K.; Zhang, D.; Zhao, M. The pricing method of drainage rights trading based on full cost method and its application. Water Econ. 2022, 40, 7. (In Chinese) [Google Scholar]
- Shen, J.; Wang, X.; Sun, F. Research on the pricing method of drainage rights trading in China under quasi-market. Water Econ. 2021, 39, 7. (In Chinese) [Google Scholar]
- Scrase, J.I.; Sheate, W.R. Re-framing Flood Control in England and Wales. Environ. Values 2005, 14, 113–137. [Google Scholar]
- Zhang, Y.; Guo, R. Scientific drainage to improve urban flooding in the UK. Henan Water Resour. South-North Water Divers. 2011, 19, 48. (In Chinese) [Google Scholar]
- Wlliott, A.H.; Trowsdale, S.A. Areview of models for low impact urban stormwater grainage. Environ. Model. Softerware 2007, 22, 394–405. [Google Scholar]
- Wang, H.-F.; Fan, Z.-W.; Luo, L.; Zhang, W. The inspiration of foreign urban rainwater utilization financial support policy to China. Water Resour. Dev. Res. 2014, 14, 12–15. (In Chinese) [Google Scholar] [CrossRef]
- Sun, F.; Du, X.; Shen, J. An asymmetric information bargaining model for pricing drainage rights transactions based on fair preferences. Resour. Ind. 2020, 22, 10. (In Chinese) [Google Scholar]
- Tian, G.; Liu, J.; Wei, B. Pricing and simulation of water discharge rights in Taihu Lake basin based on improved bilateral bidding auction model. Ecol. Econ. 2020, 36, 6. (In Chinese) [Google Scholar]
- Chen, W.; Cao, S. Application of improved bilateral call auction model in water rights trading. China Rural. Water Conserv. Hydropower 2010, 3, 3. (In Chinese) [Google Scholar]
- Son, Y.S.; Baldick, R.; Siddiqi, S. Reanalysis of “Nash Equilibrium Bidding Strategies in a Bilateral Electricity Market”. Ieee Trans. Power Syst. 2004, 19, 1243–1244. [Google Scholar]
- Markus, V. Utility of wealth with many indivisibilities—ScienceDirect. J. Math. Econ. 2017, 71, 20–27. [Google Scholar]
- Estimation of Direct and Indirect Economic Losses Caused By a Flood With Long-lasting Inundation: Application To the 2011 Thailand Flood. Ecol. Environ. Conserv. 2020, 56, e2019WR026092.
- Smith, A. On the Division of Labour. In The Wealth of Nations, Books I–III; Penguin Classics: New York, NY, USA, 1986; p. 119. [Google Scholar]
- Hirai, H.; Sato, R. Polyhedral Clinching Auctions for Two-Sided Markets. Math. Oper. Res. 2021, 47, 259–285. [Google Scholar]
- Wu, F.; You, M.; Yu, Q. A study on wealth utility-based pricing model of emission rights under multiple scenarios. Soft Sci. 2017, 31, 108–111, 140. (In Chinese) [Google Scholar] [CrossRef]
- Grant, A.; Satchell, S. Investment decisions when utility depends on wealth and other attributes. Quant. Financ. 2020, 20, 499–513. [Google Scholar]
- Pollak, R.A. Bergson-Samuelson Social Welfare Functions and the Theory of Social Choice. Q. J. Econ. 1979, 93, 73–90. [Google Scholar]
- Nash, J.F. The Bargaining Problem. Econometrica 1950, 18, 155–162. [Google Scholar]
- Gini Coefficient Analysis of Regional Differences in Energy Utilization Under the Concept of Low-carbon Ecological Environmental protection. Ecol. Environ. Conserv. 2019, 28, 2149–2160.
- Wu, F.; Cao, Q.D.; Zhang, D.; Sun, F.; Shen, J. Allocation of drainage rights of the Sunan Canal based on environmental Gini coefficient. J. Henhai Univ. Nat. Sci. Ed. 2020, 48, 6. (In Chinese) [Google Scholar]



| Buyer Bi | Seller Sj | ||||
|---|---|---|---|---|---|
| Buyer | Expected Acquisition Price oi (yuan/m3) | Expected Acquisition Volume xi (m3) | Seller | Expected Sales Price fj (yuan/m3) | Expected Sales Volume yj (m3) |
| B1 | 8.14 | 100 | S4 | 4.38 | 37.5 |
| B3 | 7.21 | 100 | S3 | 6.47 | 50 |
| B2 | 5.83 | 50 | S2 | 6.80 | 75 |
| B4 | 5.20 | 62.5 | S1 | 9.45 | 100 |
| Transaction Serial Number | Buyer Bi | Seller Sj | Expected Trading Volume (m3) | Expected Acquisition Price oi (yuan/m3) | Expected Sales Price fj (yuan/m3) |
|---|---|---|---|---|---|
| I | B1 | S4 | 37.5 | 8.14 | 4.38 |
| II | B1 | S2 | 62.5 | 8.14 | 6.80 |
| III | B3 | S3 | 50 | 7.21 | 6.47 |
| IV | B3 | S2 | 12.5 | 7.21 | 6.80 |
| Indicators (Arithmetic Average of the Previous Three Years) | B1 | S4 |
|---|---|---|
| GDP (100 million yuan) | 5911.45 | 2392.48 |
| Land area (km2) | 3063 | 3012 |
| Population (10,000 people) | 336.2 | 222.01 |
| Flooding direct economic loss (100 million yuan) | 1.44 | 0.03 |
| Indicators | Transaction I | Transaction II | Transaction III | Transaction IV | ||||
|---|---|---|---|---|---|---|---|---|
| B1 | S4 | B1 | S2 | B3 | S3 | B3 | S2 | |
| GDP | 0.05 | 0.95 | 0.36 | 0.64 | 0.58 | 0.42 | 0.1 | 0.9 |
| Land | 0.02 | 0.98 | 0.37 | 0.63 | 0.80 | 0.20 | 0.73 | 0.27 |
| Population | 0.03 | 0.97 | 0.39 | 0.61 | 0.65 | 0.35 | 0.56 | 0.44 |
| Average | 0.03 | 0.97 | 0.37 | 0.63 | 0.67 | 0.33 | 0.46 | 0.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, J.; Zhu, T.; Sun, F. A Study on the Mechanism and Pricing of Drainage Rights Trading Based on the Bilateral Call Auction Model and Wealth Utility Function. Water 2022, 14, 2269. https://doi.org/10.3390/w14142269
Shen J, Zhu T, Sun F. A Study on the Mechanism and Pricing of Drainage Rights Trading Based on the Bilateral Call Auction Model and Wealth Utility Function. Water. 2022; 14(14):2269. https://doi.org/10.3390/w14142269
Chicago/Turabian StyleShen, Juqin, Tingting Zhu, and Fuhua Sun. 2022. "A Study on the Mechanism and Pricing of Drainage Rights Trading Based on the Bilateral Call Auction Model and Wealth Utility Function" Water 14, no. 14: 2269. https://doi.org/10.3390/w14142269
APA StyleShen, J., Zhu, T., & Sun, F. (2022). A Study on the Mechanism and Pricing of Drainage Rights Trading Based on the Bilateral Call Auction Model and Wealth Utility Function. Water, 14(14), 2269. https://doi.org/10.3390/w14142269





