A Case Study of Tidal Analysis Using Theory-Based Artificial Intelligence Techniques for Disaster Management in Taehwa River, South Korea
Abstract
:1. Introduction
- i.
- analyse tidal effects of Taehwa River using theory-based deep learning modeling; and
- ii.
- evaluate contributing effect of wind on tide prediction for disaster prevention and management.
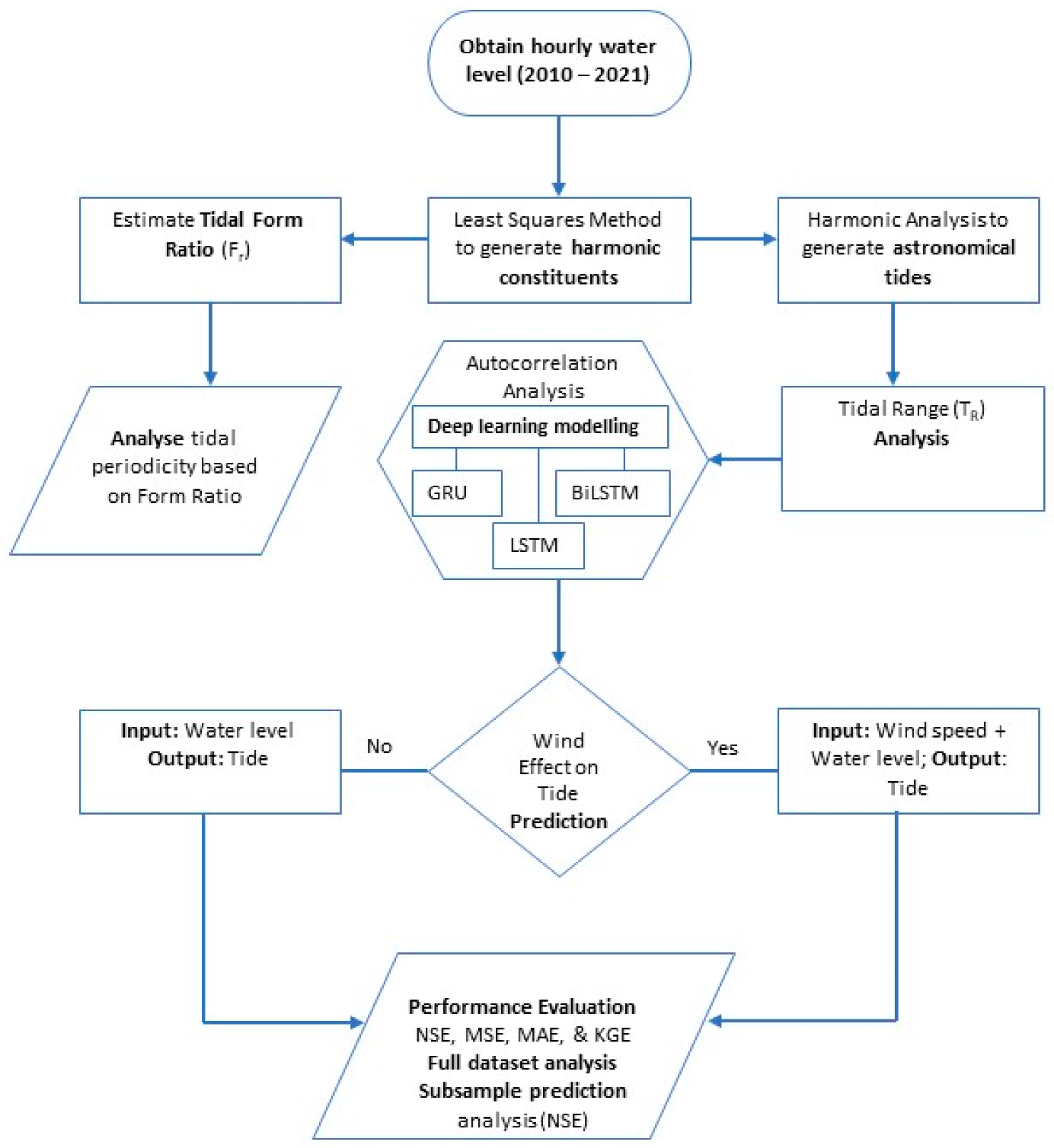
2. Materials and Methods
2.1. Study Area
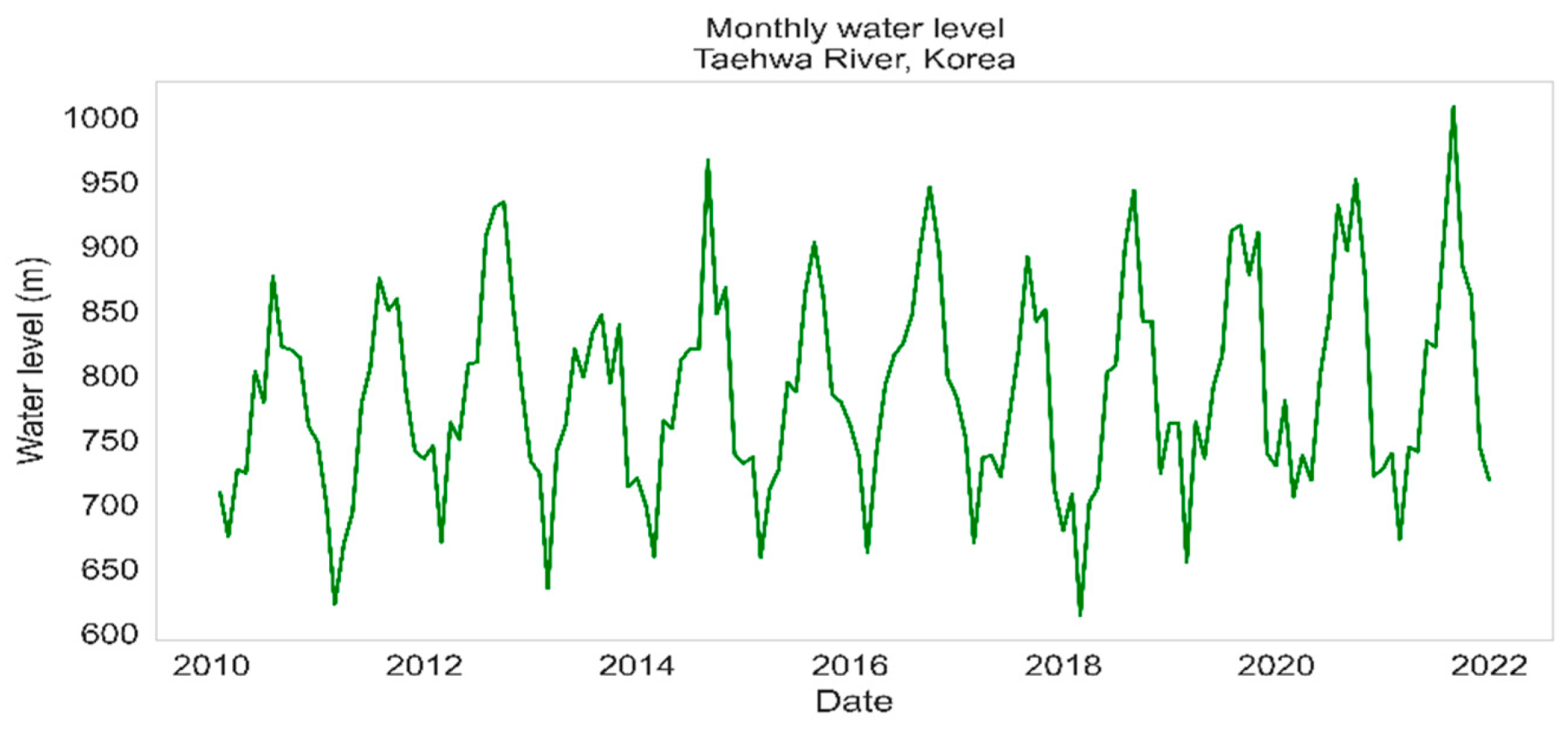
2.2. Data Collection and Model Input
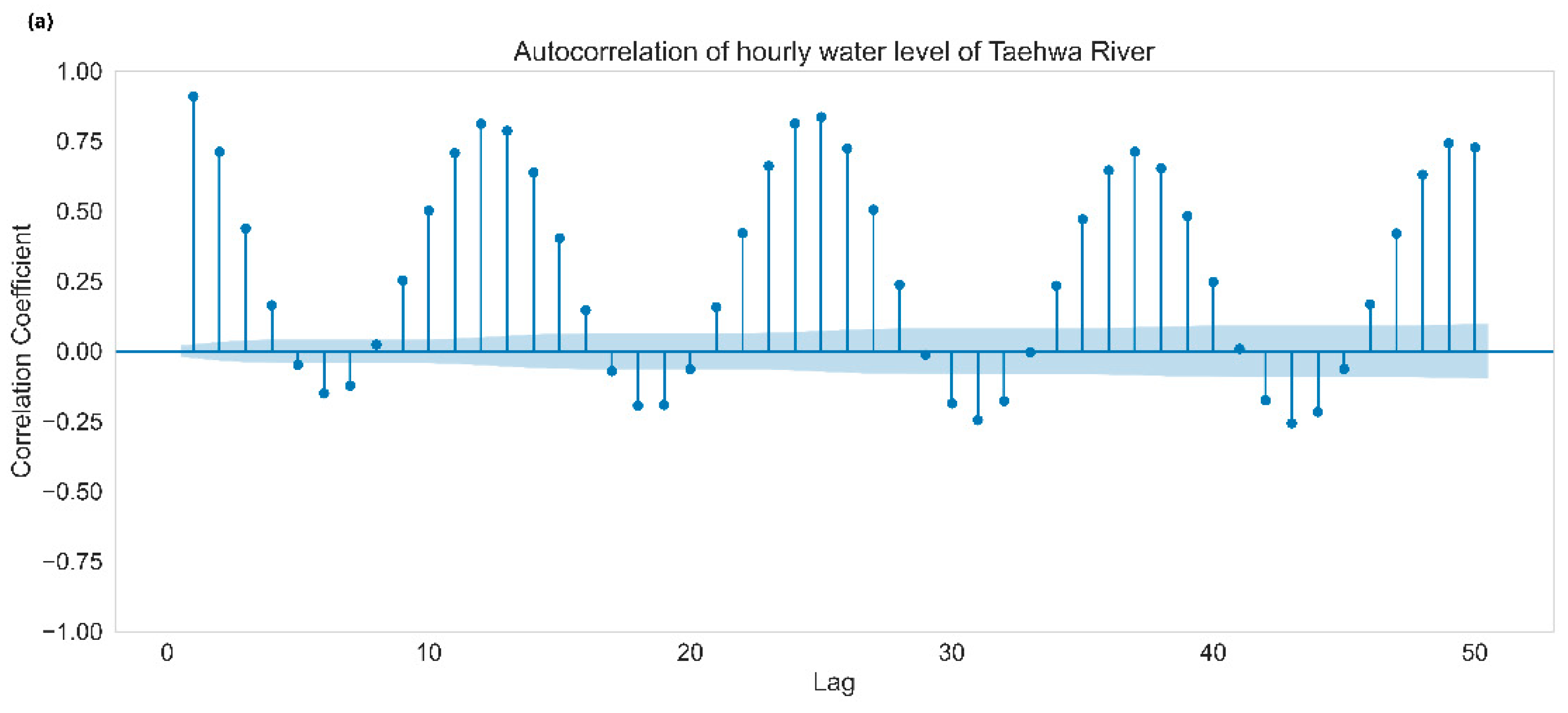
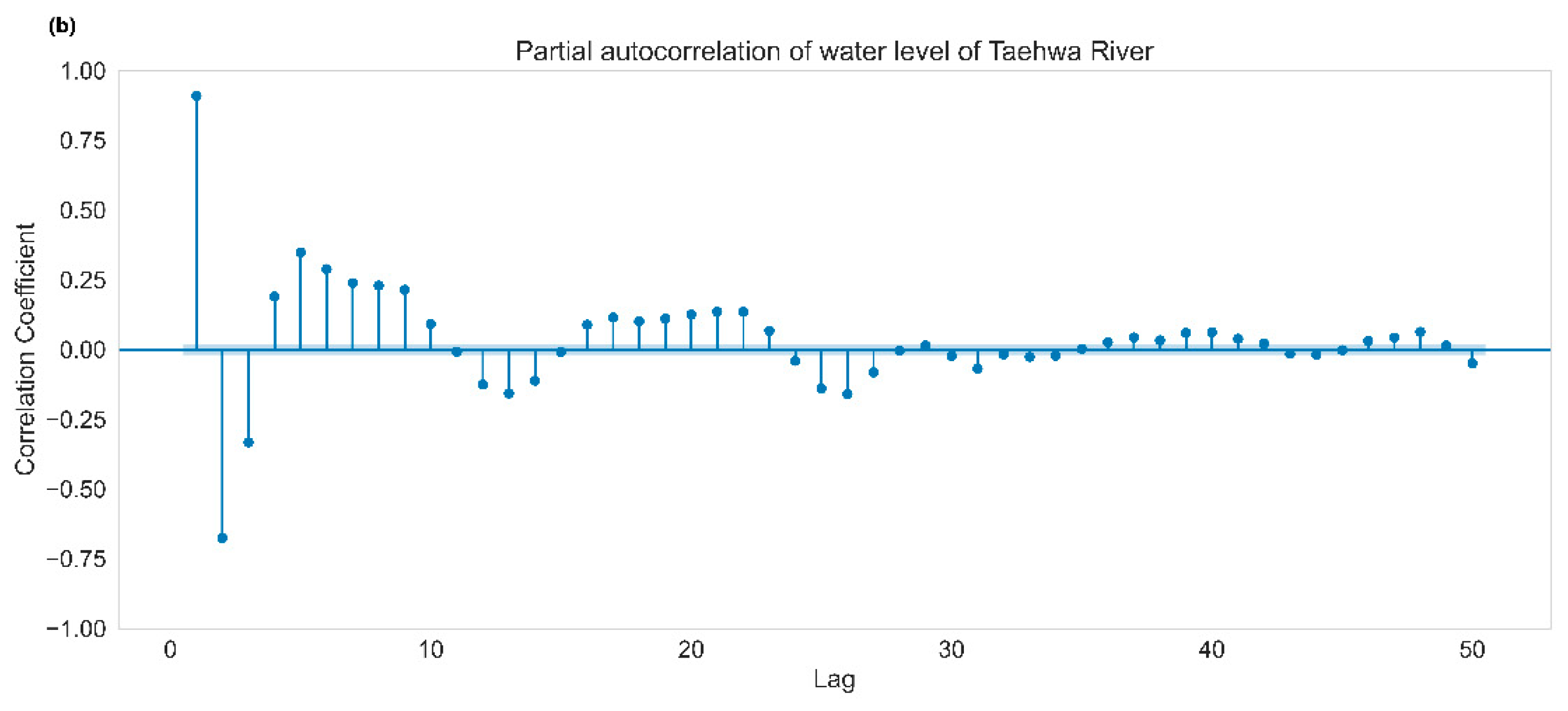
2.3. Harmonic Analysis of Water Level Data of Taehwa River
2.4. Effect of Wind on Tidal Prediction Using Deep Learning Models
- i.
- concatenating wind input with water level to predict harmonically generated tides;
- ii.
- input values of water level without wind data to predict tides.
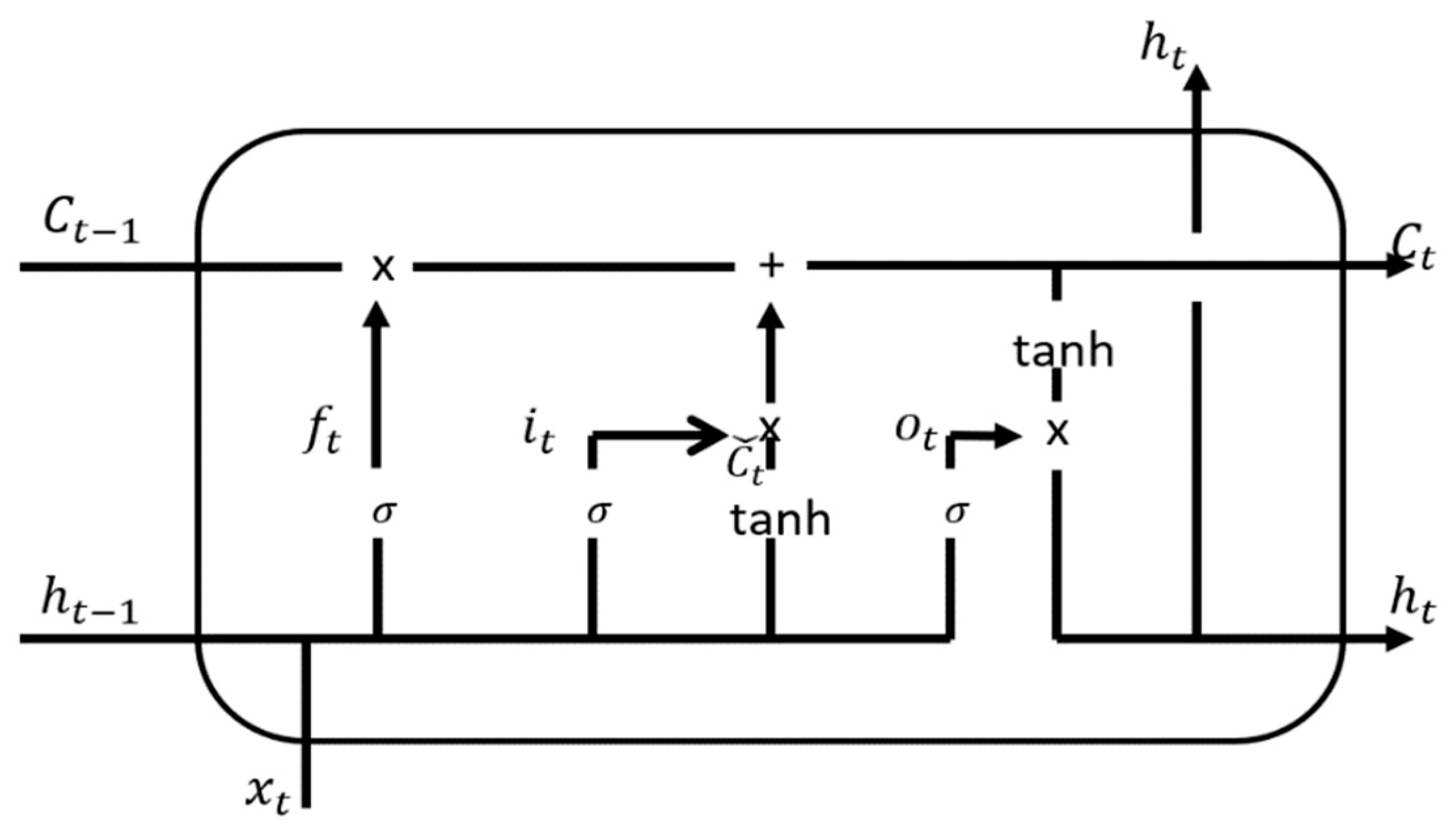
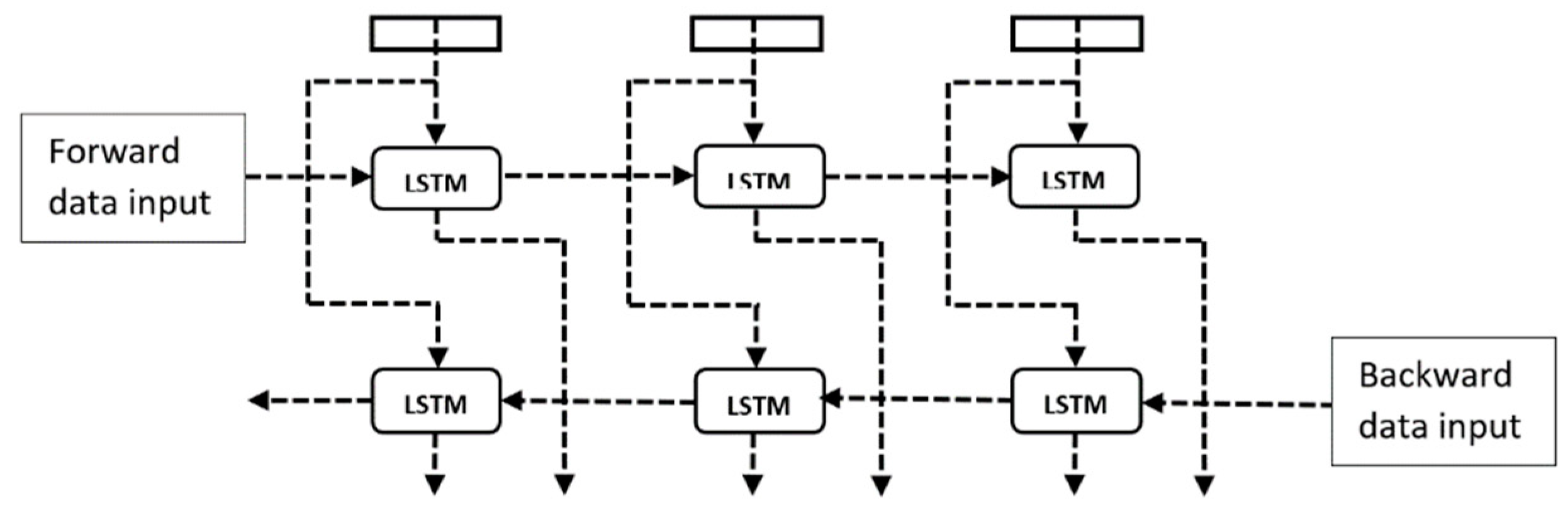
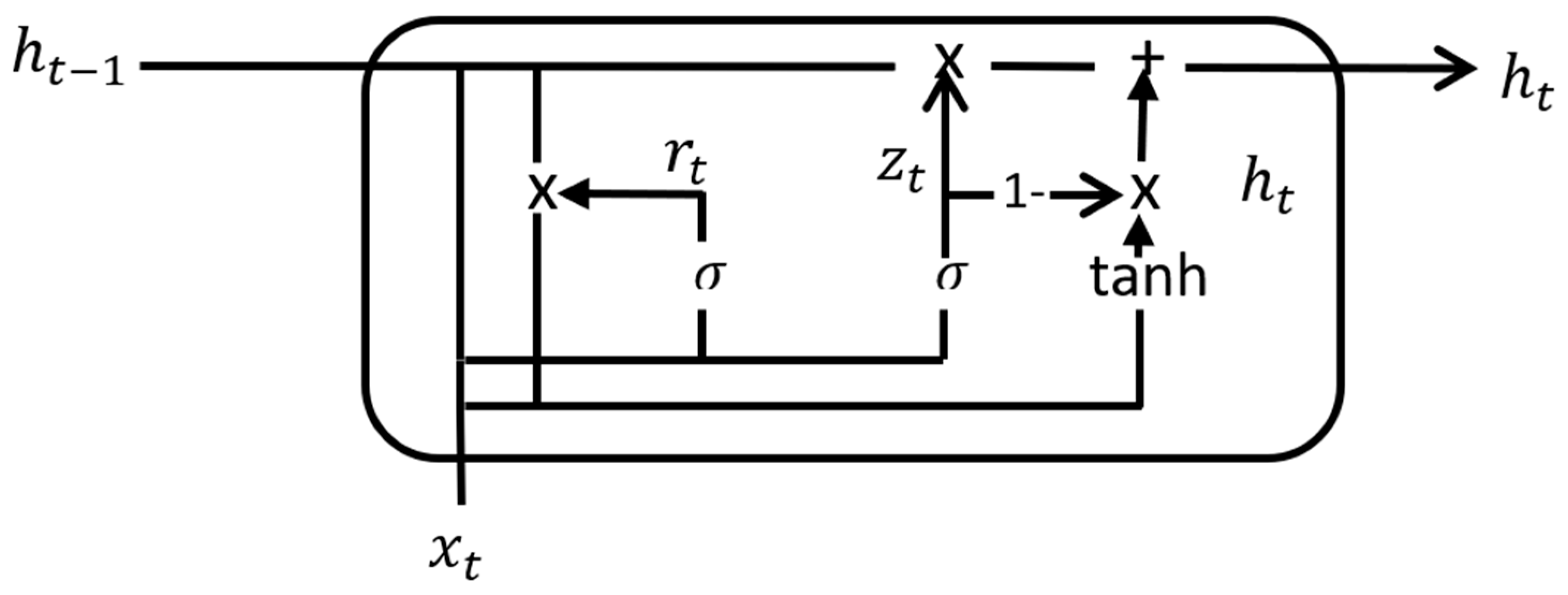
2.5. Deep Learning Model Selection
2.6. Deep Learning Model Creation
3. Results and Discussion
3.1. Results of Harmonic Analysis of the Taehwa River
3.2. Results of Tidal Range across Different Lunar Orientations
3.3. Effect of Wind Speed on Tide Prediction Using Deep Learning Models
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Granata, F.; Di Nunno, F. Artificial Intelligence models for prediction of the tide level in Venice. Stoch. Environ. Res. Risk Assess. 2021, 35, 2537–2548. [Google Scholar] [CrossRef]
- Hoitink, A.J.F.; Jay, D.A. Tidal river dynamics: Implications for deltas. Rev. Geophys. 2016, 54, 240–272. [Google Scholar] [CrossRef]
- Liu, X.; Li, M.; Chen, J.; Xu, Y.J.; Zhang, W.; Chen, Z.; Ai, W.; Hou, L.; Pan, Z. Natural and reservoir-induced channel changes in the Yangtze River Tidal Reach. J. Hydrol. 2021, 605, 127398. [Google Scholar] [CrossRef]
- Garrett, C.R. Tidal Resonance in the Bay of Fundy and Gulf of Maine. Nature 1972, 238, 441–443. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, C.; Wu, Z.; Long, Y.; Deng, B.; Liu, X. Numerical Investigation of Fresh and Salt Water Distribution in the Pearl River Estuary During a Typhoon Using a Fully Coupled Atmosphere-Wave-Ocean Model. Water 2019, 11, 646. [Google Scholar] [CrossRef] [Green Version]
- Cyriac, R.; Dietrich, J.C.; Fleming, J.G.; Blanton, B.O.; Kaiser, C.; Dawson, C.N.; Luettich, R.A. Variability in Coastal Flooding predictions due to forecast errors during Hurricane Arthur. Coast. Eng. 2018, 137, 59–78. [Google Scholar] [CrossRef]
- Gong, W.; Chen, Y.; Zhang, H.; Chen, Z. Effects of Wave–Current Interaction on Salt Intrusion During a Typhoon Event in a Highly Stratified Estuary. Estuaries Coasts 2018, 41, 1904–1923. [Google Scholar] [CrossRef]
- Li, C.; Weeks, E.; Blanchard, B.W. Storm surge induced flux through multiple tidal passes of Lake Pontchartrain estuary during Hurricanes Gustav and Ike. Estuar. Coast. Shelf Sci. 2010, 87, 517–525. [Google Scholar] [CrossRef]
- Lin, N.; Emanuel, K.A.; Smith, J.A.; Vanmarcke, E. Risk assessment of hurricane storm surge for New York City. J. Geophys. Res. Atmos. 2010, 115, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Berke, P.; Larsen, T.; Ruch, C. A computer system for hurricane hazard assessment. Comput. Environ. Urban Syst. 1984, 9, 259–269. [Google Scholar] [CrossRef]
- Sa’Adi, Z.; Ismail, A.Z.; Yusop, Z.; Yusof, Z.M. Effect of the tide on flood modeling and mapping in Kota Tinggi, Johor, Malaysia. Nat. Hazards 2022, 112, 2053–2081. [Google Scholar] [CrossRef]
- Karki, T.K. Flood resilience in Malaysian cities: A case study of two towns in Johor state. Int. J. Disaster Resil. Built Environ. 2019, 11, 329–342. [Google Scholar] [CrossRef]
- Tam, T.H.; Ibrahim, A.L.; A Rahman, M.Z.; Mazura, Z. Flood loss assessment in the Kota Tinggi. IOP Conf. Ser. Earth Environ. Sci. 2014, 18, 12120. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Xu, Y.J. Decadal-Scale Riverbed Deformation and Sand Budget of the Last 500 km of the Mississippi River: Insights Into Natural and River Engineering Effects on a Large Alluvial River. J. Geophys. Res. Earth Surf. 2018, 123, 874–890. [Google Scholar] [CrossRef]
- Yang, H.; Yang, S.; Xu, K.; Milliman, J.; Wang, H.; Yang, Z.; Chen, Z.; Zhang, C. Human impacts on sediment in the Yangtze River: A review and new perspectives. Glob. Planet. Chang. 2018, 162, 8–17. [Google Scholar] [CrossRef]
- Ralston, D.K.; Geyer, W.R. Sediment Transport Time Scales and Trapping Efficiency in a Tidal River. J. Geophys. Res. Earth Surf. 2017, 122, 2042–2063. [Google Scholar] [CrossRef]
- Chen, K.; Kuang, C.; Wang, L.; Chen, K.; Han, X.; Fan, J. Storm Surge Prediction Based on Long Short-Term Memory Neural Network in the East China Sea. Appl. Sci. 2021, 12, 181. [Google Scholar] [CrossRef]
- Di Nunno, F.; de Marinis, G.; Gargano, R.; Granata, F. Tide Prediction in the Venice Lagoon Using Nonlinear Autoregressive Exogenous (NARX) Neural Network. Water 2021, 13, 1173. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F.; Gargano, R.; de Marinis, G. Forecasting of Extreme Storm Tide Events Using NARX Neural Network-Based Models. Atmosphere 2021, 12, 512. [Google Scholar] [CrossRef]
- Riazi, A. Accurate tide level estimation: A deep learning approach. Ocean Eng. 2020, 198, 107013. [Google Scholar] [CrossRef]
- Issaka, Y.; Kumi-Boateng, B. Artificial intelligence techniques for predicting tidal effects based on geographic locations in ghana. Geod. Cartogr. 2020, 46, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Imani, M.; Kao, H.-C.; Lan, W.-H.; Kuo, C.-Y. Daily sea level prediction at Chiayi coast, Taiwan using extreme learning machine and relevance vector machine. Glob. Planet. Chang. 2017, 161, 211–221. [Google Scholar] [CrossRef]
- Sarkar, D.; Osborne, M.A.; Adcock, T.A.A. Prediction of tidal currents using Bayesian machine learning. Ocean Eng. 2018, 158, 221–231. [Google Scholar] [CrossRef]
- Feng, B.; Qian, P.; Si, Y.; Liu, X.; Yang, H.; Wen, H.; Zhang, D. Comparative Investigations of Tidal Current Velocity Prediction Considering Effect of Multi-Layer Current Velocity. Energies 2020, 13, 6417. [Google Scholar] [CrossRef]
- Lee, M.; You, Y.; Kim, S.; Kim, K.T.; Kim, H.S. Decomposition of Water Level Time Series of a Tidal River into Tide, Wave and Rainfall-Runoff Components. Water 2018, 10, 1568. [Google Scholar] [CrossRef] [Green Version]
- Shamshirband, S.; Mosavi, A.; Rabczuk, T.; Nabipour, N.; Chau, K.-W. Prediction of significant wave height; comparison between nested grid numerical model, and machine learning models of artificial neural networks, extreme learning and support vector machines. Eng. Appl. Comput. Fluid Mech. 2020, 14, 805–817. [Google Scholar] [CrossRef]
- Wang, Z.; Attar, N.F.; Khalili, K.; Behmanesh, J.; Band, S.S.; Mosavi, A.; Chau, K.-W. Monthly streamflow prediction using a hybrid stochastic-deterministic approach for parsimonious non-linear time series modeling. Eng. Appl. Comput. Fluid Mech. 2020, 14, 1351–1372. [Google Scholar] [CrossRef]
- Zheng, W.; Band, S.S.; Karami, H.; Karimi, S.; Samadianfard, S.; Shadkani, S.; Chau, K.-W.; Mosavi, A.H. Forecasting the discharge capacity of inflatable rubber dams using hybrid machine learning models. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1761–1774. [Google Scholar] [CrossRef]
- Tao, H.; Al-Khafaji, Z.S.; Qi, C.; Zounemat-Kermani, M.; Kisi, O.; Tiyasha, T.; Chau, K.-W.; Nourani, V.; Melesse, A.M.; Elhakeem, M.; et al. Artificial intelligence models for suspended river sediment prediction: State-of-the art, modeling framework appraisal, and proposed future research directions. Eng. Appl. Comput. Fluid Mech. 2021, 15, 1585–1612. [Google Scholar] [CrossRef]
- Carton, J.A. The variation with frequency of the long-period tides. J. Geophys. Res. Earth Surf. 1983, 88, 7563. [Google Scholar] [CrossRef]
- Markus, M.; Knapp, H.V.; Tasker, G.D. Entropy and generalized least square methods in assessment of the regional value of streamgages. J. Hydrol. 2003, 283, 107–121. [Google Scholar] [CrossRef] [Green Version]
- Schureman, P. Manual of Harmonic Analysis and Prediction of Tides. Special Publication 98, Coast and Geodetic Survey; U.S. Dept. of Commerce: Washington, DC, USA, 1958; p. 317. [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Cho, K.; van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder-Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1724–1734. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 30 March 2020).
- Sumich, J.L. An Introduction to the Biology of Marine Life, 6th ed.; Dubuque, I.A., Brown, W.C., Eds.; Jones & Bartlett Learning: Burlington, MA, USA, 2016; pp. 30–35. [Google Scholar]
- Ross, D.A. Introduction to Oceanography; HarperCollins: New York, NY, USA, 1995; pp. 236–242. [Google Scholar]
- Thurman, H.V. Introductory Oceanography, 7th ed.; Macmillan: New York, NY, USA, 1994; pp. 252–276. [Google Scholar]
- Golparvar, B.; Wang, R.-Q. AI-supported citizen science to monitor high-tide flooding in newport beach, California. In Proceedings of the 3rd ACM SIGSPATIAL International Workshop on Advances in Resilient and Intelligent Cities, ARIC, Seattle, WA, USA, 3 November 2020; pp. 66–69. [Google Scholar] [CrossRef]
- Kareem, K.Y.; Seong, Y.; Jung, Y. LSTM Prediction of Streamflow during Peak Rainfall of Piney River. J. Korean Soc. Disaster Secur. 2021, 14, 17–27. [Google Scholar]
- Klotz, D.; Kratzert, F.; Gauch, M.; Keefe Sampson, A.; Brandstetter, J.; Klambauer, G.; Hochreiter, S.; Nearing, G. Uncertainty estimation with deep learning for rainfall–runoff modeling. Hydrol. Earth Syst. Sci. 2022, 26, 1673–1693. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Razavi, S. Deep learning, explained: Fundamentals, explainability, and bridgeability to process-based modelling. Environ. Model. Softw. 2021, 144, 105159. [Google Scholar] [CrossRef]
- Balogun, A.-L.; Adebisi, N. Sea level prediction using ARIMA, SVR and LSTM neural network: Assessing the impact of ensemble Ocean-Atmospheric processes on models’ accuracy. Geomat. Nat. Hazards Risk 2021, 12, 653–674. [Google Scholar] [CrossRef]
- Yuk, J.-H.; Kang, J.-S.; Myung, H. Applicability Study of a Global Numerical Weather Prediction Model MPAS to Storm Surges and Waves in the South Coast of Korea. Atmosphere 2022, 13, 591. [Google Scholar] [CrossRef]

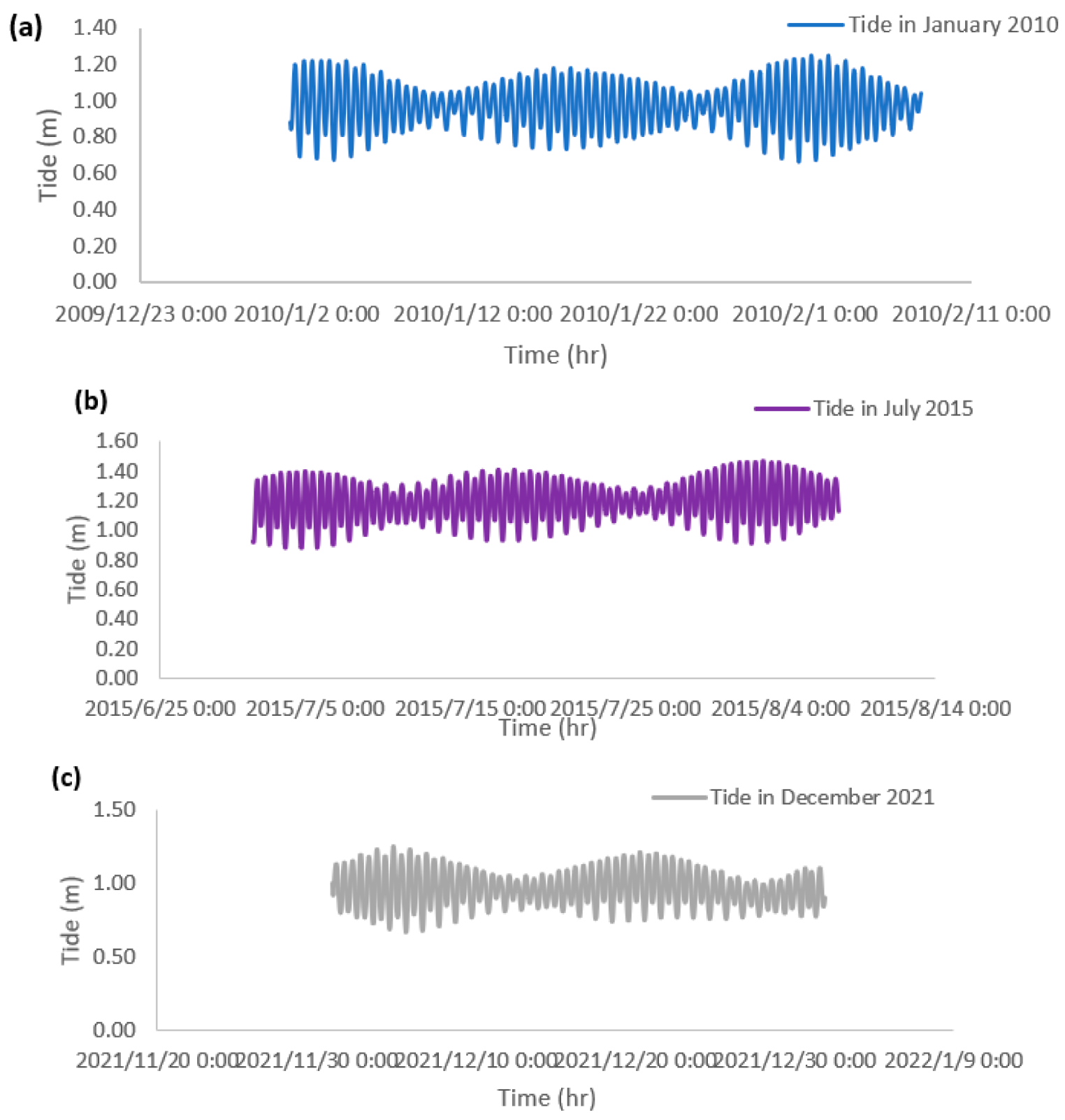
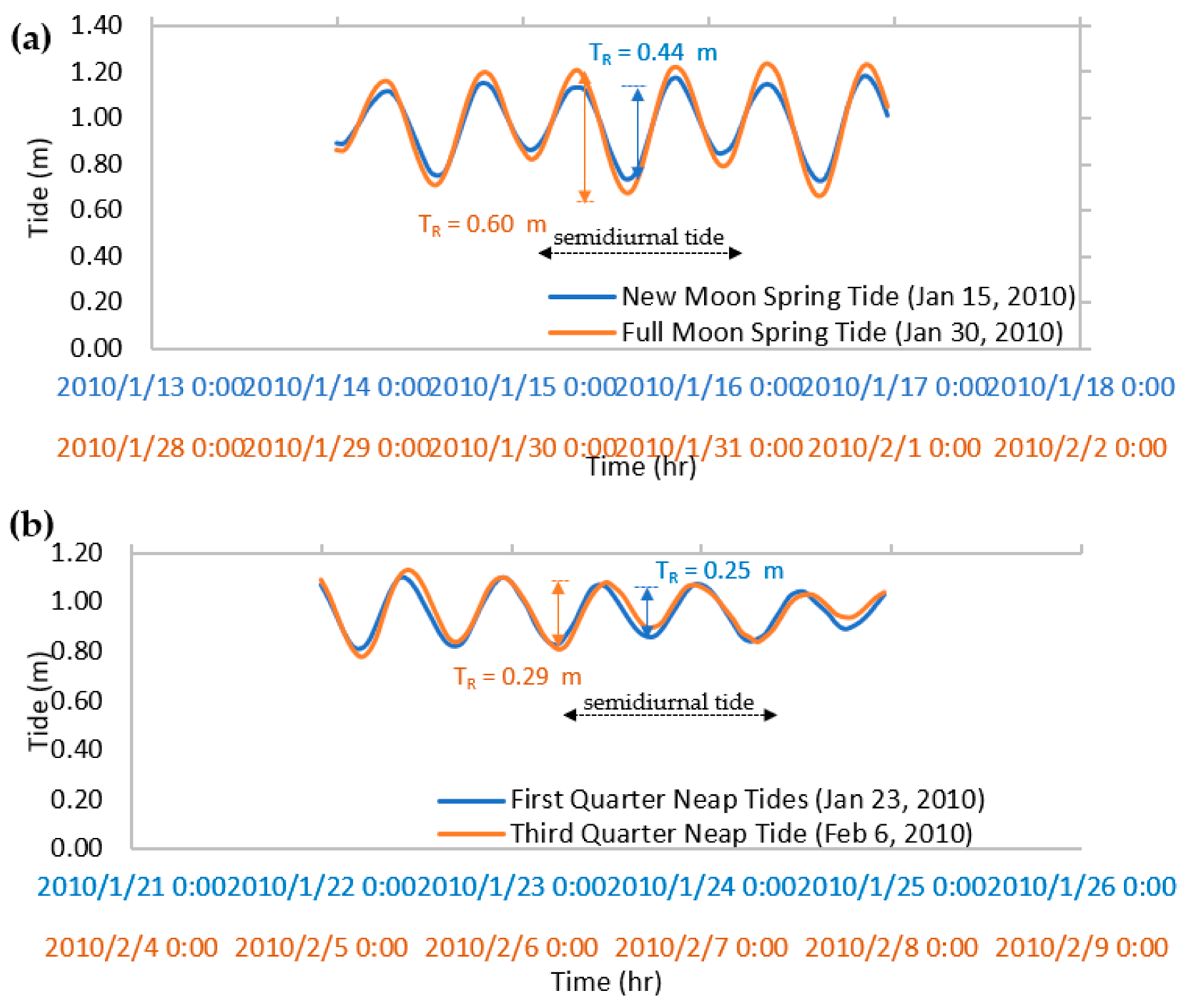
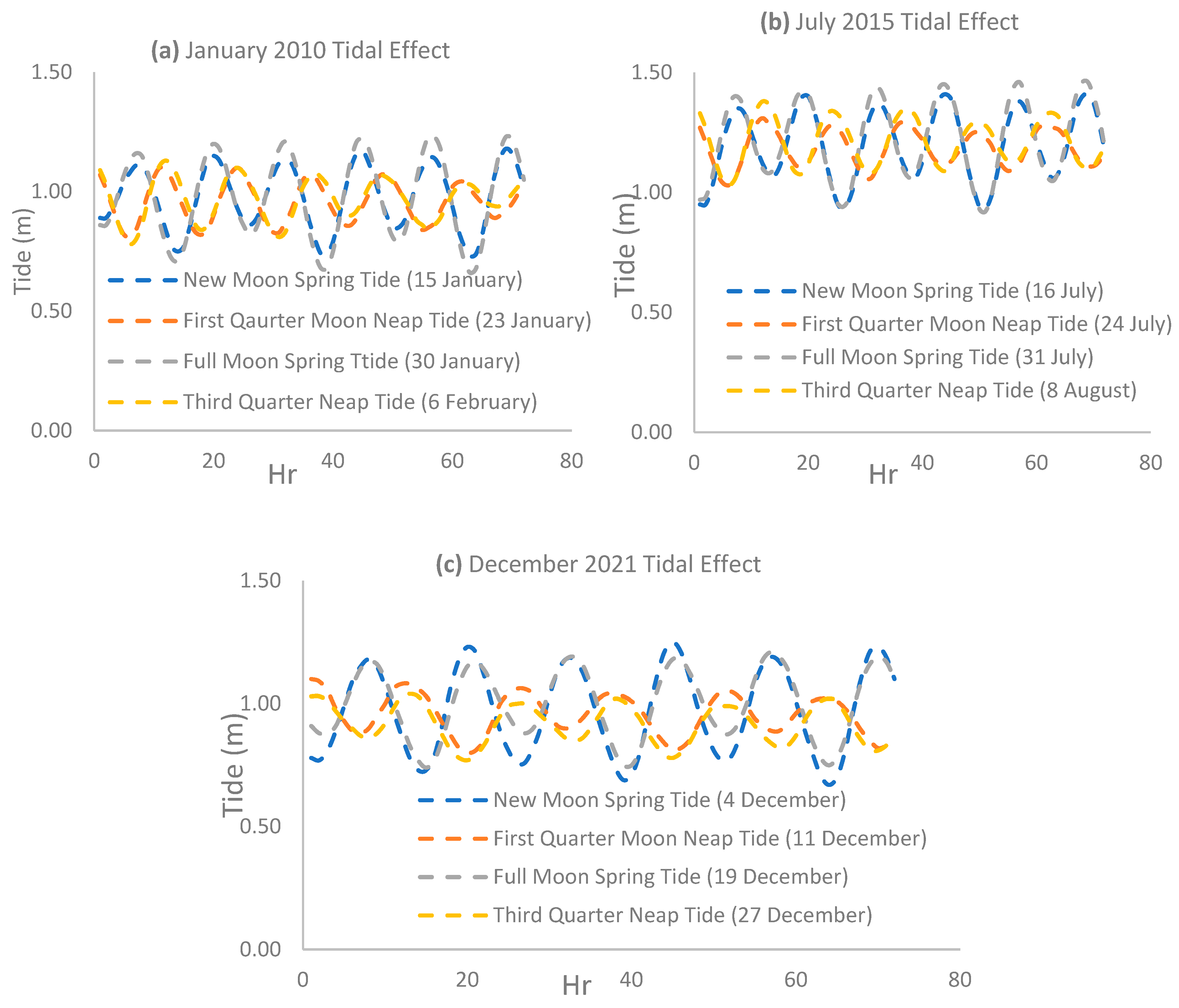

| Month | Date | Tide Type | Moon Orientation | Average Tidal Range, TR (m) | Decision |
|---|---|---|---|---|---|
| January | 15/2010 | Spring | NM | 0.44 | |
| 23/2010 | Neap | FQ | 0.25 | LTL | |
| 30/2010 | Spring | FM | 0.60 | HTL | |
| 6 February 2010 | Neap | TQ | 0.29 | ||
| July | 16/2015 | Spring | NM | 0.50 | |
| 24/2015 | Neap | FQ | 0.20 | LTL | |
| 31/2015 | Spring | FM | 0.53 | HTL | |
| 7 August 2010 | Neap | TQ | 0.23 | ||
| December | 4/2021 | Spring | NM | 0.50 | HTL |
| 11/2021 | Neap | FQ | 0.27 | LTL | |
| 19/2021 | Spring | FM | 0.43 | ||
| 27/2021 | Neap | TQ | 0.34 |
| Metrics | GRU | LSTM | BiLSTM | |||
|---|---|---|---|---|---|---|
| Prediction with No Wind | Prediction with Wind | Prediction with No Wind | Prediction with Wind | Prediction with No Wind | Prediction with Wind | |
| KGE | 0.84 | 0.80 | 0.82 | 0.87 * | 0.81 | 0.67 |
| NSE | 0.75 | 0.76 | 0.83 | 0.83 | 0.76 | 0.67 |
| MSE | 0.0059 | 0.0057 | 0.0041 | 0.0041 | 0.0055 | 0.0077 |
| MAE | 0.06 | 0.06 | 0.0502 | 0.0502 | 0.0598 | 0.073 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kareem, K.Y.; Seong, Y.; Kim, K.; Jung, Y. A Case Study of Tidal Analysis Using Theory-Based Artificial Intelligence Techniques for Disaster Management in Taehwa River, South Korea. Water 2022, 14, 2172. https://doi.org/10.3390/w14142172
Kareem KY, Seong Y, Kim K, Jung Y. A Case Study of Tidal Analysis Using Theory-Based Artificial Intelligence Techniques for Disaster Management in Taehwa River, South Korea. Water. 2022; 14(14):2172. https://doi.org/10.3390/w14142172
Chicago/Turabian StyleKareem, Kola Yusuff, Yeonjeong Seong, Kyungtak Kim, and Younghun Jung. 2022. "A Case Study of Tidal Analysis Using Theory-Based Artificial Intelligence Techniques for Disaster Management in Taehwa River, South Korea" Water 14, no. 14: 2172. https://doi.org/10.3390/w14142172






