Trends and Changes in Hydrologic Cycle in the Huanghuaihai River Basin from 1956 to 2018
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data Sources
2.2.1. Hydrological and Meteorological Data
2.2.2. Evapotranspiration Product Data
- (i)
- Data quality control. The quality control steps of data include eliminating outliers, correcting delay time, coordinate rotation (plane fitting method) and frequency response correction. Ultrasonic virtual temperature correction and density correction include eliminating the data of instrument error; eliminating the data of 1 h before and after precipitation; eliminating the data of 10 Hz original data with a loss rate of more than 3% per 30 min; and eliminating the observed data of weak turbulence at night.
- (ii)
- Data interpolation. When the missing value is less than 2 h, the effective flux before and after the time is calculated by linear interpolation. When the missing value is between 2 h and 4 d, the average diurnal variation method is used to calculate the average effective flux in the same period of 5 days before and after the adjacent period. When the missing measurement value exceeds 4 days, it may be caused by power supply or instrument failure. The linear fitting relationship between latent heat flux and air temperature, sensible heat flux and net radiation is established by selecting the observation data of the vacancy adjacent period, and the daily value is inserted according to the simulated value.
- (iii)
- Calculation of evaporation. This is carried out according to latent heat flux and vaporization latent heat of water (λ = 2.45 MJ × kg−1). The actual evaporation of the basin is calculated by Formula (1).
2.2.3. Terrestrial Water Storage Data
2.2.4. Natural Runoff Data
2.2.5. Vegetation Data
3. Methodology
3.1. Trend Test Method
3.2. Data Accuracy Evaluation
3.3. Machine Learning Algorithm
- (i)
- Random forest
- (ii)
- BP neural network
- (iii)
- Extreme learning machine
3.4. Water Balance Analysis
4. Results
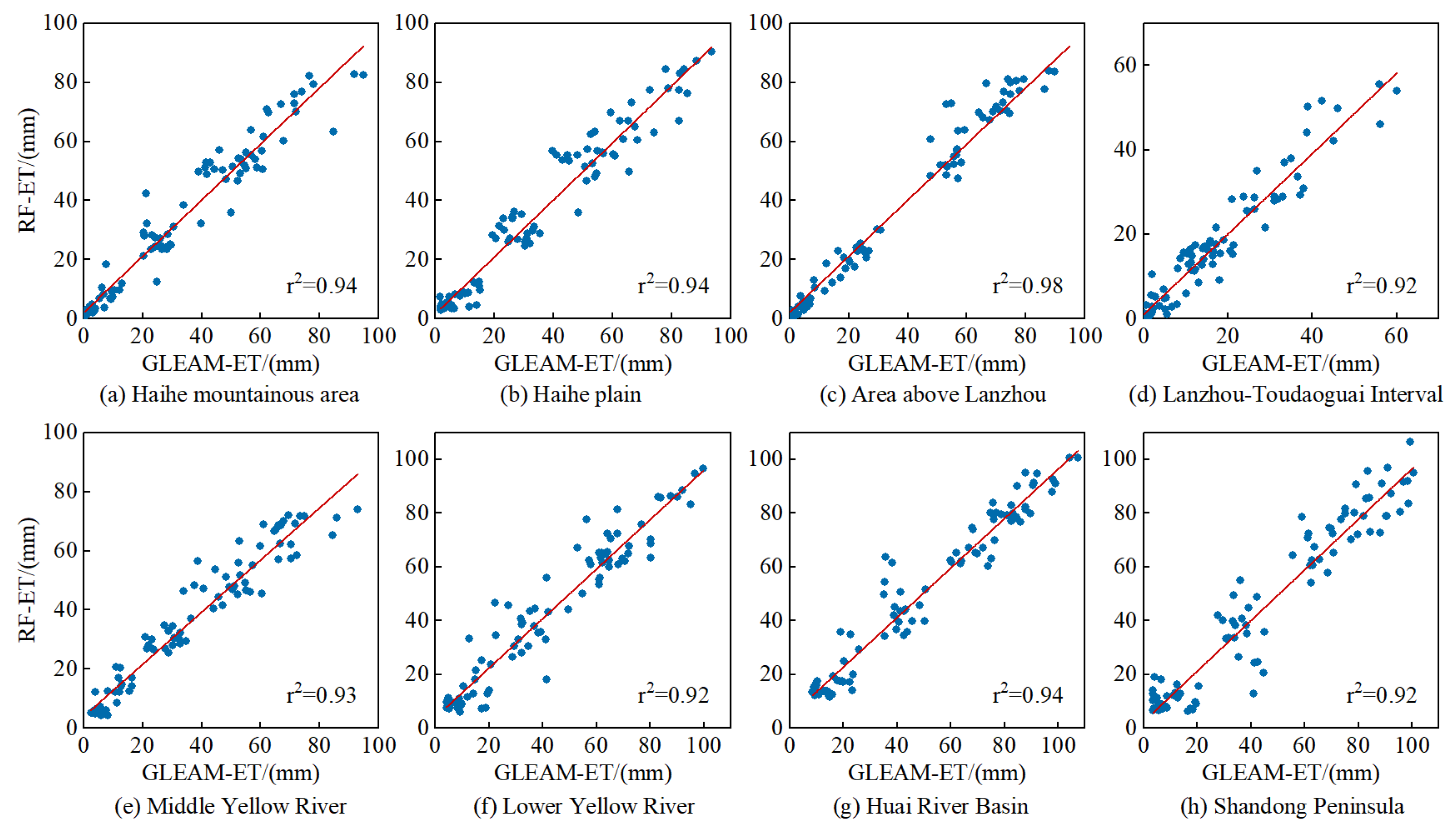
4.1. Evaluation and Extension of Evaporative Data
4.1.1. Evaluation of Evaporated Data
4.1.2. Extension of Evapotranspiration Data
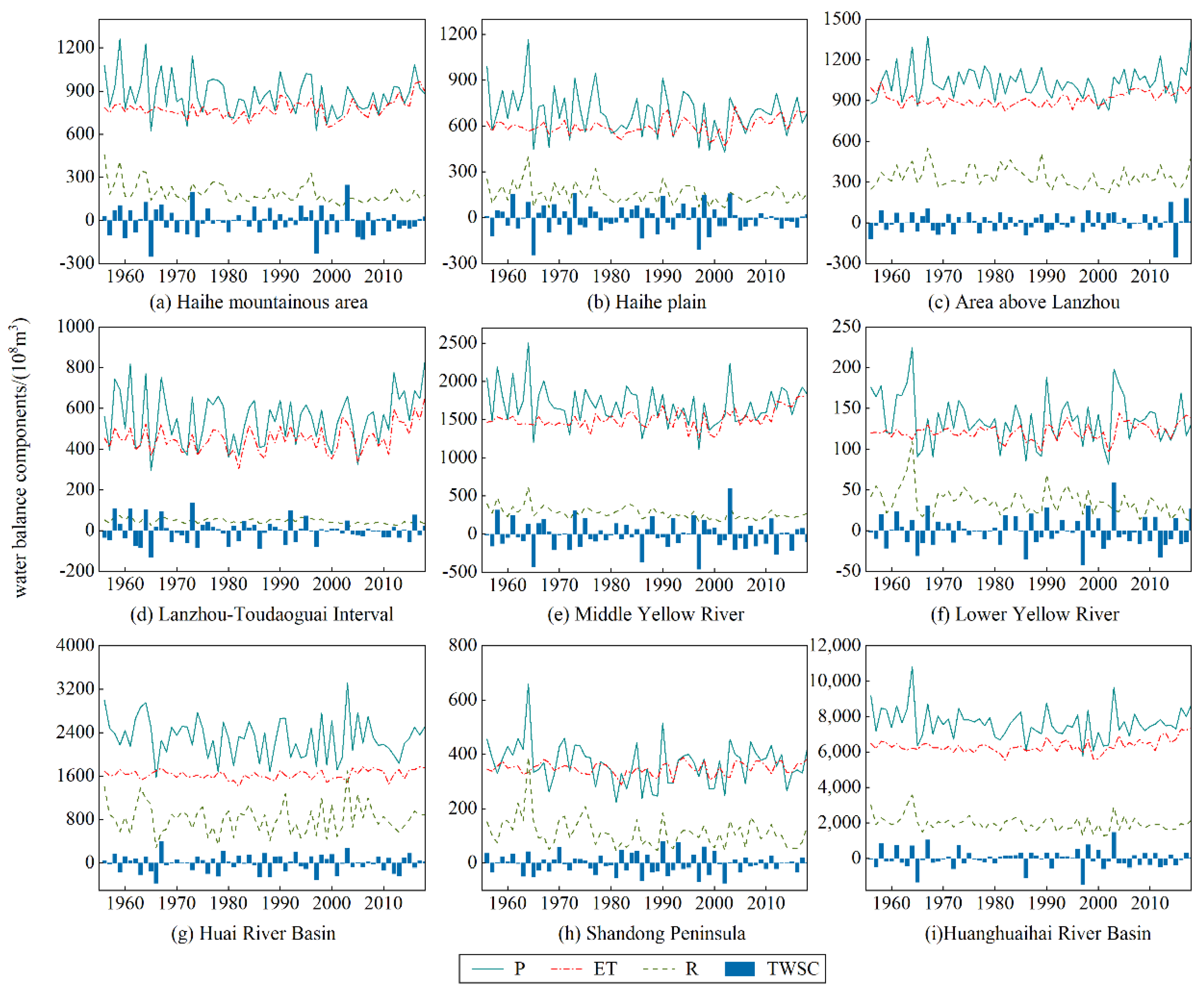
4.2. Regional Water Cycle Change
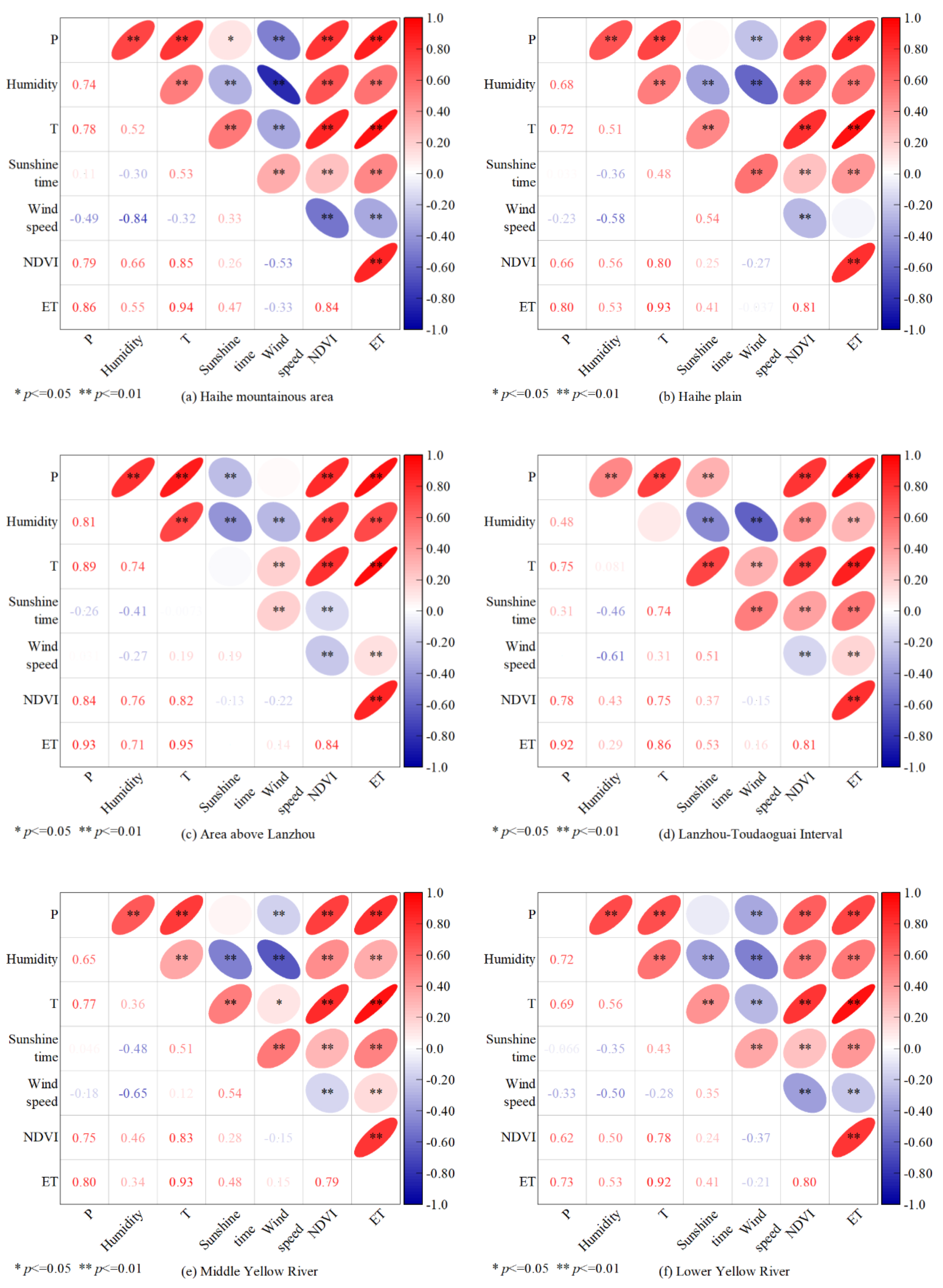
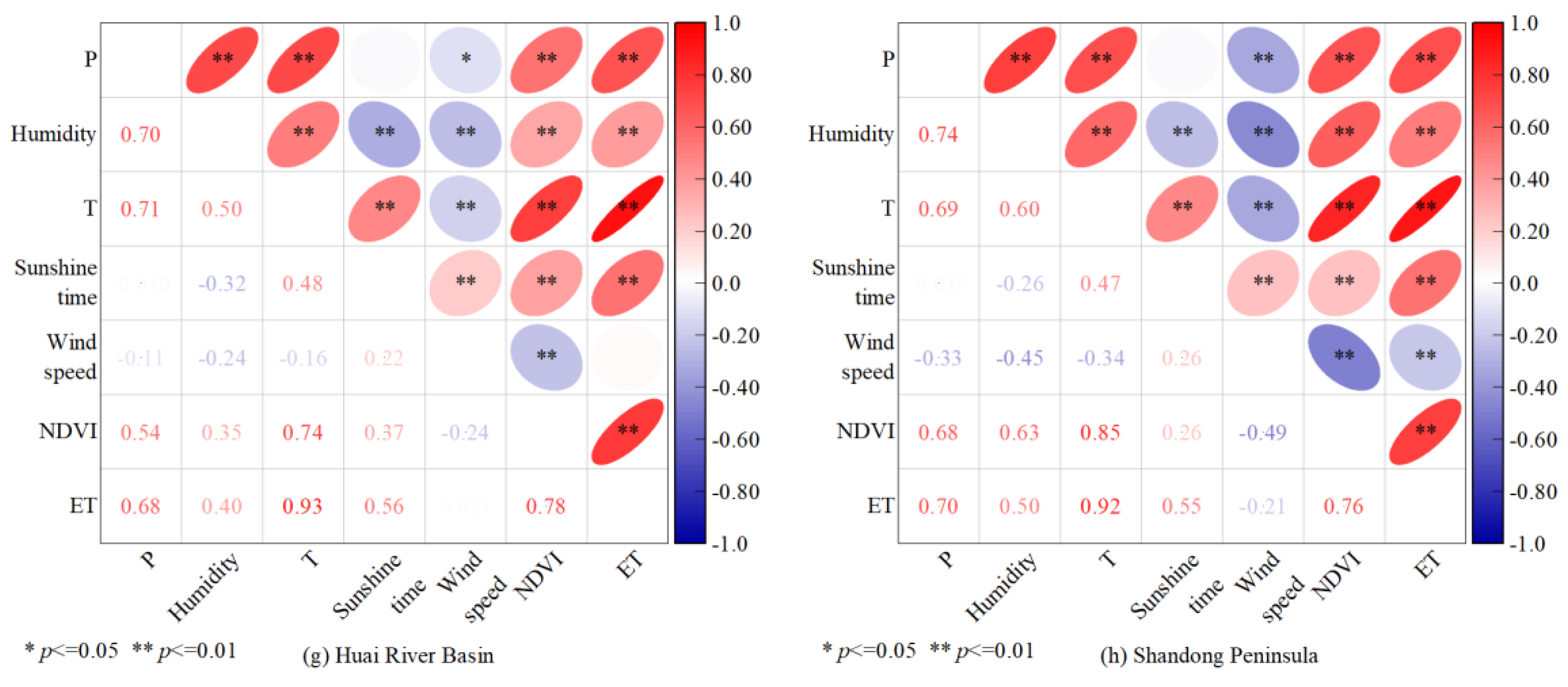
4.2.1. Evolution of Hydrological Elements
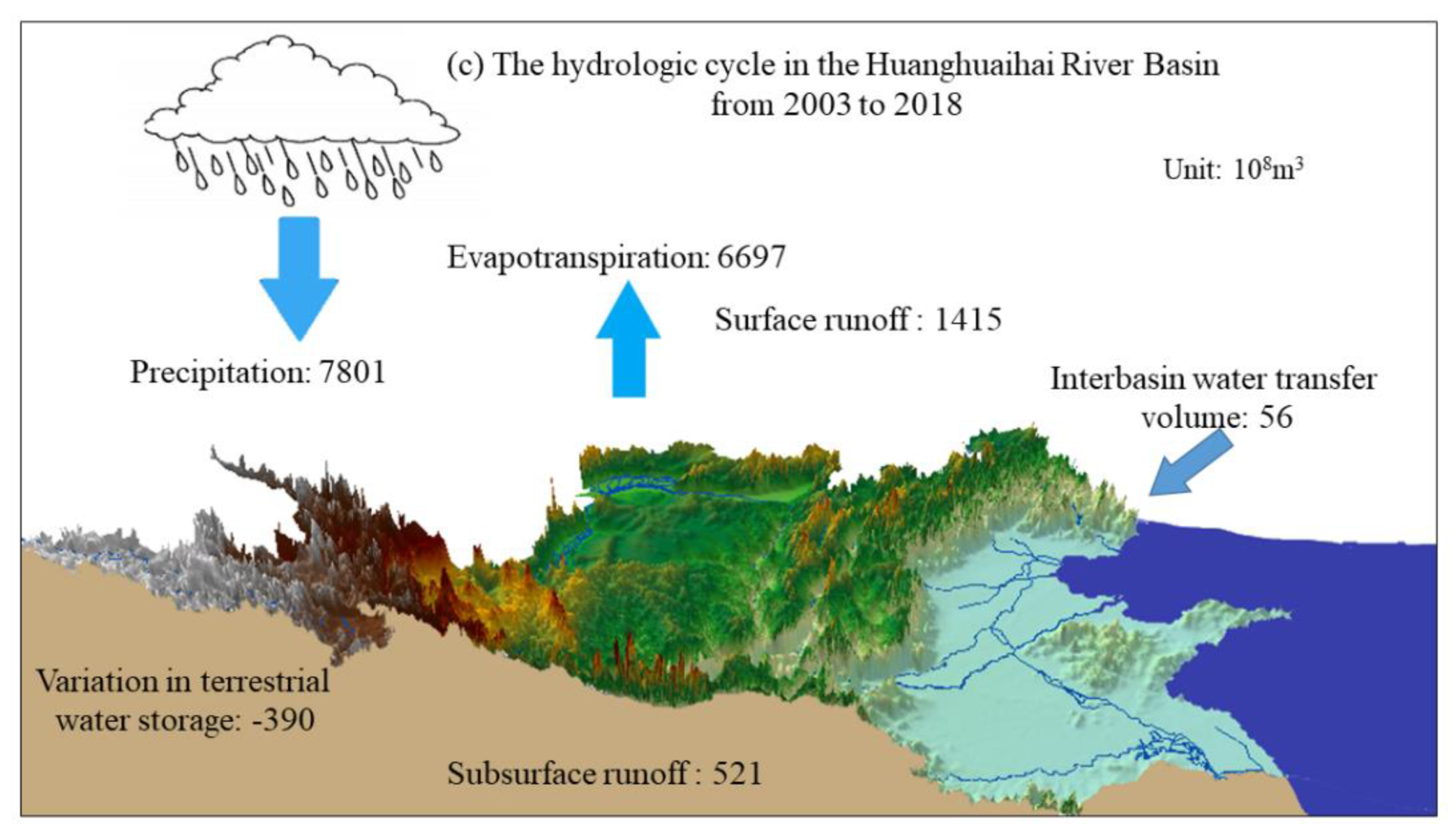
4.2.2. Variation in Water Balance
5. Discussion
6. Conclusions
- (1)
- The accuracy verification results of ET data from flux stations show that the simulation accuracy of GLEAM products in HRB is good, and the annual average ET spatial distribution tends to increase from northwest to southeast as a whole.
- (2)
- Precipitation, temperature, sunshine, humidity and NDVI are used as the influencing factors of ET. Three machine learning algorithms, BP, RF and ELM, are used to construct the ET calculation model. The r values of the three methods are all above 0.9 and the MRE values of RF are all less than 30%. The RF calculates the best results.
- (3)
- The water balance analysis of HRB shows that the income item of the basin is mainly precipitation, and the amount of water spent is mainly ET, accounting for 76% of the total amount of water spent, and TWSC of the basin is in a state of decrease. The relative errors of water balance in HRB from 1956–1979, 1980–2002 and 2003–2018 are less than ±5%, which indicates that the calculation of each element of the water cycle in HRB has reached a certain accuracy and can reflect the relationship of water balance in HRB.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef] [Green Version]
- Nasta, P.; Allocca, C.; Deidda, R.; Romano, N. Assessing the impact of seasonal-rainfall anomalies on catchment-scale water balance components. Hydrol. Earth Syst. Sci. 2020, 24, 3211–3227. [Google Scholar] [CrossRef]
- Lehmann, F.; Vishwakarma, B.D.; Bamber, J. How well are we able to close the water budget at the global scale? Hydrol. Earth Syst. Sci. 2022, 26, 35–54. [Google Scholar] [CrossRef]
- Saemian, P.; Elmi, O.; Vishwakarma, B.D.; Tourian, M.J.; Sneeuw, N. Analyzing the Lake Urmia restoration progress using ground-based and spaceborne observations. Sci. Total Environ. 2020, 739, 139857. [Google Scholar] [CrossRef] [PubMed]
- Bhattarai, N.; Mallick, K.; Stuart, J.; Vishwakarma, B.D.; Niraula, R.; Sen, S.; Jain, M. An automated multi-model evapotranspiration mapping framework using remotely sensed and reanalysis data. Remote Sens. Environ. 2019, 229, 69–92. [Google Scholar] [CrossRef]
- Long, D.; Yang, Y.; Wada, Y.; Hong, Y.; Liang, W.; Chen, Y.; Yong, B.; Hou, A.; Wei, J.; Chen, L. Deriving scaling factors using a global hydrological model to restore GRACE total water storage changes for China’s Yangtze River Basin. Remote Sens. Environ. 2015, 168, 177–193. [Google Scholar] [CrossRef]
- Tan, X.; Liu, B.; Tan, X.; Chen, X. Long-Term Water Imbalances of Watersheds Resulting From Biases in Hydroclimatic Data Sets for Water Budget Analyses. Water Resour. Res. 2022, 58, e2021WR031209. [Google Scholar] [CrossRef]
- Chen, J.; Tapley, B.; Rodell, M.; Seo, K.W.; Wilson, C.; Scanlon, B.R.; Pokhrel, Y. Basin-Scale River Runoff Estimation From GRACE Gravity Satellites, Climate Models, and In Situ Observations: A Case Study in the Amazon Basin. Water Resour. Res. 2020, 56, e2020WR028032. [Google Scholar] [CrossRef]
- Abolafia-Rosenzweig, R.; Pan, M.; Zenga, J.L.; Livneh, B. Remotely sensed ensembles of the terrestrial water budget over major global river basins: An assessment of three closure techniques. Remote Sens. Environ. 2021, 252, 112191. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, M.; Sheffield, J.; Siemann, A.L.; Fisher, C.K.; Liang, M.; Beck, H.E.; Wanders, N.; MacCracken, R.F.; Houser, P.R.; et al. A Climate Data Record (CDR) for the global terrestrial water budget: 1984–2010. Hydrol. Earth Syst. Sci. 2018, 22, 241–263. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Liang, S.; Xie, X.; Cheng, J.; Jia, K.; Li, Y.; Liu, R. Estimation of the terrestrial water budget over northern China by merging multiple datasets. J. Hydrol. 2014, 519, 50–68. [Google Scholar] [CrossRef]
- Liu, W.; Shi, C.; Zhou, Y. Trends and attribution of runoff changes in the upper and middle reaches of the Yellow River in China. J. Hydro-Environ. Res. 2021, 37, 57–66. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhou, J.; Sun, N.; Jia, B.; Hu, G. Variation Trends of Precipitation and Runoff in the Jinsha River Basin, China: 1961–2015. IOP Conf. Ser. Earth Environ. Sci. 2020, 440, 052044. [Google Scholar] [CrossRef]
- Xu, H.; Ren, Y.; Zheng, H.; Ouyang, Z.; Jiang, B. Analysis of Runoff Trends and Drivers in the Haihe River Basin, China. Int. J. Environ. Res. Public Health 2020, 17, 1577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, T.; Guo, Z.; Xia, Y.; Ferreira, V.G.; Liu, S.; Wang, K.; Yao, Y.; Zhang, X.; Zhao, C. Evaluation of twelve evapotranspiration products from machine learning, remote sensing and land surface models over conterminous United States. J. Hydrol. 2019, 578, 124105. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Y. Analysis of Dynamic Spatiotemporal Changes in Actual Evapotranspiration and Its Associated Factors in the Pearl River Basin Based on MOD16. Water 2017, 9, 832. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Liang, K.; Liu, C.; Liu, W.; Bai, P. Evaluation of different evapotranspiration products in the middle Yellow River Basin, China. Hydrol. Res. 2017, 48, 124105. [Google Scholar] [CrossRef] [Green Version]
- Sorensson, A.A.; Ruscica, R.C. Intercomparison and Uncertainty Assessment of Nine Evapotranspiration Estimates Over South America. Water Resour. Res. 2018, 54, 2891–2908. [Google Scholar] [CrossRef] [Green Version]
- Harold, L.; Waldo, L.; Cristian, M.; William, S.; Pedro, R. PISCO_HyM_GR2M: A Model of Monthly Water Balance in Peru (1981–2020). Water 2021, 13, 1048. [Google Scholar]
- Sahoo, A.K.; Pan, M.; Troy, T.J.; Vinukollu, R.K.; Sheffield, J.; Wood, E.F. Reconciling the global terrestrial water budget using satellite remote sensing. Remote Sens. Environ. 2011, 115, 1850–1865. [Google Scholar] [CrossRef]
- Munier, S.; Aires, F. A new global method of satellite dataset merging and quality characterization constrained by the terrestrial water budget. Remote Sens. Environ. 2018, 205, 119–130. [Google Scholar] [CrossRef]
- Yoon, Y.; Yoon, Y.; Kumar, S.V.; Forman, B.A.; Zaitchik, B.F.; Kwon, Y.; Kwon, Y.; Qian, Y.; Rupper, S.; Maggioni, V.; et al. Evaluating the uncertainty of terrestrial water budget components over high mountain Asia. Front. Earth Sci. 2019, 7, 120. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, N.; Zhang, Y.; Szilagyi, J.; Liu, W. Complementary-relationship-based modeling of terrestrial evapotranspiration across China during 1982-2012: Validations and spatiotemporal analyses. J. Geophys. Res. 2019, 124, 4326–4351. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. Available online: www.gleam.eu (accessed on 26 May 2021). [CrossRef]
- Ma, N.; Szilagyi, J. The CR of Evaporation: A Calibration-Free Diagnostic and Benchmarking Tool for Large-Scale Terrestrial Evapotranspiration Modeling. Water Resour. Res. 2019, 55, 7246–7274. Available online: https://data.tpdc.ac.cn/zh-hans/ (accessed on 18 February 2022). [CrossRef] [Green Version]
- Ghaderpour, E.; Abbes, A.B.; Rhif, M.; Pagiatakis, S.D.; Farah, I.R. Non-stationary and unequally spaced NDVI time series analyses by the LSWAVE software. Int. J. Remote Sens. 2020, 41, 2374–2390. [Google Scholar] [CrossRef]
- Tali, P.A.; Bhat, M.M.; Lone, F.A. Seasonal Spatio-Temporal Variability in Temperature over North Kashmir Himalayas Using Sen Slope and Mann-Kendall Test. J. Climatol. Weather. Forecast. 2021, 9, 288. [Google Scholar]
- Lichang, Y.; Fulu, T.; Yi, C.; Fengshan, L.; Jian, H. Improving terrestrial evapotranspiration estimation across China during 2000–2018 with machine learning methods. J. Hydrol. 2021, 600, 126538. [Google Scholar]
- Shabani, S.; Samadianfard, S.; Sattari, M.T.; Mosavi, A.; Shamshirband, S.; Kmet, T.; Várkonyi-Kóczy, A.R. Modeling Pan Evaporation Using Gaussian Process Regression K-Nearest Neighbors Random Forest and Support Vector Machines; Comparative Analysis. Atmosphere 2020, 11, 66. [Google Scholar] [CrossRef] [Green Version]
- Batra, K.; Gandhi, P. Neural Network-Based Prediction Model for Evaporation Using Weather Data. Agric. Res. 2022, 11, 123–128. [Google Scholar] [CrossRef]
- Deo, R.C.; Samui, P.; Kim, D. Estimation of monthly evaporative loss using relevance vector machine, extreme learning machine and multivariate adaptive regression spline models. Stoch. Environ. Res. Risk Assess. 2016, 30, 1769–1784. [Google Scholar] [CrossRef]
- Ebrahim, G. JUST: MATLAB and python software for change detection and time series analysis. GPS Solut. 2021, 25, 85. [Google Scholar]
- Minghan, C.; Xiyun, J.; Binbin, L.; Xun, Y.; Mingchao, S.; Xiuliang, J. Long time series of daily evapotranspiration in China based on the SEBAL model and multisource images and validation. Earth Syst. Sci. Data 2021, 13, 3995–4017. [Google Scholar]
- Tao, S.; Taichen, F.; Bicheng, H.; Zixuan, H.; Zhonghua, Q.; Guolin, F.; Wei, H. Trend, Seasonal, and Irregular Variations in Regional Actual Evapotranspiration Over China: A Multi-Dataset Analysis. Front. Phys. 2021, 9, 718771. [Google Scholar]
- Fubo, Z.; Shuai, M.; Yiping, W.; Linjing, Q.; Wenke, W.; Yanqing, L.; Ji, C.; Bellie, S. The role of climate change and vegetation greening on evapotranspiration variation in the Yellow River Basin, China. Agric. For. Meteorol. 2022, 316, 108842. [Google Scholar]
- Jing, F.; Yueqi, G.; Wenwu, Z.; Jun, Z.; Meng, Z.; Zhongbo, Z.; Jianxin, Q.; Jianxiong, L.; Bin, Q. Spatial-temporal variations of terrestrial evapotranspiration across China from 2000 to 2019. Sci. Total Environ. 2022, 825, 153951. [Google Scholar]
- Linshan, Y.; Qi, F.; Meng, Z.; Liuming, W.; Reza, A.M.; Adamowski, J.F.; Xiaohu, W.; Zhenliang, Y. Variation in actual evapotranspiration and its ties to climate change and vegetation dynamics in northwest China. J. Hydrol. 2022, 607, 127533. [Google Scholar]
- Yang, X.; Wang, G.; Ye, J.; Li, Y. Spatial and temporal changing analysis of terrestrial evapotranspiration in Huai River basin based on GLEAM data. Trans. Chin. Soc. Agric. Eng. 2015, 31, 133–139. [Google Scholar]
- Dang, S.; Suzhen, D.; Xinwei, G.; Wenge, Z.; Huijuan, Y. Analysis of Temporal and Spatial Variations in Actual Evapotranspiration in the Headwaters of the Yellow River Based on Remote Sensing Data. IOP Conf. Ser. Earth Environ. Sci. 2020, 571, 012066. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X. Intercomparison and evaluation of three global high-resolution evapotranspiration products across China. J. Hydrol. 2018, 566, 743–755. [Google Scholar] [CrossRef]
- Yang, X.; Yong, B.; Ren, L.; Zhang, Y.; Long, D. Multi-scale validation of GLEAM evapotranspiration products over China via ChinaFLUX ET measurements. Int. J. Remote Sens. 2017, 38, 5688–5709. [Google Scholar] [CrossRef]
- Meng, L.; Ronghao, C.; Towfiqul, I.A.R.M.; Shuanghe, S. Characteristics of surface evapotranspiration and its response to climate and land use and land cover in the Huai River Basin of eastern China. Environ. Sci. Pollut. Res. Int. 2020, 28, 683–699. [Google Scholar]
- Shuo, W.; Chenfeng, C.; Qin, D. Contributions of Vegetation Greening and Climate Change to Evapotranspiration Trend after Large-Scale Vegetation Restoration on the Loess Plateau, China. Water 2021, 13, 1755. [Google Scholar]
- Huang, H.; Han, Y.; Cao, M.; Song, J.; Xiao, H.; Cheng, W.; Kucharski, F. Spatiotemporal Characteristics of Evapotranspiration Paradox and Impact Factors in China in the Period of 1960–2013. Adv. Meteorol. 2015, 2015, 519207. [Google Scholar] [CrossRef] [Green Version]
- Jinfei, H.; Guangju, Z.; Pengfei, L.; Xingmin, M. Variations of pan evaporation and its attribution from 1961 to 2015 on the Loess Plateau, China. Nat. Hazards 2022, 111, 1199–1217. [Google Scholar]
- Tonglin, F.; Xinrong, L.; Rongliang, J.; Li, F. A novel integrated method based on a machine learning model for estimating evapotranspiration in dryland. J. Hydrol. 2021, 603, 126881. [Google Scholar]
- Yin, Z.; Wen, X.; Feng, Q.; He, Z.; Zou, S.; Yang, L. Integrating genetic algorithm and support vector machine for modeling daily reference evapotranspiration in a semi-arid mountain area. Hydrol. Res. 2017, 48, 1177–1191. [Google Scholar] [CrossRef]
- Mo, X.; Wu, J.J.; Wang, Q.; Zhou, H. Variations in water storage in China over recent decades from GRACE observations and GLDAS. Nat. Hazards Earth Syst. Sci. 2016, 16, 469–482. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Guo, B.; Zhou, Z.; Zhong, Y.; Min, L. Spatio-Temporal Variations in Groundwater Revealed by GRACE and Its Driving Factors in the Huang-Huai-Hai Plain, China. Sensors 2020, 20, 992. [Google Scholar] [CrossRef] [Green Version]
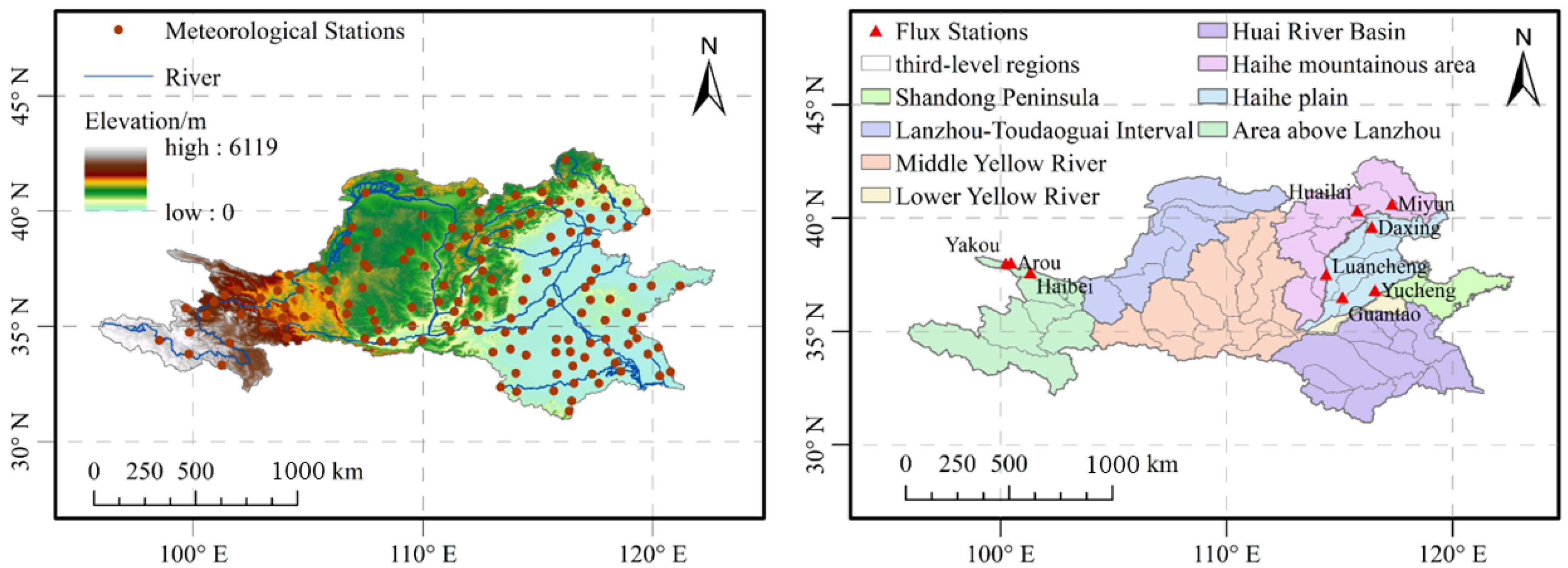



| Type | Site | Longitude | Latitude | Underlying Surface Type | Altitude/m | Time Series |
|---|---|---|---|---|---|---|
| Grassland | Haibei | 101.3 | 37.6 | Alpine meadow | 3216 | 2003–2010 |
| Arou | 100.5 | 38.0 | Alpine meadow | 3033 | 2015–2017 | |
| Yakou | 100.2 | 38.0 | Alpine meadow | 4148 | 2015–2017 | |
| Farmland | Luancheng | 114.4 | 37.5 | Double cropping rotation of Winter Wheat and summer maize in one year | 50 | 2007.10–2013.9 |
| Daxing | 116.4 | 39.6 | Corn/wheat, melon and fruit | 20 | 2008–2010 | |
| Guantao | 115.1 | 36.5 | Corn/wheat, cotton | 30 | 2008–2010 | |
| Miyun | 117.3 | 40.6 | Orchards, corn/bare land, towns | 350 | 2008–2010 | |
| Huailai | 115.8 | 40.4 | Watered field corn | 480 | 2013–2018 | |
| Yucheng | 116.6 | 36.8 | Warm temperate semi-humid dry farmland | 28 | 2003–2010 |
| Site | r | RMSE | ||||
|---|---|---|---|---|---|---|
| TEDAC | GLEAM | GLDAS | TEDAC | GLEAM | GLDAS | |
| Arou station | 0.96 | 0.96 | 0.97 | 15.03 | 18.08 | 30.28 |
| Daxing station | 0.69 | 0.76 | 0.74 | 36.57 | 26.58 | 32.40 |
| Guantao station | 0.95 | 0.93 | 0.90 | 12.83 | 12.74 | 14.51 |
| Haibei station | 0.95 | 0.94 | 0.89 | 12.41 | 15.44 | 33.80 |
| Huailai station | 0.84 | 0.84 | 0.82 | 21.69 | 17.14 | 23.31 |
| Luancheng station | 0.82 | 0.83 | 0.82 | 35.27 | 28.69 | 28.09 |
| Miyun station | 0.95 | 0.94 | 0.96 | 14.43 | 14.64 | 11.43 |
| Yucheng station | 0.73 | 0.78 | 0.73 | 31.50 | 26.85 | 28.11 |
| Yakou station | 0.90 | 0.94 | 0.92 | 15.38 | 12.95 | 16.40 |
| Research Area | RF | BP | ELM | ||||||
|---|---|---|---|---|---|---|---|---|---|
| r2 | RMSE | MRE | r2 | RMSE | MRE | r2 | RMSE | MRE | |
| Haihe mountainous area | 0.94 | 9.10 | 28.9% | 0.94 | 6.32 | 38.8% | 0.95 | 6.01 | 46.6% |
| Haihe plain | 0.94 | 7.14 | 13.6% | 0.91 | 7.98 | 33.8% | 0.92 | 7.95 | 48.1% |
| Area above Lanzhou | 0.98 | 7.85 | 21.7% | 0.98 | 4.08 | 21.8% | 0.98 | 4.00 | 20.3% |
| Lantou Interval | 0.92 | 6.46 | 18.0% | 0.91 | 4.59 | 31.5% | 0.91 | 4.72 | 23.1% |
| Middle Yellow River | 0.93 | 4.02 | 27.1% | 0.92 | 6.98 | 23.2% | 0.90 | 7.51 | 27.8% |
| Lower Yellow River | 0.92 | 4.55 | 19.7% | 0.88 | 9.95 | 27.4% | 0.88 | 10.13 | 40.2% |
| Huai River Basin | 0.94 | 6.29 | 23.5% | 0.93 | 7.60 | 18.0% | 0.92 | 8.63 | 26.9% |
| Shandong Peninsula | 0.92 | 6.19 | 21.5% | 0.89 | 10.50 | 56.3% | 0.91 | 9.61 | 37.9% |
| Zoning | Years | Income Water Quantity | Expenditure Water Quantity | Water Storage Change Value | |||
|---|---|---|---|---|---|---|---|
| p | ET | Rs | Rg | Total | TWSC | ||
| Haihe mountainous area | 1956–1979 | 924.2 | 764.8 | 187.4 | 45.1 | 997.3 | −21.8 |
| 1980–2002 | 827.5 | 754.3 | 119.5 | 48.4 | 922.2 | −118.7 | |
| 2003–2018 | 869.4 | 818.9 | 96.2 | 61.5 | 976.6 | −208.7 | |
| Haihe plain | 1956–1979 | 737.2 | 592.4 | 68.5 | 116.5 | 777.4 | −97.5 |
| 1980–2002 | 639.0 | 576.4 | 42.8 | 94.0 | 713.2 | −88.7 | |
| 2003–2018 | 683.0 | 640.5 | 43.8 | 98.9 | 783.3 | −164.9 | |
| Area above Lanzhou | 1956–1979 | 1050.3 | 904.7 | 346.4 | 1.3 | 1252.5 | 3.9 |
| 1980–2002 | 991.7 | 885.5 | 322.6 | 3.1 | 1211.2 | 42.7 | |
| 2003–2018 | 1075.2 | 963.1 | 333.8 | 1.8 | 1298.8 | 181.5 | |
| Lantou Interval | 1956–1979 | 553.2 | 443.9 | 21.2 | 32.6 | 497.6 | 57.0 |
| 1980–2002 | 513.0 | 434.4 | 19.2 | 29.3 | 482.8 | −80.0 | |
| 2003–2018 | 589.7 | 491.2 | 17.6 | 16.8 | 525.6 | −63.8 | |
| Middle Yellow River | 1956–1979 | 1748.5 | 1468.7 | 254.1 | 63.8 | 1786.7 | −76.3 |
| 1980–2002 | 1590.5 | 1479.1 | 196.6 | 63.5 | 1739.2 | −90.9 | |
| 2003–2018 | 1721.0 | 1618.9 | 171.7 | 69.3 | 1859.9 | −162.1 | |
| Lower Yellow River | 1956–1979 | 142.5 | 120.8 | 26.3 | 16.3 | 163.4 | −14.3 |
| 1980–2002 | 125.5 | 117.2 | 20.6 | 14.3 | 152.0 | −14.7 | |
| 2003–2018 | 140.2 | 128.8 | 11.8 | 13.7 | 154.2 | −12.4 | |
| Huaihe River Basin | 1956–1979 | 2384.8 | 1633.0 | 610.9 | 207.2 | 2451.1 | 18.4 |
| 1980–2002 | 2184.9 | 1584.2 | 556.7 | 203.1 | 2343.9 | −35.1 | |
| 2003–2018 | 2345.0 | 1667.1 | 663.2 | 230.3 | 2570.6 | 66.9 | |
| Shandong Peninsula | 1956–1979 | 393.0 | 351.1 | 103.9 | 36.1 | 491.2 | 3.6 |
| 1980–2002 | 328.9 | 338.9 | 57.3 | 32.1 | 428.4 | −52.8 | |
| 2003–2018 | 377.4 | 358.2 | 76.6 | 28.4 | 463.2 | −26.8 | |
| Year | Total Income Water Quantity (108 m3) | Total Expenditure Water Quantity (108 m3) | Water Storage Change Value (108 m3) | Absolute Error (108 m3) | Water Balance Relative Error |
|---|---|---|---|---|---|
| 1956–1979 | 7933.8 | 8417.1 | −127.1 | −356.1 | −4.49% |
| 1980–2002 | 7200.9 | 7992.9 | −438.3 | −353.7 | −4.91% |
| 2003–2018 | 7856.6 | 8632.1 | −390.3 | −385.3 | −4.94% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Bao, Z.; Wang, G.; Liu, C.; Jin, J. Trends and Changes in Hydrologic Cycle in the Huanghuaihai River Basin from 1956 to 2018. Water 2022, 14, 2148. https://doi.org/10.3390/w14142148
Yang X, Bao Z, Wang G, Liu C, Jin J. Trends and Changes in Hydrologic Cycle in the Huanghuaihai River Basin from 1956 to 2018. Water. 2022; 14(14):2148. https://doi.org/10.3390/w14142148
Chicago/Turabian StyleYang, Xiaotian, Zhenxin Bao, Guoqing Wang, Cuishan Liu, and Junliang Jin. 2022. "Trends and Changes in Hydrologic Cycle in the Huanghuaihai River Basin from 1956 to 2018" Water 14, no. 14: 2148. https://doi.org/10.3390/w14142148






