Selecting Suitable MODFLOW Packages to Model Pond–Groundwater Relations Using a Regional Model
Abstract
:1. Introduction
2. Materials and Methods
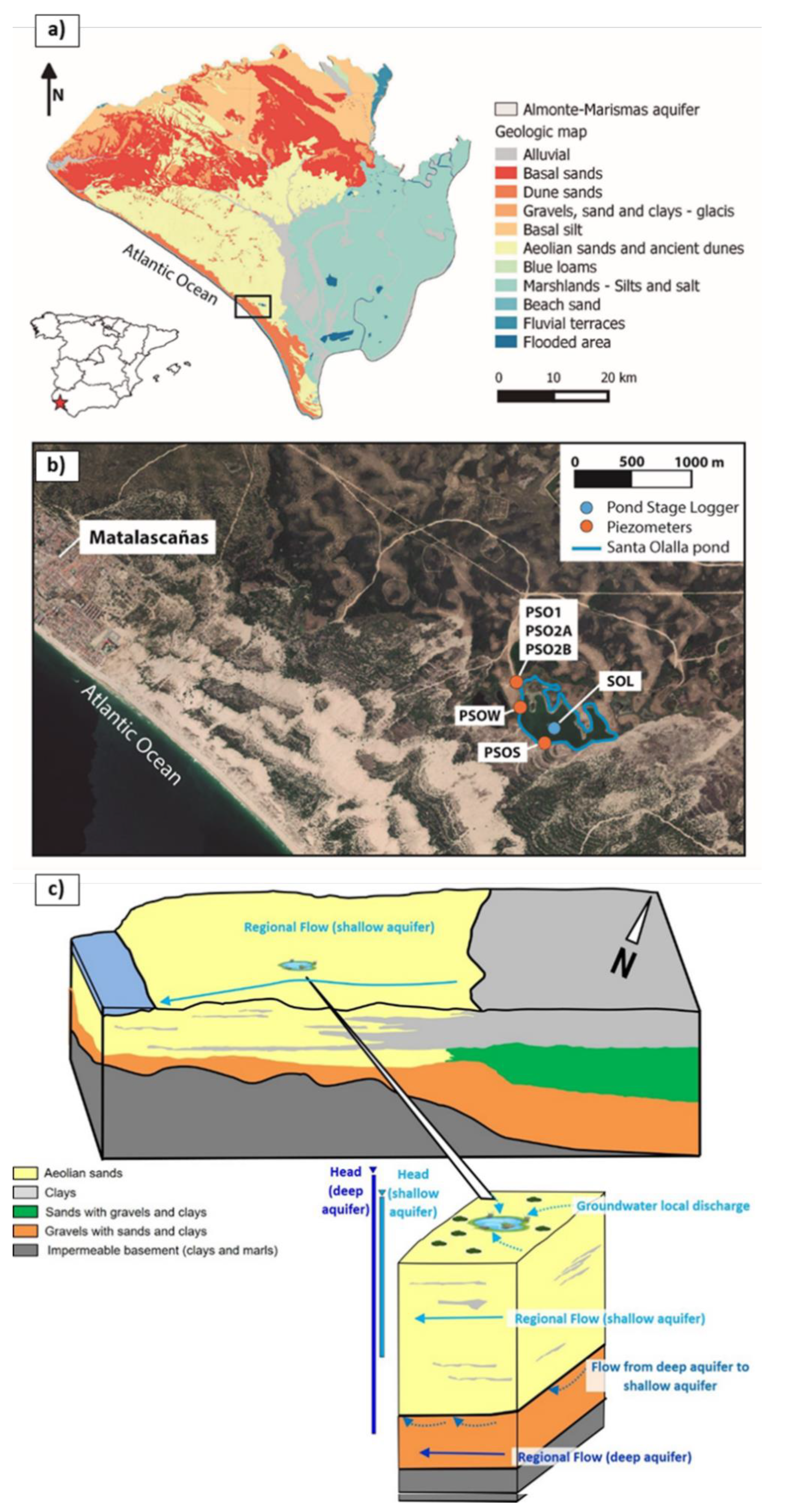
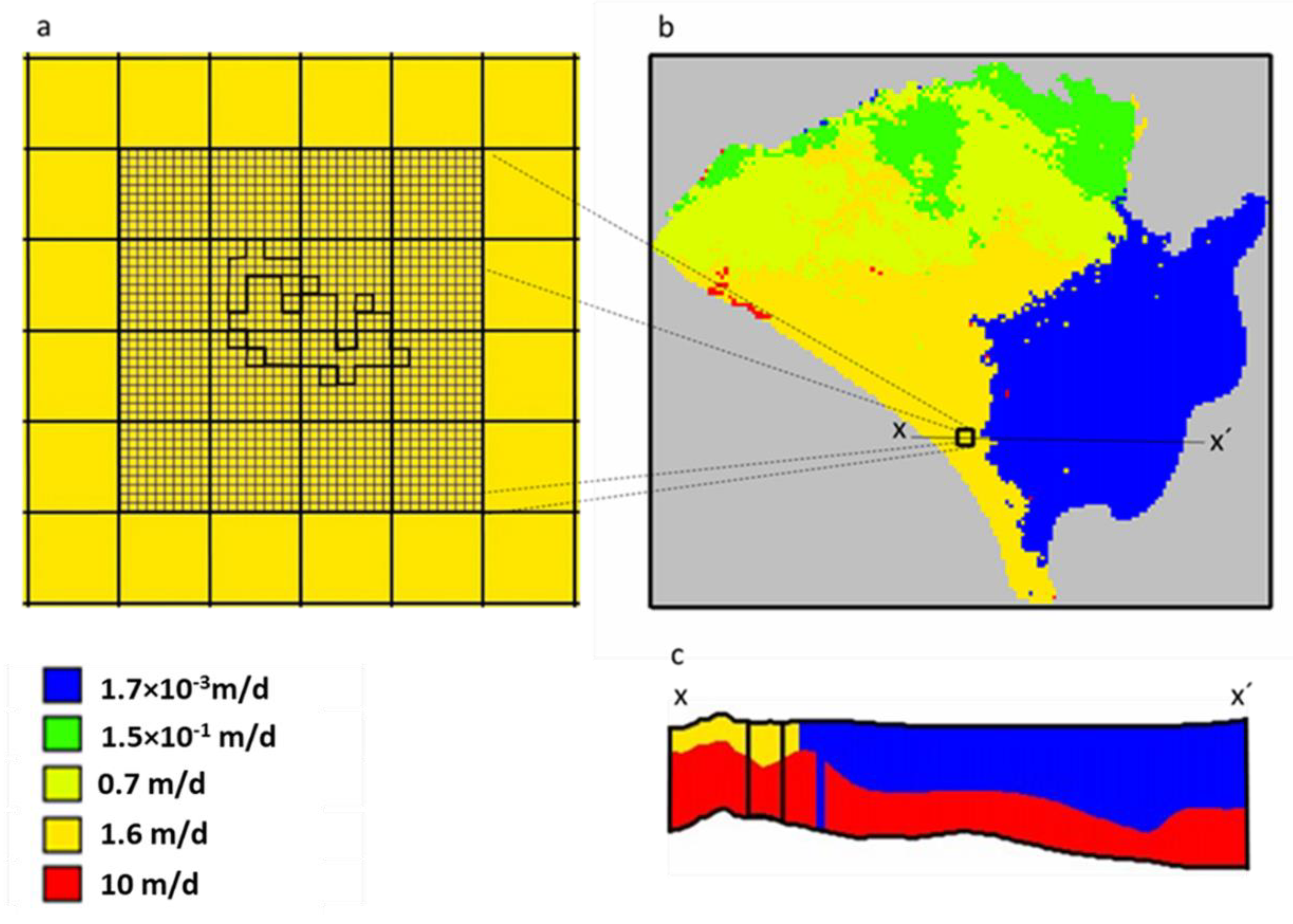
2.1. Study Area
2.2. Data
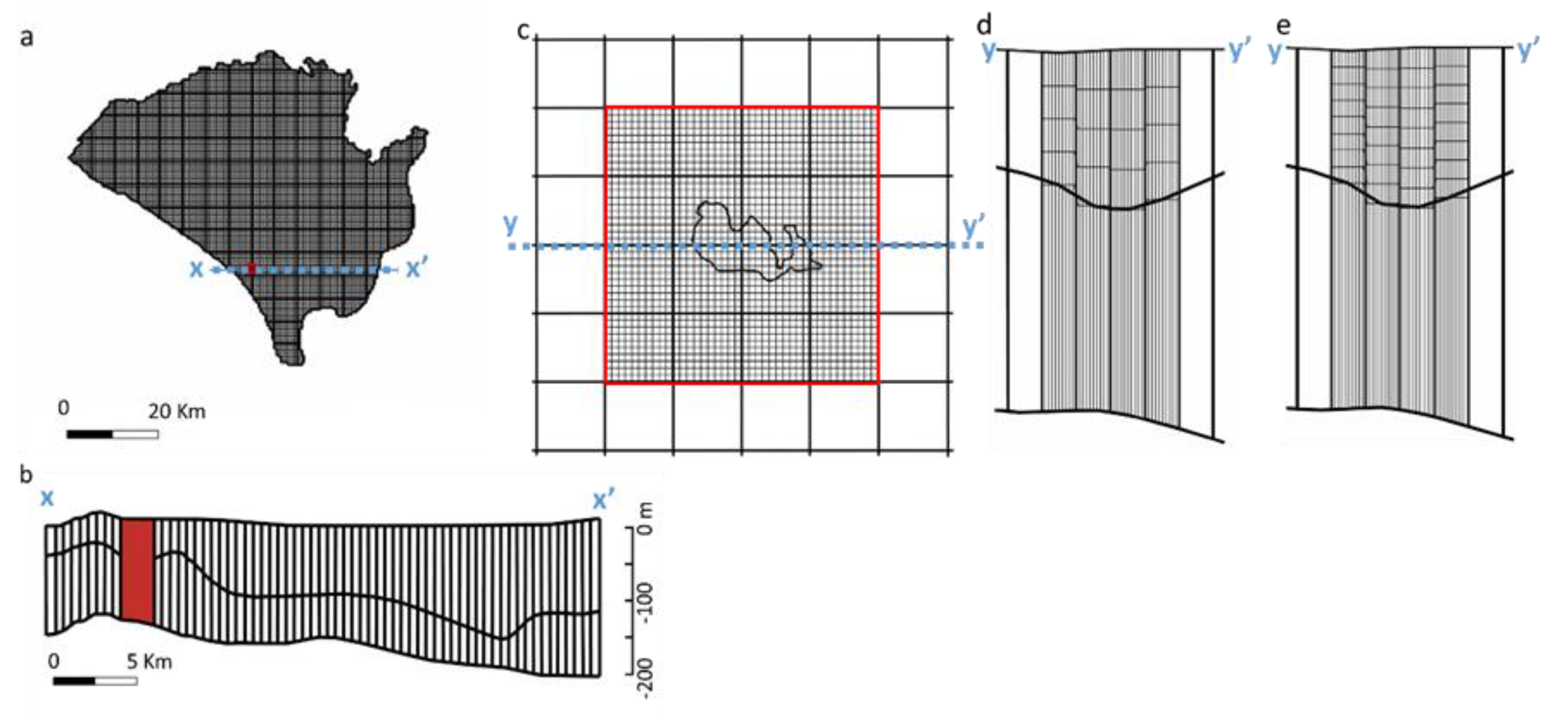
2.3. Reference Regional Groundwater Model
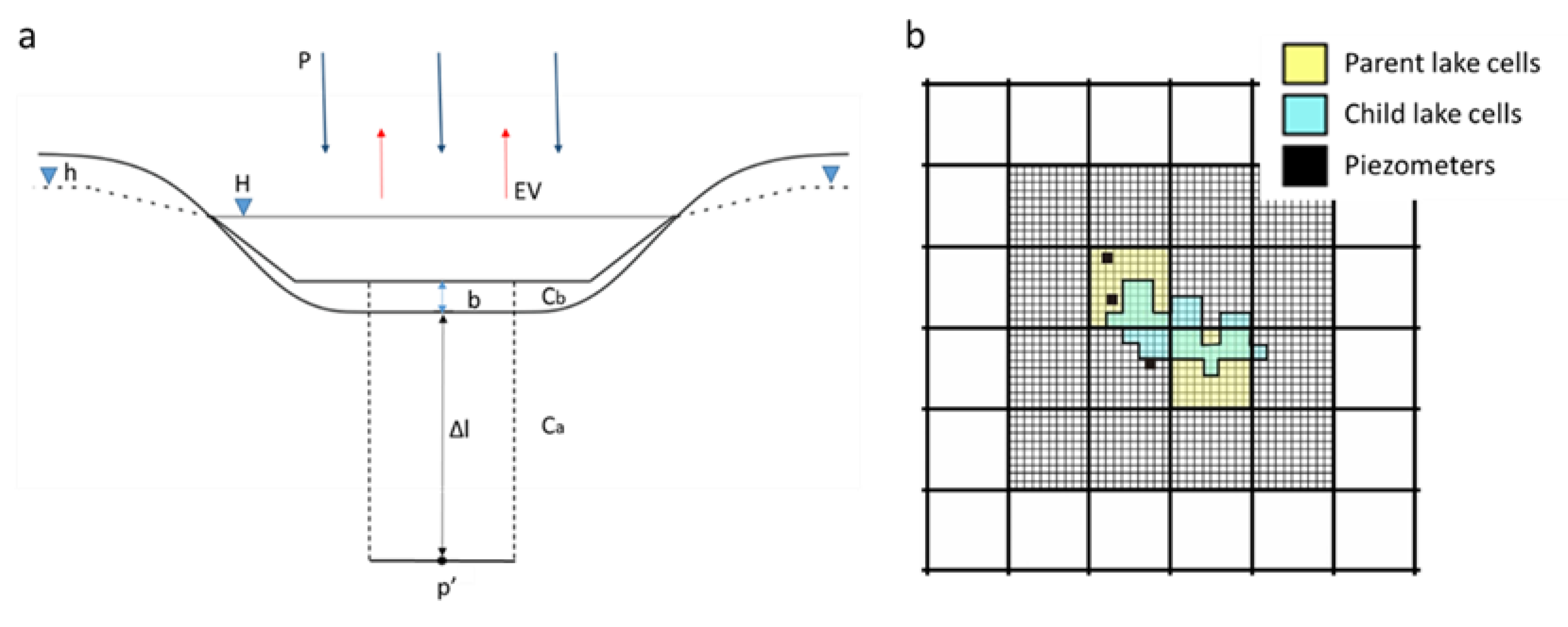
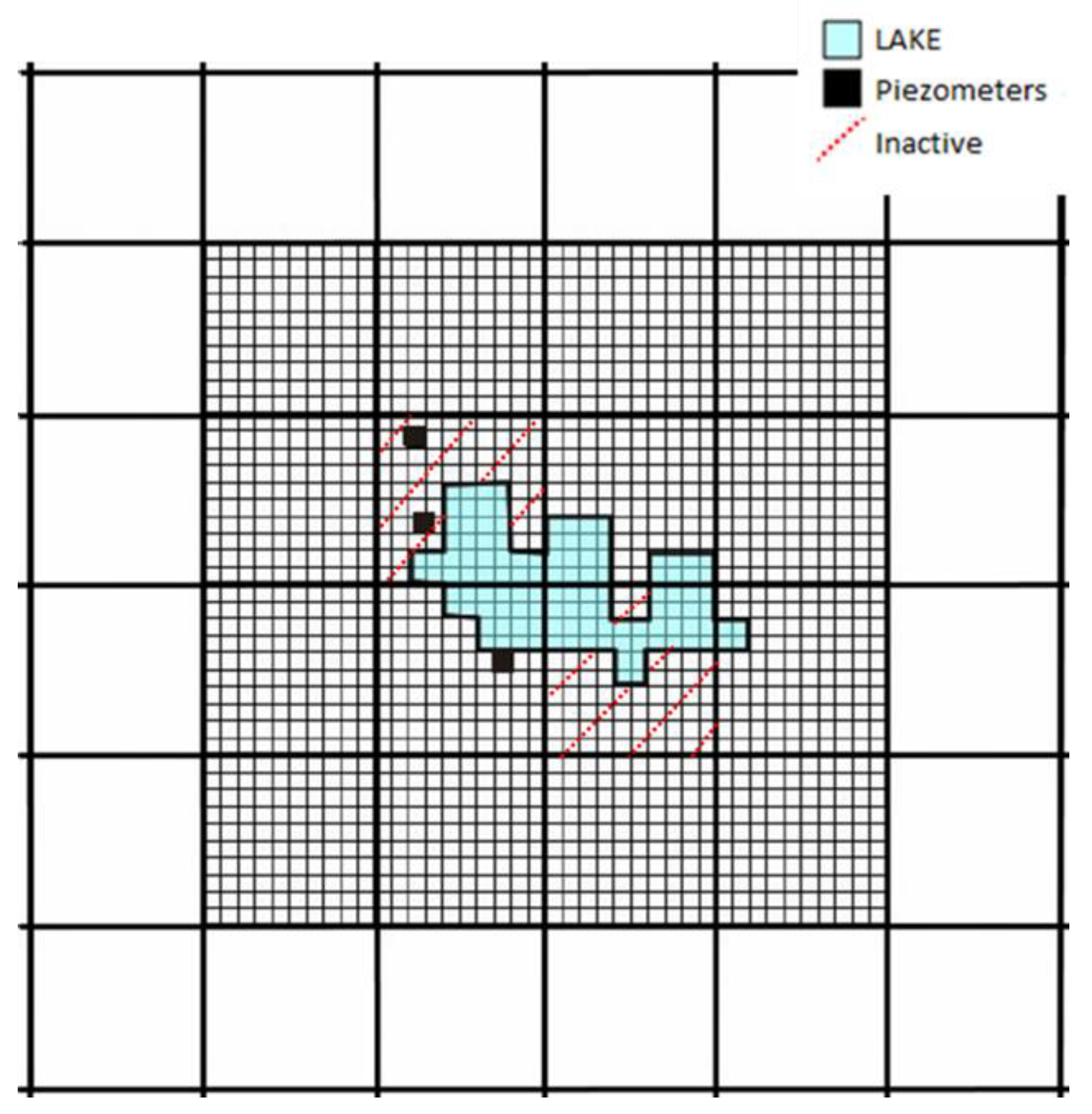
2.4. MODFLOW-LGR
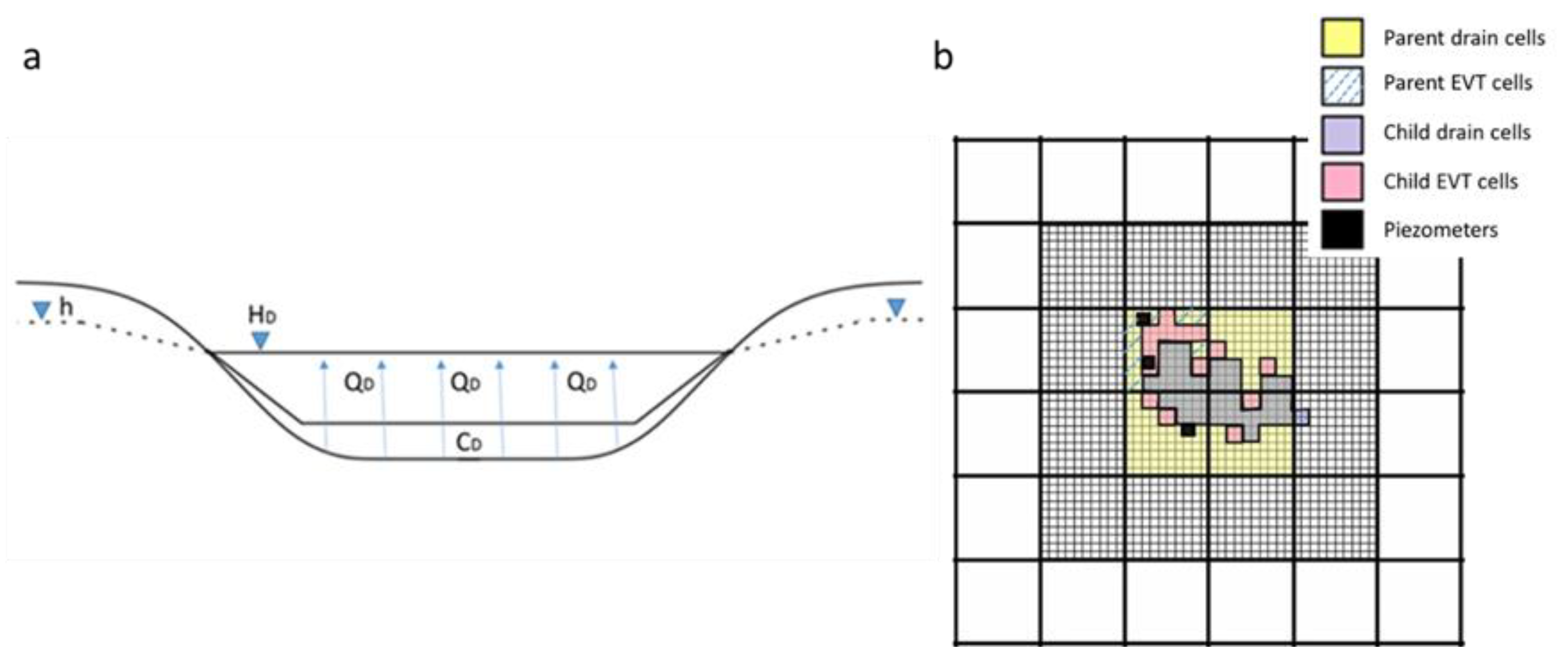
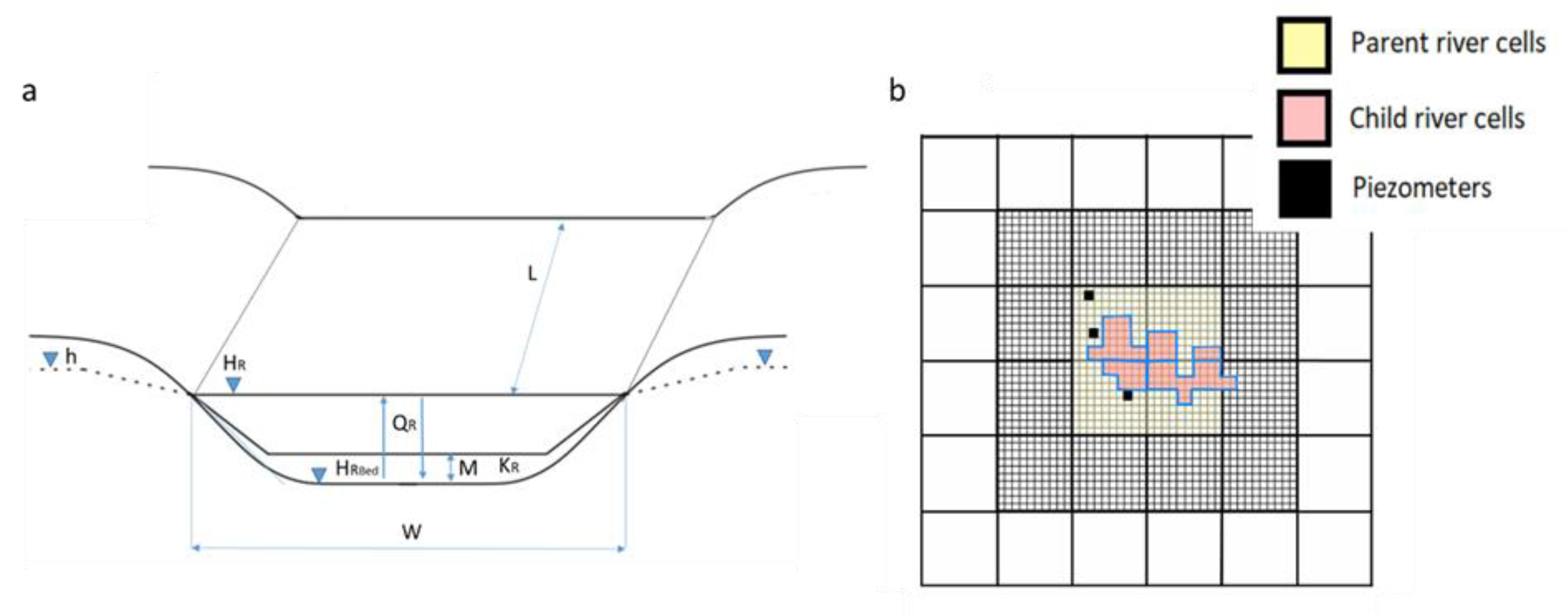
2.5. MODFLOW Boundary Conditions Representing the Pond
3. Results and Discussion
3.1. Reference Model Parent
3.2. Parent vs. Child for DRAIN Package
3.3. Parent vs. Child for RIVER Package
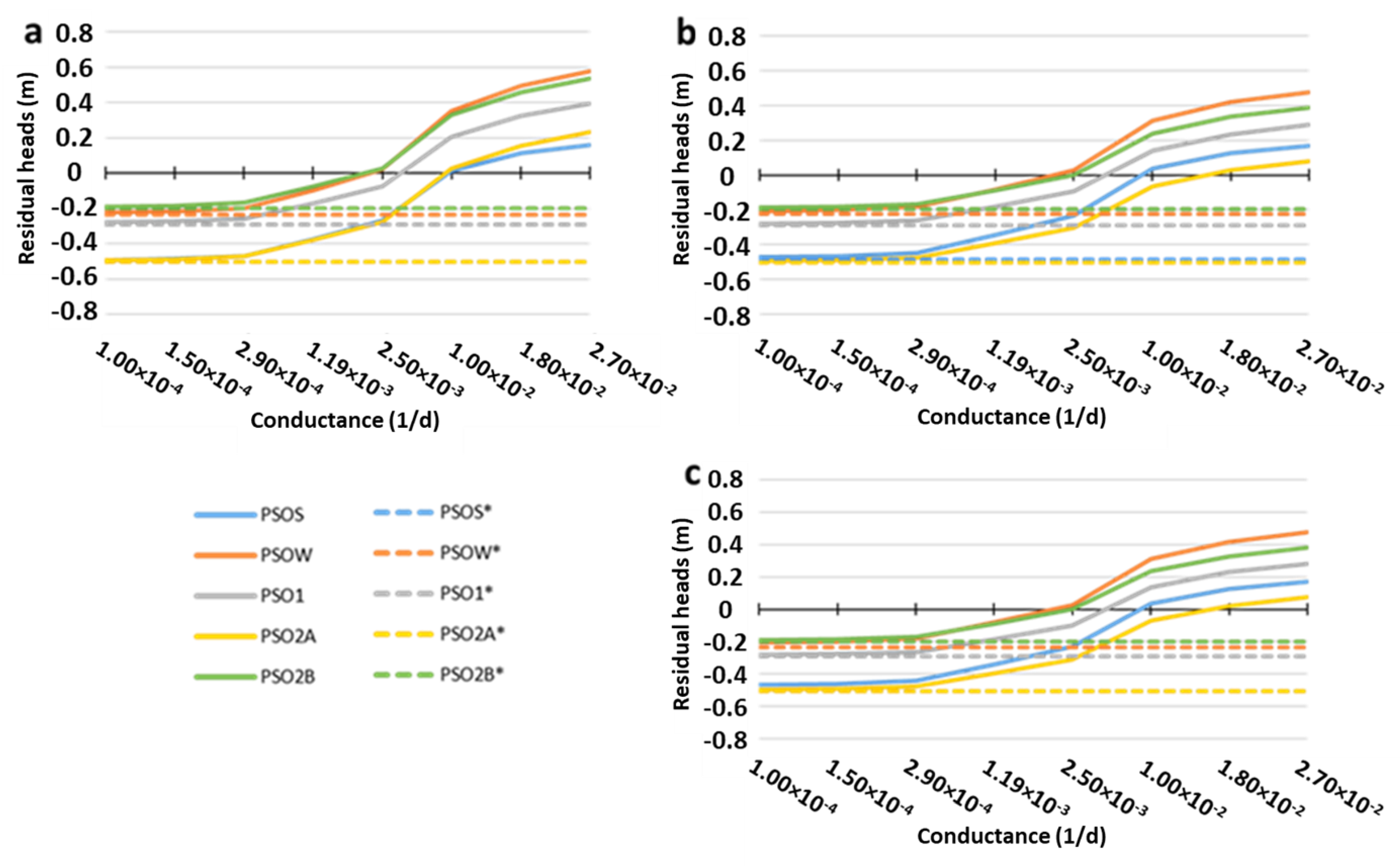
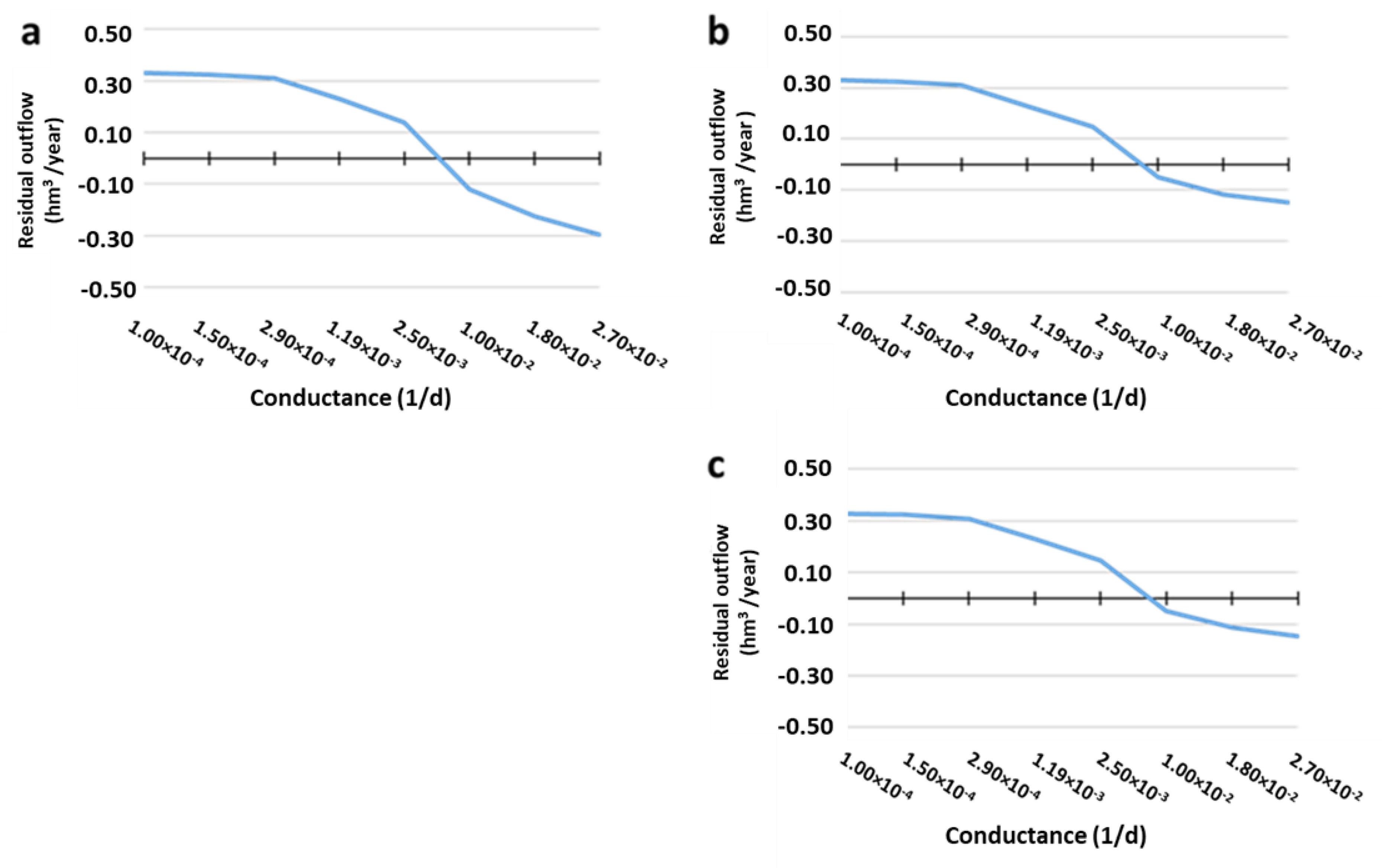
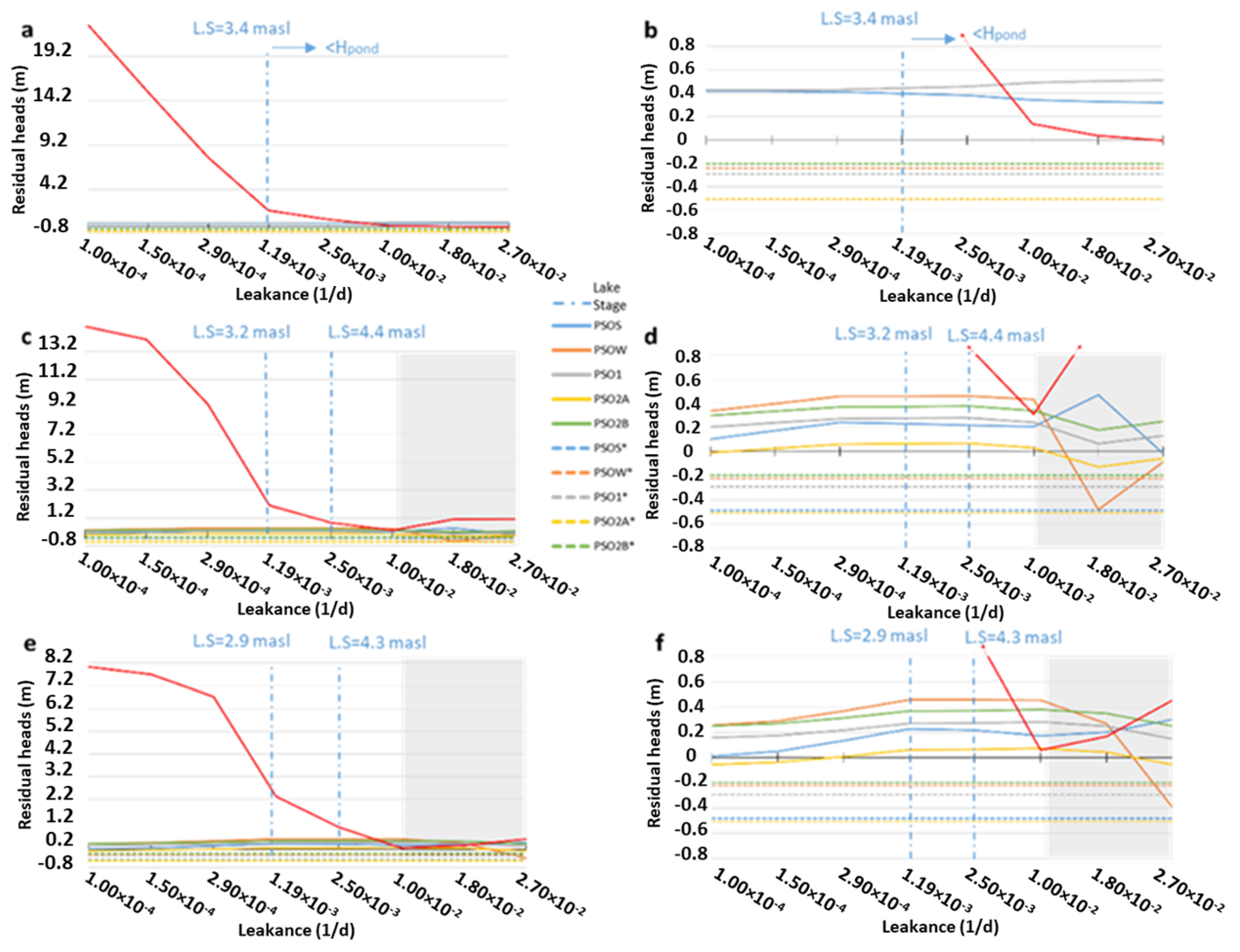
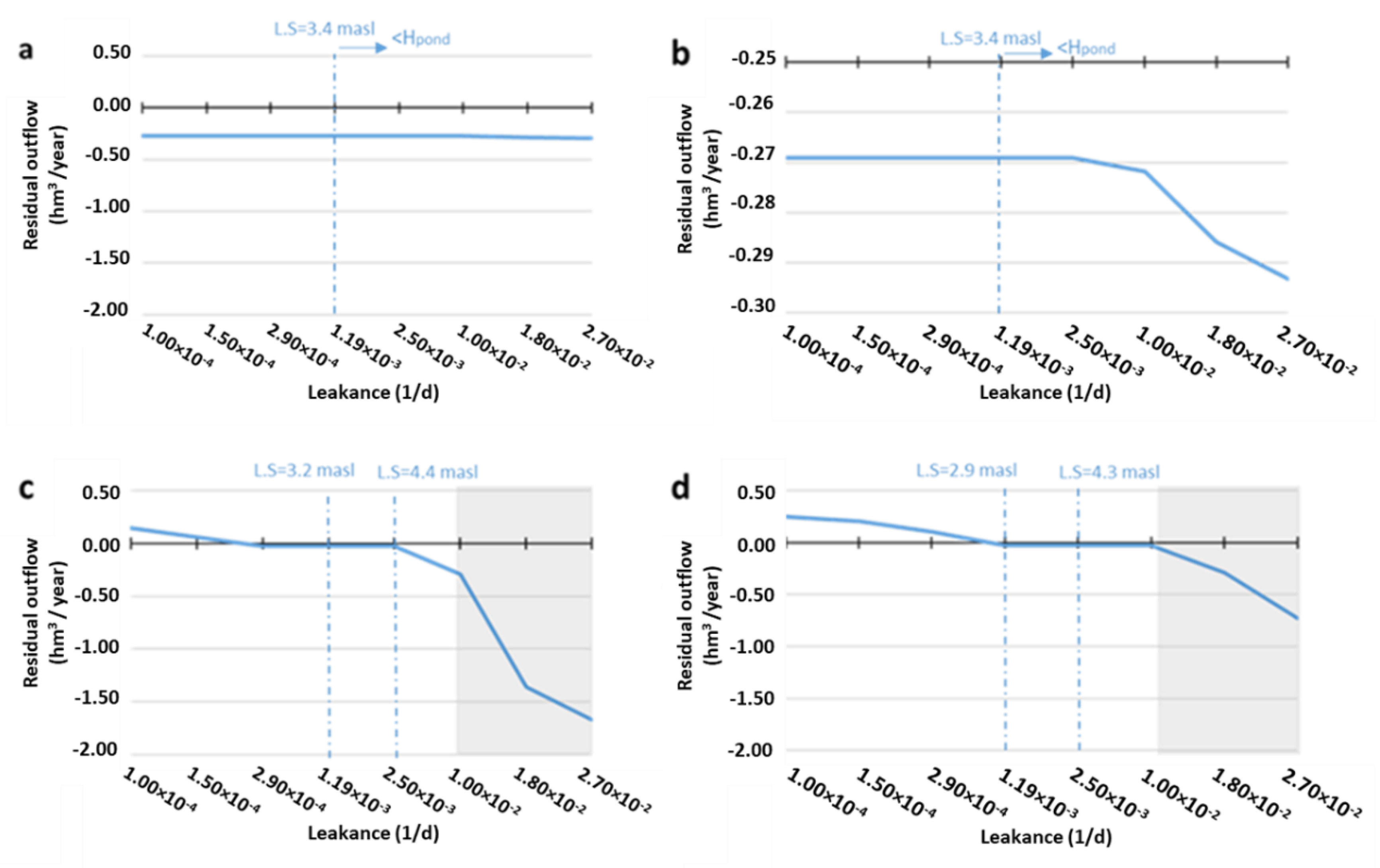
3.4. Parent vs. Child for LAKE Package
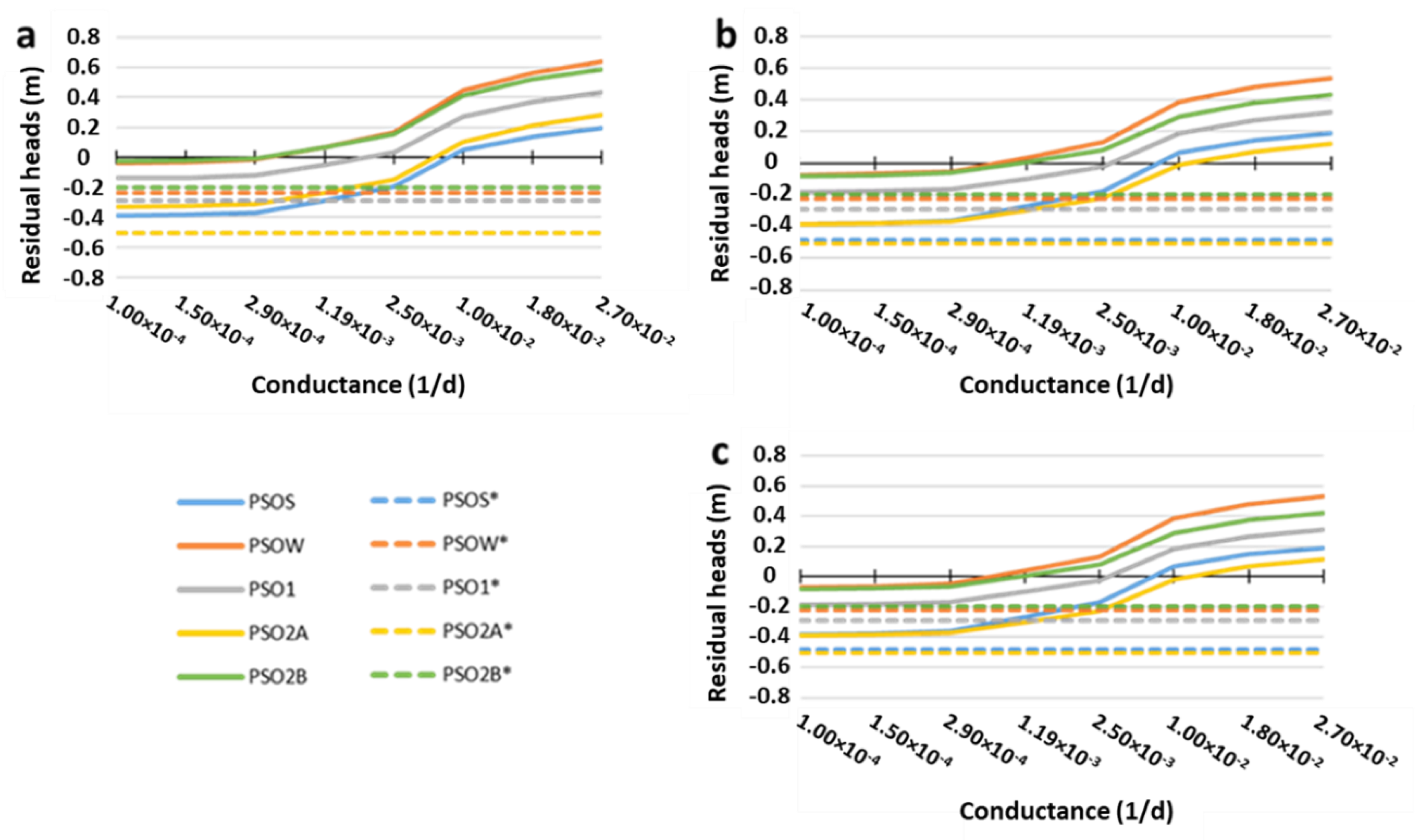
3.4.1. Piezometry Results in the Parent Model (LAKE Package)
3.4.2. Piezometry Results in the Child Models (LAKE Package)
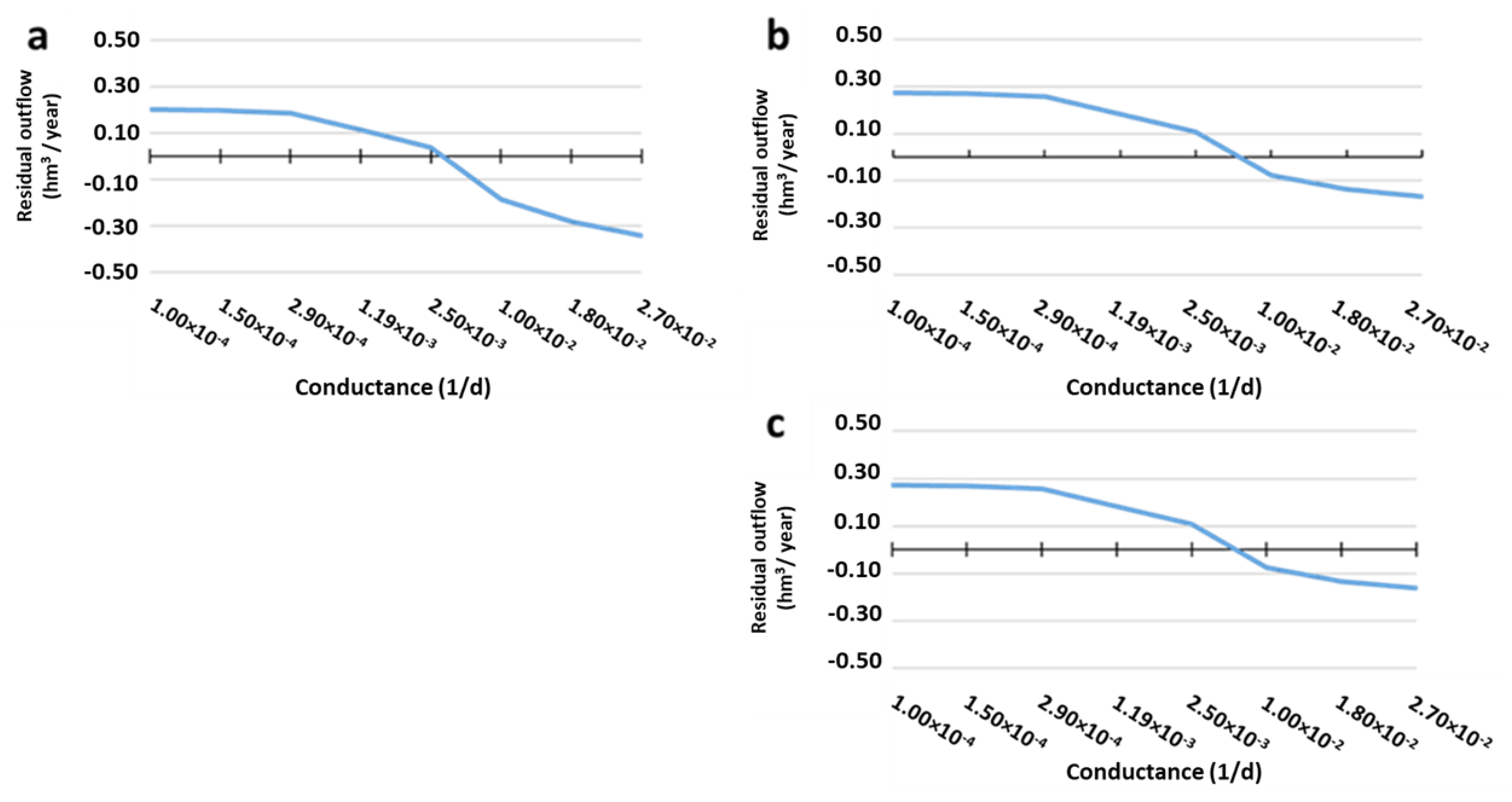
3.4.3. Outflow Results (LAKE Package)
3.5. Practical Aspects Using ModelMuse
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Harbaugh, A.W. MODFLOW-2005, The U.S. Geological Survey Modular Ground-Water Model: The Ground-Water Flow Process; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2005.
- Panday, S.; Langevin, C.D.; Niswonger, R.G.; Ibaraki, M.; Hughes, J.D. MODFLOW–USG Version 1: An Unstructured Grid Version of MODFLOW for Simulating Groundwater Flow and Tightly Coupled Processes Using a Control Volume Finite-Difference Formulation; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2013.
- Langevin, C.D.; Hughes, J.D.; Banta, E.R.; Niswonger, R.G.; Panday, S.; Provost, A.M. Documentation for the MODFLOW 6 Groundwater Flow Model; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2017.
- Mehl, S.W.; Hill, M.C. MODFLOW-LGR—Documentation of Ghost Node Local Grid Refinement (LGR2) for Multiple Areas and the Boundary Flow and Head (BFH2) Package; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2013.
- Vilhelmsen, T.N.; Christensen, S.; Mehl, S.W. Evaluation of MODFLOW-LGR in Connection with a Synthetic Regional-Scale Model. Groundwater 2012, 50, 118–132. [Google Scholar] [CrossRef] [PubMed]
- Gedeon, M.; Mallants, D. Sensitivity Analysis of a Combined Groundwater Flow and Solute Transport Model Using Local-Grid Refinement: A Case Study. Int. Assoc. Math. Geosci. 2012, 44, 881–899. [Google Scholar] [CrossRef]
- Kozar, M.D.; McCoy, K.J. Use of MODFLOW Drain package for simultating inter-basin transfer of groundwater in abandoned coal mines. J. Am. Soc. Min. Reclam. 2012, 1, 27–43. [Google Scholar]
- Peksezer-Sayit, A.; Cankara-Kadioglu, C.; Yazicigil, H. Assessment of Dewatering Requirements and their Anticipated Effects on Groundwater Resources: A Case Study from the Caldag Nickel Mine, Western Turkey. Mine Water Environ. 2015, 34, 122–135. [Google Scholar] [CrossRef]
- Zaadnoordijk, W.J. Simulating Piecewise-Linear Surface Water and Ground Water Interactions with MODFLOW. Groundwater 2009, 47, 723–726. [Google Scholar] [CrossRef]
- Yihdego, Y.; Danis, C.; Paffard, A. 3-D numerical groundwater flow simulation for geological discontinuities in the Unkheltseg Basin, Mongolia. Environ. Earth Sci. 2015, 68, 1119–1126. [Google Scholar] [CrossRef]
- Han, W.S.; Graham, J.P.; Choung, S.; Park, E.; Choi, W.; Kim, Y.S. Local-scale 696 variability in groundwater resources: Cedar Creek Watershed, Wisconsin, USA. J. Hydro-Environ. Res. 2018, 20, 38–51. [Google Scholar] [CrossRef]
- Cheng, X.; Anderson, M.P. Numerical simulation of ground-water interaction with lakes allowing for fluctuating lake levels. Groundwater 1993, 31, 929–933. [Google Scholar] [CrossRef]
- Council, G.W. ISimulating lake-groundwater interaction with Modflow. In Proceedings of the 1997 Georgia Water Resources Conference, Athens, GA, USA, 20–22 March 1997. [Google Scholar]
- Merritt, M.L.; Konikow, L.F. Documentation of a Computer Program to Simulate Lake-Aquifer Interaction Using the MODFLOW Ground-Water Flow Model and the MOC3DSolute-TransportModel; Water—Resources Investigations Report; U.S. Geological Survey: Reston, VA, USA, 2000.
- Hunt, R.J.; Haitjema, H.M.; Krohelski, J.T.; Feinstein, D.T. Simulating ground water-lake interactions: Approaches and insights. Groundwater 2003, 41, 227–237. [Google Scholar] [CrossRef]
- El-Zehairy, A.A.; Lubczynski, M.W.; Gurwin, J. Interactions of artificial lakes with groundwater applying an integrated MODFLOW solution. Hydrogeol. J. 2018, 26, 109–132. [Google Scholar] [CrossRef]
- Niswonger, R.G.; Prudic, D.E. Documentation of the Streamflow-Routing (SFR2) Package to Include Unsaturated Flow Beneath Streams: A Modification to SFR1; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2005.
- Niswonger, R.G.; Prudic, D.E.; Regan, R.S. Documentation of the Unsaturated-Zone Flow (UZF1) Package for Modeling Unsaturated Flow between the Land Surface and the Water Table with MODFLOW-2005; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2006.
- Anderson, M.P.; Hunt, R.J.; Krohelski, J.T.; Chung, K. Using High Hydraulic Conductivity Nodes to Simulate Seepage Lakes. Ground Water J. 2002, 40, 117–122. [Google Scholar] [CrossRef]
- McDonald, M.G.; Harbaugh, A.W. A Modular Three Dimensional Finite-Difference Ground-Water Flow Model; Techniques of Water-Resources Investigations; U.S. Geological Survey: Reston, VA, USA, 1988; Volume 6, p. 586.
- Jones, P.M.; Roth, J.L.; Trost, J.J.; Christenson, C.A.; Diekoff, A.L.; Erickson, M.L. Simulation and Assessment of Groundwater Flow and Groundwater and Surface-Water Exchanges in Lakes in the Northeast Twin Cities Metropolitan Area, Minnesota, 2003 through 2013. Chapter B of Water Levels and Groundwater and Surface-Water Exchanges in Lakes of the Northeast Twin Cities Metropolitan Area, Minnesota, 2002 through 2015; U.S. Geological Survey: Reston, VA, USA, 2017; ISSN 2328-0328.
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water Model—User Guide to Modularization Concepts and the Ground-Water Flow Process; Open-File Report 00-92; U.S. Geological Survey: Reston, VA, USA, 2000; p. 121.
- Dusek, P.; Veliskova, Y. Comparison of the MODFLOW modules for the simulation of the river type boundary condition. Int. J. Eng. Inf. Sci. 2017, 12, 3–13. [Google Scholar] [CrossRef]
- Brunner, P.; Simmons, C.T.; Cook, P.G.; Therrien, R. Modeling surface water-groundwater interaction with MODFLOW: Some considerations. Ground Water J. 2020, 50, 174–180. [Google Scholar] [CrossRef] [Green Version]
- Green, A.J.; Alcorlo, P.; Peeters, E.T.; Morris, E.P.; Espinar, J.L.; Bravo-Utrera, M.A.; Bustamante, J.; Díaz-Delgado, R.; Koelmans, A.A.; Mateo, R.; et al. Creating a safe operating space for wetlands in a changing climate. Front. Ecol. Environ. 2017, 15, 99–107. [Google Scholar] [CrossRef] [Green Version]
- Sacks, L.A.; Herman, J.S.; Konikow, L.F.; Vela, A.L. Seasonal dynamics of groundwater-Lake interactions of Doñana National Park, Spain. J. Hydrol. 1992, 136, 123–154. [Google Scholar] [CrossRef]
- Suso, J.; Llamas, M.R. Influence of groundwater development on the Doñana National Park ecosystems (Spain). J. Hydrol. 1993, 141, 239–269. [Google Scholar] [CrossRef]
- Serrano, L.; Zunzunegui, M. The relevance of preserving temporary ponds during drought: Hydrological and vegetation changes over a 16-year period in the Doñana National Park (south-west Spain). Aquat. Conserv. Mar. Freshw. Ecosyst. 2008, 18, 261–279. [Google Scholar] [CrossRef]
- Serrano, L.; Serrano, L. Influence of groundwater exploitation for urban water supply on temporary ponds from the Doñana National Park (SW Spain). J. Environ. Manag. 1996, 46, 229–238. [Google Scholar] [CrossRef]
- Instituto Geológico y Minero de España (IGME). Modelo Matemático del Acuífero Almonte—Marismas: Actualización y Realización en Visual Modflow 2005. 2005. Available online: https://www.researchgate.net/publication/264229860_Modelo_matematico revisado_del_acuifero Almonte-Marismas aplicación a distintas-hipotesis de gestion (accessed on 21 November 2018).
- Instituto Geológico y Minero de España (IGME). Proyecto Para la Actualización del Modelo Numérico (Visual Modflow 4.3, Igme 2007) del Sistema Acuífero Almonte-Marismas, Como Apoyo para el Desarrollo de un Modelo de Gestión y Uso Sostenible del Acuífero en el Ámbito de Doñana (Huelva-Sevilla); Instituto Geológico y Minero de España: Madrid, Spain, 2011. [Google Scholar]
- Guardiola-Albert, C.; Jackson, C.R. Potential impacts of climate change on groundwater supplies to the Doñana wetland, Spain. Wetlands 2011, 31, 907. [Google Scholar] [CrossRef] [Green Version]
- Lozano, E. Las Aguas Subterráneas en los Cotos de Doñana y su Influencia en las Lagunas. Ph.D. Thesis, Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos, Universidad Politécnica de Cataluña, Barcelona, Spain, 2004. [Google Scholar]
- Rodríguez-Rodríguez, M.; Martos-Rosillo, S.; Fernández-Ayuso, A.; Aguilar, R. Application of a flux model and segmented-Darcy approach to estimate the groundwater discharge to a shallow pond. Case of Santa Olalla pond. Geogaceta 2018, 63, 27–30. [Google Scholar]
- Salvany, J.M.; Custodio, E. Características litoestratigráficas de los depósitos pliocuaternarios del bajo Guadalquivir en el área de Doñana; implicaciones hidrogeológicas. Rev. Soc. Geol. Esp. 1995, 8, 21–31. [Google Scholar]
- Fernandez-Ayuso, A.; Aguilera, H.; Guardiola-Albert, C.; Rodriguez-Rodriguez, M.; Heredia, J.; Naranjo-Fernandez, N. Unraveling the Hydrological Behavior of a coastal Pond in Doñana National Park (Southwest Spain). Groundwater 2019, 57, 895–906. [Google Scholar] [CrossRef]
- Estación Biológica de Doñana. ICTS de la reserva biológica de Doñana. CSIC, Spain. Available online: http://icts.ebd.csic.es/datos-meteorologicos (accessed on 2 June 2018).
- FAO. Crop Evapotranspiration. In Guidelines for Computing Crop Waater Requirements; Paper 56; Food and Agriculture Organization of the United Nations Irrigation and Drainage: Rome, Italy, 1998. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. J. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Winston, R.B. ModelMuse—A Graphical User Interface for MODFLOW-2005 and PHAST; Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2009.
- Naranjo-Fernandez, N.; Guardiola-Albert, C.; Montero-Gonzalez, E. Applying 3D Geostatistical Simulation to Improve the Groundwater Management Modelling of Sedimentary Aquifers: The Case of Doñana (Southwest Spain). Water 2019, 11, 39. [Google Scholar] [CrossRef] [Green Version]
- Guardiola-Albert, C.; García-Bravo, N.; Mediavilla, C.; Martín Machuca, M. Gestión de los recursos hídricos subterráneos en el entorno de Doñana con el apoyo del modelo matemático del acuífero Almonte-Marismas. Boletín Geol. Min. 2009, 120, 361–376. [Google Scholar]
- Coleto, M.C. Funciones Hidrologicas y Biogeoquimicas de las Formaciones Palustres Hipogénicas de Los Mantos Eólicos de Los Mantos del Abalorio-Doñana (Huelva). Ph.D. Thesis, Universidad Autónoma de Madrid, Facultad de Ciencias, Madrid, Spain, 2003. [Google Scholar]
- Winston, R.B. ModelMuse Version 4—A Graphical User Interface for MODFLOW 6; Scientific Investigations Report 2019–5036; U.S. Geological Survey: Reston, VA, USA, 2019; p. 10. [CrossRef]
- Rosemberry, D.O.; Hayashi, M. Wetland Techniques; Anderson, J., Davis, C., Eds.; Springer: Dordrecht, The Netherlands, 2013; Chapter 3; Volume 1, pp. 87–225. [Google Scholar] [CrossRef]
| Source | Name | X UTM | Y UTM | Average Observed Heads (m) | Max/Min Observed Heads (m) | No. of Measurements | Well Screen Depth (m) | Sensor (Brand) |
|---|---|---|---|---|---|---|---|---|
| (ED50 H30) | (ED50 H30) | |||||||
| IGME | PSO1 | 190,112 | 4,098,731 | 6.33 | 6.78/5.84 | 1868 | 69.5 | OTT |
| MiniOrpheus | ||||||||
| IGME | PSO2A | 190,113 | 4,098,733 | 6.14 | 6.60/5.54 | 2230 | 27.5 | OTT |
| MiniOrpheus | ||||||||
| IGME | PSO2B | 190,113 | 4,098,733 | 6.44 | 6.59/5.75 | 1217 | 45 | OTT |
| Orpheus | ||||||||
| POU | PSOW | 190,142 | 4,098,479 | 6.08 | 6.48/5.46 | 2920 | 15.6 | MiniDiver |
| POU | PSOS | 190,374 | 4,098,113 | 5.45 | 5.90/4.95 | 2920 | 2.5 | MiniDiver |
| CD/A (1/d) | Obj. Function | Drain | Lake | River |
|---|---|---|---|---|
| 0.0001 | Parent | 0.32 | 517.74 | 0.76 |
| 4 Layer | 0.42 | 225.17 | 0.73 | |
| 8 Layer | 0.42 | 64.93 | 0.73 | |
| 0.00015 | Parent | 0.31 | 229.43 | 0.73 |
| 4 Layer | 0.4 | 198.21 | 0.71 | |
| 8 Layer | 0.4 | 59.65 | 0.71 | |
| 0.00029 | Parent | 0.28 | 61.02 | 0.67 |
| 4 Layer | 0.37 | 88.83 | 0.65 | |
| 8 Layer | 0.37 | 45.64 | 0.65 | |
| 0.00119 | Parent | 0.16 | 3.77 | 0.38 |
| 4 Layer | 0.21 | 4.87 | 0.37 | |
| 8 Layer | 0.21 | 5.92 | 0.37 | |
| 0.0025 | Parent | 0.11 | 1.11 | 0.17 |
| 4 Layer | 0.12 | 1.22 | 0.18 | |
| 8 Layer | 0.12 | 1.44 | 0.18 | |
| 0.01 | Parent | 0.48 | 0.45 | 0.29 |
| 4 Layer | 0.28 | 0.4 | 0.18 | |
| 8 Layer | 0.27 | 0.47 | 0.18 | |
| 0.018 | Parent | 0.87 | 0.45 | 0.65 |
| 4 Layer | 0.5 | 3.56 | 0.37 | |
| 8 Layer | 0.48 | 0.34 | 0.36 | |
| 0.027 | Parent | 1.18 | 0.45 | 0.95 |
| 4 Layer | 0.65 | 4.12 | 0.52 | |
| 8 Layer | 0.63 | 0.56 | 0.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Serrano-Hidalgo, C.; Guardiola-Albert, C.; Heredia, J.; Elorza Tenreiro, F.J.; Naranjo-Fernández, N. Selecting Suitable MODFLOW Packages to Model Pond–Groundwater Relations Using a Regional Model. Water 2021, 13, 1111. https://doi.org/10.3390/w13081111
Serrano-Hidalgo C, Guardiola-Albert C, Heredia J, Elorza Tenreiro FJ, Naranjo-Fernández N. Selecting Suitable MODFLOW Packages to Model Pond–Groundwater Relations Using a Regional Model. Water. 2021; 13(8):1111. https://doi.org/10.3390/w13081111
Chicago/Turabian StyleSerrano-Hidalgo, Carmen, Carolina Guardiola-Albert, Javier Heredia, Francisco Javier Elorza Tenreiro, and Nuria Naranjo-Fernández. 2021. "Selecting Suitable MODFLOW Packages to Model Pond–Groundwater Relations Using a Regional Model" Water 13, no. 8: 1111. https://doi.org/10.3390/w13081111






