Smoothed Particle Hydrodynamics Simulations of Water Flow in a 90° Pipe Bend
Abstract
1. Introduction
2. Governing Equations and Numerical Framework
2.1. Exact Equations
2.2. LES Filtering
2.3. The SPH Method
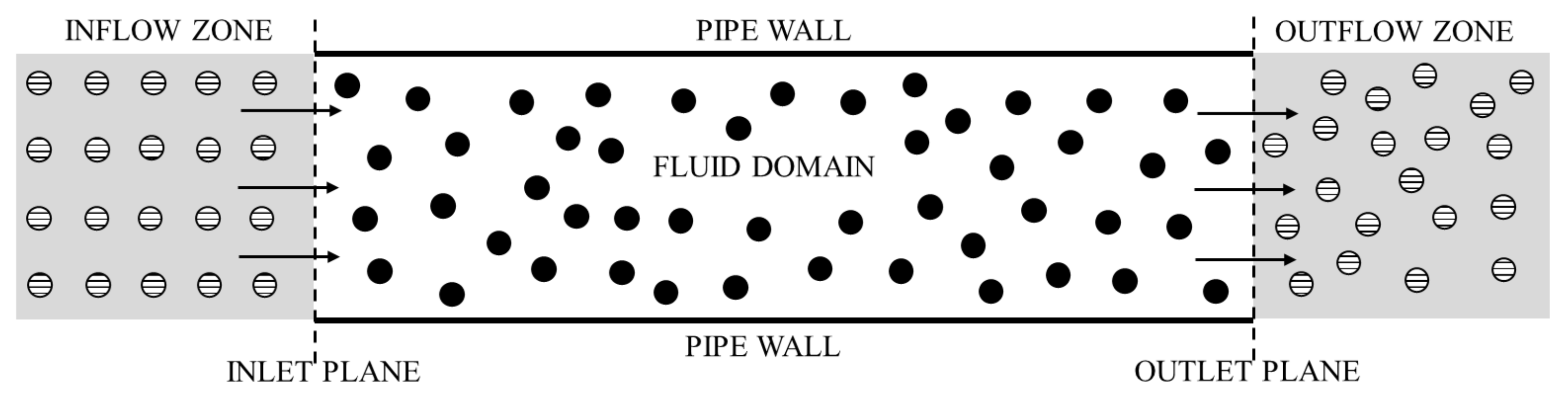
2.4. Boundary Conditions
2.5. Time Marching Scheme
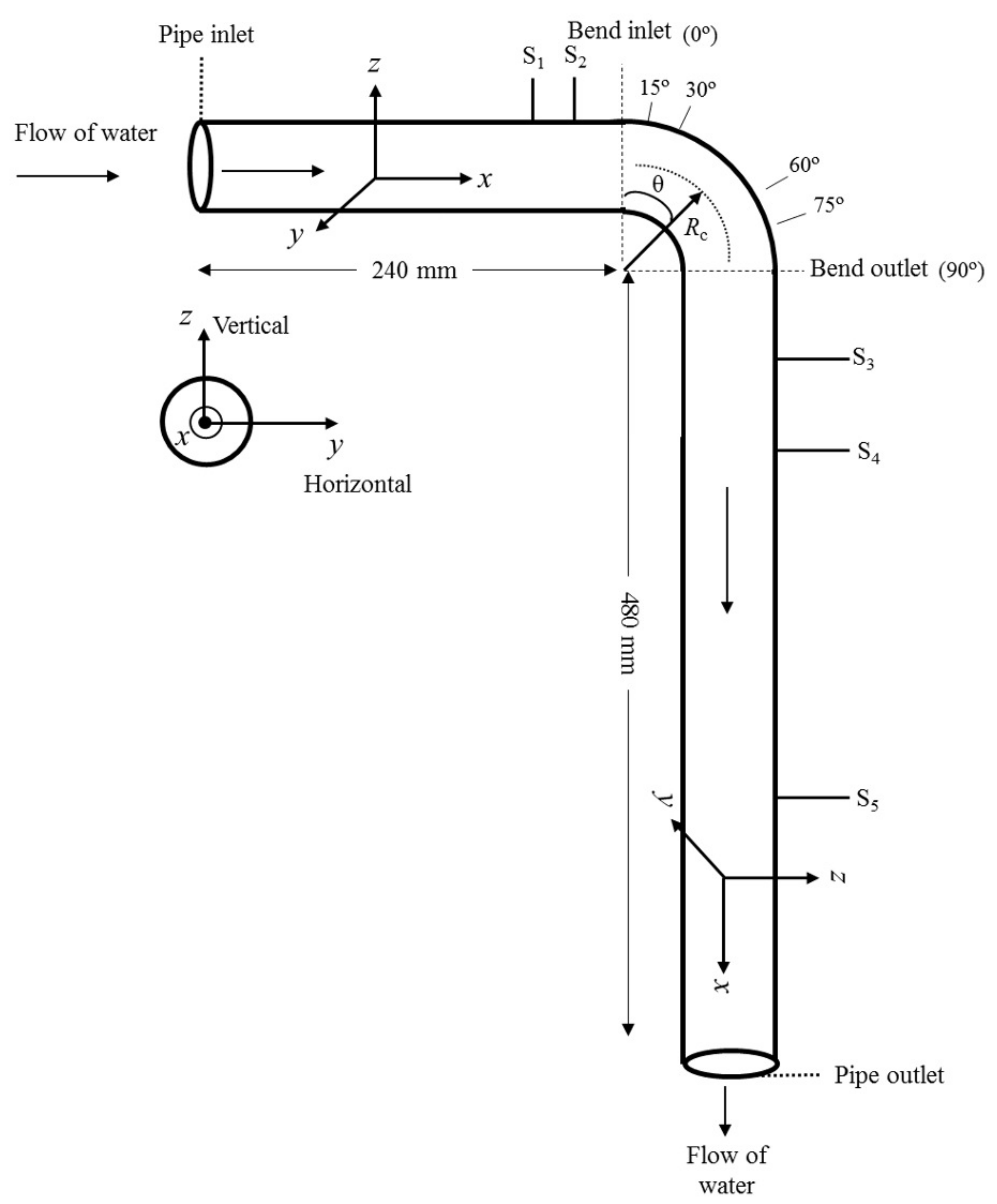
3. Pipe Bend Model Description
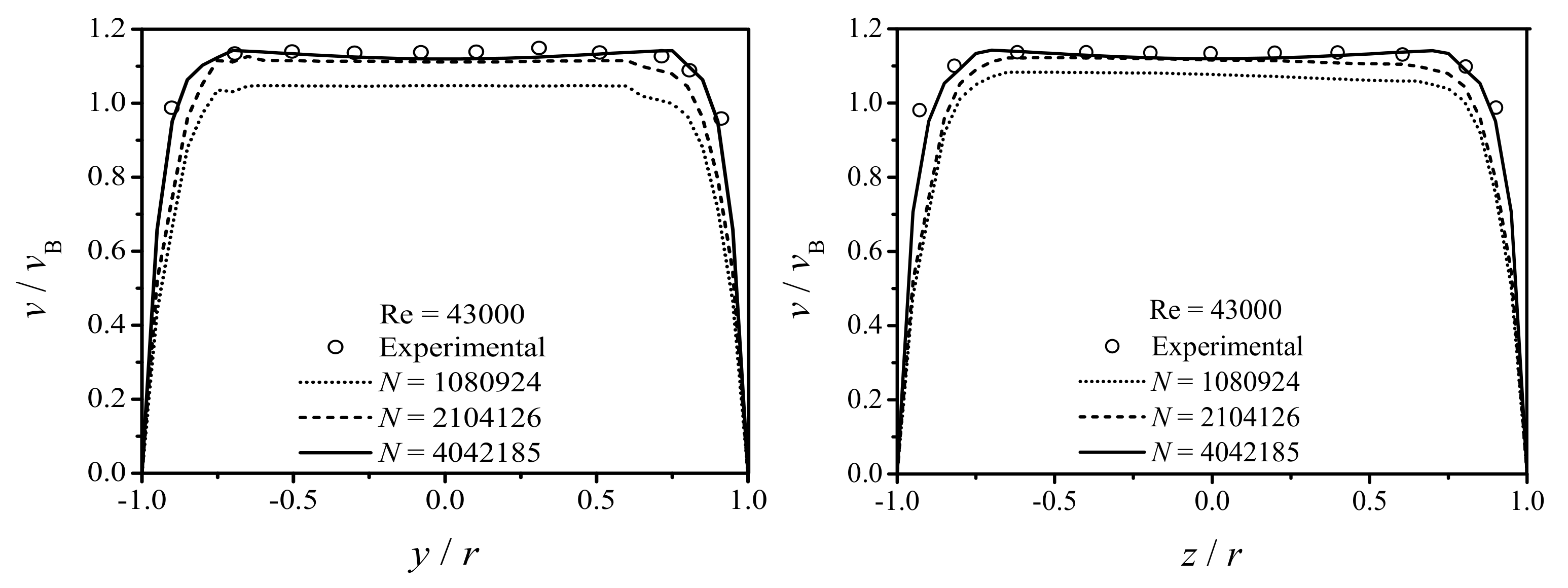
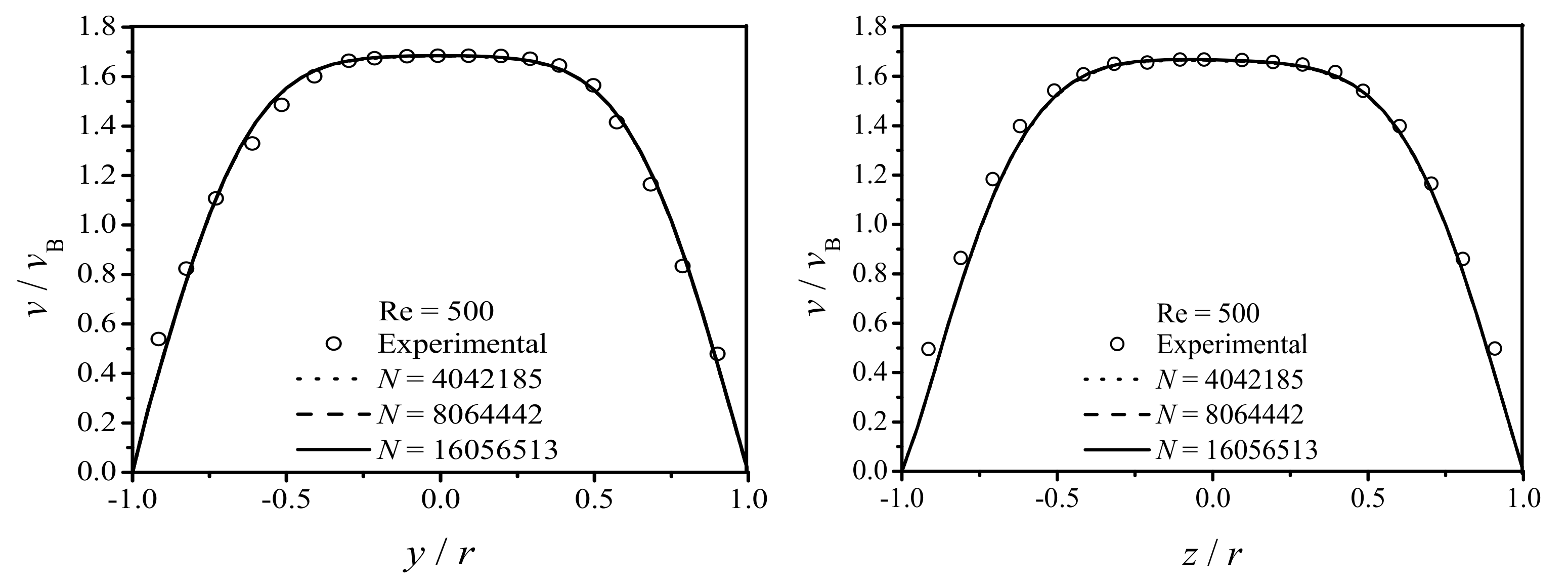
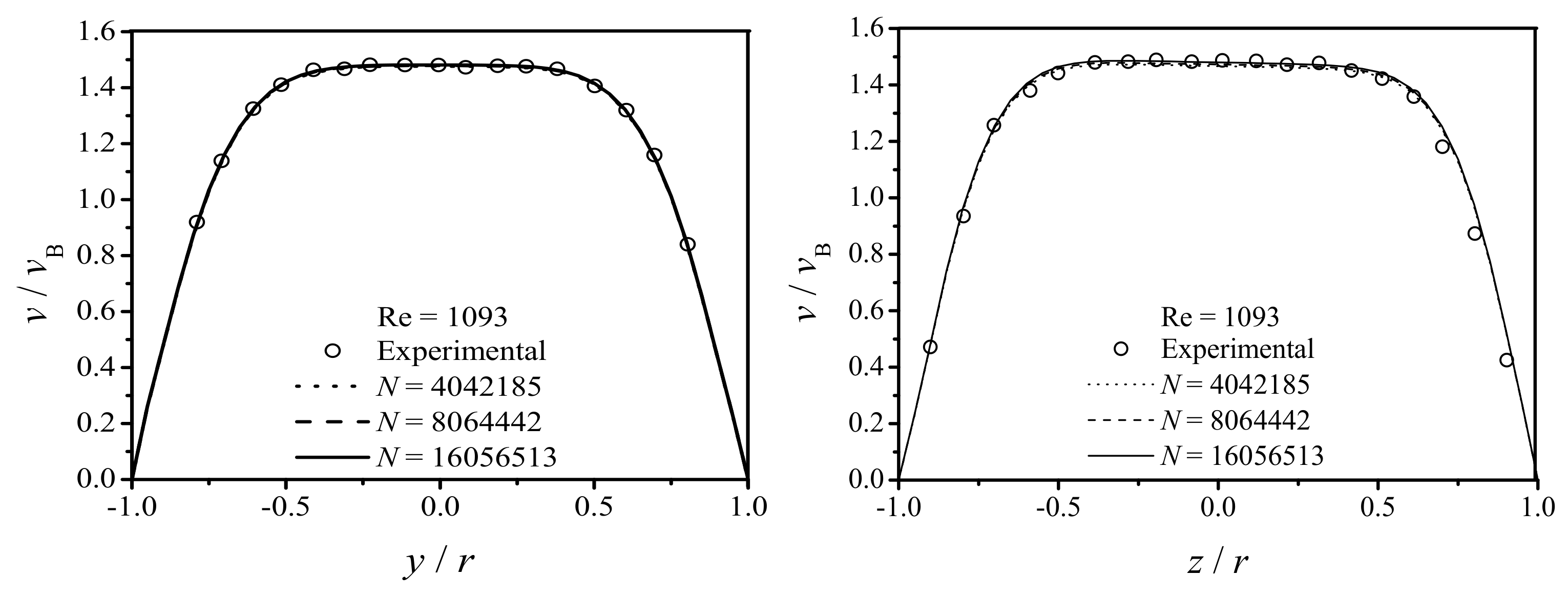
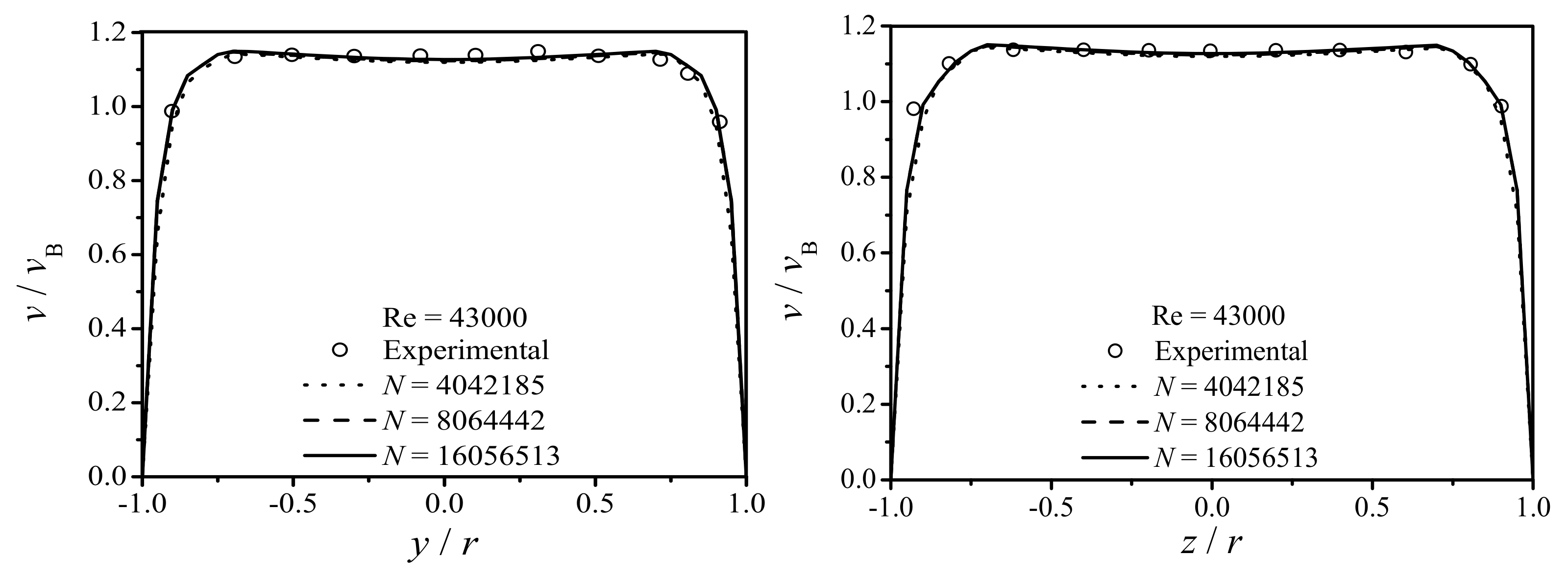
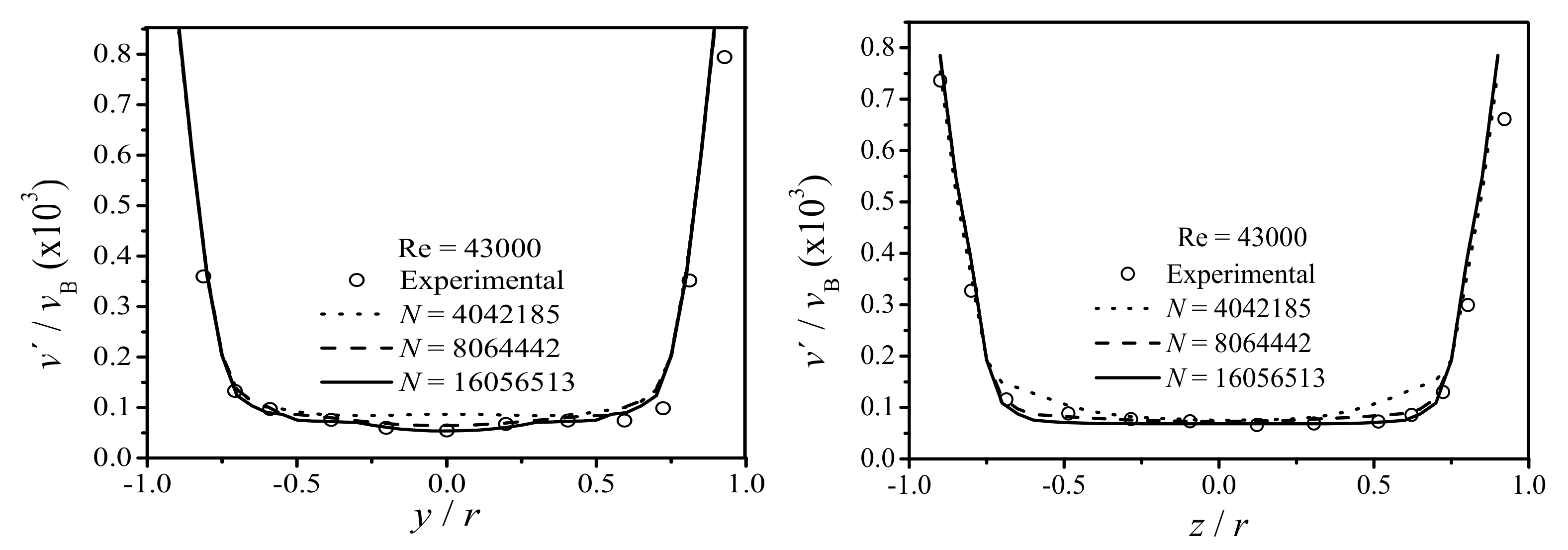
Validation and Particle Independence Test
4. Results
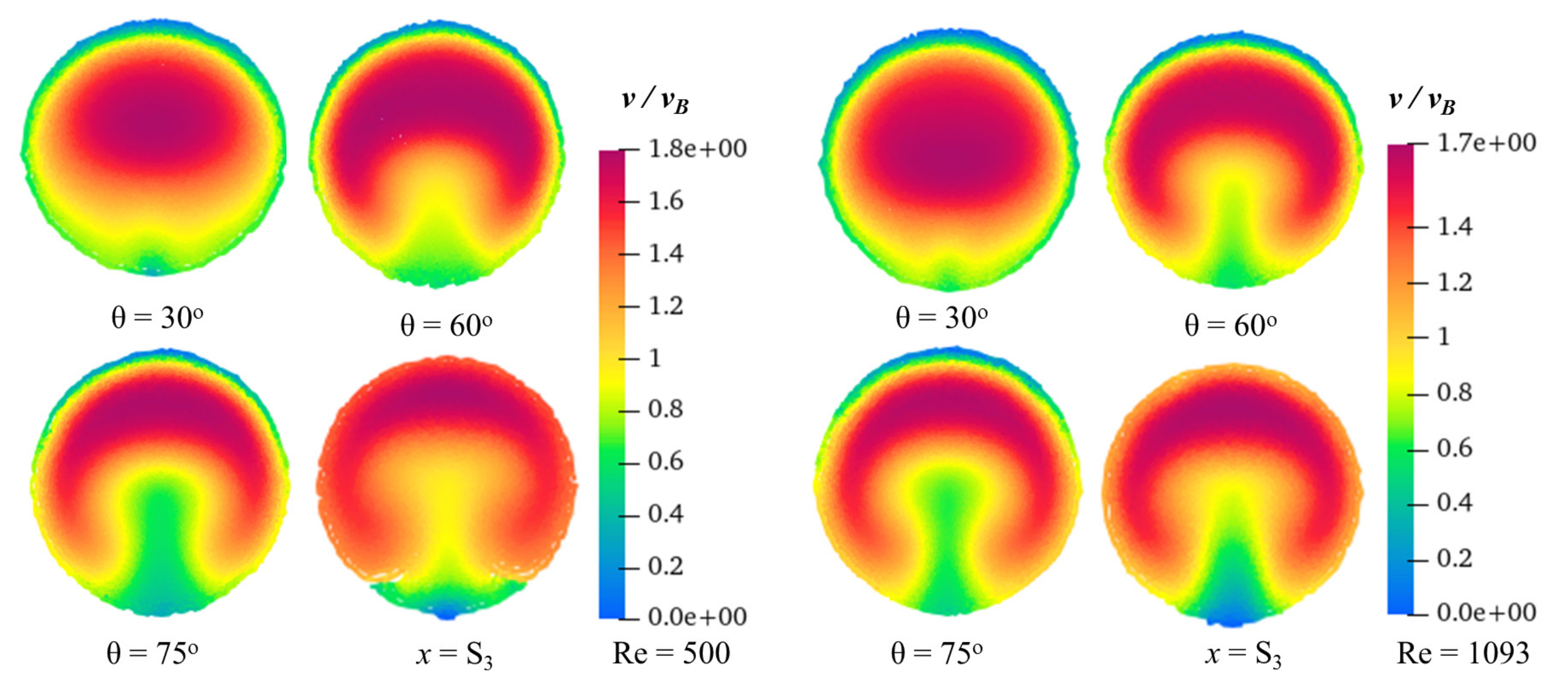
4.1. Laminar Flow
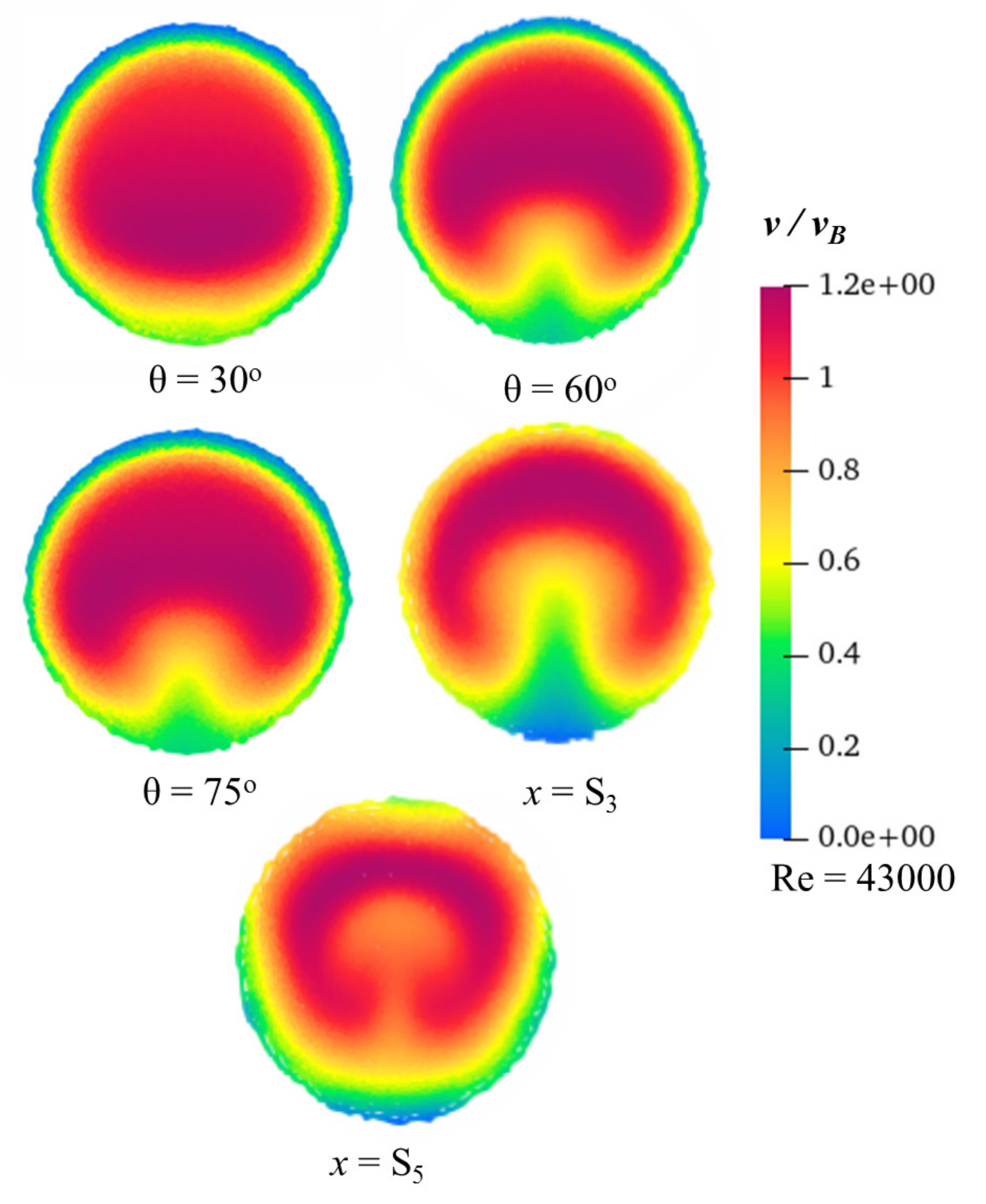
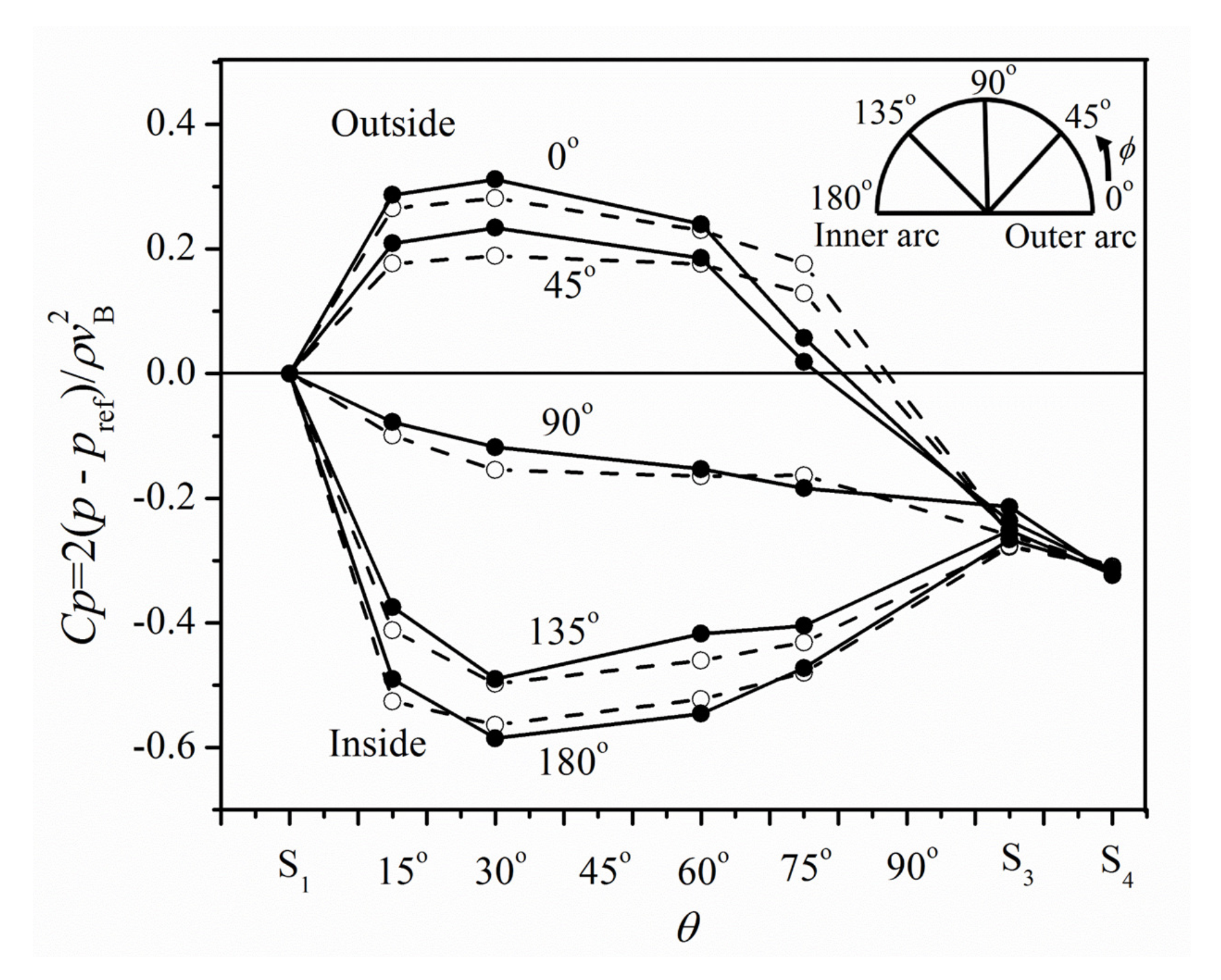
4.2. Turbulent Flow
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Enayet, M.M.; Gibson, M.M.; Taylor, A.M.K.P.; Yianneskis, M. Laser-Doppler measurements of laminar and turbulent flow in a pipe bend. Int. J. Heat Fluid Flow 1982, 3, 213–219. [Google Scholar] [CrossRef]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Exp. Fluids 1998, 25, 42–49. [Google Scholar] [CrossRef]
- Sudo, K.; Sumida, M.; Hibara, H. Experimental investigation on turbulent flow in a square-sectioned 90-degree bend. Exp. Fluids 2001, 30, 246–252. [Google Scholar] [CrossRef]
- Hellström, L.H.O.; Sinha, A.; Smits, A.J. Visualizing the very-large-scale motion in turbulent pipe flow. Phys. Fluids 2011, 23, 011703. [Google Scholar] [CrossRef]
- Verma, A.K.; Singh, S.N.; Seshadri, V. Pressure drop for the flow of high concentration solid-liquid mixture across 90° horizontal coventional circular pipe bend. Indian J. Eng. Mat. Sci. 2006, 13, 477–483. [Google Scholar]
- Rup, K.; Malinowski, L.; Sarna, P. Measurements of flow rate in square-sectioned duct bend. J. Theoret. Appl. Mech. 2011, 49, 301–311. [Google Scholar]
- Kalpakli, A.; Örlü, R. Turbulent pipe flow downstream a 90° pipe bend with and without superimposed swirl. Int. J. Heat Fluid Flow 2013, 41, 103–111. [Google Scholar] [CrossRef]
- Kim, J.; Yadav, M.; Kim, S. Characteristics of secondary flow induced by 90-degree elbow in turbulent pipe flow. Eng. Appl. Comput. Fluid Mech. 2014, 8, 229–239. [Google Scholar] [CrossRef]
- Wang, S.; Ren, C.; Sun, Y.; Yang, X.; Tu, J. A study on the instantaneous turbulent flow field in a 90-degree elbow pipe with circular section. Sci. Tech. Nucl. Inst. 2016, 2016, 5265748. [Google Scholar] [CrossRef]
- Kalpakli Vester, A.; Sattarzadeh, S.S.; Örlü, R. Combined hot-wire and PIV measurements of a swirling turbulent flow at the exit of a 90° pipe bend. J. Vis. 2016, 19, 261–273. [Google Scholar] [CrossRef]
- Kalpakli Vester, A.; Örlü, R.; Alfredsson, P.H. Turbulent flows in curved pipes: Recent advances in experiments and simulations. Appl. Mech. Rev. 2016, 68, 050802. [Google Scholar] [CrossRef]
- Van de Vosse, F.N.; van Steenhoven, A.A.; Segal, A.; Janssen, J.D. A finite element analysis of the steady laminar entrance flow in a 90° curved tube. Int. J. Numer. Meth. Fluids 1989, 9, 275–287. [Google Scholar] [CrossRef]
- Pantokratoras, A. Steady laminar flow in a 90° bend. Adv. Mech. Eng. 2016, 8, 1–9. [Google Scholar] [CrossRef]
- Röhrig, R.; Jakirlić, S.; Tropea, C. Comparative computational study of turbulent flow in a 90° pipe elbow. Int. J. Heat Fluid Flow 2015, 55, 120–131. [Google Scholar] [CrossRef]
- Dutta, P.; Saha, S.K.; Nandi, N.; Pal, N. Numerical study on flow separation in 90° pipe bend under high Reynolds number by k-ϵ modelling. Eng. Sci. Technol. Int. J. 2016, 19, 904–910. [Google Scholar]
- Wang, Z.; Orlü, R.; Schlatter, P.; Chung, Y.M. Direct numerical simulation of a turbulent 90° bend pipe flow. Int. J. Heat Fluid Flow 2018, 73, 199–208. [Google Scholar] [CrossRef]
- Hufganel, L.; Canton, J.; "Orlü, R.; Marin, O.; Merzari, E.; Schlatter, P. The three-dimensional structure of swirl-switching in bent pipe flow. J. Fluid Mech. 2018, 835, 86–101. [Google Scholar]
- Du, X.; Wei, A.; Fang, Y.; Yang, Z.; Wei, D.; Lin, C.-H.; Jin, Z. The effect of bend angle on pressure drop and flow behavior in a corrugated duct. Acta Mech. 2020, 231, 3755–3777. [Google Scholar] [CrossRef]
- Hou, Q.; Kruisbrink, A.C.H.; Pearce, F.R.; Tijsseling, A.S.; Yue, T. Smoothed particle hydrodynamics simulations of flow separation at bends. Comput. Fluids 2014, 90, 138–146. [Google Scholar] [CrossRef][Green Version]
- Alvarado-Rodríguez, C.E.; Klapp, J.; Sigalotti, L.D.G.; Domínguez, J.M.; de la Cruz Sánchez, E. Nonreflecting outlet boundary conditions for incompressible flows using SPH. Comput. Fluids 2017, 159, 177–188. [Google Scholar] [CrossRef]
- Rosić, N.M.; Kolarević, M.B.; Savić, L.M.; Dordević, D.M.; Kapor, R.S. Numerical modelling of supercritical flow in circular conduit bends using SPH method. J. Hydrodyn. 2017, 29, 344–352. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics. Annu. Rev. Astron. Astrophys. 1992, 30, 543–574. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R. Smoothed particle hydrodynamics (SPH): An overview and recent developments. Arch. Comput. Meth. Eng. 2010, 17, 25–76. [Google Scholar] [CrossRef]
- Monaghan, J.J. Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 2012, 44, 323–346. [Google Scholar] [CrossRef]
- Becker, M.; Teschner, M. Weakly compressible SPH for free surface flows. In Proceedings of the 2007 ACM SIGGRAPH/Europhysics Symposium on Computer Animation, San Diego, CA, USA, 2–4 August 2007; ACM Press: San Diego, CA, USA, 2007; pp. 32–58. [Google Scholar]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Gómez-Gesteira, M.; Rogers, B.D.; Crespo, A.J.C.; Dalrymple, R.A.; Narayanaswamy, M.; Domínguez, J.M. Sphysics—Development of a free-surface fluid solver—Part 1: Theory and formulations. Comput. Geosci. 2012, 48, 289–299. [Google Scholar] [CrossRef]
- Colagrossi, A.; Landrini, M. Numerical simulation of interfacial flows by smoothed particle hydrodynamics. J. Comput. Phys. 2003, 191, 448–475. [Google Scholar] [CrossRef]
- Lo, E.Y.M.; Shao, S. Simulation of near-shore solitary wave mechanics by an incompressible SPH method. Appl. Ocean Res. 2002, 24, 275–286. [Google Scholar]
- Bonet, J.; Lok, T.-S.L. Variational and momentum preservation aspects of smooth particle hydrodynamic formulations. Comput. Meth. Appl. Mech. Eng. 1999, 180, 97–115. [Google Scholar] [CrossRef]
- Vacondio, R.; Rogers, B.D.; Stansby, P.K.; Mignosa, P.; Feldman, J. Variable resolution for SPH: A dynamic particle coalescing and splitting scheme. Comput. Meth. Appl. Mech. Eng. 2013, 256, 132–148. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Dehnen, W.; Aly, H. Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 2012, 425, 1068–1082. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Gómez-Gesteira, M.; Dalrymple, R.A. Boundary conditions generated by dynamic particles in SPH methods. Comput. Mat. Cont. 2007, 5, 173–184. [Google Scholar]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on smoothed particle hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sigalotti, L.D.G.; Alvarado-Rodríguez, C.E.; Klapp, J.; Cela, J.M. Smoothed Particle Hydrodynamics Simulations of Water Flow in a 90° Pipe Bend. Water 2021, 13, 1081. https://doi.org/10.3390/w13081081
Sigalotti LDG, Alvarado-Rodríguez CE, Klapp J, Cela JM. Smoothed Particle Hydrodynamics Simulations of Water Flow in a 90° Pipe Bend. Water. 2021; 13(8):1081. https://doi.org/10.3390/w13081081
Chicago/Turabian StyleSigalotti, Leonardo Di G., Carlos E. Alvarado-Rodríguez, Jaime Klapp, and José M. Cela. 2021. "Smoothed Particle Hydrodynamics Simulations of Water Flow in a 90° Pipe Bend" Water 13, no. 8: 1081. https://doi.org/10.3390/w13081081
APA StyleSigalotti, L. D. G., Alvarado-Rodríguez, C. E., Klapp, J., & Cela, J. M. (2021). Smoothed Particle Hydrodynamics Simulations of Water Flow in a 90° Pipe Bend. Water, 13(8), 1081. https://doi.org/10.3390/w13081081






