Comparison of Various Growth Curve Models in Characterizing and Predicting Water Table Change after Intensive Mine Dewatering Is Discontinued in an East Central European Karstic Area
Abstract
:1. Introduction
1.1. Mining Water Extraction, a Central-Eastern European Example
1.2. Aims of the Study
2. Materials and Methods
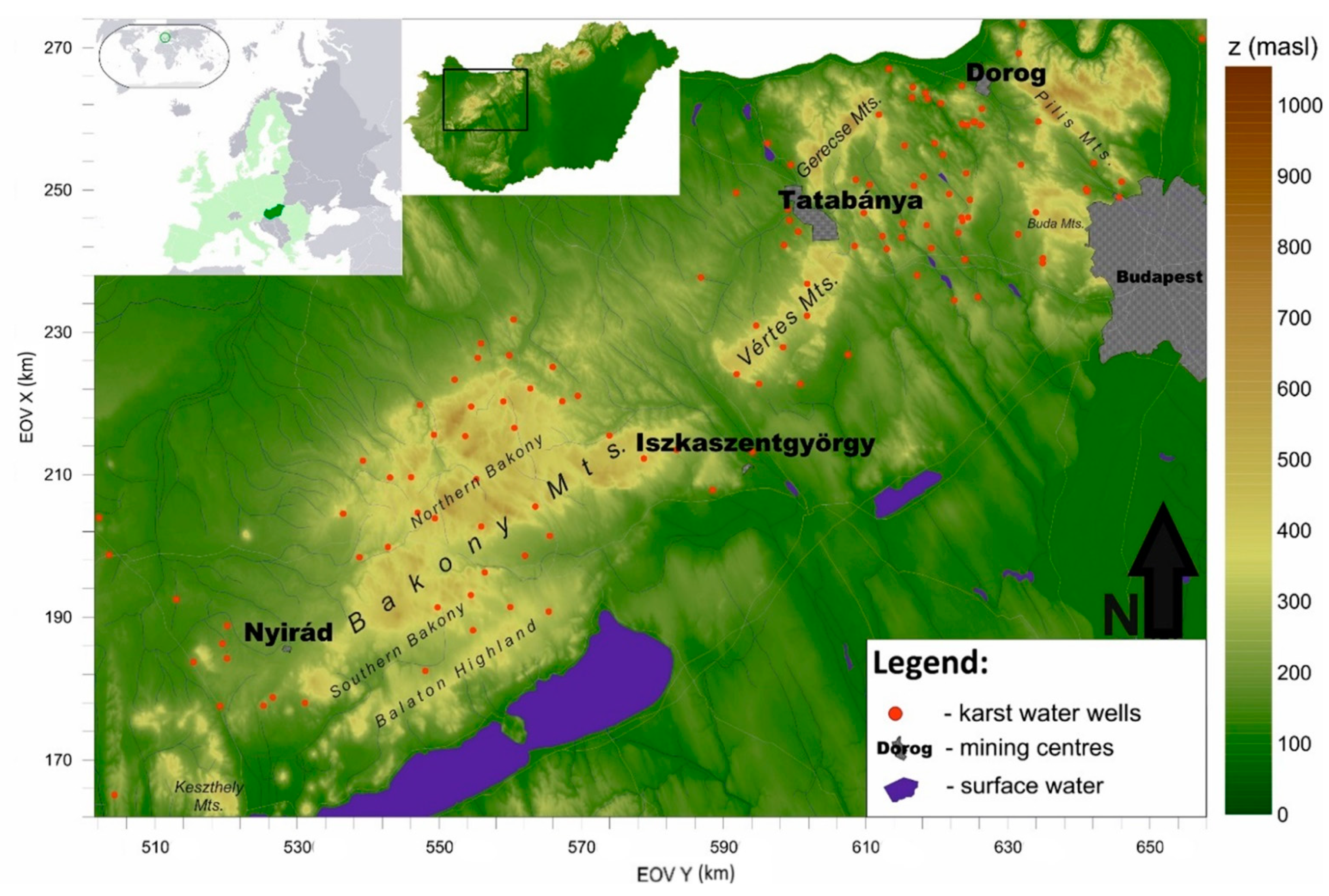
2.1. Hydrogeological Description of the Study Area
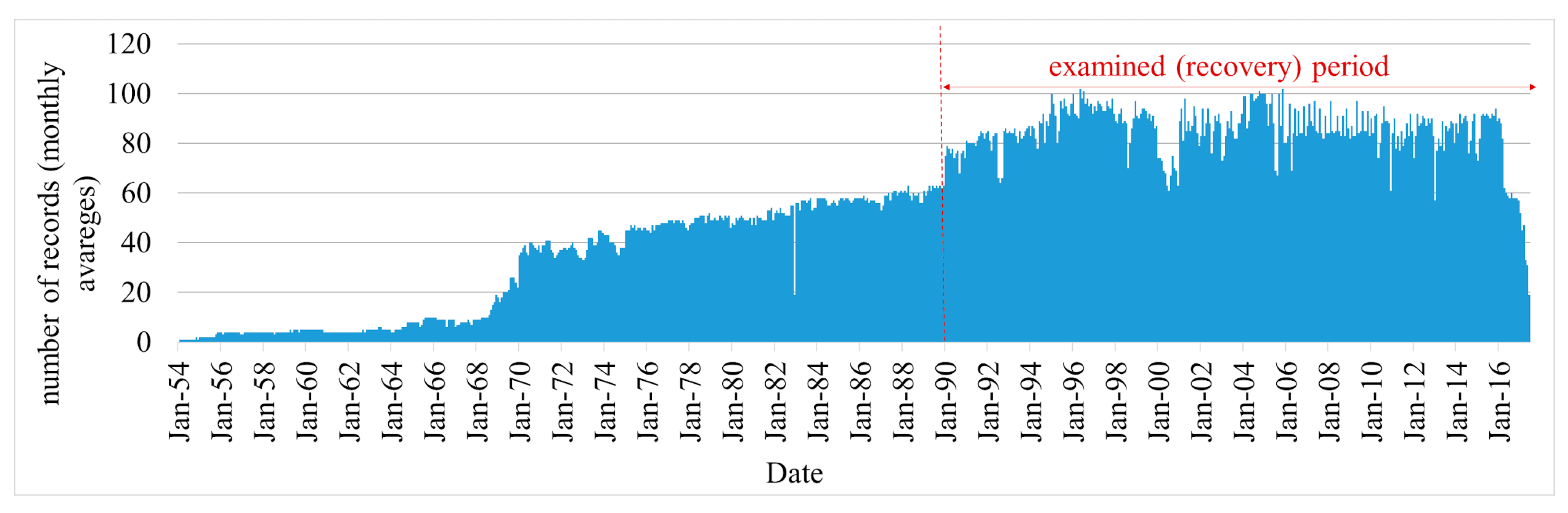
2.2. Dataset Description
2.3. Applied Methodology
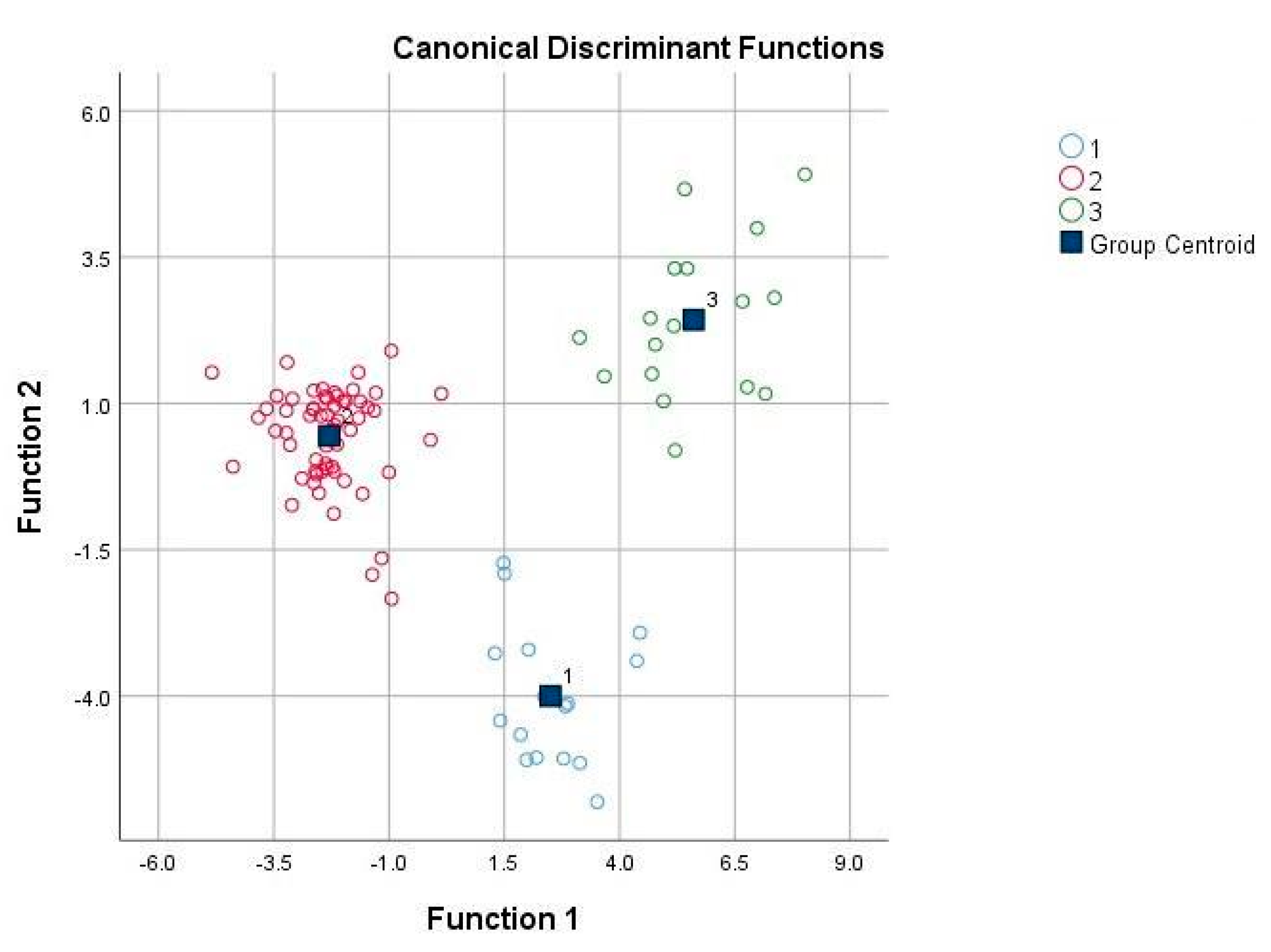
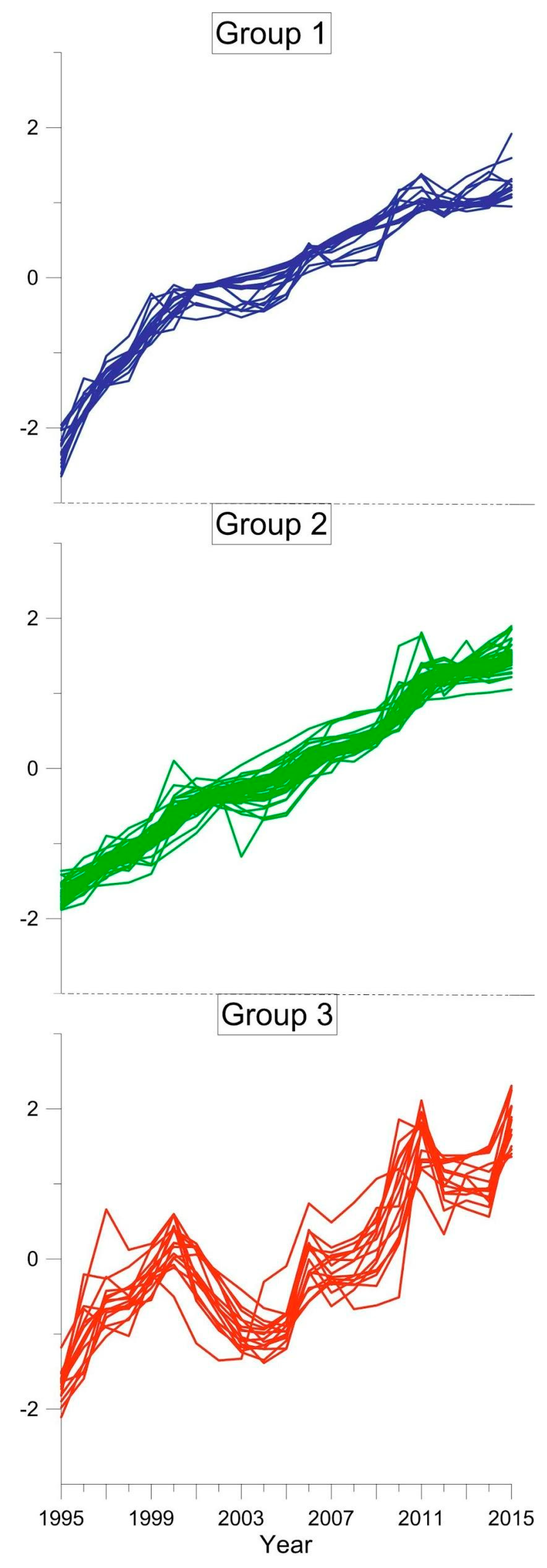
2.4. Cluster and Discriminant Analysis
2.5. Trend Estimation
2.5.1. Growth Curves
2.5.2. Model Fitting
2.6. Deterministic Model
2.7. Variography and Interpolation
2.8. Used Software
3. Results
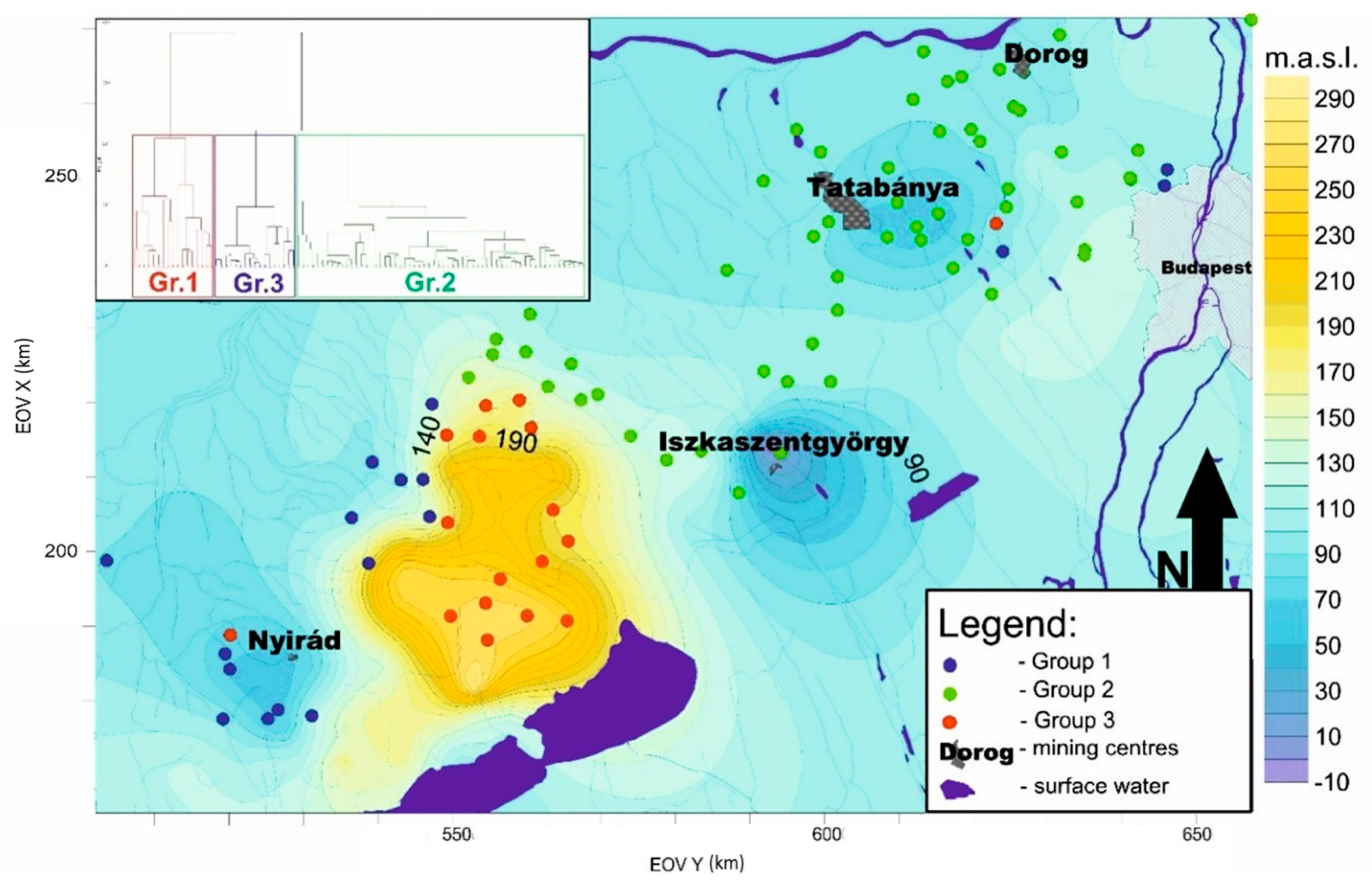
3.1. Cluster Analysis
3.2. Trend Estimation
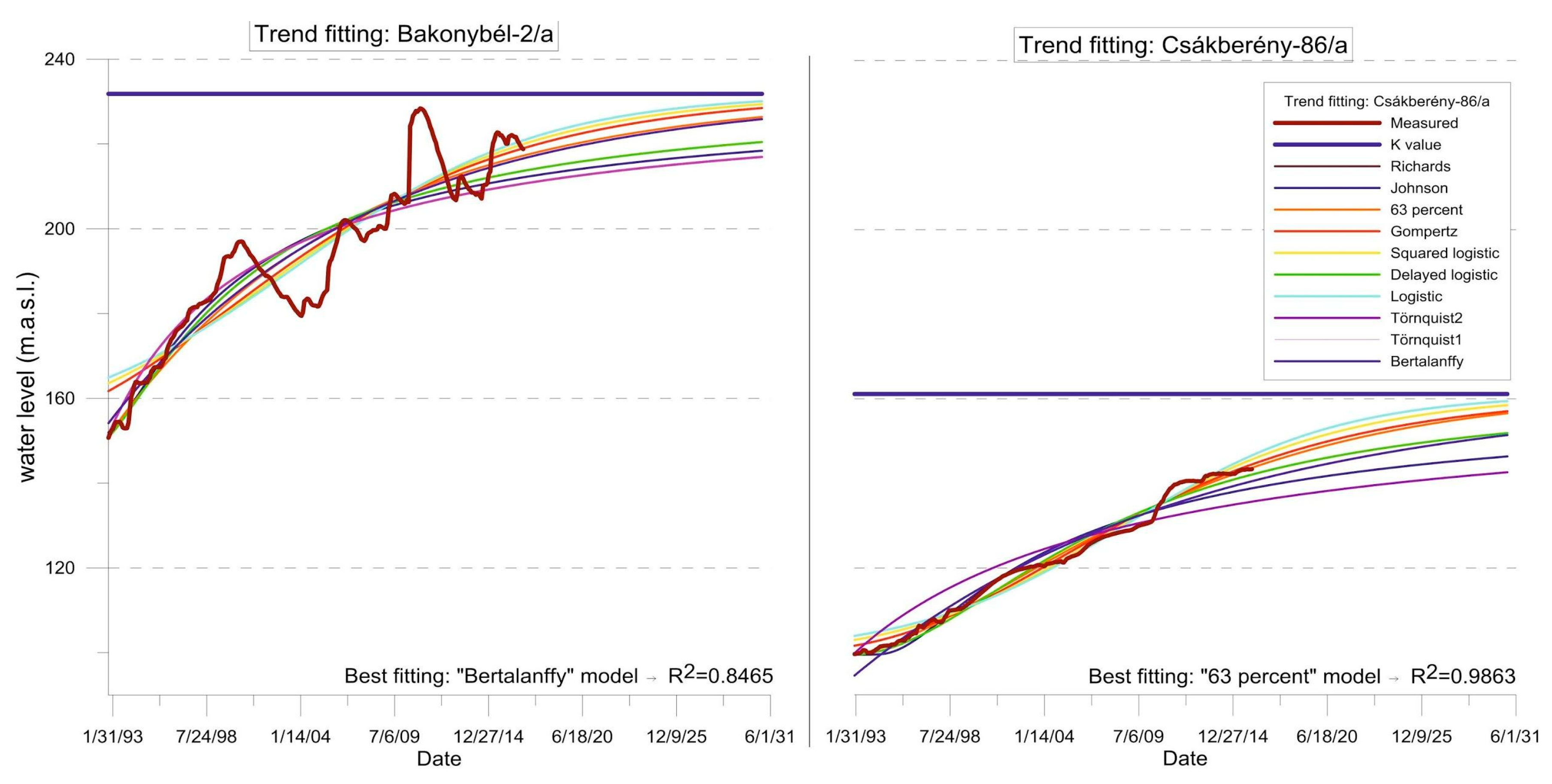
3.2.1. Determining the Best-Fitting Model
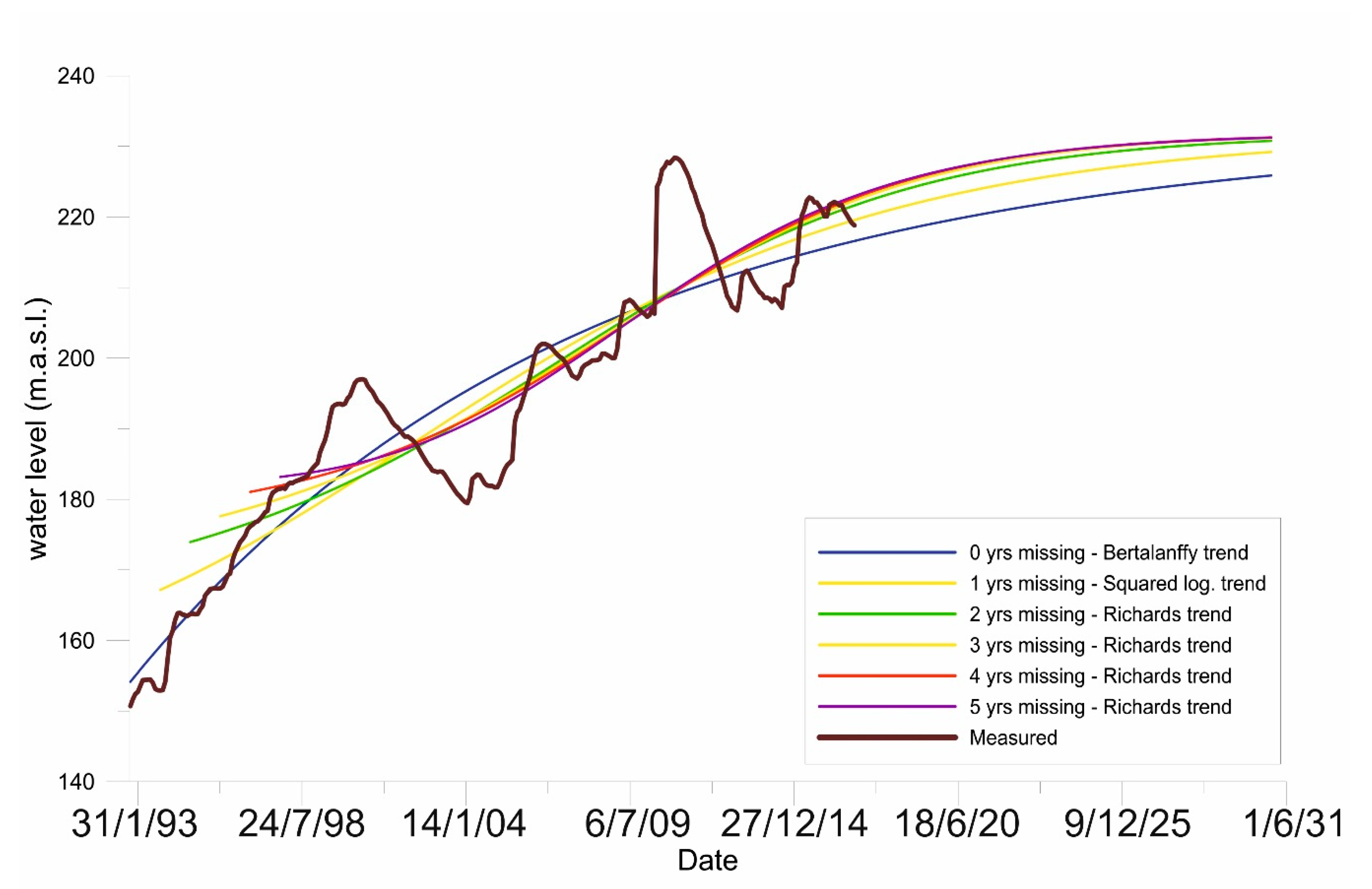
3.2.2. Limitations of Trend Estimation
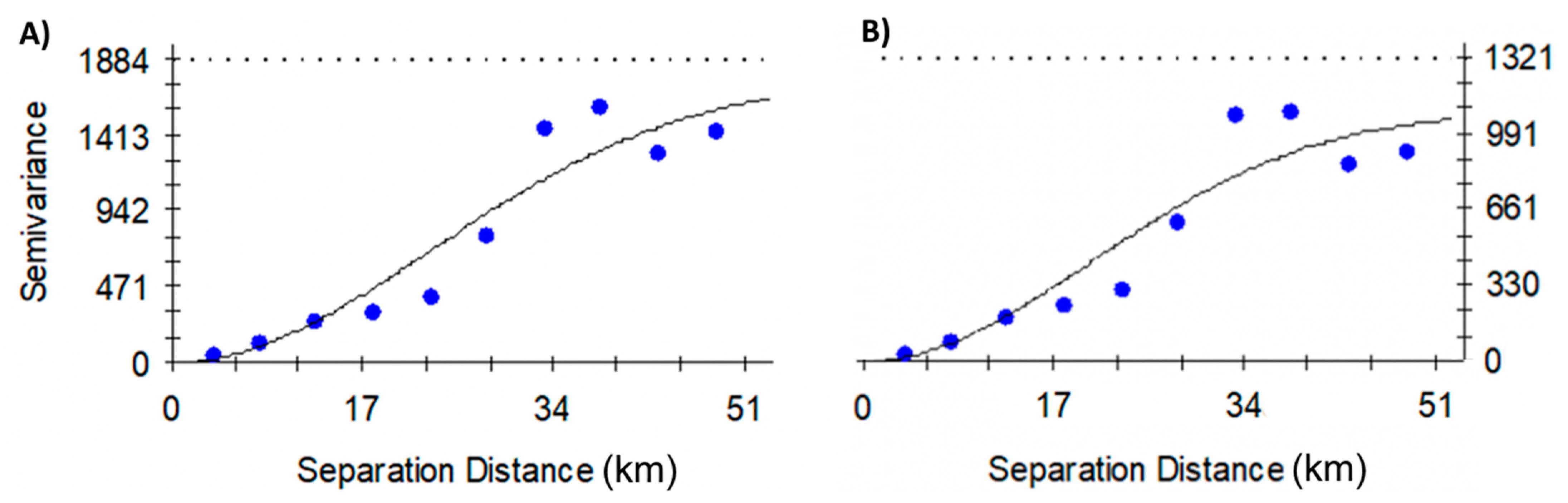
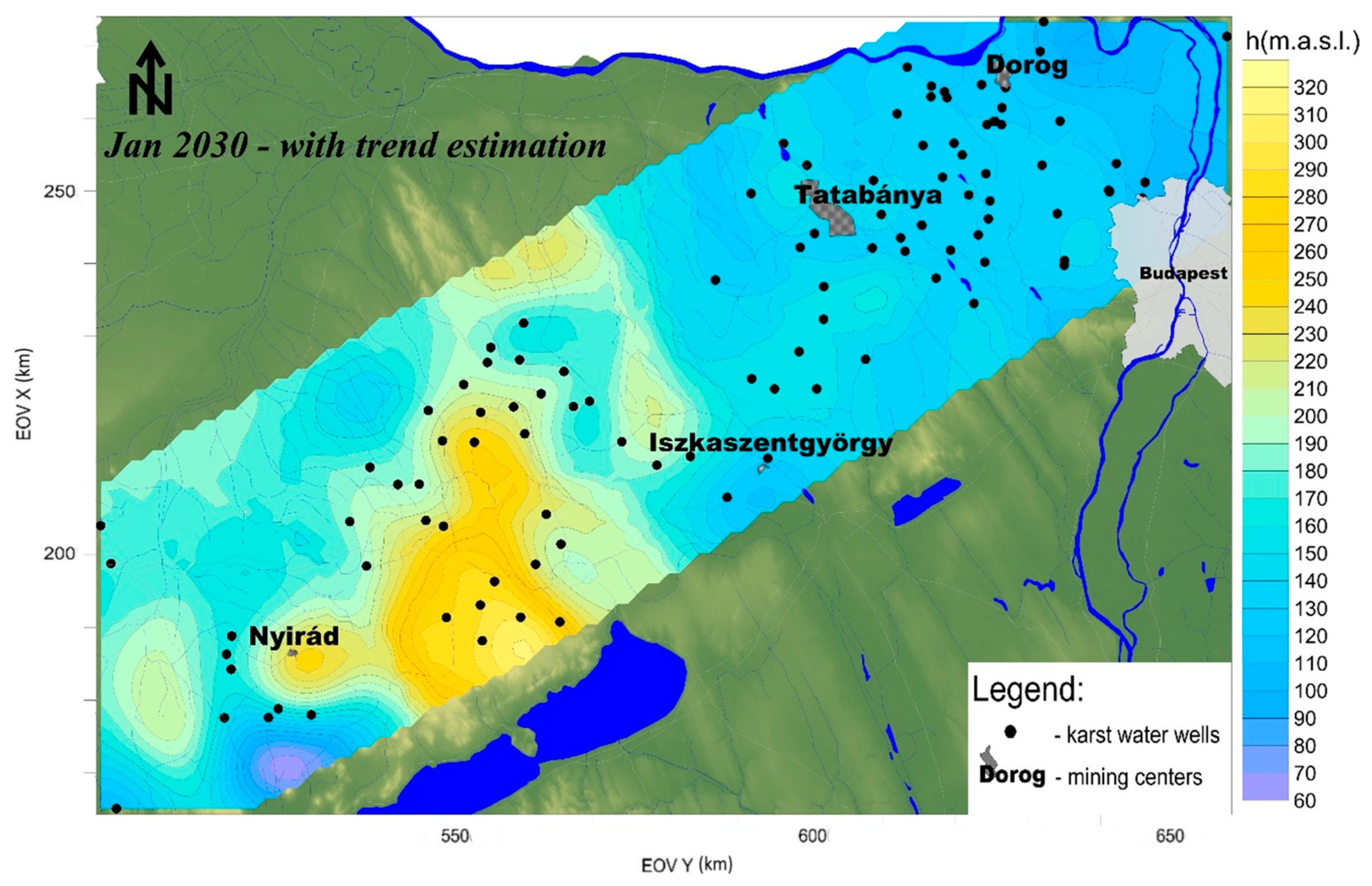
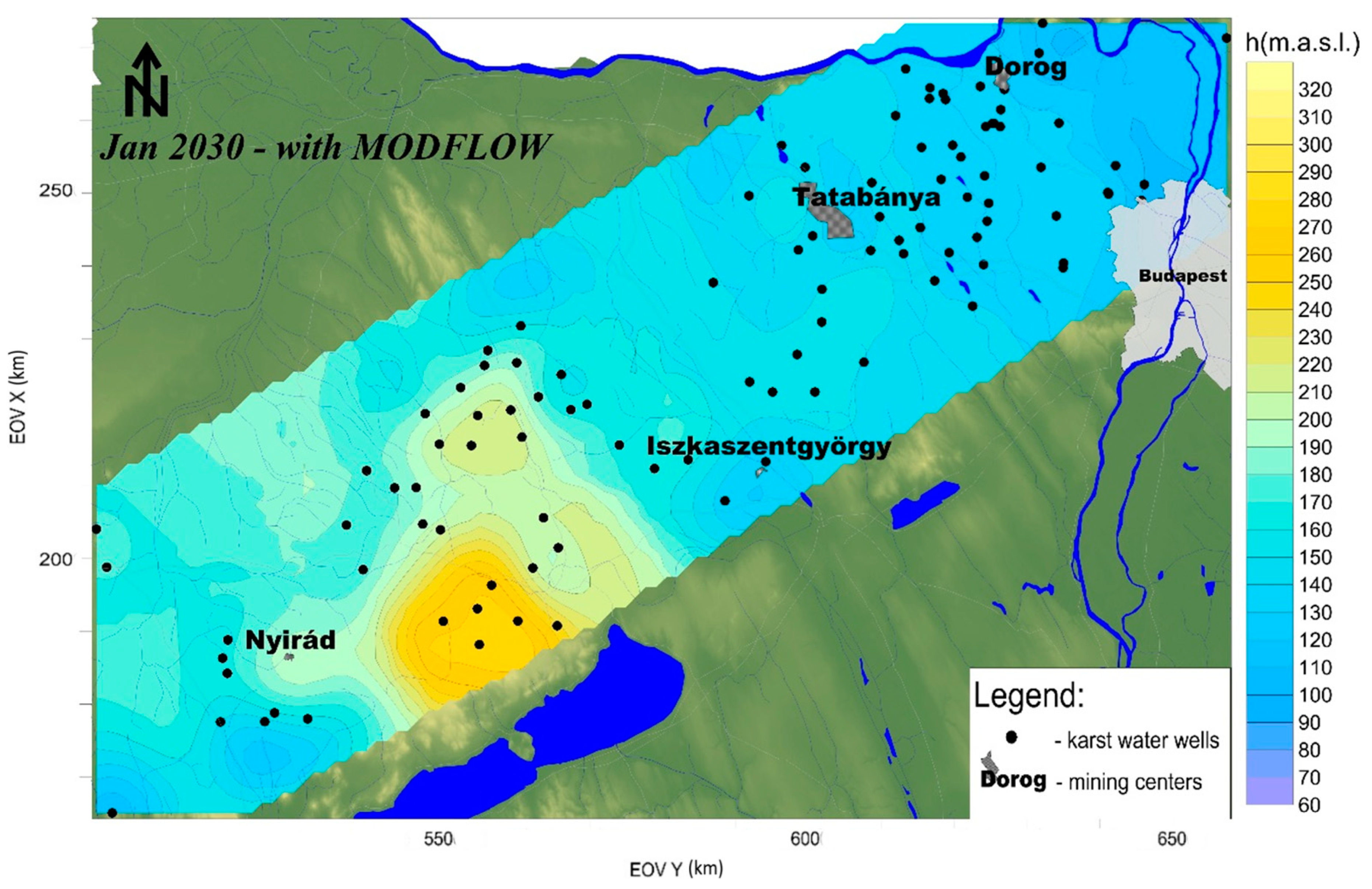
3.3. Variography and Predicted Karst Water Level Maps
4. Discussion
5. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Coulson, M. The History of Mining: The Events, technology and people involved in the industry that forged the modern world; Illustrated edition; Harriman House: Hampshire, UK, 2012. [Google Scholar]
- Brown, D.K. A History of Mining in Latin America: From the Colonial Era to the Present; University of New Mexico press: Albuquerque, NM, USA, 2012. [Google Scholar]
- Kusuma, S. Environmental Impact Assessment of a Proposed Bauxite mining using Rapid Impact Assessment Matrix Method. Int. J. Appl. Environ. Sci. 2010, 5, 29–38. [Google Scholar]
- Kamble, P.H.; Bhosale, S.M. Environmental Impact of Bauxite Mining: A Review. Int. J. Res. Appl. Sci. Eng. Technol. 2019, 7, 86–90. [Google Scholar] [CrossRef]
- Cidu, R.; Biddau, R.; Fanfani, L. Impact of past mining activity on the quality of groundwater in SW Sardinia (Italy). J. Geochem. Explor. 2009, 100, 125–132. [Google Scholar] [CrossRef]
- Howladar, M.F. Coal mining impacts on water environs around the Barapukuria coal mining area, Dinajpur, Bangladesh. Environ. Earth Sci. 2013, 70, 215–226. [Google Scholar] [CrossRef]
- Jhariya, D.C.; Khan, R.; Thakur, G.S. Impact of Mining Activity on Water Resource: An Overview study. In Proceedings of the National Seminar on Recent Practices & Innovations in Mining Industry, Raipur, India, 19–20 February 2016; pp. 271–277. [Google Scholar]
- Andrew, H.; Grigg, A.H. Hydrological response to bauxite mining and rehabilitation in the jarrah forest in south west Australia. J. Hydrol. Reg. Stud. 2017, 12, 150–164. [Google Scholar] [CrossRef]
- Apaydın, A. Dual impact on the groundwater aquifer in the Kazan Plain (Ankara, Turkey): Sand–gravel mining and over-abstraction. Environ. Earth Sci. 2012, 65, 241–255. [Google Scholar] [CrossRef]
- Huang, D.; Liu, Z.; Wang, W. Evaluating the Impaction of Coal Mining on Ordovician Karst Water through Statistical Methods. Water 2018, 10, 1409. [Google Scholar] [CrossRef] [Green Version]
- Wu, Q.; Zhou, W.F.; Li, D. Management of karst water resources in mining area: Dewatering in mines and demand for water supply in the Dongshan Mine of Taiyuan, Shanxi Province, North China. Environ. Geol. 2006, 50, 1107–1117. [Google Scholar] [CrossRef]
- Wu, Q.; Xing, L.T.; Ye, C.H.; Liu, Y.Z. The influences of coal mining on the large karst springs in North China. Env. Earth Sci. 2011, 64, 1513–1523. [Google Scholar] [CrossRef]
- Li, G.; Zhou, W. Impact of karst water on coal mining in North China. Environ. Geol. 2006, 49, 449–457. [Google Scholar] [CrossRef]
- Sherwood, J.M. Modelling Minewater Flow and Quality Changes after Coalfield Closure. Ph.D. Thesis, University of Newcastle, Newcastle upon Tyne, UK, 1997. [Google Scholar]
- Sadler, P. Predicting groundwater recovery after mine closure. In Proceedings of the Mine, Water and Environment Congress, Sevilla, Spain, 13–17 September 1999; pp. 437–444. [Google Scholar]
- Jin, W. Environmental geological hazards caused by abandoned mines and its prevention and control measures. Heilongjiang Sci. 2017, 20, 68–69. [Google Scholar]
- Zhou, J. Risk analysis on adjacent mine water inrush caused by groundwater rebound of abandoned coal mine. Saf. Coal Mines 2013, 7, 166–168. [Google Scholar]
- Wu, Q.; Wang, M.Y. Characterization of water bursting and discharge into underground mines with multi-layered groundwater flow systems in the North China coal basin. Hydrogeol. J. 2006, 14, 882–893. [Google Scholar] [CrossRef]
- Toran, L.; Bradbury, K.R. Ground-Water Flow Model of Drawdown and Recovery Near an Underground Mine. Groundwater 1988, 26, 724–733. [Google Scholar] [CrossRef]
- Younger, P.L.; Adams, R. Predicting Mine Water Rebound. Technical report; University of Newcastle: Newcastle upon Tyne, UK, 1999. [Google Scholar] [CrossRef]
- Kim, S.-M.; Choi, Y. SIMPL: A Simplified Model-Based Program for the Analysis and Visualization of Groundwater Rebound in Abandoned Mines to Prevent Contamination of Water and Soils by Acid Mine Drainage. Int. J. Environ. Res. Public Health 2018, 15, 951. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dreybrodt, W. Processes in Karst Systems: Physics, Chemistry, and Geology, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Ford, D.; Williams, P. Karst Hydrogeology and Geomorphology; John Wiley & Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- Ellman, M. Socialist Planning; Cambridge University Press: Cambridge, UK, 1979; p. 17. [Google Scholar]
- Crowley, S. Hot Coal, Cold Steel: Russian and Ukrainian Workers from the End of the Soviet Union to the Post-Communist Transformations; University of Michigan Press: Ann Arbor, MI, USA, 1997. [Google Scholar] [CrossRef]
- Haney, M.; Shkaratan, M. Mine Closure and its Impact on the Community: Five Years after Mine Closure in Romania, Russia and Ukraine; Policy Research Working Paper No. 3083; World Bank: Washington, DC, USA, 2003; Available online: https://openknowledge.worldbank.org/handle/10986/18177 (accessed on 9 April 2021).
- Nyírő, A. Tata: Collapse of the Karst Water System. Political and Economical Aspects of an Environmental Catastrophe in Hungary, 1950-2019. Studia Mundi Econ. 2020, 7, 52–58. [Google Scholar] [CrossRef]
- Tóth, M. Mikor indulnak újra a tatai források? Vízügyi Közlemények 2002, 84, 195–209. [Google Scholar]
- Körmendi, G. Tata-Tóváros, mint kedvelt fürdő- és üdülőhely (1773–1939). In A Vártól a Városig. Tata Évszázadai; Kisné Cseh, J., Ed.; Tata: Tata Város Önkormányzata, Hungary, 2004; pp. 233–253. [Google Scholar]
- Alföldi, L.; Kapolyi, L. Bányászati Karsztvízszint-süllyesztés a Dunántúli-Középhegységben; MTA Földrajztudományi Kutatóintézet: Budapest, Hungary, 2007. [Google Scholar]
- Edelényi, J.E. Geological conditions around the cone of depression arising from pumping of mine waters in the Nyirád region, western Hungary. In Annual Report of the Geological Institute of Hungary 1992-1993/II; Geological Institute of Hungary: Budapest, Hungary, 1999; pp. 121–122. [Google Scholar]
- Ballabás, G. Visszatérő karsztforrásokkal kapcsolatos településfejlesztési és környezetvédelmi lehetőségek és veszélyek Tata város példáján. In Táj, tér, Tervezés, Geográfus Doktoranduszok VIII.; Kovács, F., Ed.; Országos Konferenciája: Szeged, Hungary; SZTE TTIK Természeti Földrajzi és Geoinformatikai Tanszék: Szeged, Hungary, 2004. [Google Scholar]
- Kehl, D.; Sipos, B. A telítődési, a logisztikus és az életgörbe alakú trendfüggvények becslése Excel parancsfájl segítségével. Stat. Szle. 2009, 87, 381–411. [Google Scholar]
- Harris, T.M.; Devkota, J.P.; Khanna, V.; Eranki, P.L.; Landis, A.E. Logistic growth curve modeling of US energy production and consumption. Renew. Sustain. Energy Rev. 2018, 96, 46–57. [Google Scholar] [CrossRef]
- Pérez-Suárez, R.; López-Menéndez, A.J. Growing green? Forecasting CO2 emissions with Environmental Kuznets Curves and Logistic Growth Models. Environ. Sci. Policy 2015, 54, 428–437. [Google Scholar] [CrossRef]
- Haas, J.; Demény, A. Early dolomitisation of Late Triassic platform carbonates in the Transdanubian Range (Hungary). Sediment. Geol. 2002, 151, 225–242. [Google Scholar] [CrossRef]
- Tóth, Á. A Balaton-Felvidék Felszínalatti Vizeinek Hidraulikai Kapcsolata a Bakonnyal és a Balatonnal. Ph.D. Thesis, Eötvös Loránd Tudományegyetem, Budapest, Hungary, 2018. [Google Scholar]
- Balla, Z.; Dudko, A. Large-scale Tertiary strike-slip displacements recorded in the structure of the Transdanubian Range. Geophys. Trans. 1989, 35, 3–64. [Google Scholar]
- Bárdossy, G. Karst Bauxites: Bauxite Deposits on Carbonate Rocks, 1st ed.; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Mindszenty, A. The lithology of some Hungarian bauxites—a contribution to the palaeogeographic reconstruction. Acta Geol. Hung. 1985, 27, 441–455. [Google Scholar]
- Haas, J.; Kovács, S. Pelso Composite Unit. In Geology of Hungary; Haas, J., Ed.; Springer: Heidelberg, Germany, 2012; pp. 21–55. [Google Scholar]
- Mindszenty, A.; Szintai, M.; Tóth, K.; Szantner, F.; Nagy, T.; Gellai, M.; Baross, G. Sedimentology and depositional environment of the Csabapuszta bauxite (Paleocene/Eocene) in the South Bakony Mts., Hungary. Acta Geol. Hung. 1988, 31, 339–370. [Google Scholar]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Hatvani, I.G.; Kovács, J.; Kovácsné Székely, I.; Jakusch, P.; Korponai, J. Analysis of long-term water quality changes in the Kis-Balaton Water Protection System with time series-, cluster analysis and Wilks’ lambda distribution. Ecol. Eng. 2011, 37, 629–635. [Google Scholar] [CrossRef]
- Hubert, L.J.; Levin, J.R. A general statistical framework for assessing categorical clustering in free recall. Psychol. Bull. 1976, 83, 1072–1080. [Google Scholar] [CrossRef]
- Hatvani, I.G.; Magyar, N.; Zessner, M.; Kovács, J.; Blaschke, A.P. The Water Framework Directive: Can more information be extracted from groundwater data? A case study of Seewinkel, Burgenland, eastern Austria. Hydrogeol. J. 2014, 22, 779–794. [Google Scholar] [CrossRef]
- Márkus, L.; Borbás, E.; Daroughi, A.; Kovács, J. Characterization of Karstic Aquifer Complexity Using Fractal Dimensions. GEM—Int. J. Geomath. 2021, 12, 4. [Google Scholar]
- Wilks, S.S. Certaingeneralizations in theanalysis of variance. Biometrika 1932, 24, 471–494. [Google Scholar] [CrossRef]
- Molnár, S.; Füst, A.; Szidarovszky, F.; Molnár, M. Models in Environmental Informatics II; Department of Informatics, Szent István University: Göldöllő, Hungary, 2010. [Google Scholar]
- Hatvani, I.G.; Leuenberger, M.; Kohán, B.; Kern, Z. Geosta-tistical analysis and isoscape of ice core derived water stable isotope records in an Antarctic macro region. Polar Sci. 2017, 13, 23–32. [Google Scholar] [CrossRef]
- Molnar, S. On the convergence of the kriging method. Ann. Univ. Sci. Bp. Sect. Comput. 1985, 6, 81–90. [Google Scholar]
- Landau, S.; Everitt, B.S. A Handbook of Statistical Analyses Using SPSS, 1st ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004; p. 356. [Google Scholar]
- Bertalanffy, L. A Quantitative Theory of Organic Growth (Inquiries on Growth Laws II.). Hum. Biol. 1938, 10, 181–213. [Google Scholar]
- Törnquist, L. The Bank of Finland’s Consumption Price Index. Bank Finl. Mon. Bull. 1936, 16, 27–32. [Google Scholar]
- Törnquist, L. Collected Scientific papers of Leo Törnquist, 1st ed.; The Research Institute of the Finnish Economy: Helsinki, Finland, 1981. [Google Scholar]
- Verhulst, P.-F. Notice sur la loi que la population poursuit dans son accroissement. Corresp. Mathématique Phys. 1838, 10, 113–121. [Google Scholar]
- Pearl, R.; Reed, L.J. On the Rate of Growth of the Population of the United States since 1790 and its Mathematical Representation. In Mathematical Demography; Smith, D.P., Keyfitz, N., Eds.; Springer: Heidelberg, Germany, 1977; pp. 341–347. [Google Scholar]
- Hutchinson, G.E. Circular causal systems in ecology. Ann. N.Y. Acad. Sci. 1948, 50, 221–246. [Google Scholar] [CrossRef] [PubMed]
- Kotz, S.; Johnson, N.L.; Read, C.B. Encyclopedia of Statistical Sciences, 2nd ed.; Wiley InterScience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Gompertz, B. On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies. Philos. Trans. R. Soc. Lond. 1825, 115, 513–585. [Google Scholar]
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biometrika 1949, 36, 149–176. [Google Scholar] [CrossRef] [PubMed]
- Richards, F.J. A Flexible Growth Function for Empirical Use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Lorberer, Á. A Dunántúli-Középhegység karsztvízföldtani és vízgazdálkodási helyzetfelmérése és döntéselőkészítő értékelése; VITUKI: Budapest, Hungary, 1986. [Google Scholar]
- Kenney, J.F.; Keeping, E.S. Linear Regression and Correlation. Ch. 15 in Mathematics of Statistics, Pt. 1, 3rd ed.; Van Nostrand: Princeton, NJ, USA, 1962; pp. 252–285. [Google Scholar]
- Morton, F.I. Operational estimates of areal evapotranspiration and their significance to the science and practice of hydrology. J. Hydrol. 1983, 66, 1–76. [Google Scholar] [CrossRef]
- Afifi, A.; Clark, V.A.; May, S. Computer-Aided Multivariate Analysis, 4th ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2004. [Google Scholar]
- Matheron, G. Les Variables régionalisées et leur estimation: Une application de la théorie des fonctions aléatoires aux sciences de la nature; Masson et Cie: Échandens, Switzerland, 1965. [Google Scholar]
- Chilès, J.-P.; Delfiner, P. Modeling Spatial Uncertainty, 2nd ed.; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Kern, Z.; Erdélyi, D.; Vreča, P.; Krajcar Bronić, I.; Fórizs, I.; Kanduč, T.; Štrok, M.; Palcsu, L.; Süveges, M.; Czuppon, G.; et al. Isoscape of amount-weighted annual mean precipitation tritium (3H) activity from 1976 to 2017 for the Adriatic-Pannonian region—AP 3 H_v1 database. Earth Syst. Sci. Data 2020, 12, 2061–2073. [Google Scholar] [CrossRef]
- Hatvani, I.G.; Erdélyi, D.; Vreča, P.; Kern, Z. Analysis of the Spatial Distribution of Stable Oxygen and Hydrogen Isotopes in Precipitation across the Iberian Peninsula. Water 2020, 12, 481. [Google Scholar] [CrossRef] [Green Version]
- Tiwary, R.K. Environmental Impact of Coal Mining on Water Regime and Its Management. Water Air Soil Pollut. 2001, 132, 185–199. [Google Scholar] [CrossRef]
- Shen, B.; Poulsen, B.; Luo, X.; Qin, J.; Thiruvenkatachari, R.; Duan, Y. Remediation and monitoring of abandoned mines. Int. J. Min. Sci. Technol. 2017, 27, 803–811. [Google Scholar] [CrossRef]
- Oh, H.; Lee, S. Integration of ground subsidence hazard maps of abandoned coal mines in Samcheok, Korea. Int. J Coal Geol. 2011, 86, 58–72. [Google Scholar] [CrossRef]
- Wolkersdorfer, C. Water Management at Abandoned Flooded Underground Mines: Fundamentals, Tracer tests, Modelling, Water Treatment; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Gutiérrez, F.; Parise, M.; De Waele, J.; Jourde, H. A review on natural and human-induced geohazards and impacts in karst. Earth-Sci. Rev. 2014, 138, 61–88. [Google Scholar] [CrossRef]
- Irawan, D.E.; Puradimaja, D.J.; Notosiswoyo, S.; Soemintadiredja, P. Hydrogeochemistry of volcanic hydrogeology based on cluster analysis of Mount Ciremai, West Java, Indonesia. J. Hydrol. 2009, 376, 221–234. [Google Scholar] [CrossRef]
- Kovács, J.; Erőss, A. Statistically optimal grouping using combined cluster and discriminant analysis (CCDA) on a geochemical database of thermal karst waters in Budapest. Appl. Geochem. 2017, 84, 76–86. [Google Scholar] [CrossRef]
- Naranjo Fernández, N.; Guardiola-Albert, C.; Aguilera, H.; Serrano-Hidalgo, C.; Montero, E. Clustering Groundwater Level Time Series of the Exploited Almonte-Marismas Aquifer in Southwest Spain. Water 2020, 12, 1063. [Google Scholar] [CrossRef] [Green Version]
- Parise, M.; Closson, D.; Gutiérrez, F.; Stevanović, Z. Anticipating and managing engineering problems in the complex karst environment. Environ. Earth Sci. 2015, 74, 7823–7835. [Google Scholar] [CrossRef]
- Goldscheider, N.; Drew, D.; Worthington, S. Why karst aquifers require specific investigation techniques. In Methods in Karst Hydrogeology, 1st ed.; Goldscheider, N., Drew, D., Eds.; Taylor & Francis: London, UK, 2007; pp. 2–4. [Google Scholar]
- Palmer, A. Digital modeling of karst aquifers-Successes, failures, and promises. Spec. Pap. Geol. Soc. Am. 2006, 404, 243–250. [Google Scholar] [CrossRef]
- Rapantova, N.; Grmela, A.; Vojtek, D.; Halir, J.; Michalek, B. Ground Water Flow Modelling Applications in Mining Hydrogeology. Mine Water Environ. 2007, 26, 264–270. [Google Scholar] [CrossRef]
- He, R.; Pang, B. Sensitivity and uncertainty analysis of the Variable Infiltration Capacity model in the upstream of Heihe River basin. Proc. Int. Assoc. Hydrol. Sci. 2015, 368, 312–316. [Google Scholar] [CrossRef] [Green Version]
- Mahapatra, S.; Jha, M.; Biswal, S.; Senapati, D. Assessing Variability of Infiltration Characteristics and Reliability of Infiltration Models in a Tropical Sub-humid Region of India. Sci. Rep. 2019, 10, 1515. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Charou, E.; Stefouli, M.; Dimitrakopoulos, D.; Vasileiou, E.; Mavrantza, O.D. Using Remote Sensing to Assess Impact of Mining Activities on Land and Water Resources. Mine Water Environ. 2010, 29, 45–52. [Google Scholar] [CrossRef]
- Tóth, J. A theory of groundwater motion in small drainage basins in central Alberta, Canada. J. Geophys. Res. 1962, 67, 4375–4387. [Google Scholar] [CrossRef]
- Tóth, J. A theoretical analysis of groundwater flow in small drainage basins. J. Geophys. Res. 1963, 68, 4795–4812. [Google Scholar] [CrossRef]


| Bertalanffy | Törnquist1 | Törnquist2 | Logistic | Delayed Log | ||
| r2 = max. | % | 11.21% | 0.00% | 1.87% | 1.87% | 17.76% |
| r2 ≥ (max.—0.005) | % | 32.71% | 3.74% | 6.54% | 20.56% | 33.64% |
| Squared log | Gompertz | 63 percent | Johnson | Richards | ||
| r2 = max. | % | 0.00% | 4.67% | 28.04% | 4.67% | 29.91% |
| r2 ≥ (max.—0.005) | % | 22.43% | 31.78% | 48.60% | 17.76% | 52.34% |
| Missing Year(s) | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Number of changed time series | 13 | 26 | 28 | 35 | 38 |
| Percent of changed time series | 24.53% | 49.06% | 52.83% | 66.04% | 77.55% |
| Well | Number of Missing Year(s) | ||||||
|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | ||
| Bakonybél-2a | Best fitting function | Bertalanffy | Squared log | Richards | |||
| max. r2 | 0.85 | 0.82 | 0.80 | 0.78 | 0.76 | 0.74 | |
| January 2030 (m asl.) | 225.5 | 228.9 | 230.6 | 231.1 | 231.1 | 231.1 | |
| deviation in forecast (%) | 0.00% | 1.52% | 2.27% | 2.47% | 2.51% | 2.49% | |
| Csákberény-86a | Best fitting function | “63 percent” | Gompertz | Richards | |||
| max. r2 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.97 | |
| January 2030 (m asl.) | 156.1 | 155.6 | 155.7 | 155.4 | 157.1 | 157.9 | |
| forecast deviation (%) | 0.00% | 0.32% | 0.31% | 0.50% | 0.62% | 1.11% | |
| Duka-1 | Best fitting function | Delayed log | |||||
| max. r2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | |
| January 2030 (m asl.) | 171.5 | 171.0 | 171.5 | 171.3 | 170.6 | 170.7 | |
| forecast deviation (%) | 0.00% | 0.29% | 0.04% | 0.12% | 0.50% | 0.45% | |
| Epöl-5 | Best fitting function | “63 percent” | |||||
| max. r2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.98 | |
| January 2030 (m asl.) | 134.8 | 134.0 | 134.7 | 134.0 | 134.0 | 134.6 | |
| forecast deviation (%) | 0.00% | 0.57% | 0.07% | 0.61% | 0.62% | 0.17% | |
| Tata-Pokol | Best fitting function | “63 percent” | Gompertz | ||||
| max. r2 | 0.99 | 0.99 | 0.98 | 0.98 | 0.98 | 0.97 | |
| January 2030 (m asl.) | 146.8 | 147.4 | 147.4 | 147.0 | 147.0 | 149.9 | |
| forecast deviation (%) | 0.00% | 0.38% | 0.43% | 0.13% | 0.14% | 2.08% | |
| Well | Percentage of Original K Value | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90% | 92% | 94% | 96% | 98% | 100% | 102% | 104% | 106% | 108% | 110% | ||
| Bakonybél-2a | Best fitting function | Bertalanffy | ||||||||||
| max. r2 | 0.84 | 0.84 | 0.84 | 0.84 | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 | |
| January 2030 (m asl.) | 220.6 | 221.7 | 222.7 | 223.7 | 224.6 | 225.5 | 226.3 | 227.1 | 227.9 | 228.6 | 229.3 | |
| forecast dev. (%) | 2.15% | 1.68% | 1.23% | 0.80% | 0.39% | 0.00% | 0.37% | 0.73% | 1.07% | 1.40% | 1.71% | |
| Csákberény-86a | Best fitting function | “63 percent’ | ||||||||||
| max. r2 | 0.98 | 0.98 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| January 2030 (m asl.) | 152.7 | 153.4 | 154.2 | 154.9 | 155.5 | 156.1 | 156.7 | 157.3 | 157.8 | 158.3 | 158.8 | |
| forecast dev. (%) | 2.23% | 1.73% | 1.27% | 0.82% | 0.40% | 0.00% | 0.38% | 0.74% | 1.08% | 1.41% | 1.72% | |
| Duka-1 | Best fitting function | “63 percent” | Bertalanffy | Delayed lg | ||||||||
| max. r2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| January 2030 (m asl.) | 168.3 | 169.9 | 171.2 | 169.6 | 170.6 | 171.5 | 172.3 | 173.1 | 173.8 | 174.5 | 175.1 | |
| forecast dev. (%) | 1.86% | 0.94% | 0.15% | 1.08% | 0.52% | 0.00% | 0.48% | 0.93% | 1.36% | 1.75% | 2.12% | |
| Epöl-5 | Best fitting function | “63 percent” | Bertalanffy | |||||||||
| max. r2 | 0.9895 | 0.9899 | 0.9902 | 0.9905 | 0.9907 | 0.9909 | 0.9911 | 0.9912 | 0.9914 | 0.9915 | 0.9916 | |
| January 2030 (m asl.) | 133.35 | 133.69 | 134.00 | 134.29 | 134.56 | 134.82 | 135.06 | 135.28 | 135.49 | 135.68 | 135.78 | |
| forecast dev. (%) | 1.09% | 0.84% | 0.61% | 0.39% | 0.19% | 0.00% | 0.18% | 0.34% | 0.50% | 0.64% | 0.72% | |
| Tata-Pokol | Best fitting function | “63 percent” | ||||||||||
| max. r2 | 0.9841 | 0.9846 | 0.9851 | 0.9855 | 0.9858 | 0.9861 | 0.9863 | 0.9866 | 0.9868 | 0.9869 | 0.9871 | |
| January 2030 (m asl.) | 144.56 | 145.07 | 145.55 | 146.00 | 146.42 | 146.81 | 147.17 | 147.52 | 147.84 | 148.14 | 148.43 | |
| forecast dev. (%) | 1.53% | 1.18% | 0.86% | 0.55% | 0.27% | 0.00% | 0.25% | 0.48% | 0.70% | 0.91% | 1.10% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Modrovits, K.; Csepregi, A.; Kovácsné Székely, I.; Hatvani, I.G.; Kovács, J. Comparison of Various Growth Curve Models in Characterizing and Predicting Water Table Change after Intensive Mine Dewatering Is Discontinued in an East Central European Karstic Area. Water 2021, 13, 1047. https://doi.org/10.3390/w13081047
Modrovits K, Csepregi A, Kovácsné Székely I, Hatvani IG, Kovács J. Comparison of Various Growth Curve Models in Characterizing and Predicting Water Table Change after Intensive Mine Dewatering Is Discontinued in an East Central European Karstic Area. Water. 2021; 13(8):1047. https://doi.org/10.3390/w13081047
Chicago/Turabian StyleModrovits, Kamilla, András Csepregi, Ilona Kovácsné Székely, István Gábor Hatvani, and József Kovács. 2021. "Comparison of Various Growth Curve Models in Characterizing and Predicting Water Table Change after Intensive Mine Dewatering Is Discontinued in an East Central European Karstic Area" Water 13, no. 8: 1047. https://doi.org/10.3390/w13081047







