Abstract
Multi-objective evolutionary algorithms (MOEAs) are widely used to optimize multi-purpose reservoir operations. Considering that most outcomes of MOEAs are Pareto optimal sets with a large number of incomparable solutions, it is not a trivial task for decision-makers (DMs) to select a compromise solution for application purposes. Due to the increasing popularity of data-driven decision-making, we introduce a clustering-based decision-making method into the multi-objective reservoir operation optimization problem. Traditionally, solution selection has been conducted based on trade-off ranking in objective space, and solution characteristics in decision space have been ignored. In our work, reservoir operation processes were innovatively clustered into groups with unique properties in decision space, and the trade-off surfaces were analyzed via clustering in objective space. To attain a suitable performance, a new similarity measure, referred to as the Mei–Wang fluctuation similarity measure (MWFSM), was tailored to reservoir operation processes. This method describes time series in terms of both their shape and quantitative variation. Then, a compromise solution was selected via the joint use of two clustering results. A case study of the Three Gorges cascade reservoirs system under small and medium floods was investigated to verify the applicability of the proposed method. The results revealed that the MWFSM effectively distinguishes reservoir operation processes. Two more operation patterns with similar positions but different shapes were identified via MWFSM when compared with Euclidean distance and the dynamic time warping method. Furthermore, the proposed method decreased the selection range from the whole Pareto optimal set to a set containing relatively few solutions. Finally, a compromise solution was selected.
1. Introduction
Reservoirs are considered the most effective form of water infrastructure to realize the comprehensive utilization of water resources [1]. Generally, the objectives of a multi-purpose reservoir create conflict in nature, such as flood control, hydroelectric power generation, water supply, navigation, and ecological conservation, and there exists no single optimal solution that simultaneously satisfies all objectives [2,3]. Hence, the optimization of a multi-purpose reservoir represents a typical multi-objective optimization problem (MOP) [4,5].
MOPs can be roughly divided into three categories according to the articulation of preference [6]: (1) for a given prior articulation of preference, transformation of all but one of the objectives into constraints and sorting of the objectives based on this preference; (2) when prior preference knowledge is available during the search, interactive searching is conducted via decision-making and optimization at interleaved steps; (3) for a given posterior articulation of preference, the MOP is solved by first generating the Pareto optimal solution set, and a satisfactory solution is subsequently selected from the Pareto optimal set according to this preference [7].
Regarding optimization of the multi-objective reservoir operation, the MOP may be transformed into a single-objective optimization problem [8] or solved with multi-objective evolutionary algorithms (MOEAs) [9,10]. Due to the effectiveness of Pareto optimal set generation, MOEAs have been increasingly adopted [11,12]. In the optimization of a multi-purpose reservoir system in India, Reddy and Kumar [3] proposed a method, the multi-objective genetic algorithm (MOGA), to generate the Pareto optimal set. It has been demonstrated that the MOGA offers many alternatives to the decision-maker (DM). In the joint operation optimization of two cascade reservoirs, Chang and Chang [13] applied the non-dominated sorting genetic algorithm II (NSGA-II) [14] to solve the MOP and simultaneously minimize the shortage indices of both reservoirs. Their results demonstrated the ability of NSGA-II to attain high performance when analyzing water resource systems. Qin et al. [15] developed the multi-objective cultured differential evolution (MOCDE) approach to achieve trade-offs between two conflicting flood control goals in multi-objective reservoir optimization. It was demonstrated that the MOCDE approach is efficient and robust with an increased ability to overcome the premature convergence problem. In addition, more MOEAs have been proposed in recent works [16,17,18]. These studies focus on the development of powerful MOEAs, rather than the selection of one or several particularly apt solutions.
Regarding the abovementioned research, trade-off ranking techniques have usually been adopted to choose a solution from the results obtained with MOEAs. With a clear preference towards the objectives, methods such as the technique for order preference by similarity to ideal solution (TOPSIS), the elimination and choice translating reality (ELECTRE) [19], and the analytic hierarchy process (AHP) are common approaches to rank and select the solutions of the Pareto optimal set [20]. However, when applying MOEAs in real-world reservoir optimization problems, the DM may not have a clear articulation of preference (e.g., maximization of the total power production amount or guaranteed output). Thus, relative distance ranking [21] and new trade-off ranking [22] have been introduced to rank solutions without additional preferences.
In addition to the above ranking techniques, data-driven decision making [23] is also an effective tool. Taboada and Coit [24] applied cluster analysis to the Pareto optimal set. This data mining technique based decisions on the cluster analysis of a multi-objective optimization dataset. It successfully reduced the size of the Pareto optimal set and subsequently selected solutions. In the study of Suwal et al. [25], projection pursuit clustering (PPC) was used to sequence the optimal solutions obtained via the NSGA-II algorithm. This was conducted in the objective function space. The scheme with a larger projection value was better.
However, the above ranking methods consider the Pareto frontier in objective space (e.g., the value of power production) without considering the information involved in decision space (e.g., the process of reservoir regulation). To fully utilize the information contained in the Pareto optimal set, Dumedah [26] presented a clustering-based method for the selection of solutions from the Pareto optimal set according to the solution distribution in both objective and decision spaces. Sato and Izui [27] applied the clustering method and association rule analysis in decision space to reduce the size of the Pareto optimal set. Simplified but vital knowledge was provided to the DM in a case study of a multi-objective topology optimization problem. The results revealed that the information detected with the clustering method facilitates the discovery of particularly effective solutions.
In this study, solution selection based on clustering in both objective and decision spaces [26] was introduced into decision-making for multi-objective reservoir optimization purposes. The clustering-based method for solution selection (CMSS) was first applied to the Pareto optimal set of a multi-purpose reservoir. To enhance its capacity to cluster the time series [28] (i.e., decision variables in reservoir operation), we improved the similarity measurement approach of the Mei–Wang fluctuation similarity measure (MWFSM). The MWFSM is tailored to characterize the similarity of the decision vector in both aspects of position and shape.
The remainder of this paper is organized as follows: In Section 2, the CMSS and MWFSM are presented. The clustering algorithm adopted is introduced. A multi-objective reservoir operation optimization model is then built. In Section 3, the background of the small- and medium-flood (SMF) utilization of the Three Gorges cascade reservoirs and the input data are provided. In Section 4, optimal results of multi-objective reservoir operation are generated with NSGA-II. Clustering algorithms are employed to analyze the Pareto optimal results in objective space and decision space, respectively. The effectiveness of the MWFSM and CMSS is thereafter examined. Section 5 offers a summary of our work and presents guidelines for future work.
2. Methodology
Reservoir operation processes (e.g., water releases, water levels) are considered as the decision variables. Quantification of their similarity is key to valid clustering and guarantees a high performance of solution selection in the optimization of multi-objective reservoir operation. In this section, a new similarity measurement method, clustering algorithm, solution selection procedure, and model of multi-objective reservoir operation are presented.
2.1. Mei–Wang Fluctuation Similarity Measure
It has been acknowledged that a proper distance measure is vital in clustering [29]. Recently, a new index, Mei–Wang fluctuation (MWF) [30], has been proposed to measure the fluctuation in a given process. The MWF index outperforms other indices by characterizing fluctuation in regard to both its quantitative variation and contour changes based on the standard deviation (SD) and rotation angle. This paper introduces the MWF index into the measurement of the similarity between two reservoir operation processes.
On the basis of the MWF index, the MWFSM was developed to identify similar reservoir operation processes. The MWFSM describes both the shape and spatial position of processes, which reflect the features of the reservoir operation.
Assume two reservoir operation processes of the same length:
The calculation procedure of the MWFSM between and is as follows:
- is the index used to describe the difference in quantitative variation between and . It is calculated with Equation (2):where is the ordinate of the point , is the ordinate of the point , is the sequence number, N is the length of the process, and and are the means of and , respectively.
- is an index describing the difference between two processes in terms of contour variations. It is calculated with Equations (3)–(5):where is the angle between two line segments of and is the angle between two line segments of . The rotation angle and line segment of a process are shown in Figure 1. is selected as an example, and for or , is the rotation angle between the first line segment and a horizontal line, is the rotation angle between the last line segment and a horizontal line, and is the slope of the line segment, which is defined by Equation (5).
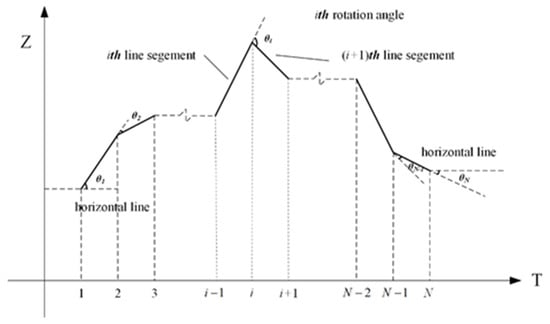 Figure 1. Diagram of rotation angle and line segment of the process.
Figure 1. Diagram of rotation angle and line segment of the process. - The MWFSM between and is calculated with Equation (6) as follows:where is the index of the MWFSM method.
2.2. Clustering by Fast Search and Find of Density Peaks
Clustering by fast search and find of density peaks (DPC) [31] is a clustering algorithm based on the density and distance developed by Rodriguez and Alessandro Liao in 2014. It has been verified that the DPC algorithm quickly determines density peaks and reduces the impact of isolated points, which is suitable for cluster analysis of large datasets [32]. In this paper, the DPC algorithm was adopted to cluster decision processes during solution selection.
In the DPC algorithm, three important parameters are defined for each point. The local density and the distance to the nearest higher-density point δ are considered to describe data points. The decision value γ is created to simplify the selection process of the cluster centers.
In regard to data point , is expressed by Equation (7):
where is the distance between points and , which is calculated via the proposed MWFSM, and is the cut-off distance, which is larger than zero. According to Equation (6), is equal to the number of points in the neighborhood area of point within a radius of . Hence, is sensitive to . However, previous research [31] has also demonstrated that a large dataset reduces the influence of on the clustering result. Conventionally, by sorting in ascending order, the top 2% of the data column is assigned to . In this paper, the value of in the case study is determined via this approach.
In addition, is defined by Equation (8) as follows:
where is calculated as the minimum distance between point and any other point with a higher density. The point with the highest value is expressed as follows:
The decision value is calculated with Equation (10).
where points with an extremely high value are chosen as cluster centers. After determination of the density peaks, the remaining points are allocated following the principle of proximity.
Suppose a dataset . The detailed process of applying the DPC to is described as below:
- Calculate distance matrix via MWFSM.
- Sort in ascending order, assign the top 2% of the data column to .
- Calculate local density according to Equation (7) for each data point in .
- Calculate distance from the nearest larger density point according to Equations (8) and (9) for each data point in .
- Calculate the decision value according to Equation (10) for each data point in .
- Sort in ascending order and record the new order.
- Construct the decision value graph where points are represented as with the ascending order in Step 6.
- Select the points of the large γ values as cluster centers according to the decision value graph.
- Allocate the remaining points following the principle of proximity.
2.3. Clustering-Based Solution Selection Method
The procedure of the CMSS is described below.
Suppose represents the reservoir operation decision process vectors in the Pareto set calculated with an MOEA, where is the number of solutions. Furthermore, represents the set of objective value vectors of the Pareto frontier.
- The DPC method is applied to set and obtains clusters of decision processes.
- The clusters generated in step 1 are ranked by size, and the decision cluster is denoted as , and the decision cluster with the largest membership is denoted as .
- An operation pattern set consisting of the solutions corresponding to the centers of the decision clusters is generated.
- The k-means algorithm is employed to cluster set and obtain objective value clusters.
- The objective value clusters are ranked in descending order, and the cluster is denoted as , and the set with the largest membership is denoted as .
- The intersection of and is considered. If the intersection set is not empty, it is denoted as . If the intersection set is empty, the intersection of and the next objective cluster is determined. This process is repeated until the intersection set is no longer empty, which is then denoted as .
- The decision process with the minimum accumulative similarity in set is identified and recommended.
- The selected solution and the operation pattern set are provided to DMs.
The core of this solution selection method is to identify solutions in high-density areas of the decision processes and objective values. is the area of the maximum concentration of the solutions in the decision space, and is considered a representative decision pattern if a typical solution is selected from this area. Analogously, a suitable robustness is achieved if the solution belongs to a representative area in objective space, e.g., . Hence, a linkage is built between the information extracted from the objective values and the knowledge acquired from the decision processes. In addition to the trade-offs between the objectives, the selected solution is also a compromise choice between the decision processes and objective values. Furthermore, the operation pattern set will help DMs better understand the reservoir operations of multi-objective optimal results.
2.4. Multi-Objective Optimization Model
During the flood period, the minimization of flood risk and ecological influences are common objectives of multi-objective reservoirs. In this section, a model of a cascade reservoir system is built considering these two objectives while meeting a variety of constraints (e.g., water balance and power output range). The decision variable of the model is the time series of the water level.
2.4.1. Objective Functions
The objective of the minimization of the ecological influences can be expressed as
where is the eco-friendly objective, is the discharge of the cascade reservoir system during the period. is the ecological flow series and is the ecological flow during the period. The definition of an ecological flow is usually based on the case study for certain purposes. When the cascade discharge process is similar to the ecological flow process, is relatively limited, and the eco-goal is better met.
The objective of flood control is to minimize the maximum flood control capacity used during the operation horizon while satisfying additional flood control constraints. This is demonstrated in the study case. The flood control objective can be expressed as
where is the maximum flood control capacity used during the operation horizon, is the average capacity used in the interval at the cascade reservoir, and is the lower bound of the volume of the cascade reservoir.
2.4.2. Constraints
- The water balance is expressed aswhere is the average storage of the cascade reservoir during the period, is the inflow of the cascade reservoir during the period, and is the outflow rate of the cascade reservoir during the period; is the duration.
- The outflow constraint is expressed aswhere is the inflow of the cascade reservoir, which is equal to the sum of the outflow of the cascade reservoir and the local inflow during the period.
- The power output constraint is given bywhere and are the minimum and maximum output power levels, respectively, of the plant during the period, and is the average output power of the plant during the period.
- The storage volume constraint is expressed aswhere and are the lower and upper bounds, respectively, of the water level of the dam during the period.
- The boundary condition limit is given bywhere and are the water levels of the cascade reservoir during the first and last periods, respectively, and is the initial water level of the dam, which is given in the case study.
The procedure of the proposed approach is illustrated in Figure 2. It is composed of three main parts. The multi-objective problem modelling is the first part. Data preparation is carried out in this part. The second part is the optimization via NSGA-II. In the solution selection part, results of NSGA-II are used as an input. The data-driven solution selection approach is carried out.
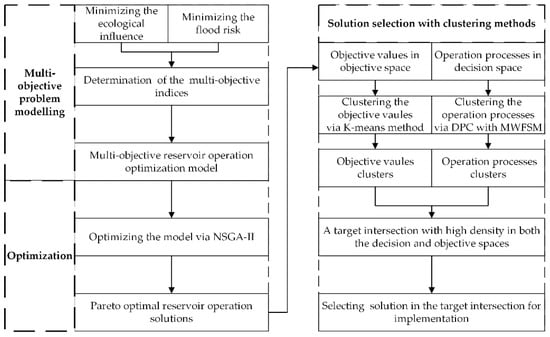
Figure 2.
Procedure of the clustering-based solution selection method.
3. Case Study
3.1. Study Area
The Three Gorges–Gezhouba cascade reservoirs, as shown in Figure 3, were selected for the case study in this work. The Three Gorges Reservoir (TGR), as the backbone project of the Yangtze River, provides comprehensive benefits while prioritizing flood control, hydroelectric generation, and navigation. Gezhouba (GZB), as a reverse regulation reservoir of the TGR, is located 38 km downstream from the TGR. In recent years, small- and medium-flood (SMF) utilization of the TGR has attracted much attention from the operators of the TGR [33]. Floods with a peak discharge between 25,000 and 55,000 m3/s are considered small and medium floods in the TGR. During small and medium floods, the objective of flood risk and ecological influence minimization is adopted.
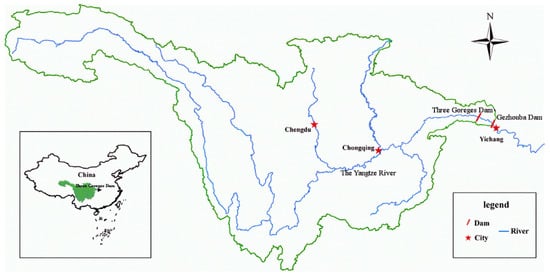
Figure 3.
The location of the Three Gorges Reservoir–Gezhouba (TGR–GZB) cascade reservoirs in China.
3.2. Input Data
In this case study, the plan period extended from 10 to 30 June. Daily inflow data of the TGR from 10 June 2012 to 30 June 2012 were adopted as input data. The initial water level of the TGR was set to 145 m, and the water level of GZB was set to a fixed value of 66 m. The maximum water level of the TGR during SMF utilization was set to 155 m according to previous research [33] as an additional flood control constraint. The daily inflow of the cascade reservoir system during the plan period is shown in Figure 4.
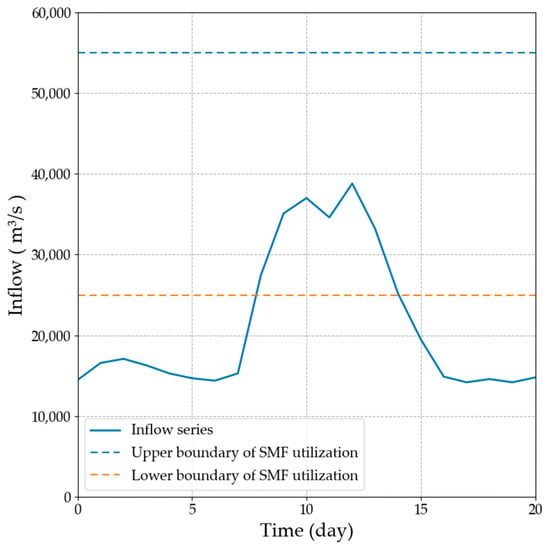
Figure 4.
Inflow of the cascade reservoir system during the operational period.
In the multi-objective reservoir optimization model, the eco-friendly objective was calculated depending on the ecological flow . According to [34], the breeding state of four major Chinese carps in the middle reaches of the Yangtze River is commonly adopted as a major indicator of the status of the ecological system. The artificial flood pulse flow satisfying the breeding conditions of these carps was adopted as . In Appendix A, the determination of the ecological flow is presented.
4. Results and Discussion
In this study, the optimization results of multi-objective reservoir operation were obtained via NSGA-II. Hereafter, the optimization results of multi-objective reservoir operation are presented. Based on the optimization results, the objective values were clustered with the k-means method, and the operation processes were separately clustered in the decision space. The centers of the decision cluster were representative patterns of reservoir operation. Solution selection was conducted via the joint use of clustering results.
4.1. NSGA-II Output and Traditional Analysis of Pareto Set
NSGA-II was implemented via MATLAB 2014a software. The population size was set to 200, and the maximum number of iterations was set to 500. The stopping criterion of the algorithm was defined as the maximum number of iterations. The crossover probability of NSGA-II was set to 0.8, and the mutation probability was fixed as (where is the number of variables for each solution). In this case study, was 21, and the mutation probability was set to 0.1. The algorithm converged after 500 iterations and generated a non-dominated set containing 200 feasible solutions satisfying all of the above model constraints. The output results of NSGA-II are shown in Figure 5.
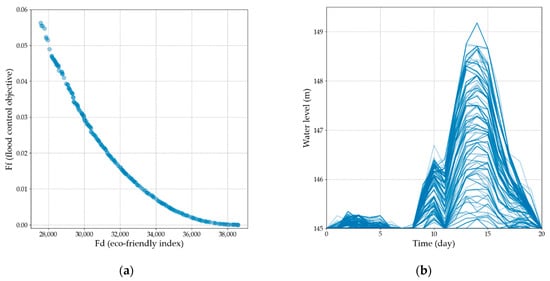
Figure 5.
Output of non-dominated sorting genetic algorithm II (NSGA-II) in the objective and decision spaces: (a) the trade-offs between the eco-friendly objective and flood control target in objective space; (b) the corresponding reservoir operation processes in decision space.
According to Figure 5a, the trade-offs between the conflicting objectives indicate that the eco-goal cannot be improved without worsening the flood control target . Corresponding decision processes in the decision space are shown in Figure 5b.
Commonly, after a Pareto optimal set is generated, researchers might select representative solutions [35]. For comparison purposes, we selected three solutions in the same way: the solution fully satisfying the eco-friendly index, the solution fully satisfying the flood control target and a medium compromise solution considering both objectives with the same importance [36]. The medium compromise solution has the closest Euclidean distance (ED) to the utopia point [37] (also called the ideal point). These three solutions are shown in Figure 6 below. Figure 6a presents the distributions of these three solutions in objective space, and Figure 6b shows the corresponding operation processes.
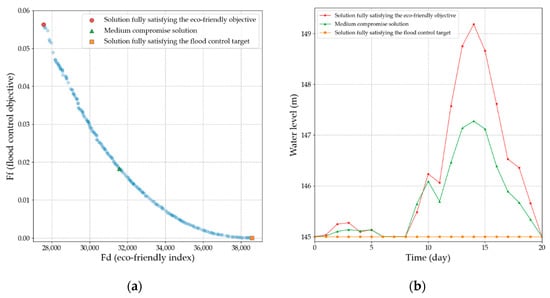
Figure 6.
Three representative solutions selected through a traditional analysis approach. (a) The objective values of the representative solutions; (b) the corresponding reservoir operation processes of the representative solutions.
4.2. Clustering of the Trade-Off Frontier
In this subsection, objective values obtained via NSGA-II were clustered through the k-means algorithm [38]. Before clustering, the two objective values were normalized via the z-score method [39]. The number of clusters in the k-means method is the most critical choice. Hence, the Calinski–Harabasz indicator (CH) [40] was adopted to determine the optimal number of clusters, which was equal to 10. To eliminate the impact of the initial centers on the k-means method, multiple computations with randomly chosen initial centroids were performed until the results stabilized.
Figure 7 shows the clustering result based on the objective values. The colored points indicate the distribution of the Pareto optimal solutions in objective space, and the stars indicate the cluster centroids. According to the clustering results in objective space, the solutions were partitioned into ten clusters.
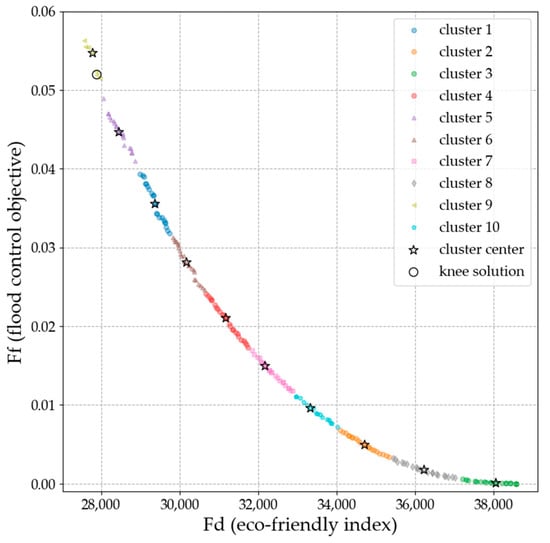
Figure 7.
Schematic diagram of the clustering results in objective space.
By clustering the Pareto set in objective space, we narrowed the selection range (200 solutions in this case study) to ten clusters with corresponding unique characteristics. In some studies [24,41], cluster analysis is adopted as a practical solutions selection approach. This approach offers the DM a set of k clusters. To make the final decision, the DM is required to select one cluster from among the k clusters. In this case study, if DMs prefer a low flood control risk to better meet the eco-friendly goal, they can choose among the solutions contained in cluster 3, which are the green circles in Figure 7. If DMs have no preference, the cluster that contains the knee region will be the focus. According to [42], cluster 9 is the knee region and a knee solution is marked in Figure 7.
4.3. Clustering of the Reservoir Operation Processes
To discover more information about the Pareto optimal results, we clustered the operation processes in the decision space to detect reservoir operation patterns, which facilitates practical water management. In this subsection, the clustering results of the reservoir operation processes obtained through DPC with the new similarity measure MWFSM (MWFSM-DPC) are presented. Compared to DPC with ED (ED-DPC) and DPC with dynamic time warping (DTW; DTW-DPC), the validity of MWFSM was verified. The MWFSM recognized more reservoir operation patterns in the high water level zone.
DPC was employed to cluster the reservoir operation processes in the decision space. To validate the MWFSM, two common methods, i.e., ED and DTW [43], were adopted as controls. ED is a classical distance measure, which is simple and intuitive to use. DTW is another well-known similarity measure, which has been widely applied in the clustering of time-series data [44]. In the DPC applications, the top 2% of the data column was assigned to . Each experiment was independently run in the same computer environment.
In this case study, the true clustering was unknown. The Silhouette method [45], as a widely used internal validity index [46], was adopted as the clustering validation measure. The Silhouette index (Sil) is a normalized summation-type index. Its value ranges between −1 and +1. The larger the value of Sil, the better the clustering results. As the internal validity indices (i.e., Sil) cannot make comparisons between clustering approaches that are generated using different similarity measures [47], Sil was used to verify the validity of the clustering results [48], not for comparison purposes.
In Table 1 below, the results of clustering and the Silhouette method are listed.

Table 1.
Results obtained via clustering in decision space.
According to the values of Sil presented in Table 1, the results of the three experiments were reliable. From clustering results, MWFSM-DPC divided the reservoir operation processes into seven clusters, whereas DTW-DPC and ED-DPC yielded five clusters. In the MWFSM-DPC experiment, the largest cluster contained 71 reservoir operation processes, whereas the other six clusters contained few processes. In the DTW and ED experiments, the largest clusters contained 53 and 97 processes, respectively. The abovementioned similarity measurement methods impose different influences on the time-series clustering results. Proper similarity measures applied in cluster algorithms could provide more useful and highly pertinent information regarding reservoir operation.
The visualizations of the clustering results of DTW-DPC, ED-DPC, and MWFSM-DPC are shown in Figure 8, Figure 9 and Figure 10 separately. Cluster centers were selected as the representative solutions. These operation patterns were divided into three categories: the high water level pattern, in which the highest water level is higher than 148 m; the medium water level pattern, in which the highest water level is between 148 and 146 m; and the low water level pattern, in which the highest water level is lower than 146 m. The results of each experiment are presented below.
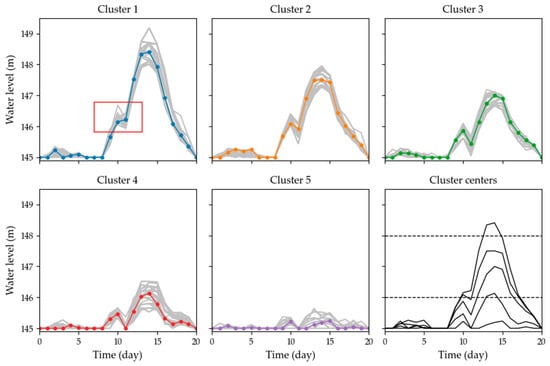
Figure 8.
Clustering results on reservoir operation processes via dynamic time warping (DTW). Clusters are drawn in each subfigure separately. The cluster centers are shown in the last subfigure.
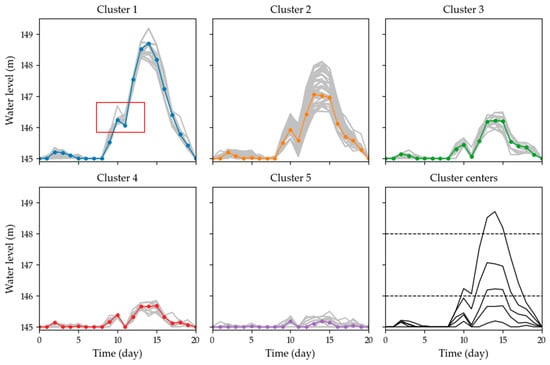
Figure 9.
Clustering results on reservoir operation processes via Euclidean distance (ED). Clusters are drawn in each subfigure separately. The cluster centers are shown in the last subfigure.
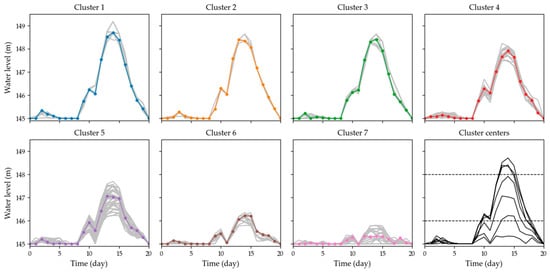
Figure 10.
Clustering results on the reservoir operation processes via Mei–Wang fluctuation similarity measure (MWFSM). Clusters are drawn in each subfigure separately. The cluster centers are shown in the last subfigure.
In Figure 8, DTW-DPC found one high water level pattern, three medium water level patterns, and one low water pattern. In Figure 9, ED-DPC yielded five clusters. One high water level pattern, two medium water level patterns and two low water patterns were identified, respectively. As shown in the red boxes of the first subfigures in Figure 8 and Figure 9, the local trends of the high water level patterns were vastly different. During the period between the eighth and twelfth days, the pattern in DTW-DPC exhibited mono-growth, in which the pattern in DTW-DPC first increased and then decreased. In DTW-DPC and ED-DPC experiments, the clusters were generated in a narrow area with a similar position in the decision space. However, the shape dissimilarity between the various processes with similar positions was not captured.
The result of MWFSM-DPC is shown in Figure 10. In Figure 10, MWFSM-DPC discovered three high water level patterns, three medium water level patterns, and one low water pattern. The patterns discovered in each experiment were similar except for the high water level patterns.
Compared with ED and DTW, the MWFSM distinguished more patterns in the high water level zone, and the mono-growth pattern and the pattern with fluctuation were both recognized. More patterns were discovered, which allowed the DM to better understand the high water level operations.
According to the above results, the MWFSM method attains distinct advantages in the clustering reservoir operation processes, where the concern is not only position similarity but also shape similarity.
4.4. Solution Selection
In this part, the CMSS results are presented. Then, the results are compared to the outcomes of the traditional recommendation method in Section 4.1 and the clustering method in Section 4.2. The advantages and shortcomings of CMSS are discussed.
According to the cluster analysis results of the objective values and the operation processes, the intersection of the two abovementioned results was determined and is presented in Table 2 below.

Table 2.
Number of solutions in the intersection between cluster 5 of MWFSM-DPC and the Pareto clusters.
The number of solutions in each intersection is provided in Table 2. The largest intersection was obtained between cluster 7 of MWFSM-DPC and cluster 10 determined via Pareto cluster analysis. Considering that the intersection describes the robustness level [26], which implies that the larger the intersection, the higher the robustness, we took the largest intersection as the new selection range. The selection range was narrowed from 200 to 22 solutions, which is illustrated in Figure 11.
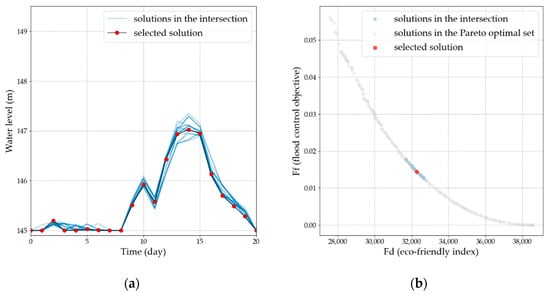
Figure 11.
Results of the clustering-based method for solution selection (CMSS) considering the MWFSM-DPC method. (a) Reservoir operation processes in decision space; (b) objective values in objective space.
The processes in the largest intersection and the intersection center are shown in Figure 11a. Corresponding objective values are shown in Figure 11b. In Figure 11a, the blue curves represent the reservoir operation processes of the solutions in the intersection. The black curve with red dots represents the center. It shows that for most solutions in the intersection, the water level slightly fluctuated during the early period and decreased to the dead water level before the main flood control operation. Another fluctuation occurred during the rising period on the 10th day, and the highest water level during the flood was observed around the 14th day. All solutions in this intersection shared the same trends except for the early period and the period of the 13th, 14th, and 15th days. It was observed that objective values of solutions around the selected solution were on the Pareto frontier or close to it, which indicates the robustness of the selected solution.
Finally, the DM can be provided with the seven patterns discovered in the decision space and the selected solution.
Via the traditional recommendation method in Section 4.1, three solutions selected from the large Pareto set are presented to the DM. The medium compromise solution is most likely recommended for implementation. As such, valuable information contained in the large Pareto optimal set is wasted at a certain point. Via trade-off cluster analysis in Section 4.2, the selection range is narrowed to 10 Pareto clusters. Further selection requires a clear preference of the DM. Otherwise, a representative solution selected from the knee region is chosen as a recommendation. In both approaches, the selection is based on the information in the objective space. The reservoir operation processes in the Pareto optimal set are not analyzed.
In the proposed approach, we innovatively clustered the processes in the decision space. The processes were assigned to certain groups with similar position and shape. Seven typical operation patterns of the Pareto optimal set were identified. Then, the set intersection operation was performed for the largest cluster in the decision space and clusters in the objective space. The selection range was narrowed to the largest intersection which contained 22 solutions. The center of the intersection was chosen as a recommendation.
Compared to the other two selection methods, the proposed approach involved the information discovered in the decision space, not only the objective values. Valuable information regarding the Pareto optimal reservoir operation processes was uncovered during the calculation.
Although the proposed approach worked without the articulation of preference from DM, robustness was a hidden preference. In addition, the CMSS was sensitive to similarity measures adopted in the clustering algorithm according to the clustering analysis results of operation processes.
5. Conclusions
To select a solution with certain properties from among the numerous solutions in the optimal Pareto set for multi-objective reservoir operation models, this study introduced the CMSS, which benefits from the information via clustering not only in objective space but also in decision space. A new similarity measure named MWFSM was developed to capture the temporal nature of the various reservoir operation processes through clustering. Due to the advantages of the additional information extracted in the decision space, the CMSS selects solutions from a large Pareto set. In this study, the CMSS was verified in a case study of the regulation of the TGR–GZB cascade reservoirs during the flood season considering the eco-goal and flood control target. MWFSM successfully identified more patterns with different shapes. The CMSS recommended a solution that acquires robustness. The feasibilities of the MWFSM and CMSS were verified. In many cases of real-world reservoir optimization problems like the case study, the DM may not have a clear articulation of preference. The CMSS can deal with this situation and select a solution with robustness.
In future research, forecast data will be analyzed instead of historical data, and the risk objective of reservoir flood operation will be imported, which may further narrow the gap between research and practice. Another advantage of CMSS is that it selected a solution automatically. It could be developed into an automated decision-making system in reservoir operation in the future.
Author Contributions
Conceptualization: Y.K., Y.M., X.W. and Y.B.; Methodology: Y.K.; Formal analysis: Y.K.; investigation: Y.K., Y.B.; Resources: Y.M.; Writing—original draft preparation, Y.K.; Writing—review and editing: Y.M., Y.B. and X.W.; Funding acquisition, Y.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (no. 91647204) and the National Natural Science Foundation of China (no. 51479140).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data presented is available under request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Determination of the Ecological Flow Based on the Indicators of Hydrologic Alteration (IHA) Method
To determine the ecological flow (i.e., the artificial flood pulse flow) of the TGR during the planning period, the IHA method [49,50] was employed.
As a result of the IHA method, nine indicators referring to high-flow pulses were chosen to develop the artificial flood pulse flow series. The results are listed in Table A1.

Table A1.
Components of the Indicators of Hydrologic Alteration (IHA) results used to develop the artificial flood pulse flow.
Table A1.
Components of the Indicators of Hydrologic Alteration (IHA) results used to develop the artificial flood pulse flow.
| Hydrologic Indicators of a High Pulse | Quantile | ||
|---|---|---|---|
| 75% | 50% | 25% | |
| Date of rise | 12 | 7 | 2 |
| Initial flow of the pulse (m3/s) | 23,500 | 21,150 | 20,250 |
| Duration of the high pulse (day) | 8 | 4 | 2 |
| No. of high pulses (times) | 2 | 1 | 1 |
| Peak flow of the high pulse (m3/s) | 30,800 | 25,450 | 21,200 |
| Rise rate (m3/s/d) | 2303 | 1932 | 1558 |
| Fall rate (m3/s/d) | −1105 | −1386 | −1766 |
| Rise duration (d) | 4 | 2 | 1 |
| Fall duration (d) | 4 | 2 | 1 |
According to the results listed in Table A1, the high pulse during the scheduling period exhibited the characteristics of a low frequency (only one or two high pulses) and a short duration (ranging from two to eight days). Comprehensively considering the above features, the number of high pulses was set to one, and the duration was set to six days. The flood pulse started to rise on the ninth day of the scheduling period. The rise and fall periods both lasted three days, and the peak flow of the high pulse was assigned a value of 25,450 m3/s. The remainder of the high pulse was assigned the corresponding value of the 50th percentile series. The ecological flow series considering one high pulse is listed in Table A2.

Table A2.
Artificial flood pulse from 10 June to 30 June at the location of the TGR.
Table A2.
Artificial flood pulse from 10 June to 30 June at the location of the TGR.
| Index Number (Day) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Discharge (m3/s) | 14,800 | 14,900 | 14,800 | 15,500 | 15,100 | 14,700 | 15,100 |
| Index Number (Day) | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| Discharge (m3/s) | 15,400 | 15,000 | 18,483 | 21,966 | 25,450 | 23,666 | 21,883 |
| Index Number (Day) | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| Discharge (m3/s) | 20,100 | 19,500 | 22,000 | 21,800 | 22,200 | 23,200 | 25,200 |
References
- Yu, Y.; Wang, C.; Wang, P.; Hou, J.; Qian, J. Assessment of multi-objective reservoir operation in the middle and lower Yangtze River based on a flow regime influenced by the Three Gorges Project. Ecol. Inform. 2017, 38, 115–125. [Google Scholar] [CrossRef]
- Labadie, J.W. Optimal operation of multireservoir systems: State-of-the-art review. J. Water Resour. Plan. Manag. 2004, 130, 93–111. [Google Scholar] [CrossRef]
- Reddy, M.J.; Kumar, D.N. Optimal reservoir operation using multi-objective evolutionary algorithm. Water Resour. Manag. 2006, 20, 861–878. [Google Scholar] [CrossRef]
- Chou, F.N.F.; Wu, C.W. Stage-wise optimizing operating rules for flood control in a multi-purpose reservoir. J. Hydrol. 2015, 521, 245–260. [Google Scholar] [CrossRef]
- Dai, L.; Zhang, P.; Wang, Y.; Jiang, D.; Dai, H.; Mao, J.; Wang, M. Multi-objective optimization of cascade reservoirs using NSGA-II: A case study of the Three Gorges-Gezhouba cascade reservoirs in the middle Yangtze River, China. Hum. Ecol. Risk Assess. 2017, 23, 814–835. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lamont, G.B.; Van Veldhuizen, D.A.; Goldberg, D.E.; Koza, J.R. Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: New York, NY, USA, 2007; ISBN 9780387310299. [Google Scholar]
- Van Veldhuizen, D.A.; Lamont, G.B. Multiobjective evolutionary algorithms: Analyzing the state-of-the-art. Evol. Comput. 2000, 8, 125–147. [Google Scholar] [CrossRef]
- Zhu, D.; Mei, Y.; Xu, X.; Chen, J.; Ben, Y. Optimal operation of complex flood control system composed of cascade reservoirs, navigation-power junctions, and flood storage areas. Water 2020, 12, 1883. [Google Scholar] [CrossRef]
- Zhou, A.; Qu, B.Y.; Li, H.; Zhao, S.Z.; Suganthan, P.N.; Zhangd, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Deb, K. Multi-objective Optimisation Using Evolutionary Algorithms: An Introduction. In Multi-Objective Evolutionary Optimisation for Product Design and Manufacturing; Springer: London, UK, 2011. [Google Scholar]
- Reed, P.M.; Hadka, D.; Herman, J.D.; Kasprzyk, J.R.; Kollat, J.B. Evolutionary multiobjective optimization in water resources: The past, present, and future. Adv. Water Resour. 2013, 51, 438–456. [Google Scholar] [CrossRef]
- Adeyemo, J.A. Reservoir operation using multi-objective evolutionary algorithms—A review. Asian J. Sci. Res. 2011, 4, 16–27. [Google Scholar] [CrossRef]
- Chang, L.C.; Chang, F.J. Multi-objective evolutionary algorithm for operating parallel reservoir system. J. Hydrol. 2009, 377, 12–20. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, J.; Lu, Y.; Li, Y.; Zhang, Y. Multi-objective Cultured Differential Evolution for Generating Optimal Trade-offs in Reservoir Flood Control Operation. Water Resour. Manag. 2010, 24, 2611–2632. [Google Scholar] [CrossRef]
- Fotovatikhah, F.; Herrera, M.; Shamshirband, S.; Chau, K.W.; Ardabili, S.F.; Piran, M.J. Survey of computational intelligence as basis to big flood management: Challenges, research directions and future work. Eng. Appl. Comput. Fluid Mech. 2018, 12, 411–437. [Google Scholar] [CrossRef]
- Zhang, X.; Luo, J.; Sun, X.; Xie, J. Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm. Eng. Optim. 2019, 51, 42–62. [Google Scholar] [CrossRef]
- Liu, D.; Huang, Q.; Yang, Y.; Liu, D.; Wei, X. Bi-objective algorithm based on NSGA-II framework to optimize reservoirs operation. J. Hydrol. 2020, 585, 124830. [Google Scholar] [CrossRef]
- Malekmohammadi, B.; Zahraie, B.; Kerachian, R. Ranking solutions of multi-objective reservoir operation optimization models using multi-criteria decision analysis. Expert Syst. Appl. 2011, 38, 7851–7863. [Google Scholar] [CrossRef]
- Tzeng, G.-H.; Huang, J.-J. Multiple Attribute Decision Making: Methods and Applications a State of the Art Survey; CRC Press: Boca Raton, FL, USA, 2011; ISBN 9781439861578. [Google Scholar]
- Kao, C. Weight determination for consistently ranking alternatives in multiple criteria decision analysis. Appl. Math. Model. 2010, 34, 1779–1787. [Google Scholar] [CrossRef]
- Jaini, N.; Utyuzhnikov, S. Trade-off ranking method for multi-criteria decision analysis. J. Multi-Criteria Decis. Anal. 2017, 24, 121–132. [Google Scholar] [CrossRef]
- Provost, F.; Fawcett, T. Data Science and its Relationship to Big Data and Data-Driven Decision Making. Big Data 2013, 1, 51–59. [Google Scholar] [CrossRef]
- Taboada, H.A.; Coit, D.W. Data mining techniques to facilitate the analysis of the pareto-optimal set for multiple objective problems. In Proceedings of the 2006 IIE Annual Conference and Exposition, Orlando, FL, USA, 20–24 May 2006. [Google Scholar]
- Suwal, N.; Huang, X.; Kuriqi, A.; Chen, Y.; Pandey, K.P.; Bhattarai, K.P. Optimisation of cascade reservoir operation considering environmental flows for different environmental management classes. Renew. Energy 2020, 158, 453–464. [Google Scholar] [CrossRef]
- Dumedah, G.; Berg, A.A.; Wineberg, M.; Collier, R. Selecting Model Parameter Sets from a Trade-off Surface Generated from the Non-Dominated Sorting Genetic Algorithm-II. Water Resour. Manag. 2010, 24, 4469–4489. [Google Scholar] [CrossRef]
- Sato, Y.; Izui, K.; Yamada, T.; Nishiwaki, S. Data mining based on clustering and association rule analysis for knowledge discovery in multiobjective topology optimization. Expert Syst. Appl. 2019, 119, 247–261. [Google Scholar] [CrossRef]
- Liao, T.W. Clustering of time series data—A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A Comprehensive Survey of Clustering Algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Wang, X.; Mei, Y.; Cai, H.; Cong, X. A new fluctuation index: Characteristics and application to hydro-wind systems. Energies 2016, 9, 114. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Wang, H.; Yu, X. Shared-nearest-neighbor-based clustering by fast search and find of density peaks. Inf. Sci. 2018, 450, 200–226. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, J.; Li, C.; Chen, F. Integrated utilization of the Three Gorges Cascade for navigation and power generation in flood season. Shuili Xuebao 2017, 48, 31–40. [Google Scholar] [CrossRef]
- Ban, X.; Diplas, P.; Shih, W.R.; Pan, B.; Xiao, F.; Yun, D. Impact of Three Gorges Dam operation on the spawning success of four major Chinese carps. Ecol. Eng. 2019. [Google Scholar] [CrossRef]
- Tsai, W.P.; Chang, F.J.; Chang, L.C.; Herricks, E.E. AI techniques for optimizing multi-objective reservoir operation upon human and riverine ecosystem demands. J. Hydrol. 2015, 530, 634–644. [Google Scholar] [CrossRef]
- Ameur, M.; Kharbouch, Y.; Mimet, A. Optimization of passive design features for a naturally ventilated residential building according to the bioclimatic architecture concept and considering the northern Morocco climate. Build. Simul. 2020, 13, 677–689. [Google Scholar] [CrossRef]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Gentle, J.E.; Kaufman, L.; Rousseuw, P.J. Finding Groups in Data: An Introduction to Cluster Analysis. Biometrics 1991, 47, 788. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. 1974, 3, 1–27. [Google Scholar]
- Taboada, H.A.; Baheranwala, F.; Coit, D.W.; Wattanapongsakorn, N. Practical solutions for multi-objective optimization: An application to system reliability design problems. Reliab. Eng. Syst. Saf. 2007, 92, 314–322. [Google Scholar] [CrossRef]
- Satopää, V.; Albrecht, J.; Irwin, D.; Raghavan, B. Finding a “kneedle” in a haystack: Detecting knee points in system behavior. Proc. Int. Conf. Distrib. Comput. Syst. 2011, 166–171. [Google Scholar] [CrossRef]
- Berndt, D.; Clifford, J. Using dynamic time warping to find patterns in time series. Knowl. Discov. Databases Workshop 1994, 398, 359–370. [Google Scholar]
- Yuan, G.; Sun, P.; Zhao, J.; Li, D.; Wang, C. A review of moving object trajectory clustering algorithms. Artif. Intell. Rev. 2017, 47, 123–144. [Google Scholar] [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; Pérez, J.M.; Perona, I. An extensive comparative study of cluster validity indices. Pattern Recognit. 2013, 46, 243–256. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Ying Wah, T. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Ruiz, L.G.B.; Pegalajar, M.C.; Arcucci, R.; Molina-Solana, M. A time-series clustering methodology for knowledge extraction in energy consumption data. Expert Syst. Appl. 2020, 160, 113731. [Google Scholar] [CrossRef]
- Wang, H.; Brill, E.D.; Ranjithan, R.S.; Sankarasubramanian, A. A framework for incorporating ecological releases in single reservoir operation. Adv. Water Resour. 2015, 78, 9–21. [Google Scholar] [CrossRef]
- Mathews, R.; Richter, B.D. Application of the indicators of hydrologic alteration software in environmental flow setting. J. Am. Water Resour. Assoc. 2007, 43, 1400–1413. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).