Introducing Non-Stationarity Into the Development of Intensity-Duration-Frequency Curves under a Changing Climate
Abstract
:1. Introduction
2. Study Area and Data Used
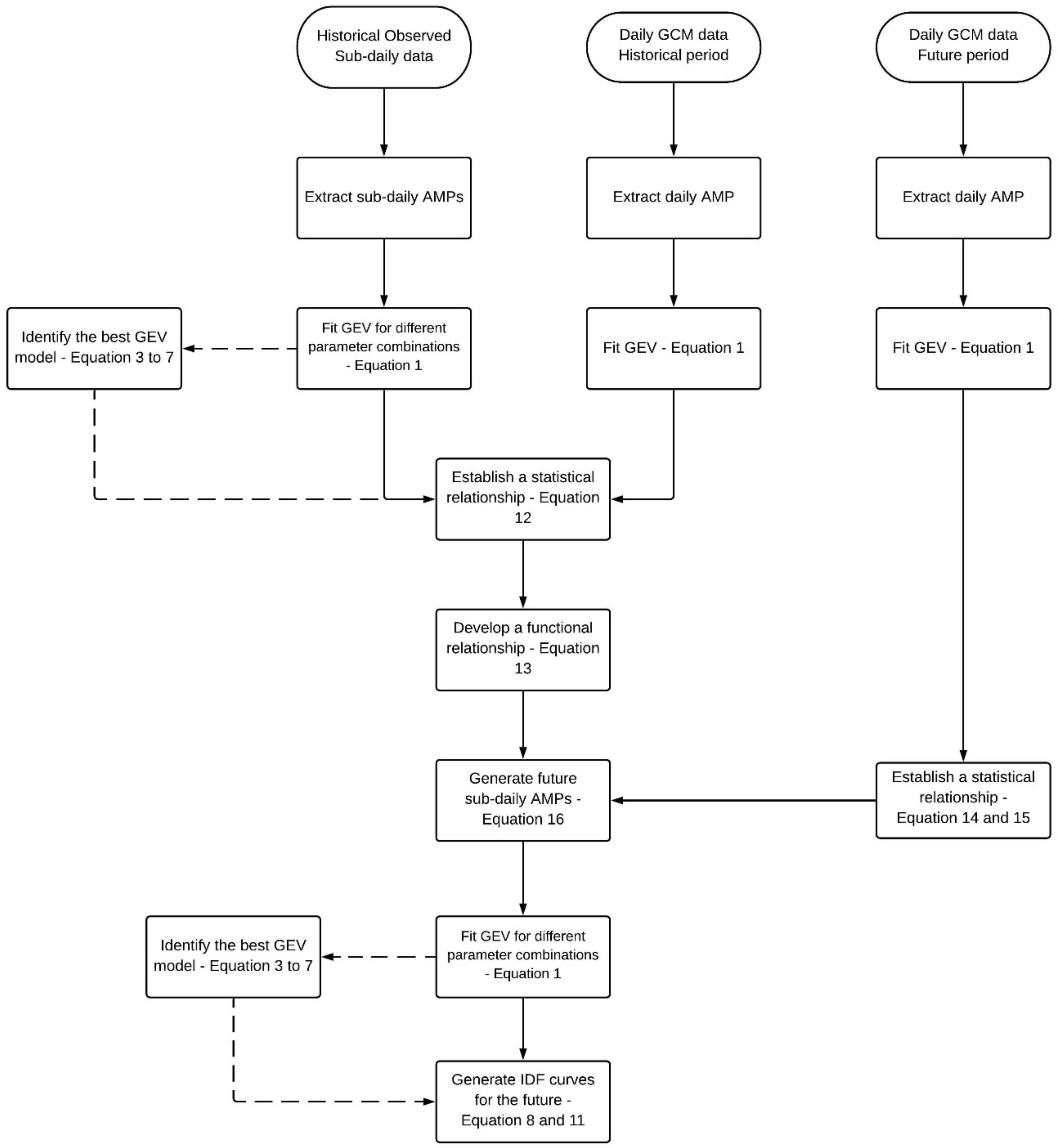
3. Methodology
- Statistical analysis: applied to fit stationary and non-stationary probability distributions to both historical and future projected data. An information criteria method is used to identify the best probability distribution model, and a significance test is performed to assess the statistical significance of the non-stationary model in comparison to the stationary one;
- Updating IDF curves for future conditions (EQMNS): a modified EQM methodology is applied to generate future sub-daily annual maximum precipitation data, and update IDF curves for future period under non-stationary conditions.
3.1. Statistical Analysis
3.1.1. Theoretical Probability Distribution
3.1.2. Identification of the Best Model
3.1.3. Rainfall Depth Estimation
3.2. Non-Stationary IDF Curves under Changing Climate
4. Results and Discussions
4.1. Trends in GEV Model Parameters in Historical Observed Data
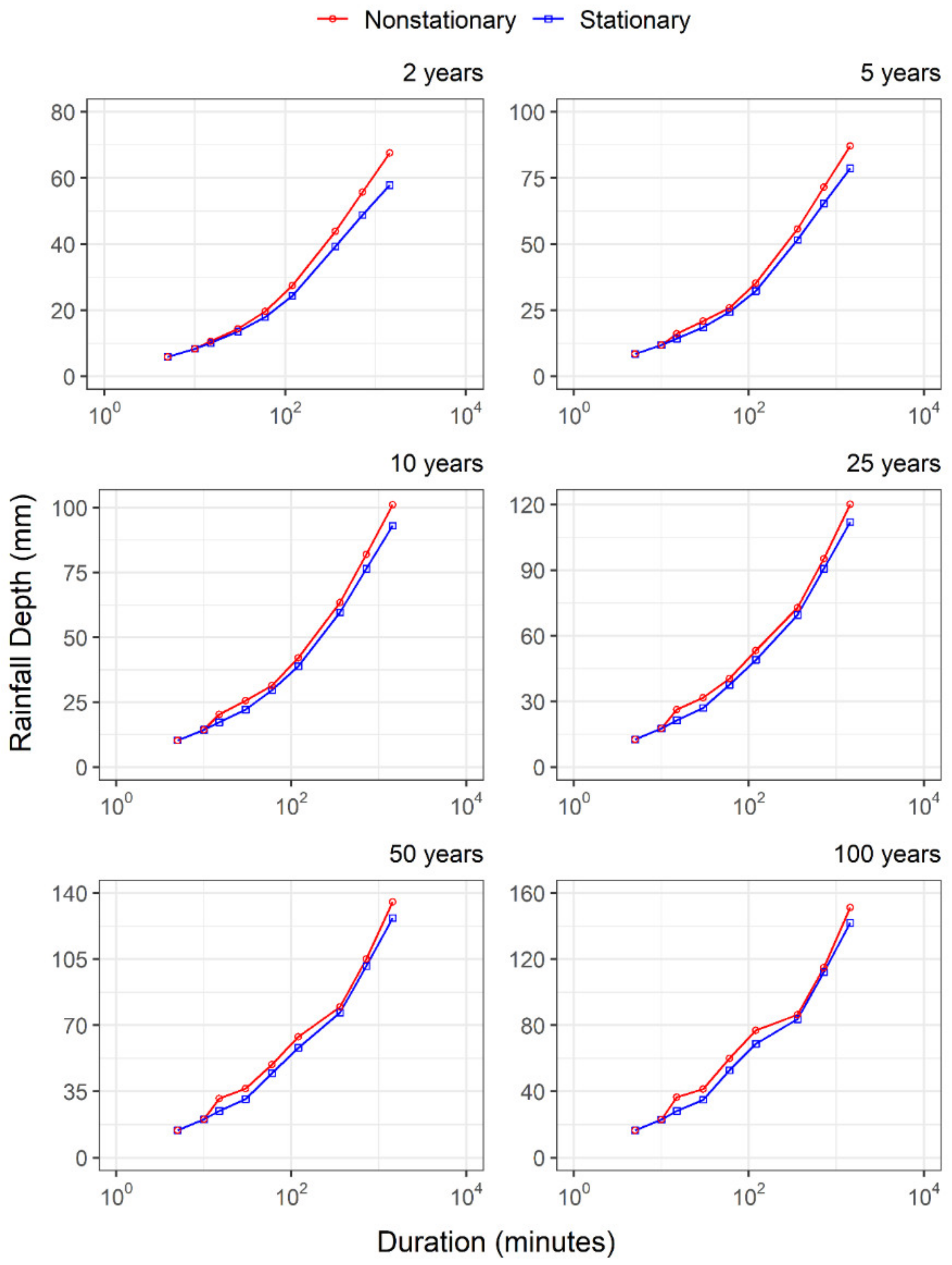
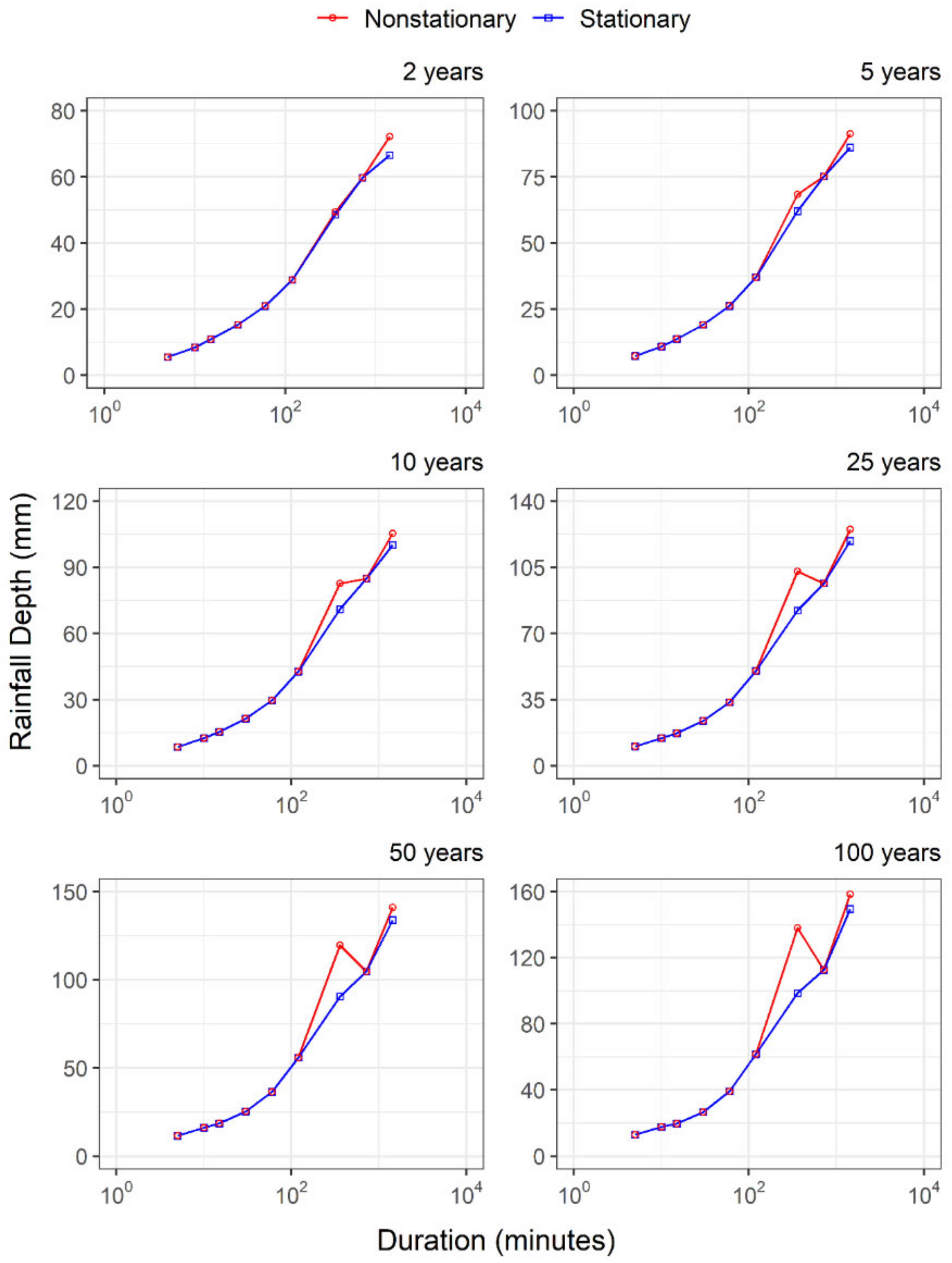
4.2. Historic IDF Relationships
4.3. Performance of the Modified Spatial Downscaling
4.4. Future IDF Curves
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mailhot, A.; Duchesne, S. Design criteria of urban drainage infrastructures under climate change. J. Water Resour. Plan. Manag. 2010, 136, 201–208. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Synthesis Report; Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernamental Panel on Climate Change; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; 151p. [Google Scholar]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berggren, K. Indicators for Urban Drainage System-Assessment of Climate Change Impacts. In Proceedings of the 11th International Conference on Urban Drainage, Munich, Germany, 31 August–5 September 2008. [Google Scholar]
- Agilan, V.; Umamahesh, N.V. Detection and attribution of non-stationarity in intensity and frequency of daily and 4-hr extreme rainfall of Hyderabad, India. J. Hydrol. 2015, 530, 677–697. [Google Scholar] [CrossRef]
- Agilan, V.; Umamahesh, N.V. What are the best covariates for developing non-stationary rainfall Intensity-Duration-Frequency relationship? Adv. Water Resour. 2017, 101, 11–22. [Google Scholar] [CrossRef]
- Willems, P.; Vrac, M. Statistical precipitation downscaling for small-scale hydrological impact investigations of climate change. J. Hydrol. 2011, 402, 193–205. [Google Scholar] [CrossRef]
- Nguyen, V.-T.-V.; Nguyen, T.-D.; Cung, A. A statistical approach to downscaling of sub-daily extreme rainfall processes for climate-related impact studies in urban areas. Water Sci. Technol. 2007, 7, 183–192. [Google Scholar] [CrossRef]
- Hassanzadeh, E.; Nazemi, A.; Elshorbagy, A. Quantile-based downscaling of precipitation using genetic programming: Application to IDF curves in Saskatoon. ASCE J. Hydrol. Eng. 2014, 19, 943–955. [Google Scholar] [CrossRef]
- Mailhot, A.; Beauregard, I.; Talbot, G.; Caya, D.; Biner, S. Future changes in intense precipitation over Canada assessed from multi-model NARCCAP ensemble simulations. Int. J. Climatol. 2012, 32, 1151–1163. [Google Scholar] [CrossRef]
- Srivastav, R.K.; Schardong, A.; Simonovic, S.P. Equidistance Quantile Matching Method for Updating IDF Curves under Climate Change. Water Resour. Manag. 2014, 28, 2539–2562. [Google Scholar] [CrossRef]
- Arnbjerg-Nielsen, K.; Willems, P.; Olsson, J.; Beecham, S.; Pathirana, A.; Gregersen, I.B.; Madsen, H.; Nguyen, V.-T.-V. Impacts of climate change on rainfall extremes and urban drainage system: A review. Water Sci. Technol. 2013, 68, 16–28. [Google Scholar] [CrossRef]
- Smid, M.; Costa, A.C. Climate projections and downscaling techniques: A discussion for impact studies in urban systems. Int. J. Urban Sci. 2018, 22, 277–307. [Google Scholar] [CrossRef] [Green Version]
- Ganguli, P.; Coulibaly, P. Assessment of future changes in intensity-duration-frequency curves for Southern Ontario using North American (NA)-CORDEX models with non-stationary methods. J. Hydrol. Reg. Stud. 2019, 22, 100587. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Navarro, A.; Moreno, R.; Sánchez, J.L.; Gárcia-Ortega, E. Regional climate models: 30 years of dynamical downscaling. Atmos. Res. 2020, 235, 104785. [Google Scholar] [CrossRef]
- Cannon, A.J.; Innocenti, S. Projected intensification of sub-daily and daily rainfall extremes in convection-permitting climate models simulations over North America: Implications for future intensity-duration-frequency curves. Nat. Hazards Earth Syst. Sci. 2019, 19, 421–440. [Google Scholar] [CrossRef] [Green Version]
- Prein, A.F.; Rasmussen, R.; Castro, C.L.; Dai, A.; Minder, J. Special issue: Advances in convection-permitting climate modeling. Clim. Dyn. 2020, 55, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Madsen, H.; Ang, P.H. A comparison of different regional climate models and statistical downscaling methods for extreme rainfall estimation under climate change. Atmos. Res. 2012, 103, 119–128. [Google Scholar] [CrossRef]
- Maraun, D. Bias correcting climate change simulations—A critical review. Curr. Clim. Change Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef] [Green Version]
- Herath, S.M.; Sarukkalige, P.R.; Nguyen, V.-T.-V. A spatial temporal downscaling approach to development of IDF relations for Perth airport region in the context of climate change. Hydrol. Sci. J. 2015, 61, 2061–2070. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, T.-H.; Nguyen, V.-T.-V. Linking climate change to urban storm drainage system design: An innovative approach to modeling of extreme rainfall processes over different spatial and temporal scales. J. Hydroenviron. Res. 2020, 29, 80–95. [Google Scholar] [CrossRef]
- Bi, E.G.; Gachon, P.; Vrac, M.; Monette, F. Which downscaled rainfall data for climate change impact studies in urban areas? Review of current approaches and trends. Theor. Appl. Climatol. 2017, 127, 685–699. [Google Scholar] [CrossRef]
- Schardong, A.; Simonovic, S.P.; Sandink, D. Computerized Tool for the Development of Intensity-Duration-Frequency Curves under a Changing Climate: User’s Manual v.3; Water Resources Research Report no. 104; Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering: London, ON, Canada, 2018; 80p, ISBN 978-0-7714-3108. Available online: https://www.eng.uwo.ca/research/iclr/fids/publications/products/104.pdf (accessed on 8 March 2021).
- Hassazandeh, E.; Nazemi, A.; Adamowski, J.; Nguyen, T.-H.; Van-Nguyen, V.-T. Quantile-based downscaling of rainfall extremes: Notes on methodological functionality, associated uncertainty and application in practice. Adv. Water Resour. 2019, 131, 103371. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationarity precipitation intensity-duration-frequency curves for infrastructure design in a changing climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yilmaz, A.G.; Pereira, B.J.C. Extreme rainfall non-stationarity investigation and intensity-frequency-duration relationship. ASCE J. Hydrol. Eng. 2014, 19, 1160–1172. [Google Scholar] [CrossRef] [Green Version]
- Sugahara, S.; da Rocha, R.P.; Silveira, R. Non-stationary frequency analysis of extreme daily rainfall in Sao Paulo, Brazil. Int. J. Climatol. 2009, 29, 1339–1349. [Google Scholar] [CrossRef]
- Simonovic, S.P.; Schardong, A.; Sandink, D.; Srivastav, R. A web-based tool for the development of Intensity Duration Frequency curves under changing climate. Environ. Model. Softw. 2016, 81, 136–153. [Google Scholar] [CrossRef]
- Sandink, D.; Simonovic, S.P.; Schardong, A.; Srivastav, R. A decision support system for updating and incorporating climate change impacts into rainfall intensity-duration-frequency curves: Review of the stakeholder involvement process. Environ. Model. Softw. 2016, 84, 193–209. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen–Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef] [Green Version]
- Schardong, A.; Simonovic, S.P.; Gaur, A.; Sandink, D. Web-based tool for the development of intensity duration frequency curves under changing climate at gauged and ungauged locations. Water 2020, 12, 1243. [Google Scholar] [CrossRef]
- Maurer, E.P.; Hidalgo, H.G.; Dettinger, M.D.; Cayan, D.R. The utility of daily large-scale climate data in the assessment of climate change impacts on daily streamflow in California. Hydrol. Earth Syst. Sci. 2010, 14, 1125–1138. [Google Scholar] [CrossRef] [Green Version]
- Gudmundsson, L.; Bremnes, J.; Haugen, J.; Engen-Skaugen, T. Technical note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef] [Green Version]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: London, UK, 2001. [Google Scholar]
- Alaya, M.A.B.; Zwiers, F.; Zhang, X. An evaluation of block-maximum based estimation of very long return period precipitation extremes with a large ensemble climate simulation. J. Clim. 2020, 33, 6957–6970. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Change 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y. Non-stationary analysis of the frequency and intensity of heavy precipitation over Canada and their relations to large-scale climate patterns. Clim. Dyn. 2016, 48, 2983–3001. [Google Scholar] [CrossRef]
- Rangulina, G.; Reitan, T. Generalized extreme value shape parameter and its nature for extreme precipitation using long term series and the Bayesian approach. Hydrol. Sci. J. 2017, 62, 863–879. [Google Scholar] [CrossRef]
- Katz, R.W. Statistics of extremes in hidrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef] [Green Version]
- El Adlouni, S.; Ouarda, T.B.M.J.; Zhang, X.; Roy, R.; Bobée, B. Generalized maximum likelihood estimators for the non-stationary generalized extreme value method. Water Resour. Res. 2007, 43, W03410. [Google Scholar] [CrossRef]
- Beguería, S.; Angulo-Martinez, M.; Vincente-Serrano, S.M.; López-Moreno, J.I.; El-Kenawy, A. Assessing trends in extreme precipitation events intensity and magnitude using non-stationary peaks-over-threshold analysis: A case study in northeast Spain from 1930 to 2006. Int. J. Climatol. 2011, 31, 2101–2114. [Google Scholar] [CrossRef] [Green Version]
- Ouarda, T.B.M.J.; Yousef, L.A.; Charron, C. Non-stationary intensity-duration-frequency curves integrating information concerning teleconnections and climate change. Int. J. Climatol. 2018, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Naghettini, M.; Pinto, E.J.A. Hidrologia Estatística; CPRM Serviço Geológico do Brasil: Belo Horizonte, Brasil, 2007.
- Katz, R.W. Statistical methods for non-stationary extremes. In Extremes in a Changing Climate: Detection, Analysis and Uncertainty; AghaKouchak, A., Easterling, D., Schubert, K.H.S., Sorooshian, S., Eds.; Springer: London, UK, 2013; pp. 15–37. [Google Scholar]
- Gilleland, E. Extreme Value Analysis Version 2.0-10. 2019. Available online: http://www.ral.ucar.edu/staff/ericg/extRemes (accessed on 8 March 2021).
- Burnham, K.P.; Anderson, D.R. Multimodel inference: Understanding AIC and BIC in model selection. Sociol. Methods Res. 2004, 33, 261–304. [Google Scholar] [CrossRef]
- Li, J.; Evans, J.; Johnson, F.; Sharma, A. A comparison of methods for estimating climate change impact of design rainfall using high-resolution RCM. J. Hydrol. 2017, 547, 413–427. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes? J. Clim. 2015. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011; Available online: http://www.R-project.org (accessed on 1 April 2021).
- Silva, D.F.; Simonovic, S.P. Development of Non-Stationary Rainfall Intensity Duration Frequency Curves for Future Climate Conditions; Water Resources Research Report no. 106; Facility for Intelligent Decision Support, Department of Civil and Environmental Engineering: London, ON, Canada, 2020; 49p, ISBN 978-0-7714-3138-8. Available online: https://www.eng.uwo.ca/research/iclr/fids/publications/products/106.pdf (accessed on 8 March 2021).
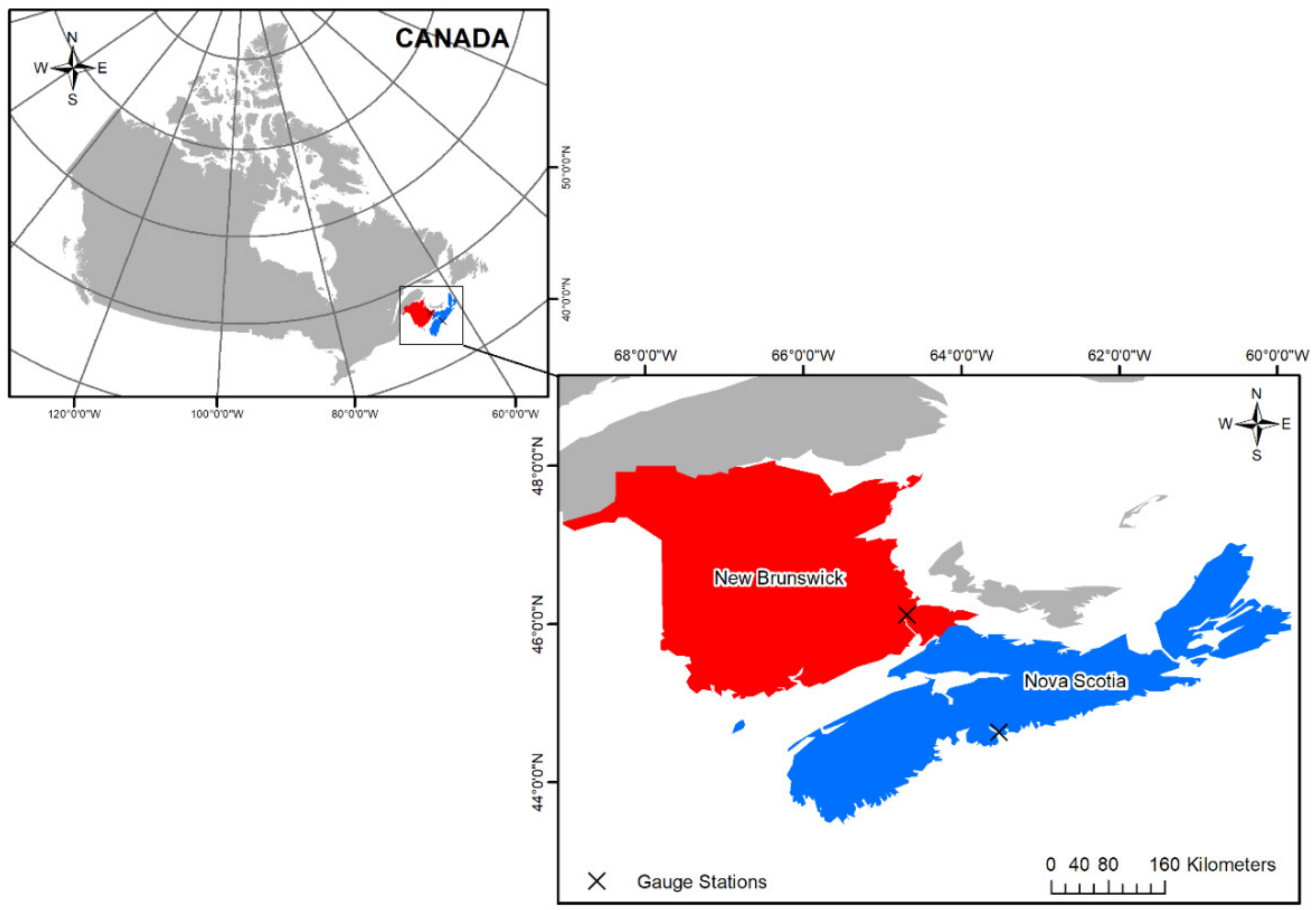
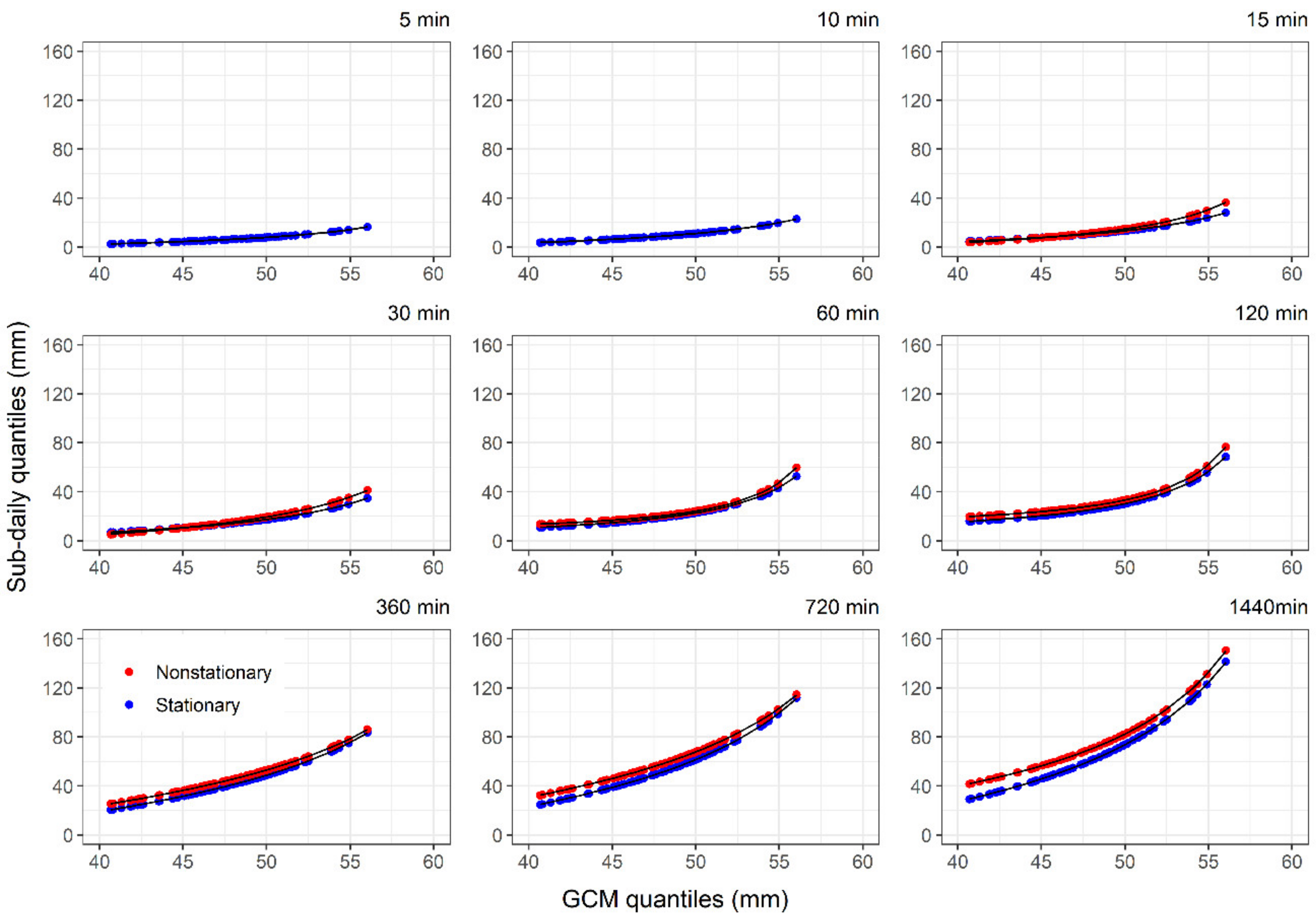
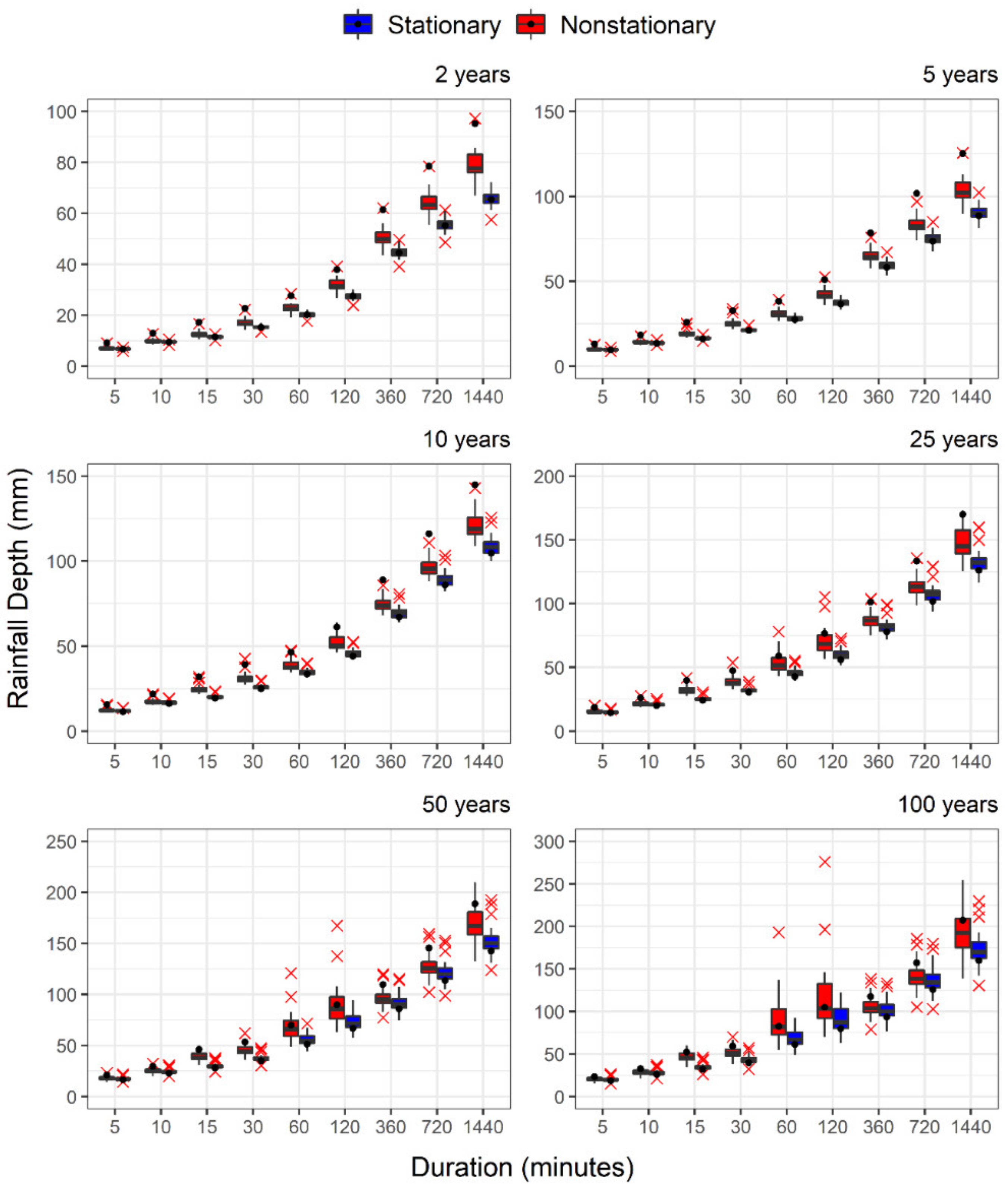
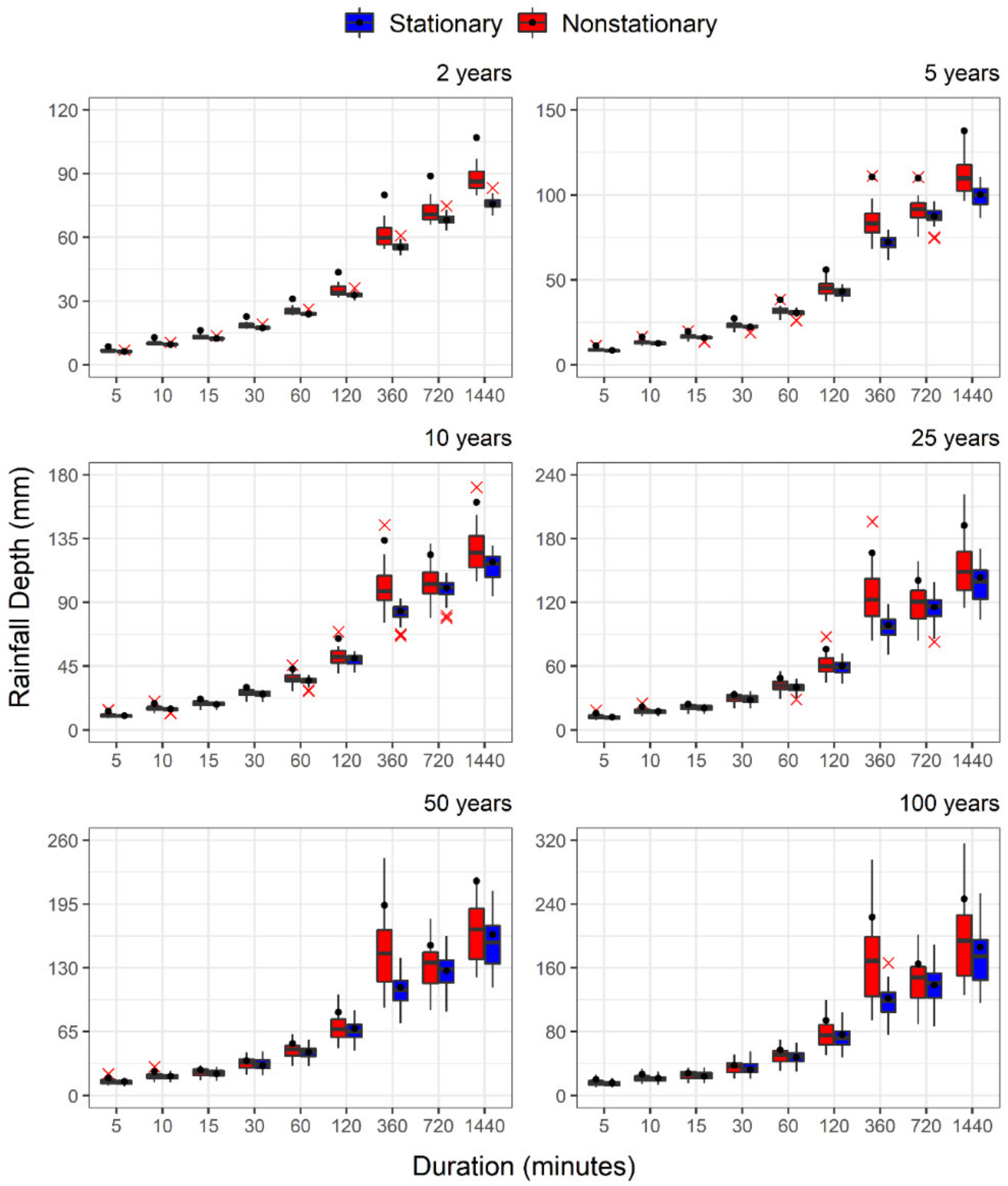

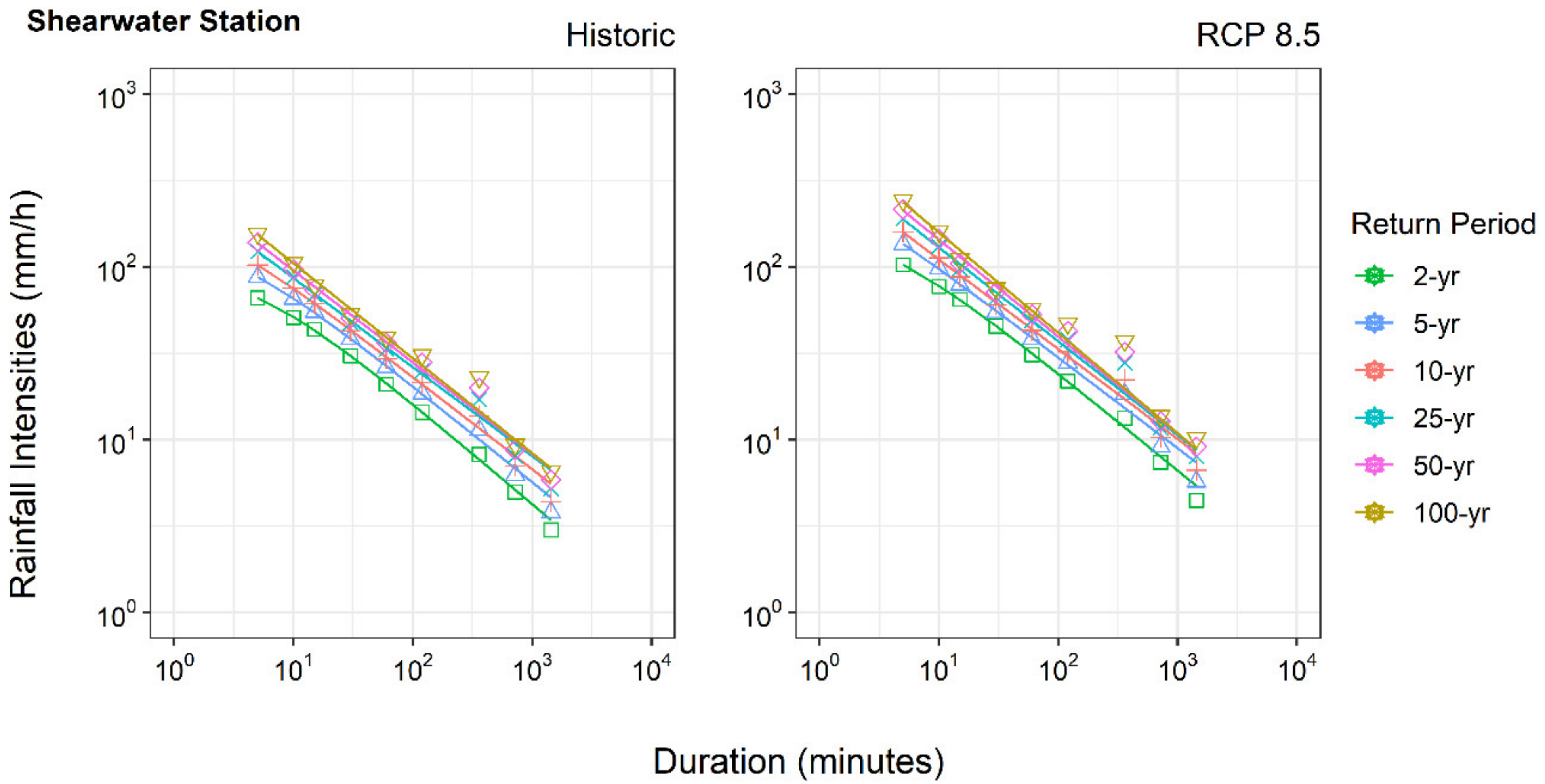
| Study Area | Station Name | Station ID | Latitude x Longitude | Data Availability |
|---|---|---|---|---|
| Moncton | Moncton INTL A | 8103201 | 46°7′ N 64°41′ W | 1946–2016 (67 years) |
| Halifax | Shearwater RCS | 8205092 | 46°7′ N 64°41′ W | 1955–2016 (59 years) |
| Model | Country | Centre Name | Spatial Resolution (Longitude vs. Latitude) |
|---|---|---|---|
| bcc-csm1-1 | China | Beijing Climate Center, China Meteorological Administration | 2.8 × 2.8 |
| bcc-csm1-1-m | China | Beijing Climate Center, China Meteorological Administration | 2.8 × 2.8 |
| BNU-ESM | China | College of Global Change and Earth System Science | 2.8 × 2.8 |
| CanESM2 | Canada | Canadian Centre for Climate Modeling and Analysis | 2.8 × 2.8 |
| CCSM4 | USA | National Center of Atmospheric Research | 1.25 × 0.94 |
| CESM1-CAM5 | USA | National Center of Atmospheric Research | 1.25 × 0.94 |
| CNRM-CM5 | France | Centre National de Recherches Meteorologiques and Centre Europeen de Recherches et de Formation Avancee en Calcul Scientifique | 1.4 × 1.4 |
| CSIRO-Mk3-6-0 | Australia | Australian Commonwealth Scientific and Industrial Research Organization in collaboration with the Queensland Climate Change Centre of Excellence | 1.8 × 1.8 |
| FGOALS-g2 | China | IAP (Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing, China) and THU (Tsinghua University) | 2.55 × 2.48 |
| GFDL-CM3 | USA | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 |
| GFDL-ESM2G | USA | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 |
| HadGEM2-AO | United Kingdom | Met Office Hadley Centre | 1.25 × 1.875 |
| HadGEM2-ES | United Kingdom | Met Office Hadley Centre | 1.25 × 1.875 |
| IPSL-CM5A-LR | France | Institut Pierre Simon Laplace | 3.75 × 1.8 |
| IPSL-CM5A-MR | France | Institut Pierre Simon Laplace | 3.75 × 1.8 |
| MIROC5 | Japan | Japan Agency for Marine-Earth Science and Technology | 1.41 × 1.41 |
| MIROC-ESM | Japan | Japan Agency for Marine-Earth Science and Technology | 2.8 × 2.8 |
| MIROC-ESM-CHEM | Japan | Japan Agency for Marine-Earth Science and Technology | 2.8 × 2.8 |
| MPI-ESM-LR | Germany | Max Planck Institute for Meteorology | 1.88 × 1.87 |
| MPI-ESM-MR | Germany | Max Planck Institute for Meteorology | 1.88 × 1.87 |
| MRI-CGCM3 | Japan | Meteorological Research Institute | 1.1 × 1.1 |
| NorESM1-M | Norway | Norwegian Climate Center | 2.5 × 1.9 |
| NorESM1-ME | Norway | Norwegian Climate Center | 2.5 × 1.9 |
| GFDL-ESM2M | USA | National Oceanic and Atmospheric Administration’s Geophysical Fluid Dynamic Laboratory | 2.5 × 2.0 |
| GEV Model | |
|---|---|
| ID | Specification |
| I | F ( |
| II | F ( |
| III | F ( |
| IV | F (; |
| V | F ( |
| VI | F ( |
| VII | F ( |
| VIII | F ( |
| IX | F ( |
| Duration (Minutes) | Best GEV-Type | Stationary GEV Model | Best GEV Model (95th Percentile) | LR-Test (p-Value) | ||||
|---|---|---|---|---|---|---|---|---|
| Location | Scale | Shape | Location | Scale | Shape | |||
| 5 | I | 5.18 | 2.10 | 0.07 | 5.18 | 2.10 | 0.07 | - |
| 10 | I | 7.32 | 2.92 | 0.07 | 7.32 | 2.92 | 0.07 | - |
| 15 | VI | 8.92 | 3.35 | 0.09 | 9.01 | 4.27 | 0.14 | 0.043 |
| 30 | V | 12.03 | 4.12 | 0.08 | 12.33 | 5.51 | 0.06 | 0.030 |
| 60 | II | 16.22 | 4.60 | 0.22 | 18.06 | 4.10 | 0.31 | 0.011 |
| 120 | VII | 22.22 | 5.63 | 0.23 | 25.46 | 5.19 | 0.30 | 0.047 |
| 360 | II | 35.30 | 11.07 | −0.02 | 39.97 | 10.78 | −0.03 | 0.041 |
| 720 | II | 43.59 | 14.35 | 0.02 | 50.68 | 13.86 | 0.004 | 0.016 |
| 1440 | II | 51.44 | 17.45 | 0.05 | 61.62 | 15.95 | 0.08 | 0.002 |
| Duration (Minutes) | Best GEV-Type | Stationary GEV Model | Best GEV Model (95th Percentile) | LR Test (p-Value) | ||||
|---|---|---|---|---|---|---|---|---|
| Location | Scale | Shape | Location | Scale | Shape | |||
| 5 | I | 4.98 | 1.46 | 0.07 | 4.98 | 1.46 | 0.07 | - |
| 10 | I | 7.67 | 2.16 | 0.001 | 7.67 | 2.16 | 0.001 | - |
| 15 | I | 9.88 | 2.80 | −0.13 | 9.88 | 2.80 | −0.13 | - |
| 30 | I | 13.88 | 3.95 | −0.16 | 13.88 | 3.95 | −0.16 | - |
| 60 | I | 19.17 | 4.94 | −0.06 | 19.17 | 4.94 | −0.06 | - |
| 120 | I | 26.30 | 6.95 | 0.04 | 26.30 | 6.95 | 0.04 | - |
| 360 | V | 44.24 | 11.94 | −0.004 | 43.93 | 14.67 | 0.14 | 0.044 |
| 720 | I | 54.57 | 14.34 | −0.06 | 54.57 | 14.34 | −0.06 | - |
| 1440 | II | 60.59 | 16.05 | 0.08 | 66.61 | 15.05 | 0.12 | 0.030 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feitoza Silva, D.; Simonovic, S.P.; Schardong, A.; Avruch Goldenfum, J. Introducing Non-Stationarity Into the Development of Intensity-Duration-Frequency Curves under a Changing Climate. Water 2021, 13, 1008. https://doi.org/10.3390/w13081008
Feitoza Silva D, Simonovic SP, Schardong A, Avruch Goldenfum J. Introducing Non-Stationarity Into the Development of Intensity-Duration-Frequency Curves under a Changing Climate. Water. 2021; 13(8):1008. https://doi.org/10.3390/w13081008
Chicago/Turabian StyleFeitoza Silva, Daniele, Slobodan P. Simonovic, Andre Schardong, and Joel Avruch Goldenfum. 2021. "Introducing Non-Stationarity Into the Development of Intensity-Duration-Frequency Curves under a Changing Climate" Water 13, no. 8: 1008. https://doi.org/10.3390/w13081008







