Characterizing Groundwater Interaction with Lakes and Wetlands Using GIS Modeling and Natural Water Quality Measurements
Abstract
:1. Introduction
1.1. Background and Previous Work
1.2. Study Site
2. Methods
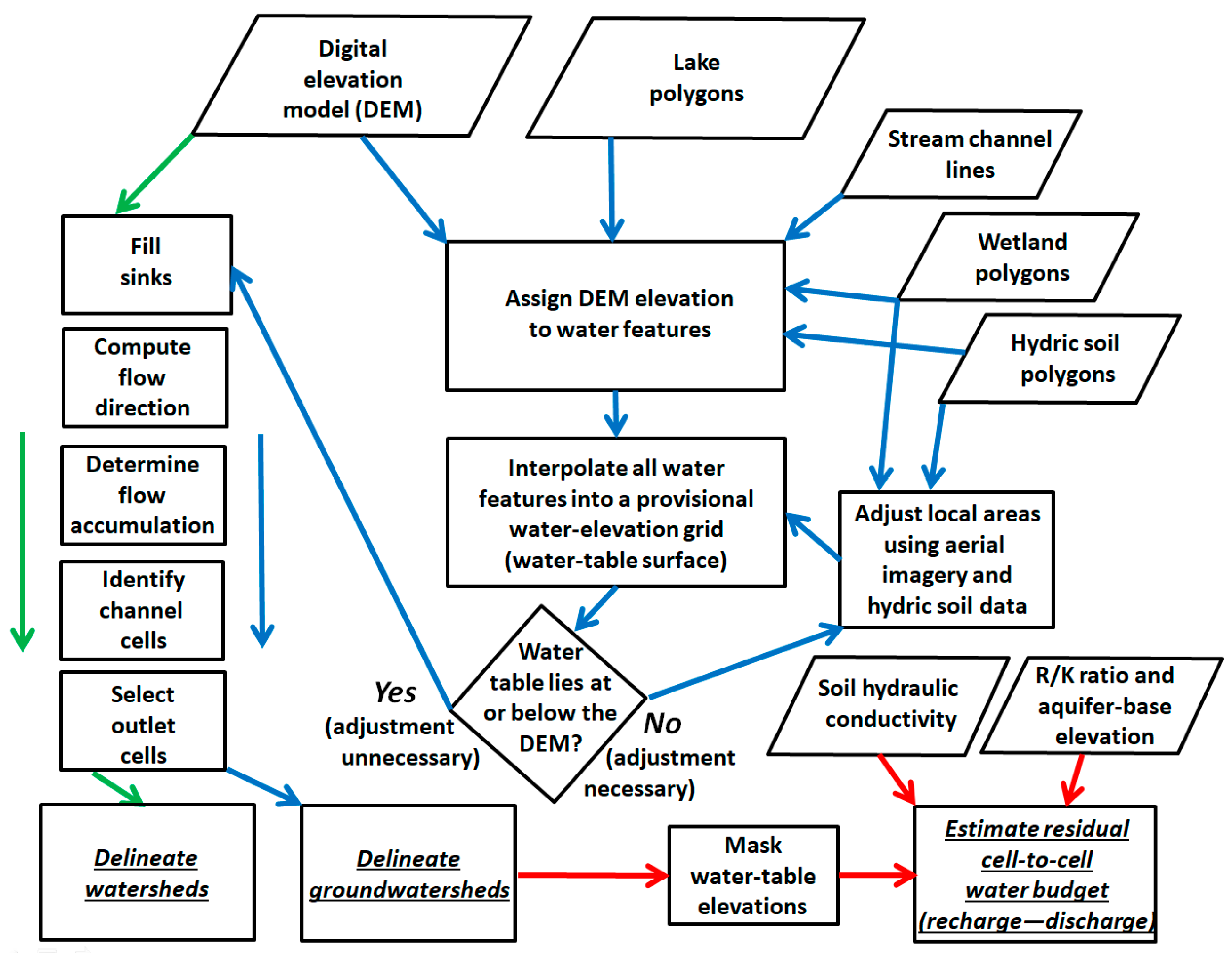
2.1. Approach and Data
- (1)
- Generate a local and regional water-table surface from a DEM and associated lake, stream, wetland, and hydric soil elevation data.
- (2)
- Use the water-table surface to delineate groundwatersheds for lakes and wetlands (blue arrows), which are then compared to topographic (surface) watersheds (green arrows) to determine the relative importance of groundwater and surface water for selected lakes.
- (3)
- Based on the water-table surface, flow accumulation is computed. Groundwater flow paths are derived from this step and coupled with the location of lakes and wetlands.
- (4)
- Recharge–discharge across the landscape is mapped by combining data from the water-table surface, saturated soil hydraulic conductivity, and an analytical technique to estimate the maximum depth of groundwater–surface water interaction.
2.2. Interpolation of the Water-Table Surface
- The polygon was listed as a hydric soil and was described as frequently ponded, which is a closed depression that contains water and has more than a 50% chance of occurring in any given year under normal weather conditions [41];
- The soils represented by the polygon covered small parts of the raster where additional water-table elevation control was necessary, including areas where the water-table surface lay above the DEM.
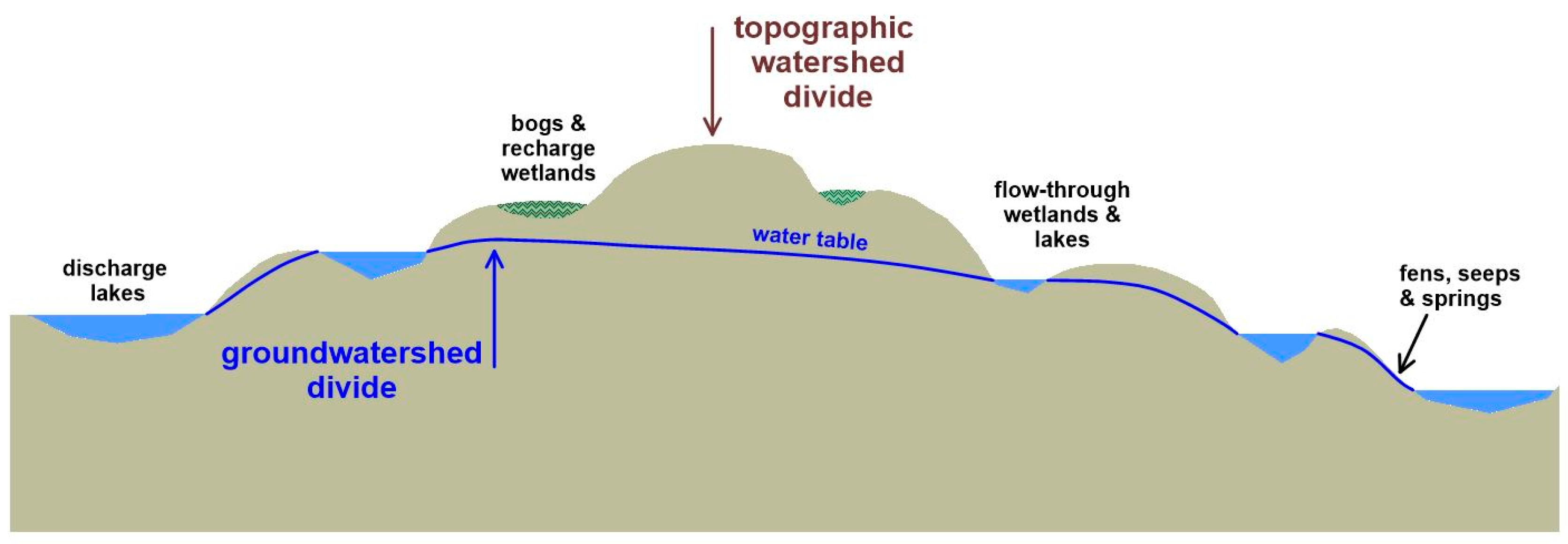
2.3. Groundwater Flow Pathlines and Groundwatersheds
2.4. Mapping Recharge–Discharge
2.5. Field Methods
- The probe was rinsed with deionized water before and after each measurement;
- Algae, floating vegetation, and disturbance of bottom sediments were avoided when taking measurements;
- For each measurement of pH and specific conductance, the probe was placed approximately 10 cm below the water surface and swirled gently until the values stabilized, approximately 60 s;
- At least one measurement was taken near the center of the waterbody and additional measurements were taken in each quadrant, at each site coordinates were recorded for each location with a Garmin eTrex 30x GPS receiver (Olathe, KS, USA).
3. Results
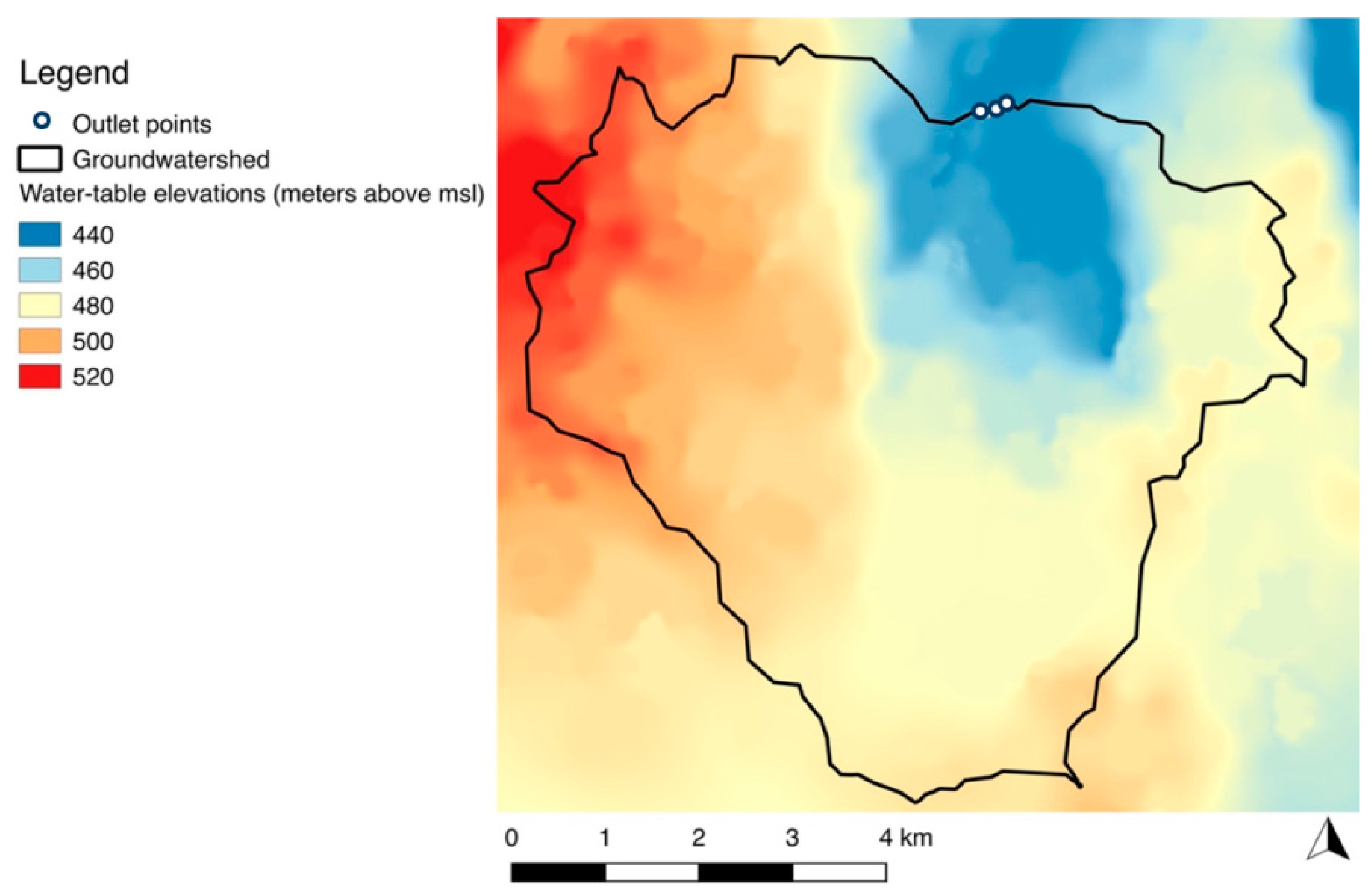
3.1. Water-Table Surface
3.2. Groundwater Flow Paths
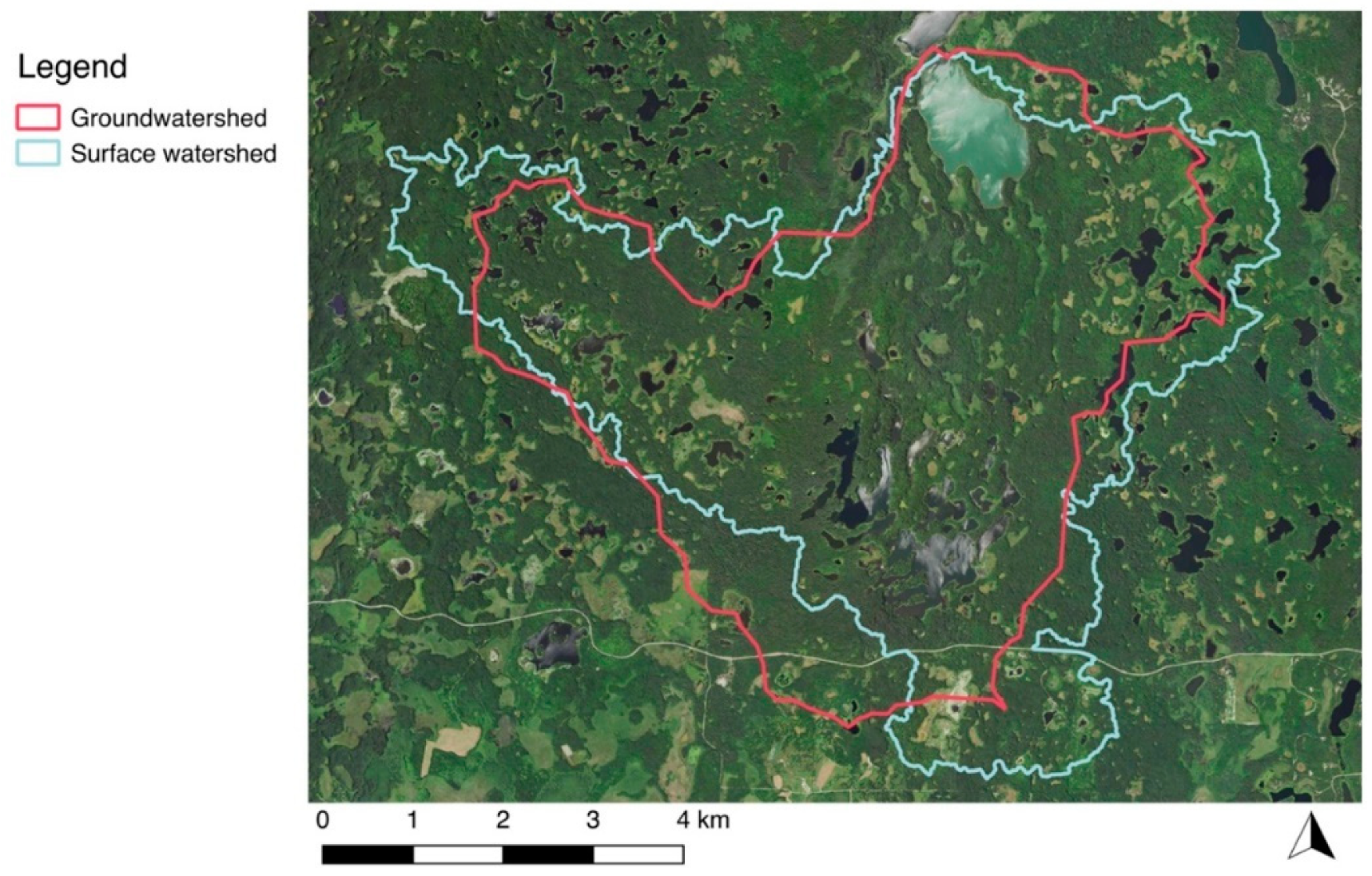
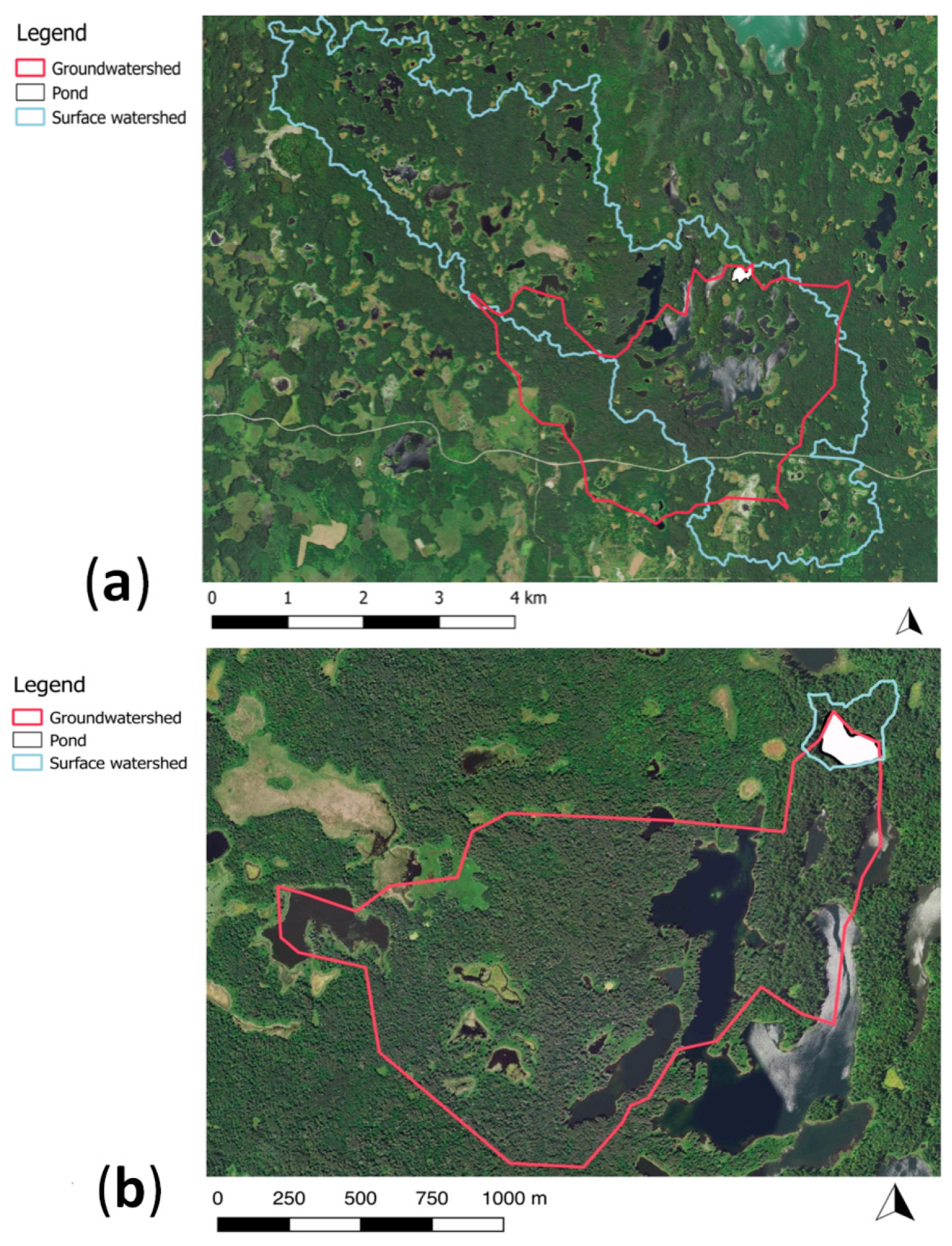
3.3. Watersheds
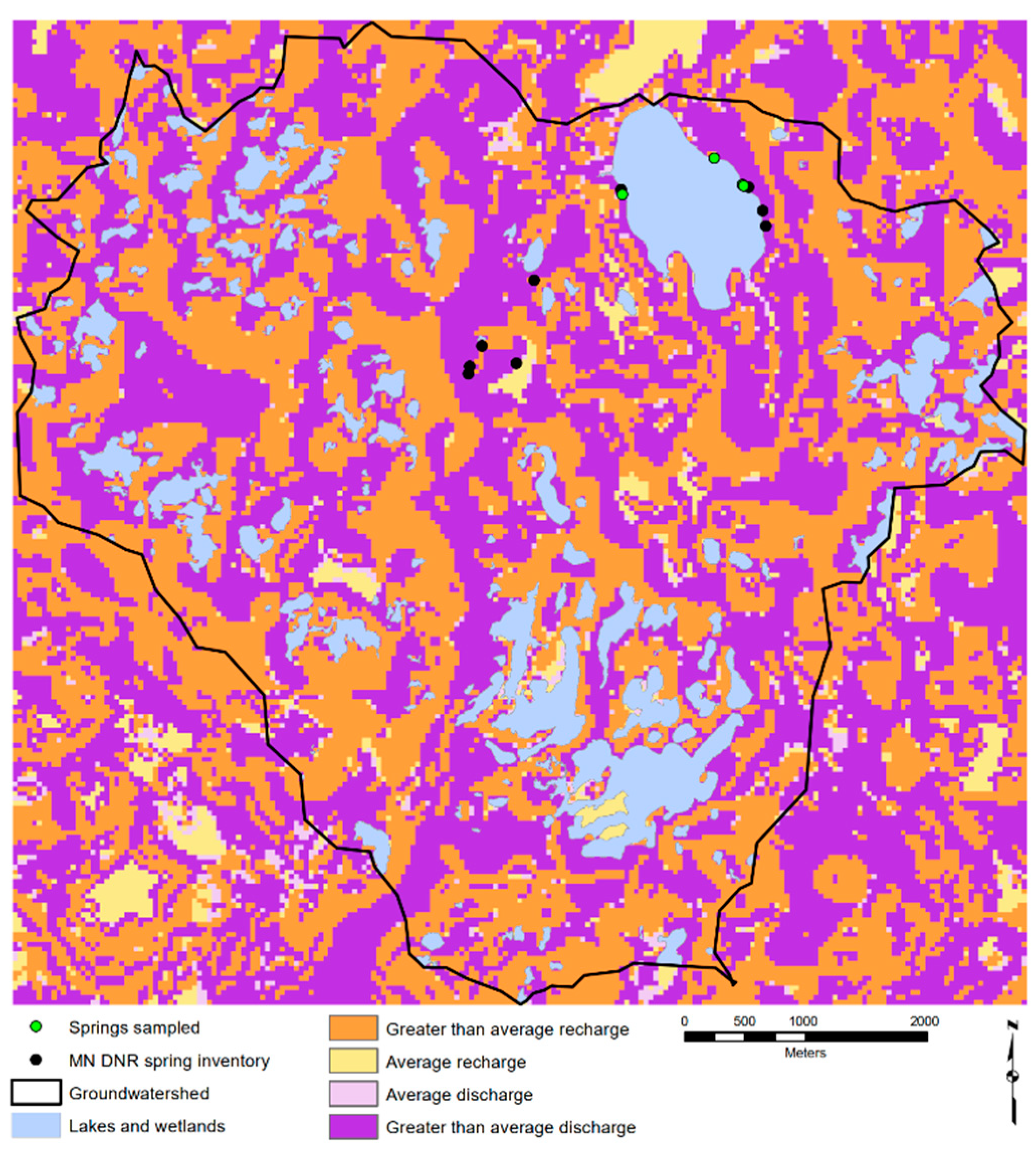
3.4. Spatial Distribution of Recharge and Discharge
4. Discussion
4.1. Water-Table Surface
4.2. Groundwater Flow Paths and Field Measurements
4.3. Watersheds and Field Measurements
4.4. Recharge–Discharge Map
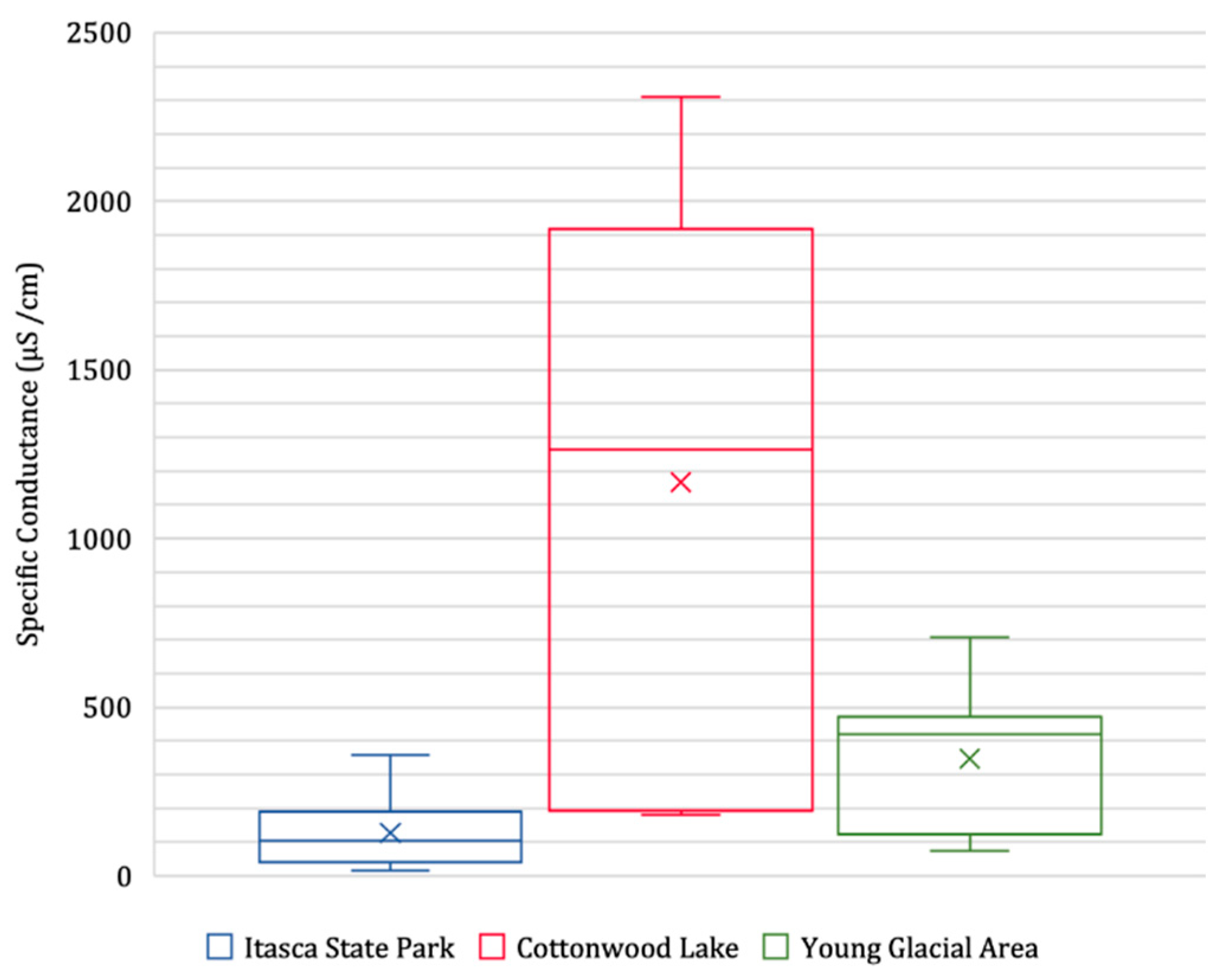
4.5. Specific Conductance, Flow Paths, and Mapped Glacial Sediments
4.6. Specific Conductance Variability Compared to the Missouri Coteau and Young Glacial Area
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
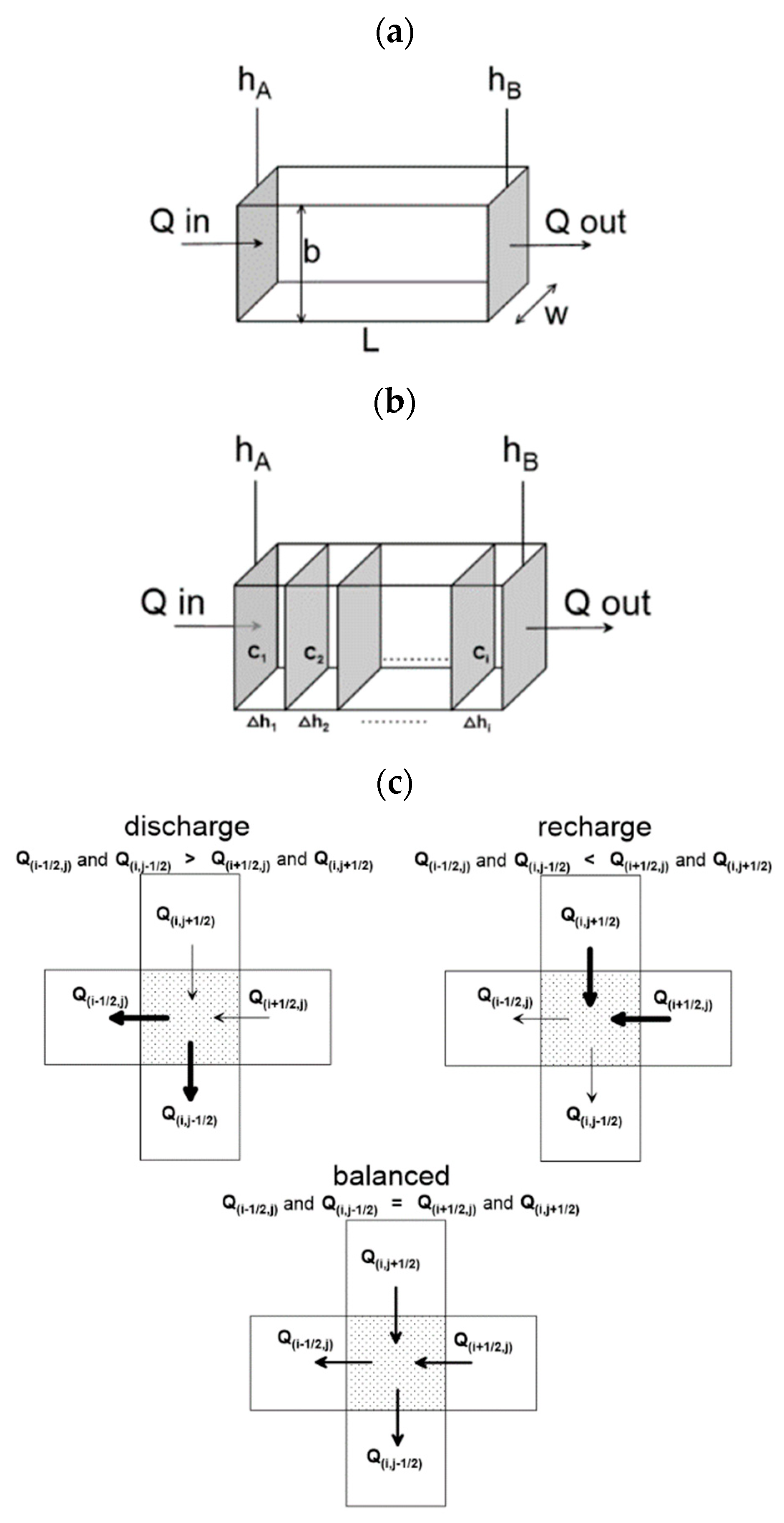
Appendix A. Application of a Water Table–Land-Surface Interaction Model to Estimate the Recharge Rate and Hydraulic Conductivity
- Introduction and Background
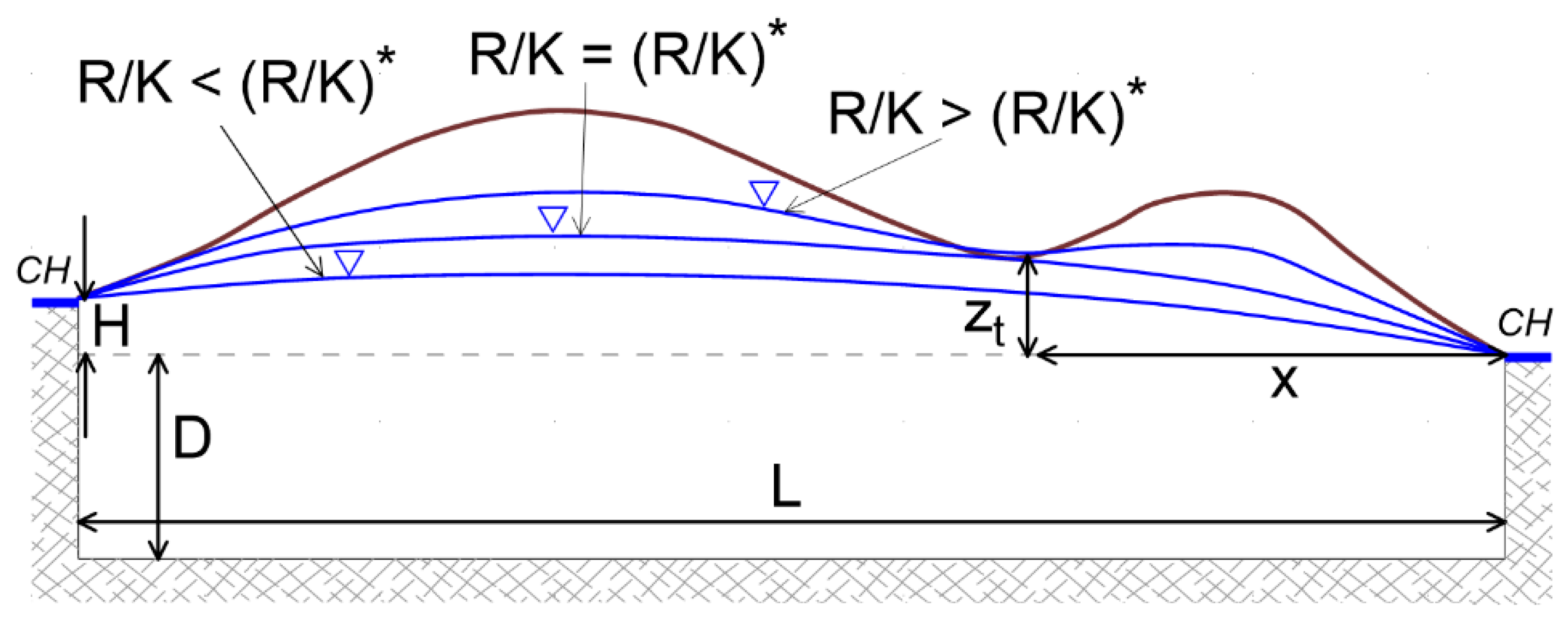
- B.
- Theory and Methods
| Variable | Units | Definition |
|---|---|---|
| R | L/T | recharge |
| K | LT | hydraulic conductivity |
| De | L | equivalent depth accounting for vertical resistance to flow below drain level |
| zt | L | topographic elevation |
| H | L | elevation difference between two drains |
| x | L | horizontal distance between reference drain and water-table outcrop |
| L | L | horizontal distance between two drains |
| D | L | depth to horizontal impervious base below reference drain |
| r0 | L | radius of circular drains |
| F(u) | – | function of u (in this case u is assumed to be <0.5 and the Dagan approximation is used) |
| u | – | function of L and D |
| Profile | Feature | X-Coordinate | Y-Coordinate |
|---|---|---|---|
| 1 start | Elk Lake | 332,160 | 5,227,785 |
| 1 end | Basswood Creek | 327,628 | 5,219,859 |
| 2 start | Lake Itasca | 335,416 | 5,228,917 |
| 2 end | Basswood Creek | 329,433 | 5,218,795 |
| 3 start | Lake Itasca | 331,321 | 5,229,574 |
| 3 end | Basswood Creek | 325,783 | 5,221,396 |
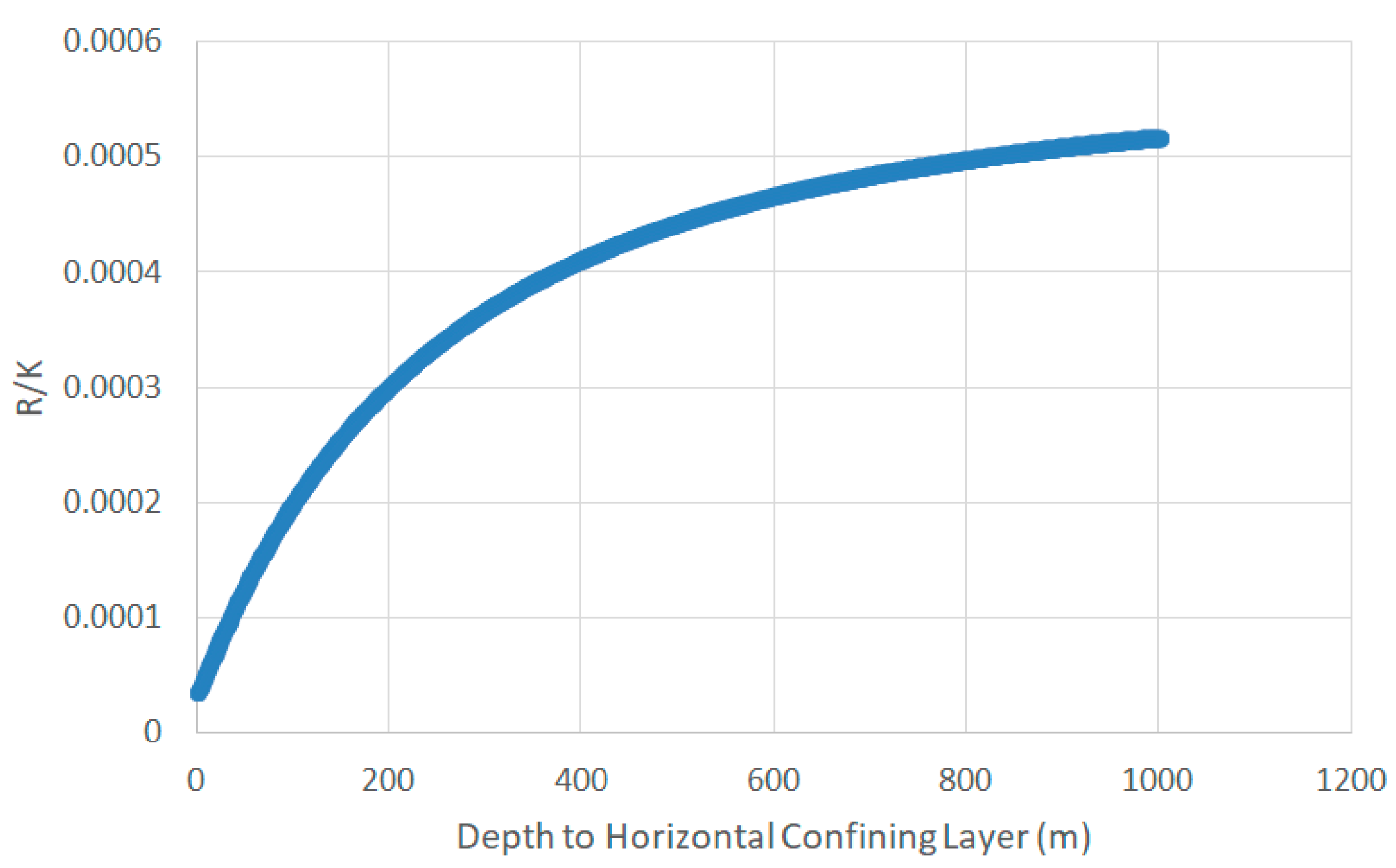
- C.
- Results and Discussion
| Profile | Average K (m/day) | R (m/day) | Expected R/K |
|---|---|---|---|
| 1 | 9.6 | 4 × 10−4 | 4.3 × 10−5 |
| 2 | 2.3 | 4 × 10−4 | 1.8 × 10−4 |
| 3 | 3.2 | 4 × 10−4 | 1.3 × 10−4 |
| Profile | Average K (m/day) | R (m/day) | Expected R/K |
|---|---|---|---|
| 1 | 9.6 | 4 × 10−4 | 4.3 × 10−5 |
| 2 | 2.3 | 4 × 10−4 | 1.8 × 10−4 |
| 3 | 3.2 | 4 × 10−4 | 1.3 × 10−4 |
References
- Mitsch, W.J.; Gosselink, J.G. Wetlands, 4th ed.; Wiley: Hoboken, NJ, USA, 2007; ISBN 978-0471699675. [Google Scholar]
- Winter, T.C. Relation of streams, lakes, and wetlands to groundwater flow systems. Hydrogeol. J. 1999, 7, 28–45. [Google Scholar] [CrossRef]
- Winter, T.C.; Harvey, J.W.; Franke, O.L.; Alley, W.M. Ground Water and Surface Water-A Single Resource, Circular 1139; U.S. Government Printing Office: Washington, DC, USA, 1998.
- Haitjema, H.M. On the residence time distribution in idealized groundwatersheds. J. Hydrol. 1995, 172, 127–146. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O.; Labaugh, J.W. Where does the ground water in small watersheds come from? GroundWater 2003, 41, 989–1000. [Google Scholar] [CrossRef]
- Woodward, S.J.R.; Wöhling, T.; Stenger, R. Uncertainty in the modelling of spatial and temporal patterns of shallow groundwater flow paths: The role of geological and hydrological site information. J. Hydrol. 2016, 534, 680–694. [Google Scholar] [CrossRef]
- Gerla, P.J. Estimating the ground-water contribution in wetlands using modeling and digital terrain analysis. Wetlands 1999, 19, 394–402. [Google Scholar] [CrossRef]
- Zhang, W.; Montgomery, D.R. Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Huang, G.H. A study on DEM-derived primary topographic attributes for hydrologic applications: Sensitivity to elevation data resolution. Appl. Geogr. 2008, 28, 210–223. [Google Scholar] [CrossRef]
- Habtezion, N.; Tahmasebi Nasab, M.; Chu, X. How does DEM resolution affect microtopographic characteristics, hydrologic connectivity, and modelling of hydrologic processes? Hydrol. Process. 2016, 30, 4870–4892. [Google Scholar] [CrossRef]
- Sørensen, R.; Seibert, J. Effects of DEM resolution on the calculation of topographical indices: TWI and its components. J. Hydrol. 2007, 347, 79–89. [Google Scholar] [CrossRef]
- Winter, T.C.; Carr, M.R. Hydrologic Setting of Wetlands in the Cottonwood Lake Area, Stutsman County, North Dakota, Water Resources Investigations 80–99; U.S. Government Printing Office: Washington, DC, USA, 1980.
- Jaworska-Szulc, B. Role of the lakes in groundwater recharge and discharge in the Young Glacial Area, northern Poland. Groundwater 2016, 54, 603–611. [Google Scholar] [CrossRef]
- Gerla, P.J. Can pH and electrical conductivity monitoring reveal spatial and temporal patterns in wetland geochemical processes? Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 699–728. [Google Scholar]
- Black, P.E. Watershed Hydrology, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1996; ISBN 978-1575040271. [Google Scholar]
- Seelig, B.; DeKeyser, S. Water Quality and Wetland Function in the Northern Prairie Pothole Region, Circular WQ-1313; North Dakota State University: Fargo, ND, USA, 2006. [Google Scholar]
- Schwintzer, C.R.; Tomberlin, T.J. Chemical and physical characteristics of shallow ground waters in northern Michigan bogs, swamps, and fens. Am. J. Bot. 1982, 69, 1231–1239. [Google Scholar] [CrossRef]
- Heinselman, M.L. Landscape Evolution, Peatland Types, and the Environment in the Lake Agassiz Peatlands Natural Area, Minnesota. Ecol. Monogr. 1970, 40, 235–261. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology, 4th ed.; Pearson: Upper Saddle River, NJ, USA, 2000; ISBN 978-0130882394. [Google Scholar]
- Drever, J.I. The Geochemistry of Natural Waters, 2nd ed.; Prentice Hall: North Saddle River, NJ, USA, 1997; ISBN 978-0132727907. [Google Scholar]
- Glaser, P.H. Vegetation and Water Chemistry. In Patterned Peatlands of Minnesota; Wright, H.E., Coffin, B.A., Aaseng, N.E., Eds.; University of Minnesota Press: Saint Paul, MN, USA, 1992; pp. 15–26. ISBN 978-0-8166-1917-7. [Google Scholar]
- Tucker, C.S.; D’Abramo, L.R. Managing High pH in Freshwater Ponds, Publication 4604; Southern Regional Aquaculture Center: College Station, TX, USA, 2008. [Google Scholar]
- Clymo, R.S. Ion exchange in Sphagnum and its relation to bog ecology. Ann. Bot. 1963, 27, 309–324. [Google Scholar] [CrossRef]
- Clymo, R.S.; Hayward, P.M. The ecology of Sphagnum. In Bryophyte Ecology; Smith, A.J.E., Ed.; Chapman and Hall: New York, NY, USA, 1982; pp. 229–290. ISBN 978-94-009-5893-7. [Google Scholar]
- Gorham, E.; Eisenreich, S.J.; Ford, J.; Santlemann, M.V. The chemistry of bog water. In Chemical Processes of Lakes; Stumm, W., Ed.; John Wiley and Sons: New York, NY, USA, 1985; pp. 339–362. ISBN 978-0471882619. [Google Scholar]
- Beaty, J.E.; Kroeker, T.S.; Nance, D.P.; Sayini, S. Water Resource Availability in the Maumee River Basin, Indiana; Indiana Department of Natural Resources: Indianapolis, Indiana, 1996.
- Logan, T.J. Water quality. In Environmental Hydrology; Ward, A.D., Elliot, W.J., Eds.; Lewis Publishers: Boca Raton, FL, USA, 1995; pp. 311–334. ISBN 978-0873718868. [Google Scholar]
- Wolock, D.M.; Fan, J.; Lawrence, G.B. Effects of basin size on low-flow stream chemistry and subsurface contact time in the neversink river watershed, New York. Hydrol. Process. 1997, 11, 1273–1286. [Google Scholar] [CrossRef]
- Minnesota Department of Natural Resources Itasca State Park. Available online: https://www.dnr.state.mn.us/state_parks/park.html?id=spk00181#information (accessed on 2 August 2019).
- Wright, H.E., Jr. History of the Landscape in the Itasca Region; Geological Society of America: Boulder, CO, USA, 1993. [Google Scholar]
- Carney, L.M.; Mooers, H.D. Landform assemblages and glacial history of a portion of the Itasca moraine, north-central Minnesota. In Contributions to Quaternary Studies in Minnesota Report of Investigations 49; Patterson, C.J., Wright, H.E.J., Eds.; Minnesota Geological Survey: Minneapolis, MN, USA, 1998; pp. 85–96. ISSN 0076-9177. [Google Scholar]
- Megard, R.O.; Bradbury, J.P.; Dean, W.E. Climatic and Limnologic Setting of Elk Lake; Geological Society of America: Boulder, CO, USA, 1993. [Google Scholar]
- Hobbs, H.C.; Goebel, J.E. S-01 Geologic Map of Minnesota, Quaternary Geology. Available online: http://hdl.handle.net/11299/60085 (accessed on 1 August 2019).
- Minnesota Geospatial Information Office MnTOPO Viewer. Available online: http://arcgis.dnr.state.mn.us/maps/mntopo/ (accessed on 2 August 2019).
- Minnesota Department of Natural Resources Wetland Inventory Update. Available online: https://www.dnr.state.mn.us/eco/wetlands/nwi_proj.html (accessed on 2 August 2019).
- Minnesota Geospatial Information Office 2017 NAIP Aerial Imagery Metadata, Web Mapping Service. Available online: ftp://ftp.gisdata.mn.gov/pub/gdrs/data/pub/us_mn_state_mngeo/base_naip_2017_airphotos/metadata/metadata.html (accessed on 2 August 2019).
- U.S. Geological Survey National Hydrography Dataset. Available online: https://www.usgs.gov/core-science-systems/ngp/tnm-delivery/ (accessed on 12 August 2019).
- Natural Resources Conservation Service Web Soil Survey (SSURGO). Available online: https://websoilsurvey.nrcs.usda.gov/ (accessed on 12 August 2019).
- Wieczorek, M.E. Area-and Depth-Weighted Averages of Selected SSURGO Variables for the Conterminous United States and District of Columbia; Data Series 866; U.S. Government Printing Office: Washington, DC, USA, 2014.
- Cowardin, L.M.; Carter, V.; Golet, F.C.; LaRoe, E.T. Classification of Wetlands and Deepwater Habitats of the United States; U.S. Government Printing Office: Washington, DC, USA, 1979.
- Natural Resources Conservation Service Hydric Soils. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/main/soils/use/hydric/ (accessed on 12 August 2019).
- Hutchinson, M.F. ANUDEM Version 5.3 User Guide; The Australian National University: Canberra, AU, Australia, 2011; p. 26. [Google Scholar]
- Adams, R. Methods for Estimating Water-Table Elevation and Depth to Water Table GW-04; Minnesota Department of Natural Resources: Saint Paul, MN, USA, 2016. [Google Scholar]
- Hutchinson, M.F. Calculation of hydrologically sound digital elevation models. In Proceedings of the Third International Symposium on Spatial Data Handling; International Geographical Union, Commission on Geographical Data Sensing and Processing, Sydney, Australia, 14–17 August 1988; Dept. of Geography, Ohio State University: Columbus, OH, USA, 1988; p. 421. [Google Scholar]
- Young, D.M. Iterative Solution of Large Linear Systems; Academic Press: Cambridge, MA, USA, 1971; ISBN 978-0127730509. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2013; ISBN 978-1421407944. [Google Scholar]
- Tarboton, D.G.; Bras, R.L.; Rodriguez-Iturbe, I. On the extraction of channel networks from digital elevation data. Hydrol. Process. 1991, 5, 81–100. [Google Scholar] [CrossRef]
- Jenson, S.K.; Domingue, J.O. Extracting topographic structure from digital elevation data for geographic information system analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Helsel, D.R.; Hirsch, R.M. Statistical methods in water resources. In Techniques of Water-Resource Investigations Book 4: Hydrologic Analysis and Interpretation; U.S. Geological Survey: Washington, DC, USA, 2002. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, The U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process. U.S. Geol. Surv. Tech. Methods 2005, 16, 55. [Google Scholar]
- Dupuit, J. Mouvement de l’eau a travers le terrains permeables. Seances Acad. Sci. 1857, 45, 92–96. [Google Scholar]
- Bresciani, E.; Goderniaux, P.; Batelaan, O. Hydrogeological controls of water table-land surface interactions. Geophys. Res. Lett. 2016, 43, 9653–9661. [Google Scholar] [CrossRef]
- Hooghoudt, S.B. General Consideration of the Problem of Detailed Dewatering and Infiltration through Parallel Running Drains, Trenches, Ditches, and Canals. No. 7 in the Series: Contributions to the Knowledge of Some Physical Quantities of the Ground Series, #7; Algemeene Landsdrukkerij: The Hague, The Netherlands, 1940. [Google Scholar]
- Smith, E.A.; Westenbroek, S.M. Potential Groundwater Recharge for the State of Minnesota Using the Soil-Water Balance Model 1996–2010, Scientific Investigations Report 2015-5038; U.S. Government Printing Office: Washington, DC, USA, 2015.
- Minnesota Pollution Control Agency. Water Chemistry Assessment Protocol for Wetland Monitoring Sites; Minnesota Pollution Control Agency: Saint Paul, MN, USA, 2015. [Google Scholar]
- HANNA Instruments HI 9813-5; HI 9813-6 Portable pH/EC/TDS/°C Meters Manual. Available online: https://hannainst.com/downloads/dl/file/id/1159/man9813_22_09_10.pdf (accessed on 1 August 2019).
- Minnesota Department of Natural Resources Minnesota Spring Inventory. Available online: https://www.dnr.state.mn.us/waters/groundwater_section/springs/msi.html (accessed on 2 August 2019).
- Freeze, A.; Cherry, J.A. Groundwater; Prentice Hall: Upper Saddle River, NJ, USA, 1979; ISBN 978-0133653120. [Google Scholar]
- Novotny, E.; Murphy, D.; Stefan, H. Road Salt Effects on the Water Quality of Lakes in the Twin Cities Metropolitan Area, Project Report No. 505; St. Anthony Falls Laboratory: Minneapolis, MN, USA, 2007. [Google Scholar]
- Cormier, S.M.; Wilkes, S.P.; Zheng, L. Relationship of land use and elevated ionic strength in Appalachian watersheds. Environ. Toxicol. Chem. 2013, 32, 296–303. [Google Scholar] [CrossRef] [Green Version]
- Minnesota Department of Natural Resources Surface-Water Watersheds vs. Ground-Water Watersheds. Available online: https://www.dnr.state.mn.us/watersheds/surface_ground.html (accessed on 2 August 2019).
- Mięsiak-Wójcik, K.; Turczyński, M.; Sposób, J. Diverse sediment permeability and implications for groundwater exchange in closed lake-wetland catchments (West Polesie, east Poland). Wetlands 2018, 38, 779–792. [Google Scholar] [CrossRef] [Green Version]
- Rosenberry, D.O. Unsaturated-zone wedge beneath a large, natural lake from Little Sand Water seeps out of the than Belle Taine. Seepage-meter data indicate water is seeping out of Belle Upper Bottle. Water Resour. Res. 2000, 36, 3401–3409. [Google Scholar] [CrossRef] [Green Version]
- Cravens, S.J.; Ruedisili, L.C. Water Movement in Till of East-Central South Dakota. Groundwater 1987, 25, 555–561. [Google Scholar] [CrossRef]
- van der Kamp, G.; Hayashi, M. Groundwater-wetland ecosystem interaction in the semiarid glaciated plains of North America. Hydrogeol. J. 2009, 17, 203–214. [Google Scholar] [CrossRef]
- LaBaugh, J.W.; Mushet, D.M.; Rosenberry, D.O.; Euliss, N.H.; Goldhaber, M.B.; Mills, C.T.; Nelson, R.D. Changes in pond water levels and surface extent due to climate variability alter solute sources to closed-basin prairie-pothole wetland ponds, 1979 to 2012. Wetlands 2016, 36, 343–355. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O. Hydrology of prairie pothole wetlands during drought and deluge: A 17-year study of the Cottonwood Lake wetland complex in North Dakota in the perspective of longer term measured and proxy hydrological records. Clim. Chang. 1998, 40, 189–209. [Google Scholar] [CrossRef]
- Winter, T.C.; Rosenberry, D.O.; Buso, D.C.; Merk, D.A. Water source to four U.S. wetlands: Implications for wetland management. Wetlands 2001, 21, 462–473. [Google Scholar] [CrossRef]
- Shjeflo, J.B. Evapotranspiration and the Water Budget of Prairie Potholes in North Dakota, Professional Paper 585-B; U.S. Government Printing Office: Washington, DC, USA, 1968.
- Sloan, C.E. Ground-Water Hydrology of Prairie Potholes in North Dakota, Professional Paper 585-C; U.S. Government Printing Office: Washington, DC, USA, 1972.
- Eisenlohr, W.S.J. Hydrologic Investigations of Prairie Potholes in North Dakota, 1959–1968; U.S. Government Printing Office: Washington, DC, USA, 1972.
- Hem, J.D. Study and Interpretation of the Chemical Characteristics of Natural Water, 3rd ed.; Water-Supply Paper 2254; U.S Government Printing Office: Washington, DC, USA, 1985.
- Vaughan, S. Groundwater Report: Mississippi River-Headwaters Watershed; Minnesota Pollution Control Agency: St. Paul, MN, USA, 2017. [Google Scholar]
- Leibowitz, S.G.; Vining, K.C. Temporal connectivity in a prairie pothole complex. Wetlands 2003, 23, 13–25. [Google Scholar] [CrossRef]
- Heagle, D.; Hayashi, M.; Kamp, G.V.D. Surface-subsurface salinity distribution and exchange in a closed-basin prairie wetland. J. Hydrol. 2013, 478, 1–14. [Google Scholar] [CrossRef]
- Anderson, R.Y. The Varve Chronometer in Elk Lake: Record of Climatic Variability and Evidence for Solar-Geomagnetic-14C-Climate Connection; Geological Society of America: Boulder, CO, USA, 1993. [Google Scholar]
- Whitlock, C.; Bartlein, P.J.; Watts, W.A. Vegetation history of Elk Lake. Spec. Pap. Geol. Soc. Am. 1993, 276, 251–274. [Google Scholar]
- Bartlein, P.J.; Whitlock, C. Paleoclimatic Interpretation of the Elk Lake Pollen Record; Geological Society of America: Boulder, CO, USA, 1993. [Google Scholar]
- Clark, J.S. Fire, Climate Change, and Forest Processes during the Past 2000 Years; Geological Society of America: Boulder, CO, USA, 1993. [Google Scholar]
- Niswonger, R.G.; Panday, S.; Ibaraki, M. MODFLOW-NWT, A Newton Formulation for MODFLOW-2005 U.S. Geological Survey Techniques and Methods 6-A37; U.S. Government Printing Office: Washington, DC, USA, 2011.
- Hunt, R.J.; Feinstein, D.T. MODFLOW-NWT: Robust Handling of Dry Cells Using a Newton Formulation of MODFLOW-2005. Ground Water 2012, 50, 659–663. [Google Scholar] [CrossRef]
- van der Molen, W.H.; Wesseling, J. A solution in closed form and a series solution to replace the tables for the thickness of the equivalent layer in Hooghoudt’s drain spacing formula. Agric. Water Manag. 1991, 19, 1–16. [Google Scholar] [CrossRef]
- Dagan, G. Spacing of Drains by an Approximate Method. J. Irrig. Drain. Div. 1964, 90, 41–66. [Google Scholar] [CrossRef]
- Conrad, O.; Bechtel, B.; Bock, M.; Dietrich, H.; Fischer, E.; Gerlitz, L.; Wehberg, J.; Wichmann, V.; Böhner, J. System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 1991, 8, 1991–2007. [Google Scholar] [CrossRef] [Green Version]
- Minnesota Department of Natural Resources National Wetland Inventory for Minnesota. Available online: https://gisdata.mn.gov/dataset/water-nat-wetlands-inv-2009-2014 (accessed on 2 August 2019).
- Jirsa, M.A.; Bauer, E.J.; Boerboom, T.J.; Chandler, V.W.; Lively, R.S.; Mossler, J.H.; Runkel, A.C.; Setterholm, D.R. OFR10-02, Preliminary Bedrock Geologic Map of Minnesota; Minnesota Geological Survey: St. Paul, MN, USA, 2010. [Google Scholar]
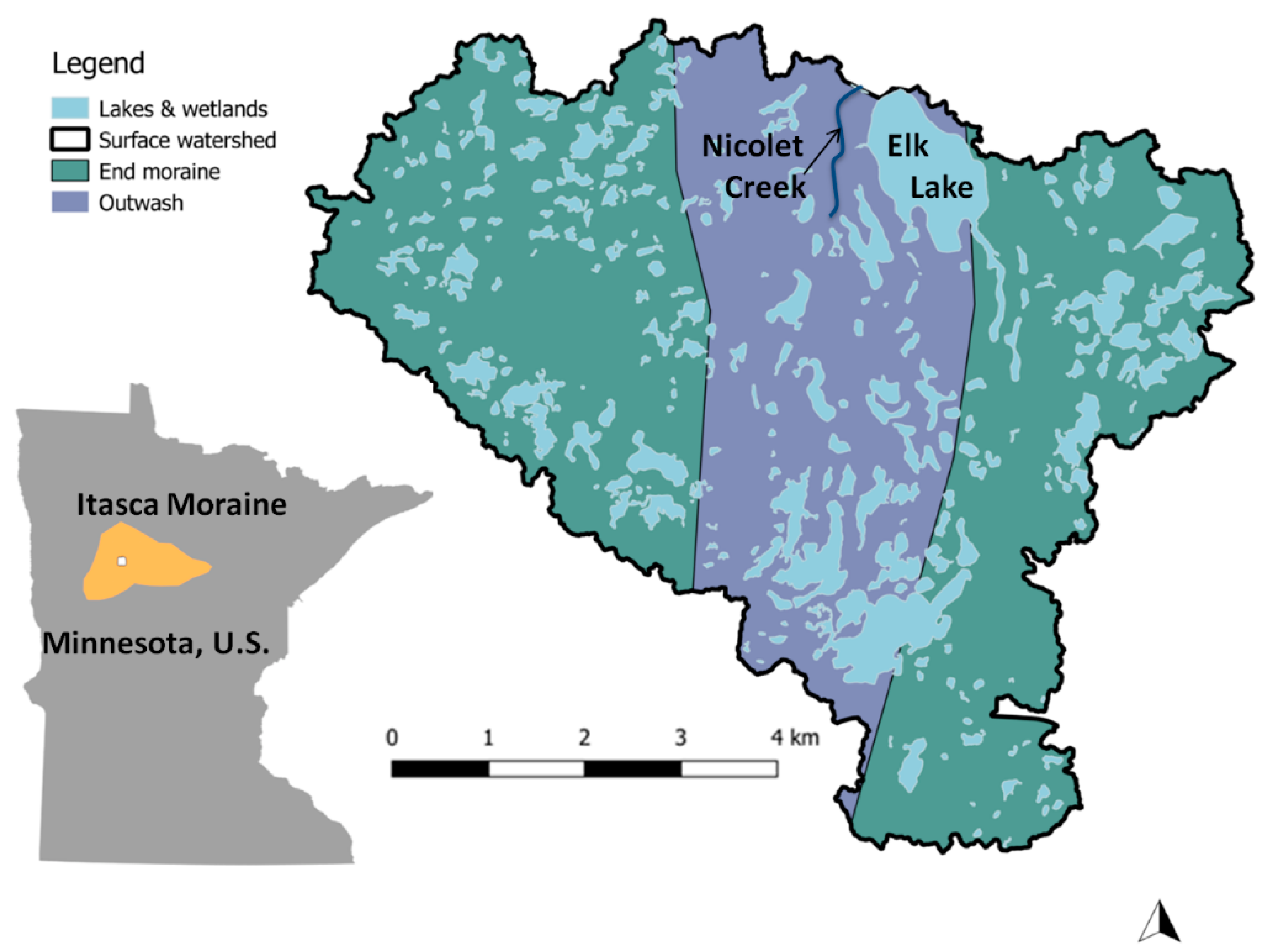
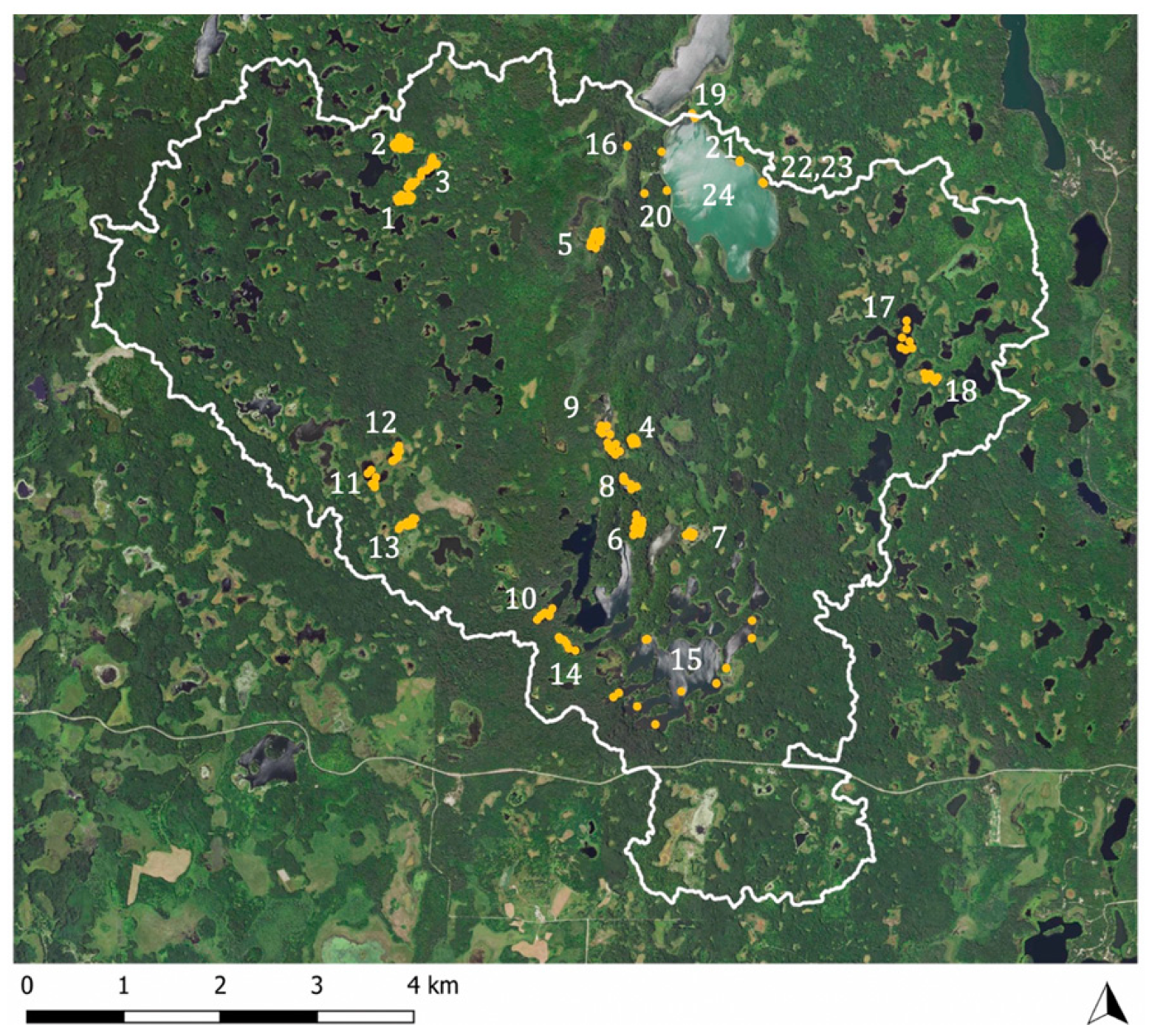
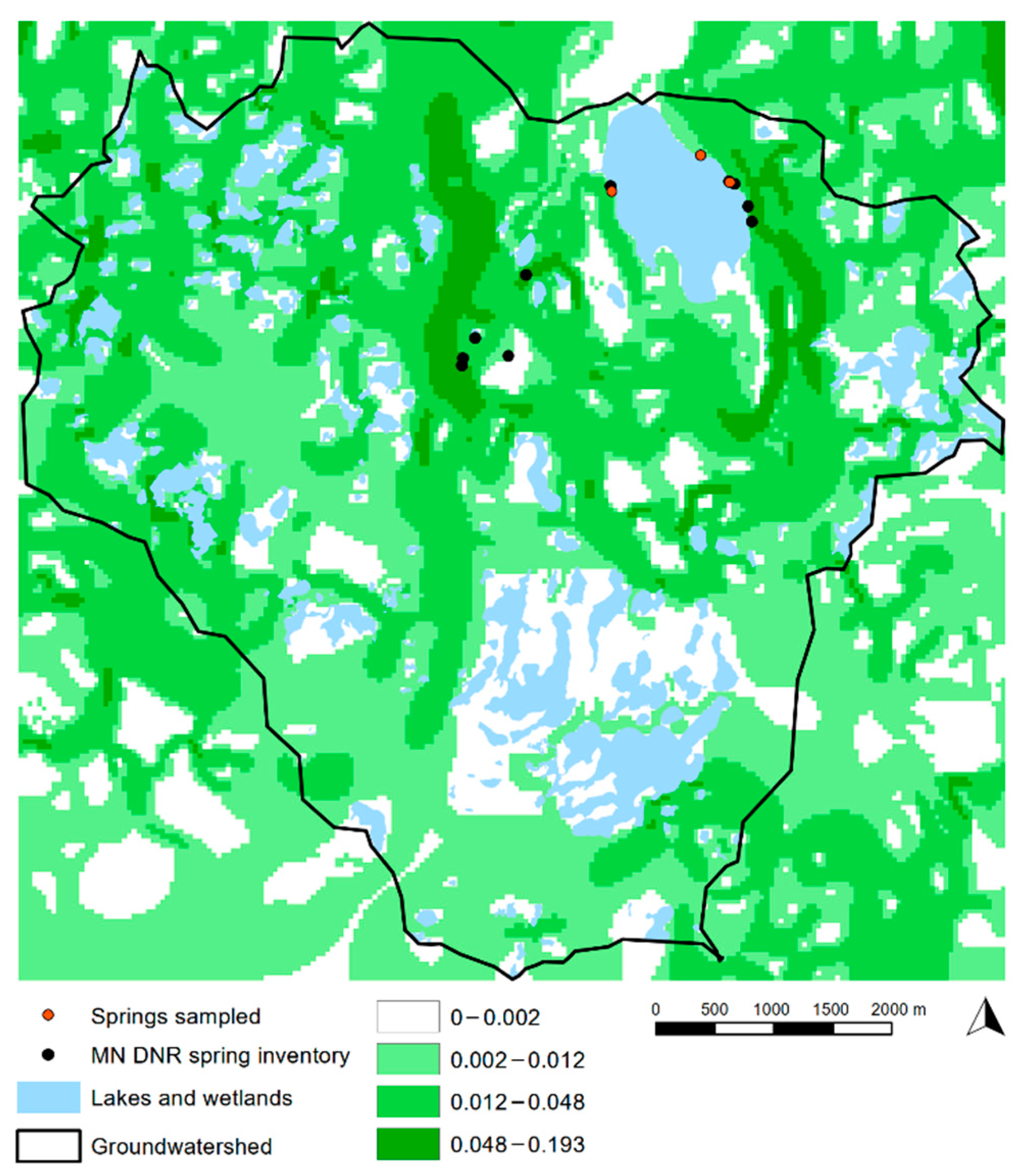
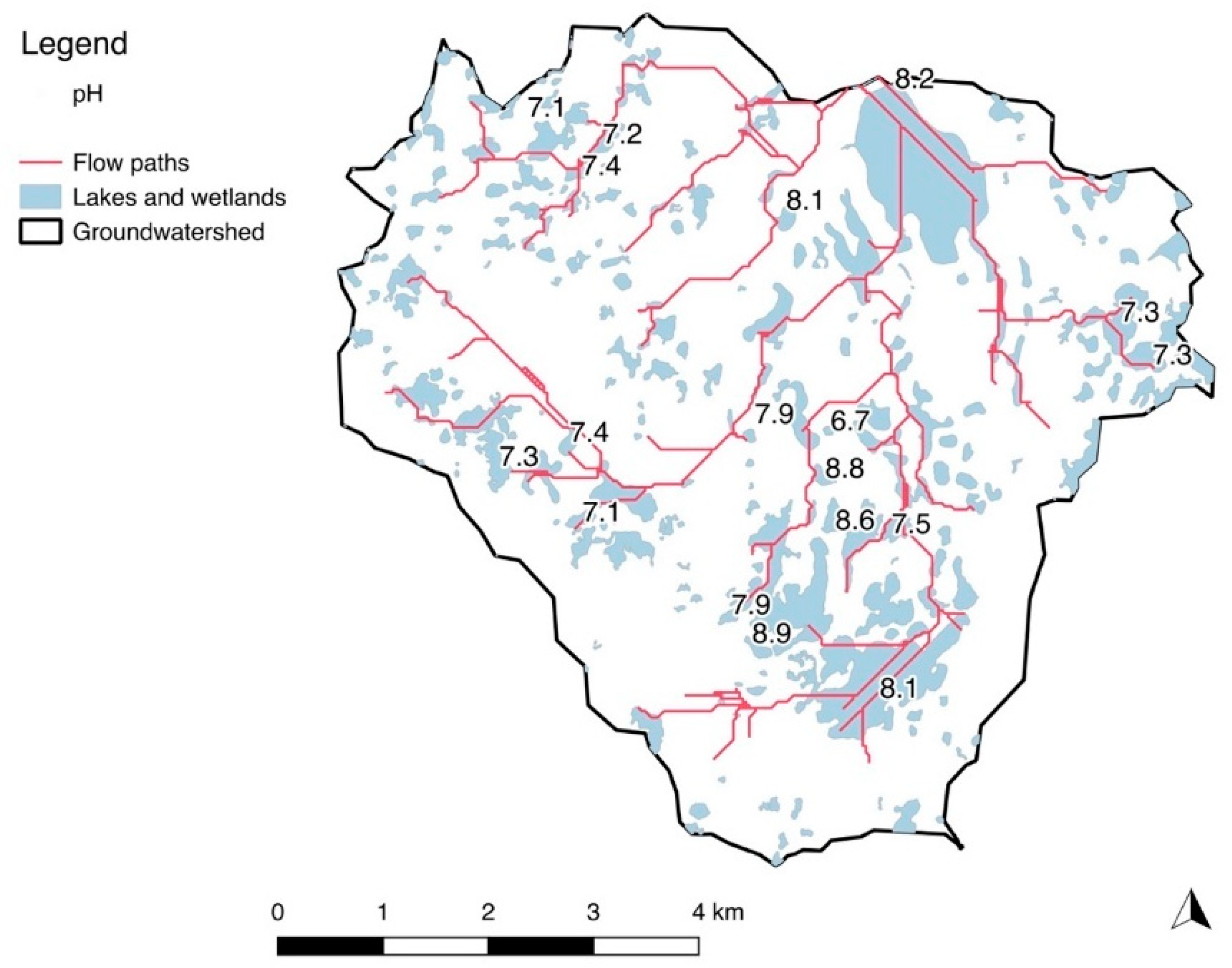
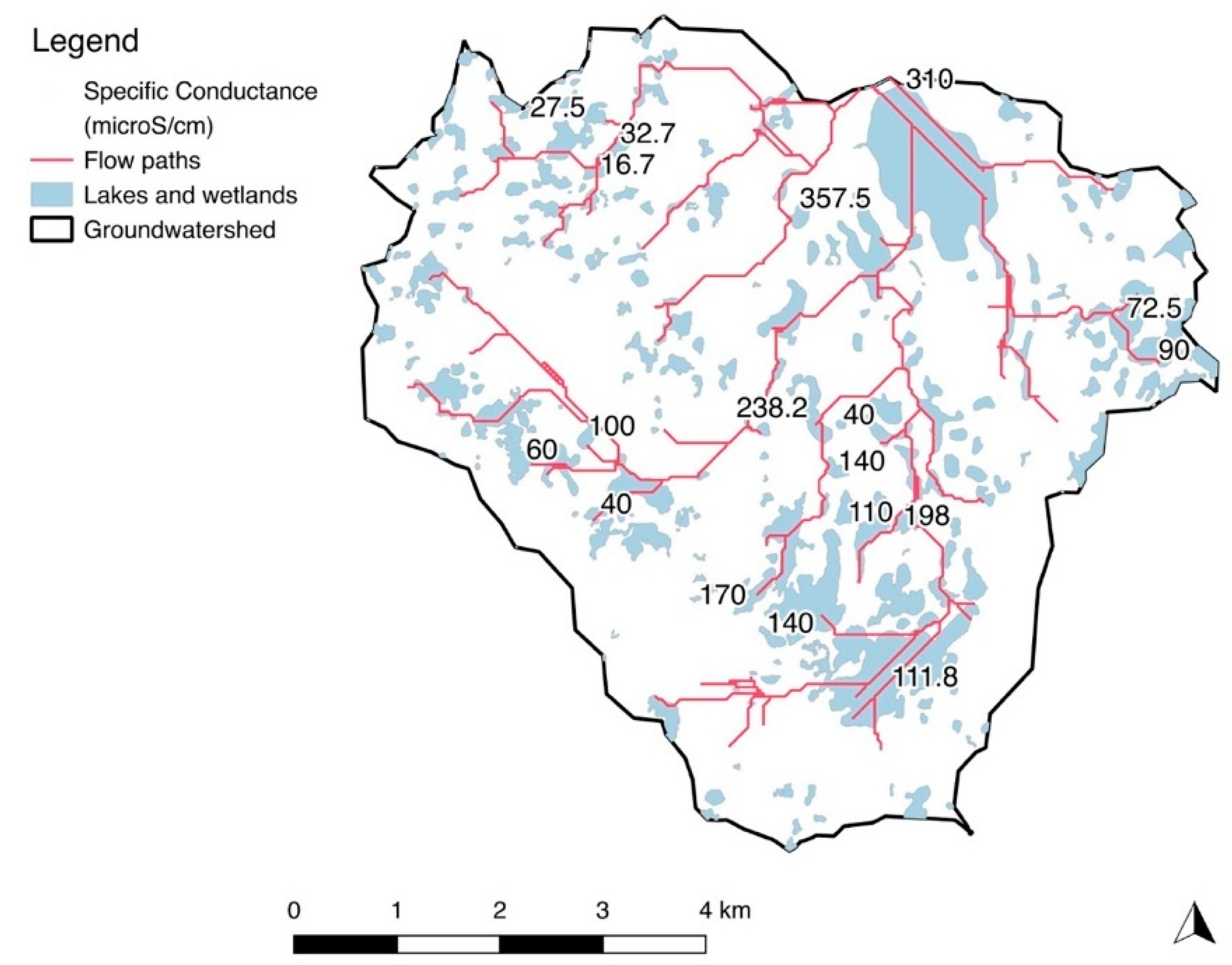
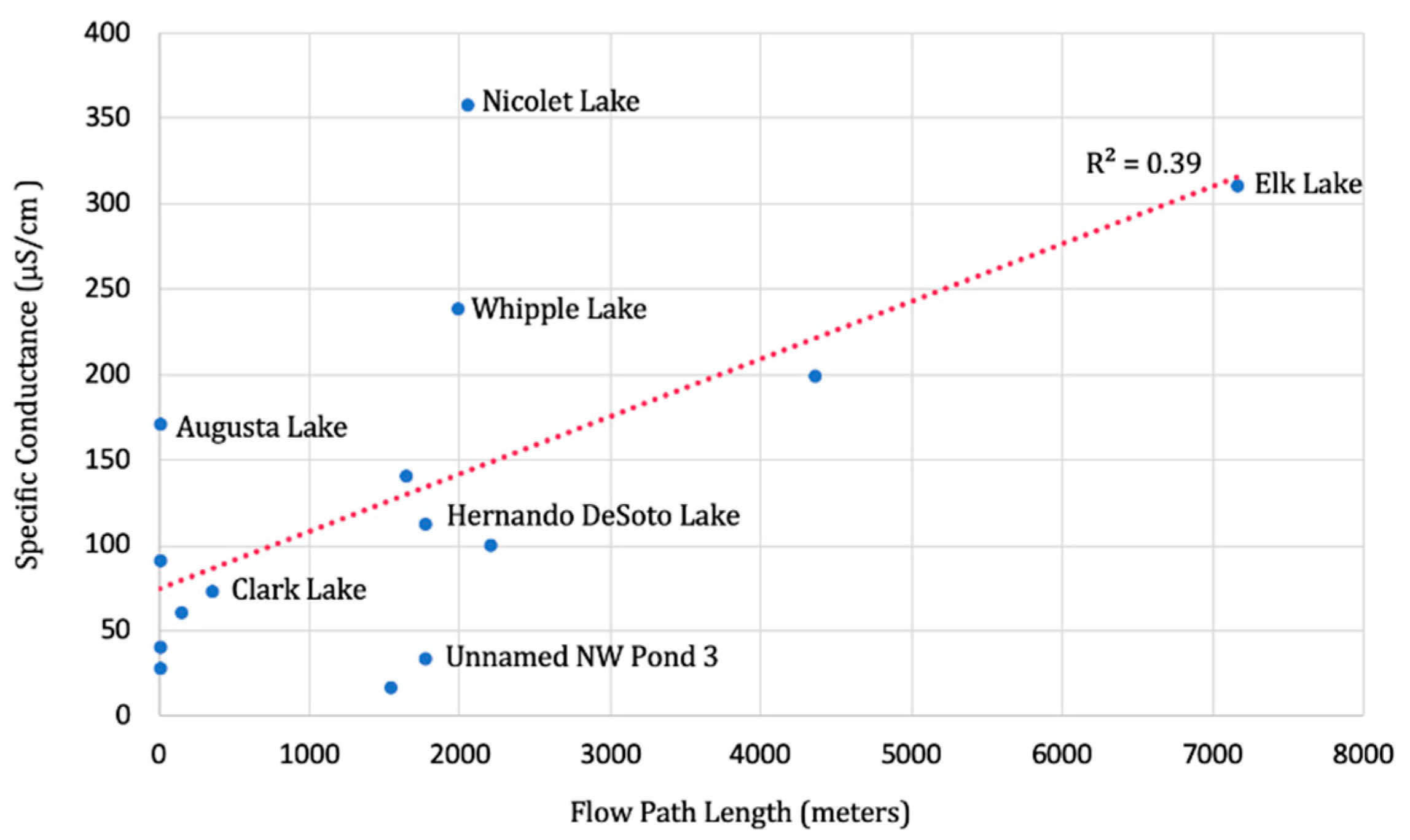
| Location | Name | Date (Sept. 2018) | Avg. Specific Conductance (µS/cm) | Flow Path Length (m) | Avg. pH | Surface Watershed (km2) | Ground-Watershed (km2) | SW/GW Ratio | SW/GW Log Ratio |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Unnamed NW pond 1 | 1 | 16.7 | 1535 | 7.4 | 0.145 | 0.355 | 0.4 | −0.39 |
| 2 | Unnamed NW pond 2 | 1 | 27.5 | 0 | 7.1 | 0.145 | 0.355 | 0.4 | −0.39 |
| 3 | Unnamed NW pond 3 | 1 | 32.7 | 1764 | 7.2 | 4.37 | 3.08 | 1.4 | 0.15 |
| 4 | Bog near Whipple Lake | 8 | 40 | - | 6.7 | 0.013 | 0.008 | 1.6 | 0.22 |
| 5 | Nicolet Lake | 8 | 357.5 | 2047 | 8.1 | 0.213 | 1.833 | 0.1 | −0.93 |
| 6 | Triplet Lakes | 8 | 110 | - | 8.6 | 0.201 | 0.033 | 6.1 | 0.79 |
| 7 | Unnamed pond nr. Little Elk Lk. | 8 | 198 | 4359 | 7.5 | 20.8 | 9.56 | 2.2 | 0.34 |
| 8 | Unnamed pond nr. Whipple Lk. | 8 | 140 | 1638 | 8.8 | 0.069 | 1.73 | 0.0 | −1.40 |
| 9 | Whipple Lake | 8 | 238.2 | 1982 | 7.9 | 0.874 | 2.10 | 0.4 | −0.38 |
| 10 | Augusta Lake | 15 | 170 | 0 | 7.9 | 0.202 | 0.549 | 0.4 | −0.43 |
| 11 | Unnamed SW pond 1 | 15 | 60 | 146 | 7.3 | 5.20 | 0.856 | 6.1 | 0.78 |
| 12 | Unnamed SW pond 2 | 15 | 100 | 2205 | 7.4 | 6.07 | 3.97 | 1.5 | 0.18 |
| 13 | Unnamed SW pond 3 | 15 | 40 | 0 | 7.1 | 0.748 | 0.383 | 2.0 | 0.29 |
| 14 | Horn Lake | 15 | 140 | - | 8.9 | 0.092 | 0.226 | 0.4 | −0.39 |
| 15 | Hernando DeSoto Lake | 18 | 111.8 | 1771 | 8.1 | 2.01 | 8.00 | 0.3 | −0.60 |
| 16 | Nicolet Creek | 18 | 430 | - | 7.5 | - | - | - | - |
| 17 | Clark Lake | 22 | 72.5 | 350 | 7.3 | 3.87 | 1.73 | 2.2 | 0.35 |
| 18 | Unnamed pond nr. Clark Lk. | 22 | 90 | 0 | 7.3 | 1.99 | 0.592 | 3.4 | 0.53 |
| 19 | Chambers Creek | 29 | 380 | - | 8.2 | - | - | - | - |
| 20 | Elk Lake spring 1 | 29 | 590 | - | 7.4 | - | - | - | - |
| 21 | Elk Lake spring 2 | 29 | 570 | - | 7.2 | - | - | - | - |
| 22 | Elk Lake spring 3 | 29 | 550 | - | 7.4 | - | - | - | - |
| 23 | Elk Lake spring 4 | 29 | 610 | - | 7.5 | - | - | - | - |
| 24 | Elk Lake | 29 | 310 | 7164 | 8.2 | 37.1 | 33.2 | 1.1 | 0.05 |
| Date | Nicolet Creek | Chambers Creek | Total |
|---|---|---|---|
| 20 June 2017 | 0.06 | 0.03 | 0.09 |
| 21 September 2017 | 0.09 | 0.07 | 0.16 |
| 16 May 2018 | 0.18 | 1.0 | 1.18 |
| 21 June 2018 | 0.03 | 0.03 | 0.06 |
| Cell Size | Sum (Raw) | Sum (Filled) |
|---|---|---|
| 10 | −3.84 | −4.35 |
| 20 | −6.08 | −6.13 |
| 30 | −1.16 | −2.46 |
| 40 | −0.54 | −0.56 |
| 50 | −15.89 | −16.14 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Speldrich, B.; Gerla, P.; Tschann, E. Characterizing Groundwater Interaction with Lakes and Wetlands Using GIS Modeling and Natural Water Quality Measurements. Water 2021, 13, 983. https://doi.org/10.3390/w13070983
Speldrich B, Gerla P, Tschann E. Characterizing Groundwater Interaction with Lakes and Wetlands Using GIS Modeling and Natural Water Quality Measurements. Water. 2021; 13(7):983. https://doi.org/10.3390/w13070983
Chicago/Turabian StyleSpeldrich, Brianna, Philip Gerla, and Emma Tschann. 2021. "Characterizing Groundwater Interaction with Lakes and Wetlands Using GIS Modeling and Natural Water Quality Measurements" Water 13, no. 7: 983. https://doi.org/10.3390/w13070983
APA StyleSpeldrich, B., Gerla, P., & Tschann, E. (2021). Characterizing Groundwater Interaction with Lakes and Wetlands Using GIS Modeling and Natural Water Quality Measurements. Water, 13(7), 983. https://doi.org/10.3390/w13070983








